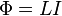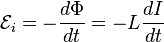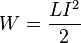Определение коэффициента самоиндукции катушки индуктивности
Цель
работы: определение коэффициента
самоиндукции катушки методом измерения
ее полного электрического сопротивления
(импеданса) по переменному и постоянному
току.
Приборы
и оборудование: катушка индуктивности
(L),
переменное сопротивление (Rпер.),
источник постоянного тока (ε),
миллиамперметр переменного и постоянного
тока (мА), вольтметр переменного тока
(~V),
вольтметр постоянного тока (=V),
генератор электрических колебаний
(ЗГ),
источник постоянного тока (ε).
Теоретические
сведения
В
пространстве, окружающем электрические
токи и постоянные магниты, возникает
силовое поле, называемое магнитным.
Наличие его обнаруживается по
силовому действию на внесенные проводники
или постоянные магниты.
Ампер
установил, что сила
,
с которой магнитное поле действует на
элемент проводника
с
током прямо пропорциональна силе тока
I
и вектор-ному произведению элемента
на магнитную индукцию:
.
Модуль силы Ампера
вычисляется по формуле
,
где
–
угол между векторами
и
;
и
.
Таким
образом, вектор магнитной индукции
является силовой характеристикой
магнитного поля. Последнее
изображают с помощью линий магнитной
индукции – линий, касательные к которым
в каждой точке совпадают с направлением
вектора
.
Магнитная стрелка устанавливается
вдоль касательной к линии магнитной
индукции,
причем ее северный конец N указывает
направление вектора
.
Закон
Ампера позволяет определить единицу
измерения магнитной индукции. Пусть
элемент проводника
c
током
силой
I
перпендикулярен
линиям магнитной индукции однородного
поля. Тогда модуль силы Ампера равен
,
при
=π/2
и sin=1.
Откуда
.
Единица измерения
магнитной индукции – Тесла (Тл).
1
Тесла – магнитная индукция однородного
поля, действующего с силой в 1Н на каждый
метр длины прямолинейного проводника,
расположенного перпендикулярно линиям
магнитной индукции, если по этому
проводнику
идет ток силой 1А:
.
Потоком
вектора магнитной индукции (магнитным
потоком) через площадку
dS
называется скалярная физическая
величина, равная
,
где
Вn
= Вcos
– проекция вектора
на направление единичного вектора
нормали
к
площадке dS;
– угол между векторами
и
;
–
вектор, модуль которого равен dS
(),
а направление совпадает с направлением
нормали
к
площадке dS
(рис. 1).
Рис. 1
Для
однородного поля и плоской поверхности,
перпендикулярной вектору
,
Вn
= В = const
и Ф=ВS.
Из
последней формулы определяется единица
измерения магнитного
потока – Вебер (Вб).
1
Вебер – магнитный поток, проходящий
через плоскую поверхность площадью
1м2,
перпендикулярную линиям магнитной
индукции однородного
поля, индукция которого равна 1 Тесле:
1Вб=1Тл
1м2.
Теорема Гаусса
для магнитного поля: поток вектора
магнитной индукции через любую замкнутую
поверхность равен нулю, т.е.
.
Эта
теорема отражает отсутствие магнитных
зарядов, вследствие чего линии
магнитной индукции не имеют ни начала,
ни конца и являются замкнутыми.
Электрический
ток, идущий по замкнутому контуру, в
окружающем пространстве создает
магнитное поле, индукция которого,
по закону Био-Савара-Лапласа, прямо
пропорциональна
силе тока. Поэтому магнитный поток Ф
пропорционален силе тока
I
в контуре:
Ф
= LI,
где L
– коэффициент самоиндукции, или
индуктивность контура. Из этого выражения
определяется единица измерения
индуктивности – Генри (Гн).
1
Генри – индуктивность
такого контура, магнитный поток
самоиндукции которого при силе тока в
1А
равен 1 Веберу:
Фарадей
открыл закон: при изменении магнитного
потока, пронизывающего поверхность,
натянутую на замкнутый проводящий
контур, в последнем возникает
электродвижущая сила (ЭДС) индукции:
Знак
«минус» в этой формуле является
математическим выражением правила
Ленца: индукционный ток в контуре имеет
всегда такое направление, при котором
создаваемое им магнитное поле препятствует
изменению магнитного потока.
Таким
образом, при изменении силы тока в
контуре изменяется и сцепленный
с ним магнитный поток и, следовательно,
индуцируется ЭДС.
Возникновение
ЭДС в проводящем контуре при изменении
в нем силы тока называется самоиндукцией.
Применяя
к самоиндукции закон Фарадея, получим,
что ЭДС самоиндукции
Если
контур не деформируется, то L=const
и
.
Значит,
на концах катушки возникает ЭДС
самоиндукции, препятствующая изменению
силы тока.
Определение
коэффициента самоиндукции
Рассмотрим
электрическую цепь, состоящую из катушки
индуктивности L.
Катушка имеет активное (омическое)
сопротивление
R
и индуктивное (реактивное) сопротивление
ωL,
где ω
– циклическая частота переменного тока;
L
– индуктивность катушки. Будем
считать, что омическое сопротивление
катушки сосредоточено в сопротивлении
R,
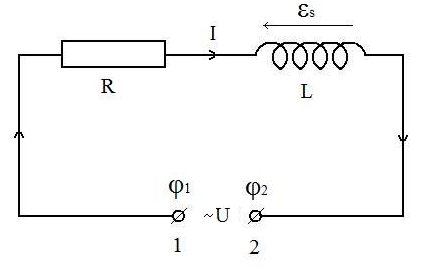
включенном последовательно с ней (рис.
2). На контакты 1 и 2 подается переменное
напряжение ~U
с циклической частотой ω.
Пусть
в данный момент времени потенциал
первого контакта φ1
больше потенциала второго контакта φ2.
Тогда ток I
идет слева направо.
Допустим,
что сила тока I
увеличивается, т.е.
> 0.
Тогда,
согласно закону Фарадея, на концах
катушки L
возникает ЭДС самоиндукции, направление
которой противоположно направлению
тока I
в цепи:
.
Если
входное напряжение ~U
изменяется по гармоническому закону,
то
U
= Um
cosωt = φ1
– φ2
,
где
Um
– амплитуда напряжения.
Рис. 2
Запишем закон Ома
для этого неоднородного участка цепи:
. (1)
Тогда
и
(2)
Частное решение
дифференциального уравнения (2) имеет
вид
,
(3)
где
Im
– амплитуда силы тока, –
начальная фаза колебаний тока.
Найдем первую
производную:
.
(4)
Выражения (7.3) и
(7.4) подставим в формулу (7.2):
,
.
(5)
Пусть
(6)
и

(7)
Подставим выражения
(6) и (7) в формулу (5):
.
Отсюда
(8)
Равенство
(7.8) будет справедливо для любого момента
времени t
при условии
γ-β=0 и γ = β. Тогда из (8)
получаем
,
(9)
причем
.
Из равенства (9)
следует, что
(10)
является полным
электрическим сопротивлением (импедансом)
участка цепи, включающим активное
сопротивление R
и индуктивное сопротивление ωL
катушки индуктивности.
На
практике с помощью вольтметра и амперметра
измеряются эффективные
(действующие)
значения переменных напряжений и силы
тока, связанные
с амплитудами следующим образом:
и
.
Значит
.
(11)
Из выражения (10)
получаем
(ωL)2=Z2
–
R2
и
(12)
Следовательно,
измеряя полное электрическое
сопротивление
Z
катушки индуктивности при переменном
токе и ее омическое сопротивление R
при постоянном токе, можно найти
индуктивность катушки L.
Порядок выполнения
работы
-
Собрать
рабочую схему для определения полного
электрического
сопротивления
Z(импеданса)
катушки индуктивности
при переменном токе
(рис. 3).
Рис.3
-
Установить
максимальное значение переменного
сопротивления Rпер.. -
Включить
генератор ЗГ. -
Изменяя
сопротивление Rпер.,
получить пять значений силы тока Iэффи измерить соответствующие напряжения
Uэфф
на катушке индуктивности. -
Результаты
измерений занести в таблицу 1.
Таблица 1
|
№ опыта |
Іэф, |
Uэф, |
Z, |
Zср, |
|
1 |
||||
|
2 |
||||
|
3 |
||||
|
4 |
||||
|
5 |
-
По
формуле (11) вычислить полные сопротивления
Z
катушки индуктивности и найти их
среднее значение Zср
. -
Собрать
схему для определения омического
сопротивления R катушки индуктивности
при постоянном токе, рис.4.
9.
Изменяя
сопротивление Rпер.,
получить пять значений силы тока I
и измерить соответствующие напряжения
U
на катушке индуктивности.
10 .
Результаты измерений занести в таблицу
2.
Таблица 2
|
№ опыта |
І, |
U, |
R, |
Rср, |
|
1 |
||||
|
2 |
||||
|
3 |
||||
|
4 |
||||
|
5 |
11. Вычислить
омические сопротивления R
катушки индуктивности и найти их
среднее значение Rср..
12.
По формуле
при
частоте ν=1000
Гц определить коэффициент самоиндукции
L
катушки.
Рис. 4
Контрольные вопросы
-
Что такое магнитное
поле? Что такое линии индукции магнитного
поля? -
Как
формулируется закон Ампера? Единица
измерения индукции магнитного
поля. -
Дать определение
потока вектора магнитной индукции.
Единица его измерения. -
Что такое
индуктивность контура? Единица ее
измерения.
-
Сформулировать
закон Фарадея и правило Ленца. -
В чем заключается
явление самоиндукции? Э Д С. самоиндукции
катушки.
-
Явление взаимной
индукции. Практическое применение
этого явления. -
Написать уравнения
Максвелла в интегральной форме.
9.
Вывести рабочие формулы для расчета
полного сопротивления (импеданса) и
коэффициента
самоиндукции катушки индуктивности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сергей Сергеевич Соев
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Определение самоиндукции. Направление ЭДС самоиндукции
Замкнутый контур с током создает поток магнитной индукции (Ф) через поверхность S, которая ограничена этим контуром. Электродвижущая сила индукции ($mathcal E$) появляется при любом изменении магнитного потока через поверхность (S), которую охватывает контур с током. Значит, если изменять силу тока в контуре, то в контуре появляется ЭДС. Такое явление называется явлением самоиндукции.
Правило Ленца
Направление вектора магнитной индукции поля, которое создает ток, определяется правилом правого винта, $mathcal E$ в контуре связана с изменением потока правилом левого винта, значит, ЭДС самоиндукции направлена так, что препятствует изменению силы тока, которым она вызвана. Это правило называют правилом Ленца.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Индуктивность контура
Сила тока в контуре связывается с магнитным потоком с помощью выражения:
[Ф=LI left(1right),]
где $L$ называют индуктивностью (коэффициентом самоиндукции) контура. Индуктивность контура равна магнитному потоку в процессе самоиндукции контура по которому течет ток силой в 1А.
Если среда не является ферромагнитной и контур не деформируется, ЭДС самоиндукции запишется как:
[{{mathcal E}}_{samInd}=-Lfrac{dI}{dt}left(2right),]
где t — время.
Линейная зависимость в формуле (1) между магнитным потоком и силой тока наблюдается если магнитная проницаемость среды ($mu $) в которой находится контур не зависит от
магнитной индукции ($overrightarrow{B}$), то есть в отсутствии ферромагнетиков. Надо отметить, что форма уравнения (1) не изменится для любых веществ. Кроме того при постоянной
силе тока поток вектора магнитной индукции изменяется с изменение формы и размеров контура.
Как уже отмечалось, L зависит от среды, в которой находится контур, его геометрических размеров и формы:
[L=frac{{mu }_0}{4pi }intlimits_S{dSointlimits_l{frac{mu }{r^3}}}{left[overrightarrow{dl} overrightarrow{r}right]}_nleft(3right),]
где $mu $ — относительная магнитная проницаемость среды, $overrightarrow{r}$- радиус-вектор, который проводится от элемента контура с током ($overrightarrow{dl}$) к элементу поверхности dS, поверхности S которая ограничена рассматриваемым контуром, индекс n означает проекцию на нормаль к dS. Для жесткого контура и в отсутствии ферромагнетиков L=const.
Основной единицей коэффициента самоиндукции в системе СИ является генри (Гн).
[1Гн=1Вб/1А left(4right).]
«Коэффициент самоиндукции (индуктивность) контура» 👇
Пример 1
Задание: Получите формулу, для вычисления коэффициента самоиндукции бесконечно длинного соленоида. Если даны n — число витков соленоида на единицу длины, V- объем соленоида, $ mu – $магнитная проницаемость среды.
Решение:
Если по соленоиду течет ток I, то внутри соленоида возникает однородное магнитное поле, индукция (В) которого равна:
[B={mu }_0mu nI left(1.1right),]
где $n$ — количество витков соленоида на единицу его длины ($n=frac{N}{l}$), $N$ — суммарное количество витков, $l$ — длина соленоида.
В таком случае поток вектора магнитной индукции ($Ф’$) через любой виток соленоида равна:
[Ф’=B left(1.2right),]
где $S$ — площадь витка соленоида, она же площадь соленоида. Тогда полный поток (Ф) через все витки равен c учетом (1.1) и (1.2):
[Ф=NФ=nlBS={mu }_0mu n^2I Slleft(1.3right).]
По определению коэффициент самоиндукции связан с магнитным потоком и силой тока выражением:
[Ф=LIleft(1.4right).]
Сравниваем формулы (1.3) и (1.4), получаем:
[L={mu }_0mu n^2V ,]
где $V$ — объем соленоида.
На практике индуктивность соленоида рассчитывают в соответствии с формулой:
[L={kmu }_0mu n^2V ,]
где $k$ — коэффициент который зависит от отношения длины соленоида ($l$) к диаметру его витков (d). Так при $l/d=0,1 k=0,2;; при l/d=10 kapprox 1.$Ответ: $L={mu }_0mu
n^2V.$
Пример 2
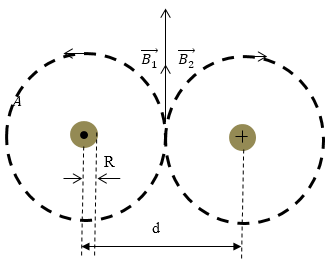
Задание: Получите формулу, для вычисления коэффициента самоиндукции двухпроводной линии. Если даны R — радиусы проводов, d- расстояние между проводами, $mu =1- $магнитная
проницаемость среды.
Рис. 1
Решение:
Двухпроводная цепь — это два длинных параллельных проводника, которые входят в цепь тока. Токи в проводах направлены в противоположные стороны.
Найдем магнитный поток через площадь, которая ограничена осями проводов для отрезка длины l.
Рассмотрим один провод. Магнитное поле такого тока имеет осевую симметрию с центром на оси провода. Силовые линии поля при этом окружности с центрами на оси симметрии. По модулю значение магнитной индукции во всех точках силовой линии одинаково. Возьмем в качестве кривой циркуляции $A$ силовую линию радиуса r, тогда по теореме о циркуляции запишем:
[ointlimits_A{overrightarrow{B}dr}=Bcdot 2pi r (2.1)]
Для области внутри провода ($x
[Bcdot 2pi r={mu }_0frac{I}{pi R^2}pi r^2={mu }_0frac{I}{R^2}r^2to B=frac{{mu }_0I}{2pi R^2}rleft(2.2right).]
Для области вне провода ($xge R$) магнитная индукция поля равна:
[Bcdot 2pi r={mu }_0Ito B=frac{{mu }_0I}{2pi r}left(2.3right).]
Соответственно поток ($Ф_{rle R}$) через часть площади ($dS=lrdr$)внутри провода будет равен:
[Ф_{rle R}=frac{{mu }_0Il}{2pi R^2}intlimits^R_0{r}dr=frac{{mu }_0Il}{4pi }left(2.4right).]
Поток ($Ф_{rge R}$) через остальную часть площади (при $rge R$) имеет вид:
[Ф_{rge R}=frac{{mu }_0Il}{2pi }intlimits^d_R{frac{dr}{r}=frac{{mu }_0Il}{2pi }}lnfrac{R}{d}left(2.5right).]
Полный поток от одного провода можно найти как сумму потоков из выражений (2.4) и (2.5):
[Ф=frac{{mu }_0Il}{4pi }+frac{{mu }_0Il}{2pi }lnfrac{R}{d}=frac{{mu }_0Il}{2pi }left(frac{1}{2}+lnfrac{R}{d}right)left(2.6right).]
Так как токи в проводах имеют противоположное направление, значит направления полей одинаковы. Поток от двух проводов в два раза больше, чем от одного. Значит:
[Ф’=2Ф.]
Зная, что:
[Ф’=ILto L=frac{Ф’}{I}left(2.7right),]
получим, что:
[L=2cdot frac{{mu }_0l}{2pi }left(frac{1}{2}+lnfrac{R}{d}right)=frac{{mu }_0l}{pi }left(frac{1}{2}+lnfrac{R}{d}right).]
Ответ: $L=frac{{mu }_0l}{pi }left(frac{1}{2}+lnfrac{R}{d}right).$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Как было установлено опытным путём, вокруг любого проводника с током создаётся магнитное поле. Мы знаем, магнитный поток Ф, проходящий через контур прямо пропорционален индукции В магнитного поля и площади S, охватываемой проводником Индукция В магнитного поля, созданного проводником с током, в каждой точке пространства вокруг этого проводника пропорциональна силе тока I в проводнике. Следовательно, магнитный поток Ф через данный проводящий контур (S = const) прямо пропорционален силе тока в контуре:
Ф =LI
В СИ единицей индуктивности является Генри (Гн).
L = Ф / I,
1 Гн = 1Вб / 1А.
Контур, в котором электрический ток с силой 1 Ампер создаёт магнитный поток 1 Вебер, обладает индуктивностью 1 Генри.
Постоянный ток I, протекающий через контур индуктивностью L, создаёт вокруг контура магнитный поток Ф, равный
Ф = LI
Что произойдёт с данным контуром при выключении тока?
Ток прекратится, магнитное поле исчезнет. Вспомним, исчезновение магнитного потока — это его изменение от начального значения Ф = LI до нуля. Согласно закону электромагнитной индукции, изменения магнитного потока через контур должно вызывать появление ЭДС индукции равной:
Εis = -∆Ф/∆t = -L (∆I/∆t)
Явление возникновения ЭДС индукции, вызванной изменением силы тока в самом контуре называется самоиндукцией.
С изменением тока в контуре пропорционально меняется и магнитный поток через поверхность, которая ограничена этим контуром. По закону электромагнитной индукции, изменение магнитного потока приводит к возбуждению в этом контуре индуктивной ЭДС.
Единицей индуктивности 1 Генри обладает такой контур, в котором при изменении силы тока на 1 Ампер за 1 секунду возникает ЭДС самоиндукции в 1 Вольт.
По правилу Ленца, ЭДС самоиндукции при уменьшении силы тока в контуре действует в направлении поддержания силы тока неизменной, при увеличении силы тока в контуре ЭДС самоиндукции препятствует увеличению тока.
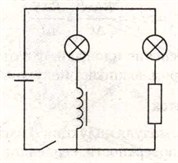
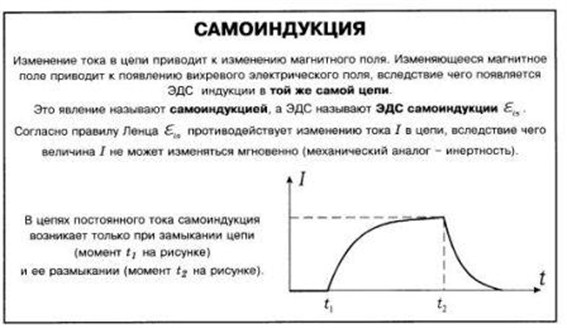
Для обнаружения явления самоиндукции можно использовать электрическую цепь, представленную на схеме:
В данной цепи параллельно включены резистор и катушка с железным сердечником, последовательно с резистором и катушкой включены электрические лампы. Электрическое сопротивление резистора равно электрическому сопротивлению катушки на постоянном токе, поэтому при параллельном подключении их к источнику тока лампы должны гореть одинаково ярко.
Проведём несколько опытов. При замыкании цепи лампа в цепи катушки загорается заметно позднее, чем лампа в цепи резистора. Это можно объяснить тем, что катушка с железным сердечником обладает большой индуктивностью, ЭДС самоиндукции препятствует возрастанию тока при включении.
Обе лампы вспыхивают при отключении источника тока. Ток в цепи катушки и резистора создаёт ЭДС самоиндукции, возникающую при уменьшении силы тока в катушке. Это показывает, что магнитное поле не только способно действовать на движущие заряды, но и обладает определённым запасом энергии. Именно за счёт энергии магнитного поля возникает ток в цепи при отключении её от источника тока.
При изменении силы тока в проводнике в последнем возникает вихревое электрическое поле. Это поле тормозит электроны при возрастании силы тока и ускоряет их при убывании электрического тока в этом проводнике.
Явление самоиндукции играет очень важную роль в элекротехнике и радиотехнике. Индуктивность цепи оказывает существенное влияние на прохождение по цепи переменного электрического тока.
Остались вопросы? Не знаете, что такое самоиндукция?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 мая 2020 года; проверки требуют 9 правок.
Самоиндукция — это явление возникновения ЭДС индукции в проводящем контуре[1] (в цепи) при изменении протекающего через контур тока.
При изменении тока в контуре пропорционально меняется[2] и магнитный поток через поверхность, ограниченную этим контуром[3]. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС.
Это явление и называется самоиндукцией. Стоит отметить, что данное понятие родственно понятию взаимоиндукции, являясь как бы его частным случаем.
Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока — убыванию (сонаправлена с током). Явление самоиндукции проявляется в замедлении процессов исчезновения и установления тока[4].
При сопоставлении силы электрического тока со скоростью в механике и электрической индуктивности с массой в механике ЭДС самоиндукции сходна с силой инерции.
Величина ЭДС самоиндукции пропорциональна скорости изменения силы (переменного) тока 
.
Коэффициент пропорциональности 
Самоиндукция и синусоидальный ток[править | править код]
В случае синусоидальной зависимости тока, текущего через катушку, от времени, ЭДС самоиндукции в катушке отстаёт от тока по фазе на 


Для расчёта более или менее сложных схем, содержащих индуктивные элементы, то есть витки, катушки и т. п. устройства, в которых наблюдается самоиндукция, (особенно, полностью линейных, то есть не содержащих нелинейных элементов[5]) в случае синусоидальных токов и напряжений применяют метод комплексных импедансов или, в более простых случаях, менее мощный, но более наглядный его вариант — метод векторных диаграмм.
Заметим, что всё описанное применимо не только непосредственно к синусоидальным токам и напряжениям, но и практически к произвольным, поскольку последние могут быть практически всегда разложены в ряд или интеграл Фурье и таким образом сведены к синусоидальным.
В более или менее непосредственной связи с этим можно упомянуть о применении явления самоиндукции (и, соответственно, катушек индуктивности) в разнообразных колебательных контурах, фильтрах, линиях задержки и других разнообразных схемах электроники и электротехники.
Самоиндукция и скачок тока[править | править код]
За счёт явления самоиндукции в электрической цепи с источником ЭДС при замыкании цепи ток устанавливается не мгновенно, а через какое-то время. Аналогичные процессы происходят и при размыкании цепи, при этом (при резком размыкании) величина ЭДС самоиндукции может в этот момент значительно превышать ЭДС источника.
Чаще всего в обычной жизни это используется в катушках зажигания автомобилей. Типичное напряжение зажигания при напряжении питающей батареи 12 В составляет 7-25 кВ. Впрочем, превышение ЭДС в выходной цепи над ЭДС батареи здесь обусловлено не только резким прерыванием тока, но и коэффициентом трансформации, поскольку чаще всего используется не простая катушка индуктивности, а катушка-трансформатор, вторичная обмотка которой как правило имеет во много раз большее количество витков (то есть, в большинстве случаев схема несколько более сложная, чем та, работа которой полностью объяснялось бы через самоиндукцию; однако физика её работы и в таком варианте отчасти совпадает с физикой работы схемы с простой катушкой).
Это явление применяется и для поджига люминесцентных ламп в стандартной традиционной схеме (здесь речь идёт именно о схеме с простой катушкой индуктивности — дросселем).
Кроме того, явление самоиндукции надо учитывать всегда при размыкании контактов, если ток течёт по нагрузке с заметной индуктивностью: возникающий скачок ЭДС может приводить к пробою промежутка между контактами и/или другим нежелательным эффектам, для подавления которых в этом случае, как правило, необходимо принимать разнообразные специальные меры, например устанавливать диод в обратном включении параллельно выводам катушки (дросселя).
См. также[править | править код]
- Взаимоиндукция
- Электрический генератор
- Катушка индуктивности
Примечания[править | править код]
- ↑ Контур может быть и многовитковым — в частности, катушкой. В этом случае, так же как и в случае одиночного контура, строго говоря, контур должен быть замкнутым (например, через вольтметр, измеряющий ЭДС), но на практике при (очень) большом количестве витков различие ЭДС в полностью замкнутом контуре и в контуре с разрывом (геометрически даже большим по сравнению с размером катушки) может быть пренебрежимо малым.
- ↑ Поскольку магнитный поток через контур пропорционален току в контуре. Для тонкого жёсткого контура (для случая которого, это утверждение и является точным) точная пропорциональность очевидна исходя из закона Био-Савара, так как согласно этому закону вектор магнитной индукции прямо пропорционален току, а поток этого вектора (что и называется магнитным потоком) через фиксированную (она не меняется при жёстком контуре) поверхность тогда тоже пропорционален току. Формально это записывается в виде равенства:
, где
— магнитный поток,
— коэффициент самоиндукции,
— ток в контуре.
- ↑ В случае сложной формы контура, например, если контур многовитковый (катушка), поверхность, ограниченная контуром (или, как говорят, «натянутая на контур») оказывается достаточно сложной, что ничуть не меняет сути описываемого явления. Для упрощения понимания случая многовитковых контуров (катушек) можно (приближённо) считать поверхность, натянутую на такой контур, состоящей из множества (стопки) поверхностей, каждая из которых натянута на свой отдельный единичный виток.
- ↑ Калашников С. Г., Электричество, М., ГИТТЛ, 1956, гл. IX «Электромагнитная индукция», п. 107 «Исчезновение и установление тока», с. 221 – 224;
- ↑ Сами индуктивные элементы являются линейными, то есть подчиняются линейному дифференциальному уравнению, приведённому в статье выше. Впрочем, это уравнение в реальности выполняется лишь приближённо, так что индуктивные элементы являются линейными также лишь приближённо (хотя иногда и с крайне хорошей точностью). Также в реальности встречаются отклонения от идеального уравнения, носящие линейный характер (например, связанные с упругими деформациями катушки в линейном приближении).
Ссылки[править | править код]
- Про самоиндукцию и взаимоиндукцию из «Школы для электрика»
1). Индуктивность (или коэффициент самоиндукции) – коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность, краем которой является этот контур.
В формуле
Ф – магнитный поток, I – ток в контуре, L – индуктивность.
Нередко говорят об индуктивности прямого длинного провода. В этом случае и других (особенно – в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведённое выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.
Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока:
Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.
При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током:
Практически участки цепи со значительной индуктивностью выполняют в виде катушек индуктивности. Элементами малой индуктивности (применяемыми для больших рабочих частот) могут быть одиночные (в том числе и неполные) витки или даже прямые проводники; при высоких рабочих частотах необходимо учитывать индуктивность всех проводников.
Для имитации индуктивности, т.е. ЭДС на элементе, пропорциональной и противоположной по знаку скорости изменения тока через этот элемент, в электронике используются и устройства, не основанные на электромагнитной индукции (см. Гиратор); такому элементу можно приписать определённую эффективную индуктивность, используемую в расчётах полностью (хотя вообще говоря с определёнными ограничивающими условиями) аналогично тому, как используется обычная индуктивность.
Обозначение и единицы измерения:
В системе единиц СИ индуктивность измеряется в генри, сокращённо Гн. Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать напряжение в один вольт.
В вариантах системы СГС – системе СГСМ и в гауссовой системе индуктивность измеряется в сантиметрах (1 Гн = 109 см; 1 см = 1 нГн); для сантиметров в качестве единиц индуктивности применяется также название абгенри. В системе СГСЭ единицу измерения индуктивности либо оставляют безымянной, либо иногда называют статгенри (1 статгенри ≈ 8,987552·1011 генри, коэффициент перевода численно равен 10-9 от квадрата скорости света, выраженной в см/с).
Символ L, используемый для обозначения индуктивности, был принят в честь Эмилия Христиановича Ленца (Heinrich Friedrich Emil Lenz). Единица измерения индуктивности названа в честь Джозефа Генри(Joseph Henry). Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года.
Материал из Википедии — свободной энциклопедии
2). Индуктивность, коэффициент самоиндукции (L) – отношение потокосцепления самоиндукции цепи к силе тока в ней. Характеризует связь потокосцепления самоиндукции с силой тока контура. Измеряется в генри (Г). Индуктивность кольцевой катушки L=μaW2S/l, где W – количество витков; S – поперечное сечение катушки; l – длина катушки; μa – магнитная проницаемость среды.
Словарь по электротехнике