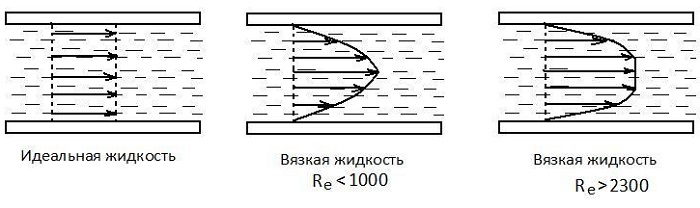
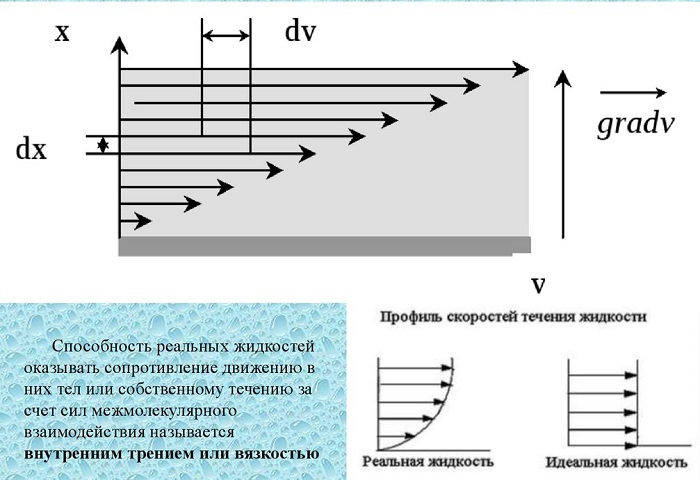
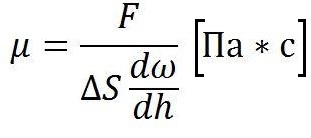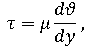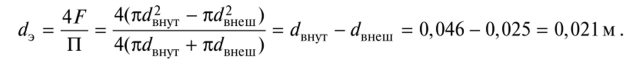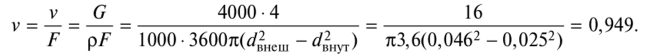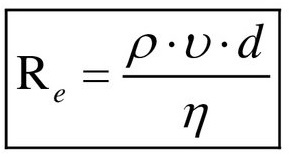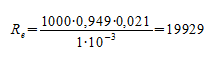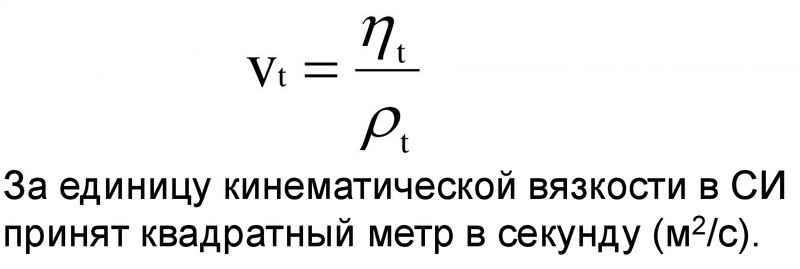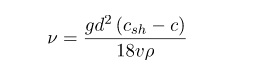Коэффициент вязкости – это величина, используемая для обозначения силы внутреннего трения текучих веществ. Вязкость – разновидность явлений переноса. Жидкости и газы оказывают сопротивление перемещению двух слоев относительно друг друга. Эта особенность характерна для текучих веществ, связана с движением частиц, из которых и состоят вещества.
Вязкость называют внутренним трением. В его основе находится хаотическое движение молекул, передающих импульс между слоями. Такие импульсные обмены выравнивают скорости перемещения слоев.
Коэффициент динамической вязкости
Численное обозначение абсолютной вязкости является индексом сопротивляемости испытуемых веществ взаимному перемещению или скольжению их слоев.
Единицей измерения коэффициента в системе СИ приняты паскаль-секунды:
Физическая основа динамического показателя заключается в его соответствии касательному напряжению, которое происходит между слоями вещества, перемещающимися относительно друг друга, при условии расстояния между ними, равного единице длины, и на скорости, равной единице.
Вязкость жидкости
Вязкость жидкости определяется формулой, в которой динамический коэффициент определяет пропорциональность скорости движения слоев и расстояния между ними:
-
τ – касательное напряжение;
-
µ – показатель пропорциональности, который является динамическим индексом вещества.
Закон вязкости жидкости был установлен Ньютоном в конце 17 века. Абсолютный показатель зависит от типа газа или жидкости, температуры веществ.
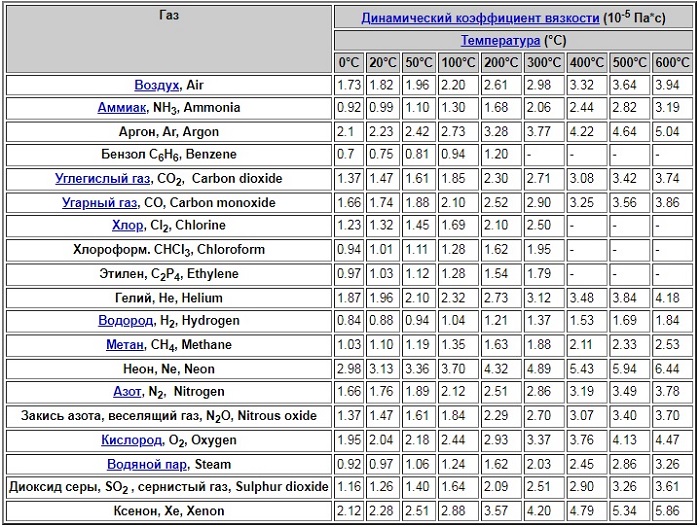
Коэффициент динамической вязкости газа
Для основных газов величины коэффициента при температуре 0 – 600 градусов Цельсия представлены в таблице:
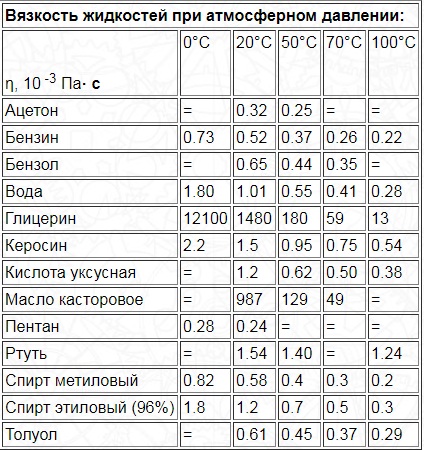
Коэффициент вязкости жидкостей
Для органических жидкостей показания напрямую зависят от температуры. Ниже приведена таблица со значениями абсолютного индекса для веществ при температурах от 0 до 100 градусов Цельсия.
Единица измерения – миллипаскаль-секунды, что соответствует сантипуазам.
Коэффициент динамической вязкости жидкостей уменьшается при условии нагревания вещества. Другими словами, чем выше температура жидкости, тем менее вязкой она становится.
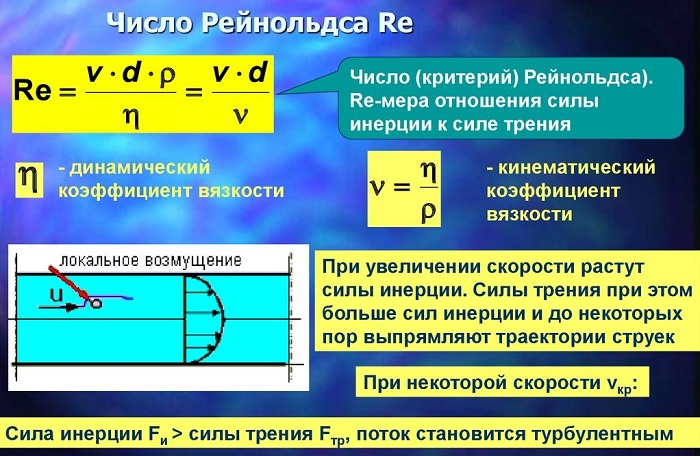
Связь коэффициента вязкости с числами Рейнольдса и силой трения
Английский механик, физик и инженер Оскар Рейнольдс установил (1876 — 1883 гг.), что характер течения зависит от величины, не имеющей размерностью, и называемой числом Re.
Число Рейнольдса используют для отображения соотношения кинематической энергии вещества к энергопотерям на установленной длине в условиях внутреннего трения.
Примеры решения задач
Попробуем решить следующую задачу.
Установить тип движения жидкого вещества по трубам теплообменника, имеющего структуру «труба в трубе». Параметры внутренней трубы – 25*2 мм, внешней – 50*2,5 мм. Массовый расход воды составляет 4000 кг/ч (обозначение G). Плотность жидкости – 1000 кг/м3. Абсолютный индекс составляет 1•10-3 Па*с.
Действие 1.
Следует узнать эквивалентный диаметр сечения межтрубного пространства:
Действие 2.
Определение скорости воды на основе уравнения расхода:
Действие 3.
По формуле Рейнольдса найти число Re:
Подставляя значения, получаем:
Ответ: режим перемещения воды в межтрубном пространстве является турбулентным.
Коэффициент кинематической вязкости
Кинематическая вязкость – это индекс, который отображает отношение абсолютного показателя вещества к его плотности при установленной температуре.
Физическая формула соотношения выглядит и единицы измерения можно увидеть на картинке:
Действие 4. Вычисление кинематического показателя, исходя из формулы:
Подставив в уравнение полученные и имеющиеся расчетные данные, получим кинематический индекс вещества.
Заключение
Физический смысл коэффициента вязкости заключается в том, что он демонстрирует, чему равна величина F внутреннего трения, действующая на 1 ед. площади поверхности соприкасающихся слоев при единичном градиенте скорости.
Размерность данной величины и перевод из одних единиц измерения в другие показаны на картинке:
вязкая жидкость–
это подчиняющаяся в своём течении закону
вязкого трения Ньютона,
то есть касательное
напряжение и градиент скорости линейно
зависимы.
Коэффициент пропорциональности между
этими величинами известен как вязкость.
Простое
уравнение, описывающее силы вязкости,
возникающие в ньютоновской жидкости
(которые во многом определяют ее
поведение), основано на сдвиговом
течении:
,
где
— касательное
напряжение,
вызываемое жидкостью [Па]
—
динамический
коэффициент вязкости — коэффициент
пропорциональности [Па·с]
—
производная
скорости в направлении, перпендикулярном
направлению сдвига [с−1].
7. Движение тела в вязкой жидкости. Формула Стокса для шарика и границы ее
применимости.
На
тело, движущееся в жидкости или газе,
действуют две силы (равнодействующую
их обозначим R),
одна из которых (Rx)
направлена в сторону, противоположную
движению тела (всторону потока), — лобовое
сопротивление, а
вторая (Ry)
перпендикулярна этому направлению
— подъемная
сила
Формула Стокса — Эйнштейна
Величина
подвижности не всегда легко определяется,
поэтому если предположить, что числа
Рейнольдса малы,
то для силы сопротивления, испытываемой
макроскопическим шариком (частицей),
можно использовать формулу
Стокса
где
— вязкость жидкости,
—
радиус частицы.
Таким
образом, получается выражение:
8. Течение в трубах. Закон Пуазейля и границы его применимости. Гидравлическое сопротивление.
Уравнение или закон
Пуазёйля (закон
Хагена — Пуазёйля или закон Хагена —
Пуазёйля) — закон, определяющий
расход жидкости при установившемся
течении вязкой несжимаемой жидкости в
тонкой цилиндрической трубе круглого
сечения.

где
-
—
расход
жидкости в трубопроводе; -
—
диаметр
трубопровода;
Закон
Пуазёйля работает только при ламинарном
течении и
при условии, что длина трубки превышает
так называемую длину начального участка,
необходимую для развитияламинарного
течения в
трубке.
гидравлическое
сопротивление —
безвозвратные потери удельной
энергии (переход
её в теплоту)
на участках гидравлических систем
(системгидропривода, трубопроводах,
другом гидрооборудовании), обусловленные
наличием вязкого трения
Гидравлические
потери принято разделять на два вида:
-
потери
на трение по длине —
возникают при равномерном течении, в
чистом виде — в прямых трубах постоянного
сечения, они пропорциональны длине
трубы; -
местные
гидравлические потери —
обусловлены т. н. местными
гидравлическими сопротивлениями —
изменениями формы и размера канала,
деформирующими поток.
9. Ламинарное и турбулентное течение. Число Рейнольдса.
Ламина́рное
тече́ние —
течение, при котором жидкость или газ перемещается
слоями без перемешивания и пульсаций
(то есть беспорядочных быстрых изменений
скорости и давления).
Турбулентное течение течение жидкости
или газа, характеризующееся беспорядочным,
нерегулярным перемещением его объёмов
и их интенсивным перемешиванием
но в целом имеющее плавный, регулярный
характер.
Число
Рейно́льдса (
), —
безразмерная величина, характеризующая
отношение нелинейного и диссипативного
членов в уравнении
Навье — Стокса[1].
Число Рейнольдса также считается критерием
подобия течения
вязкой жидкости.
Число
Рейнольдса определяется следующим
соотношением:
где
-
— плотность среды,
кг/м3; -
—
характерная скорость,
м/с; -
—
характерный
размер, м; -
— динамическая
вязкость среды,
Н·с/м2; -
— кинематическая
вязкость среды,
м2/с(
) ; -
—
объёмная
скорость потока; -
—
площадь
сечения трубы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
6-я лекция.
23.03.12
6. КИНЕМАТИКА И ДИНАМИКА РЕАЛЬНОЙ ЖИДКОСТИ-2
6.1 Уравнение Бернулли для потока реальной (вязкой) жидкости.
6.2 Мощность потока.
6.3 Коэффициент Кориолиса.
6.4 Гидравлические потери (общие сведения).
6.5 Местные потери.
6.6. Потери энергии на трение по длине
Рекомендуемые материалы
6.7.Примеры использования уравнения Бернулли в технике
6.1.Уравнение Бернулли для потока реальной (вязкой) жидкости.
При выводе уравнения Бернулли для потока реальной (вязкой) жидкости необходимо учесть: неравномерность распределения скоростей по сечению и потери энергии. Эти явления соответствуют вязкой жидкости.
При движении жидкости из-за влияния вязкости происходит торможение потока. Наибольшие значения скорость достигает в центральной части потока, по мере приближения к стенке она уменьшается почти до нуля. Пример распределения скоростей показан на рис. 6.1.
Из-за неравномерного распределения скоростей происходит скольжение или сдвиг одних слоев по другим и между слоями возникают касательные напряжения или напряжения трения. Движение вязкой жидкости сопровождается вращением частиц, вихреобразованием и перемешиванием.
При движении реальной жидкости на преодоление сопротивлений, связанных с вязкостью, требуются затраты энергии, поэтому удельная энергия движущейся вязкой жидкости не остается постоянной, как в случае идеальной жидкости, а уменьшается вдоль потока.
При выводе уравнения Бернулли для потока вязкой жидкости вместо неравномерного распределения скоростей рассматриваются средние скорости и средние значения удельной энергии жидкости в данном сечении. Измерение скорости в различных точках сечения потока выполнить сложно, измерение средней скорости потока выполнить проще и они могут быть сделаны с большей точностью.
Для потока вязкой жидкости делается допущение: принимается, что в пределах рассматриваемых поперечных сечений потока, справедлив основной закон гидростатики и гидростатический напор есть величина одинаковая для всех точек данного сечения.
6.2. Мощность потока
Мощностью потока называется полная энергия, которую проносит поток через данное сечение в единицу времени.
Мощностью называется отношение работы, выполненной за определенный промежуток времни к длительности этого промежутка. Например, для гидроцилиндра
где давление p = ρgh, , работа А =pghS*L, массовый расход δQm = ρW/t = ρ(L*S) /t
Выразим работу, как произведение силы или произведение давления р на площадь S гидроцилиндра на ход – L, который поршень проходит под действием этой силы. Это выражение мощности гидравлического потока подведенного к гидроцилиндру.
Элементарные струйки, составляющие поток обладают различной энергией.
Мощность элементарной струйки это произведение полной удельной энергии струйки жидкости в виде третьей формы уравнения Бернулли в данной точке
gН= gz + p/(ρ) + (V2/2), (6.1)
на элементарный массовый расход струйки
δQm = ρ(V*δS /δt),
где V – скорость в сечении δS струйки .
Это произведение позволяет выразить мощность струйки:
δN = gH*δQm = (gz + p/ρ + v2/2)*ρ* v*δS = P*δQ (6.2)
Мощность всего потока найдем, как интеграл от предыдущего выражения по площади S:

Учитывая, допущение о том, что гидростатический напор для всех элементарных струек в сечении потока есть величина постоянная, получим мощность потока:

6.3 Коэффициент Кориолиса
Для определения полной удельной мощности потока разделим мощность потока на средний массовый расход: Qm = ρQ = 

Умножив и разделив последний член на V

где α – безразмерный коэффициент Кориолиса, учитывающий неравномерность распределения скоростей и равный

Умножив числитель и знаменатель на ρ/2, получим: коэффициент Кориолиса представляет собой отношение действительной кинетической энергии потока в данном сечении к кинетической энергии того же потока и в том же сечения, но при равномерном распределении скоростей, поскольку интеграл от dm = ρ*VdS – масса потока в данном сечении:
Возьмем два сечения реального потока, первое и второе, и обозначим средние значения полного напора жидкости в этих сечениях соответственно Нср1 и Нср2. Тогда
Н ср1 = Нср2 + Σhп,
где Σhп – суммарная потеря полного напора на участке между рассматриваемыми сечениями.
Это уравнение Бернулли для потока вязкой жидкости:

От уравнения для элементарной струйки идеальной жидкости это уравнение отличается четвертым членом – потерей полного напора, и коэффициентами Кориолиса, учитывающим неравномерность распределения скоростей. Скорости, входящие в это уравнение, являются средними скоростями в первом и тором сечениях потока.
Это уравнение Бернулли применимо не только для жидкостей, но для газов при условии, что скорость их движения значительно меньше скорости звука.
Графически это уравнение представляется диаграммой подобно уравнению Бернулли для идеальной жидкости с учетом потерь напора. Потери напора вдоль потока возрастают.
Уравнение Бернулли для струйки идеальной жидкости – это закон сохранения механической энергии.
Уравнение Бернулли для потока реальной жидкости – уравнение баланса энергии с учетом потерь.
Энергия, теряемая жидкостью на рассматриваемом участке течения превращается в тепловую форму энергии.
Хотя удельная теплоемкость жидкостей велика и тепловая энергия непрерывно рассеивается, повышение температуры рабочей жидкости в гидросистемах бывает значительным. Процесс преобразования механической энергии в тепловую необратим, обратное превращение тепловой энергии в механическую здесь невозможно.
Уменьшение среднего значения полной удельной энергии жидкости вдоль потока, отнесенное к единице его длины, называется гидравлическим уклоном.
6.4 Гидравлические потери .
Гидравлические потери удельной энергии, выраженные напором или давлением, зависят от формы и размеров трубопровода, скорости течения и вязкости жидкости.
При турбулентном режиме движения жидкости гидравлические потери пропорциональны скоростям во второй степени, в единицах длины
h п = ζ V2 ср /(2g), (6.9)
где ζ – безразмерный коэффициент местного сопротивления; V – средняя скорость потока (обычно – в сечении трубопровода перед местным сопротивлением или после него). В единицах давления
pп = ρghп = ζρ V2 ср /2. (6.10)
Безразмерный коэффициент потерь ζ – дзета называется коэффициентом сопротивления и равен отношению величины потерянного напора к скоростному напору.
Гидравлические потери разделяют на местные потери и потери на трение по длине.
Значение ζ вообще зависит от формы местного сопротивления, шероховатости его стенок, условий входа и выхода из него жидкости и основного критерия динамического подобия напорных потоков – числа Рейнольдса.
Число Рейнольдса обычно относят к сечению трубопровода, в котором находится местное сопротивление

где V и Q – средняя скорость потока и расход в трубе; D – диаметр трубы; ν- кинематическая вязкость жидкости.
Для большинства местных сопротивлений в трубопроводах при числах Рейнольдса Re > 105 имеет место турбулентная автомодельность – потери напора пропорциональны скорости во второй степени и коэффициент сопротивления не зависит от Re (квадратичнаνя зона сопротивления).
В тех местных сопротивлениях, где основной является вихревая потеря напора (например, резкое изменение сечения трубопровода, диафрагмы и др.), автомодельность устанавливается при значительно меньших числах Рейнольдса Re≥104.
Число Рейнольса определяет режим течения жидкости. При его значении меньше Re≤2300 режим течения жидкости называется ламинарным, от слова ламина – слой или слоистым.
Ламинарным движением жидкости называется режим ее течения упорядоченным слоями без ее перемешивания.
Струи жидкости, находящиеся на разном удалении от оси движутся с различными скоростями. Наибольшую скорость имеет осевая струйка, при стенках скорость равна нулю.
Увеличение скорости понижает устойчивость ламинарного течения и нарушает его режим. На устойчивость ламинарного режима оказывают влияние вязкость жидкости, плотность, скорость движения частиц, а также диаметр трубопровода.
При увеличении скорости струйки разрываются, разрыву предшествует образование волнообразных колебаний. При усилении колебаний струйка полностью перемешивается с окружающей жидкостью. Движение частиц производит впечатление беспорядочных вихрей. При числах Рейнольса больше Re>2300 режим течения жидкости становится турбулентным.
Турбулентным движением жидкости называется режим ее течения неупорядоченным слоями с их перемешиванием.
6.5.Местные потери
Местные потери энергии вызваны изменениями формы и размера трубопровода, вызывающими деформацию потока. Жидкости, протекая через местные сопротивления, изменяет скорость и образует вихри. После отрыва потока от стенок вихри образуют области, в которых частицы жидкости движутся в основном по замкнутым траекториям.
Примеры местных сопротивлений приведены на рис. 6.3. Здесь же показаны отрывы потока и вихреобразование.
Каждое местное сопротивление характеризуется значением коэффициента сопротивления ζ, которое приближенно можно считать постоянным для данной формы местного сопротивления.
6.6. Потери энергии на трение по длине
Эти потери возникают в прямых трубах постоянного сечения и при равномерной скорости течения, возрастают пропорционально длине трубы (рис.6.4).
Потери энергии на трение по длине связаны с внутренним трением в жидкости, эти потери можно определять по формуле для гидравлических потерь, т. е.
h тр = ζ тр v2/(2g).
Поскольку длины труб разные, коэффициент потерь на трение ζтр связывают с относительной длиной трубы l/d.
Коэффициент потерь на трение участка круглой трубы с длиной равной ее диаметру
l = d обзначают буквой λ –лямбда, если длина трубы l не равна диаметру d, коэффициент потерь будет в l/d раз больше:
ζ тр = λ* l/d .
Формула для определения потерь на трение по длине называется формулой Вейсбаха – Дарси.
(6.11)
или в единицах давления

Коэффициент λ, входящий в формулы для определения потерь по длине называется “коэффициентом потерь на трение по длине”, или “коэффициентом Дарси”.
Физический смысл коэффициента λ. При равномерном движении в трубе длиной l и диаметром d, имеет место равновесие сил, действующих на объем: сил давления и силы трения. Это равновесие выражается равенством
πd2pтр/4 – πdlτ0 = 0,
где τ0 — напряжение трения на стенке трубы.
Так как 

λ есть величина, пропорциональная отношению напряжения от силы трения на стенке трубы к динамическому давлению, определяемому по средней скорости.
6.6. Применение уравнения Бернулли в технике
6.6.1. Расходомер Вентури – устройство, устанавливаемое в трубопроводах и выполняющее сужение потока — дросселирование (рис.6.5).
Расходомер состоит из двух участков — плавно сужающегося сопла и постепенно расширяющегося диффузора. Скорость потока в суженном месте возрастает, а давление падает. Возникает перепад давлений, который измеряется двумя пьезометрами и дифференциальным U-образным манометром.
В сечении 1-1 перед сужением скорость потока равна V1, давление Р1, площадь сечения S1 , а в cечении 2-2: V2, P2 ,S2 , разность показаний пьезометров, присоединенных к сечениям ΔН.
Запишем для сечений 1-1 и 2-2 потока уравнение Бернулли и уравнение расхода, считая распределение скоростей равномерным.
где hм — потеря напора между сечениями 1-1 и 2-2.
Объемный расход
где С — величина постоянная для данного расходомера.
Зная величину С, можно найти расход в трубопроводе по формуле. Коэффициент С можно определить теоретически, но лучше найти его экспериментально при тарировании расходомера.
Вместо пьезометров для измерения перепада давлений в расходомере можно применить дифференциальный манометр, заполненный ртутью. Над ртутью в трубках находится жидкость с плотностью ρ, поэтому можно записать для уровня 0-0, уравнение статики
Р1+ρgΔh= Р2+ρртgΔh, (Р1– Р2 ) = ρртgΔh – ρgΔh, (Р1– Р2 ) =ΔНρg, откуда
6.6.2. Карбюратор поршневых двигателей внутреннего сгорания служит для подсоса бензина и смешивания его с потоком воздуха (рис. 6.6). Поток воздуха засасываемого в двигатель, сужается в том месте, где установлен распылитель бензина (трубка диаметром d). Скорость воздуха этом сечении возрастает, а давление по закону Бернулли падает. Благодаря пониженному давлению бензин подсасывается в поток воздуха.
Найдем соотношение между массовыми расходами бензина Qб и воздуха Qв при заданных размерах D и d и коэффициентах сопротивления воздушного канала (до сечения 2-2) и жиклера ζж (сопротивлением бензотрубки пренебрегаем).
Записав уравнение Бернулли для потока воздуха (сечение 1-1 и 2-2), а затем для потока бензина (сечение 1-1 и 2-2), получим (при z1= z2‚ и α= 1):
откуда
Учитывая, что массовые расходы
получим
Таким образом, обеспечивается постоянство соотношения расходов бензина и воздуха.
Струйный насос (эжектор) состоит из плавно сходящегося насадка А (рис.6.6), осуществляющего сжатие потока, и постепенно расширяющейся трубки С, установленной на некотором расстоянии от насадка в камере В.
Вследствие увеличения скорости потока в струе на выходе из насадка и по всей камере В значительно понижается. В расширяющейся трубке скорость уменьшается, а давление возрастает приблизительно до атмосферного (если жидкость вытекает в атмосферу), следовательно в камере В давление обычно меньше атмосферного, т. е. возникает разрежение (вакуум). Под действием разрежения жидкость из нижнего резервуара всасывается по трубе D в камеру В, где происходят слияние и дальнейшее перемешивание двух потоков.
Трубка полного напора ( трубка Пито) служит для измерения скорости в трубе (рис. 1.34). Если установить в этом потоке трубку, повернутую под углом 90°, отверстием навстречу потоку и пьезометр, то жидкость в этой трубке поднимается над уровнем в пьезометре на высоту равную скоростному напору.
“3. Освещение” – тут тоже много полезного для Вас.
Объясняется это тем, что скорость v частиц жидкости, попадающих в отверстие трубки, уменьшается до нуля, а давление, следовательно, увеличивается на величину скоростного напора. Измерив разность высот подъема жидкости в трубке Пито и пьезометре, легко определить скорость жидкости в данной точке. На этом же принципе основано измерение скорости полета самолета. На рис.6.7 показана схема самолетной скоростной трубки (насадка) для измерения малых по сравнению со скоростью звука скоростей полета.
Запишем уравнение Бернулли для струйки , которая набегает на трубку вдоль ее оси, а затем растекается по ее поверхности. Для сечений 0-0 (невозмущенный поток) и 1-1 (где v =0), получаем

Так как боковые отверстия трубки приближенно воспринимают давление невозмущенного потока, р2 ≈ р0 , следовательно, из предыдущего имеем
Рефераты, дипломные, курсовые работы — бесплатно: Библиофонд!
Определение коэффициента гидравлического трения
В уравнении Бернулли, записанном для двух сечений потока вязкой жидкости (обозначения общепринятые):
(1)
где представляет собой суммарную величину потерянного напора:
, (2)
где – потери напора по длине расчетного участка трубопровода, вызванные трением жидкости о стенки, называются путевыми потерями;
– потери напора на коротких участках трубопровода, обусловленные изменением формы или размеров (иногда и того и другого одновременно), называемые потерями в местных сопротивлениях, или местными потерями напора.
В данной работе рассматриваются путевые потери. Согласно уравнению неразрывности для потока вязкой несжимаемой жидкости (ρ = const):
(3)
Обратите внимание
При течении жидкости в горизонтально расположенном трубопроводе (z1=z2) постоянного сечения (S1=S2) скорость в начале и конце расчетного участка будет одинаковыми (V1=V2) и уравнение Бернулли примет вид:
(4)
Путевые потери определяются по формуле Дарси – Вейсбаха:
, (5)
где λ – безразмерный коэффициент гидравлического трения (коэффициент Дарси);
L – длина расчетного участка трубопровода;
d – диаметр трубопровода;
J – средняя скорость потока.
Экспериментально установлено, что коэффициент гидравлического трения в общем случае зависит от режима течения, характеризуемого числом Рейнольдса (Re), и состояния внутренней поверхности трубопровода, характеризуемой относительной шероховатостью (ε). Влияние этих факторов на величину λ при ламинарном и турбулентном режимах течения проявляется по-разному.
При ламинарном режиме, т.е. (ν – кинематический коэффициент вязкости) состояние поверхности стенки не влияет на сопротивление движению жидкости и λ = f (Re). Значение коэффициента λ в этом случае определяется по теоретической формуле Пуазейля:
(6)
Подставляя это выражение в (5), получим формулу для определения путевых потерь при ламинарном течении в виде:
, (7)
где
Из (7) следует, что в ламинарном потоке потери напора по длине трубопровода (путевые потери) прямо пропорциональны средней скорости течения жидкости.
Турбулентный режим течения характеризуется интенсивным перемешиванием жидкости как в поперечном (по сечению потока), так и в продольном (по длине потока) направлениях.
Однако в диапазоне чисел Рейнольдса непосредственно вблизи стенок трубопровода существует слой движущейся жидкости, течение в котором сохраняется ламинарным. Этот слой называется ламинарным подслоем или ламинарной пленкой.
Толщина ламинарной пленки (δЛ) зависит от режима течения δЛ = f (Re) и с увеличением числа Рейнольдса δЛ уменьшается.
Важно
Стенки любого тракта имеют естественную шероховатость поверхности, первоначально обусловленную материалом и технологией изготовления трубопровода и меняющуюся при его эксплуатации вследствие взаимодействия материала трубопровода с рабочей жидкостью. Средняя высота выступов шероховатости (Δ) называется абсолютной шероховатостью. В зависимости от соотношения между δЛ и Δ (см. рис 1) трубы или стенки рассматривают как гидравлически гладкие или гидравлически шероховатые.
Рис. 1
Если δЛ > Δ, ламинарный подслой как бы сглаживает шероховатость стенки: поток не получает дополнительной турбулизации от шероховатости, поскольку образующиеся на вершинах выступов шероховатости вихри подавляются ламинарной пленкой. Труба, в которой выступы шероховатости находятся в пределах толщины ламинарного подслоя, называется гидравлически гладкой.
Если δЛ < Δ, выступы шероховатости, оказавшись в турбулентном ядре потока, вносят дополнительное возмущение в обтекающую их жидкость, что приводит к увеличению сопротивления и, следовательно, потерь напора. Такая труба является гидравлически шероховатой.
В зависимости от режима течения, одна и та же труба может быть как гидравлически гладкой, так и гидравлически шероховатой, поскольку с ростом числа Рейнольдса толщина ламинарного подслоя уменьшается, и, наоборот – с увеличением Re, δЛ возрастает.
Естественная шероховатость всегда неравномерна, так как выступы имеют различные формы, размеры и расположения. Поэтому вводится понятие эквивалентной (или равномерно-зернистой) абсолютной шероховатости ΔЭ.
Эта искусственно создаваемая шероховатость, например, путем наклеивания на стенки трубы песчинок одного размера (одной фракции) и на одинаковых расстояниях друг от друга, обеспечивает создание сопротивления трубопровода, равного сопротивления при естественной шероховатости.
Значения абсолютной (Δ) и эквивалентной (ΔЭ) шероховатости для труб из некоторых материалов приведены в таблице 1.
Таблица 1.
| № п/п | Материал и состояние труб | Δ,мм | ΔЭ,мм |
| 1 | Трубы из стекла, латуни или медные, новые | 0,0015…0,01 | 0,001…0,01 |
| 2 | Трубы стальные, бесшовные (цельнопотянутые), новые, чистые | 0,02…0,1 | 0,02…0,5 |
| 3 | Трубы стальные, сварные, новые, чистые | 0,03…0,12 | 0,03…0,1 |
| 4 | Трубы стальные, бывшие в употреблении | 0,2…1,2 | 0,2…1,25 |
| 5 | Трубы чугунные, новые | 0,25…1,0 | 0,2…0,5 |
| 6 | Трубы чугунные, бывшие в употреблении | 0,5…1,4 | 0,5…1,5 |
При определении λ учитывается не абсолютная шероховатость, а ее отношение к диаметру (или радиусу) трубы, т.е. относительная шероховатость:
;
Это обусловлено тем, что одна и та же абсолютная шероховатость оказывает большее влияние на сопротивление движению в трубопроводе меньшего диаметра.
Предложено большое количество эмпирических и полуэмпирических формул для определения коэффициента гидравлического трения λ, учитывающих особенности течения при турбулентном режиме. Эти особенности в конечном итоге сказываются на зависимости путевых потерь от средней скорости течения.
Совет
Так, для гидравлически гладких труб потери напора по длине пропорциональны средней скорости в степени 1,75.
В переходной области от гидравлически гладких к шероховатым трубам () на величину λ оказывают влияние одновременно два фактора: число Рейнольдса и относительная шероховатость, т.е. в переходной области λ = f (Re, ε).
В этой области, называемой зоной доквадратного сопротивления, потери напора по длине пропорциональны средней скорости в степени 1,74…2.
Для гидравлически шероховатых труб, когда ламинарная пленка практически полностью разрушается, коэффициент λ уже не зависит от Re, а определяется лишь относительной шероховатостью, т.е. λ = f (ε).
Эта область называется зоной квадратичного сопротивления, т. к. hl ~ J2, или автомодельной областью, так как независимость λ от Re означает, что потери напора по длине, определяемые по формуле (5) пропорциональны квадрату средней скорости.
Начало этой области определяется условием .
Определение λ по приведенным в таблице 2 и другим формулам облегчается использованием таблиц и номограмм, содержащихся в учебных и справочных пособиях.
При проведении данной работы рассматриваются режимы течения в гидравлически гладких трубах.
Таблица 2
| Зона сопротивления, режим | Границы зоны | Расчетные формулы | Зависимость потерь напора от скорости |
| 1. Ламинарный | ;ф. Пуазейля | hl ~ J | |
| 2. Зона гладкостенного сопротивления | ;ф. Блазиуса | hl ~ J1,75 | |
| ф. Конакова | |||
| 3. Зона доквадратичного сопротивления | ф. Кольбрука Уайта | hl ~ J1,75 ¸ 2 | |
| ф. Альтшуля | |||
| 4. Зона квадратичного сопротивления | ф. Прандтля-Никурадзе | hl ~ J2 | |
| ф. Шифринсона |
Описание установки.
Принципиальная схема экспериментальной установки, используемой для определения коэффициента гидравлического трения λ приведена на рис. 2.
Экспериментальный участок трубопровода круглого сечения длиной L подсоединен к напорному баку 5, в который из водовода через вентиль 1 и успокоительную сетку 3 непрерывно подается вода. Излишки воды из бака сливаются через переливную трубу 4. Поэтому в баке может поддерживаться постоянный уровень.
Расход воды через экспериментальный участок регулируется вентилем 7 (вентиль на входе в экспериментальный участок полностью открыт во время всего эксперимента). После прохождения экспериментального участка вода сливается в мерный бак 8, на входе из которого имеется кран 9. Для измерения температуры воды установлен термометр 2.
Обратите внимание
Установка снабжена пьезометрическим щитом 6, на котором установлены пьезометры для измерения потерь по длине.
Рис. 4
Литература
1. Башта Т.М. и др. Гидравлика, гидромашины и гидроприводы. – М.: Машиностроение, 1984, 424 с.
2. Идельчик И.Е. Справочник по гидравлическим сопротивлениям. – М.: Машиностроение, 1975. – 559 с.
3. Установка для изучения потерь напора при турбулентном установившемся движении (тип ГВ5). – Одесоргнаучкомплектснаб. – 39 с.
Источник: https://www.BiblioFond.ru/view.aspx?id=479280
Коэффициенты гидравлического трения и местных сопротивлений
Гидравлический расчет
Цель гидравлического расчета – определение величины сопротивления, вносимую теплообменником в систему технологических трубопроводов, и мощности, необходимой для перемещения теплоносителей, выбор насоса, работающего на сеть Теплоносители должны подаваться в теплообменный аппарат под некоторым избыточным давлением для того, чтобы преодолеть гидравлическое сопротивление аппарата и системы технологических трубопроводов за аппаратом, переместить теплоноситель из одной точки пространства в другую (например, поднять его) и иметь возможность сообщить ему дополнительную скорость. При этом теплоноситель должен обладать достаточной энергией в заданной точке технологической схемы. Потери энергии жидкостью и газами при движении, обусловленные внутренним трением, определяют величину гидравлического сопротивления. Различают потери напора по длине hɩ и потери в местных сопротивлениях h(м.с), обусловленные изменением скорости потока по величине или направлению. Полное гидравлическое сопротивление потоку, движущемуся в закрытых каналах теплообменных аппаратах (потери напора) (в м),
(3.1)
Потери напора по длине оценивают по формуле Дарси-Вейсбаха
(3.2)
а местные сопротивления (потери в местных сопротивлениях) — по формуле Вейсбаха
(3.3)
где λ — гидравлический коэффициент трения;- общая длина потока теплоносителя в аппарате, м; d3KB — эквивалентный диаметр потока, м;- коэффициент местного сопротивления, отнесенный к средней скорости потока; ω- средняя скорость потока, м/с; g = 9,81 — ускорение свободного падения, м/с2.
С учетом (3.2) и (3.3) формула (3.1) приобретает вид
(3.4)
или (в Па)
(3.5)
где р — плотность теплоносителя, кг/м3.
При значительных изменениях температуры рабочей
Совет
среды и большой высоте вертикальных каналов возникают дополнительные потери энергии, обусловленные местными ускорениями потока вследствие изменения плотности теплоносителя,Py(в Па), а также потери на преодоление подъемных сил (самотяги) в вертикальных каналах теплообменника [6].
При постоянном сечении канала
(3.6)
гдеи- скорости, м/с;и- плотности теплоносителей во входном и выходном сечениях потока, кг/м3. В случае нагревания теплоносителяРУ положительно, в случае охлаждения — отрицательно.
Подъемная сила и равное ей по величине сопротивление самотягиРС (в Па), возникающее вследствие того, что вынужденному движению нагретой жидкости в нисходящих каналах противодействует сила, направленная вверх, определяются следующим соотношением:
(3.7)
гдеи pi- плотность холодного и нагретого теплоносителя,кг/м3; h — высотавертикального канала, м.
При нисходящем движении нагретой жидкости величина самотяги является дополнительным сопротивлением канала, при восходящем движении сопротивление канала уменьшается на величинуРС.
Полное гидравлическое сопротивление теплообменника (Па)
(3.8)
Мощность N (в кВт), необходимая для перемещения теплоносителя через аппарат,
(3.9)
а мощность(в кВт), потребляемая электродвигателем насоса (или вентилятора),
(З.10)
Важно
где V — объемный расход теплоносителя, м3/с;- полное гидравлическое сопротивление сети, Па [33, с. 18-19];- общий КПД насосной (вентиляционной) установки.
Разбивка трубопровода насосной установки на участки: всасывающая линия, участок напорного трубопровода от насоса до теплообменника, теплообменник, участок напорного трубопровода от теплообменника до конечной точки
Трубопровод состоит из всасывающей и напорной линий. Всасывающая линия — трубопровод от источника (приемного бака) до насоса. Напорная линия — участок трубопровода от насоса до конечной точки трубопровода в расчетной схеме с включенным в него теплообменником:
— участок напорного трубопровода от насоса до теплообменника; — теплообменник;
— участок напорного трубопровода от теплообменника до конечной точки трубопровода.
Разбивка трубопровода на перечисленные участки обусловлена отличиями ни них либо скоростей движения теплоносителей, либо их температур, а в конечном итоге — разными значениями чисел Рейнольдса.
Выбор типа и марки насоса
Решающим фактором при выборе типа насоса являются физико-химические свойства перекачиваемой жидкости. При этом учитываются также заданная подача и рассчитанный требуемый напор насоса.
Марку насоса выбирают по полю характеристик V-H насосов выбранного типа, соответствующую этим параметрам (V и Hтр).
В заданиях на проектирование, приводимых в разделе 6, целесообразно использовать лопастные насосы.
Гидравлический расчет
Цель гидравлического расчета – определение величины сопротивления, вносимую теплообменником в систему технологических трубопроводов, и мощности, необходимой для перемещения теплоносителей, выбор насоса, работающего на сеть Теплоносители должны подаваться в теплообменный аппарат под некоторым избыточным давлением для того, чтобы преодолеть гидравлическое сопротивление аппарата и системы технологических трубопроводов за аппаратом, переместить теплоноситель из одной точки пространства в другую (например, поднять его) и иметь возможность сообщить ему дополнительную скорость. При этом теплоноситель должен обладать достаточной энергией в заданной точке технологической схемы. Потери энергии жидкостью и газами при движении, обусловленные внутренним трением, определяют величину гидравлического сопротивления. Различают потери напора по длине hɩ и потери в местных сопротивлениях h(м.с), обусловленные изменением скорости потока по величине или направлению. Полное гидравлическое сопротивление потоку, движущемуся в закрытых каналах теплообменных аппаратах (потери напора) (в м),
(3.1)
Потери напора по длине оценивают по формуле Дарси-Вейсбаха
(3.2)
а местные сопротивления (потери в местных сопротивлениях) — по формуле Вейсбаха
(3.3)
где λ — гидравлический коэффициент трения;- общая длина потока теплоносителя в аппарате, м; d3KB — эквивалентный диаметр потока, м;- коэффициент местного сопротивления, отнесенный к средней скорости потока; ω- средняя скорость потока, м/с; g = 9,81 — ускорение свободного падения, м/с2.
С учетом (3.2) и (3.3) формула (3.1) приобретает вид
(3.4)
или (в Па)
(3.5)
где р — плотность теплоносителя, кг/м3.
При значительных изменениях температуры рабочей
Совет
среды и большой высоте вертикальных каналов возникают дополнительные потери энергии, обусловленные местными ускорениями потока вследствие изменения плотности теплоносителя,Py(в Па), а также потери на преодоление подъемных сил (самотяги) в вертикальных каналах теплообменника [6].
При постоянном сечении канала
(3.6)
гдеи- скорости, м/с;и- плотности теплоносителей во входном и выходном сечениях потока, кг/м3. В случае нагревания теплоносителяРУ положительно, в случае охлаждения — отрицательно.
Подъемная сила и равное ей по величине сопротивление самотягиРС (в Па), возникающее вследствие того, что вынужденному движению нагретой жидкости в нисходящих каналах противодействует сила, направленная вверх, определяются следующим соотношением:
(3.7)
гдеи pi- плотность холодного и нагретого теплоносителя,кг/м3; h — высотавертикального канала, м.
При нисходящем движении нагретой жидкости величина самотяги является дополнительным сопротивлением канала, при восходящем движении сопротивление канала уменьшается на величинуРС.
Полное гидравлическое сопротивление теплообменника (Па)
(3.8)
Мощность N (в кВт), необходимая для перемещения теплоносителя через аппарат,
(3.9)
а мощность(в кВт), потребляемая электродвигателем насоса (или вентилятора),
(З.10)
Важно
где V — объемный расход теплоносителя, м3/с;- полное гидравлическое сопротивление сети, Па [33, с. 18-19];- общий КПД насосной (вентиляционной) установки.
Коэффициенты гидравлического трения и местных сопротивлений
Коэффициент гидравлического трения λ в общем случае зависит от режима течения теплоносителя и шероховатости стенки канала. При ламинарном режиме движения (Re < 2300) λ зависит только от режима движения и определяется по формуле Пуазейля
λ = A/Re ,(3.11)
где Re = ωd/v — число Рейнольдса; А — коэффициент, зависящий от формы поперечного сечения канала и от его размеров (табл. 3.1). При турбулентном режиме движения и числах Рейнольдса от 2300 до105 (промежуточная зона) λ является функцией и числа Re , и шероховатости стенки канала, а при Re106 (квадратичная зона) — функцией только относительной шероховатости и практически не зависит от Re.
Обратите внимание
В справочной и специальной литературе приводятся многочисленные эмпирические формулы для расчета коэффициента трения λ при турбулентном режиме движения
жидкостей в трубах. Наиболее распространены формулы Никурадзе
(3.12)
и Шифринсона
(3.13)
для квадратичной зоны и формулы Колбрука
(3.14)
и Альтшуля
(3.15)
для промежуточной зоны, где- эквивалентная шероховатость, учитывающая не только среднюю высоту выступов, но и их форму, расположение в плане и пр.
Под эквивалентной шероховатостью понимается такая высота выступов равнозернистой шероховатости, которая при введении ее в формулы для λ (содержащие кэ) позволяет вычислить коэффициент трения λ для данной категории труб в реальных условиях (табл. 3.2)
Таблица 3.1
Значение коэффициента А для некоторых сечений
| Форма сечения | А |
| Круг | |
| Квадрат | |
| Равносторонний треугольник | |
| Кольцо | |
| Прямоугольник а/b = 0 | |
| а/b = 0,1 | |
| а/b = 0,2 | |
| а/b = 0,25 | |
| а/b = 0,33 | |
| а/b = 0,5 | |
| Эллипс — главная полуось b, вспомогательная | |
| полуось а | |
| а/b = 0,1 | |
| а/b = 0,3 | |
| а/b = 0,5 | |
| а/b = 0,7 |
Таблица 3.2
Значения эквивалентной шероховатости кэ для труб из разных материалов [25]
| Трубы | Состояние труб | кэ, мм |
| Тянутые из стекла и цветных металлов | Новые технически гладкие | 0-0,002 |
| Бесшовные стальные | Новые и чистые | 0,01-0,02 |
| Стальные сварные | После нескольких лет эксплуатации Новые и чистые С незначительной коррозией после очистки | 0,15-0,3 0,03-0,1 0,1-0,2 |
| Умеренно заржавевшие | 0,3-0,7 | |
| Старые заржавевшие Сильно заржавевшие или с большими | 0,8-1,5 2-4 | |
| отложениями | ||
| Оцинкованные железные | Новые и чистые | 0,1-0,2 |
| После нескольких лет эксплуатации | 0,4-0,7 | |
| Чугунные | Новые без покрытия | 0,2-0,5 |
| Бывшие в употреблении | 0,5-1,5 | |
| Очень старые | До З |
Для металлических труб кэ =(0,5/0,7)[18].
Если высота выступовв трубе меньше толщины вязкого подслоя
(3.16)
то шероховатость стенок не влияет на величину коэффициента λ и при турбулентном режиме движения потока. Такие трубы называются гидравлически гладкими.
При турбулентном режиме движения λ для гидравлически гладких труб определяют по формулам Блазиуса (4 ·10 3 < Re < 105)
(3.17)
и Прандтля (Re > 10 5 )
(3.18)
Так как толщина вязкого подслоя=f(Re) , труба может быть шероховатой при одном расходе жидкости и гидравлически гладкой — при другом. Поэтому при выборе расчетной формулы необходимо проверить трубу на шероховатость для конкретных условий ее эксплуатации.
Для расчета гидравлического сопротивления при турбулентном движении жидкости в каналах некруглого сечения вместо фигурирующего в формулах (3.12)-(3.18) диаметра трубопровода должен подставляться эквивалентный диаметр(в м), определяемой формулой [2, 18]
(3.19)
где S — площадь поперечного сечения потока, м2; П — смоченный периметр, м.
Кривизна канала несколько увеличивает его гидравлическое сопротивление. Она учитывается введением поправочного коэффициента φ, который может быть представлен как функция отношения радиуса изгиба R к диаметру трубы d [26]:
3.0 < R/d < 12;
(3.20)
При R/d < 3 кривизну канала следует учитывать через коэффициент местных сопротивлений, а при R/d > 12 коэффициент φ = 1.
Теплоносители, движущиеся в трубах и каналах рекуперативных теплообменных аппаратов, нагреваются или охлаждаются. При этом изменяется вязкость теплоносителей, а следовательно, и сопротивление трения. Влияние изменяемости вязкости, температуры и направления теплового потока на сопротивление трения для ламинарного и турбулентного режимов в
технически гладких трубах учитывается симплексом (Рrст/Рr)1/3 [39].
Важно
По данным [27], гидравлическое сопротивление при ламинарном движении в теплообменных трубах зависит от естественной конвекции, что учитывается поправочным множителем= 1 + 0,22(GrPr/Re)0,15.
Тогда при неизотермическом течении расчетная формула для ламинарного режима будет иметь вид
(3.21)
где Re, Pr, Gr — числа Рейнольдса, Прандтля и Грасгофа, определенные для средней температуры теплоносителя; Ргст — число Прандтля, рассчитанное для теплоносителя при температуре стенки трубы.
Поправка к коэффициенту трения, связанная с естественной конвекцией, зависит главным образом от температурного напораи средней скорости ω варьируется в пределах 1,5-2,1, причем нижний предел относится к малым температурным напорам (10 °C) и большим скоростям (ω1 м/с), а верхний — к большим температурным напорам (100 °C) и малым скоростям (ω0,1 м/с).
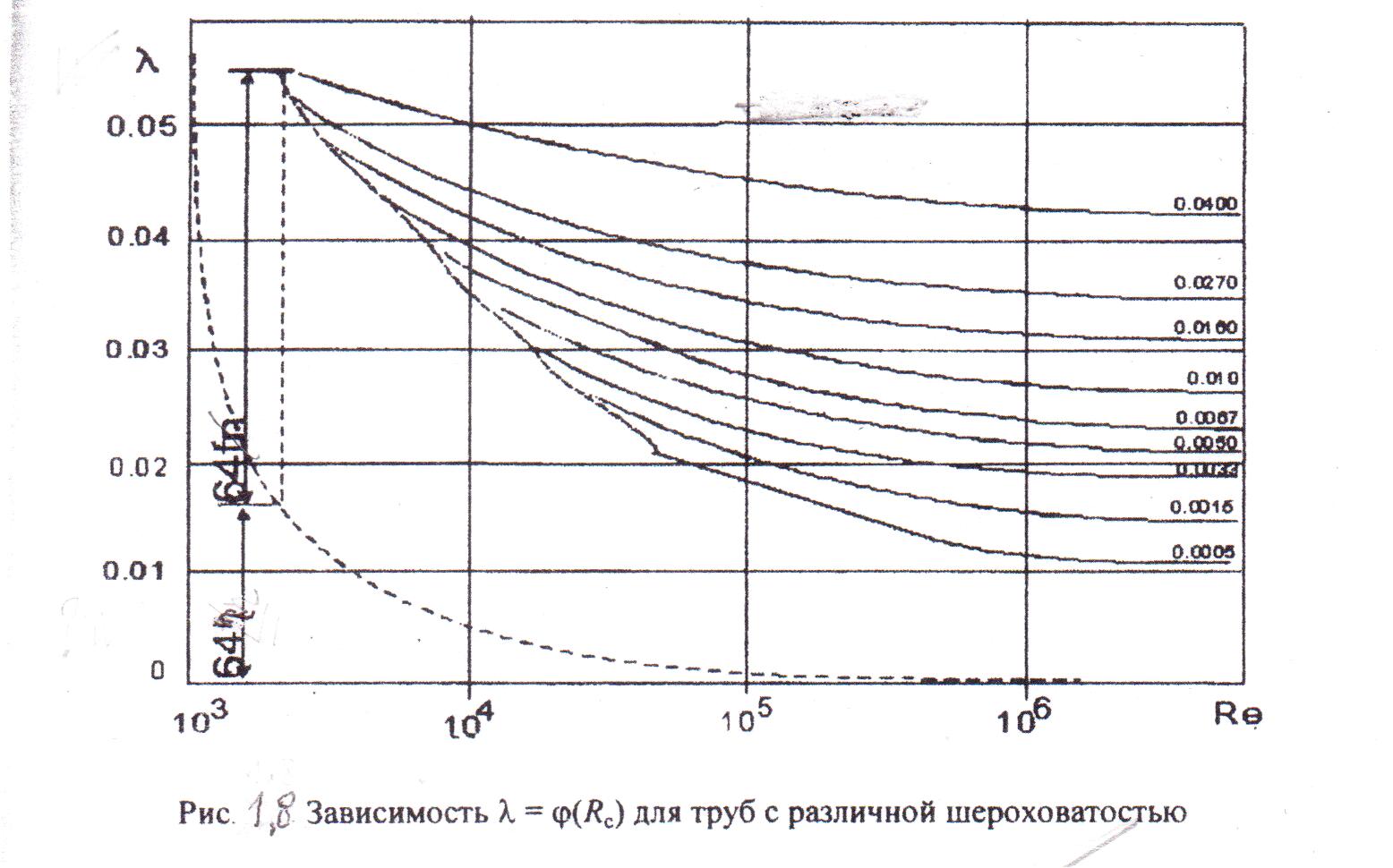
Коэффициент местных сопротивленийобусловливается не только вязкостью и скоростью течения основного потока, но и геометрической формой и размерами препятствий на пути потока.
Коэффициенты разных местных сопротивлений находят, как правило, опытным путем. Таблицы значений этих коэффициентов (табл. 3.
3 [23, 34]) или формулы для их определения содержатся в справочниках и руководствах по гидравлике.
| Виды сопротивления | Значение |
| Входная и выходная камеры (удар и поворот) Поворот на 180° из одной секции в другую через промежуточную камеру То же через колено в секционных подогревателях и теплообменниках типа «труба в трубе» (R/d < 3) Вход в межтрубное пространство под углом 90° к рабочему потоку Поворот на 180° в U-образной трубке Переход из одного элемента в другой (межтрубный поток) Поворот на 180° через перегородку в межтрубном пространстве Огибание перегородок, поддерживающих трубы Вход в межтрубное пространство под углом 90° и выход из него Вход в трубное пространство и выход из него Поперечное движение в межтрубном пространстве между перегородками (п, – число рядов труо) | 1.5 2.5 2.0 1.5 0,5 2.5 1.5 0,5 1,0 1,0 |
Окончание табл.3.3
| Внезапное расширение | |
| Внезапное сужение Проходной вентиль d = 50 мм при полном открытии Нормальная задвижка Проходной кран Угольник 90° | 4,6 0,5 — 1,0 0,6 — 2,0 1,0 — 2,0 |
*Коэффициент отнесен к средней скорости перед местным сопротивлением, в остальных случаях — к средней скорости за сопротивлением.
Источник: https://cyberpedia.su/7×1553.html
Шероховатость полиэтиленовых труб. Расчет гидравлических потерь давления в трубопроводе из пластмасс
Гидравлический расчет является важной составляющей процесса выбора типоразмера трубы для строительства трубопровода. В нормативной литературе по проектированию этот ясный с точки зрения физики вопрос основательно запутан.
На наш взгляд, это связано с попыткой описать все варианты расчета коэффициента трения, зависящего от режима течения, типа жидкости и ее температуры, а также от шероховатости трубы, одним (на все случаи) уравнением с вариацией его параметров и введением всевозможных поправочных коэффициентов.
При этом краткость изложения, присущая нормативному документу, делает выбор величин этих коэффициентов в значительной степени произвольным и чаще всего заканчивается номограммами, кочующими из одного документа в другой.
С целью более подробного анализа предлагаемых в документах методов расчета представляется полезным вернуться к исходным уравнениям классической гидродинамики [1].
Совет
Потеря напора, связанная с преодолением сил трения при течении жидкости в трубе, определяется уравнением:
где: L и D длина трубопровода и его внутренний диаметр, м; ? — плотность жидкости, кг/м3; w — средняя объемная скорость, м/сек, определяемая по расходу Q, м3/сек:
λ — коэффициент гидравлического трения, безразмерная величина, характеризующая соотношение сил трения и инерции, и именно ее определение и есть предмет гидравлического расчета трубопровода. Коэффициент трения зависит от режима течения, и для ламинарного и турбулентного потока определяется по-разному. Для ламинарного (чисто вязкого режима течения) коэффициент трения определяется теоретически в соответствии с уравнением Пуазейля: λ = 64/Re (2) где: Re — критерий (число) Рейнольдса. Опытные данные строго подчиняются этому закону в пределах значений Рейнольдса ниже критического (Re < 2320). При превышении этого значения возникает турбулентность. На первом этапе развития турбулентности (3000 < Re < 100000) коэффициент трения также очень точно определяется классическим уравнением Блязиуса: λ = 0,3164 Re -0,25 (3)
В несколько расширенном диапазоне чисел Рейнольдса (4000 < Re < 6300000) применяют уравнение ВТИ, также ставшее классическим:
λ = 1,01 lg(Re) -2,5 (4)
Для значений Re > 100000 предложено много расчетных формул, но практически все они дают один и тот же результат [1 — 3].
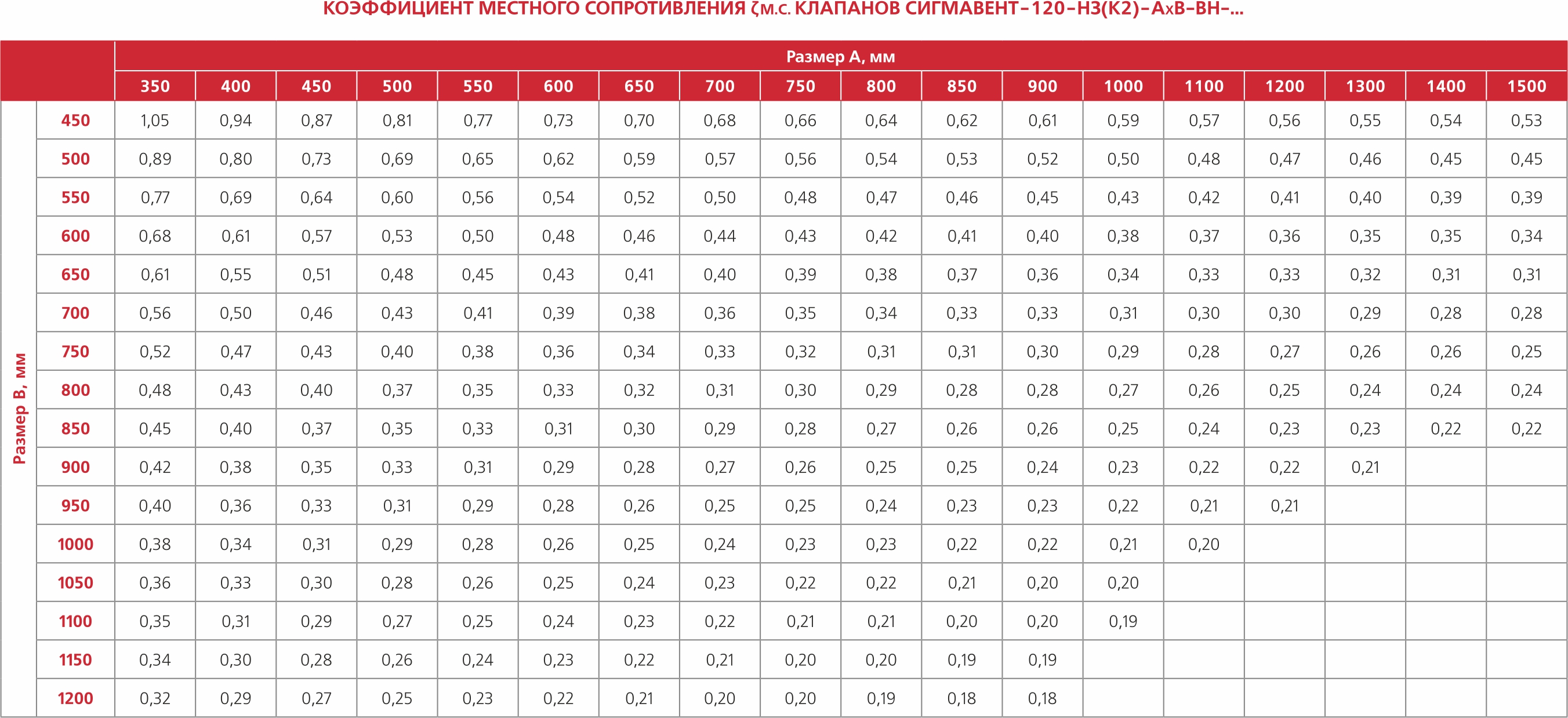
На рис.1 показано, как «работают» уравнения (2) — (4) в указанном диапазоне чисел Рейнольдса, который достаточен для описания всех реальных случаев течения жидкости в гидравлически гладких трубах. Рис.1
Шероховатость стенки трубы влияет на гидравлическое сопротивление только при турбулентном потоке, но и в этом случае, из-за наличия ламинарного пограничного слоя существенно сказывается только при числах Рейнольдса, превышающих некоторое значение, зависящее от относительной шероховатости ξ/D, где ξ — расчетная высота бугорков шероховатости, м.
Труба, для которой при течении жидкости выполняется условие:
считается гидравлически гладкой, и коэффициент трения определяется по уравнениям (2) — (4).
Для чисел Re больше определенных неравенством (5) коэффициент трения становится величиной постоянной и определяется только относительной шероховатостью по уравнению:
которое после преобразования дает:
Гидравлическое понятие шероховатости не имеет ничего общего с геометрией внутренней поверхности трубы, которую можно было бы инструментально промерить.
Исследователи наносили на внутреннюю поверхность модельных труб четко воспроизводимую и измеряемую зернистость, и сравнивали коэффициент трения для модельных и реальных технических труб в одних и тех же режимах течения.
Обратите внимание
Этим определяли диапазон эквивалентной гидравлической шероховатости, которую следует принимать при гидравлических расчетах технических труб. Поэтому уравнение (6) точнее следует записать:
где: ξ э — нормативная эквивалентная шероховатость (Таблица 1).
Таблица 1 [1, 2]
| Вид трубопровода | ξ э, мм |
| Стальные новые оцинкованные | 0,1 — 0,2 |
| Стальные старые, чугунные старые, керамические | 0,8 — 1,0 |
| Чугунные новые | 0,3 |
| Бетонированные каналы | 0,8 — 9,0 |
| Чистые трубы из стекла | 0,0015 — 0,01 |
| Резиновый шланг | 0,01 — 0,03 |
Данные таблицы 1 получены для традиционных на тот период материалов трубопроводов.
В период 1950-1975 годов западные гидродинамики аналогичным способом определили ξ э труб из полиэтилена и ПВХ разных диаметров, в том числе и после длительной эксплуатации.
Получены значения эквивалентной шероховатости в пределах от 0,0015 до 0,0105 мм для труб диаметром от 50 до 300 мм [3]. В США для собранного на клеевых соединениях трубопровода из ПВХ этот показатель принимается 0,005 мм [3].
В Швеции, на основе фактических потерь давления в пятикилометровом трубопроводе из сваренных встык полиэтиленовых труб диаметром 1200 мм, определили, что ξ э = 0,05 мм [3].
В российских строительных нормах в случаях, относящихся к полимерным (пластиковым) трубам, их шероховатость либо совсем не упоминается [5 — 8], либо принимается: для водоснабжения и канализации — «не менее 0,01 мм» [9], для газоснабжения ξ э = 0,007 мм [10].
Натурные измерения потерь давления на действующем газопроводе из полиэтиленовых труб наружным диаметром 225 мм длиной более 48 км показали, что ξ э< 0,005 мм [11].
Вот, пожалуй, и все, чем положения классической гидродинамики могут помочь при анализе нормативной документации, посвященной гидравлическому расчету трубопроводов. Напомним, что
Re = w D/ν (7)
где: ν — кинематическая вязкость жидкости, м2/сек.
Первый вопрос, который следует решить раз и навсегда — являются ли полимерные (пластиковые) трубы, имеющие, как показано выше, уровень шероховатости, от ≈ 0,005 мм для труб малых диаметров, до ≈ 0,05 мм для труб большого диаметра , гидравлически гладкими.
В Таблице 2 для труб различных диаметров по уравнениям (5) и (7) определены значения расходных скоростей движения воды при температуре 20°С (ν = 1,02*10-6 м2/сек), выше которых труба не может считаться гидравлически гладкой.
Для полимерных (пластиковых) труб шероховатость плавно повышали с увеличением диаметра, как это оговорено выше; для новых и старых стальных труб — принимали минимальные значения из Таблицы 1.
Важно
Отметим, что критические скорости в старых стальных трубопроводах в 10 раз ниже, чем в новых, и их шероховатость не может не учитываться при расчете гидравлических потерь напора.
Таблица 2
Для трубопроводов внутри зданий предельными значениями скорости воды в трубопроводах являются: для отопительных систем — 1,5 м/сек [7];
для водопровода — 3 м/сек [8].
Для наружных сетей мы таких ограничений в нормативной документации [4 — 9] не нашли, но если оставаться пределах, определенных таблицей 2, можно сделать однозначный вывод — полимерные (пластиковые) трубы являются, безусловно, гладкими.
Оставляя предельное значение скорости, w = 3 м/сек, определим, что при течении воды в трубах диаметром 20-1000 мм число Рейнольдса лежит в диапазоне 50000-2500000, то есть для расчета коэффициента трения течения воды в полимерных (пластиковых) трубах вполне корректно использовать уравнения (3) и (4). Уравнение (4) вообще охватывает весь диапазон режимов течения.
В нормативной документации, посвященной проектированию систем водоснабжения [4 — 9], уравнение для определения удельных потерь напора (Па/м либо м/м) дается в развернутом относительно диаметра трубы и скорости движения воды виде:
где: К — набор всевозможных коэффициентов, n и m — показатели степеней при диаметре D, м и скорости w, м/сек.
Уравнение Блязиуса (3), наиболее удобное для подобного преобразования, для воды при 20°С при 3000 < Re < 100000 принимает вид:
но оно действует при Re < 100000. Для расчетов при Re > 100000 следует пользоваться модификацией уравнения (4).
В ISO TR 10501 [4] для пластмассовых труб при 4000 < Re < 150000 предлагается:
Для диапазона чисел Рейнольдса 150000< Re < 1000000 проводится незначительная модификация (см. рис. 1) уравнения:
Источник: https://polyplastic.ua/news/news-111.html
Коэффициент гидравлического трения и местного сопротивления
Во Всесоюзном теплотехническом институте Г. А. Муриным проведено исследование потери давления от трения в стальных трубах. Были испытаны обычные стальные трубы промышленного назначения, т. е. трубы с действительной реальной шероховатостью: новые и бывшие в употреблении различного сортамента с внутренним диаметром от 40 до 143 мм.
Трубы имели шероховатость в виде зернистой и оспенной коррозии, налета, окалины, отдулин, продольных борозд, расположенных параллельно оси трубы и по винтовой линии, продольных швов, поперечных круговых борозд, волн. Результаты испытания показали, что в обычных стальных трубах в переходной области (Re=104… 105) сопротивление трения с увеличением числа Рейнольдса постепенно уменьшается.
Г. А. Муриным дано следующее выражение коэффициента трения для гидравлически гладких труб (ламинарный пограничный слой закрывает абсолютную шероховатостьвнутренних стенок трубы):
Эта формула объединяет формулы Блазиуса и Никурадзе для гидравлически гладких труб.
Испытаниями ВТИ установлено, что в переходной области от гладких труб к шероховатым коэффициент гидравлического трения λявляется сложной функцией числа Re и относительной шероховатости k/d:
Совет
На рис. V.1 показаны полученная зависимость λ от числа Re и отношения диаметра трубы d к абсолютной шероховатости k.
Те же испытания подтверждают правильность формулы Никурадзе для шероховатых труб (пограничный ламинарный слой не закрывает абсолютную шероховатость внутренних стенок):
Для определения относительной шероховатости k/d замерялась фактическая потеря давления на трение по длине трубы при определенной скорости воды в ней.
Подставляя в формулу (V.18) значение X, найденное из опыта, определяли значение d/k, а так как диаметр трубы известен, то вычисляли величину абсолютной шероховатости трубы k.
Для теплопроводов центральных систем отопления, согласно опытным данным, полученным ВТИ, абсолютную шероховатость следует принимать k=0,2 мм.
На нижней плавной кривой (см. рис. V.1) показана зависимость λ от Re для гладких труб. Видно, что с увеличением относительной шероховатости в трубах переходная область наступает при меньшем числе Re.
На этом же рисунке пунктирной линией показаны другие переходные числа Re2np> за пределами которых трубы становятся шероховатыми.
М. И. Кисейным и В. М. Зусманобичем на основе данных испытании приводятся формулы расчета для переходной области турбулентного течения от гладких труб к шероховатым.
При обработке опытных данных трубы диаметром от 15 до 200 мм отнесены к первой группе и от 200 до 1000 мм 7-ко второй группе.
Обратите внимание
Для первой груцпы труб даются следующие расчетные формулы: в переходной области от гидравлически гладких труб к шероховатым
первое переходное число Re от области гладких труб к переходной области
авторы указывают, что формулы (V.17) и (V.18) действительны только для чисел Re≥4000;
второе переходное число Re от переходной области к шероховатым трубам (но только для труб с абсолютной шероховатостью k=0,2 мм)
Для чисел Re≥Re2np труба считается шероховатой и коэффициент сопротивления трению X следует определять по формуле (V.18).
Для второй группы труб даются следующие формулы:
Данные расчета по этим формулам имеют расхождение с опытными в пределах ±3%. Эмпирические формулы М. И. Киссина и В. М. Зусмановича позволяют с достаточно большой точностью определить потерю давления оттрения.
Проведенный ими анализ результатов испытаний ВТИ показал, что течение воды в трубах систем центрального отопления в основном происходит в переходной области от гладки труб к шероховатым.По приведенным формулам составлены таблицы для гидравлического расчета теплопроводов.
Потеря давления в местных сопротивлениях зависит в основном от геометрической формы препятствий на пути потока жидкости. На величину потери в местных сопротивлениях оказывает влияние также характер распределения скорости в сечении потока при входе его в рассматриваемый элемент теплопровода.
Распределение скорости, в свою очередь, зависит от формы других препятствий на пути потока и их расстояния от рассматриваемого элемента сети.
Вследствие этого суммарные потери давления от нескольких близко расположенных местных сопротивлений (например, тройника и крана, крана и нагревательного прибора и т. п.
), как правило, не равны арифметической сумме этих сопротивлений, определенных порознь.
Важно
Поэтому сопротивления часто повторяющихся узлов систем отопления, состоящих из нескольких близко расположенных фасонных частей, определяют обычно экспериментальным путем. Значения коэффициентов местных сопротивлений отдельных элементов сети приведены в справочной литературе.
В ряде источников рекомендуется принимать коэффициент местного сопротивления для тройника на проходе ζ=1; для тройника на ответвлении £=1,5; для крестовины на проходе ζ=2.
Как показывают теоретические расчеты, приведенные значения коэффициентов местных сопротивлений несколько завышены, однако для облегчения расчетов теплопроводов систем отопления часто пользуются этими данными. При внезапном сжатии потока и увеличении скорости в сечении f3 (рис. V.2) происходит потеря давления.
Значение ζСж относится к большей скорости, т. е. к скорости в сечении f3; величина его зависит от отношения площади после сужения потока f3 к площади до сжатия потока f3.
2.3. Расчет по варианту
Вариант-13
Расчет параметров линейной гидравлической цепи из последовательного соединения элементов RГ1, RГ2, …. RГ; проведём согласно гидравлической схеме на рисунке 1.1
Рисунок 1.1 –Схема для расчета параметров линейной гидравлической цепи
1. Расчет скоростей потоков в элементах гидравлической цепи:
, где=кг/. По условию, в рабочем режиме
Q=250/ч == 69,4*/c, т.е. Q0,0694/c.
G=*Q=/ч =69,4 кг/с, G69,4 кг/с.
Согласно условию, внутренние диаметры сечений (i=1,…,5): d1=d2=200мм=0,2м, т.е. d1=d2=D1
d3=d4=d5=180мм=0,18м, т.е d3=d4=d5=D2
Скорости потока в сечениях (i=1,2):
v1=v2===м/с, т.е. v1=v22,21 м/с
В сечениях (i=3,4,5): v3=v4=v5===2,72863097 м/с, т.е. v3=v4=v52,73 м/с.
Итого: скорость потока в сечениях линейных элементов:
1) v1=v22,21 м/с
2) v3=v4=v52,73 м/с.
2. Расчет давлений на участках гидравлической цепи
2.1. Гидравлические сопротивления:
=>, Тогда согласно рисунка 1.1:
Участок (1,2) элемент 1:, при d1=D1=0,2м; l1=2м
Участок (2,3) элемент 2:
, при d2=D1=0,2м; l2=2м; v2=2,21 м/с;
439,8
Участок (3,4) элемент 3:
, при d3=D2=0,18м; l3=2,5м; v3=2,73 м/с;
Участок (4,5) элемент 4:
, при d4=D2=0,18м; l4=2,5м; v4=2,73 м/с;
Участок (5,6) элемент 5:
, при d5=D2=0,18м; l5=2,5м; v5=2,73 м/с;
Итого:
1: i(1,2):
2: i(2.3):439,8
3: i(3,4):
4: i(4,5):
5: i(5,6):
2.2. Давления на элементах цепи:
Pi=GRГi , для участков гидравлической цепи:
P1=P2= 69,4кг/с * R1,2=69,4*439,8=30,5 Па
P3=P4=P5= 69,4кг/с * R3,4,5= 69,4*33,62= 2,33 Па
Заключение
Расходуемое в системе давление, Па, должно быть меньше расчетного циркуляционного давления, определяемого по формуле IV.50, на 10%, т. е.
где l — длина участков наиболее невыгодного циркуляционного кольца теплопроводов, м;
Совет
R—удельная линейная потеря давления от трения (пo длине 1 м трубы) на соответствующих участках, Па/м;
Z—потеря давления на местные сопротивления на тех же участках, Па.
Искусственное давление Δpн, создаваемое насосом, принимается; а) для зависимых систем отопления, присоединяемых к тепловым сетям через элеваторы или смесительные насосы, исходя из располагаемой разности давления на вводе и коэффициента смешения; б) для независимых систем отопления, присоединяемых к тепловым сетям через теплообменники или к котельным без перспективы присоединения к тепловым сетям, исходя из предельно допустимой скорости движения воды в теплопроводах (по табл. IV.1), возможности увязки потери давления в циркуляционных кольцах систем и технико-экономических расчетов.
Ориентируясь на величину средней удельной линейной потери давления RCp, сначала определяют предварительные, а затем (с учетом потери на местные сопротивления) окончательные диаметры теплопроводов.
Расчет теплопроводов начинают с основного наиболее неблагоприятного циркуляционного кольца, которым следует считать:
а) в насосной системе с тупиковым движением воды в магистралях — кольцо через наиболее нагруженный и отдаленный от теплового пункта стояк;
б) в насосной системе с попутным движением воды — кольцо через средний наиболее нагруженный стояк;
’в) в гравитационной системе — кольцо, у которого в зависимости от располагаемого циркуляционного давления, значение RcР будет наименьшим..
Средняя ориентировочная величина линейной потери давления в теплопроводах расчетного циркуляционного кольца определяется по формуле ,
где k — коэффициент, учитывающий долю потери давления на местные сопротивления от общей величины расчетного циркуляционного давления; для систем отопления с естественной циркуляцией &=0,5, для систем отопления с искусственной циркуляцией 0,35;
Σl — общая длина последовательно соединенных участков расчетного кольца, м.
Обратите внимание
Зная Rcp и расход воды Gy4, находят соответствующий им диаметр участка по таблицам для расчета теплопроводов.
При расчете по характеристикам сопротивления определяют удельную характеристику сопротивления, Па/(кг/ч)2;
и по приложению 1 находят соответствующий ей диаметр участка.
Увязка потерь давления в циркуляционных кольцах должна производиться с учетом только тех участков, которые не являются общими для сравниваемых колец.
Расхождение (невязка) в расчетных потерях давления на параллельно соединенных участках отдельных колец системы допускается при тупиковом движении воды до 15%, при попутном движении воды в магистралях ±5%.
Расчет участков сети. Потери давления на участках сети могут быть определены с использованием табличных значений удельных линейных потерь давления R, Па/м, или характеристик сопротивления S, Па(кг/ч)2.
Первый способ дает более точные значения потерь давления на трение и используется, как правило, при расчете систем с естественной циркуляцией, где скорость движения воды относительно небольшая и коэффициент гидравлического трения не пропорционален квадрату скорости.
При расчете по характеристикам сопротивления используют осредненные значения коэффициентов гидравлического трения из области значительной скорости, где без заметной погрешности применима квадратичная зависимость, в связи с чем по этому способу рассчитываются насосные однотрубные системы отопления.
Список использованной литературы
1. Зайцева Н.К., Цубанов А.Г., Синица С.И. Тепловые сети сельскохозяйственных предприятий и населенных пунктов. Методические указания. — Мн.: БГАТУ, 2003.
Важно
2. Справочник по теплоснабжению сельского хозяйства. Л.С. Герасимович, А.Г. Цубанов, и др. — Мн.: Ураджай, 1993.
3. Зайцева Н.К., Андрейчик А.Е. Источники и системы теплоснабжения. Методические указания к практическим работам. — Мн.: БГАТУ 2005.
4. Зайцева Н.К., Цубанов А.Г., Синица С.И. Тепловые сети сельскохозяйственных предприятий и населенных пунктов. Методические указания — Мн.: БГАТУ 1996.
5. Системы теплоснабжения жилых микрорайонов и промышленных предприятий: методические указания к курсовой работе по курсу «Источники и системы теплоснабжения предприятий» /сост. З.Г. Марьина. – Архангельск: Издательство АГТУ, 2006. – 22 с.
6. Соколов Е.Я. Теплофикация и тепловые сети. – М.: Энергоиздат, 1988. – 376 с.
7. Наладка и эксплуатация водяных тепловых сетей: Справочник / В.М. Манюк, Я.И. Каплинский и др. М.: Стройиздат, 1988. – 432 с.
8. Справочник по теплоснабжению и вентиляции, книга 1./Р.В. Щекин С.М. Кореневский и др. – Киев: Будивельник, 1976. – 416 с.
Источник: https://megaobuchalka.ru/9/37393.html
Расчет гидравлического сопротивления трубопроводов
Потерянный напор складывается из сопротивления на прямом участке трубы (или сопротивления трения) hтр и местных сопротивлений hм.с., то есть:
hпот.=hтр.+hм.с.
Сопротивление трения или сопротивление на прямом участке трубы, обусловленное вязкостными свойствами жидкости и шероховатостью трубы, можно рассчитать из уравнения Дарси-Вейсбаха:
м ,
Па ,
| где l, d — | соответственно длина и диаметр трубы, м; |
| l — | безразмерный коэффициент трения, зависящий от режима течения, то есть величины критерия Re, и шероховатости трубы. |
В случае гидравлически гладких труб коэффициент трения зависит только от режима течения (то есть величины критерия Re) и может быть рассчитан по формулам.
Для гидравлически гладкой трубы толщина ламинарного слоя вблизи стенок трубы D > е (е – высота выступов шероховатости).
В этом случае ламинарный пограничный слой, будучи практически недвижим (скорость среды равна нулю), закрывает выступы шероховатости и «защищает» поверхность трубы от контакта с турбулентным ядром потока.
Для гидравлически гладких труб коэффициент трения подсчитывается по следующим формулам
В случае шероховатых труб (обычно это оговорено условиями задачи) коэффициент трения находится графически.
В этом случае нужно рассчитать критерий Рейнольдса, найти соотношение, где е – высота выступов шероховатости,
dэкв – эквивалентный диаметр труб.
Местные сопротивления обусловлены изменением величины скорости или ее направления. Такие сопротивления создаются разнообразными устройствами, устанавливаемыми на трубопроводе: кранами, вентилями, задвижками, заслонками, шиберами, измерительными устройствами. Повороты, вход и выход из трубы, сужения, расширения также создают местное сопротивление.
Формулы для расчета местных сопротивлений:
, Па,
, м ст. жидк.
где x — коэффициент местных сопротивлений
Сопротивление сети, то есть полный напор, который нужно преодолеть насосу для поднятия жидкости на какую-либо высоту, складывается из следующих компонентов:
Dрс =Dрск +Dртр +Dрмс +Dрпод +Dрдоп ,
Совет
где Dрск ,Dртр ,Dрмс –затраты энергии на создание скоростного напора, и преодоление сопротивления трения, местных сопротивлений соответственно.
Dрпод = r ·g·hпод – затраты энергии на подъем жидкости на высоту hпод, Па;
Dрдоп = (р2 – р1) – затраты энергии на преодоление разности давлений в приемном и расходном резервуарах.
Введем понятиесеть – связанные между собой с помощью трубопроводов с использованием задвижек, отводов и т.д., аппараты технологической схемы.
В этом случае сопротивление сети будет включать в себя
· скоростной напор,
· потери на преодоление сопротивления трения,
· потери на преодоление суммы всех местных сопротивлений,
· потери на преодоление подъема на высоту,
· разность давлений между нагнетающей и всасывающей линией насоса.
Сопротивление сети в развернутом виде:
Па, м ст.жидк.
Дата добавления: 2017-09-01; просмотров: 2986;
Источник: https://poznayka.org/s95997t1.html
Содержание
- Классификация морских течений
- Основы теории дрейфовых течений
- Основы теории геострофических течений
- Расчёт геострофических течений по альтиметрическим данным спутников
- Расчёт геострофических течений по океанографическим данным
- Основные черты поверхностной циркуляции вод Мирового океана
Классификация морских течений
Морскими течениями называются поступательные перемещения водных масс в морях и океанах, характеризующиеся направлением, скоростью и устойчивостью. Направление показывает, куда движутся водные массы, скорость задаётся в м/с или узлах. Устойчивость — это вероятность в процентах преобладающего направления. Эта характеристика была введена после того, как стало возможным проводить длительные (до года) наблюдения за течением в одной и той же точке. Оказалось, что направление течения меняется. Однако в некоторых случаях одно из направлений, как правило, наблюдалось чаще других. Оно и указывалось как направление течения в данной точке с определённой вероятностью (устойчивость).
Морские течения могут быть классифицированы по следующим признакам:
1. По силам, их вызывающим:
- ветровые или дрейфовые течения, возникающие в результате трения при движении ветра над поверхностью воды;
- градиентные течения, обусловленные горизонтальным градиентом давления, который возникает при наклоне поверхности моря относительно некоторой изопотенциальной (уровенной) поверхности. Градиенты давления могут создаваться изменением атмосферного давления и неравномерным распределением плотности морской воды в горизонтальном направлении;
- приливные течения, возникающие в результате воздействия на водные массы приливообразующих сил Луны и Солнца.
2. По устойчивости:
- постоянные или квазипостоянные — мало изменяются по скорости в течение сезона или года, наблюдаются в одних и тех же районах океана и характеризуются генеральным направлением (например, Гольфстрим);
- периодические — течения, направление и скорость которых повторяются через примерно равные промежутки времени и в определённой последовательности (приливные течения);
- непериодические (временные) — течения, вызванные непериодическим действием внешних сил (например, кратковременным действием ветра).
3. По глубине расположения:
- поверхностные — в слое воды от поверхности до глубины 10–15 м;
- подповерхностные — сразу же под поверхностным течением, но в направлении противоположном ему;
- придонные — в слое воды, прилегающем ко дну;
- глубинные — течения в толще воды между поверхностным и придонным.
4. По физико-химическим свойствам:
- тёплые — температура воды в течении выше, чем температура окружающих вод;
- холодные — температура воды в течении ниже температуры окружающих вод.
Течения с температурой окружающих вод иногда называют нейтральными.
Основы теории дрейфовых течений
В кинематике жидкостей применяются два различных метода описания движения: метод Лагранжа и метод Эйлера. В первом из них движение жидкости задаётся путём указания зависимости координат всех её частиц от времени.
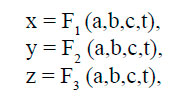
где a, b, c — координаты частицы в момент времени t = 0. Величины a, b, c и t называются переменными Лагранжа. Если из уравнений исключить время, то можно получить уравнение траектории частицы. Проекции на оси координат векторов скорости частицы будут равны:
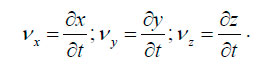
Метод Эйлера является основным в гидроаэродинамике. Движение жидкости определяется путём задания поля скоростей жидкости в пространстве:
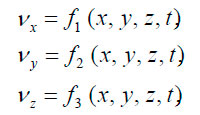
где vx, vy и vz — проекции скорости жидкости по осям в момент времени t в точке пространства.
Запишем уравнение движения в декартовых координатах для составляющих по осям Ox и Oy. В таком виде оно называется уравнением Навье — Стокса:

В настоящее время система уравнений (4.1) не решается без кардинальных упрощений (допущений). Поэтому теоретическое решение расчёта скорости ветровых течений было выполнено Экманом при следующих допущениях:
vt — составляющая скорости течения в направлении ветра.
С учётом принятых допущений уравнения (4.1) принимают вид:
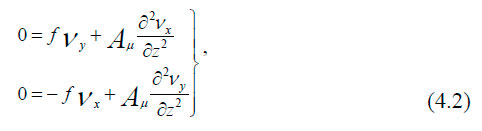
где f = 2ωsinφ — параметр Кориолиса; ω — угловая скорость вращения Земли; φ — географическая широта.
Таким образом, сила трения и сила Кориолиса на поверхности вращающейся Земли находятся в равновесии. Уравнения (4.2) имеют решения:
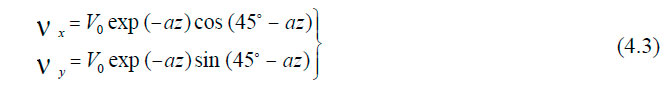
при условии, что ветер дует в северном направлении (T = Tyz).
Константы, входящие в уравнение, будут равны:

где Vо — абсолютная величина скорости течения на морской поверхности; ρw – плотность воды.
Анализ решения уравнений даёт нам следующие характеристики ветровых течений:
1. На поверхности z = 0.
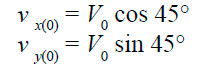
Таким образом, течение на поверхности Vо направлено на северо-восток. В общем случае в Северном полушарии поверхностное течение направлено под углом 45° вправо от направления дующего ветра, а в Южном — влево.
2. С удалением от поверхности z увеличивается, следовательно, Vо будет уменьшаться по закону
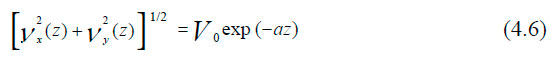
и поворачивать вправо в Северном полушарии.
3. Так как скорость течения уменьшается по экспоненте, то глубина, на которую распространяется течение, может быть выбрана произвольно. Экман предложил считать нижней границей такого слоя глубину, на которой вектор скорости течения направлен противоположно вектору поверхностной скорости:

Величина D известна в литературе как «слой Экмана».
Для вычисления силы трения ветра о поверхность воды Экман использует формулу:

где ρa — плотность воздуха, принимаемая равной
1,25 кг/м3; С — коэффициент трения, который был принят Экманом равным С = 1,6 × 10-3; W10 — скорость ветра, измеренная на высоте 10 м.
Для нахождения абсолютной скорости на поверхности воды Vо Экман воспользовался эмпирической формулой, которая, по-видимому, была ему известна из литературы:
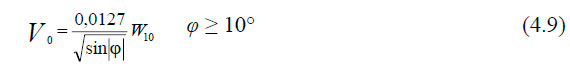
Затем, подставляя (4.9) и (4.8) в (4.4), находим Aμ и из уравнения (4.7) получаем:

В качестве примера в табл. 4.1 приведены вычисленные по формуле (4.10) толщины слоя Экмана для широт 15 и 45 градусов.
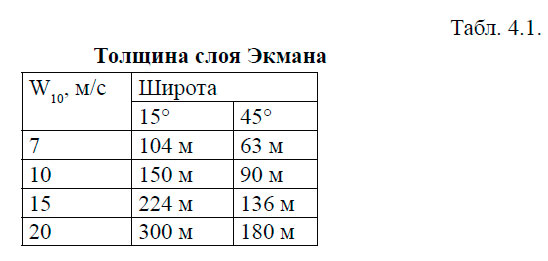
Работа Экмана была опубликована в 1905 г. И вот уже более 100 лет проблема изучения ветровой циркуляции продолжается. Для того, чтобы применить теоретические выводы Экмана к расчёту ветровых течений, необходимо знать два параметра: коэффициент турбулентной вязкости Aμ и силу трения ветра о поверхность воды Т (тангенциальное напряжение). Несмотря на большие успехи, достигнутые в изучении турбулентности и расчёта тангенциального напряжения, практически во всех учебниках, учебных пособиях и нормативных документах для расчёта ветровых течений рекомендуется формула (4.9). Авторство этой формулы не установлено. В некоторых работах просто указывается, что она получена по наблюдениям за сносом судов.
Специальные эксперименты для проверки теории Экмана были проведены в конце XX в. Эти эксперименты показали, что теория Экмана достаточно точно описывает течения на временных интервалах порядка нескольких суток. В частности, предположение об установившемся течении справедливо, когда продолжительность воздействия ветра превышает маятниковые сутки.
На основании экспериментов Ralph и Niiler получили следующие формулы для вычисления толщины слоя Экмана и абсолютной скорости поверхностного течения Vо:

Скорость ветра задаётся в м/с.
Таким образом, полученная толщина слоя DЕ практически совпадает со значением, вычисленным Экманом (4.10), а скорость поверхностного течения почти в два раза меньше (4.9).
Угол между направлением ветра и поверхностным течением зависит от широты; в средних широтах он составляет 45° (рис. 4.1).
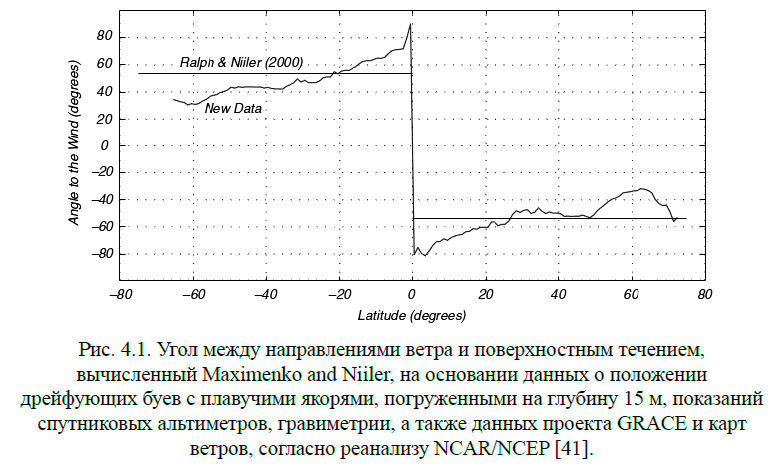
Основы теории геострофических течений
В толще воды океана, не испытывающей влияния приповерхностного слоя Экмана, в результате возникновения горизонтального градиента давления при наличии уклона водной поверхности развиваются геострофические (градиентные) течения. При горизонтальных масштабах, превышающих несколько десятков километров, и временных периодах свыше нескольких суток эта толща воды находится в состоянии геострофического равновесия. Это означает, что горизонтальный градиент давления почти полностью компенсируется силой Кориолиса, источником которой является развившееся течение. Для расчёта скорости геострофических течений требуется упростить уравнения (4.1).
Рассматривается установившееся течение в однородном по плотности океане, вязкие члены в уравнении движения пренебрежительно малы (силы внутреннего трения). Основные силы, действующие в вертикальном направлении — вертикальный градиент давления и сила тяжести, сбалансированы. В этом случае уравнения движения принимают вид:
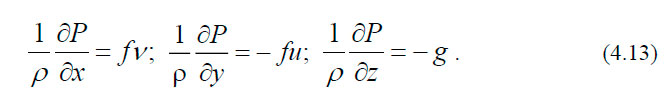
Эти уравнения известны как геострофические уравнения. Они применимы к потокам с горизонтальным масштабом, превышающим 50 км.
Уравнения (4.13) можно переписать в виде:
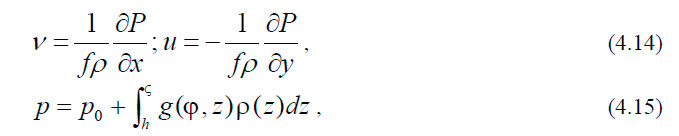
где po — атмосферное давление при z = 0; ς — возвышение морской поверхности над поверхностью z = 0; h — глубина.
При записи уравнений (4.13–4.15) принимается левая система координат: ось Oy направлена в сторону наибольшего уклона, а ось Oz — к центру Земли.
Подразумевается, что g зависит от широты и глубины, а ρ — от глубины.
Расчёт геострофических течений по альтиметрическим данным спутников
Система спутниковой альтиметрии состоит из радара, который измеряет высоту спутника над земной (морской) поверхностью, и системы слежения для определения высоты спутника в геоцентрической системе координат. Спутниковый альтиметр измеряет высоту спутника над поверхностью моря. Вычитая это значение из высоты орбиты, получаем уровень моря относительно центра Земли. Форма морской поверхности в спокойном состоянии практически совпадает с геоидом. В общем же случае она отклоняется от поверхности геоида под воздействием сил, вызывающих течения.
В слое небольшой толщины (несколько метров от поверхности) можно считать значения g и ρ постоянными. Тогда давление на уровенной поверхности, находящейся, например, на глубине 1 м будет равно:

Подставив (4.16) в уравнения (4.14), получаем выражения для составляющих скорости поверхностного течения uп и vп:
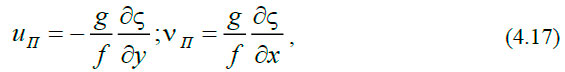
где g — ускорение силы тяжести; f — параметр Кориолиса; ς — возвышение уровня над уровенной поверхностью.
Таким образом, согласно уравнению (4.17) составляющие скорости поверхностного геострофического течения пропорциональны наклону морской поверхности. Если форма геоида нам известна, то величина наклона может быть измерена методами спутниковой альтиметрии (рис. 4.2).
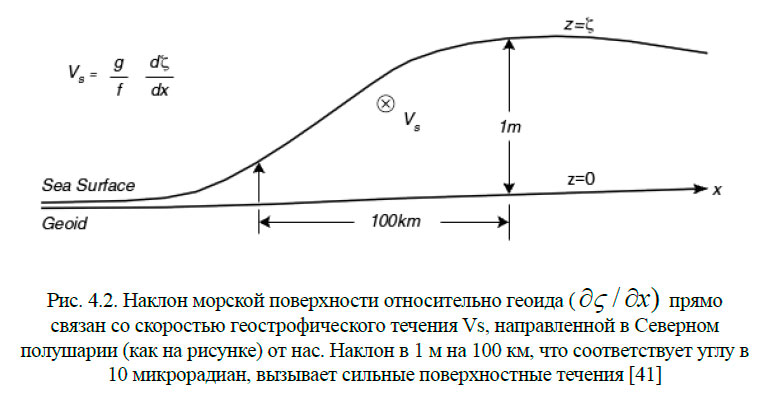
Исследование постоянных поверхностных течений проводится по альтиметрическим данным спутников, осреднённым за длительный период. Погрешность определения формы геоида при расчёте течений может быть существенной при осреднении на площади масштабом больше 100 км2. Форма геоида достаточно хорошо изучена на более мелком масштабе (с пространственным разрешением больше 100 км) в результате специальных проектов по изучению гравитационного поля Земли GRACE и GOCE. Спутники этих проектов были запущены с российского космодрома Плисецк в 2002 и 2009 гг. соответственно. Спутники программы GOCE закончили работу в 2013 году. Одна из целей программы — определить геоид с точностью 1–2 см и достичь пространственного разрешения меньше 100 км. Эти системы проводят гравиметрические измерения с точностью, достаточной для того, чтобы не учитывать погрешность определения формы геоида.
Расчёт геострофических течений по океанографическим данным
Исследование геострофических течений по распределению температуры, солёности, плотности и давлению получил название динамического метода. В результате воздействия внешних сил формируется наклон поверхности моря и горизонтальная неоднородность плотности воды. Это приводит к возникновению горизонтального градиента давления. Возникает течение. Оно развивается и становится установившимся, т. е. сила горизонтального градиента уравновешивается силой Кориолиса. В отечественной литературе геострофические течения, обусловленные горизонтальным градиентом плотности воды, называются плотностными течениями. С помощью динамического метода можно рассчитывать не только поверхностные течения, но и глубинные.
Итак, движение вызывается градиентом горизонтального давления. Если бы мы имели совершенно определённую отсчётную поверхность (в предыдущем случае это геоид), то расчёт течений не представлял бы труда. Рассчитав поле плотности по уравнению состояния морской воды, можно было бы рассчитать давление в каждой точке, а затем течения по уравнениям (4.14, 4.15). В реальных условиях положение такой поверхности неизвестно. Поэтому все расчёты ведутся от так называемой «нулевой поверхности», т. е. предполагается, что на некоторой глубине существует поверхность, на которой горизонтальный градиент давления равен нулю.
Возьмём, например, глубину 1000 м на двух океанографических станциях (рис. 4.3 а). Между точками существует градиент давления Δp = pA − pB вследствие разности плотностей. Предположим, что ρ = const. Для того чтобы градиент сохранился, нужно поднять точку А и градиент давления будет обусловлен разностью высот ΔН, а линия А1В будет представлять собой изобарическую поверхность (рис. 4.3 б).
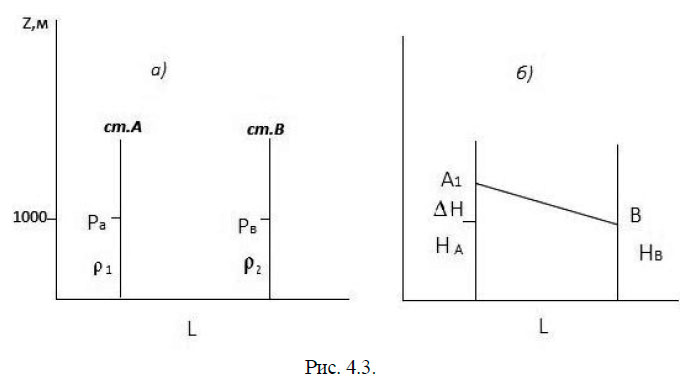
Следовательно:
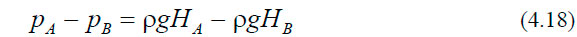
Величину gH = D по предложению Бьеркнеса принято называть динамической высотой. Динамическая высота — это не геометрическая величина, а работа, которую нужно совершить, чтобы переместить единицу массы по линии отвеса на расстояние Н. При измерении глубины в динамических метрах D = 0,1 gH, где Н — глубина в геометрических метрах. Динамическая высота используется как вертикальная координата z.
Таким образом, при вычислении скорости течения мы переходим от разности давления к разности динамических высот:
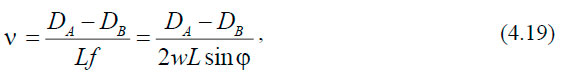
где L — расстояние между океанографическими станциями.
Течение направлено под углом 90° вправо от направления уклона в Северном полушарии и влево — в Южном.
При выводе формулы (4.19) было принято, что на глубине залегания нулевой поверхности течение отсутствует. Если это условие не соблюдается, то формула (4.19) будет содержать погрешность, равную неучтённой скорости течения на этой поверхности. Расчёт динамических глубин производится следующим образом:
изменение давления dp при изменении глубины на dH будет равно:

Далее в расчётах интеграл заменяется суммой, а вместо удельного объёма используется условный удельный объём vt,s,p.
Подавляющее большинство расчётов течений динамическим методом выполнено относительно нулевой поверхности. Выбору этой поверхности посвящена обширная литература. Наиболее часто применяется метод, предложенный Дефантом. На графиках изменения с глубиной разностей динамических глубин изобарических плоскостей он обнаружил слой, в котором эти разности становятся постоянными. Дефант предположил, что этот слой почти неподвижен и принял его за слой, прилегающий к нулевой поверхности.
Границы применимости геострофических уравнений.
Принцип геострофического равновесия может быть применён к течениям протяжённостью в несколько сотен километров и временными периодами более нескольких суток. Равновесие подразумевает отсутствие какого-либо ускорения потока, а это означает, что течения в океанах никогда бы не изменялись. Важными ограничениями, которые присущи геострофическому приближению, являются:
- Геострофические течения не могут изменяться во времени, поскольку установившееся течение не предполагает ускорения потока. При горизонтальных масштабах 50 км и менее ускорения потока неизбежны.
- Геострофические уравнения не применимы в экваториальной полосе ±2°, где сила Кориолиса стремится к нулю (sinφ → 0).
- Геострофическое равновесие не учитывает сил трения.
- Динамический метод расчёта позволяет рассчитать течения только по отношению к нулевой поверхности, т. е. с течениями на другой глубине. Это может быть приемлемо для больших глубин. На небольших глубинах, например, в районе континентального шельфа он не слишком пригоден.
Точность расчётов. Сравнение измеренных и рассчитанных скоростей течений даёт следующие результаты. По данным спутниковой альтиметрии в системе течения Куросио на участке длиной 12,5 км разность между измеренными и рассчитанными течениями составила ±16 см/с для течений со скоростью до 150 см/с, т. е. около 10 %.
Сравнение измеренных скоростей и рассчитанных динамическим методом проводилось в системе течения Гольфстрим. Скорости, измеренные на глубинах до 500 м в центральных областях течения, были на 10–25 см/с больше, чем расчётные. Максимальная скорость в центре течения превышала 150 см/с. Таким образом, погрешность также составила около 10 %.
Основные черты поверхностной циркуляции вод Мирового океана
Осреднённые по времени поверхностные течения в океанах традиционно изображаются в виде «Схемы течений Мирового океана». В основу такой схемы положены главным образом данные океанографических наблюдений. Характерные черты океанической циркуляции рассмотрим на рис. 4.4, заимствованном из работы. Изображённая на схеме циркуляция вод соответствует современным представлениям о поверхностной циркуляции вод Мирового океана, основанным на данных, накопленных в течение более чем столетия наблюдений.
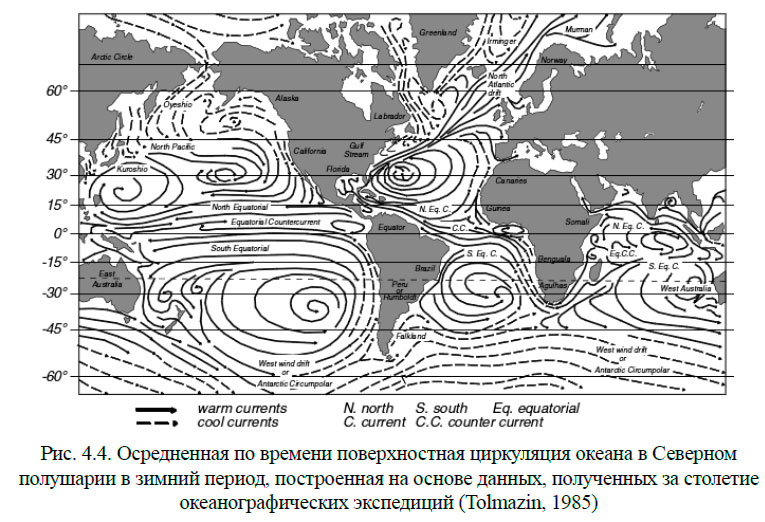
Течения поверхностных вод Атлантического и Тихого океана имеют много общих черт. В обоих океанах течения образуют два огромных антициклонических круговорота, которые разделяются экваториальными противотечениями. В южной части Индийского океана циркуляция в общих чертах сходна с циркуляцией в южных частях этих океанов. В северной части Индийского океана циркуляция обусловлена муссонами, и в периоды летнего и зимнего муссонов картина циркуляции полностью меняется.
Течения, образующие круговороты, значительно отличаются по скоростям на различных участках круговорота. Западные пограничные течения представляют собой узкие, глубокие, с чёткими границами потоки (Гольфстрим, Куросио).
Течения, направленные к экватору на другой стороне океанов — Бенгальское, Калифорнийское, Перуанское, — широкие, слабые потоки с расплывчатыми границами.
Экваториальные течения. Северное и Южное пассатные течения в Атлантическом и Тихом океане являются частью антициклонических круговоротов этих океанов. Между ними располагаются межпассатные противотечения, направленные на восток.
Южное пассатное течение, несущее воды на запад, существует и в южной части Индийского океана. В северной части океана располагается Муссонное течение, которое при северо-восточном муссоне направлено на запад. В этот период наблюдается и Межпассатное противотечение. В период юго-западного муссона направление Муссонного течения меняется на восточное.
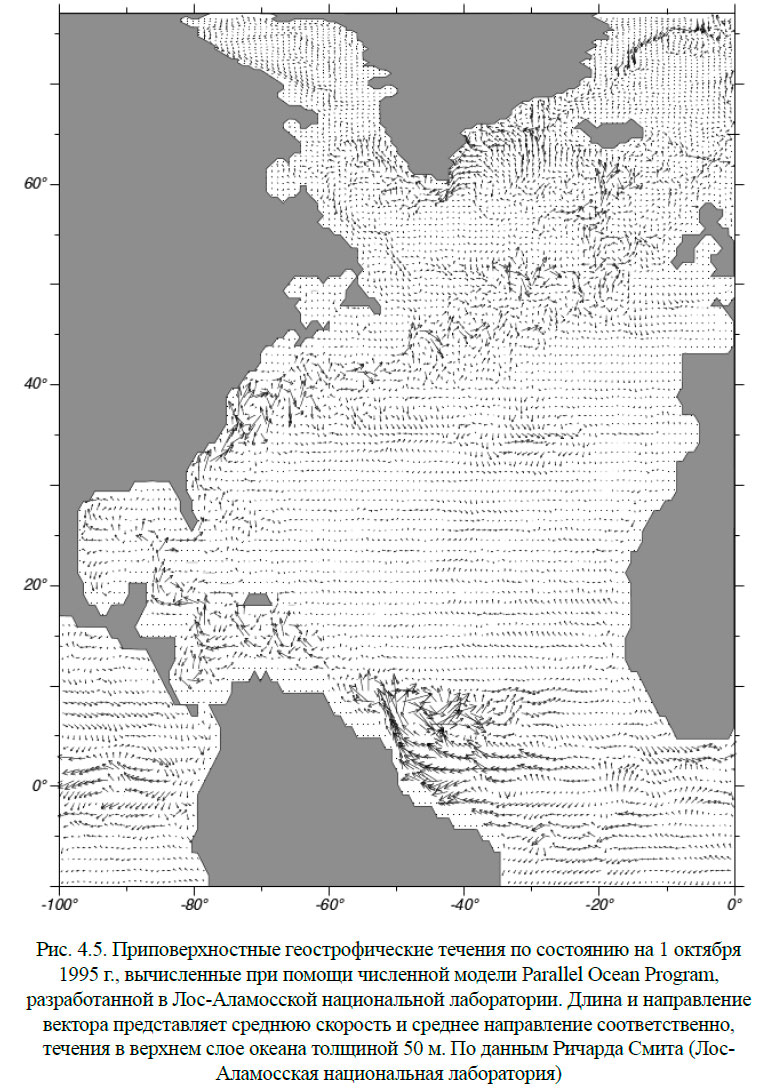
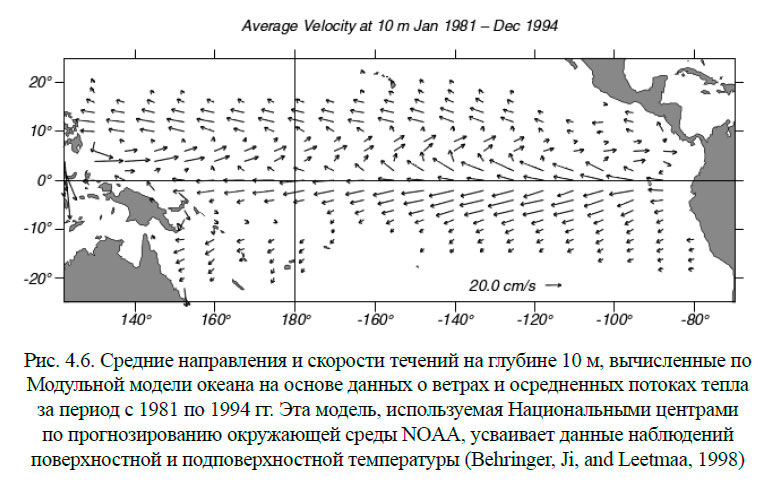
В Южном полушарии отсутствие суши и широкий (300 миль) и глубокий (3000 м) пролив Дрейка между Южной Америкой и Антарктидой создают условия для беспрепятственного водообмена между всеми океанами в системе течения Западных ветров.
На современном этапе исследования глобальной системы океанических течений применяется математическое моделирование. Эти модели имитируют течения в реальном океане, с реальным рельефом дна, учитывают вязкость воды и нелинейные компоненты уравнения движения. Однако модели должны соответствовать возможностям современных компьютеров, а это означает, что в уравнения движения вносятся и будут и дальше вноситься различные упрощения (допущения). Существуют различные типы глобальных и региональных моделей Мирового океана. В заключение приведём два рисунка из работы (рис. 4.5, 4.6.). Читатель может самостоятельно сравнить их с рисунком (4.4).
Литература
Гидрометеорологическое Обеспечение Мореплавания – Глухов В.Г., Гордиенко А.И., Шаронов А.Ю., Шматков В.А. [2014]