Как найти коэффициент силы тяжести

Содержание:

Сила тяжести:

Почему все подброшенные вверх тела падают на Землю ? Почему на санках легко съезжать с горки, а вверх их нужно тянуть?

Подбросьте вверх мяч. Поднявшись на некоторую высоту, он начнёт двигаться вниз и упадёт на Землю. Парашютист, выпрыгнувший из самолёта, падает вниз и после раскрытия парашюта. С появлением дождевой тучи на Землю падает густой дождь. Как бы высоко мы не прыгали вверх, всегда опускаемся на Землю.

Все тела, находящиеся на Земле или вблизи неё, взаимодействуют с ней: Земля притягивает тела, а они притягивают Землю.

Поскольку масса у Земли очень большая, то в результате взаимодействия с нею заметно изменяют свои скорости и положения именно тела, а Земля практически остаётся на месте.

Силу, с которой Земля притягивает к себе любое тело, называют силой тяжести.

От чего зависит сила тяжести

Из опыта с яблоками, выполненного ранее, можем сделать вывод, что на два яблока, подвешенных на пружине, действует сила тяжести больше, чем на одно, так как масса двух яблок больше массы одного. Силу тяжести обозначают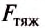

Единицей силы тяжести, как и любой другой, в СИ является один ньютон (1Н). Эта единица названа в честь английского учёного Исаака Ньютона, впервые сформулировавшего основные законы движения тел и законы тяготения. 1 ньютон (1 Н) равен силе тяжести, которая действует на тело массой приблизительно 102 г.

Тогда на тело массой 1кг действует сила тяжести 9,81 Н, т. е.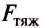

Как, пользуясь единицей силы 1 Н, определить силу тяжести, которая действует на тело любой массы?

Поскольку на тело массой 1 кг действует сила тяжести 9,81 Н, то на тело массой т будет действовать сила тяжести, в т раз большая.

Чтобы определить силу тяжести 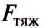, действующую на тело, нужно постоянную для данной местности величину 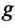= 9,81  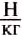умножить на массу тела 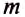, выраженную в килограммах: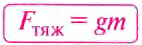 

Но притяжение существует не только между Землёй и телами на ней или вблизи неё. Все тела притягиваются друг к другу. Например, притягиваются между собой Земля и Луна, Солнце и Земля или другие планеты, корабли в море, предметы в комнате. Вследствие притяжения Земли к Луне на Земле возникают приливы и отливы (рис. 69).

Вода в океанах поднимается дважды в сутки на несколько метров.

Благодаря силе тяжести атмосфера удерживается возле Земли, реки текут сверху вниз, Луна удерживается возле Земли, планеты двигаются по орбитам вокруг Солнца.

Явление притяжения всех тел Вселенной друг к другу называют всемирным тяготением.

Исаак Ньютон доказал, что сила притяжения между телами тем больше, чем больше массы этих тел и чем меньше расстояние между телами. Если бы сила тяжести на Земле вдруг исчезла, то все незакреплённые на ее поверхности тела от любого небольшого толчка разлетелись бы во все стороны в космическом пространстве.

Каково направление силы тяжести

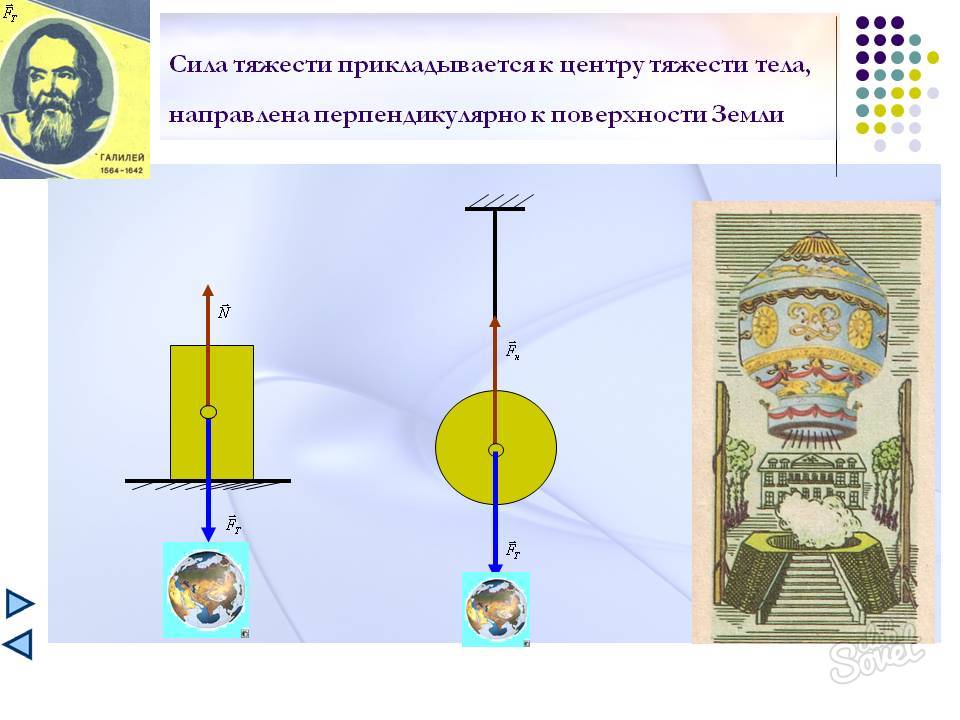
Опыт. Если взять отвес или привязанный к нити какой-либо предмет (рис. 70), то увидим, что нить с грузиком вследствие действия на него силы тяжести всегда направлена к Земли вдоль прямой, которую называют вертикалью.

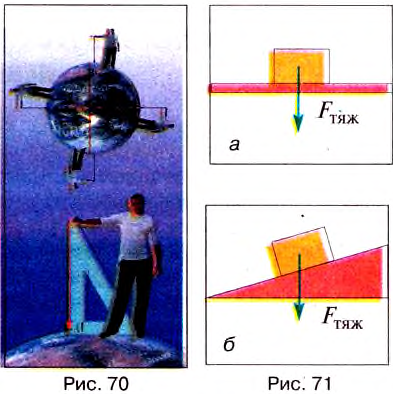
Выполнив этот опыт во всех точках Земли, учёные убедились, что сила тяжести всегда направлена к центру Земли.

Силу тяжести изображают в виде вертикальной стрелки, направленной вниз и приложенной к определённой точке тела (рис. 71 а, б).

Кстати:

Кроме планет с их спутниками вокруг Солнца двигаются малые планеты, которые еще называют астероидами. Наибольшая из них – Церера – имеет статус карликовой планеты и радиусом почти в 20 раз, а по массе в 7500 раз меньше Земли. Сила тяжести на ней настолько мала, что человек, оттолкнувшись от поверхности планеты, мог бы улететь с нее.

Вот как описывает основатель теории космонавтики К,Э. Циолковский в рассказе “Путь к звездам” условия пребывания человека на этом астероиде: “На Земле я могу свободно нести еще одного человека такого же веса, как я. На Весте так же легко могу нести в 30 раз больше. На Земле я могу подпрыгнуть на 50см. На Весте такое же усилие дает прыжок в 30м. Это высота десятиэтажного дома или огромной сосны. Там легко перепрыгивать через рвы и ямы шириной с крупную реку. Можно перепрыгнуть через 15-метровые деревья и дома. И это без разгона”.

Сила тяготения

Все тела возле Земли падают на ее поверхность, если их ничто не удерживает. В чем причина этого явления?

Как тела падают на Землю

Рассмотрим фотографию падения шарика, на которой положение шарика фиксировалось на пленке через равные интервалы времени (рис. 45). Если линейкой отмерить расстояние между изображениями шарика в различные моменты времени, то можно заметить, что эти расстояния постепенно увеличиваются. Это свидетельствует о том, что скорость шарика при падении постепенно увеличивается.

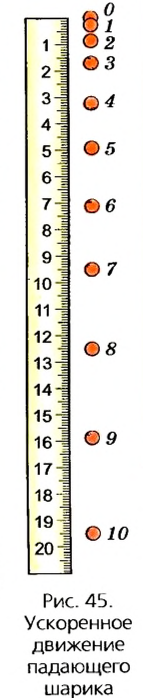
Как увеличивается скорость падающего тела

Если вспомнить определение силы, по которому сила изменяет скорость тела, то можно сделать вывод, что на шарик действует сила, направленная к Земле.

Силу, действующую на каждое тело со стороны Земли, называют силой тяготения.

Измерения показывают, что скорость тела, падающего на поверхность Земли при отсутствии сопротивления воздуха, каждую секунду увеличивается на 9,8 .

Как рассчитать силу тяготения

Если знать массу тела, то можно рассчитать силу тяготения. Способ таких расчетов подсказывают результаты опытов.

Возьмем динамометр и подвесим к нему гирьку массой 102 г, стрелка динамометра остановится на отметке 1 Н. Если подвесить два таких груза, то динамометр покажет силу 2 Н и т. д. С этого опыта можно сделать вывод, что сила тяжести пропорциональна массе тела.

Сила тяготения пропорциональна массе тела:

Коэффициент пропорциональности 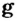равен приблизительно

Для расчетов при решении задач иногда принимают, что

Если знать такую зависимость силы тяготения от массы, то можно заранее рассчитать ее значение.

Например, необходимо определить, что покажет динамометр, если на его крючок повесить гирю массой 500 г.

Дано:

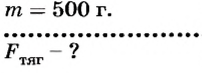
Решение

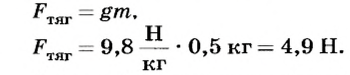
Ответ. Стрелка динамометра покажет 4,9 Н.

Какая природа силы тяготения

Сила тяготения является проявлением общего закона природы, действующего во всей Вселенной закона всемирного тяготения. Открытый и сформулированный в XVII в. английским физиком Ньютоном, он утверждает, что сила гравитационного притяжения во Вселенной пропорциональна массам взаимодействующих тел и зависит от расстояния между ними.

где R — расстояние между телами, m₁ и m₂ — массы взаимодействующих тел, 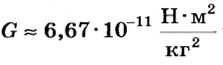 — гравитационная постоянная.

Сила тяготения, как проявление гравитационного взаимодействия Земли, является следствием взаимодействия всех тел с Землей. Поэтому в расчетах силы тяготения пользуются только массой данного тела. Характеристики Земли отображены в обобщенной форме в коэффициенте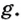

Работа силы тяжести

Каждая сила, действующая на движущееся тело, совершает работу. Проанализируем более подробно работу, совершаемую силой тяжести. При небольших расстояниях от поверхности Земли сила тяжести постоянна и по модулю равна mg. Пусть тело массой m падает с высоты h₁ до высоты h₂ (рис. 132). Модуль перемещения 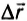 равен при этом h₁ –h₂ . Так как направления перемещения и силы совпадают, то работа силы тяжести положительна и равна:
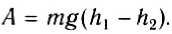    (1)

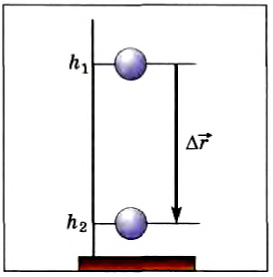
Рис. 132

Высоты h₁ и h₂  можно отсчитывать от любого уровня. Это может быть уровень поверхности Земли, пола класса или поверхности стола и т. д. Высоту выбранного уровня принимают равной пулю. Поэтому этот уровень называют нулевым.

Если тело падает с высоты h до нулевого уровня, то работа силы тяжести:

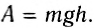   (2)

Теперь выясним, какую работу совершает сила тяжести, если тело движется не по вертикали. Для этого рассмотрим движение тела по наклонной плоскости. Пусть тело массой m совершило перемещение 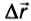, равное по модулю длине наклонной плоскости (рис. 133). Работа силы тяжести в этом случае равна: 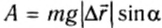, где 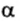— угол между вектором перемещения и вектором силы тяжести. Из рисунка видно, что 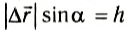. Поэтому

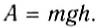
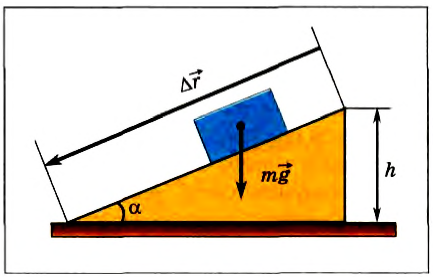
Рис. 133

Мы получили для работы силы тяжести такое же выражение, как и в случае движения тела по вертикали (см. формулу (2)). Отсюда следует, что работа силы тяжести не зависит от того, движется ли тело по вертикали или проходит более длинный путь по наклонной плоскости. Работа силы тяжести определяется только изменением высоты относительно некоторого уровня.

Теперь докажем, что работа силы тяжести определяется формулой (2) при движении по любой траектории. Например, некоторое тело бросили горизонтально с высоты h (рис. 134). Как известно, траекторией такого движения является парабола. Мысленно разобьем траекторию на маленькие участки 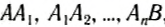, такие, что их можно считать прямыми линиями. Каждый из них можно считать маленькой наклонной плоскостью, а движение по траектории AB рассматривать как движение по множеству наклонных плоскостей. Работа силы тяжести на каждой из них равна произведению силы тяжести на изменение высоты. Например, на участке А₂А₃ работа равна mg(h₂-h₃). Полную же работу силы тяжести на всем пути найдем, сложив работу на каждом участке:

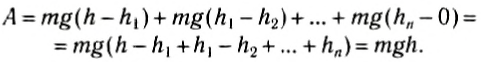
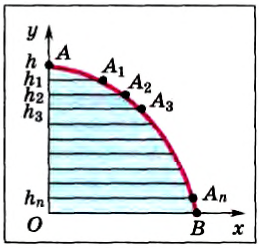
Рис. 134

Таким образом, работа силы тяжести не зависит от формы траектории движения тела и всегда равна произведению модуля силы тяжести на разность высот в начальном и конечном положениях тела, т. е. вычисляется но формуле (1). Отсюда следует, что если тело движется по замкнутой траектории, где начальное и конечное положения тела совпадают, то работа силы тяжести равна нулю. Такие силы, работа которых не зависит от формы траектории, а определяется только начальным и конечным положениями тела в пространстве, называются потенциальными или консервативными. Другое определение потенциальных сил: это такие силы, работа которых по замкнутой траектории равна нулю.

Для потенциальных сил можно ввести понятие потенциальной энергии. Действительно, формула (I) может быть переписана следующим образом:

A = mg(h_l – h₂)= -(mgh₂– mgh₁).    (3)

Правая часть этого равенства представляет собой изменение величины mgh, взятое с противоположным знаком.

Понятие кинетической энергии, изменение которой равно работе сил, действующих на тело. Теперь мы встретились еще с одной величиной, изменение которой (но с противоположным знаком) тоже равно работе силы — в данном случае работе силы тяжести. Величину, равную mgh, называют потенциальной энергией П тела в гравитационном поле. Тогда формулу (3) можно записать в виде:
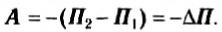    (4)

Говорят, что работа силы тяжести равна убыли потенциальной энергии тела в гравитационном поле Земли.
Если тело падает с высоты h до нулевого уровня, то работа силы тяжести равна его начальной потенциальной энергии:

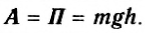
Следовательно, потенциальная энергия тела, поднятого на некоторую высоту, равна работе силы тяжести при падении тела с этой высоты. Например, этим пользуются при забивании свай на строительных площадках (рис. 135). Чтобы поднять тело с нулевого уровня на эту же высоту, должна быть совершена работа другой силой, направленной против силы тяжести.

Рис. 135

Потенциальная энергия зависит от положения тела относительно нулевого уровня и, следовательно, от координат тела. Так как пулевой уровень может быть выбран произвольно, то и потенциальная энергия определяется неоднозначно. Однако физический смысл имеет разность потенциальных энергий тела ΔП, а эта разность не зависит от выбора нулевого уровня.

Сила тяжести является силой, с которой Земля притягивает тело. Тело обладает потенциальной энергией, потому что оно взаимодействует с Землей. Не было бы Земли, не было бы и силы притяжения, а следовательно, и потенциальной энергии тела. Поэтому потенциальная энергия — это энергия взаимодействия, в данном случае тела и Земли.

Главные выводы:

1. Работа силы тяжести не зависит от формы траектории, а определяется начальным и конечным положениями тела.
2. Работа силы тяжести равна нулю, если тело возвращается в исходное положение.
3. Сила тяжести является потенциальной силой.
4. Потенциальная энергия тела, поднятого на некоторую высоту, равна работе силы тяжести при падении тела с этой высоты.
5. Потенциальная энергия — это энергия взаимодействия тел.

Сила тяжести и напряженность гравитационного поля

Как вы знаете, по современным научным представлениям взаимное притяжение между телами осуществляется посредством особого вида материи – гравитационного поля. Каждое тело вокруг себя создает гравитационное поле. Как и другие физические поля, гравитационное поле имеет свою силовую характеристику – напряженность гравитационного поля.

Напряженность гравитационного поля – это векторная физическая величина, равная отношению силы притяжения, действующей на материальную точку (тело) в гравитационном поле, к его массе:

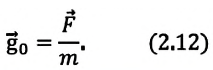
Где 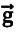 – напряженность гравитационного поля,  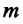– масса материальной точки (тела),  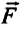– сила притяжения, действующая на материальную точку в гравитационном поле.

От чего зависит модуль напряженности гравитационного поля

Чтобы ответить на этот вопрос, определим модуль напряженности гравитационного поля для произвольной точки на поверхности Земли и на высоте 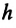от поверхности Земли:

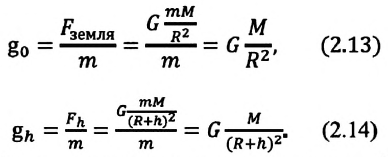
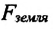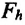Здесь и  — силы притяжения на поверхности Земли и на высоте h соответственно,  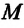— масса Земли,  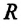— радиус Земли.

• Заказать решение задач по физике

Модуль напряженности гравитационного поля в некоторой точке прямо пропорционален массе источника данного поля и обратно пропорционален

квадрату расстояния до этой точки. Модуль напряженности гравитационного поля не зависит от массы тела, помещенного в это поле. Вектор напряженности гравитационного поля в произвольной точке поля направлен вдоль радиуса к центру источника поля (b). В данной точке гравитационного поля модуль и направление напряженности гравитационного поля совпадают с модулем и направлением ускорения свободного падения.

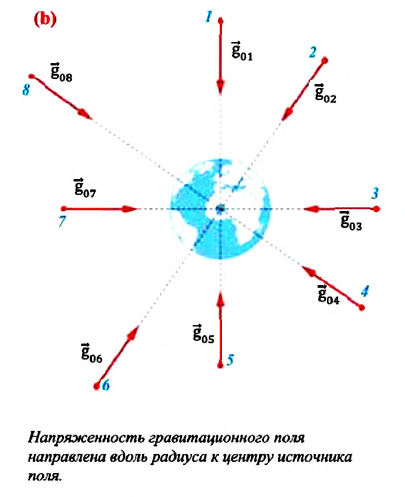
Являются ли напряженность гравитационного поля и ускорение свободного падения одной и той же величиной

На помещенное в гравитационное поле произвольное тело действует сила притяжения со стороны источника поля. В результате тело получает ускорение (ускорение свободного падения), направленное к центру источника поля (например, центру Земли). Это ускорение сообщается телу действующей на него силой тяжести гравитационного поля.

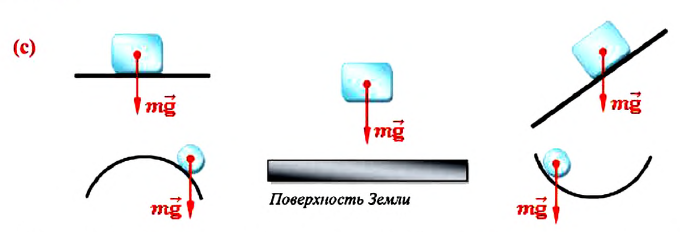
Сила тяжести – это сила, с которой Земля (планета) притягивает тела. Сила тяжести равна произведению массы тела, помещенного в гравитационное поле Земли (планеты), на ускорение свободного падения:

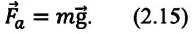
Сила тяжести всегда приложена к центру массы тела и направлена вертикально вниз (перпендикулярно к горизонтальной поверхности) к центру Земли (планеты) (с).

Из вышесказанного ясно, что понятия “напряженность гравитационного поля” и “ускорение свободного падения” имеют разный физический смысл. Так, напряженность гравитационного поля появляется в случае возникновения поля, а ускорение свободного падения возникает в результате действия силы тяжести при помещении в это поле произвольного тела (пробное тело).

Сила тяжести и вес тела

Если выпустить из рук карандаш, он обязательно упадет. Если поставить рюкзак на скамейку, она (хоть и незаметно для глаз) прогнется. Если подвесить к резиновому шнуру какое-нибудь тело, шнур растянется. Все это — следствия притяжения Земли. При этом репортажи с космических станций демонстрируют нам вроде бы «исчезновение» земного притяжения — космонавты и все вещи на борту находятся в состоянии невесомости.

Гравитационное взаимодействие:

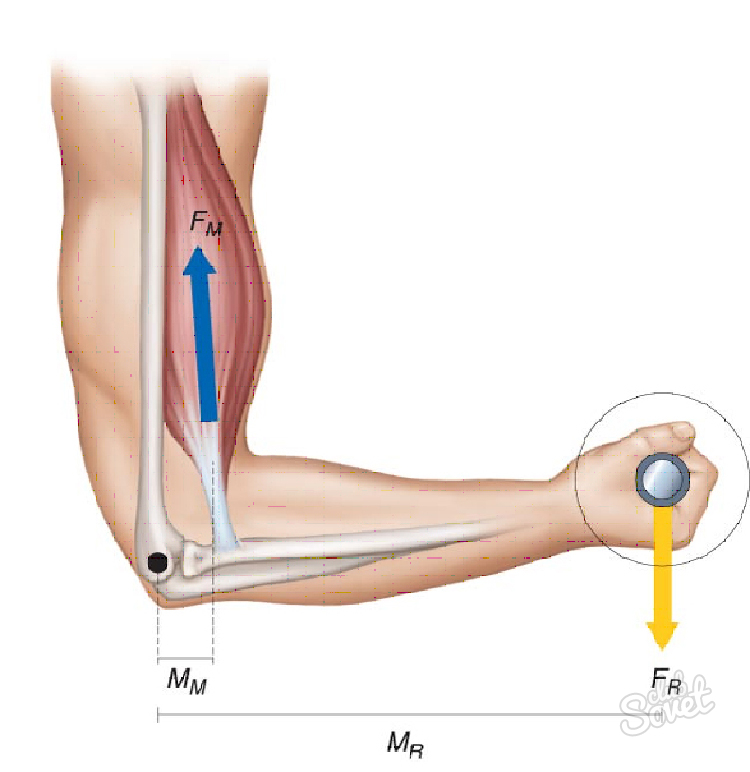
Почему любой предмет, например выпущенный из руки карандаш, капля дождя, лист дерева и т. д., падает вниз? Почему стрела, выпущенная из лука, не летит все время прямо, а в конце концов падает на землю? Почему Луна движется вокруг Земли? Причина всех этих явлений в том, что Земля притягивает к себе все тела (рис. 20.1).

При этом все тела притягивают к себе Землю. Например, притяжение к Луне вызывает на Земле приливы и отливы (рис. 20.2). В результате притяжения к Солнцу наша планета и все другие планеты Солнечной системы движутся вокруг Солнца по определенным орбитам. В 1687 г. Исаак Ньютон сформулировал закон, согласно которому между всеми телами Вселенной существует взаимное притяжение. Такое взаимное притяжение объектов называют гравитационным взаимодействием или всемирным тяготением. Опираясь на опыты и математические расчеты, Ньютон доказал, что интенсивность гравитационного взаимодействия увеличивается с увеличением масс взаимодействующих тел. Именно поэтому легко убедиться в том, что всех нас притягивает Земля, и при этом мы совсем не ощущаем притяжение соседа по парте.

В физике силу гравитационного притяжения Земли, действующую на тела вблизи ее поверхности*, называют силой тяжести.

Сила тяжести 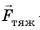— это сила, с которой Земля притягивает к себе тела, находящиеся на ее поверхности или вблизи нее.

Сила тяжести приложена к телу, которое притягивается Землей, и направлена вертикально вниз, к центру Земли (рис. 20.3).

Многочисленными опытами доказано, что сила тяжести, действующая на тело, прямо пропорциональна массе этого тела: 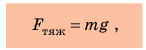где 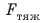— значение силы тяжести; m — масса тела; g — коэффициент пропорциональности, который называют ускорением свободного падения.

Будем считать, что, когда говорят «вблизи поверхности Земли», имеют в виду расстояние, не превышающее нескольких десятков километров.

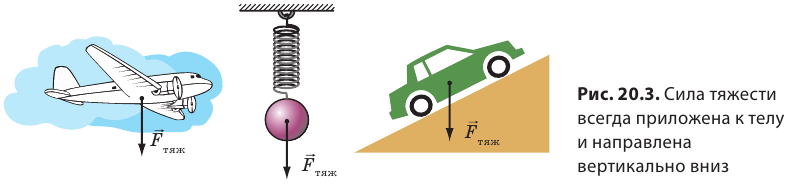
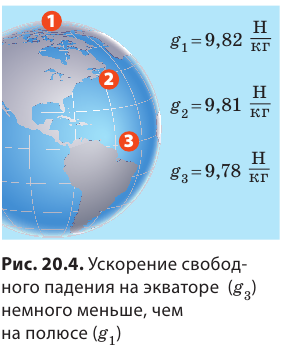
Вблизи поверхности Земли ускорение свободного падения равно приблизительно 9,8 ньютона на килограмм: 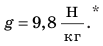Значение ускорения свободного падения несущественно изменяется на экваторе и полюсах Земли (рис. 20.4), при подъеме над поверхностью Земли и при спуске в шахту. Используя рис. 20.4, определите, на сколько сила тяжести, действующая на вас, на экваторе меньше, чем на полюсе.

Что физики называют весом тела

Из-за притяжения к Земле все тела сжимают или прогибают опору либо растягивают подвес. Сила, которая характеризует такое действие тел, называется весом тела (рис. 20.5).

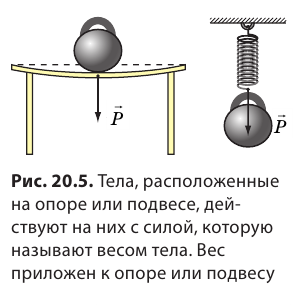
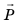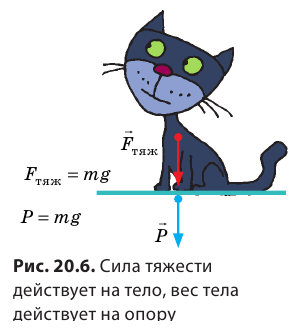
Вес тела — это сила, с которой вследствие притяжения к Земле тело давит на горизонтальную опору или растягивает вертикальный подвес. Единица веса в СИ, как и любой другой силы,— ньютон 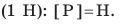Если тело находится в состоянии покоя или прямолинейного равномерного движения, то его вес совпадает по направлению с силой тяжести и равен ей по значению: P=mg. Однако в отличие от силы тяжести, которая приложена к телу, вес приложен к опоре или подвесу (рис. 20.6).

Для упрощения расчетов в случаях, когда большая точность не существенна, можно считать, что g= 10 Н/кг.

Состояние невесомости

Вы наверняка хорошо знаете термин «невесомость», но его значение многие понимают неправильно. Например, считают, что невесомость — это состояние, которое наблюдается только в космосе, где нет воздуха, или там, где отсутствует гравитация. Но это не так! Отсутствие воздуха само по себе не вызывает невесомости, а от гравитации вообще не спрячешься — во Вселенной нет ни одного уголка, где бы не действовали силы всемирного тяготения*. На самом деле невесомость — это отсутствие веса. Уберите у тела опору или подвес — и оно окажется в состоянии невесомости. (Обратите внимание: сопротивление воздуха тоже является своего рода опорой!)

Невесомость — это такое состояние тела, при котором тело не действует на опору или подвес. Тело вблизи поверхности Земли находится в состоянии невесомости, если на него действует только одна сила — сила тяжести. На короткое время невесомость легко создать и дома. Можно, например, подпрыгнуть — и вы на мгновение окажетесь в состоянии невесомости: в данном случае, пока выдвигаетесь вниз, сопротивление воздуха пренебрежимо мало и можно считать, что на вас действует только сила тяжести. Постоянно в состоянии невесомости находятся космические орбитальные станции и все, что на них находится (рис. 20.7). Это связано с тем, что космические корабли «постоянно падают» на Землю из-за ее притяжения и в то же время остаются на орбите благодаря своей огромной скорости. У нетренированного человека длительное пребывание в состоянии невесомости, как правило, сопровождается тошнотой, нарушением работы мышц, вестибулярного аппарата**, нервными расстройствами, именно поэтому космонавты проходят серьезную физическую подготовку (рис. 20.8).

Плотность материи в нашей Вселенной очень мала (2-3 атома Гидрогена на 1 м³), потому во Вселенной в среднем очень мала и гравитация. Ее называют микрогравитацией. Вестибулярный аппарат — орган чувств у людей и позвоночных животных, воспринимающий изменение положения тела в пространстве и направление движения. Этот орган отвечает, например, за способность человека различать в темноте, где верх, а где низ.

Итоги:

Во Вселенной все тела притягиваются друг к другу. Такое взаимное притяжение тел называют всемирным тяготением. Сила тяжести — сила, с которой Земля притягивает к себе тела, находящиеся на ее поверхности или вблизи нее. Сила тяжести вычисляется по формуле 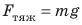и направлена вертикально вниз, к центру Земли. Вес 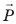тела — это сила, с которой вследствие притяжения к Земле тело действует на горизонтальную опору или вертикальный подвес. Следует различать силу тяжести и вес тела: сила тяжести приложена к самому телу, а вес — к опоре или подвесу; вес тела равен по значению силе тяжести (P=mg) только в состоянии покоя тела или его равномерного прямолинейного движения. Когда тело движется под действием только силы тяжести, то оно находится в состоянии невесомости (его вес равен нулю).

Эти два понятия используются для одного и того же – для определения количества материи в условиях Земли. Именно по тому, что цель у них одинаковая и происходит некая запутанность в их определении. Необходимо понять и разделять эти способы определения количества материи на Земле только по способу определения.

Масса.

Способ определения количества материи – масса. Определим инструментарий данного способа: это скорость и время. Описания метода: берётся определённое количество материи и придаётся этой материи определённая скорость и после достижения установленной скорости происходит остановка материи о преграду с весовым датчиком. На терминале датчика определяется воздействие материи на преграду. Для простоты, время остановки прировняем нулю. В связи с этим остаётся только одно значение, влияющее на воздействие материи на опору – это скорость.

Но скорость не является величиной постоянной для внутреннего наблюдателя и по этому её можно назвать иллюзорной. Смоделируем, что будет происходить с инерционной массой с увеличением энергии окружающего пространства в два раза.

При увеличении энергии окружающего пространства в два раза произойдёт замедление течения времени так же в два раза и произойдёт сжимание пространственных координат в 2√2 раза. Именно деформация осей координат и времени и приводит к деформации восприятия скорости. Скорость увеличится в √2 раза. Это говорит о том, что одна и та же скорость в разных областях пространства с различной энергией окружающего пространства различна, хоть и для внутреннего наблюдателя кажется одинаковой. А энергия – это квадрат скорости. Исходя из этого можно утверждать, что масса прямо пропорционально зависит от энергии окружающего пространства и при увеличении энергии окружающего пространства в два раза – увеличивается и масса так же в два раза. Но необходимо уточнить данное утверждение, что это справедливо только для системы координат внутреннего наблюдателя, так как для единой системы координат масса не меняется и не меняется абсолютная энергия заключённая в материи.

Запишем формулу изменения массы материи для внутреннего наблюдателя:

M1 = M0 / ∆T,

Где M1 – это инерционная масса материи после изменения энергии окружающего пространства.

M0 – это инерционная масса материи до изменения энергии окружающего пространства.

∆T – это коэффициент изменение скорости течения времени, где

∆T = T1 / T0

Если энергия пространства увеличивается, то соответственно время замедляет свой ход и коэффициент изменения скорости течения времени меньше единицы. А если энергия пространства уменьшается, то соответственно время ускоряет свой ход и коэффициент изменения скорости течения времени больше единицы.

Сила тяжести.

Сила тяжести так же является способом определения количества материи, но инструментарий используется совсем другой. Для определения силы тяжести используется такое понятие как пространственный ветер и энергия этого пространственного ветра. Материя же выступает в роли некоего паруса. В условиях Земли, для определения силы тяжести тело должно быть неподвижно по отношению к Земле. Давайте смоделируем изменение энергии окружающего пространства и посмотрим, что будет с силой тяжести. Если энергия окружающего пространства увеличится в два раза, то произойдёт следующее:

Скорость пространственного ветра в единой системе координат не изменится, а для внутреннего наблюдателя она увеличится пропорционально изменению скорости течения времени. То есть существующая скорость 11,2 км/с превратится в 22,4 км/с, а время замедлится в два раза и превратится из 1141 с. в 570 с. Согласно формуле ускорения А = ∆V/T мы получаем, что ускорение свободного падения на Земле увеличится в 4 раза.

Напишем зависимость через время, как энергетический коэффициент:

А = ∆V/T

А1 = А0 / ∆T2

Это значит, что изменение ускорения свободного падения на Земле будет происходить пропорционально по квадратичной зависимости от энергии окружающего пространства или от времени. Но это только ускорение. Для определения силы тяжести справедлива формула Ньютона, в которой роль паруса исполняет такая количественная составляющая материи, как масса, а в роли энергообмена – ускорение свободного падения на Земле.

F = AM

F1 = A1M1 = M0 / ∆T x А0 / ∆T2 = A0M0 / ∆T3 = F0 / ∆T3

Из этого выражения видно насколько различны масса и сила тяжести. Любое изменение инерционной массы приводит к кубическому изменению силы тяжести, при всех равных условиях и в системе координат внутреннего наблюдателя.

Как найти силу тяжести

Сила тяжести – величина, на которую тело притягивается к земле под действием ее притяжения. Данный показатель напрямую зависит от веса человека или массы предмета. Чем больше вес, тем он выше. В этой статье мы расскажем, как найти силу тяжести.

1

Из школьного курса физики: сила притяжения прямо пропорциональна весу тела. Рассчитать величину можно по формуле F=m*g, где g – коэффициент, равный 9,8 м/с². Соответственно для человека, который весит 100 кг, сила притяжения равна 980. Стоит отметить, что на практике все немного иначе, и на силу тяжести влияет множество факторов.

Факторы, влияющие на силу тяжести:

• расстояние от земли;
• географическое расположение тела;
• время суток.

2

Запомните, что на северном полюсе постоянная g равна не 9,8, а 9,83. Это возможно из-за наличия в земле залежей полезных ископаемых, которые обладают магнитными свойствами. Незначительно увеличивается коэффициент в местах залежей железной руды. На экваторе коэффициент равен 9,78.

3

Если тело находится не на земле или в движении, то для определения силы притяжения необходимо знать ускорение предмета. Для этого можно воспользоваться специальными приборами – секундомером, спидометром или акселерометром. Для расчета ускорения определите конечную и начальную скорости движения объекта. Отнимите от конечной величины начальную скорость, а полученную разницу разделите на время, за которое предмет прошел расстояние.

4

Можно подсчитать ускорение, подвигав предмет. Для этого необходимо передвинуть тело из состояния покоя. Теперь расстояние умножьте на два. Полученную величину разделите на время, возведенное в квадрат. Этот способ расчета ускорения подходит, если тело вначале находится в состоянии покоя.

5

Если имеется спидометр, то для определения ускорения необходимо возвести в квадрат начальную и конечную скорости тела. Найдите разницу квадратов конечной и начальной скоростей. Полученный результат разделите на время, умноженное на 2. Если тело движется по окружности, то оно имеет свое ускорение, даже при постоянной скорости. Для нахождения ускорения возведите скорость тела в квадрат и разделите на радиус окружности, по которой оно движется. Радиус необходимо указывать в метрах.

6

Для определения мгновенного ускорения используйте акселерометр. Если вы получили отрицательное значение ускорения, это значит, что предмет тормозит, то есть его скорость уменьшается. Соответственно при положительном значении предмет разгоняется, а его скорость увеличивается. Помните, коэффициент 9,8 можно использовать лишь в том случае, если сила тяжести определяется для предмета, который находится на земле. Если тело установлено на опору, следует учесть сопротивление опоры. Эта величина зависит от материала, из которого изготовлена опора.

Если тело волочат не в горизонтальном направлении, то стоит взять во внимание угол, на который отклоняется предмет от горизонта. В итоге формула будет иметь следующий вид: F=m*g – Fтяги*sin. Измеряется сила тяжести в ньютонах. Для проведения расчетов используйте скорость, измеренную в м/с. Для этого поделите скорость в км/час на 3,6.

Явление
тяготения. Сила тяжести

«Был этот свет глубокой тьмой окутан.

Да будет свет! И вот явился Ньютон»

Александр Поуп

Еще на первых темах были приведены
примеры падения тел на Землю. Мяч, камень, перо или листик – все эти тела
падают на Землю. Тогда было сказано, что это обусловлено явлением всемирного
тяготения. В этой теме будет идти речь об этом явлении более подробно. Не
одно десятилетие и даже не одно столетие люди пытались объяснить данное
явление.

В древности люди считали, что Земля –
это центр Вселенной, а все остальное вращается вокруг неё. Людей интересовало не только
движение тел на Земле, но и на небе. Исходя из множества наблюдений,
выяснилось, что многие планеты двигаются вокруг Земли более чем странно. Они то
движутся вперед, то начинают выписывать какие-то петли, двигаясь назад, а потом
снова начинают своё движение вперёд. Древнегреческий ученый, Клавдий
Птолемей, выпустил целое собрание из тринадцати книг, в котором он обобщал
астрономические и математические знания древнегреческого мира.

Чтобы объяснить движение планет,
Птолемеем рисовались специальные окружности, специальные сферы, количество
которых доходило до нескольких десятков – настолько Птолемей не хотел
отказываться от теории о том, что Земля лежит в центре Вселенной. Кстати, также
нелепо Птолемеем объяснялось явление смены времени суток.

Однако смог отказаться от такой
теории Николай Коперник. Он решил, что Солнце находится в центре
Вселенной, и все планеты вращаются именно вокруг Солнца.

Конечно, сегодня, глупо говорить о
том, что Солнце находится в центре Вселенной, но, тем не менее, Коперник
оказался прав: наблюдаемые с Земли планеты действительно вращаются вокруг
Солнца. Этим легко объяснялось непонятное ранее движение планет (поскольку
все они двигались не вокруг Земли, а вокруг Солнца, и сама Земля – тоже
вращалась вокруг Солнца). В системе Коперника все стало гораздо яснее –
не надо было придумывать никаких многочисленных сфер и окружностей, которые так
усердно рисовал Птолемей в своих небесных картах.

Ранее говорилось, изменение
скорости или направления движения тел может быть вызвано только силой.

Лишь в XVII веке Робертом Гуком впервые было высказано
предположение о том, что Земля притягивается к Солнцу, и именно этим
объясняется характер её движения.

Таким образом, получалось, что движение
планет обеспечивается Солнцем, а точнее силой взаимодействия между планетами и
Солнцем. Чуть позднее Исаак Ньютон предположил, что раз сила направлена
в сторону изменения скорости, то это значит, что именно Солнце заставляет двигаться
другие планеты, поскольку планеты обращаются вокруг него. Именно таким
образом появились первые знания о явлении тяготения. Итак, явление
всемирного тяготения – это явление взаимного притяжения между всеми телами
во Вселенной. То есть, не только между Солнцем и планетами существует
тяготение, но и между самими планетами тоже. Не только Земля притягивает к себе
все тела, находящиеся на ней, но и сами тела притягиваются друг к другу.
Правда, это притяжение очень незначительно, по сравнению с земным притяжением,
поэтому, притяжение между другими телами не заметно.

Исаак Ньютон в одной из своих работ сформулировал
закон всемирного тяготения, о котором подробно будет говориться позже.
Ньютон строго доказал, что притяжение между телами тем больше, чем больше
массы этих тел. Также, притяжение между телами тем меньше, чем больше
расстояние между этими телами. Именно исходя из этого закона, можно себе
представить, насколько незначительно притяжение тел на Земле друг к другу, по
сравнению с притяжением между этими телами и Землёй.

Сила, с которой Земля притягивает к
себе тело, называется силой тяжести. Сила тяжести, как и любая другая сила, обозначается буквой _тяж.
Индекс «тяж», указывает, что это именно сила тяжести. Необходимо запомнить,
что сила тяжести всегда направлена вертикально вниз. Исходя из
закона всемирного тяготения, сила тяжести, действующая на тело, прямо
пропорциональна массе этого тела. Поэтому более тяжёлым называем то тело,
которое имеет большую массу. Может возникнуть вопрос: «а какое расстояние
может быть между Землёй и телом, покоящимся на её поверхности?». За
расстояние между телами принимается расстояние между центрами этих тел.
То есть, расстояние между Землёй и телом на её поверхности равно радиусу
Земли. Из курса географии известно, что Земля не является идеальным шаром,
а немного сплюснута у полюсов. Поэтому, на полюсах сила тяжести, действующая
на тело, будет немного больше, чем сила тяжести, действующая на это же тело на
экваторе.

Аналогично, если альпинист поднимется
на высокую гору, то сила тяжести, действующая на него, станет немного меньше,
чем сила тяжести, действовавшая на альпиниста у подножья горы.

Итак, сила тяжести прямо
пропорциональна массе тела.

                                                            F_тяж = mg

Коэффициентом пропорциональности в
этой зависимости является, так называемый, коэффициент g. Коэффициент g равен

g = 9,8 Н/кг

То есть, на тело, масса которого
равна 1/9,8 кг, действует сила тяжести F_тяж в 1 Н.

Надо сказать, что сила тяжести на
других планетах может сильно отличаться, поскольку каждая планета имеет свой
собственный коэффициент g.
Например, на Луне коэффициент g = 1,6 Н/кг, что примерно в шесть
раз меньше, чем на Земле.

На Меркурии коэффициент g = 3,7 Н/кг. Меркурий – это наиболее близкая и
наименьшая из основных планет Солнечной системы. Масса этой планеты почти в
19 раз меньше массы Земли. А вот самая
большая планета Солнечной системы – Юпитер, в 317 раз массивнее Земли. Там
коэффициент g ≈ 25 Н/кг/ Этот
коэффициент зависит от размеров и массы небесного тела.

Вообще изучение Солнечной системы, да
и космического пространства в целом очень важно для понимания процессов,
происходящих на Земле.

Упражнения.

Задача 1. Найдите силу тяжести, действующую
на тело, масса которого составляет 20 кг. Какова будет сила тяжести, действующая на это же тело на Луне?

Задача 2. Определите, какая сила тяжести будет
больше: сила тяжести, действующая на тело массой 300 г на Юпитере или сила тяжести, действующая на тело массой 700 г, на Земле?

Основные выводы:

– Явление всемирного тяготения
– это явление взаимного притяжения между всеми телами во
Вселенной.

– Сила притяжения между двумя
телами зависит от массы этих тел и от расстояния между ними.

– Сила тяжести прямо
пропорциональна массе тела

F_тяж = mg

– g – коэффициент пропорциональности, который на Земле равен

g = 9,8 Н/кг

На этой странице находится ответ на вопрос Как обозначается коэффициент тяжести?, из категории
Физика, соответствующий программе для 5 – 9 классов. Чтобы посмотреть
другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов
подберите похожие вопросы и ответы в категории Физика. Ответ, полностью
соответствующий критериям вашего поиска, можно найти с помощью простого
интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе.
Обратите внимание на варианты ответов других пользователей, которые можно не
только просмотреть, но и прокомментировать.