Как найти коэффициент скорости химической реакции

Правило Вант-Гоффа — эмпирическое правило, позволяющее в первом приближении оценить влияние температуры на скорость химической реакции в небольшом температурном интервале (обычно от 0 °C до 100 °C). Якоб Хендрик Вант-Гофф на основании множества экспериментов сформулировал следующее правило:

При повышении температуры на каждые 10 градусов константа скорости гомогенной элементарной реакции увеличивается в два—четыре раза.

Уравнение, которое описывает это правило, следующее:

${displaystyle V_{2}=V_{1}cdot gamma ^{frac {T_{2}-T_{1}}{10}},}$

где $V_{2}$ — скорость реакции при температуре $T_{2}$ , $V_{1}$ — скорость реакции при температуре $T_{1}$ , gamma — температурный коэффициент реакции (если он равен 2, например, то скорость реакции будет увеличиваться в 2 раза при повышении температуры на 10 градусов).

Следует помнить, что правило Вант-Гоффа применимо только для реакций с энергией активации 60—120 кДж/моль в температурном диапазоне 10—400 °C. Правилу Вант-Гоффа также не подчиняются реакции, в которых принимают участие громоздкие молекулы, например, белки в биологических системах.

Температурную зависимость скорости реакции более корректно описывает уравнение Аррениуса.

Из уравнения Вант-Гоффа температурный коэффициент вычисляется по формуле

${displaystyle gamma =(V_{2}/V_{1})^{10/(T_{2}-T_{1})}.}$

Источник

Скорость химической реакции – основное понятие химической кинетики, выражающее отношения количества
прореагировавшего вещества (в молях) к отрезку времени, за которое произошло взаимодействие.

Скорость реакции отражает изменение концентраций реагирующих веществ за единицу времени. Единицы измерения для гомогенной реакции:
моль/л * сек. Физический смысл в том, что каждую секунду какое-то количество одного вещества превращается в
другое в единице объема.

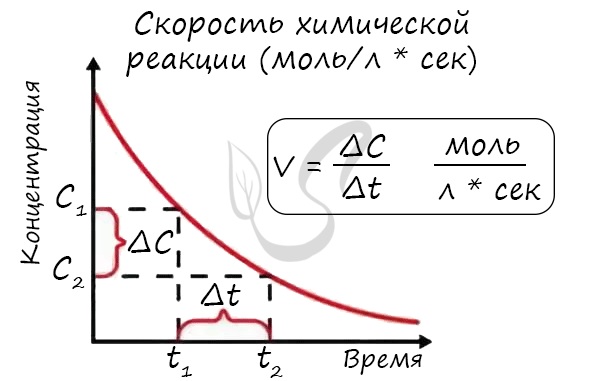
Мне встречались задачи, где была дана молярная концентрация вещества до реакции и после, время и объем. Требовалось посчитать скорость
реакции. Давайте решим подобное несложное задание для примера:

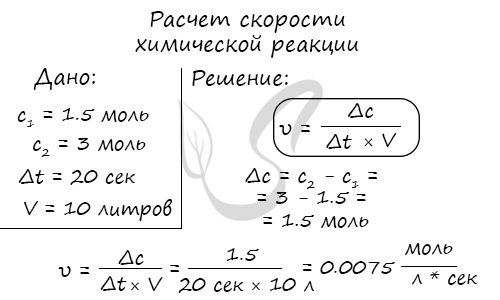
Молярная концентрация вещества до реакции составляла 1.5 моль/л по итогу реакции – 3 моль/л. Объем смеси 10 литров, реакция заняла 20 секунд.
Рассчитайте скорость реакции.

Влияние природы реагирующих веществ

При изучении агрегатных состояний веществ возникает вопрос: где же быстрее всего идут реакции: между газами, растворами или твердыми веществами?

Запомните, что самая высокая скорость реакции между растворами, в жидкостях. В газах она несколько ниже.

Если реакция гетерогенная: жидкость + твердое вещество, газ + твердое вещество, жидкость + газ, то большую роль играет площадь соприкосновения
реагирующих веществ.

Очевидно, что большой кусок железа, положенный в соляную кислоту, будет гораздо дольше реагировать с ней, нежели чем измельченное
железо – железная стружка.

Химическая активность также играет важную роль. Например, отвечая на вопрос “какой из металлов Fe или Ca быстрее прореагирует с серой?” мы отдадим
предпочтение кальцию, так как в ряду активности металлов он стоит левее железа, а значит кальций активнее железа.

Иного подхода требуют реакции металлов с водой, где нужно учитывать радиус атома. Например, отвечая на вопрос “какой из металлов Li или K быстрее прореагирует с водой?” мы отдадим предпочтение калию, так как калий имеет больший радиус атома. Калий будет быстрее взаимодействовать с водой, чем литий.

Иногда для верного ответа на вопрос о скорости реакции требуется знание активности кислот. Мы подробнее обсудим эту тему в гидролизе, однако сейчас
я замечу: чем сильнее (активнее) кислота, тем быстрее идет реакция.

Например, реакцию магния с серной кислотой протекает гораздо быстрее реакции магния с уксусной кислотой. Причиной этому служит то, что серная кислота
относится к сильным (активным) кислотам, а активность уксусной кислоты меньше, она является слабой кислотой.

Как я уже упомянул, слабые и сильные кислоты и основания изучаются в теме гидролиз.

Влияние изменения концентрации

Влияние концентрации “прямо пропорционально” скорости реакции: при увлечении концентрации реагирующего вещества скорость реакции повышается, при
уменьшении – понижается.

Замечу деталь, которая может оказаться важной, если в реакции участвуют газы: при увеличении давления концентрация вещества на единицу объема
возрастает (представьте, как газ сжимается). Поэтому увеличение давление, если среди исходных веществ есть газ, увеличивает скорость реакции.

Закон действующих масс устанавливает соотношение между концентрациями реагирующих веществ и их продуктами. Скорость простой реакции
aA + bB → cC определяют по уравнению:

υ = k × С^a_A × С^b_B

Физический смысл константы скорости – k – в том, что она численно равна скорости реакции при том условии, что концентрации реагирующих
веществ равны 1. Обратите внимание, что стехиометрические коэффициенты уравнения переносятся в степени – a и b.

Записанное выше следствие закона действующих масс нужно не только “зазубрить”, но и понять. Поэтому мы решим пару задач, где потребуется
написать подобную формулу.

Окисление диоксида серы протекает по уравнению: 2SO_2(г) + O₂ = 2SO_3(г). Как изменится скорость этой реакции,
если объемы системы уменьшить в три раза?

По итогу решения становится ясно, что скорость реакции в таком случае возрастет в 27 раз.

Решим еще одну задачу. Дана реакция синтеза аммиака: N₂ + ЗН₂ = 2NH₃. Как изменится скорость прямой реакции
образования аммиака, если уменьшить концентрацию водорода в два раза?

В результате решения мы видим, что при уменьшении концентрации водорода в два раза скорость реакции замедлится в 8 раз.

Влияние изменения температуры на скорость реакции

Постулат, который рекомендую временно взять на вооружение: “Увеличение температуры увеличивает скорость абсолютно любой химической реакции: как
экзотермической, так и эндотермической. Исключений нет!”

Очень часто в заданиях следующей темы – химическом равновесии, вас будут пытаться запутать и ввести в заблуждение, но вы не поддавайтесь
и помните про постулат!

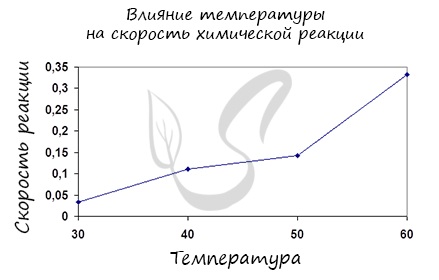
Итак, влияние температуры на скорость реакции “прямо пропорционально”: чем выше температура, тем выше скорость реакции – чем ниже
температура, тем меньше и скорость реакции. Однако, как и в случае с концентрацией, это больше чем простая “пропорция”.

Правило Вант-Гоффа, голландского химика, позволяет точно оценить влияние температуры на скорость химической реакции. Оно звучит так:
“При повышении температуры на каждые 10 градусов константа скорости гомогенной элементарной реакции увеличивается в два — четыре раза”

В формуле, написанной выше, используются следующие обозначение:

υ₁ – скорость реакции при температуре t₁
υ₂ – скорость реакции при температуре t₂
γ – температурный коэффициент, который может быть равен 2-4

Если по итогам решения задач у вас получится температурный коэффициент меньше 2 или больше 4, то, скорее всего, где-то вы допустили ошибку.
Используйте этот факт для самопроверки.

Для тренировки решим пару задач, в которых потребуется использование правило Вант-Гоффа.

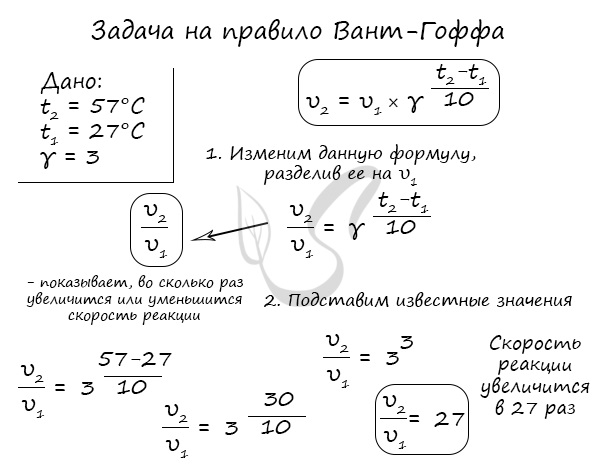
Как изменится скорость гомогенной реакции при повышении температуры от 27°C до 57°C при температурном коэффициенте, равном трем?

Иногда в задачах требуется рассчитать температурный коэффициент, как, например, здесь: “Рассчитайте, чему равен температурный коэффициент
скорости, если известно, что при понижении температуры от 250°C до 220°C скорость реакции уменьшилась в 8 раз”.

Катализаторы и ингибиторы

Катализатор (греч. katalysis — разрушение) – вещество, ускоряющее химическую реакцию, но не участвующее в ней. Катализатор не расходуется в химической реакции.

Многие химические реакции в нашем организме протекают с участием катализаторов – белковых молекул, ферментов. Без катализаторов
подобные реакции шли бы сотни лет, а с катализаторами идут одну долю секунды.

Катализом называют явление ускорения химической реакции под действием катализатора, а химические реакции, идущие с участием катализатора
– каталитическими.

Ингибитор (лат. inhibere – задерживать) – вещество, замедляющее или предотвращающее протекание какой-либо химической реакции.

Ингибиторы применяют для замедления коррозии металла, окисления топлива, старения полимеров. Многие лекарственные вещества
являются ингибиторами.

Так при лечении гастрита – воспаления желудка (греч. gaster – желудок) или язв часто назначаются ингибиторы протонной помпы – химические вещества,
которые блокирует выработку HCl слизистой желудке. В результате этого соляная кислота прекращает воздействие на поврежденную стенку желудка,
воспаление стихает.

Данная статья написана Беллевичем Юрием Сергеевичем и является его интеллектуальной собственностью. Копирование, распространение
(в том числе путем копирования на другие сайты и ресурсы в Интернете) или любое иное использование информации и объектов
без предварительного согласия правообладателя преследуется по закону. Для получения материалов статьи и разрешения их использования,
обратитесь, пожалуйста, к Беллевичу Юрию.

Источник

Температурный коэффициент скорости реакции

Возрастание
скорости реакции с ростом температуры
принято характеризовать температурным
коэффициентом скорости реакции , числом,
показывающим, во сколько раз возрастает
скорость данной реакции при повышении
температуры системы на 10°С. Температурный
коэффициент различных реакций различен.
При обычных температурах его значение
для большинства реакций находится в
пределах от 2… 4.

Температурный
коэффициент определяют в соответствии
с так называемым «правилом Вант-Гоффа»,
которое математически выражается
уравнением

v₂/v₁
= ⁽^T₂^–^T₁^)/10,

где
v₁
и v₂
–
скорости реакции при температурах Т₁
и Т₂;

температурный коэффициент реакции.

Так,
например, если 
= 2, то при Т₂
–
Т₁
= 50°С v₂/v₁
= 2⁵
= 32, т.е. реакция ускорилась в 32 раза,
причем это ускорение никак не зависит
от абсолютных величин Т₁
и Т₂,
а только от их разности.

Энергия
активации,
разность между значениями средней
энергии частиц (молекул, радикалов,
ионов и др.), вступающих в элементарный
акт химической реакции, и средней энергии
всех частиц, находящихся в реагирующей
системе. Для различных химических
реакций Э. а. изменяется в широких
пределах — от нескольких до ~ 10 дж./
моль. Для
одной и той же химической реакции
значение Э. а. зависит от вида функций
распределения молекул по энергиям их
поступательного движения и внутренним
степеням свободы (электронным,
колебательным, вращательным). Как
статистическую величину Э. а. следует
отличать от пороговой энергии, или
энергетического барьера, — минимальной
энергии, которой должна обладать одна
пара сталкивающихся частиц для протекания
данной элементарной реакции.

Аррениуса
уравнение,
температурная зависимость константы
скорости
к элементарной
хим. реакции:

где
A-предэкспоненциальныи множитель
(размерность совпадает с размерностью
к), Е_а
-энергия
активации, обычно принимающая положит.
значения, Т-абс. температура, k-постоянная
Больцмана. Принято приводить Е_а
в расчете не
на одну молекулу.
а на число частиц N_A
= 6,02*10²³
(постоянная Авогадро) и выражать в
кДж/моль; в этих случаях в уравнении
Аррениуса величину k
заменяют
газовой
постоянной
R. График
зависимости 1nк от 1/kT
(аррениусов
график) – прямая линия, отрицательный
наклон которой определяется энергией
активации
Е_аи
характеризует положит. температурную
зависимость к.

Скорость
химической реакции —
изменение количества одного из реагирующих
веществ за единицу времени в единице
реакционного пространства. Является
ключевым понятием химической
кинетики.
Скорость химической реакции —
величина всегда положительная, поэтому,
если она определяется по исходному
веществу (концентрация
которого убывает в процессе реакции),
то полученное значение домножается на
−1.

Например
для реакции:

выражение
для скорости будет выглядеть так:

Скорость
химической реакции в каждый момент
времени пропорциональна концентрациям
реагентов, возведенным в некоторые
степени.

Для
элементарных
реакций
показатель степени при значении
концентрации каждого вещества часто
равен его стехиометрическому коэффициенту,
для сложных реакций это правило не
соблюдается. Кроме концентрации на
скорость химической реакции оказывают
влияние следующие факторы:

природа
реагирующих веществ,
наличие
катализатора,
температура
(правило
Вант-Гоффа),
давление,
площадь
поверхности реагирующих веществ.

Если
мы рассмотрим самую простую химическую
реакцию A + B → C, то мы заметим, что
мгновенная
скорость химической реакции величина
непостоянная.

Катализа́тор —
химическое
вещество,
ускоряющее
реакцию,
но не входящее в состав продуктов
реакции^[1].
Количество катализатора, в отличие от
других реагентов, после реакции не
изменяется. Важно понимать, что катализатор
участвует в реакции. Обеспечивая более
быстрый путь для реакции, катализатор
реагирует с исходным веществом,
получившееся промежуточное соединение
подвергается превращениям и в конце
расщепляется на продукт и катализатор.
Затем катализатор снова реагирует с
исходным веществом, и этот каталитический
цикл многократно (до миллиона
раз)^[^{источник?}^]
повторяется.

Катализаторы
подразделяются на гомогенные
и гетерогенные.
Гомогенный катализатор находится в
одной фазе
с реагирующими веществами, гетерогенный —
образует самостоятельную фазу, отделённую
границей раздела от фазы, в которой
находятся реагирующие вещества ^[1].
Типичными гомогенными катализаторами
являются кислоты и основания. В качестве
гетерогенных катализаторов применяются
металлы, их оксиды и сульфиды.

Реакции
одного и того же типа могут протекать
как с гомогенными, так и с гетерогенными
катализаторами. Так, наряду с растворами
кислот применяются имеющие кислотные
свойства твёрдые Al₂O₃,
TiO₂,
ThO₂,
алюмосиликаты, цеолиты. Гетерогенные
катализаторы с основными свойствами:
CaO, BaO, MgO ^[1].

Гетерогенные
катализаторы имеют, как правило, сильно
развитую поверхность, для чего их
распределяют на инертном носителе
(силикагель,
оксид
алюминия,
активированный
уголь
и др.).

Для
каждого типа реакций эффективны только
определённые катализаторы. Кроме уже
упомянутых кислотно-основных,
существуют катализаторы
окисления-восстановления;
для них характерно присутствие переходного
металла
или его соединения (Со⁺³,
V₂O₅+MoO₃).
В этом случае катализ осуществляется
путём изменения степени окисления
переходного металла.

Много
реакций осуществлено при помощи
катализаторов, которые действуют через
координацию
реагентов у атома или иона переходного
металла (Ti,
Rh,
Ni).
Такой катализ называется координационным.

Если
катализатор обладает хиральными
свойствами, то из оптически неактивного
субстрата получается оптически активный
продукт.

В
современной науке и технике часто
применяют системы
из нескольких катализаторов,
каждый из которых ускоряет разные стадии
реакции ^[2][3].
Катализатор также может увеличивать
скорость одной из стадий каталитического
цикла, осуществляемого другим
катализатором. Здесь имеет место «катализ
катализа», или катализ
второго уровня
(Имянитов).

В
биохимических реакциях роль катализаторов
играют ферменты.

Катализаторы
следует отличать от инициаторов.
Например, перекиси
распадаются на свободные
радикалы,
которые могут инициировать радикальные
цепные
реакции.
Инициаторы расходуются в процессе
реакции, поэтому их нельзя считать
катализаторами.

Ингибиторы
иногда ошибочно считают отрицательными
катализаторами. Но ингибиторы, например,
цепных радикальных реакций, реагируют
со свободными радикалами и, в отличие
от катализаторов, не сохраняются. Другие
ингибиторы (каталитические яды)
связываются с катализатором и его
дезактивируют, здесь имеет место
подавление катализа, а не отрицательный
катализ. Отрицательный катализ в принципе
невозможен: он обеспечивал бы для реакции
более медленный путь, но реакция,
естественно, пойдёт по более быстрому,
в данном случае, не катализированному,
пути.

Диспе́рсная
систе́ма —
это образования
из двух или более числа
фаз (тел),
которые совершенно или практически не
смешиваются и не реагируют друг с другом
химически. Первое из веществ (дисперсная
фаза)
мелко распределено во втором (дисперсионная
среда).
Если фаз несколько, их можно отделить
друг от друга физическим способом
(центрифугировать, сепарировать и т. д.).

Обычно
дисперсные системы — это коллоидные
растворы,
золи.
К дисперсным системам относят также
случай твёрдой дисперсной среды, в
которой находится дисперсная фаза.

Наиболее
общая классификация дисперсных систем
основана на различии в агрегатном
состоянии дисперсионной
среды и дисперсной фазы. Сочетания трех
видов агрегатного состояния позволяют
выделить девять видов дисперсных систем.
Для краткости записи их принято обозначать
дробью, числитель которой указывает на
дисперсную фазу, а знаменатель на
дисперсионную среду, например для
системы «газ в жидкости» принято
обозначение Г/Ж.

Дисперсная фаза	Дисперсионная среда	Название и пример
Газообразная	Газообразная	Дисперсная система не образуется
Жидкая	Газообразная	Аэрозоли: туманы, облака
Твёрдая	Газообразная	Аэрозоли (пыли, дымы), порошки
Газообразная	Жидкая	Газовые эмульсии и пены
Жидкая	Жидкая	Эмульсии: нефть, крем, молоко
Твёрдая	Жидкая	Суспензии и золи: пульпа, ил, взвесь, паста
Газообразная	Твёрдая	Пористые тела
Жидкая	Твёрдая	Капиллярные системы: жидкость в пористых телах, грунт, почва
Твёрдая	Твёрдая	Твёрдые гетерогенные системы: сплавы, бетон, ситаллы, композиционные материалы

Коллоидные
растворы. Коллоидное состояние характерно
для многих веществ, если их частицы
имеют размер от 1 до 500 нм. Легко показать,
что суммарная поверхность этих частиц
огромна. Если предположить, что частицы
имеют форму шара с диаметром 10 нм, то
при общем объеме этих частиц
1
см³
они будут иметь

площадь
поверхности порядка 10 м2. Как указывалось
ранее поверхностный слой характеризуется
поверхностной энергией и способностью
адсорбировать те или иные частицы, в
том числе ионы

из
раствора. Характерной особенностью
коллоидных частиц является наличие на
их поверхности заряда, обусловленного
избирательной адсорбцией ионов.
Коллоидная частица имеет сложное
строение. Она включает в себя ядро,
адсорбированные ионы, противоины и
растворитель. Существуют лиофильные
(гид.

роф
ильные) коллоиды, в которых растворитель
взаимодейстиует с ядрами частиц,
илнофобные (гидрофобные) коллоиды, в
которых растворитель не взаимодействует
с ядрами

частиц.
Растворитель входит в состав гидрофобных
частиц лишь как сольватная оболочка
адсорбированных ионов или при наличии
стабилизаторов (ПАВ), имеющих лиофобную
и лиофильные части.

Приведем
несколько примеров коллоидных частиц:

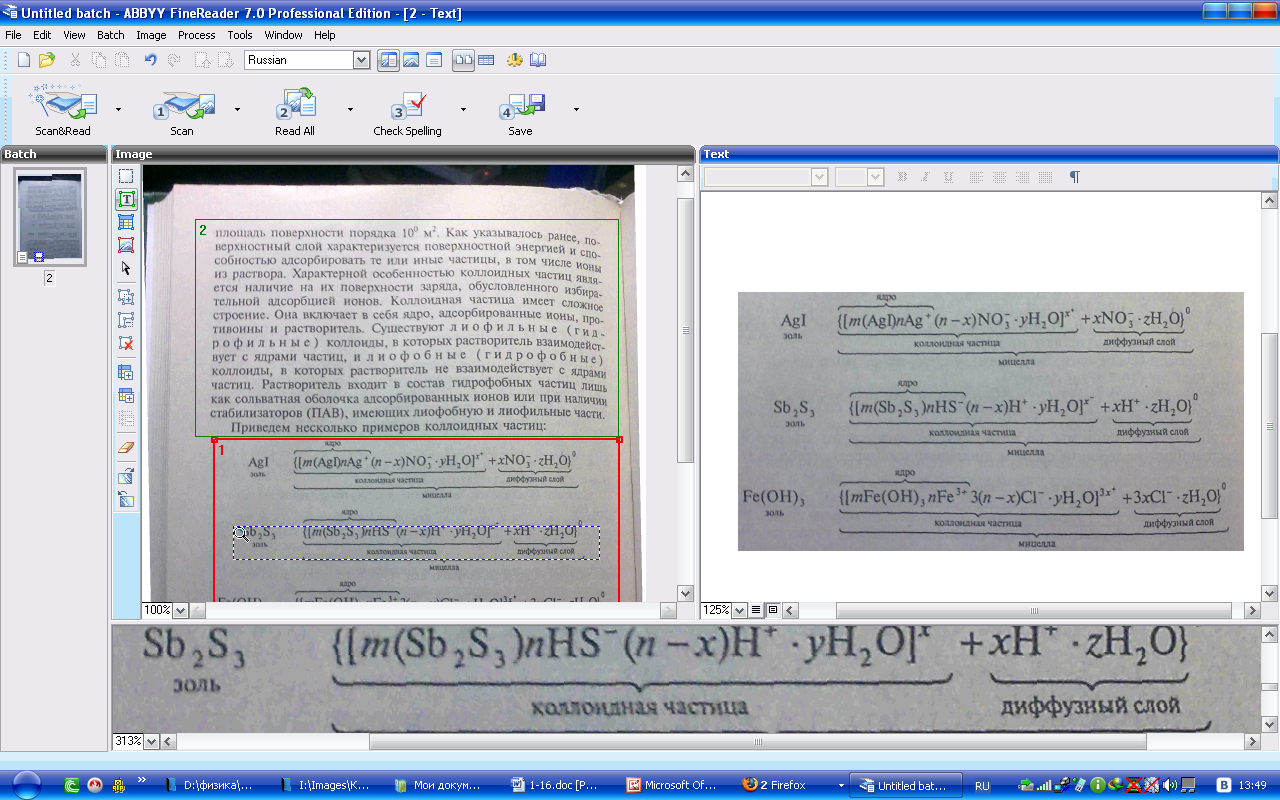
Как.
видно, ядро состоит из электронейтрального
агрегата частиц с адсорбированными
ионами элементов, входящих в состав
ядра (в данных примерах ионами Аg⁺,
НS-,
Fе³⁺).
Коллоидная час-шца кроме ядра имеет
противоионы и молекулы растворителя.
Адсорбированные ионы и противоионы
с растворителем образуют адсорбированный
слой. Суммарно заряд частицы равен
разности зарядов адсороированных
ионов и противоионов. Вокруг частиц
находится д и ф ф у з н ы й с л о и и о
н о в, заряд которых равен иряду коллоидной
частицы. Коллоидная частица и диффузный
слои образуют электронейтральную
мицеллу

Мицеллы (уменьшительное
от лат. mica —
частица, крупинка) — частицы в
коллоидных
системах,
состоят из нерастворимого в данной
среде ядра очень малого размера,
окруженного стабилизирующей оболочкой
адсорбированных
ионов
и молекул
растворителя.
Например, мицелла сульфида
мышьяка
имеет строение:

{(As₂S₃)_m•nHS⁻•(n-x)H⁺}^x-•хН⁺

Средний
размер мицелл от 10⁻⁵
до 10⁻⁷см.

Коагуляция
– разделение коллоидного раствора на
две фазы – растворитель и студнеобразную
массу, или загустевание раствора в
результате укрупнения частиц растворенного
вещества

Пептизация
— процесс перехода коллоидного осадка
или геля в коллоидный раствор под
действием жидкости или добавленных к
ней веществ, хорошо адсорбирующихся
осадком или гелем, называемых в этом
случае пептизаторами (например, пептизация
жиров под действием желчи).

Пептизация
— разъединение агрегатов частиц гелей
(студней) или рыхлых осадков под влиянием
определенных веществ — пептизаторов
после коагуляции коллоидных растворов.
В результате пептизации осадок (или
гель) переходит во взвешенное состояние.

РАСТВОРЫ,
однофазные
системы, состоящие из двух или более
компонентов. По своему агрегатному
состоянию растворы могут быть твердыми,
жидкими или газообразными.

Растворимость,
способность вещества образовывать с
другим веществом (или веществами)
гомогенные смеси с дисперсным
распределением компонентов (см. Растворы).
Обычно растворителем
считают вещество, которое в чистом виде
существует в том же агрегатном состоянии,
что и образовавшийся раствор. Если до
растворения
оба вещества находились в одном и том
же агрегатном состоянии, растворителем
считается вещество, присутствующее в
смеси в существенно большем кол-ве.

Растворимость
определяется физическим и химическим
сродством молекул
растворителя и растворяемого вещества,
соотношением энергий взаимодействием
однородных и разнородных компонентов
раствора. Как правило, хорошо растворимы
друг в друге подобные по физ. и хим.
свойствам вещества (эмпирич. правило
“подобное растворяется в подобном”).
В частности, вещества, состоящие из
полярных
молекул,
и вещества с ионным типом связи хорошо
раств. в полярных растворителях (воде,
этаноле,
жидком аммиаке), а неполярные вещества
хорошо раств. в неполярных растворителях
(бензоле, сероуглероде).

Согласно
теории, предложенной Дж. Гильдебрандом
(1935), взаимная растворимость неэлектролитов
возрастает с уменьшением разности их
параметров растворимости
d=(Е/V)^1/2,
где Е-теплота испарения,
V-полярный объем. Параметр растворимости
– одно из осн. понятий, определяющих
когезионные свойства веществ в конденсир.
состояниях; важная технол. характеристика
полимеров
и растворителей, лакокрасочных
материалов
и т.п. (см. Когезия). Р. мн. электролитов
возрастает пропорционально кубу
диэлектрич. проницаемости растворителя.
Обычно более растворимы электролиты
с большей склонностью к сольватации
растворителем; образование кристаллогидратов
обычно увеличивает растворимость солей.

Растворимость
данного вещества зависит от температуры
и давления
соответствует общему принципу смещения
равновесий (см. Ле Шателье-Брауна
принцип). Концентрация
насыщенного раствора при данных условиях
численно определяет Р. вещества в данном
растворителе и также наз. растворимостью.
Пересыщенные растворы содержат большее
кол-во растворенного вещества, чем это
соответствует его растворимости,
существование пересыщенных растворов
обусловлено кинетич. затруднениями
кристаллизации
(см. Зарождение новой фазы). Для
характеристики растворимости
малорастворимых веществ используют
произведение
активностей
ПА (для растворов, близких по своим
свойствам к идеальному – произведение
растворимости ПР).

Способы
выражения концентрации растворов.

1)
Массовая доля раствора ω (х). Выражается
отношением массы растворенного вещества
m(х) к массе раствора.

Является
величиной безразмерной или выражается
в процентах:

Например,
15%-ный раствор: массовая доля ω (х) = 0,15

2)
Молярная концентрация раствора С(х).
Выражается отношением количества
растворенного вещества n(x) к объему
раствора, выраженному в литрах.

Т.к.
количество вещества n(x) выражается
отношением массы вещества m(x) к его
молярной массе M(x), то молярную концентрацию
раствора удобно выразить как

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
01.05.2015354.02 Кб230725259_F7873_baranenko_a_v_holodilnye_mashiny.pdf
#
#
#
#
01.05.20156.82 Mб301.doc
#
#
#

Источник

Химическая кинетика

Напечатано::	Гость
Дата:	среда, 24 мая 2023, 19:55

Описание

Законы химической термодинамики позволяют определить направление и предел протекания возможного при данных условиях химического процесса, а также его энергетический эффект. Однако термодинамика не может ответить на вопросы о том, как осуществляется данный процесс и с какой скоростью. Эти вопросы – механизм и скорость химической реакции – и являются предметом химической кинетики.

1. Скорость химической реакции
- 1.1. Кинетическое уравнение химической реакции. Порядок реакции
- 1.2. Реакции нулевого порядка
- 1.3. Реакции первого порядка
- 1.4. Реакции второго порядка
- 1.5. Методы определения порядка реакции

1. Скорость химической реакции

Дадим определение основному понятию химической кинетики – скорости химической реакции:

Скорость химической реакции есть число элементарных актов химической реакции, происходящих в единицу времени в единице объема (для гомогенных реакций) или на единице поверхности (для гетерогенных реакций).

Скорость химической реакции есть изменение концентрации реагирующих веществ в единицу времени.

Первое определение является наиболее строгим; из него следует, что скорость химической реакции можно также выражать как изменение во времени любого параметра состояния системы, зависящего от числа частиц какого-либо реагирующего вещества, отнесенное к единице объема или поверхности – электропроводности, оптической плотности, диэлектрической проницаемости и т.д. и т.п. Однако наиболее часто в химии рассматривается зависимость концентрации реагентов от времени. В случае односторонних (необратимых) химических реакций (здесь и далее рассматриваются только односторонние реакции) очевидно, что концентрации исходных веществ во времени постоянно уменьшаются (ΔС_исх < 0), а концентрации продуктов реакции увеличиваются (ΔС_прод > 0). Скорость реакции считается положительной, поэтому математически определение средней скорости реакции в интервале времени Δt записывается следующим образом:

(II.1)

В различных интервалах времени средняя скорость химической реакции имеет разные значения; истинная (мгновенная) скорость реакции определяется как производная от концентрации по времени:

(II.2)

Графическое изображение зависимости концентрации реагентов от времени есть кинетическая кривая (рисунок 2.1).

Рис. 2.1 Кинетические кривые для исходных веществ (А) и продуктов реакции (В).

Истинную скорость реакции можно определить графически, проведя касательную к кинетической кривой (рис. 2.2); истинная скорость реакции в данный момент времени равна по абсолютной величине тангенсу угла наклона касательной:

Рис. 2.2 Графическое определение V_ист.

(II.3)

Необходимо отметить, что в том случае, если стехиометрические коэффициенты в уравнении химической реакции неодинаковы, величина скорости реакции будет зависеть от того, изменение концентрации какого реагента определялось. Очевидно, что в реакции

2Н₂ + О₂ → 2Н₂О

концентрации водорода, кислорода и воды изменяются в различной степени:

ΔС(Н₂) = ΔС(Н₂О) = 2 ΔС(О₂).

Скорость химической реакции зависит от множества факторов: природы реагирующих веществ, их концентрации, температуры, природы растворителя и т.д.

Одной из задач, стоящих перед химической кинетикой, является определение состава реакционной смеси (т.е. концентраций всех реагентов) в любой момент времени, для чего необходимо знать зависимость скорости реакции от концентраций. В общем случае, чем больше концентрации реагирующих веществ, тем больше скорость химической реакции. В основе химической кинетики лежит т. н. основной постулат химической кинетики:

Скорость химической реакции прямо пропорциональна произведению концентраций реагирующих веществ, взятых в некоторых степенях.

Т. е. для реакции

аА + bВ + dD + … → еЕ + …

можно записать

(II.4)

Коэффициент пропорциональности k есть константа скорости химической реакции. Константа скорости численно равна скорости реакции при концентрациях всех реагирующих веществ, равных 1 моль/л.

Зависимость скорости реакции от концентраций реагирующих веществ определяется экспериментально и называется кинетическим уравнением химической реакции. Очевидно, что для того, чтобы записать кинетическое уравнение, необходимо экспериментально определить величину константы скорости и показателей степени при концентрациях реагирующих веществ. Показатель степени при концентрации каждого из реагирующих веществ в кинетическом уравнении химической реакции (в уравнении (II.4) соответственно x, y и z) есть частный порядок реакции по данному компоненту. Сумма показателей степени в кинетическом уравнении химической реакции (x + y + z) представляет собой общий порядок реакции. Следует подчеркнуть, что порядок реакции определяется только из экспериментальных данных и не связан со стехиометрическими коэффициентами при реагентах в уравнении реакции. Стехиометрическое уравнение реакции представляет собой уравнение материального баланса и никоим образом не может определять характера протекания этой реакции во времени.

В химической кинетике принято классифицировать реакции по величине общего порядка реакции. Рассмотрим зависимость концентрации реагирующих веществ от времени для необратимых (односторонних) реакций нулевого, первого и второго порядков.

1.1. Кинетическое уравнение химической реакции. Порядок реакции

Т. е. для реакции

аА + bВ + dD + … → еЕ + …

можно записать

(II.4)

1.2. Реакции нулевого порядка

Для реакций нулевого порядка кинетическое уравнение имеет следующий вид:

(II.5)

Скорость реакции нулевого порядка постоянна во времени и не зависит от концентраций реагирующих веществ; это характерно для многих гетерогенных (идущих на поверхности раздела фаз) реакций в том случае, когда скорость диффузии реагентов к поверхности меньше скорости их химического превращения.

1.3. Реакции первого порядка

Рассмотрим зависимость от времени концентрации исходного вещества А для случая реакции первого порядка А → В. Реакции первого порядка характеризуются кинетическим уравнением вида (II.6). Подставим в него выражение (II.2):

(II.6)

(II.7)

После интегрирования выражения (II.7) получаем:

(II.8)

Константу интегрирования g определим из начальных условий: в момент времени t = 0 концентрация С равна начальной концентрации С_о. Отсюда следует, что g = ln С_о. Получаем:

(II.9)

Рис. 2.3 Зависимость логарифма концентрации от времени для реакций первого порядка.

Т.о., логарифм концентрации для реакции первого порядка линейно зависит от времени (рис. 2.3) и константа скорости численно равна тангенсу угла наклона прямой к оси времени.

(II.10)

Из уравнения (II.9) легко получить выражение для константы скорости односторонней реакции первого порядка:

(II.11)

Еще одной кинетической характеристикой реакции является период полупревращения t_1/2 – время, за которое концентрация исходного вещества уменьшается вдвое по сравнению с исходной. Выразим t_1/2 для реакции первого порядка, учитывая, что С = ½С_о:

(II.12)

Отсюда

(II.13)

Как видно из полученного выражения, период полупревращения реакции первого порядка не зависит от начальной концентрации исходного вещества.

1.4. Реакции второго порядка

Для реакций второго порядка кинетическое уравнение имеет следующий вид:

(II.14)

либо

(II.15)

Рассмотрим простейший случай, когда кинетическое уравнение имеет вид (II.14) или, что то же самое, в уравнении вида (II.15) концентрации исходных веществ одинаковы; уравнение (II.14) в этом случае можно переписать следующим образом:

(II.16)

После разделения переменных и интегрирования получаем:

(II.17)

Постоянную интегрирования g, как и в предыдущем случае, определим из начальных условий. Получим:

(II.18)

Таким образом, для реакций второго порядка, имеющих кинетическое уравнение вида (II.14), характерна линейная зависимость обратной концентрации от времени (рис. 2.4) и константа скорости равна тангенсу угла наклона прямой к оси времени:

(II.19)

(II.20)

Рис. 2.4 Зависимость обратной концентрации от времени для реакций второго порядка.

Если начальные концентрации реагирующих веществ C_о,А и C_о,В различны, то константу скорости реакции находят интегрированием уравнения (II.21), в котором C_А и C_В – концентрации реагирующих веществ в момент времени t от начала реакции:

(II.21)

В этом случае для константы скорости получаем выражение

(II.22)

Порядок химической реакции есть формально-кинетическое понятие, физический смысл которого для элементарных (одностадийных) реакций заключается в следующем: порядок реакции равен числу одновременно изменяющихся концентраций. В случае элементарных реакций порядок реакции может быть равен сумме коэффициентов в стехиометрическом уравнении реакции; однако в общем случае порядок реакции определяется только из экспериментальных данных и зависит от условий проведения реакции. Рассмотрим в качестве примера элементарную реакцию гидролиза этилового эфира уксусной кислоты (этилацетата), кинетика которой изучается в лабораторном практикуме по физической химии:

СН₃СООС₂Н₅ + Н₂О → СН₃СООН + С₂Н₅ОН

Если проводить эту реакцию при близких концентрациях этилацетата и воды, то общий порядок реакции равен двум и кинетическое уравнение имеет следующий вид:

(II.23)

При проведении этой же реакции в условиях большого избытка одного из реагентов (воды или этилацетата) концентрация вещества, находящегося в избытке, практически не изменяется и может быть включена в константу скорости; кинетическое уравнение для двух возможных случаев принимает следующий вид:

1) Избыток воды:

(II.24)

(II.25)

2) Избыток этилацетата:

(II.26)

(II.27)

В этих случаях мы имеем дело с так назывемой реакцией псевдопервого порядка. Проведение реакции при большом избытке одного из исходных веществ используется для определения частных порядков реакции.

1.5. Методы определения порядка реакции

Проведение реакции в условиях, когда концентрация одного из реагентов много меньше концентрации другого (других) и скорость реакции зависит от концентрации только этого реагента, используется для определения частных порядков реакции – это т.н. метод избыточных концентраций или метод изолирования Оствальда. Порядок реакции по данному веществу определяется одним из перечисленных ниже методов.

Графический метод заключается в построении графика зависимости концентрации реагента от времени в различных координатах. Для различных частных порядков эти зависимости имеют следующий вид:

Порядок реакции	Зависимость концентрации от времени
1
2
3

Если построить графики этих зависимостей на основании опытных данных, то лишь одна из них будет являться прямой линией. Если, например, график, построенный по опытным данным, оказался прямолинейным к координатах lnC = f(t), то частный порядок реакции по данному веществу равен единице.

Метод подбора кинетического уравнения заключается в подстановке экспериментальных данных изучения зависимости концентрации вещества от времени в кинетические уравнения различных порядков. Подставляя в приведённые в таблице уравнения значения концентрации реагента в разные моменты времени, вычисляют значения константы скорости. Частный порядок реакции по данному веществу равен порядку того кинетического уравнения, для которого величина константы скорости остаётся постоянной во времени.

Порядок реакции	Выражение для константы скорости
1
2
3

Метод определения времени полупревращения заключается в определении t_1/2 для нескольких начальных концентраций. Как видно из приведённых в таблице уравнений, для реакции первого порядка время полупревращения не зависит от C_o, для реакции второго порядка – обратно пропорционально C_o, и для реакции третьего порядка – обратно пропорционально квадрату начальной концентрации.

Порядок реакции	Выражение для периода полупревращения
1
2
3

По характеру зависимости t_1/2 от C_o нетрудно сделать вывод о порядке реакции по данному веществу. Данный метод, в отличие от описанных выше, применим и для определения дробных порядков.

Источник

Температурный коэффициент некоторой химической реакции равен 4. Как изменится скорость этой химической реакции при нагревании реакционной смеси от 20 до 50 градусов?

Решение задачи

Зависимость скорости химической реакции от температуры определяет правило Вант-Гоффа, которым мы воспользуемся при решении задачи.

Правило Вант-Гоффа: скорость большинства химических реакций при повышении температуры на каждые 10 возрастает в 2-4 раза.

Математически правило Вант-Гоффа выражается формулой:

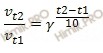
где:

– температурный коэффициент;

– скорость химической реакции при температурах , соответственно.

Учитывая то, что по условию задачи температурный коэффициент равен 4, а температура повысилась на 30 градусов, вычислим, как изменилась скорость химической реакции:

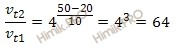
Таким образом, скорость химической реакции увеличилась в 64 раза.

Ответ: скорость химической реакции увеличилась в 64 раза.

Источник

Влияние природы реагирующих веществ

Влияние изменения концентрации

Влияние изменения температуры на скорость реакции

Катализаторы и ингибиторы

Температурный коэффициент скорости реакции

Химическая кинетика

Описание

Оглавление

1. Скорость химической реакции