Как найти коэффициент смещения зубчатого колеса

Параметры и обозначения Расчетные формулы
и указания Числовые значения шестерни
ведущей шестерни ведомой
(колеса) – 90 Модуль, m,мм – 8 Угол наклона зуба на делительной окружности β 17.2342 Угол профиля α – 20 Коэффициент высоты головки h_a – 1 Коэффициент граничной высоты h₁ – 2 Коэффициент радиального зазора (для стандартного контура) c>=0.25 – 0.25 Коэффициент высоты модификации головки h_g – 0.4 Коэффициент глубины модификации головки Δ – 0.008 Коэффициент смещения (коррекции) – x₁= 0.35 x₂= 0.3 Размер притупления продольной кромки вершины зубьев – k₁=1.5 k₂=1.5 Ширина венца у шестерни, – b₁=55 b₂=55 Расчет основных геометрических параметров Делительное межосевое расстояние, a, мм 376.92322 Угол профиля в торцовой плоскости α_t^o 20.86085 Расчет межосевого расстояния при заданных коэффициентах смещения Угол зацепления в торцовой плоскости inv α_tw^o Межосевое расстояние, мм Коэффициент суммы смещени ∑x=x₁+x₂ Делительный диаметр, мм d = z m /cos(β ) Передаточное число u = z₁ / z₂ Начальный диаметр, мм d_w1 = 2 a_w /(u+1);
d_w2 = 2 a_w u/(u+1) Коэффициент воспринимаемого смещения y = (a_w -a ) / m Коэффициент уравнительного смещения Δy = ∑x – y Диаметр вершин зубьев, мм d_a = d +2 (h_a+x-Δy)m; Диаметр впадин, мм d_f = d – 2 (h_a+c-x)m; Диаметр притупления кромок вершин зубьев, мм d_k = d_a – 2 k Расчет размеров для контроля номинальной поверхности зуба. Расчет размеров для контроля торцового профиля зуба. Основной диаметр, мм d_b = d cos(α_t) Угол профиля зуба в точке на окружности вершин, α_a^o α_a = acos(d_b/d_a) Угол профиля зуба в точке на окружности притупления кромок вершин, α_k^o α_k = acos(d_b/d_k) Радиус кривизны активного профиля зуба в нижней точке (без учета притупления), мм ρ_p1 = a_w sin(α_tw)-0,5 d_b2 tan(α_a2)
ρ_p2 = a_w sin(α_tw)-0,5 d_b1 tan(α_a1) Радиус кривизны активного профиля зуба в нижней точке (c учетом притупления), мм ρ_p1 = a_w sin(α_tw)-0,5 d_b2 tan(α_k2)
ρ_p2 = a_w sin(α_tw)-0,5 d_b1 tan(α_k1) Угол развернутости активного профиля зуба в нижней точке, ν_p^o ν_p = 2 ρ_p / d_b Диаметр окружности нижних точек активных профилей зубьев, d_p мм Расчет размера для контроля контактной линии поверхности зуба. Основной угол наклона β_b^o β_b=asin(sin(β) cos(α)) Дополнительный расчет при модификации головки исходного контура. Радиус кривизны профиля зуба в начальной точке модификации головки, мм., ρ_g ρ_g = 0.5 d₁ sin(α_t)+(h_a-h_b+x)m/ sin(α_t) Угол развернутости профиля зуба, соответствующий начальной точке модификации головки. ν_g^o ν_g = 2 ρ_g/ d_b Диаметр окружности нижних точек активных профилей зубьев, d_p мм Угол линии модификации головки торцового исходного контура в начальной точке модификации.α_tM^o Справедливы, если линия модификации головки исходного контура – прямая.
Диаметр основной окружности эвольвенты, являющейся линией модификации головки зуба, мм Справедливы, если линия модификации головки исходного контура – прямая.
d_bM = d cos(α_tM) Нормальная глубина модификации торцового профиля головки зуба, мм.Δ_at Справедливы, если линия модификации головки исходного контура – прямая.

Если имеется притупление продольной кромки зуба
Дополнительный расчет при модификации головки исходного контура. Расчет размеров для контроля взаимного положения разноименных профилей зубьев.
Расчет постоянной хорды и высоты до постоянной хорды. Постоянная хорда, мм s_c = [ (π / 2) (cos(α))² + x sin(2 α)] m Радиус кривизны разноименных профилей зуба в точках, определяющих постоянную хорду, мм ρ_s = 0.5 ( d_b tan(α_t)+ s_c cos(β_b) / cos(α) ) Условие ρ_s > ρ_p Высота до постоянной хорды, мм h_c = 0.5 ( d_a – d -s_c tan(α)) Расчет длины общей нормали. Угол профиля в точке на концентрической окружности диаметра d_x =d + 2 x m, ^o Расчетное число зубьев в длине общей нормали Длина общей нормали, мм W=[π ( Z_W – 0,5) + 2 x tan(α) + Z inv(α_t )] m cos(α) Радиус кривизны разноименных профилей зубьев в точках, определяющих длину общей нормали, мм ρ_g = 0,5 W cos(β_b) Радиус кривизны профиля зуба в точке на окружности вершин, мм ρ_a = 0,5 d_a sin(α_a) Должно выполняться условие ρ_p < ρ_W < ρ_α ρ_s < ρ_g Для косозубых зубчатых колес W < b / sin(β_b) Расчет толщины по хорде и высоты до хорды. Угол профиля в точке на концентрической окружности заданного диаметра d_y

d_y = d₁ α_y = acos[ (d₁/d_y ) ⋅ cos(α_t) ] в нижней активной точке зуба d_p α_y = acos[ (d₁/d_p ) ⋅ cos(α_t) ] Окружная толщина зуба на заданном диаметре d_y в нижней активной точке зуба d_y Угол наклона линии зуба соосной цилиндрической поверхности диаметра d_y β_y = atan [ (d_y ⋅ tan(β) / d ] β_p = atan [ (d_p ⋅ tan(β) / d ] Половина угловой толщины зуба эквивалентного зубчатого колеса, соответствующая концентрической окружности диаметра , град ψ_yv = (s_ty / d_y) ⋅ cos(β_y)³ ψ_pv = (s_ty / d_p) ⋅ cos(β_p)³ Толщина по хорде, мм s_y = d_y ⋅ sin(ψ_yv) / cos(β_y)² s_p = d_p ⋅ sin(ψ_pv) / cos(β_p)² Высота до хорды, мм h_ay = 0.5 [d_a – d_y + d_y ⋅ (1 – cos(ψ_yv)) / cos(β_y)²] h_py = 0.5 [d_a – d_p + d_p ⋅ (1 – cos(ψ_pv)) / cos(β_p)²] Расчет размера по роликам (шарикам). Диаметр ролика (шарика), мм.
при a=20 град. рекомендуется D = 1,7 ⋅ m Угол профиля на концентрической окружности, проходящей через центр шарика α_D^o Диаметр концентрической окружности, проходящей через центр шарика, проходящей через центр шарика, мм d_D = d ⋅ cos(α_t) / cos(a_D) Радиус кривизны разноименных профилей зубьев в точках контакта поверхности ролика (шарика) с главными поверхностями зубьев, мм ρ_M = 0,5 ⋅ (d_b ⋅ tan(a_D) – D ⋅ cos(β_b)) Размер по роликам (шарикам) зубчатых колес с числом зубьев (в торцовом сечении), мм четным M = d_D + D

нечетным M = d_D ⋅ cos(90^o / z) + D Минимальный размер по роликам (шарикам) косозубых зубчатых колес с нечетным числом зубьев, а также с четным числом зубьев при β >45°
Минимальный размер по роликам (шарикам) косозубых зубчатых колес с четным числом зубьев β < 45° совпадает с размером в торцовом сечении β_D = atan(cos(α_t) ⋅ tan(β) / cos(a_D)) при z четным γ = 0
при z нечетным γ = 180 / z λ – корень уравнения
sin(γ + λ) ⋅ tan²(β_D) – λ = 0 Должны выполняться условия ρ_p <  ρ_M < ρ_α d_D + D > d_a d_D – D > d_f Нормальная толщин s_n = ( π / 2 + 2 ⋅ x ⋅ tan(α) )⋅ m Расчет размеров для контроля взаимного положения одноименных профилей зубьев Шаг зацепления, мм P_a = π ⋅ m ⋅ cos(α) Осевой шаг зубьев, мм P_x = π ⋅ m / sin(β) Ход зуба, мм P_z = z ⋅ P_x Проверка качества зацепления по геометрическим показателям
Проверка отсутствия подрезания зуба Коэффициент наименьшего смещения x_min = h₁ – h_a – z ⋅ sin²(α_t) / 2 ⋅ cos(β) подрезание зуба исходной производящей рейкой x ≥ x_min Проверка отсутствия интерференции зубьев Радиус кривизны в граничной точке профиля зуба, мм ρ₁ = 0,5 ⋅ d ⋅ sin(α_t) – (h₁ – h_a – x) ⋅ m / sin(α_t) интерференция зубьев ρ₁ ≤ ρ_p Проверка коэффициента перекрытия Коэффициент торцового перекрытия
При наличии притупления продольной кромки вершин зубьев ε_α = [z₁ ⋅ tan(α_a1) + z₂ ⋅ tan(α_a2) – (z₁+z₂ ) ⋅ tan(α_tw) ] / ( 2 ⋅ π)
ε_αk = [z₁ ⋅ tan(α_k) + z₂ ⋅ tan(α_k2) – (z₁+z₂ ) ⋅ tan(α_tw) ] / ( 2 ⋅ π)
прямозубые ε_α > 1,2
косозубые ε_α > 1,0 Коэффициент осевого перекрытия ε _β = b_w / ρ_x > 1,0
b_w – рабочая ширина венца Коэффициент перекрытия ε = ε_α + ε _β > 2 Угол профиля зуба в начальной точке модификации головки cos(α_g) = d_b / d_g Часть коэффициента торцового перекрытия, определяемая участками торцовых профилей зубьев, совпадающих с главными профилями ε_αM = [z₁ ⋅ tan(α_g1) + z₂ ⋅ tan(α_g2) – (z₁+z₂ ) ⋅ tan(α_tw) ] / ( 2 ⋅ π) Угол наклона линии вершины зуба tan(β_α) = tan(β) ⋅ d_a / d Нормальная толщина на поверхности вершин, мм
s_na > 0.4 m

Анализ качественных показателей зубчатой передачи

Анализ зубчатой передачи

Провести анализ качественных показателей зубчатой передачи – значит решить сложную оптимизационную задачу, содержащую большое количество параметров. Инженерам такие задачи приходится решать очень часто. Связано это с тем, что невозможно создать одинаково хорошее решение во всех аспектах – всегда приходится принимать определенные уступки.

Поэтому для проведения оптимизации каждый из параметров рассматривается по отдельности. Выделяется область его оптимальных значений, а затем все полученные области накладываются друг на друга с выделение такого решения, которое будет не самым лучшим, а удовлетворять наиболее важным требованиям надежности, экономичности и безопасности.

Качественные показатели зубчатой передачи – совокупность параметров, характеризующих зубчатых передачу с точки зрения надежности, контактной прочности, плавности передачи вращающего момента и долговечности. К таким параметрам относятся:

• коэффициент торцевого перекрытия
• коэффициенты удельного скольжения
• коэффициент удельного давления
• приведенные толщины зубьев по окружности вершин

Проведите расчет качественных показателей онлайн в калькуляторе, а затем приступайте к анализу! Задано межосевое расстояние? Тебе сюда!

Алгоритм анализа качественных показателей:

• Определить исходные данные из текста задания.
• Выбрать коэффициент смещения для колеса исходя из рекомендаций.
• Провести расчет геометрических параметров и качественных показателей, варьируя значения коэффициента смещения шестерни.
• Выделить область подрезания из условия:

  $$Xgeq X_{min}$$

• Выделить область заострения из условия:

  $$S_{a}^{*}geq [S_{a}^{*}]_{доп}$$

• Выделить область технического заострения из условия:

  $$varepsilon_alphageq[varepsilon_alpha]_{доп}$$

• Определить область допустимых решений/значений (ОДР/ОДЗ)
• Оценить потенциально возможные значения коэффициента смещения шестерни по наличию стандартного инструмента, равномерному износу колес.

Результатом анализа является график качественных показателей и выбранный коэффициент смещения шестерни. Пример полученного графика:

График качественных показателей

Мы подготовили небольшое видео, в котором изложены основные этапы анализа качественных показателей:

Параметры, определяющие ОДР

Коэффициент смещения – величина, равная отношению смещения производящего исходного контура к нормальному модулю цилиндрического зубчатого колеса. В зависимости от величины и знака этого смещения различают зубчатые передачи:

• Положительные – составленные из колес с положительными смещениями или когда положительное смещение одного колеса больше отрицательного смещения другого (рис. а).
• Нулевые или равносмещенные – составленные из зубчатых колес без смещения или с равными, но противоположенными по знаку смещениями (рис. б).
• Отрицательные – составленные из колес с отрицательными смещениями или когда отрицательное смещение одного колеса больше положительного смещения другого (рис. в).

Виды зубчатых передач

Подрезание – негативное последствие, возникающее, когда точка B_l активного участка линии зацепления выходит за границы зоны сопряженного контакта (B_{l}N). Возникновение подрезания происходит при неграмотном выборе коэффициента смещения, в случае, когда не выполняется условие:

$$Xgeq X_{min}=h_{a}^{*}cdotdfrac{Z_{min}-Z}{Z_{min}}$$

где

$$Z_{min}=dfrac{2cdot h_{a}{*}}{sin^2(alpha)}$$

(alpha) – угол главного профиля;

(Z) – число зубьев проектируемого зубчатого колеса;

(h_{a}^{*}) – коэффициент высоты головки зуба.

Иллюстрация возникновения подрезания при изменении коэффициента смещения проектируемого колеса:

Возникновение подрезания

Для стандартного инструмента число зубьев, при котором колесо может быть нарезано без смещения, должно быть больше (17).

Заострение – негативное последствие, вызванное заострением вершины зуба по окружности вершин при увеличении коэффициента смещения. При проектировании передачи следует избегать заострения, для этого необходимо выполнение следующего условия:

$$S_{a}^{*}geq [S_{a}^{*}]_{доп}$$

$$S_{a}^{*}=dfrac{S_{a}}{m_{t}}$$

т. е. приведенная толщина зуба по окружности вершин должна быть больше некоторого принятого допустимого значения, которое выбирают в пределах от (0.2…0.45).

Техническое заострение – явление, возникающее при малом значении коэффициента перекрытия. Тогда в каждый момент времени в зацеплении находится меньше определенного значения пар зубьев в зацеплении.

В предельном случае, когда коэффициент перекрытия меньше (1), после выхода очередной пары зубьев из зацепления, следующая пара еще не входит в зацепление. В результате возникают циклические нагрузки из-за удара зубьев ведущей шестерни о зубья ведомого колеса. Это явление называют стук.

При многократных ударах, способствующих возникновению шума, возникает техническое заострение, т. е. негативное последствие связанное с разрушением зубьев возникает уже в процессе работы.

Коэффициентом перекрытия (varepsilon_{gamma}) называется величина отношения угла перекрытия зубчатого колеса (varphi_alpha) к его угловому шагу (tau), где под углом перекрытия понимают угол, на который поворачивается колесо за время зацепления одной пары зубьев.

Для цилиндрических колес различают:

• полное (varepsilon_{gamma})
• торцевое (varepsilon_{alpha})
• осевое перекрытие (varepsilon_{beta})

Коэффициент торцевого перекрытия (varepsilon_{alpha}) может быть определен следующим образом:

$$varepsilon_{alpha}=dfrac{varphi_{alpha 1}}{tau_1}=dfrac{varphi_{alpha2}}{tau_2}=dfrac{g_{alpha}}{p_b}=dfrac{g_{alpha f}+g_{alpha b}}{p_b}$$

где

$$g_{alpha f}=l_{PN_2}-l_{B_1N_2}=arccosleft(dfrac{r_{b2}}{r_{a2}}right)$$

$$g_{alpha a}=l_{PN_1}-l_{B_2N_1}=arccosleft(dfrac{r_{b1}}{r_{a1}}right)$$

$$p_b=picdot m cdot cos(alpha)$$

$$r_{b_i}=mcdot Z_i cdot cosleft(dfrac{alpha}{2}right)$$

(alpha) – угол главного профиля исходного контура;

К определению коэффициента перекрытия

Обозначения (l_{B_1N_2}, l_{PN_2}) и т. д. – длины с чертежа.

Коэффициент перекрытия определяет величину зоны контакта двух пар зубьев, когда одновременно зацепляются два последовательно расположенных зуба. Так как до окончания зацепления одной пары зубьев следующая пара должна войти в контакт, в прямозубых передачах следует обеспечивать (varepsilon_alphageq1.05…1.25).

Допустимое значение коэффициента перекрытия выбирается исходя из назначения передачи и точности ее изготовления. Максимальное значение коэффициента перекрытия для зубчатых колес, обработанных инструментом со стандартным исходным производящим контуром, составляет (varepsilon_alpha=1.98).

Коэффициент удельного давления (nu) характеризует влияние формы зуба на контактную прочность и используется для оценки контактных напряжений в высшей кинематической паре. В курсовом проекте по ТММ в месте контакта имеет место сухое трение, поэтому данный коэффициент изменяется незначительно при любом значении коэффициента смещения.

Коэффициенты удельного скольжения (lambda_1, lambda_2) характеризуют скольжение при геометрических расчетах зубчатой передачи, которые, в свою очередь, определяют величину износа активного профиля в высшей кинематической паре. Износ шестерни с увеличение коэффициента смещения уменьшается, и, наоборот, очень быстро увеличивается при приближении к минимальному значению этого коэффициента. Зависимость изменения износа колеса меняется не сильно в области рассматриваемых значений коэффициентов смещения шестерни.

Приведенные толщины зубьев по окружности вершин (S_{a1}^{*}, S_{a2}^{*}) – величины, равные отношению толщины зуба по окружности вершин к модулю передачи, характеризующие степень утоньшения вершины зуба. Применяются для нахождения ограничения коэффициента смещения шестерни по условию отсутствия заострения. С увеличением коэффициента смещения шестерни этот параметр равномерно убывает для шестерни и возрастает для колеса.

Построение станочного и рабочего зацепления доступно на сайте. Проектирование планетарных механизмов и определение передаточного отношения методом Л. П. Смирнова рассмотрено подробно в разделе.

Коэффициент
смещения. Взаимное
положение колеса и заготовки при
нарезании зубьев можно охарактеризовать
положением делительной прямой
инструментальной рейки относительно
делительной окружности нарезаемого
колеса (рис. 5.7); расстояние между ними
называют смещением
исходного контура,
его выражают в количестве модулей, как
xm.

Рис. 5.7

Безразмерную
величину x
называют
коэффициентом
смещения;
это алгебраическая величина и здесь
различают три случая, показанные рис.
5.7, а
– в. Нарезая
зубья при различных коэффициентах
смещения, можно целенаправленно влиять
на размеры и форму этих зубьев, а также
на свойства колес и составленных из них
передач.

Часть
параметров и размеров зубчатого колеса
не зависит от коэффициента смещения; к
таковым относятся:

модуль
m;

угол
профиля эвольвенты на делительной
окружности (равен
углу профиля исходного контура) ;

шаг
по дуге основной окружности
(основной шаг)

.
(5.12)

Значения
этих трех параметров у нарезаемого
колеса те же, что и у зуборезного
инструмента.

Также
не зависят от x:

диаметр
делительной окружности
(делительный диаметр)

;
(5.13)

диаметр
основной окружности
(основной диаметр)

.
(5.14)

При
нарезании зубьев поверхность их вершин
не формируется, т.е. диаметр
окружности вершин колеса

(диаметр вершин) остается равным диаметру
заготовки; следовательно, нарезание
зубьев – это попросту удаление материала
из впадин колеса.

а б Рис. 5.8

На
рис. 5.8 изображены профиль зуба реечного
производящего контура (а)
и формируемый им при нарезании профиль
зуба колеса (б).
Во время нарезания начальная прямая 2
производящей рейки перекатывается без
скольжения по делительной окружности
колеса.

На
указанных профилях отмечены соответствующие
друг другу точки и участки профилей; в
частности:

 эвольвентный
участок AL
профиля нарезаемого зуба формируется
прямолинейным участком
профиля зуба рейки;

 переходная
кривая LF
на профиле зуба колеса формируется
круговой кромкой
профиля
зуба рейки;

 вершина
зуба рейки, параллельная ее делительной
прямой 1, формирует окружность впадин
диаметра
колеса.

Очевидно,
что часть профиля зуба рейки, расположенная
выше точки
,
в профилировании нарезаемого зуба не
участвует.

Найдем
размеры колеса, зависящие от коэффициента
смещения x:

толщина
зуба по дуге делительной окружности
(делительная толщина зуба) колеса

;
(5.15)

диаметр
окружности впадин
(диаметр впадин)

,

(5.16)

или

.
(5.17)

Важным
параметром, характеризующим профиль
эвольвентного зуба, является положение
нижней граничной точки
L
эвольвенты
(рис.
5.8) – общей точки эвольвенты и переходной
кривой. При нарезании зубьев указанная
точка профиля формируется точкой
зуборезной рейки; исходя из этого для
точкиL
наиболее просто можно найти угол профиля
:

тангенс угла профиля
в нижней граничной точке эвольвенты

.
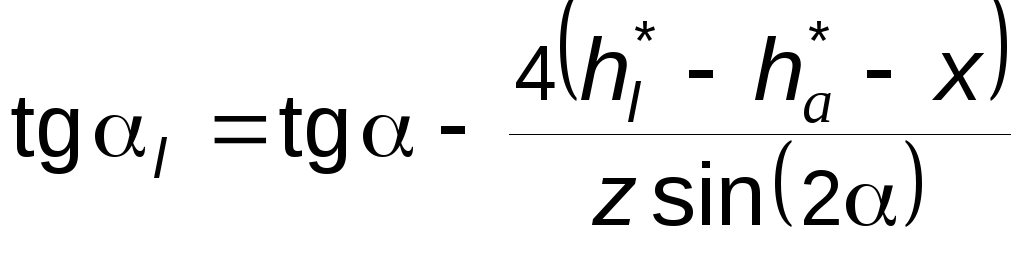
(5.18)

Согласно (5.5), диаметр
окружности граничных точек

;
(5.19)

при
,
или при

(5.20)

а б Рис. 5.9

эвольвента
в точке L
плавно сопрягается с переходной
кривой
(рис. 5.9,а);
при нарушении этого условия наблюдается
подрезание зубьев
(рис. 5.9, б),
которое выражается в том, что переходная
кривая пересекает эвольвенту несколько
выше основной окружности. В этом случае
формула (5.19) не справедлива.

Величину
называюткоэффициентом
наименьшего смещения исходного контура
(коэффициентом
наименьшего смещения).

Из
(5.18) также видно, что у колеса, имеющего
z
зубьев и нарезанного с коэффициентом
смещения x,
подрезание отсутствует, если

.
(5.21)

Величину

называют наименьшим
числом зубьев свободным от подрезания
(наименьшим
числом зубьев).

Подрезание
ослабляет зуб у основания, укорачивает
эвольвентный участок профиля и его
обычно стараются избегать; условием
отсутс–твия подрезания является
соблюдение любого из неравенств:

;

;.

Рис. 5.10

Толщина
зуба
по дуге окружности заданного диаметра.

Угол
профиля в точке Y,
принадлежащей окружности диаметра
(рис. 5.10), равен

;
(5.22)

если
эта точка принадлежит делительной
окружности (т.е.
),
угол профиляравен углу профиля исходного контура,
так как

.

В таком случае из рис.
5.10 следует, что искомая толщина зуба
равна

.
(5.23)

Формулу
(5.23) используют, например, для нахождения
толщины зуба
по дуге окружности вершин: приимеем

;
(5.24)

.
(5.25)

Окружность,
на которой расположена точка пересечения
двух разноименных эвольвент, ограничивающих
профиль одного и того же зуба, называют
окружностью
заострения (рис.
5.10); ее диаметр
находят
из условия равенства нулю правой части
выражения (5.25):

;
(5.26)

.
(5.27)

Формулой
(5.23) пользуются также для нахождения
толщины зуба
по дуге основной окружности(основной
толщины зуба); при
из (5.22) имееми тогда

.
(5.28)

При
проектировании зубчатых передач обычно
стремятся, чтобы толщина зуба
была не меньше некоторой минимально
допустимой величины. Часто применяют
такие нормы:

	– для колес с поверхностным упрочнением зубьев;
– для зубьев без поверхностного упрочнения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #