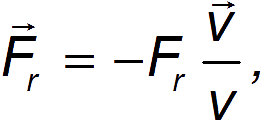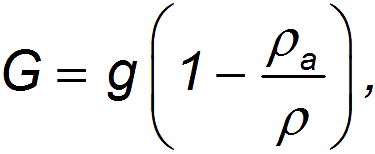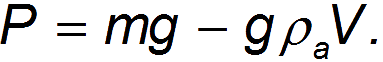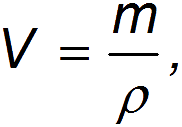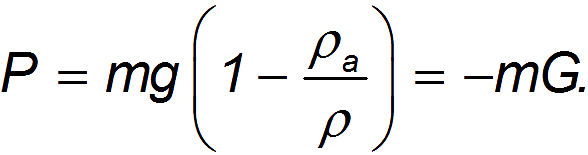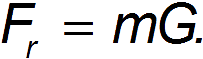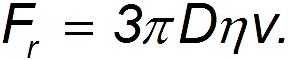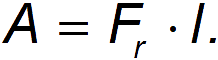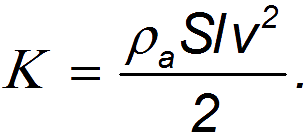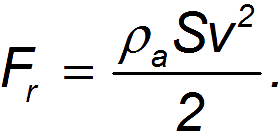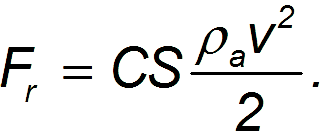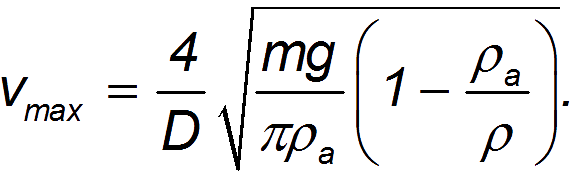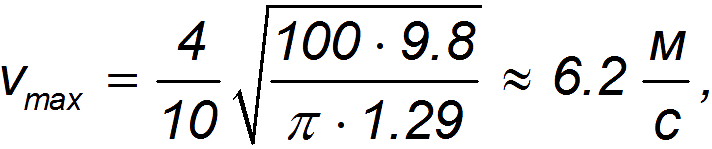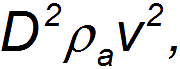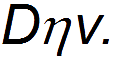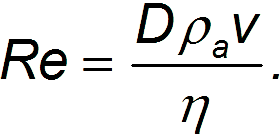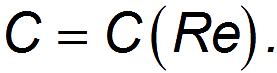Сила сопротивления зависит от размеров и формы тела и скорости перемещения тела в среде, возникающая при его движении и затормаживает это движение. Сила сопротивления отличается от силы трения тем, что последняя рассматривает характер взаимодействия друг с другом твердых тел. Можно наблюдать, когда один элемент двигается по поверхности другого. Вектор силы сопротивления имеет направление противоположное движению.
Работа силы сопротивления видна на примере: при свободном падении листка с дерева на него действует сила сопротивления воздуха, которую можно сравнить с силой тяжести. В связи с этим, ускорение падающего листка будет не таким, как от ускорения свободного падения.
Аналогично с перемещением в жидкости, если тело погружается в воду плавно, то сопротивление воды будет меньше, чем при прыжке в нее.
Чему равна сила сопротивления
В числовом выражении общая сила сопротивления равна силе, которую следует приложить для равномерного передвижения тела по ровной горизонтальной поверхности. Определяется третьим законом Ньютона.
Формулы 1 — 3
Сила сопротивления прямо пропорциональна массе тела и вычисляется по формуле:
[F=mu * m * g]
где [boldsymbol{mu}] коэффициент материала изготовления опоры, выбирается по таблице;
g – постоянная величина равная 9,8 м/с2.
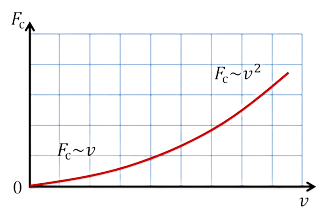
Для тел с небольшой скоростью сила сопротивления рассчитывается как произведение коэффициента сопротивления материала (a) и силы, провоцирующую движение предмета (v).
[F=v a]
где v — скорость движения предмета, a — коэффициент сопротивления среды.
При высоких скоростях или больших размеров предметов, силу сопротивления вычисляют пропорционально квадрату скорости.
[F=c v^{2}]
Зависимость силы от сопротивления определяется для каждой среды отдельно. Сила сопротивления среды растет, с ростом скорости движения предмета в среде.
От чего зависит сила сопротивления
На величину силы сопротивления влияют следующие факторы:
- особенности и плотность среды, например, у жидкости плотность выше, чем у газа;
- форма тела, у предметов с вытянутыми обтекаемыми вдоль движения формами сопротивление меньше, чем с расположенными перпендикулярно движению гранями;
- скорость движения.
В зависимости от воздействия на движущиеся предметы различают несколько типов силы сопротивления:
- Сила сопротивления качению [P_{f}]. Зависит от вида и состояния опорной поверхности, скорости перемещения, силы давления воздуха и прочее. Коэффициент сопротивлению качению f зависит типа и состояния опорной поверхности, его значение уменьшается, при повышении давления и температуры.
- Сила сопротивления воздуха [P_{B}] возникает при разных показателях давления. В аэродинамике называется лобовым сопротивлением. Показатель будет выше с ростом вихреобразования в передней и задней частях объекта движения. Величина вихреобразования зависит от формы передвигаемых предметов.
Понятие силы электрического сопротивления
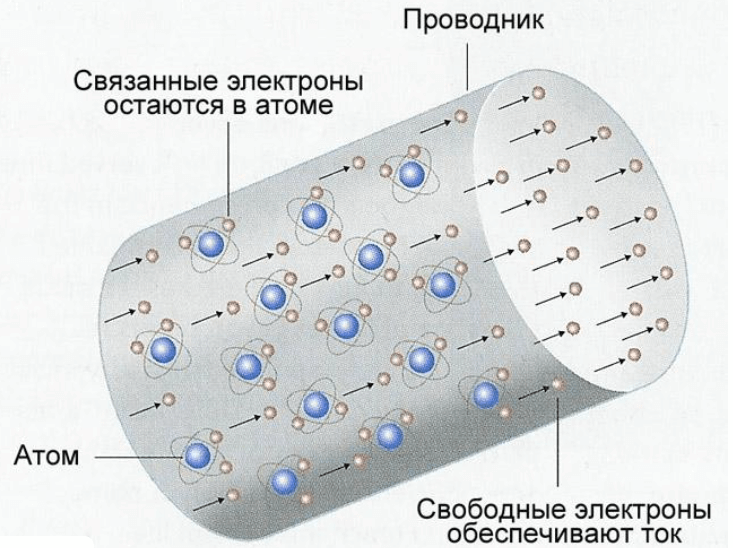
Строение металлических проводников объясняет наличие сопротивления. Свободные электроны движутся по проводнику встречая ионы кристаллической решетки. При контакте с ними другие электроны теряют часть своей энергии. У проводников с отличающимся атомным строением будет разное сопротивление току. Поэтому чем выше сопротивление проводника, тем проводимость электрического тока будет меньше.
Формулы 4 — 5
Электрическое сопротивление в физике обозначают R, измеряется в Ом. Сопротивление равно 1 Ом, если на концах проводника возникает напряжение в 1 Вольт при силе тока равной 1 Ампер.
Формула сопротивления силы тока:
[R=rho frac{l}{S}]
где l – длина проводника; S – площадь сечения; ρ – удельное сопротивление.
Сила электрического сопротивления зависит от материала проводника, его длины, формы и температуры. Удельное сопротивление отличается у различных материалов.
Удельное сопротивление [boldsymbol{(rho)}] — сопротивление проводника длиной 1м и обладающего площадью поперечного сечения [boldsymbol{1м^{2}}]. Обозначается в Ом*м. К примеру, удельное сопротивления меди [1,7 * 10^{-8} Oм * м], это значит, что у медного проводника длиной [1м^{2}] сопротивление равно [1,7 * 10^{-8} Ом].
Сопротивление проводника будет расти с увеличением температуры:
[rho=rho_{o}(1+alpha Delta T)]
где [boldsymbol{rho_{0}}] – обозначает удельное сопротивление при [T_{0}=293 mathrm{~K}left(20^{circ} mathrm{C}right), Delta T=T-T_{0}], α – температурный коэффициент сопротивления [left(K^{-1}right)].
При нагревании движение частиц материала возрастает и создает препятствия для направленного движения электродов. Количество столкновений свободных электронов с ионами кристаллической решетки увеличивается.
Такое свойство применимо в термометрах сопротивления, измеряют температуру исходя из зависимости температуры и сопротивления с высокой точностью измерения.
Нет времени решать самому?
Наши эксперты помогут!
Формула силы тока и сопротивление
Формула 6
Законом Ома для участка цепи называют взаимосвязь между силой тока (I), напряжением (U) и сопротивлением (R) проводника на практике установлена Г. Омом.
[I=frac{U}{R}]
Материалы с низким удельным сопротивлением считаются проводниками, они эффективно проводят электрический ток. С высоким удельным сопротивлением – диэлектрики, их используют как изоляторы. Промежуточное положение занимают полупроводники.
Пример
Найти силу тока в проводнике длиной 100 мм, сечением 0,5 мм2 изготовленном из меди, если напряжение на его концах 6,8 В.
Решение:
Запишем формулу закона Ома и найдем сопротивление через силу тока : [I=frac{U}{R}]
Для определения силы тока I, нужно определить сопротивление R. С помощью формулы с удельным сопротивлением преобразуем формулу для закона Ома:
[begin{array}{r}
R=rho frac{l}{S} \
I=frac{U S}{rho l}
end{array}]
Подставляем значения в формулу:
[I=frac{6,8 * 0,5}{0,017 * 100}=2 mathrm{~A}]
Значение ρ для меди берется из таблиц.
Ответ: 2А
Коэффициент сопротивления
Коэффициент сопротивления дает возможность учитывать потери энергии при движении тела. Чаще всего рассматривают два типа движения: движение по поверхности и движение в веществе (жидкости или газе). Если рассматривают движение по опоре, то обычно говорят о коэффициенте трения. В том случае, если рассматривают движение тела в жидкости или газе, то имеют в виду коэффициент сопротивления формы.
Определение коэффициента сопротивления (трения) скольжения
Речь идет о коэффициенте трения скольжения, который зависит от совокупных свойств трущихся поверхностей и является безразмерной величиной. Коэффициент трения зависит от: качества обработки поверхностей, трущихся тел, присутствия на них грязи, скорости движения тел друг относительно друга и т.д. Коэффициент трения определяют эмпирически (опытным путем).
Определение коэффициент сопротивления (трения) качения
Данный коэффициент, имеет размерность длины. Основной его единицей в системе СИ будет метр.
Определение коэффициента сопротивления формы
Иногда, если рассматривают движение вытянутого тела, то считают:
где V — объем тела.
Рассматриваемый коэффициент сопротивления является безразмерной величиной. Он не учитывает эффектов на поверхности тел, поэтому формула (3) может стать не пригодна, если рассматривается вещество, которое имеет большую вязкость. Коэффициент сопротивления (C) является постоянной величиной пока число Рейнольдса (Re) является неизменным. В общем случае .
Если тело имеет острые ребра, то эмпирически получено, что для таких тел коэффициент сопротивления остается постоянным в широкой области чисел Рейнольдса. Так опытным путем получено, что для круглых пластинок поставленных поперек воздушного потока, при значения коэффициента сопротивления находятся в пределах от 1,1 до 1,12. При уменьшении числа Рейнольдса (
) закон сопротивления переходит в закон Стокса, который для круглых пластинок имеет вид:
Сопротивление шаров было исследовано для широкой области чисел Рейнольдса до Для
получили:
При ,
.
В справочниках представлены коэффициенты сопротивления для круглых цилиндров, шаров и круглых пластинок в зависимости от числа Рейнольдса.
В авиационной технике задача о нахождении формы тела с минимальным сопротивлением имеет особое значение.
Примеры решения задач
коэффициент сопротивления
- коэффициент сопротивления
-
damping coefficient
Шифр IFToMM: —
Теория механизмов и машин. Терминология: Учеб. пособие. — М.: Изд-во МГТУ им. Н.Э. Баумана.
.
2004.
Смотреть что такое «коэффициент сопротивления» в других словарях:
-
коэффициент сопротивления ζ — Отношение потерянного давления к скоростному (динамическому) давлению в условленном (принятом) проходном сечении. [ГОСТ Р 52720 2007, статья 6.13] Источник: ГО … Словарь-справочник терминов нормативно-технической документации
-
коэффициент сопротивления — сопротивление Взятое с противоположным знаком отношение диссипативной силы или момента к соответствующей обобщенной скорости для линейной системы (см. примечание к термину характеристика восстанавливающей силы (момента)). [ГОСТ 24346 80] Тематики … Справочник технического переводчика
-
КОЭФФИЦИЕНТ СОПРОТИВЛЕНИЯ — отношение тяглового усилия к массе перевозимой л. повозки с грузом. Зависит от кач ва дороги и устройства колес. При увеличении К. с. л, вынуждена развивать большее тяговое усилие для перевозки неизменяющегося груза. Для повозок на желез. ходу К … Справочник по коневодству
-
Коэффициент сопротивления — 102. Коэффициент сопротивления Сопротивление Взятое с противоположным знаком отношение диссипативной силы или момента к соответствующей обобщенной скорости для линейной системы (см. примечание к термину 94) Источник: ГОСТ 24346 80: Вибрация.… … Словарь-справочник терминов нормативно-технической документации
-
коэффициент сопротивления (ξ) — 6.13 коэффициент сопротивления (ξ) коэффициент гидравлического сопротивления Нр. Отношение потерянного давления к скоростному (динамическому) давлению в условленном (принятом) проходном сечении. Примечание Для запорной арматуры коэффициент… … Словарь-справочник терминов нормативно-технической документации
-
коэффициент сопротивления парашюта — коэффициент сопротивления сп Отношение силы сопротивления парашюта к произведению площади парашюта на скоростной напор. [ГОСТ 21452—88] Тематики парашютные системы Синонимы коэффициент сопротивления … Справочник технического переводчика
-
коэффициент сопротивления качению колеса — f Условная количественная характеристика сопротивления качению колеса, равная отношению силы сопротивления качению колеса к его нормальной нагрузке: [ГОСТ 17697 72] Тематики автомобили, качение колеса Обобщающие термины характеристики… … Справочник технического переводчика
-
коэффициент сопротивления (в трубопроводной арматуре) — коэффициент сопротивления Отношение потерянного давления к скоростному (динамическому) давлению в условленном (принятом) проходном сечении. Примечание Для запорной арматуры коэффициент сопротивления указывается при полностью открытом положении… … Справочник технического переводчика
-
коэффициент сопротивления боковому уводу шины — коэффициент сопротивления уводу шины Ky Первая производная боковой силы колеса по углу бокового увода: [ГОСТ 17697 72] Тематики автомобили, качение колеса Обобщающие термины коэффициенты, характеризующие упругие свойства шины колеса … Справочник технического переводчика
-
Коэффициент сопротивления диффузии водяного пара — m – отношение паропроницаемости воздуха к паропроницаемости материала или рассматриваемого однородного изделия. Данное отношение характеризует относительное значение сопротивления изделия водяному пару и слоя воздуха равной толщины при той… … Энциклопедия терминов, определений и пояснений строительных материалов
-
коэффициент сопротивления (среды) — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN friction factor … Справочник технического переводчика
Зависимость электрического сопротивления от температуры
Содержание
- 1 Сопротивление
- 2 Коэффициент сопротивления
- 2.1 Газы
- 2.2 Жидкости
- 3 Сверхпроводимость
- 4 Применение
- 4.1 Резистор
- 4.2 Терморезистор
- 4.3 Термометр сопротивления
- 4.4 Газ
- 5 Заключение
- 6 Видео по теме
При проектировании электрических схем, инженеры сталкиваются с тем, что проводники обладают определенным сопротивлением, на которое оказывают влияния температурные колебания. Статья даст подробное описание, что такое зависимость сопротивления от температуры и как температура влияет на проводимость различных веществ — металлов, газов и жидкостей. Дополнительно будет приведена формула расчета такой зависимости.
Сопротивление
Сопротивлением называется способность проводника пропускать через себя электрический ток. Единицей измерения данной физической величины является Ом. На принципиальных схемах эта величина обозначается буквой «R». На величину сопротивления любого проводника электрическому току влияет его структура. Двигаясь внутри структуры, свободные электроны сталкиваются с атомами и электронами, которые замедляют их движение. Чем их концентрация больше, тем выше будет само электрическое сопротивление.
О способности проводников проводит электрический ток судят по величине его удельного сопротивления. Удельное сопротивление проводника — это сопротивление протеканию тока через проводник из любого вещества с площадью поперечного сечения 1 м² и длиной один метр. Обозначается в физике данная величина буквой «ρ». Данный параметр является табличной величиной и измеряется в системе СИ как Ом×м (может также измеряться в Ом×см и Ом×мм²/м).
Коэффициент сопротивления
Во время работы электрических цепей прослеживается прямая зависимость сопротивления металлов от температуры. Это явление называют коэффициентом температурного сопротивления. Оно определяет соотношение сопротивления к температурным изменениям. Объясняется это явление следующим образом: с повышением температуры структура проводника получает долю тепловой энергии, вследствие чего эта энергия увеличивает скорость движения атомов. В результате повышается вероятность их столкновения со свободными электронами. Чем чаще происходят эти столкновения, тем ниже будет проводимость.
Можно провести простой опыт: в электрическую схему из аккумулятора и омметра подключим кусок медной проволоки. При таком подключении схема будет иметь строго определенное значение сопротивления. Далее надо будет нагреть медную проволоку. В момент нагрева можно заметить, что сопротивление всей схемы растет, а после остывания проводника оно наоборот уменьшается. На основании такого опыта довольно просто прослеживается температурная зависимость сопротивления проводника.
Температурный коэффициент отображает увеличение сопротивления при изменении температуры вещества на 1 градус. Для максимально чистого металла это значение равняется 0.004 °С-1. То есть, при увеличении температуры на 10 градусов, электрическая проводимость в металлах изменится на 4 % в большую сторону. Данная величина обозначается буквой «α». При расчете сопротивления через удельное сопротивление используется такая формула:
В данной зависимости:
- «R» — сопротивление, Ом;
- «l» — длина проводника, м;
- «s» — поперечное сечение проводника, м²;
- «ρ» — значение удельного сопротивления, Ом×м.
Зависимость проводимости металлического проводника от температуры можно проследить с помощью таких выражений:
Для металлов все предельно просто — изменение температуры приводит к увеличению его сопротивления. Ниже будет дано описание этой зависимости для газов, которые по своей природе являются диэлектриками.
Для закрепления материала, решим следующую задачу:
Имеется стальной проводник, диаметр которого равен один миллиметр, а длина его составляет 100 метров. Определите сопротивление такого проводника из стали, если величина удельного сопротивления стального проводника составляет 12×10-8 Ом×м.
Решение:
d=1 мм;
l=100 м;
ρ=13×10-8 Ом×м;
R–?
Определяем сопротивление проводника по формуле:
R=ρ(l/S)
где S является площадью поперечного сечения. Определить площадь можно с помощью формулы:
S= π×r2= π×d2/22=3.14×(1×10-3)2/4=3.14×10-6/4=0.785×10-6м2
После этого можно определить сопротивление:
R=12×10-8×100/(0.785×10-6)=15.287 Ом
Газы
Газы не являются проводниками, но их проводимость так же зависит от температуры. Происходит это за счет так называемого эффекта ионизации. Ионизация в газах происходит за счет насыщения их жидкостью или иными веществами, которые способны проводить электрический ток. Проследить то, как увеличивается сопротивление при повышении температуры газа можно на таком опыте.
К схеме с амперметром и аккумулятором добавим 2 металлические пластины, которые не соприкасаются друг с другом. Такая электрическая цепь является разомкнутой. Между пластинами поместим зажженную горелку. При нагреве происходит смещение стрелки амперметра в сторону увеличения. То есть такую цепь можно считать замкнутой. На основании этого можно сделать вывод, что с ростом температуры воздух ионизируется, происходит снижение его сопротивления и увеличение проводимости заряженных электронов. Данный эффект называют пробоем изоляционного слоя газа, зависящий от степени их ионизации и величины протекающего напряжения. Подобное явление знакомо каждому из нас — это грозовой разряд.
Жидкости
В жидкостях прослеживается обратная зависимость. С увеличением температуры, сопротивление жидкого проводника уменьшается. Для электролита свойственно правило отрицательного значения температурного коэффициента — а˂0. Удельное сопротивление электролита рассчитывается следующим образом:
ρ= ρ0(1+ αt) или R=R0(1+ αt), где а˂0.
При этом увеличившееся значение температуры электролита сопровождается уменьшением сопротивления и ростом его проводимости.
Сверхпроводимость
Снижение температуры металлических проводников сильно увеличивает их проводимость. Это связано с тем, что в структуре вещества замедляется движение атомов и электронов, благодаря чему снижается вероятность их столкновения со свободными электронами. При температуре абсолютного 0 (–273 градуса Цельсия) возникает явление падения до нуля сопротивления проводника. Зависимость сопротивления проводника от температуры при абсолютном 0 — сверхпроводимость.
Температура, при которой обычный проводник становится сверхпроводником, называется критической. Она будет разной для различных чистых металлов и сплавов. Все будет зависеть от их структуры, химического состава и структуры кристаллов. Например, серое олово с алмазной структурой является полупроводником. Но белое олово при своей тетрагональной кристаллической ячейке, мягкости и плавкости, переходит в состояние сверхпроводника при температуре 3.70 К. Также при критической температуре прослеживается целый ряд других способностей:
- Повышение частоты переменного тока вызывает рост сопротивления, значение гармоник с периодом световой волны.
- Способность удерживать величину силы тока ранее приложенного, а затем отключенного источника.
Металл или сплав может перейти в состояние сверхпроводника и при нагревании. Такое явление называют высокотемпературной проводимостью. Ответ на вопрос, почему от высокой температуры сопротивление металлов снижается, может довольно просто объяснить их кристаллическая структура. В момент нагрева до критических значений, электроны перестают хаотично перемещаться внутри структуры вещества. Они выстраиваются в цепочку. Такое построение не мешает движению свободных электронов, а значит падает общее сопротивление. Переход в состояние высокотемпературной проводимости начинается с порога 1000К и этот показатель выше, чем точка кипения азота.
Применение
Свойство проводников изменять сопротивление при определённой температуре используют для создания различных элементов электрических схем и измерительных приборов. О них будет рассказано далее в данной статье.
Резистор
Сопротивление устройств старого типа сильно зависело от их нагрева. При нагревании проводимость резистора пропорционально изменялась в меньшую сторону. Для электрических цепей требуется идеальный резистор, который обладает наивысшим коэффициентом проводимости. Для снижения нагрева при производстве данных устройств теперь используется материал, имеющий малую зависимость сопротивления от температуры нагрева. Это позволило применять резисторы с малым сопротивлением для цепей с большим напряжением.
Терморезистор
Существует отдельная группа резисторов, которые применяют для измерения температуры. Особенностью такого устройства является то, что он может снижать свою проводимость при нагреве. При этом он отключает цепь при достижении определенного порогового значения.
Термометр сопротивления
Это прибор был разработан для измерения температуры среды. Он состоит из тонкой платиновой проволоки, защитного чехла и корпуса. Прибор имеет стабильную реакцию на перепады температуры. Измеряемой величиной в данном устройстве служит сопротивление этой проволоки из платины. Чем выше будет температура, тем сопротивление соответственно будет больше. Понижение сопротивления так же фиксируется, так как в этот момент меняются проводимость и сопротивление. Для измерения температуры термометром сопротивления, в настоящее время применяются проволочные индикаторы из разнообразных металлов. В зависимости от свойств используемого металла, погрешность устройства может составлять не более 0.1 %. Благодаря этому достигается очень высокая точность измерения температуры.
Газ
Самый известный нам газовый проводник — это люминесцентная лампа. Газ нагревается за счет увеличения напряжения между анодом и катодом лампы.
Известным жидкостным проводником является щелочной аккумулятор. При понижении температуры нарушается структура жидкости и изменяется ее сопротивление.
Нагрев провоцирует движение атомов и электронов, увеличивая сопротивление и зарядный ток устройства.
Заключение
В данной статье мы рассмотрели, как зависит сопротивление от температуры. Металлы, газы и жидкости имеют свойства изменять свою проводимость и сопротивление при температурных перепадах. Это свойство изменения электрического сопротивления используются для измерения температуры среды. Наибольшая точность измерений температуры в настоящее время достигается за счет применения современных материалов, даже в бытовой технике.
Видео по теме
Сопротивление является одним из основных объектов, описанных в гидродинамике, который используется для объяснения движения твердого тела и жидкости. Сила сопротивления рассматривается как противодействующая сила в воздушной среде, пропорциональная движению тела над жидкостью.
Коэффициент сопротивления — это безразмерная величина, определяющая сопротивление, оказываемое объекту в жидкой среде, такой как воздух и вода. Коэффициент аэродинамического сопротивления зависит от формы, угла наклона и скорости потока в аэродинамике. Включая все эти условия, давайте узнаем, как рассчитать коэффициент сопротивления через этот пост.
Как рассчитать коэффициент сопротивления без учета силы сопротивления?
Коэффициенты сопротивления обычно описываются с использованием силы сопротивления. Коэффициенты сопротивления всегда зависят от площади поверхности и плотность жидкости, над которой находится объект двигается. Предположим, мы не знаем о силе сопротивления, действующей на объект, тогда как рассчитать коэффициент сопротивления?
предполагать тело движется в воздухе; на него действует сила, противодействующая движению тела. Поскольку тело находится в движении, оно имеет определенную скорость. Мы можем рассчитать коэффициент сопротивления, используя законы движения Ньютона, не используя силу сопротивления, используя конечную скорость.
Суммарная сила, действующая на тело над жидкостью, определяется выражением
F=мг–FD
Где FD сила сопротивления;
от Второй закон движения Ньютона, результирующая сила равна F = ma
Следовательно, сила сопротивления может быть приравнена к чистой силе как
ма=мг–FD
Но ма=0; поэтому FD= мг
Предположим, что тело имеет плотность ρ, площадь поперечного сечения A и скорость тела v. Сила сопротивления, противодействующая движению, определяется как
FD=1/2 ρ СDV2A
Где FD сила сопротивления, CD это коэффициент лобового сопротивления.
Но сила сопротивления равна весу тела в жидкости. Следовательно, приведенное выше уравнение можно изменить как
мг= 1/2 ρ СDV2A
Переставляя члены, мы получаем коэффициент лобового сопротивления как
CD= 2мг/ρv2A
Как рассчитать коэффициент аэродинамического сопротивления цилиндра?
Силу сопротивления цилиндра можно определить, разложив площадь цилиндра.
Рассмотрим цилиндрическое тело, плавающее в жидкости. Тело испытывает некоторое сопротивление, которое возражает против движения цилиндра.
Коэффициент лобового сопротивления обычно определяется по формуле
CD = 2FD/ ρв2A
Где; ρ — плотность цилиндра, FD — сила сопротивления, v — скорость цилиндра, движущегося в жидкости, A — площадь цилиндра.
Площадь цилиндра определяется выражением
А=2πр+2πр2
А=2πr(ч+г)
Подставив значение площади цилиндра в приведенное выше уравнение коэффициента лобового сопротивления, получим
CD= 2FD/ ρв2A(2 πr(h+r))
CD= ρv2(πr(ч+r)
Как рассчитать коэффициент сопротивления шара?
Коэффициент сопротивления сферы включает в себя тот же процесс, что и коэффициент сопротивления цилиндра. Вычислив площадь сферы, можно найти сферу с коэффициентом лобового сопротивления как
Площадь сферы определяется уравнением
А = 4πr2
Коэффициент аэродинамического сопротивления определяется выражением
CD= 2FD/ρv2A
Подставляя площадь сферы в приведенное выше уравнение, мы получаем
CD= 2FD/ρv2(4 πr2)
CD= ФD/ρv2(2πr2)
CD= ФD/2ρv2(πr2)
Как рассчитать коэффициент аэродинамического сопротивления парашюта?
Сила сопротивления в парашюте действует противоположно сила гравитации; следовательно, парашютист замедляется при падении с парашюта.
Когда парашютист ныряет с парашютом, его скорость определяется гравитационным притяжением. При раскрытии парашюта будет увеличиваться площадь поверхности, а значит будет больше воздуха и скорость автоматически замедляется из-за сопротивление воздуха.
Сначала рассмотрите свободное падение парашюта; скорость водолаза считается a=-g, так как из-за сопротивления воздуха парашют медленно движется вверх. Но результирующая сила действует вниз, что намного больше, чем сила сопротивления.
Величина сила сопротивления из-за конечной скорости дан кем-то
|FD|=СD v
Где компакт-диск коэффициент трения, v — конечная скорость.
Суммарная действующая сила определяется выражением
∑F=FD–мг=0
FD= мг
CD vтерминал = мг
CD=мг/об.терминал
Как рассчитать коэффициент лобового сопротивления в cfd?
Для точной оценки коэффициента сопротивления широко используется вычислительная гидродинамика (CFD). Существует различное программное обеспечение, которое поможет вам рассчитать коэффициент аэродинамического сопротивления, используя предоставленные вам данные.
Тяжелые объекты, такие как транспортные средства, проектируются с помощью аэродинамики с использованием анализа CFD. Пример коэффициент трения Расчет с использованием моделирования Autodesk показан ниже:
Для получения точных результатов следуйте приведенным ниже методам.
- Для расчета необходимо использовать большую воздушную область, чтобы избежать искусственного ускорения из-за воздуха.
- Необходимо создать мелкую сетку объекта.
- Запустите расчет для нескольких итераций, чтобы получить точный результат.
- Всегда используйте площадь поперечного сечения объекта, которая уже определена.
Когда вы открываете программное обеспечение, необходимо выполнить следующие шаги
- Выберите соответствующий инструмент стены
- Внешняя поверхность объекта должна быть выбрана
- Появится флажок, затем выберите Ньютон и нажмите «Рассчитать для вывода».
- Выберите «всего FX»; направление движения объекта, то поставить формулу.
CD=2FD/ρv2A
Как рассчитать коэффициент лобового сопротивления по числу Рейнольдса?
Течение объекта в жидкости, тормозящее сопротивление, рассчитывается по эмпирической формуле с использованием числа Рейнольдса.
Число Рейнольдса для объекта плотности D и площадь поперечного сечения влияют на коэффициент лобового сопротивления. Коэффициент аэродинамического сопротивления уменьшается по мере Число Рейнольдса увеличивается.
Число Рейнольдса определяется как
Re={ρvD/µ}
Где ρ — плотность объекта, D — диаметр, μ — вязкость, v — скорость.
Стокс дал формулу для силы сопротивления как функции некоторого постоянного числа как
FD=6πμRv
Для большего значения Re, CD уменьшается по мере того, как скорость изменяется в терминах квадратного значения.
Сила сопротивления может быть записана как
FD=ΔpAw=1/2 СdAf{vмк/л2}ReL2
Гдеw влажная площадь, Аf является передней области.
Переставляя члены, мы получаем коэффициент аэродинамического сопротивления как функцию безразмерного числа, называемого числом Бежана, как отношение Aw и аf as
CD = 2 {Аw/Af}{Be/ReL2)
Где Be={Δpl^2/µD}, называемое числом Бежана
Как найти нулевой коэффициент подъемной силы?
Безразмерный параметр, характеризующий силу сопротивления при нулевой подъемной силе самолета с учетом его размеров, скорости и высоты, называется коэффициентом сопротивления при нулевой подъемной силе.
Как правило, коэффициент сопротивления при нулевой подъемной силе отражает паразитное сопротивление, описывающее обтекаемость самолета.
Математически коэффициент сопротивления при нулевой подъемной силе определяется как
CD, 0 = CD-СD, I
CD — коэффициент лобового сопротивления, а CД, я — коэффициент индуктивного сопротивления.
Полное сопротивление находится по формуле.
CD={550ηP/(1/2)ρ0Σс (1.47 В)3
Где η — КПД тяги, а P — мощность двигателя, ρ0 — плотность воздуха на уровне моря, σ — плотность атмосферы, s — площадь крыла, v — скорость.
Упрощая вышеприведенное уравнение, получаем
CD= 1.456 * 105(η P/Σsv3)
Индуцированное сопротивление определяется выражением
CD,i= {СL2/ π ARɛ}
Где CL — коэффициент подъемной силы, AR — удлинение, ε — эффективность.
Подставляя значение коэффициента подъемной силы
CD,i={4.822*104/ARɛΣ2v4}
Подставляя и вычисляя, получаем коэффициент сопротивления при нулевой подъемной силе
Как найти минимальный коэффициент лобового сопротивления?
Симметричный обтекаемый аэродинамический профиль обеспечивает минимальный коэффициент лобового сопротивления.
Минимальное сопротивление можно определить как
CD=CD0+кСL2
Где CD0 сопротивление профиля и CL — подъемное сопротивление, а k — коэффициент подъемной силы.
Для минимального коэффициента лобового сопротивления
dCDdCL=0
Учитывая, что самолет находится в прямолинейном и горизонтальном полете, минимальное сопротивление должно иметь максимальное аэродинамическое качество, т. е.
{d2CL/Округ КолумбияD2}<0
Разделив первое уравнение на CL,
Мы получаем
CLCD=CD/CL+кСL
Решенные проблемы
Найдите коэффициент лобового сопротивления лодки, плавающей на воде плотностью 1.2 кг/м.3 а площадь поперечного сечения 7м2 и движется со скоростью 23 м/с и массой лодки 66 кг.
Решение:
Дано – плотность ρ=1.2 кг/м3
Площадь поперечного сечения A=7м2
Масса лодки m=66кг.
Скорость лодки v=23м/с
Ускорение свободного падения g = 9.8 м/с.2
Коэффициент лобового сопротивления определяется выражением
CD={2мг/ρv2A}
CD={2(66*9.8)}{1.2*232*7}
CD={1293.6/4443.6}
CD= 0.291
В жидкости движется тело, площадь увлажнения которого равна 3 м, а площадь фронта 33 м. Число Рейнольдса длины пути равно 0.19, а число Бежана — 0.96. Вычислите коэффициент сопротивления данного тела.
Решение:
Коэффициент аэродинамического сопротивления CD для заданного числа Рейнольдса определяется выражением
CD= 2 {Аw/Af}{Be/ReL2}
CD=2{3/36}{0.96/0.192}
CD= 4.43.
Сферический предмет радиусом 2 м брошен в воздух, сила сопротивления которого равна 123 Н, а плотность равна 1.34 кг/м.3, а скорость объекта в воздухе 34 м/с. Как рассчитать коэффициент аэродинамического сопротивления по предоставленным данным?
Решение:
Дано – радиус объекта r=2м
Сила сопротивления, действующая на объект FD= 123N
Скорость объекта v=34 м/с
Плотность ρ=1.34 кг/м3
Площадь сферы A=4πr2
A = 50.24 м2
Коэффициент аэродинамического сопротивления определяется выражением
CD={2FD/ ρ v2A}
CD={2(123)/1.34*342*50.24}
CD= 3.16 × 10-3
9.4. Движение тел в среде с сопротивлением
Со времен опытов Галилея на Пизанской башне известно, что все тела падают в поле силы тяжести с одинаковым ускорением g.
Однако каждодневная практика указывает на другое: легкое перышко падает медленнее тяжелого металлического шарика. Понятна и причина этого — сопротивление воздуха.
Уравнения движения. Если ограничиться случаем поступательного движения невращающихся тел в неподвижной среде с сопротивлением, то сила сопротивления будет направлена против скорости. В векторном виде ее можно записать как
где 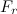

В приведенных уравнениях учтена также выталкивающая сила Архимеда, действующая на тело: ускорение свободного падения g заменено на меньшую величину
где 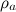
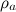
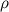
Действительно, вес 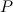
Выражая объём 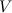
приходим к выражению
При наличии сопротивления воздуха скорость падающего тела не может расти безгранично. В пределе она стремится к некоторому установившемуся значению, которое зависит от характеристик тела. Если тело достигло установившейся скорости падения 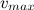
Сила сопротивления 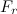
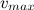
Число Рейнольдса. Разумеется, уравнения движения тела в жидкости невозможно даже начать решать, пока нам ничего неизвестно о модуле 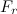
Ламинарное течение жидкости демонстрируется на опыте, показанном на рис. 13.
Как уже отмечалось в главе 9.3, при относительном движении слоёв жидкости или газа между этими слоями возникают силы сопротивления движению, которые называются силами внутреннего трения. Эти силы обусловлены особым свойством текучих тел — вязкостью, которая характеризуется численно коэффициентом вязкости 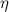
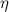
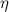
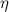
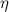
Между движущимся телом и средой всегда существуют силы сцепления, так что непосредственно вблизи поверхности тела слой газа (жидкости) полностью задерживается, как бы «прилипая» к нему. Он трется о следующий слой, который слегка отстает от тела. Тот, в свою очередь, испытывает силу трения со стороны еще более удаленного слоя и т.д. Совсем далекие от тела слои можно считать покоящимися. Теоретический расчет внутреннего трения для движения шарика диаметром D приводит к формуле Стокса:
Подставляя формулу Стокса в выражение для силы сопротивления при установившемся движении, находим выражение для установившейся скорости падения шарика в среде:
Видно, что чем легче тело, тем меньше скорость его падения в атмосфере. Полученное уравнение объясняет нам, почему пушинка падает медленнее,чем стальной шарик.
При решении реальных задач, например, вычислении установившейся скорости падения парашютиста при затяжном прыжке, не следует забывать, что сила трения пропорциональна скорости тела лишь для относительно медленного ламинарного встречного потока воздуха. При увеличении скорости тела вокруг него возникают воздушные вихри, слои перемешиваются, движение в какой-то момент становится турбулентным, и сила сопротивления резко возрастает. Внутреннее трение (вязкость) перестает играть сколько бы то ни было заметную роль.
Рис. 9.15 Фотография струи жидкости при переходе от ламинарного течения к турбулентному (число Рейнольдса Re=250)
Возникновение силы сопротивления можно тогда представить себе следующим образом. Пусть тело прошло в среде путь 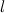
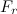
Если площадь поперечного сечения тела равна 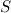
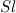
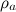
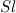

Эта энергия не появилась ниоткуда: она создана за счет работы внешних сил по преодолению силы сопротивления. Стало быть, A=К, откуда
Мы видим, что теперь сила сопротивления сильнее зависит от скорости движения, становясь пропорциональной ее второй степени (ср. с формулой Стокса). В отличие от сил внутреннего трения ее часто называют силой динамического лобового сопротивления.
Однако предположение о полном увлечении частиц среды движущимся телом оказывается слишком сильным. В реальности любое тело так или иначе обтекается потоком, что уменьшает силу сопротивления. Принято использовать так называемый коэффициент сопротивления C, записывая силу лобового сопротивления в виде:
При турбулентном потоке в некотором интервале скоростей C не зависит от скорости движения тела, но зависит от его формы: скажем, для диска он равен единице, а для шара примерно 0,5.
Подставляя формулу для силы лобового сопротивления в выражение для силы сопротивления при установившемся движении, приходим к иному, нежели ранее полученная формула, выражению для установившейся скорости падения шара (при C = 0,5):
Применяя найденную формулу к движению парашютиста весом 100 кг с поперечным размером парашюта 10 м, находим
что соответствует скорости приземления при прыжке без парашюта с высоты 2 м. Видно, что для описания движения парашютиста больше подходит формула, соответствующая турбулентному потоку воздуха.
Выражение для силы сопротивления с коэффициентом сопротивления удобно использовать во всем интервале скоростей. Поскольку при малых скоростях режим сопротивления меняется, то коэффициент сопротивления в области ламинарного течения и в переходной области к турбулентному течению будет зависеть от скорости тела. Однако прямая зависимость C от 
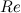
Число Рейнольдса — это параметр, описывающий смену режима при переходе от ламинарного течения к турбулентному. Таким параметром может служить отношение силы лобового сопротивления к силе внутреннего трения. Подставляя в формулу для силы сопротивления выражение для площади поперечного сечения шара 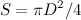
а величина силы внутреннего трения — выражением
Отношение этих двух выражений и есть число Рейнольдса:
Если речь идет не о движении шара, то под D понимается характерный размер системы (скажем, диаметр трубы в задаче о течении жидкости). По самому смыслу числа Рейнольдса ясно, что при его малых значениях доминируют силы внутреннего трения: вязкость велика и мы имеем дело с ламинарным потоком. При больших значениях числа Рейнольдса, наоборот, доминируют силы динамического лобового сопротивления и поток становится турбулентным.
Число Рейнольдса имеет огромное значение при моделировании реальных процессов в меньших (лабораторных) масштабах. Если для двух течений разных размеров числа Рейнольдса одинаковы, то такие течения подобны, и возникающие в них явления могут быть получены одно из другого простым изменением масштаба измерения координат и скоростей. Поэтому, например, на модели самолета или автомобиля в аэродинамической трубе можно предугадать и изучить процессы, которые возникнут в процессе реальной эксплуатации.
Коэффициент сопротивления. Итак, коэффициент сопротивления в формуле для силы сопротивления зависит от числа Рейнольдса:
Эта зависимость имеет сложный характер, показанный (для шара) на рис. 9.16. Теоретически получить эту кривую трудно, и обычно используют зависимости, экспериментально измеренные для данного тела. Однако возможна качественная ее интерпретация.
Рис. 9.16. Зависимость коэффициента сопротивления от числа Рейнолъдса (римскими цифрами показаны области значений Re; которым соответствуют различные режимы течения воздушного потока)
Область I. Здесь число Рейнольдса очень мало ( 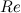
При 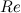
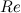
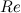
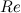
Область III. Эта область соответствует развитому турбулентному течению потока вокруг шара, а с этим режимом мы уже встречались выше. Характерные здесь значения числа Рейнольдса лежат в интервале 2·10 4 5 .
При движении тело оставляет за собой турбулентный след, за пределами которого течение ламинарно. Вихревой турбулентный след легко наблюдать, например, за кормой корабля. Часть поверхности тела непосредственно примыкает к области турбулентного следа, а его передняя часть — к области ламинарного течения. Граница между ними на поверхности тела называется линией отрыва. Физической причиной возникновения силы сопротивления является разность давлений на передней и задней поверхностях тела. Оказывается, что положение линии отрыва определяется свойствами пограничного слоя и не зависит от числа Рейнольдса. Поэтому коэффициент сопротивления примерно постоянен в этом режиме.
Область IV. Однако такой режим обтекания тела не может поддерживаться до сколь угодно больших значений 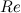
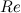
Источник
Силами сопротивления
называются силы, препятствующие движению
автомобиля. Эти силы направлены против
его движения.
движении на подъеме, характеризуемом
высотой Hп,
длиной проекции Вп
на
горизонтальную плоскость и углом
подъема дороги α, на автомобиль действуют
следующие силы сопротивления (рис.
3.12): сила сопротивления качению Рк,
равная
сумме сил сопротивления качению
передних (РК|)
и задних (РК2)
колес, сила сопротивления подъему
Рп,
сила
сопротивления воздуха Д и сила
сопротивления разгону РИ.
Силы
сопротивления качению и подъему
связаны с особенностями дороги. Сумма
этих сил называется силой сопротивления
дороги РД.
Рис.
3.13. Потери энергии на внутреннее
трение в шине:
а
— точка,
соответствующая максимальным
значениям нагрузки и прогиба
шины
Сила сопротивления качению
Возникновение
силы сопротивления качению при движении
обусловлено потерями энергии на
внутреннее трение в шинах, поверхностное
трение шин о дорогу и образование колеи
(на деформируемых дорогах).О потерях
энергии на внутреннее трение в шине
можно судить по рис. 3.13, на котором
приведена зависимость между вертикальной
нагрузкой на колесо и деформацией шины
— ее прогибом fш.
При
движении колеса по неровной поверхности
шина, испытывая действие переменной
нагрузки, деформируется. Линия αО,
которая
соответствует возрастанию нагрузки,
деформирующей шину, не совпадает с
линией аО,
отвечающей
снятию нагрузки. Площадь области,
заключенной между указанными кривыми,
характеризует потери энергии на
внутреннее трение между отдельными
частями шины (протектор, каркас, слои
корда и др.).
Потери
энергии на трение в шине называются
гистерезисом, а линия ОαО
— петлей
гистерезиса.
Потери
на трение в шине необратимы, так как при
деформации она нагревается и из нее
выделяется теплота, которая рассеивается
в окружающую среду. Энергия, затрачиваемая
на деформацию шины, не возвращается
полностью при последующем восстановлении
ее формы.
Сила
сопротивления качению Рк
достигает
наибольшего значения при движении
по горизонтальной дороге. В этом случае
где
G
— вес
автомобиля, Н; f
— коэффициент сопротивления качению.
При
движении на подъеме и спуске сила
сопротивления качению уменьшается
по сравнению с Рк
на
горизонтальной дороге, и тем значительнее,
чем они круче. Для этого случая движения
сила сопротивления качению
где α — угол
подъема, °.

силу сопротивления качению, можно
определить мощность, кВт,
затрачиваемую на
преодоление этого сопротивления:
где
v
—скорости
автомобиля,м/c2
Для
горизонтальной дороги соs0°=1
и
З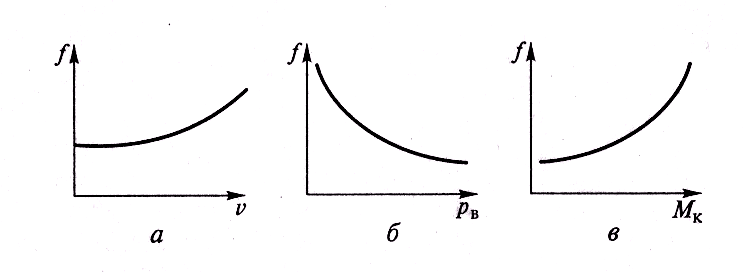
силы сопротивления качениюРк
и
мощности NК
от
скорости автомобиля v
показаны
на рис. 3.14
Коэффициент сопротивления качению
Коэффициент
сопротивления качению существенно
влияет на потери энергии при движении
автомобиля. Он зависит от многих
конструктивных и эксплуатационных
Рис 3.15. Зависимости
коэффициента сопротивления качению от
Скорости движения (а), давления воздуха в шине (б) и момента, передаваемого через колесо (в)
факторов
и определяется экспериментально. Его
средние значения для различных дорог
при нормальном давлении воздуха в шине
составляют 0,01 …0,1.Рассмотрим влияние
различных факторов на коэффициент
сопротивления качению.
Скорость
движения.
При изменении скорости движения в
интервале 0…50 км/ч коэффициент
сопротивления качению изменяется
незначительно и его можно считать
постоянным в указанном диапазоне
скоростей.
При
повышении скорости движения за пределами
указанного интервала коэффициент
сопротивления качению существенно
увеличивается (рис. 3.15, а)
вследствие
возрастания потерь энергии в шине на
трение.
Коэффициент
сопротивления качению в зависимости
от скорости движения можно приближенно
рассчитать по
формуле
где
—
скорость
автомобиля, км/ч.
Тип
и состояние покрытия дороги.
На дорогах с твердым покрытием
сопротивление качению обусловлено
главным образом деформациями шины.
При
увеличении числа дорожных неровностей
коэффициент сопротивления качению
возрастает.
На
деформируемых дорогах коэффициент
сопротивления качению определяется
деформациями шины и дороги. В этом случае
он зависит не только от типа шины, но и
от глубины образующейся колеи и
состояния грунта.
Значения
коэффициента сопротивления качению
при рекомендуемых уровнях давления
воздуха и нагрузки на шину и средней
скорости движения на различных дорогах
приведены ниже:
Асфальто-
и цементобетонное шоссе:
в
хорошем состоянии
………………………………. 0,007…0,015
в
удовлетворительном состоянии
…………… 0,015…0,02
Гравийная
дорога в хорошем состоянии …. 0,02…0,025
Булыжная
дорога в хорошем состоянии…… 0,025…0,03
Грунтовая
дорога сухая, укатанная …………..
0,025…0,03
Песок…………………………………………………………..
0,1…0,3
Обледенелая
дорога, лед …………………………. 0,015…0,03
Укатанная
снежная дорога ………………………..
0,03…0,05
Тип
шины.
Коэффициент сопротивления качению во
многом зависит от рисунка протектора,
его износа, конструкции каркаса и
качества материала шины. Изношенность
протектора, уменьшение числа слоев
корда и улучшение качества материала
приводят к падению коэффициента
сопротивления качению вследствие
снижения потерь энергии в шине.
Давление
воздуха в шине.
На дорогах с твердым покрытием при
уменьшении давления воздуха в шине
коэффициент сопротивления качению
повышается (рис. 3.15, б).
На
деформируемых дорогах при снижении
давления воздуха в шине уменьшается
глубина колеи, но возрастают потери
на внутреннее трение в шине. Поэтому
для каждого типа дороги рекомендуется
определенное давление воздуха в шине,
при котором коэффициент сопротивления
качению имеет минимальное значение.
Нагрузка
на колесо.
При увеличении вертикальной нагрузки
на колесо коэффициент сопротивления
качению существенно возрастает на
деформируемых дорогах и незначительно
— на дорогах с твердым покрытием.
Момент,
передаваемый через колесо.
При передаче момента через колесо
коэффициент сопротивления качению
возрастает (рис. 3.15, в)
вследствие
потерь на проскальзывание шины в месте
ее контакта с дорогой. Для ведущих колес
значение коэффициента сопротивления
качению на 10… 15 % больше, чем для ведомых.
Коэффициент
сопротивления качению оказывает
существенное влияние на расход
топлива и, следовательно, на топливную
экономичность автомобиля. Исследования
показали, что даже небольшое уменьшение
этого коэффициента обеспечивает
ощутимую экономию топлива. Поэтому
неслучайно стремление конструкторов
и исследователей создать такие шины,
при использовании которых коэффициент
сопротивления качению будет незначительным,
но это весьма сложная проблема.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сопротивление является одним из основных объектов, описанных в гидродинамике, который используется для объяснения движения твердого тела и жидкости. Сила сопротивления рассматривается как противодействующая сила в воздушной среде, пропорциональная движению тела над жидкостью.
Коэффициент сопротивления — это безразмерная величина, определяющая сопротивление, оказываемое объекту в жидкой среде, такой как воздух и вода. Коэффициент аэродинамического сопротивления зависит от формы, угла наклона и скорости потока в аэродинамике. Включая все эти условия, давайте узнаем, как рассчитать коэффициент сопротивления через этот пост.
Как рассчитать коэффициент сопротивления без учета силы сопротивления?
Коэффициенты сопротивления обычно описываются с использованием силы сопротивления. Коэффициенты сопротивления всегда зависят от площади поверхности и плотность жидкости, над которой находится объект двигается. Предположим, мы не знаем о силе сопротивления, действующей на объект, тогда как рассчитать коэффициент сопротивления?
предполагать тело движется в воздухе; на него действует сила, противодействующая движению тела. Поскольку тело находится в движении, оно имеет определенную скорость. Мы можем рассчитать коэффициент сопротивления, используя законы движения Ньютона, не используя силу сопротивления, используя конечную скорость.
Суммарная сила, действующая на тело над жидкостью, определяется выражением
F=мг–FD
Где FD сила сопротивления;
от Второй закон движения Ньютона, результирующая сила равна F = ma
Следовательно, сила сопротивления может быть приравнена к чистой силе как
ма=мг–FD
Но ма=0; поэтому FD= мг
Предположим, что тело имеет плотность ρ, площадь поперечного сечения A и скорость тела v. Сила сопротивления, противодействующая движению, определяется как
FD=1/2 ρ СDV2A
Где FD сила сопротивления, CD это коэффициент лобового сопротивления.
Но сила сопротивления равна весу тела в жидкости. Следовательно, приведенное выше уравнение можно изменить как
мг= 1/2 ρ СDV2A
Переставляя члены, мы получаем коэффициент лобового сопротивления как
CD= 2мг/ρv2A
Как рассчитать коэффициент аэродинамического сопротивления цилиндра?
Силу сопротивления цилиндра можно определить, разложив площадь цилиндра.
Рассмотрим цилиндрическое тело, плавающее в жидкости. Тело испытывает некоторое сопротивление, которое возражает против движения цилиндра.
Коэффициент лобового сопротивления обычно определяется по формуле
CD = 2FD/ ρв2A
Где; ρ — плотность цилиндра, FD — сила сопротивления, v — скорость цилиндра, движущегося в жидкости, A — площадь цилиндра.
Площадь цилиндра определяется выражением
А=2πр+2πр2
А=2πr(ч+г)
Подставив значение площади цилиндра в приведенное выше уравнение коэффициента лобового сопротивления, получим
CD= 2FD/ ρв2A(2 πr(h+r))
CD= ρv2(πr(ч+r)
Как рассчитать коэффициент сопротивления шара?
Коэффициент сопротивления сферы включает в себя тот же процесс, что и коэффициент сопротивления цилиндра. Вычислив площадь сферы, можно найти сферу с коэффициентом лобового сопротивления как
Площадь сферы определяется уравнением
А = 4πr2
Коэффициент аэродинамического сопротивления определяется выражением
CD= 2FD/ρv2A
Подставляя площадь сферы в приведенное выше уравнение, мы получаем
CD= 2FD/ρv2(4 πr2)
CD= ФD/ρv2(2πr2)
CD= ФD/2ρv2(πr2)
Как рассчитать коэффициент аэродинамического сопротивления парашюта?
Сила сопротивления в парашюте действует противоположно сила гравитации; следовательно, парашютист замедляется при падении с парашюта.
Когда парашютист ныряет с парашютом, его скорость определяется гравитационным притяжением. При раскрытии парашюта будет увеличиваться площадь поверхности, а значит будет больше воздуха и скорость автоматически замедляется из-за сопротивление воздуха.
Сначала рассмотрите свободное падение парашюта; скорость водолаза считается a=-g, так как из-за сопротивления воздуха парашют медленно движется вверх. Но результирующая сила действует вниз, что намного больше, чем сила сопротивления.
Величина сила сопротивления из-за конечной скорости дан кем-то
|FD|=СD v
Где компакт-диск коэффициент трения, v — конечная скорость.
Суммарная действующая сила определяется выражением
∑F=FD–мг=0
FD= мг
CD vтерминал = мг
CD=мг/об.терминал
Как рассчитать коэффициент лобового сопротивления в cfd?
Для точной оценки коэффициента сопротивления широко используется вычислительная гидродинамика (CFD). Существует различное программное обеспечение, которое поможет вам рассчитать коэффициент аэродинамического сопротивления, используя предоставленные вам данные.
Тяжелые объекты, такие как транспортные средства, проектируются с помощью аэродинамики с использованием анализа CFD. Пример коэффициент трения Расчет с использованием моделирования Autodesk показан ниже:
Для получения точных результатов следуйте приведенным ниже методам.
- Для расчета необходимо использовать большую воздушную область, чтобы избежать искусственного ускорения из-за воздуха.
- Необходимо создать мелкую сетку объекта.
- Запустите расчет для нескольких итераций, чтобы получить точный результат.
- Всегда используйте площадь поперечного сечения объекта, которая уже определена.
Когда вы открываете программное обеспечение, необходимо выполнить следующие шаги
- Выберите соответствующий инструмент стены
- Внешняя поверхность объекта должна быть выбрана
- Появится флажок, затем выберите Ньютон и нажмите «Рассчитать для вывода».
- Выберите «всего FX»; направление движения объекта, то поставить формулу.
CD=2FD/ρv2A
Как рассчитать коэффициент лобового сопротивления по числу Рейнольдса?
Течение объекта в жидкости, тормозящее сопротивление, рассчитывается по эмпирической формуле с использованием числа Рейнольдса.
Число Рейнольдса для объекта плотности D и площадь поперечного сечения влияют на коэффициент лобового сопротивления. Коэффициент аэродинамического сопротивления уменьшается по мере Число Рейнольдса увеличивается.
Число Рейнольдса определяется как
Re={ρvD/µ}
Где ρ — плотность объекта, D — диаметр, μ — вязкость, v — скорость.
Стокс дал формулу для силы сопротивления как функции некоторого постоянного числа как
FD=6πμRv
Для большего значения Re, CD уменьшается по мере того, как скорость изменяется в терминах квадратного значения.
Сила сопротивления может быть записана как
FD=ΔpAw=1/2 СdAf{vмк/л2}ReL2
Гдеw влажная площадь, Аf является передней области.
Переставляя члены, мы получаем коэффициент аэродинамического сопротивления как функцию безразмерного числа, называемого числом Бежана, как отношение Aw и аf as
CD = 2 {Аw/Af}{Be/ReL2)
Где Be={Δpl^2/µD}, называемое числом Бежана
Как найти нулевой коэффициент подъемной силы?
Безразмерный параметр, характеризующий силу сопротивления при нулевой подъемной силе самолета с учетом его размеров, скорости и высоты, называется коэффициентом сопротивления при нулевой подъемной силе.
Как правило, коэффициент сопротивления при нулевой подъемной силе отражает паразитное сопротивление, описывающее обтекаемость самолета.
Математически коэффициент сопротивления при нулевой подъемной силе определяется как
CD, 0 = CD-СD, I
CD – коэффициент лобового сопротивления, а CД, я – коэффициент индуктивного сопротивления.
Полное сопротивление находится по формуле.
CD={550ηP/(1/2)ρ0Σс (1.47 В)3
Где η — КПД тяги, а P — мощность двигателя, ρ0 — плотность воздуха на уровне моря, σ — плотность атмосферы, s — площадь крыла, v — скорость.
Упрощая вышеприведенное уравнение, получаем
CD= 1.456 * 105(η P/Σsv3)
Индуцированное сопротивление определяется выражением
CD,i= {СL2/ π ARɛ}
Где CL — коэффициент подъемной силы, AR — удлинение, ε — эффективность.
Подставляя значение коэффициента подъемной силы
CD,i={4.822*104/ARɛΣ2v4}
Подставляя и вычисляя, получаем коэффициент сопротивления при нулевой подъемной силе
Как найти минимальный коэффициент лобового сопротивления?
Симметричный обтекаемый аэродинамический профиль обеспечивает минимальный коэффициент лобового сопротивления.
Минимальное сопротивление можно определить как
CD=CD0+кСL2
Где CD0 сопротивление профиля и CL – подъемное сопротивление, а k – коэффициент подъемной силы.
Для минимального коэффициента лобового сопротивления
dCDdCL=0
Учитывая, что самолет находится в прямолинейном и горизонтальном полете, минимальное сопротивление должно иметь максимальное аэродинамическое качество, т. е.
{d2CL/Округ КолумбияD2}<0
Разделив первое уравнение на CL,
Мы получаем
CLCD=CD/CL+кСL
Решенные проблемы
Найдите коэффициент лобового сопротивления лодки, плавающей на воде плотностью 1.2 кг/м.3 а площадь поперечного сечения 7м2 и движется со скоростью 23 м/с и массой лодки 66 кг.
Решение:
Дано – плотность ρ=1.2 кг/м3
Площадь поперечного сечения A=7м2
Масса лодки m=66кг.
Скорость лодки v=23м/с
Ускорение свободного падения g = 9.8 м/с.2
Коэффициент лобового сопротивления определяется выражением
CD={2мг/ρv2A}
CD={2(66*9.8)}{1.2*232*7}
CD={1293.6/4443.6}
CD= 0.291
В жидкости движется тело, площадь увлажнения которого равна 3 м, а площадь фронта 33 м. Число Рейнольдса длины пути равно 0.19, а число Бежана — 0.96. Вычислите коэффициент сопротивления данного тела.
Решение:
Коэффициент аэродинамического сопротивления CD для заданного числа Рейнольдса определяется выражением
CD= 2 {Аw/Af}{Be/ReL2}
CD=2{3/36}{0.96/0.192}
CD= 4.43.
Сферический предмет радиусом 2 м брошен в воздух, сила сопротивления которого равна 123 Н, а плотность равна 1.34 кг/м.3, а скорость объекта в воздухе 34 м/с. Как рассчитать коэффициент аэродинамического сопротивления по предоставленным данным?
Решение:
Дано – радиус объекта r=2м
Сила сопротивления, действующая на объект FD= 123N
Скорость объекта v=34 м/с
Плотность ρ=1.34 кг/м3
Площадь сферы A=4πr2
A = 50.24 м2
Коэффициент аэродинамического сопротивления определяется выражением
CD={2FD/ ρ v2A}
CD={2(123)/1.34*342*50.24}
CD= 3.16 × 10-3