Как найти коэффициент сопротивления воздуха

Как найти коэффициент сопротивления воздуха

Трение между воздухом и другим объектом называется сопротивлением воздуха. Рассмотрим, как определить сопротивление воздуха при падении объекта.

Сопротивление воздуха падающего объекта можно рассчитать, умножив плотность воздуха на коэффициент сопротивления, умноженный на площадь, на два, а затем умножив на скорость.

Сила тяжести и сопротивление воздуха — две силы естественного поля, которые двигают все на Земле. Формула сопротивления воздуха для сферы, доказательство формулы сопротивления воздуха, формула сопротивления воздуха для свободного падения и то, как получить среднее сопротивление воздуха, будут рассмотрены более подробно.

Как рассчитать сопротивление воздуха падающего предмета?

Скорость, площадь и форма объекта, проходящего через воздух, влияют на сопротивление воздуха. Проверим, как оценить сопротивление воздуха падающего предмета.

Чтобы определить, какое сопротивление воздуха будет испытывать падающий предмет, используйте формулу FD = 1 / 2 ρv2CDА. В этом уравнении FD означает перетаскивание, ρ – плотность жидкости, v для относительной скорости объекта относительно жидкости, CD для коэффициента лобового сопротивления и A для площади поперечного сечения.

Задача: Огромный пассажирский самолет летит со скоростью 250.0 метров в секунду. A = 500 квадратных метров крыльев самолета подвергаются ветру. Коэффициент аэродинамического сопротивления CD = 0.024. Плотность воздуха ρ = 0.4500 кг на кубический метр на высоте самолета. Какому сопротивлению воздуха подвергается пассажирский самолет?

Решение: Даны данные,

А = 500 квадратных метров

CD = 0.024

ρ = 0.4500 кг на кубический метр

Сопротивление воздуха падающего предмета определяется выражением

FD = 1/2 ρv2CDA

FD =(0.4500 кг/м3 × 0.025 × 510.0 м2)/2 (250.0 м/с) 2

FD = (0.4500 кг/м3 × 0.025 × 510.0 м2)/2 (62500 м2/s2)

FD = 179296 кг.м/с2

Как рассчитать сопротивление воздуха при движении снаряда?

Объект или частица называется снарядом, а его движение называется движением снаряда. Посмотрим, как можно рассчитать сопротивление воздуха при движении снаряда.

Скорость, ускорение, и перемещение должно быть включено при описании движения снаряда в целом, как описано ниже,

  • По осям x и y мы должны расположить их составные части. Предположим, что все силы, кроме силы тяжести, ничтожны.
  • Компоненты ускорения тогда чрезвычайно прямолинейны, если положительное направление определено как восходящее, ay = -g = – 0.98 м / с.2 (-32 фут/с2).
  • Поскольку гравитация вертикальна,x = 0. аx = 0 указывает, что vx = V0x, или что начальная и конечная скорости в направлении x равны.
  • При этих ограничениях на ускорение и скорость кинематическое уравнение x (t) = x0 + (вx) среднийt для движения в униформе гравитационное поле можно записать через уравнение v2y (т) = v2oy + 2аy (г – г0), куда входят и остальные кинематические уравнения движения с ускорением с постоянным ускорением.
  • Кинематические уравнения движения в однородном гравитационном поле переходят в кинематические уравнения сy = -г, аx = 0.
  • Горизонтальное движение, v0x= Vx, х = х0 + Vxt.
  • Вертикальное движение, у = у0 + ½ (в0y + Vy)т; вy = Voy – гт; у = уo + Voyт – ½ гт2, v2y = V2oy – 2г (у – уo).

Задача: Снаряд взлетает в воздух во время фейерверка под углом 75.00 над горизонтом с начальной скоростью 70.0 м/с. Снаряд рассчитан так, что взрыватель сработает именно тогда, когда он будет на максимальной высоте над землей.

  • а. Рассчитайте высоту взрыва снаряда.
  • б. Через какое время снаряд выстрелит и взорвется?
  • в. Что происходит с горизонтальным положением снаряда при его взрыве?
  • д. Как далеко в целом продвинулся объект от места запуска до самой высокой точки?

Решение: (а) Под «высотой» мы подразумеваем высоту над начальной точкой или высоту. Когда vy = 0 достигается высшая точка любой траектории, известная как вершина. Мы используем следующее уравнение, чтобы получить y, потому что мы знаем начальное местоположение, начальную и конечную скорости и начальное положение:

v2y = V2oy – 2г (у – у0)

Уравнение упрощается тем, что yo и vy оба равны нулю.

0 = в2oy – 2г.

Вычислив y, мы получаем, y = v2oy/ 2г.

Теперь нам нужно выяснить, какова начальная компонента скорости y, или v0y, является. Его можно рассчитать по формуле v0y=v0sin θ, где v0 обозначает начальную скорость 70.0 м/с и θo=75° обозначает начальный угол. Таким образом-

v0y=v0sin θ = (70.0 м/с) sin750 = 67.6 м/с и-

у = (67.6 м/с)2 / 2(9.80 м/с2)

у = 233 м.

Начальная вертикальная скорость и максимальная высота положительны, потому что вверх положительна, а ускорение, вызванное силой тяжести, отрицательно. Снаряд с начальной вертикальной составляющей скорости 67.6 м/с достигнет максимальной высоты 233 м. Также имейте в виду, что максимальная высота зависит только от вертикальной составляющей начальной скорости (без учета сопротивления воздуха).

(b) Существуют различные способы определить, когда снаряд достигает высшей точки, как и во многих физических задачах. Самый простой подход в этой ситуации — использовать vy=v0y -гт. Это уравнение становится vy= 0 на вершине

0 = в0y− гт

или,

т = voy/g = (67.6 м/с) / (9.80 м/с2)

t = 6.90 с.

Другой способ найти время – использовать y = yo + ½ (в0y + Vy) т.

в) Сопротивление воздуха мало, следовательно, ах и ау равны нулю. И, как упоминалось ранее, горизонтальная скорость постоянна. Как показывают уравнения x=x0+vxт, где х0 равно нулю, горизонтальное перемещение равно горизонтальной скорости, умноженной на время. Таким образом,

х = vxt,

Когда vx – компонент x скорости, определяется выражением

vx = V0cosθ = (70.0 м/с) cos75°=18.1 м/с.

Поскольку оба движения имеют одинаковое время t, x равно

х = (18.1 м/с) × 6.90 с = 125 м.

Без сопротивления воздуха горизонтальное движение имеет постоянную скорость. Горизонтальное смещение, наблюдаемое здесь, может помочь предотвратить травму зрителей от падающих пиротехнических фрагментов. Немалую роль при взрыве снаряда играет сопротивление воздуха, и многие осколки падают сразу внизу.

(d) Нахождение размера и направления смещения в самой высокой точке — это все, что здесь требуется, поскольку горизонтальная и вертикальная составляющие смещения уже рассчитаны:

s→ = 125 см + 233 см; |ŝ|=√ (1252 + 2332) = 264 м; Φ = загар -1 (233/125) = 61.8°

Как рассчитать сопротивление воздуха при конечной скорости?

Сопротивление воздуха по величине эквивалентно весу падающего тела с предельной скоростью. Рассмотрим метод расчета сопротивления воздуха при предельной скорости.

  • Используя второй закон Ньютона для падающего объекта в качестве отправной точки, мы можем определить сопротивление воздуха при конечной скорости: Fg + Far = ма.
  • Для определения сопротивления воздуха при заданной скорости используются следующие два типа сопротивления воздуха: Far = – bv альтернативно, Far = – бв2.
  • Для расчета сопротивления воздуха при конечной скорости используется закон Ньютона для определения сопротивления воздуха при конечной скорости, поскольку ускорение равно нулю. мг – бв = 0; мг – бв2 = 0.
  • Чтобы определить сопротивление воздуха при заданной скорости, ответом на задачу о скорости является vT = мг/б. Альтернативой является то, что vT  = √(мг/б).

Если m представляет массу в килограммах, g — квадрат ускорения свободного падения, а b — произвольная величина.

Задача: При падении из состояния покоя объект массой 55 кг испытывает силу сопротивления воздуха, определяемую Far = -15В2. Определить конечную скорость объекта.

Решение: используйте формулу vT = √ (мг/б) для определения конечной скорости силы сопротивления вида Far = -bv2. Добавляя к уравнению, получаем,

vT = √(55) × (9.81)/15)

vT = 5.99 м / с

Как рассчитать коэффициент сопротивления воздуха?

Коэффициент сопротивления изменяется как квадратное отношение относительной скорости объекта. Рассмотрим метод расчета коэффициента сопротивления воздуха.

Коэффициент сопротивления воздуха рассчитывается по уравнению с = Fвоздух /v2. В расчете Фвоздух – силовое сопротивление, а c – силовая постоянная в этом уравнении. Жидкости, обычно вода в спортивной среде, также подвержены силе трения, которая не ограничивается только воздухом.

Сопротивление жидкости, сопротивление воздуха и сопротивление — все это относится к одному и тому же.

Проблема: Если объект движется со скоростью 22 мс-1 столкнуться с сопротивлением воздуха 50 Н, какова постоянная силы?

Решение: Даны данные,

v = 22 мс-1

Fвоздух = 50 Н

Формула для коэффициента сопротивления воздуха:

с = Fвоздух /v2

Замените указанные значения в формуле выше. Затем,

с = 50/(22)2

с = 0.103

Как рассчитать аэродинамическое сопротивление парашюта?

Вес пульсирует на шнуре, когда парашют раскрывается. Рассмотрим, как определить аэродинамическое сопротивление парашюта.

  • Чтобы определить аэродинамическое сопротивление парашюта. Уравнение для силы сопротивления парашюта, также известной как его сила сопротивления ветру, имеет вид F.D = 1 / 2 ρv2CDА. Где, ФD – сила сопротивления, r – плотность воздуха, Cd — коэффициент лобового сопротивления, A — площадь парашюта, а v — скорость в воздухе.
  • Чтобы определить сопротивление воздуха парашюта по квадрату скорости, сопротивление возрастает.
  • Чтобы определить сопротивление воздуха парашюта, нет никакой чистой силы, действующей на ракету, когда сопротивление равно весу. F = D – W = 0.
  • Cd = 2 Фd / ρв2A = W для определения аэродинамического сопротивления парашюта.
  • И, наконец, V = sqrt (2W/Cdρ A) используется для определения аэродинамического сопротивления парашюта.

При сравнении двух предметов те, у которых больший вес, меньший коэффициент лобового сопротивления, меньшая плотность газа или меньшая площадь, движутся с большей скоростью.

Как найти сопротивление воздуха через массу и ускорение?

Единственной силой, воздействующей на людей поначалу, является гравитация, которая толкает их со скоростью -9.8 м/с2. Давайте посмотрим, как можно рассчитать сопротивление воздуха, используя массу и ускорение.

  • Чтобы найти сопротивление воздуха с массой и ускорением, мы можем использовать некоторую алгебру, чтобы получить ускорение объекта с точки зрения чистой внешней силы и массы объекта (a = F/m).
  • Чистая внешняя сила (F = W – D) равна разнице между силами веса и силы сопротивления. Тогда ускорение объекта определяется выражением a = (W – D) / m.

Задача: Автомобиль массой около 29 кг движется из Калькутты в Раджастхан со скоростью 50 метров в секунду, а гусеница нагружена железом и весит 84 кг. Определить силу сопротивления автомобиля.

Решение: Даны данные,

Ускорение = 50 м/с2

Вес = 84 кг

Масса = 29 кг

Мы знаем, что a = (W – D) / m

50 = (84 – Д)/ 29

1450 = 84 – Д

-Д = 1450 – 84

Д = – 1366 Н

График сопротивления воздуха

Когда частички воздуха сталкиваются с передней частью объекта, он замедляется. Давайте проверим этот график сопротивления воздуха.

Кредит изображения – График сопротивления воздуха by Кропоткино 113 (говорить) (CC-BY-SA-3.0)

За счет уменьшения угла выпуска можно свести к минимуму влияние сопротивления воздуха на горизонтальную составляющую траектории снаряда. Расстояние и скорость, или скорость, обратно пропорциональны.

Как рассчитать сопротивление воздуха по скорости?

Чем больше частиц воздуха воздействует на объект, тем больше его общее сопротивление увеличивается с площадью поверхности. Давайте рассмотрим, как определить сопротивление воздуха на основе скорости.

Формула, используемая для определения сопротивления воздуха по скорости: c = Fv.2. Сила сопротивления воздуха представлена ​​в технике буквой F, постоянная силы представлена ​​буквой c, а скорость объекта представлена ​​буквой v. Существует линейная зависимость между сопротивлением воздуха и величиной сопротивления воздуха. плотность.

Между скоростью и сопротивлением воздуха создается квадратичная зависимость. Площадь передней кромки объекта, движущегося по воздуху, определяет, какое сопротивление воздуха он будет испытывать. Сопротивление воздуха увеличивается с увеличением площади.

Задача: Если сопротивление воздуха тела равно 34 Н, а силовая постоянная равна 0.04, какова его скорость?

Данные приведены, Fвоздух = 34 Н и с = 0.04

Формула сопротивления воздуха:

Fвоздух = резюме2

v2 = 34 / 0.04

v2 = 850

v = 29.15 м / с.

Как рассчитать силу сопротивления воздуха?

Сила сопротивления воздуха измеряется в Ньютонах (Н). Рассмотрим, как определить силу сопротивления воздуха.

Fвоздух = – резюме2 уравнение, используемое для определения силы сопротивления воздуха. Фвоздух – силовое сопротивление, а c – силовая постоянная в этом уравнении. Знак минус показывает, что объект движется в направлении, противоположном направлению сопротивления воздуха.

Задача: силовая постоянная для самолета, движущегося со скоростью 50 мс.-1 составляет 0.05. Определить сопротивление воздуха.

Решение: Даны данные,

Скорость воздуха, v = 50

Силовая постоянная, c = 0.05

Сила воздуха определяется выражением

F = – резюме2

F = (-) 0.05 × 50 × 50

F = – 125 Н.

Формула сопротивления воздуха для шара

Зависимость между силой сопротивления, действующей на тело, и сопротивлением воздуха обратная. Давайте посмотрим на формулу сопротивления воздуха шара.

Коэффициент сопротивления воздуха для сферических материалов можно рассчитать по следующей формуле: Cd = 2 Фd / ρв2A, где для сферических материалов-

  • Cd = коэффициент сопротивления воздуха, 
  • Fd сопротивление воздуха по Ньютону, 
  • А – площадь формы в плане в квадратных метрах,
  • ρ = плотность сферы, выраженная в килограммах на кубический метр,
  • А вязкость вещества, выраженная в метрах в секунду, известна как v.

Задача: Плотность воздуха 0.4500 кг/м3, а самолет, летящий на высоте, имеет скорость 250 м/с. 500 м2 Крылья самолета открыты ветру. На самолет действует сила сопротивления воздуха 168750 Н. Выполните расчет коэффициента лобового сопротивления.

Решение: Приведенные данные, Сопротивление воздуха для сферических материалов, Fd = 168750 Н

Плотность, ρ = 0.4500 кг/м3

Площадь поперечного сечения, А = 500 м2

Скорость, v = 250 м/с

Мы знаем, что для сферических материалов

Cd = 2 Фd / ρв2A

Cd = 2 × 168750 / (0.4500 × 2502 × 500)

Cd = 0.025

Как рассчитать среднее сопротивление воздуха?

Сопротивление воздуха — это разновидность жидкостного трения, которое влияет на падающие в воздухе предметы. Давайте посмотрим, как определить среднее сопротивление воздуха.

Умножив плотность воздуха, коэффициент сопротивления, площадь и скорость на два, можно рассчитать среднее сопротивление воздуха, которое будет испытывать падающий объект. Гравитация заставляет объекты двигаться вниз, в отличие от трения воздуха, которое действует противоположным образом и замедляет скорость.

Сопротивление воздуха возрастает по мере увеличения площади поверхности, на которую падают предметы.

Заключение

Сопротивление воздуха – это сила, которую испытывает объект при прохождении через воздух, где, если человек движется быстрее, сила сопротивления воздуха возрастает. Безразмерный коэффициент сопротивления CD, который рассчитывается как CD = ФD/1/2 ρАв2 где ρ — плотность жидкости (в данном случае воздуха). Площадь поперечного сечения объекта A = (1/4) ΠD2, а его скорость v.

Источник

При движении электромобиля (автомобиля) на скоростях, превышающих скорость пешехода, заметное влияние оказывает сила сопротивления воздуха. Для расчета силы сопротивления воздуха используют следующую эмпирическую формулу:

Fвозд. = Cx*S*ρ*ν2/2

Где:

Fвозд. – сила сопротивления воздуха, Н
Cx – коэффициент сопротивления воздуха (коэффициент обтекаемости) , Н*с2/(м*кг) . Cx определяется эксперементально для каждого кузова.
ρ – плотность воздуха (1,29кг/м3 при нормальных условиях)
S – лобовая площадь электромобиля (автомобиля) , м2. S является площадью проекции кузова на плоскость, перпендикулярную продольной оси.
ν – скорость электромобиля (автомобиля) , км/ч

Для расчета разгонных характеристик электромобиля (автомобиля) следует учитывать силу сопротивления разгону (силу инерции) . Причем, нужно учитывать не только инерцию самого электромобиля, но и влияние момента инерции вращающихся масс внутри электромобиля (ротор, коробка передач, кардан, колеса) . Далее приведена формула расчета силы сопротивления разгону:

Fин. = m*a*σвр

Где:

Fин. – сила сопротивления разгону, Н
m – масса электромобиля, кг
a – ускорение электромобиля, м/с2
σвр – коэффициент учета вращающихся масс

Приблизительно коэффициент учета вращающихся масс σвр можно рассчитать по формуле:

σвр=1,05 + 0,05*u2кп

Где uкп – передаточное число коробки передач

Осталось описать силу сцепления колес с дорогой. Однако, данная сила в дальнейших расчетах малоприменима, поэтому пока оставим ее на-потом.

И вот, мы уже имеем представление об основных силах, действующих на электромобиль (автомобиль) . Знание этого теоретического вопроса вскоре сподвигнет нас на изучение следующего вопроса – вопроса расчета характеристик электромобиля, необходимых для обоснованного выбора двигателя, аккумуляторной батареи и контроллера.

Читайте также: Электромобиль (автомобиль) – расчет параметров двигателя

Copyright © Дмитрий Спицын, 2007.

Данная страница создана с помощью Smart HTML Editor

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 4 апреля 2019 года; проверки требуют 14 правок.

Четыре силы, действующие на самолёт

Лобовое сопротивление — сила, препятствующая движению тел в жидкостях и газах. Лобовое сопротивление складывается из двух типов сил: сил касательного (тангенциального) трения, направленных вдоль поверхности тела, и сил давления, направленных по нормали к поверхности. Сила сопротивления является диссипативной силой и всегда направлена против вектора скорости тела в среде. Наряду с подъёмной силой является составляющей полной аэродинамической силы.

Сила лобового сопротивления обычно представляется в виде суммы двух составляющих: сопротивления при нулевой подъёмной силе и индуктивного сопротивления. Каждая составляющая характеризуется своим собственным безразмерным коэффициентом сопротивления и определённой зависимостью от скорости движения.

Лобовое сопротивление может способствовать как обледенению летательных аппаратов (при низких температурах воздуха), так и вызывать нагревание лобовых поверхностей ЛА при сверхзвуковых скоростях ударной ионизацией.

Траектории трёх объектов (угол запуска — 70°, Distance — расстояние, Height — высота). Чёрный объект не испытывает никакого сопротивления и движется по параболе, на голубой объект действует закон Стокса, на зелёный объект — закон вязкости Ньютона

Поток и форма
препятствия		 Сопротивление
формы 		Влияние

вязкости на трение

Flow plate.svg 0% ~100 %
Flow foil.svg ~10% ~90 %
Flow sphere.svg ~90% ~10 %
Flow plate perpendicular.svg 100% 0%

Сопротивление при нулевой подъёмной силе[править | править код]

Эта составляющая сопротивления не зависит от величины создаваемой подъёмной силы и складывается из профильного сопротивления крыла, сопротивления элементов конструкции самолёта, не вносящих вклад в подъёмную силу, и волнового сопротивления. Последнее является существенным при движении с около- и сверхзвуковой скоростью, и вызвано образованием ударной волны, уносящей значительную долю энергии движения. Волновое сопротивление возникает при достижении самолётом скорости, соответствующей критическому числу Маха, когда часть потока, обтекающего крыло самолёта, приобретает сверхзвуковую скорость. Критическое число М тем больше, чем больше угол стреловидности крыла, чем более заострена передняя кромка крыла и чем оно тоньше.

Сила сопротивления направлена против скорости движения, её величина пропорциональна характерной площади S, плотности среды ρ и квадрату скорости V:

{displaystyle F=C_{F}{frac {rho V^{2}}{2}}S}
{displaystyle C_{F}} — безразмерный аэродинамический коэффициент сопротивления, получается из критериев подобия, например, чисел Рейнольдса и Фруда в аэродинамике.

Определение характерной площади зависит от формы тела:

  • в простейшем случае (шар) — площадь поперечного сечения;
  • для крыльев и оперения — площадь крыла/оперения в плане;
  • для пропеллеров и несущих винтов вертолётов — либо площадь лопастей, либо ометаемая площадь винта;
  • для подводных объектов обтекаемой формы — площадь смачиваемой поверхности;
  • для продолговатых тел вращения, ориентированных вдоль потока (фюзеляж, оболочка дирижабля) — приведённая волюметрическая площадь, равная V2/3, где V — объём тела.

Мощность, требуемая для преодоления данной составляющей силы лобового сопротивления, пропорциональна кубу скорости ({displaystyle P=Fcdot V=C_{F}{dfrac {rho V^{3}}{2}}S}).

Индуктивное сопротивление в аэродинамике[править | править код]

Индуктивное сопротивление (англ. lift-induced drag) — это следствие образования подъёмной силы на крыле конечного размаха. Несимметричное обтекание крыла приводит к тому, что поток воздуха сбегает с крыла под углом к набегающему на крыло потоку (т. н. скос потока). Таким образом, во время движения крыла происходит постоянное ускорение массы набегающего воздуха в направлении, перпендикулярном направлению полёта, и направленном вниз. Это ускорение, во-первых, сопровождается образованием подъёмной силы, а во-вторых — приводит к необходимости сообщать ускоряющемуся потоку кинетическую энергию. Количество кинетической энергии, необходимое для сообщения потоку скорости, перпендикулярной направлению полёта, и будет определять величину индуктивного сопротивления. На величину индуктивного сопротивления оказывает влияние не только величина подъёмной силы (так, в случае отрицательной работы подъёмной силы направление вектора индуктивного сопротивления противоположно вектору силы, обусловленной тангенсальным трением), но и её распределение по размаху крыла. Минимальное значение индуктивного сопротивления достигается при эллиптическом распределении подъёмной силы по размаху.
При проектировании крыла этого добиваются следующими методами:

  • выбором рациональной формы крыла в плане;
  • применением геометрической и аэродинамической крутки;
  • установкой вспомогательных поверхностей — вертикальных законцовок крыла.

Индуктивное сопротивление пропорционально квадрату подъёмной силы Y, и обратно пропорционально площади крыла S, его удлинению lambda , плотности среды ρ и квадрату скорости V:

{displaystyle F_{i}=C_{F_{i}}{frac {rho V^{2}}{2}}S={frac {C_{y}^{2}}{pi lambda }}{frac {rho V^{2}}{2}}S={frac {1}{pi lambda }}{frac {Y^{2}}{{frac {rho V^{2}}{2}}S}}}

Таким образом, индуктивное сопротивление вносит существенный вклад при полёте на малой скорости (и, как следствие, на больших углах атаки). Оно также увеличивается при увеличении веса самолёта.

Суммарное сопротивление[править | править код]

Является суммой всех видов сил сопротивления:

{displaystyle F=F_{0}+F_{i}}

Так как сопротивление при нулевой подъёмной силе F_{0} пропорционально квадрату скорости, а индуктивное F_{i} — обратно пропорционально квадрату скорости, то они вносят разный вклад при разных скоростях. С ростом скорости F_{0} растёт, а {displaystyle F_{i}} — падает, и график зависимости суммарного сопротивления F от скорости («кривая потребной тяги») имеет минимум в точке пересечения кривых F_{0} и F_{i}, при которой обе силы сопротивления равны по величине. При этой скорости самолёт обладает наименьшим сопротивлением при заданной подъёмной силе (равной весу), а значит, наивысшим аэродинамическим качеством.

Мощность, требуемая для преодоления силы паразитного сопротивления, пропорциональна кубу скорости, а мощность, требуемая для преодоления индуктивного сопротивления, обратно пропорциональна скорости, поэтому суммарная мощность тоже имеет нелинейную зависимость от скорости. При некоторой скорости мощность (а значит, и расход топлива) становится минимальной — это скорость наибольшей продолжительности полёта (барражирования). Скорость, при которой достигается минимум отношения мощности (расхода топлива) к скорости полёта, является скоростью максимальной дальности полёта или крейсерской скоростью.

См. также[править | править код]

  • Эффект Бартини
  • Парадокс Даламбера
  • Закон Стокса
  • Коэффициент аэродинамического сопротивления автомобиля

Литература[править | править код]

  • Юрьев Б. Н. Экспериментальная аэродинамика. Часть II Индуктивное сопротивление, НКОП СССР, 1938, 275 с.

Ссылки[править | править код]

  • Аэродинамическое сопротивление — статья из Большой советской энциклопедии. 
  • Аэродинамическое сопротивление — статья из Физической энциклопедии
Источник

Сила сопротивления воздуха

Все составляющие
сопротивления воздуха трудно определяются
аналитически. Поэтому в практике нашла
применение эмпирическая формула, имеющая
для диапазона скоростей движения,
характерного для реального автомобиля,
следующий вид:

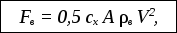
Frame5

где сх
– безразмерный
коэффициент
обтекаемости воздухом,
зависящий от формы тела; ρв
– плотность воздуха ρв=
1,202…1,225 кг/м3;
А
– площадь миделева сечения (площадь
поперечной проекции) автомобиля, м2;
V
– скорость автомобиля, м/с.

В литературе
встречается коэффициент
сопротивления воздуха
kв:

Fв
= kв
А V2,
где kв
=сх
ρв/2,
–коэффициент сопротивления воздуха,
Нс2/м4.

…и фактор
обтекаемости qв:
qв
= kв
· А.

Если вместо сх
подставить сz,
то получим аэродинамическую подъемную
силу.

Площадь миделева
сечения для авто:

А=0,9 · Вmax
· Н,

где Вmax
– наибольшая колея автомобиля, м; Н
– высота автомобиля, м.

Сила приложена в
метацентре, при этом создаются моменты.

Скорость сопротивления
потока воздуха с учетом ветра:

,
где β
– угол между направлениями движения
автомобиля и ветра.

Сх
некоторых автомобилей

ВАЗ 2101…07

0,48

Оpel
astra Sedan

HatchBack

Wagon

0,33

ВАЗ 2108…15

0,47…0,43

0,36

ВАЗ 2110

0,33

0,35

ВАЗ 2111

0,36

Peugeot 307

0,36

ВАЗ 2112

0,34

Land
Rover Free
Lander

0,44

ВАЗ 2102…04

0,48

Ford Maverick

0,44

ВАЗ 2121…214

0,536

автобус

> 0,7

ВАЗ 2123

0,455

грузовик

> 0,85

М2141

0,35

грузовик с
прицепом

> 1,25

      1. Сила сопротивления подъему

Fп
= Gа
sin
α.

В дорожной практике
величину уклона обычно оценивают
величиной подъема полотна дороги ,
отнесенную к величине горизонтальной
проекции дороги, т.е. тангенсом угла, и
обозначают i,
, выражая полученное значение в процентах.
При относительно небольшой величине
уклона допустимо в расчетных формулах
при определении силы сопротивления
подъему использовать не sin
α., а величину i
в относительных
значениях. При больших значениях
величины уклона замена sin
α величиной тангенса (i/100)недопустима.

      1. Сила сопротивления разгону

При разгоне
автомобиля происходит разгон поступательно
движущейся массы авто и разгон вращающихся
масс, увеличивающих сопротивление
разгону. Это увеличение можно учесть в
расчетах, если считать, что массы
автомобиля движутся поступательно, но
использовать некую эквивалентную массу
mэ,
несколько большей ma
( в классической
механике это выражается уравнением
Кенига)

Используем метод
Н.Е. Жуковского, приравняв кинетическую
энергии поступательно движущейся
эквивалентной массы сумме энергий:

,

где Jд
– момент инерции маховика двигателя и
связанных с ним деталей, Н·с2·м
(кг·м2);
ωд
– угловая скорость двигателя, рад/с; Jк
–момент инерции одного колеса.

Так как ωк
= Vа/rk,
ωд
= Vа·iкп
·io/rk,
rk
= rk0,

то получим
.

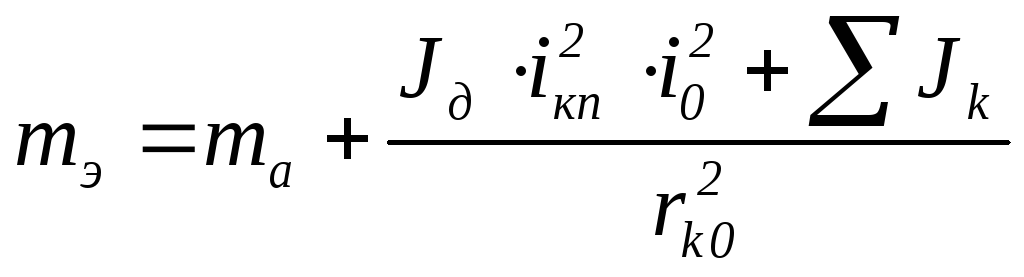Момент инерции
J
узлов трансмиссии автомобилей, кг· м2

Автомобиль

Маховик
с
коленвалом Jд

Ведомые колеса

(2 колеса с
тормозными барабанами), Jк1

Ведущие колеса

(2 колеса с
тормозными барабанами и с полуосями)
Jк2

ВАЗ 2101

0,13

1,1

1,42

ВАЗ 2121

0,13

–

9,47

УАЗ 31514

0,37

–

13,0

ГАЗ 3110

0,32

2,44

2,52

ГАЗ 53А

0,52

18,0

35,6

КАМАЗ 5320

2,11

23,3

98,5

Произведем замену:
mэ
= mа
· δ,

где.

Если автомобиль
загружен не полностью:
.

Если автомобиль
идет накатом: δ
= 1 + δ2

Сила сопротивления
разгону автомобиля (инерции): Fи
= mэ
· аа
= δ
· mа
· аа.

В первом приближении
можно принять: δ
= 1,04+0,04 iкп2

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

На расход топлива, в особенности при больших скоростях движения, значительное влияние оказывает сопротивление воздуха (аэродинамическое сопротивление), сила аэродинамического сопротивления пропорциональна квадрату скорости и рассчитывается по формуле
Pv = cx·S·v2·ρ/2,
где S – площадь фронтальной проекции автомобиля, м2; v – скорость движения автомобиля относительно воздуха, м/с; ρ – плотность воздуха, кг/м3; cх – коэффициент аэродинамического сопротивления.
Аэродинамическое сопротивление не зависит от массы автомобиля [2]. Площадь фронтальной проекции автомобиля определяется формой кузова и требованиям по обеспечению комфортного расположения водителя и пассажиров на сиденьях. Например, автомобиль большого класса может быть ниже, чем малого, так как сиденья у него зачастую располагаются ниже. У автомобиля малого класса из-за его небольшой массы и длины сиденья расположены выше над полом, и поэтому расстояние между передними и задними сиденьями меньше. Более прямое расположение водителя и пассажиров в автомобиле малого класса требует его большей высоты, но меньшей длины. Площади фронтальных проекций обоих автомобилей при этом почти одинаковы, но низкий и длинный кузов автомобиля большого класса аэродинамически более выгоден.
Мощность двигателя, необходимая для преодоления аэродинамического сопротивления, пропорциональна, следовательно, кубу скорости:
Nv = Pv·v/3600 (кВт),
где v — относительная скорость движения автомобиля, км/ч.
Коэффициент аэродинамического сопротивления, как видно из таблицы, представленной ниже, изменяется в широком диапазоне в зависимости от формы кузова автомобиля.
Аэродинамическое сопротивление различных автомобилей Кузов автомобиля
Мощность, необходимая для преодоления
аэродинамического сопротивления (кВт),
40 км/ч 80 км/ч 120 км/ч
Открытый четырёхместный 1,18 – 1,47 9,6 – 11 .8 31,0 – 40,5
Закрытый, с наличием углов и граней 0,96 – 1,18 8,0 – 9,6 26,4 – 30,8
Закрытый, с закруглением углов и граней 0,80 – 0,96 6,6 – 8,0 22,0 – 26,4
Закрытый понтонообразный 0,66 – 0,80 5,2 – 6,6 17,6 – 22,0
Закрытый, хорошо обтекаемый 0,52 – 0,66 3,7 – 5,2 13,2 – 17,6
Закрытый, аэродинамически совершенный 0,33 – 0,44 2,6 – 3,3 9,8 – 11,0
Коэффициент аэродинамического сопротивления устанавливается продувкой автомобиля или его макета в аэродинамической трубе или приближенно в ходе эксплуатационных испытаний. При испытаниях в аэродинамической трубе на макетах получаются менее точные значения, чем при тех же испытаниях на реальных автомобилях. Это вызвано тем, что на изменение сопротивления воздуха оказывают влияние неточности изготовления некоторых узлов и деталей автомобиля: ручек дверей, днища кузова, бамперов, зеркал заднего вида и т. д. Кроме того, значительное влияние на величину сх оказывает воздух, проходящий в кузов для охлаждения и вентиляции.

При больших скоростях движения автомобиля аэродинамическое сопротивление является преобладающим.

На рисунке ниже показано изменение мощностей, необходимых для преодоления сопротивления качению Nf и аэродинамического сопротивления Nv в зависимости от скорости v для автомобиля среднего класса. При скорости 60 км/ч мощности, необходимые для преодоления сопротивления качению и сопротивления воздуха, равны, что характерно для данного вида автомобилей. По сумме потребляемых мощностей можно убедиться в важности сопротивления воздуха. При скорости 80 км/ч мощность, затрачиваемая на его преодоление, в 4 раза больше, чем при скорости 40 км/ч, а при скорости выше, чем 120 км/ч, общая мощность, необходимая для движения, растет почти пропорционально кубу скорости автомобиля.

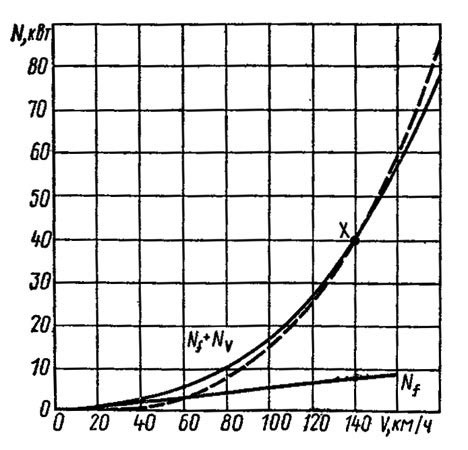
1

При определении мощности двигателя, необходимой для достижения максимальной скорости, большей той, которую обеспечивает номинальная мощность установленного на автомобиле двигателя, можно использовать без значительной ошибки следующее соотношение:

N2 = N1·(v2/v1)3,

где N2 – требуемая мощность, кВт; N1 – достигнутая максимальная мощность, кВт; v2 – требуемая скорость, км/ч; v1 – достигнутая максимальная скорость, км/ч.

Через точку X – максимальная мощность N1 при максимальной скорости v1 – проведена кривая зависимости мощности от куба скорости. Разница между этой кривой и линией мощности, требуемой для движения при максимальной скорости, незначительна.

Показанная сумма мощностей сопротивления качению Nf и аэродинамического сопротивления Nv представляет собой мощность сопротивления равномерному движению автомобиля по горизонтальному участку дороги при безветрии.

Источник

Добавить комментарий