- Home
- Statistics
- t-Test Calculator
Student’s t-test calculator for test of significance (hypothesis) for single mean, difference between two means & two equal sample sizes (paired t-test) by using t-statistic (t0) & critical value of t (te) for small samples of population in statistical surveys & experiments. This calculator is featured to generate the complete work for test of significance for small samples using one or two tailed t-test may helpful for grade school students to solve t-test worksheet or homework problems.
t-Test & it’s Applications
Statistics & probability functions are used in almost every fields such as math, science, engineering, finance, health, digital networks, data processing, social concerns, etc to research & analyze the data distributions to draw conclusions to improve the quality of process or services. Regardless of any fields, user can analyze, model, design & test any statistical surveys or experiments by using these below calculators to get the summary of data.
Student’s t-Test Formulas
In the theory of statistics & probability, the below formulas are the mathematical representation to estimate the t-statistic for the test of significance for sample mean with unknown population variance, difference between two sample means with equal but unknown population variance & related samples with unknown population variance. Users may refer these below formulas to know what are all the parameters are being used in the test of hypothesis for small samples. Users may use this one or two tailed t-test calculator to verify the estimation along with the complete work for test of significance using t-distribution table.
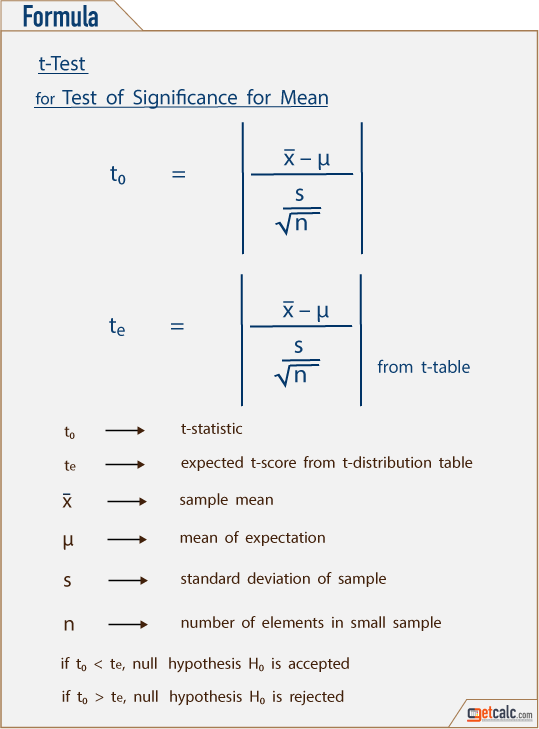
Critical Value (Rejected Region) from T-Distribution Table
In student’s t-test, the t-distribution table is used to find the critical value of te at a stated level of significance such as 0.10, 0.50, 0.90, 0.99 level. For example, 1%, 5% & 25% significance represented by t0.01, t0.05 and t0.25. This expected of t-value or t-critical te is compared with calculated or t-statistic t0 in the statistical experiments to accept or reject the hypothesis H0. The critical value of 5% for two tailed test lies on both sides of the distribution with the rejection area of tν = t0.025 on each sides. In other words, tν at the significance level of 0.20 for single tailed t-test is equal to tν at the significance level of 0.10 on both sides. The critical value or rejection region of t-distribution for small samples can be obtained by referring the t-distribution table at stated level of significance such as 1%, 5%, 9%, 10% or 50% etc or 0.10, 0.50, 0.90, 0.99 etc.
Test of Significance using t-Test
The difference between the sample mean or means is not significant, if the calculated or t-statistic t0 value is lesser than the rejection region value (t-critical) from the t-table. Therefore, the null hypothesis H0 is accepted. The difference between the sample mean or means is significant, if the calculated or t-statistic t0 value is greater than the rejection region (t-critical) value from the t-table. Therefore, the null hypothesis H0 is rejected.
Solved Example Calculations
Предположим, что надо сравнить между собой результаты выполнения тестов на внимание в двух группах. Чтобы узнать различаются ли группы между собой необходимо вычислить t-критерий Стьюдента для независимых выборок.
1. Внесем данные по группам в таблицу:
| № | Результаты группы №1 (сек.) | Результаты группы №2 (сек.) |
| 1 | 30 | 46 |
| 2 | 45 | 49 |
| 3 | 41 | 52 |
| 4 | 38 | 55 |
| 5 | 34 | 56 |
| 6 | 36 | 40 |
| 7 | 31 | 47 |
| 8 | 30 | 51 |
| 9 | 49 | 58 |
| 10 | 50 | 46 |
| 11 | 51 | 46 |
| 12 | 46 | 56 |
| 13 | 41 | 53 |
| 14 | 37 | 57 |
| 15 | 36 | 44 |
| 16 | 34 | 42 |
| 17 | 33 | 40 |
| 18 | 49 | 58 |
| 19 | 32 | 54 |
| 20 | 46 | 53 |
| 21 | 41 | 51 |
| 22 | 44 | 57 |
| 23 | 38 | 56 |
| 24 | 50 | 44 |
| 25 | 37 | 42 |
| 26 | 39 | 49 |
| 27 | 40 | 50 |
| 28 | 46 | 55 |
| 29 | 42 | 43 |
Шаг 2. Проверить распределения на нормальность.
Шаг 3. Рассчитать среднее арифметическое, стандартное отклонение и количество человек в каждой группе.
| Результаты группы №1 (сек.) | Результаты группы №2 (сек.) |
Шаг 4. Вычисляем эмпирическое значения по формуле t-критерия Стьюдента для независимых выборок
Шаг 5. Вычисляем степени свободы.
Шаг 6. Определяем по таблице критических значений t-Стьюдента уровень значимости.
Значение 6,09 больше чем значение 3,473 следовательно уровень значимости меньше 0,001
Шаг 7. Если уровень значимости меньше 0,05 делается вывод о наличи различий между группами. Таким образом между двумя группами есть различия в скорости выполнения тестов на внимание.
| Расчет критерия Т-Стьюдента для независимых выборок | |
| Расчет критерия Т-Стьюдента для независимых выборок в SPSS | Пример критерия Т-Стьюдента для независимых выборок в SPSS |
| Расчет критерия Т-Стьюдента для независимых выборок в Excell | Пример критерия Т-Стьюдента для независимых выборок в Excell |
| Критерий Т-Стьюдента для независимых выборок |
Пример расчета t-критерия Стьюдента для независимых выборок
Предположим, что надо сравнить между собой результаты выполнения тестов на внимание в двух группах.
Чтобы узнать различаются ли группы между собой необходимо вычислить t-критерий Стьюдента для независимых выборок.
1. Внесем данные по группам в таблицу:
| № | Результаты группы №1 (сек.) | Результаты группы №2 (сек.) |
| 1 | 30 | 46 |
| 2 | 45 | 49 |
| 3 | 41 | 52 |
| 4 | 38 | 55 |
| 5 | 34 | 56 |
| 6 | 36 | 40 |
| 7 | 31 | 47 |
| 8 | 30 | 51 |
| 9 | 49 | 58 |
| 10 | 50 | 46 |
| 11 | 51 | 46 |
| 12 | 46 | 56 |
| 13 | 41 | 53 |
| 14 | 37 | 57 |
| 15 | 36 | 44 |
| 16 | 34 | 42 |
| 17 | 33 | 40 |
| 18 | 49 | 58 |
| 19 | 32 | 54 |
| 20 | 46 | 53 |
| 21 | 41 | 51 |
| 22 | 44 | 57 |
| 23 | 38 | 56 |
| 24 | 50 | 44 |
| 25 | 37 | 42 |
| 26 | 39 | 49 |
| 27 | 40 | 50 |
| 28 | 46 | 55 |
| 29 | 42 | 43 |
Шаг 2.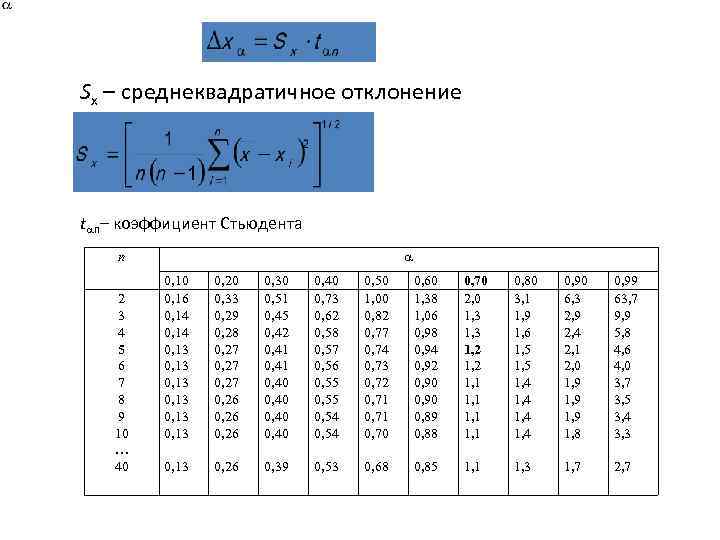
Проверить распределения на нормальность.
Шаг 3. Рассчитать среднее арифметическое, стандартное отклонение и количество человек в каждой группе.
| Результаты группы №1 (сек.) | Результаты группы №2 (сек.) |
Шаг 4. Вычисляем эмпирическое значения по формуле t-критерия Стьюдента для независимых выборок
Шаг 5. Вычисляем степени свободы.
Шаг 6. Определяем по таблице критических значений t-Стьюдента уровень значимости.
Значение 6,09 больше чем значение 3,473 следовательно уровень значимости меньше 0,001
Шаг 7. Если уровень значимости меньше 0,05 делается вывод о наличи различий между группами. Таким образом между двумя группами есть различия в скорости выполнения тестов на внимание.
| Расчет критерия Т-Стьюдента для независимых выборок | |
| Расчет критерия Т-Стьюдента для независимых выборок в SPSS | Пример критерия Т-Стьюдента для независимых выборок в SPSS |
| Расчет критерия Т-Стьюдента для независимых выборок в Excell | Пример критерия Т-Стьюдента для независимых выборок в Excell |
| Критерий Т-Стьюдента для независимых выборок |
T Формула распределения | Вычислить распределение T студентов
Формула для расчета распределения T (которое также широко известно как распределение T Стьюдента) показана как вычитание среднего значения генеральной совокупности (среднее значение второй выборки) из среднего значения выборки (среднего значения первой выборки), которое составляет [ x̄ – μ ], которое затем делится на стандартное отклонение средних значений, которое изначально делится на квадратный корень из n, который представляет собой количество единиц в этой выборке [s ÷ √(n)].
Т-распределение — это вид распределения, который выглядит почти как кривая нормального распределения или кривая нормального распределения, но с немного более толстым и коротким хвостом. Если размер выборки мал, то это распределение будет использоваться вместо нормального распределения.
t = (x̄ – μ) / (s/√n)
Распределение Стьюдента возникает при оценке среднего нормально распределенной выборки в случаях когда количество экземпляров выборки мало и стандартное отклонение неизвестно. Впервые было исследовано Вильямом Госсетом в начале XX века, который выпускал свои работы под псевдонимом Стьюдент.
Функция плотности вероятности
Функция плотности вероятности распределения Стьюдента имеет вид:
где n — количество степеней свободы и – Гамма-функция
Функция распределения
Функция распределения может быть выражена через Гамма функцию и гипергеометрическую функцию следующим образом:
Распределение Стьюдента
Точность вычисления
Знаков после запятой: 5
Значение функции распределения
График плотности вероятности
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Функция распределения
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Квантильная функция
-квантилем распределения Стьюдента называется число такое, что , где Fn — функция распределения Стьюдента.
Обратная (квантильная) функция распределения не имеет простого представления, результат ее вычисления, в литературе представлен в виде таблиц.
Калькулятор ниже вычисляет значение этой функции при помощи статистического пакета jStat:
Квантильная функция распределения Стьюдента
Точность вычисления
Знаков после запятой: 2
