Сжатие данных алгоритмом Хаффмана
Время на прочтение
15 мин
Количество просмотров 54K
Вступление
В данной статье я расскажу вам о широко известном алгоритме Хаффмана, и вы наконец разберетесь, как все там устроено изнутри. После прочтения вы сможете своими руками(а главное, головой) написать архиватор, сжимающий реальные, черт подери, данные! Кто знает, быть может именно вам светит стать следующим Ричардом Хендриксом!
Да-да, об этом уже была статья на Хабре, но без практической реализации. Здесь же мы сфокусируемся как на теоретической части, так и на программерской. Итак, все под кат!
Немного размышлений
В обычном текстовом файле один символ кодируется 8 битами(кодировка ASCII) или 16(кодировка Unicode). Далее будем рассматривать кодировку ASCII. Для примера возьмем строку s1 = «SUSIE SAYS IT IS EASYn». Всего в строке 22 символа, естественно, включая пробелы и символ перехода на новую строку — ‘n’. Файл, содержащий данную строку будет весить 22*8 = 176 бит. Сразу же встает вопрос: рационально ли использовать все 8 бит для кодировки 1 символа? Мы ведь используем не все символы кодировки ASCII. Даже если бы и использовали, рациональней было бы самой частой букве — S — дать самый короткий возможный код, а для самой редкой букве — T (или U, или ‘n’) — дать код подлиннее. В этом и заключается алгоритм Хаффмана: необходимо найти оптимальный вариант кодировки, при котором файл будет минимального веса. Вполне нормально, что у разных символов длины кода будут отличаться — на этом и основан алгоритм.
Кодирование
Почему бы символу ‘S’ не дать код, например, длиной в 1 бит: 0 или 1. Пусть это будет 1. Тогда второму наиболее встречающемуся символу — ‘ ‘(пробел) — дадим 0. Представьте себе, вы начали декодировать свое сообщение — закодированную строку s1 — и видите, что код начинается с 1. Итак, что же делать: это символ S, или же это какой-то другой символ, например A? Поэтому возникает важное правило:
Ни один код не должен быть префиксом другого
Это правило является ключевым в алгоритме. Поэтому создание кода начинается с частотной таблицы, в которой указана частота (количество вхождений) каждого символа:

Символы с наибольшим количеством вхождений должны кодироваться наименьшим
возможным
количеством битов. Приведу пример одной из возможных таблиц кодов:

Таким образом, закодированное сообщение будет выглядеть так:
10 01111 10 110 1111 00 10 010 1110 10 00 110 0110 00 110 10 00 1111 010 10 1110 01110
Код каждого символа я разделил пробелом. По-настоящему в сжатом файле такого не будет!
Вытекает вопрос:
как этот салага придумал код
как создать таблицу кодов? Об этом пойдет речь ниже.
Построение дерева Хаффмана
Здесь приходят на выручку бинарные деревья поиска. Не волнуйтесь, здесь методы поиска, вставки и удаления не потребуются. Вот структура дерева на java:
class BinaryTree {
private Node root;
public BinaryTree() {
root = new Node();
}
public BinaryTree(Node root) {
this.root = root;
}
...
}
public class Node {
private int frequence;
private char letter;
private Node leftChild;
private Node rightChild;
...
}
Это не полный код, полный код будет ниже.
Вот сам алгоритм построения дерева:
- Создать объект Node для каждого символа из сообщения(строка s1). В нашем случае будет 9 узлов(объектов Node). Каждый узел состоит из двух полей данных: символ и частота
- Создать объект Дерева(BinaryTree) для кажлого из узлов Node. Узел становится корнем дерева.
- Вставить эти деревья в приоритетную очередь. Чем меньше частота, тем больше приоритет. Таким образом, при извлечении всегда выбирается дерево наименьшей частотой.
Далее нужно циклически делать следующее:
- Извлечь два дерева из приоритетной очереди и сделать их потомками нового узла (только что созданного узла без буквы). Частота нового узла равна сумме частот двух деревьев-потомков.
- Для этого узла создать дерево с корнем в данном узле. Вставить это дерево обратно в приоритетную очередь. (Так как у дерева новая частота, то скорее всего она встанет на новое место в очереди)
- Продолжать выполнение шагов 1 и 2, пока в очереди не останется одно дерево — дерево Хаффмана
Рассмотрим данный алгоритм на строке s1:

Здесь символ «lf»(linefeed) обозначает переход на новую строку, «sp» (space) — это пробел.
А что дальше?
Мы получили дерево Хаффмана. Ну окей. И что с ним делать?
Его и за бесплатно не возьмут
А далее, нужно отследить все возможные пути от корня до листов дерева. Условимся обозначить ребро 0, если оно ведет к левому потомку и 1 — если к правому. Строго говоря, в данных обозначениях, код символа — это путь от корня дерева до листа, содержащего этот самый символ.
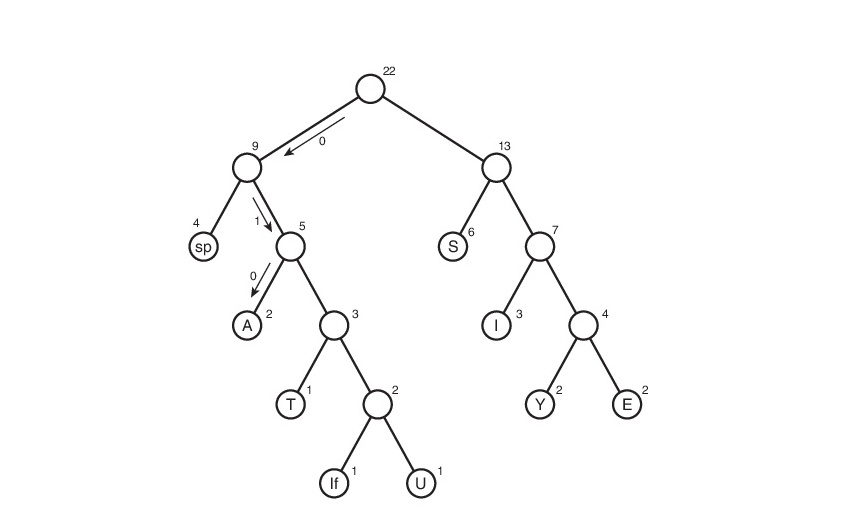
Таким макаром и получилась таблица кодов. Заметим, что если рассмотреть эту таблицу, то можно сделать вывод о «весе» каждого символа — это длина его кода. Тогда в сжатом виде исходный файл будет весить: 2 * 3 + 2*4 + 3 * 3 + 6 * 2 + 1 * 4 + 1 * 5 + 2 * 4 + 4 * 2 + 1 * 5 = 65 бит. Вначале он весил 176 бит. Следовательно, мы уменьшили его аж в 176/65 = 2.7 раза! Но это утопия. Такой коэффициент вряд ли будет получен. Почему? Об этом пойдет речь чуть позже.
Декодирование
Ну, пожалуй, осталось самое простое — декодирование. Я думаю, многие из вас догадались, что просто создать сжатый файл без каких-либо намеков на то, как он был закодирован, нельзя — мы не сможем его декодировать! Да-да, мне было тяжело это осознать, но придется создать текстовый файл table.txt с таблицей сжатия:
01110
00
A010
E1111
I110
S10
T0110
U01111
Y1110
Запись таблицы в виде ‘символ’«код символа». Почему 01110 без символа? На самом деле он с символом, просто средства java, используемые мной при выводе в файл, символ перехода на новую строку — ‘n’ -конвертируют в переход на новую строку(как бы это глупо не звучало). Поэтому пустая строка сверху и есть символ для кода 01110. Для кода 00 символом является пробел в начале строки. Сразу скажу, что
нашему коэффициенту хана
этот способ хранения таблицы может претендовать на самый нерациональный. Но он прост для понимания и реализации. С удовольствием выслушаю Ваши рекомендации в комментариях по поводу оптимизации.
Имея эту таблицу, очень просто декодировать. Вспомним, каким правилом мы руководствовались, при создании кодировки:
Ни один код не должен являться префиксом другого
Вот тут-то оно и играет облегчающую роль. Мы читаем последовательно бит за битом и, как только полученная строка d, состоящая из прочтенных битов, совпадает с кодировкой, соответствующей символу character, мы сразу знаем что был закодирован символ character (и только он!). Далее записываем character в декодировочную строку(строку, содержащую декодированное сообщение), обнуляем строку d, и читаем дальше закодированный файл.
Реализация
Пришло время
унижать мой код
писать архиватор. Назовем его Compressor.
Начнем с начала. Первым делом пишем класс Node:
public class Node {
private int frequence;//частота
private char letter;//буква
private Node leftChild;//левый потомок
private Node rightChild;//правый потомок
public Node(char letter, int frequence) { //собственно, конструктор
this.letter = letter;
this.frequence = frequence;
}
public Node() {}//перегрузка конструтора для безымянных узлов(см. выше в разделе о построении дерева Хаффмана)
public void addChild(Node newNode) {//добавить потомка
if (leftChild == null)//если левый пустой=> правый тоже=> добавляем в левый
leftChild = newNode;
else {
if (leftChild.getFrequence() <= newNode.getFrequence()) //в общем, левым потомком
rightChild = newNode;//станет тот, у кого меньше частота
else {
rightChild = leftChild;
leftChild = newNode;
}
}
frequence += newNode.getFrequence();//итоговая частота
}
public Node getLeftChild() {
return leftChild;
}
public Node getRightChild() {
return rightChild;
}
public int getFrequence() {
return frequence;
}
public char getLetter() {
return letter;
}
public boolean isLeaf() {//проверка на лист
return leftChild == null && rightChild == null;
}
}
Теперь деревце:
class BinaryTree {
private Node root;
public BinaryTree() {
root = new Node();
}
public BinaryTree(Node root) {
this.root = root;
}
public int getFrequence() {
return root.getFrequence();
}
public Node getRoot() {
return root;
}
}
Приоритетная очередь:
import java.util.ArrayList;//да-да, очередь будет на базе списка
class PriorityQueue {
private ArrayList<BinaryTree> data;//список очереди
private int nElems;//кол-во элементов в очереди
public PriorityQueue() {
data = new ArrayList<BinaryTree>();
nElems = 0;
}
public void insert(BinaryTree newTree) {//вставка
if (nElems == 0)
data.add(newTree);
else {
for (int i = 0; i < nElems; i++) {
if (data.get(i).getFrequence() > newTree.getFrequence()) {//если частота вставляемого дерева меньше
data.add(i, newTree);//чем част. текущего, то cдвигаем все деревья на позициях справа на 1 ячейку
break;//затем ставим новое дерево на позицию текущего
}
if (i == nElems - 1)
data.add(newTree);
}
}
nElems++;//увеличиваем кол-во элементов на 1
}
public BinaryTree remove() {//удаление из очереди
BinaryTree tmp = data.get(0);//копируем удаляемый элемент
data.remove(0);//собственно, удаляем
nElems--;//уменьшаем кол-во элементов на 1
return tmp;//возвращаем удаленный элемент(элемент с наименьшей частотой)
}
}
Класс, создающий дерево Хаффмана:
public class HuffmanTree {
private final byte ENCODING_TABLE_SIZE = 127;//длина кодировочной таблицы
private String myString;//сообщение
private BinaryTree huffmanTree;//дерево Хаффмана
private int[] freqArray;//частотная таблица
private String[] encodingArray;//кодировочная таблица
//----------------constructor----------------------
public HuffmanTree(String newString) {
myString = newString;
freqArray = new int[ENCODING_TABLE_SIZE];
fillFrequenceArray();
huffmanTree = getHuffmanTree();
encodingArray = new String[ENCODING_TABLE_SIZE];
fillEncodingArray(huffmanTree.getRoot(), "", "");
}
//--------------------frequence array------------------------
private void fillFrequenceArray() {
for (int i = 0; i < myString.length(); i++) {
freqArray[(int)myString.charAt(i)]++;
}
}
public int[] getFrequenceArray() {
return freqArray;
}
//------------------------huffman tree creation------------------
private BinaryTree getHuffmanTree() {
PriorityQueue pq = new PriorityQueue();
//алгоритм описан выше
for (int i = 0; i < ENCODING_TABLE_SIZE; i++) {
if (freqArray[i] != 0) {//если символ существует в строке
Node newNode = new Node((char) i, freqArray[i]);//то создать для него Node
BinaryTree newTree = new BinaryTree(newNode);//а для Node создать BinaryTree
pq.insert(newTree);//вставить в очередь
}
}
while (true) {
BinaryTree tree1 = pq.remove();//извлечь из очереди первое дерево.
try {
BinaryTree tree2 = pq.remove();//извлечь из очереди второе дерево
Node newNode = new Node();//создать новый Node
newNode.addChild(tree1.getRoot());//сделать его потомками два извлеченных дерева
newNode.addChild(tree2.getRoot());
pq.insert(new BinaryTree(newNode);
} catch (IndexOutOfBoundsException e) {//осталось одно дерево в очереди
return tree1;
}
}
}
public BinaryTree getTree() {
return huffmanTree;
}
//-------------------encoding array------------------
void fillEncodingArray(Node node, String codeBefore, String direction) {//заполнить кодировочную таблицу
if (node.isLeaf()) {
encodingArray[(int)node.getLetter()] = codeBefore + direction;
} else {
fillEncodingArray(node.getLeftChild(), codeBefore + direction, "0");
fillEncodingArray(node.getRightChild(), codeBefore + direction, "1");
}
}
String[] getEncodingArray() {
return encodingArray;
}
public void displayEncodingArray() {//для отладки
fillEncodingArray(huffmanTree.getRoot(), "", "");
System.out.println("======================Encoding table====================");
for (int i = 0; i < ENCODING_TABLE_SIZE; i++) {
if (freqArray[i] != 0) {
System.out.print((char)i + " ");
System.out.println(encodingArray[i]);
}
}
System.out.println("========================================================");
}
//-----------------------------------------------------
String getOriginalString() {
return myString;
}
}
Класс, содержащий который кодирует/декодирует:
public class HuffmanOperator {
private final byte ENCODING_TABLE_SIZE = 127;//длина таблицы
private HuffmanTree mainHuffmanTree;//дерево Хаффмана (используется только для сжатия)
private String myString;//исходное сообщение
private int[] freqArray;//частотаная таблица
private String[] encodingArray;//кодировочная таблица
private double ratio;//коэффициент сжатия
public HuffmanOperator(HuffmanTree MainHuffmanTree) {//for compress
this.mainHuffmanTree = MainHuffmanTree;
myString = mainHuffmanTree.getOriginalString();
encodingArray = mainHuffmanTree.getEncodingArray();
freqArray = mainHuffmanTree.getFrequenceArray();
}
public HuffmanOperator() {}//for extract;
//---------------------------------------compression-----------------------------------------------------------
private String getCompressedString() {
String compressed = "";
String intermidiate = "";//промежуточная строка(без добавочных нулей)
//System.out.println("=============================Compression=======================");
//displayEncodingArray();
for (int i = 0; i < myString.length(); i++) {
intermidiate += encodingArray[myString.charAt(i)];
}
//Мы не можем писать бит в файл. Поэтому нужно сделать длину сообщения кратной 8=>
//нужно добавить нули в конец(можно 1, нет разницы)
byte counter = 0;//количество добавленных в конец нулей (байта в полне хватит: 0<=counter<8<127)
for (int length = intermidiate.length(), delta = 8 - length % 8;
counter < delta ; counter++) {//delta - количество добавленных нулей
intermidiate += "0";
}
//склеить кол-во добавочных нулей в бинарном предаствлении и промежуточную строку
compressed = String.format("%8s", Integer.toBinaryString(counter & 0xff)).replace(" ", "0") + intermidiate;
//идеализированный коэффициент
setCompressionRatio();
//System.out.println("===============================================================");
return compressed;
}
private void setCompressionRatio() {//посчитать идеализированный коэффициент
double sumA = 0, sumB = 0;//A-the original sum
for (int i = 0; i < ENCODING_TABLE_SIZE; i++) {
if (freqArray[i] != 0) {
sumA += 8 * freqArray[i];
sumB += encodingArray[i].length() * freqArray[i];
}
}
ratio = sumA / sumB;
}
public byte[] getBytedMsg() {//final compression
StringBuilder compressedString = new StringBuilder(getCompressedString());
byte[] compressedBytes = new byte[compressedString.length() / 8];
for (int i = 0; i < compressedBytes.length; i++) {
compressedBytes[i] = (byte) Integer.parseInt(compressedString.substring(i * 8, (i + 1) * 8), 2);
}
return compressedBytes;
}
//---------------------------------------end of compression----------------------------------------------------------------
//------------------------------------------------------------extract-----------------------------------------------------
public String extract(String compressed, String[] newEncodingArray) {
String decompressed = "";
String current = "";
String delta = "";
encodingArray = newEncodingArray;
//displayEncodingArray();
//получить кол-во вставленных нулей
for (int i = 0; i < 8; i++)
delta += compressed.charAt(i);
int ADDED_ZEROES = Integer.parseInt(delta, 2);
for (int i = 8, l = compressed.length() - ADDED_ZEROES; i < l; i++) {
//i = 8, т.к. первым байтом у нас идет кол-во вставленных нулей
current += compressed.charAt(i);
for (int j = 0; j < ENCODING_TABLE_SIZE; j++) {
if (current.equals(encodingArray[j])) {//если совпало
decompressed += (char)j;//то добавляем элемент
current = "";//и обнуляем текущую строку
}
}
}
return decompressed;
}
public String getEncodingTable() {
String enc = "";
for (int i = 0; i < encodingArray.length; i++) {
if (freqArray[i] != 0)
enc += (char)i + encodingArray[i] + 'n';
}
return enc;
}
public double getCompressionRatio() {
return ratio;
}
public void displayEncodingArray() {//для отладки
System.out.println("======================Encoding table====================");
for (int i = 0; i < ENCODING_TABLE_SIZE; i++) {
//if (freqArray[i] != 0) {
System.out.print((char)i + " ");
System.out.println(encodingArray[i]);
//}
}
System.out.println("========================================================");
}
}
Класс, облегчающий запись в файл:
import java.io.File;
import java.io.PrintWriter;
import java.io.FileNotFoundException;
import java.io.FileOutputStream;
import java.io.IOException;
import java.io.Closeable;
public class FileOutputHelper implements Closeable {
private File outputFile;
private FileOutputStream fileOutputStream;
public FileOutputHelper(File file) throws FileNotFoundException {
outputFile = file;
fileOutputStream = new FileOutputStream(outputFile);
}
public void writeByte(byte msg) throws IOException {
fileOutputStream.write(msg);
}
public void writeBytes(byte[] msg) throws IOException {
fileOutputStream.write(msg);
}
public void writeString(String msg) {
try (PrintWriter pw = new PrintWriter(outputFile)) {
pw.write(msg);
} catch (FileNotFoundException e) {
System.out.println("Неверный путь, или такого файла не существует!");
}
}
@Override
public void close() throws IOException {
fileOutputStream.close();
}
public void finalize() throws IOException {
close();
}
}
Класс, облегчающий чтение из файла:
import java.io.FileInputStream;
import java.io.EOFException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.Closeable;
import java.io.File;
import java.io.IOException;
public class FileInputHelper implements Closeable {
private FileInputStream fileInputStream;
private BufferedReader fileBufferedReader;
public FileInputHelper(File file) throws IOException {
fileInputStream = new FileInputStream(file);
fileBufferedReader = new BufferedReader(new InputStreamReader(fileInputStream));
}
public byte readByte() throws IOException {
int cur = fileInputStream.read();
if (cur == -1)//если закончился файл
throw new EOFException();
return (byte)cur;
}
public String readLine() throws IOException {
return fileBufferedReader.readLine();
}
@Override
public void close() throws IOException{
fileInputStream.close();
}
}
Ну, и главный класс:
import java.io.File;
import java.nio.charset.MalformedInputException;
import java.io.FileNotFoundException;
import java.io.IOException;
import java.nio.file.Files;
import java.nio.file.NoSuchFileException;
import java.nio.file.Paths;
import java.util.List;
import java.io.EOFException;
public class Main {
private static final byte ENCODING_TABLE_SIZE = 127;
public static void main(String[] args) throws IOException {
try {//указываем инструкцию с помощью аргументов командной строки
if (args[0].equals("--compress") || args[0].equals("-c"))
compress(args[1]);
else if ((args[0].equals("--extract") || args[0].equals("-x"))
&& (args[2].equals("--table") || args[2].equals("-t"))) {
extract(args[1], args[3]);
}
else
throw new IllegalArgumentException();
} catch (ArrayIndexOutOfBoundsException | IllegalArgumentException e) {
System.out.println("Неверный формат ввода аргументов ");
System.out.println("Читайте Readme.txt");
e.printStackTrace();
}
}
public static void compress(String stringPath) throws IOException {
List<String> stringList;
File inputFile = new File(stringPath);
String s = "";
File compressedFile, table;
try {
stringList = Files.readAllLines(Paths.get(inputFile.getAbsolutePath()));
} catch (NoSuchFileException e) {
System.out.println("Неверный путь, или такого файла не существует!");
return;
} catch (MalformedInputException e) {
System.out.println("Текущая кодировка файла не поддерживается");
return;
}
for (String item : stringList) {
s += item;
s += 'n';
}
HuffmanOperator operator = new HuffmanOperator(new HuffmanTree(s));
compressedFile = new File(inputFile.getAbsolutePath() + ".cpr");
compressedFile.createNewFile();
try (FileOutputHelper fo = new FileOutputHelper(compressedFile)) {
fo.writeBytes(operator.getBytedMsg());
}
//create file with encoding table:
table = new File(inputFile.getAbsolutePath() + ".table.txt");
table.createNewFile();
try (FileOutputHelper fo = new FileOutputHelper(table)) {
fo.writeString(operator.getEncodingTable());
}
System.out.println("Путь к сжатому файлу: " + compressedFile.getAbsolutePath());
System.out.println("Путь к кодировочной таблице " + table.getAbsolutePath());
System.out.println("Без таблицы файл будет невозможно извлечь!");
double idealRatio = Math.round(operator.getCompressionRatio() * 100) / (double) 100;//идеализированный коэффициент
double realRatio = Math.round((double) inputFile.length()
/ ((double) compressedFile.length() + (double) table.length()) * 100) / (double)100;//настоящий коэффициент
System.out.println("Идеализированный коэффициент сжатия равен " + idealRatio);
System.out.println("Коэффициент сжатия с учетом кодировочной таблицы " + realRatio);
}
public static void extract(String filePath, String tablePath) throws FileNotFoundException, IOException {
HuffmanOperator operator = new HuffmanOperator();
File compressedFile = new File(filePath),
tableFile = new File(tablePath),
extractedFile = new File(filePath + ".xtr");
String compressed = "";
String[] encodingArray = new String[ENCODING_TABLE_SIZE];
//read compressed file
//!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!check here:
try (FileInputHelper fi = new FileInputHelper(compressedFile)) {
byte b;
while (true) {
b = fi.readByte();//method returns EOFException
compressed += String.format("%8s", Integer.toBinaryString(b & 0xff)).replace(" ", "0");
}
} catch (EOFException e) {
}
//--------------------
//read encoding table:
try (FileInputHelper fi = new FileInputHelper(tableFile)) {
fi.readLine();//skip first empty string
encodingArray[(byte)'n'] = fi.readLine();//read code for 'n'
while (true) {
String s = fi.readLine();
if (s == null)
throw new EOFException();
encodingArray[(byte)s.charAt(0)] = s.substring(1, s.length());
}
} catch (EOFException ignore) {}
extractedFile.createNewFile();
//extract:
try (FileOutputHelper fo = new FileOutputHelper(extractedFile)) {
fo.writeString(operator.extract(compressed, encodingArray));
}
System.out.println("Путь к распакованному файлу " + extractedFile.getAbsolutePath());
}
}
Файл с инструкциями readme.txt предстоит вам написать самим 🙂
Заключение
Наверное, это все что я хотел сказать. Если у вас есть что сказать по поводу
моей некомпетентности
улучшений в коде, алгоритме, вообще любой оптимизации, то смело пишите. Если я что-то недообъяснил, тоже пишите. Буду рад услышать вас в комментариях!
P.S.
Да-да, я все еще здесь, ведь я не забыл про коэффициент. Для строки s1 кодировочная таблица весит 48 байт — намного больше исходного файла, да и про добавочные нули не забыли(количество добавленных нулей равно 7)=> коэффициент сжатия будет меньше единицы: 176/(65 + 48*8 + 7)=0.38. Если вы тоже это заметили, то
только не по лицу
вы молодец. Да, эта реализация будет крайне неэффективной для малых файлов. Но что же происходит с большими файлами? Размеры файла намного превышают размер кодировочной таблицы. Вот здесь-то алгоритм работает как-надо! Например, для монолога Фауста архиватор выдает реальный (не идеализированный) коэффициент, равный 1.46 — почти в полтора раза! И да, предполагалось, что файл будет на английском языке.
UPD
Выпустил upgrade: добавил GUI + изменил алгоритм обработки исходного текста так, чтобы не читать весь файл в память. Короче, кидаю ссылку на git для любознательных: сами всё увидите.
Благодарности
Как и автор каждой хорошей книги, я созидал эту статью не без помощи других людей. Имхо, очень мало людей сделало что-то крутое в одиночку.
Огромное спасибо Исаеву Виталию Вячеславовичу за небходимую теоретическую поддержку.
Также, часть материала этой статьи взята из книги Роберта Лафоре «Data Structures and Algorithms in Java». Если сомневаетесь как или окуда начать свой путь в теории алгоритмов и структур данных — берите, не прогадаете.
Алгоритм Хаффмана — жадный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью. Был разработан в 1952 году аспирантом Массачусетского технологического института Дэвидом Хаффманом при написании им курсовой работы[1]. В настоящее время используется во многих программах сжатия данных.
В отличие от алгоритма Шеннона — Фано, алгоритм Хаффмана остаётся всегда оптимальным и для вторичных алфавитов m2 с более чем двумя символами.
Этот метод кодирования состоит из двух основных этапов:
- Построение оптимального кодового дерева.
- Построение отображения код-символ на основе построенного дерева.
Классический алгоритм Хаффмана[править | править код]
Идея алгоритма состоит в следующем: зная вероятности появления символов в сообщении, можно описать процедуру построения кодов переменной длины, состоящих из целого количества битов. Символам с большей вероятностью ставятся в соответствие более короткие коды. Коды Хаффмана обладают свойством префиксности (то есть ни одно кодовое слово не является префиксом другого), что позволяет однозначно их декодировать.
Классический алгоритм Хаффмана на входе получает таблицу частотностей символов в сообщении. Далее на основании этой таблицы строится дерево кодирования Хаффмана (Н-дерево).[2]
- Символы входного алфавита образуют список свободных узлов. Каждый лист имеет вес, который может быть равен либо вероятности, либо количеству вхождений символа в сжимаемое сообщение.
- Выбираются два свободных узла дерева с наименьшими весами.
- Создается их родитель с весом, равным их суммарному весу.
- Родитель добавляется в список свободных узлов, а два его потомка удаляются из этого списка.
- Одной дуге, выходящей из родителя, ставится в соответствие бит 1, другой — бит 0. Битовые значения ветвей, исходящих от корня, не зависят от весов потомков.
- Шаги, начиная со второго, повторяются до тех пор, пока в списке свободных узлов не останется только один свободный узел. Он и будет считаться корнем дерева.
Допустим, у нас есть следующая таблица абсолютных частотностей:
| Символ | А | Б | В | Г | Д |
|---|---|---|---|---|---|
| Абсолютная частотность | 15 | 7 | 6 | 6 | 5 |
Этот процесс можно представить как построение дерева, корень которого — символ с суммой вероятностей объединенных символов, получившийся при объединении символов из последнего шага, его n0 потомков — символы из предыдущего шага и т. д.
Чтобы определить код для каждого из символов, входящих в сообщение, мы должны пройти путь от листа дерева, соответствующего текущему символу, до его корня, накапливая биты при перемещении по ветвям дерева (первая ветвь в пути соответствует младшему биту). Полученная таким образом последовательность битов является кодом данного символа, записанным в обратном порядке.

Построение дерева для данного примера
Для данной таблицы символов коды Хаффмана будут выглядеть следующим образом.
| Символ | А | Б | В | Г | Д |
|---|---|---|---|---|---|
| Код | 0 | 100 | 101 | 110 | 111 |
Поскольку ни один из полученных кодов не является префиксом другого, они могут быть однозначно декодированы при чтении их из потока. Кроме того, наиболее частый символ сообщения А закодирован наименьшим количеством бит, а наиболее редкий символ Д — наибольшим.
При этом общая длина сообщения, состоящего из приведённых в таблице символов, составит 87 бит (в среднем 2,2308 бита на символ). При использовании равномерного кодирования общая длина сообщения составила бы 117 бит (ровно 3 бита на символ). Заметим, что энтропия источника, независимым образом порождающего символы с указанными частотностями, составляет ~2,1858 бита на символ, то есть избыточность построенного для такого источника кода Хаффмана, понимаемая как отличие среднего числа бит на символ от энтропии, составляет менее 0,05 бита на символ.
Классический алгоритм Хаффмана имеет ряд существенных недостатков. Во-первых, для восстановления содержимого сжатого сообщения декодер должен знать таблицу частотностей, которой пользовался кодер. Следовательно, длина сжатого сообщения увеличивается на длину таблицы частотностей, которая должна посылаться впереди данных, что может свести на нет все усилия по сжатию сообщения. Кроме того, необходимость наличия полной частотной статистики перед началом собственно кодирования требует двух проходов по сообщению: одного для построения модели сообщения (таблицы частотностей и Н-дерева), другого – для собственно кодирования. Во-вторых, избыточность кодирования обращается в ноль лишь в тех случаях, когда вероятности кодируемых символов являются обратными степенями числа 2. В-третьих, для источника с энтропией, не превышающей 1 (например, для двоичного источника), непосредственное применение кода Хаффмана бессмысленно.
Адаптивное сжатие[править | править код]
Адаптивное сжатие позволяет не передавать модель сообщения вместе с ним самим и ограничиться одним проходом по сообщению как при кодировании, так и при декодировании.
В создании алгоритма адаптивного кодирования Хаффмана наибольшие сложности возникают при разработке процедуры обновления модели очередным символом. Теоретически можно было бы просто вставить внутрь этой процедуры полное построение дерева кодирования Хаффмана, однако, такой алгоритм сжатия имел бы неприемлемо низкое быстродействие, так как построение Н-дерева — это слишком большая работа, и производить её при обработке каждого символа неразумно. К счастью, существует способ модифицировать уже существующее Н-дерево так, чтобы отобразить обработку нового символа. Наиболее известными алгоритмами перестроения являются алгоритм Фоллера-Галлагера-Кнута (FGK) и алгоритм Виттера.
Все алгоритмы перестроения дерева при считывании очередного символа включают в себя две операции:
Первая — увеличение веса узлов дерева. Вначале увеличиваем вес листа, соответствующего считанному символу, на единицу. Затем увеличиваем вес родителя, чтобы привести его в соответствие с новыми значениями веса потомков. Этот процесс продолжается до тех пор, пока мы не доберемся до корня дерева. Среднее число операций увеличения веса равно среднему количеству битов, необходимых для того, чтобы закодировать символ.
Вторая операция — перестановка узлов дерева — требуется тогда, когда увеличение веса узла приводит к нарушению свойства упорядоченности, то есть тогда, когда увеличенный вес узла стал больше, чем вес следующего по порядку узла. Если и дальше продолжать обрабатывать увеличение веса, двигаясь к корню дерева, то дерево перестанет быть деревом Хаффмана.
Чтобы сохранить упорядоченность дерева кодирования, алгоритм работает следующим образом. Пусть новый увеличенный вес узла равен W+1. Тогда начинаем двигаться по списку в сторону увеличения веса, пока не найдем последний узел с весом W. Переставим текущий и найденный узлы между собой в списке, восстанавливая таким образом порядок в дереве (при этом родители каждого из узлов тоже изменятся). На этом операция перестановки заканчивается.
После перестановки операция увеличения веса узлов продолжается дальше. Следующий узел, вес которого будет увеличен алгоритмом, — это новый родитель узла, увеличение веса которого вызвало перестановку.
Канонические коды Хаффмана[править | править код]
Проблема обычного алгоритма сжатия по Хаффману — недетерминированность. Для похожих последовательностей могут получиться разные деревья, так и одно дерево без правильной сериализации может соответствовать разным последовательностям. Для избежания применяют канонические коды Хаффмана.
В этом алгоритме не строится дерево Хаффмана[3].
Состоит из двух этапов:
- Подсчёт длины кода для какого-то символа
- Составление кода.
Подсчёт длины[править | править код]
- Посчитаем частотность для каждого символа
- Отсортируем их в лексикографическом порядке.
- В массив запишем частотность каждой буквы.
- Слева приписываем массив той же длины, но с порядковыми номерами из правого массива. Левый массив получается списком указателей на элементы правой части.
- В левой части делаем не возрастающую пирамиду. Но heap будет не по значению элементов массива, а по значению на ссылаемый элемент массива.
- Самый левый элемент указывает на символ из правого массива с наименьшей частотностью. Его можно удалить следующим образом:
- Правую половину не трогаем
- Первый элемент массива заменяем на самый правый элемент левого массива, якобы сдвигая границу разделения.
- Проверяем условия правильности пирамиды, если что-то не так, то надо повторить «хипизацию».
- Убирается первый элемент левой части массива и объединяется ранее убранным. Сумма их частотностей записывается в границу между левым и правым массивом.
- На место удалённого элемента в левой части записывается индекс массива куда добавили сумму частотностей на прошлом шаге.
- Из-за того объединили два элемента нужно изменить значения этих элементов массива ссылкой на родителя, куда их положили.
- Повторяем, в куче слева не останется 1 элемент.
- В правой части массива получились ссылки на элементы, объеднияющие 2 символа. Поэтому идём по массиву по ссылкам, инкрементируя уровень погружения.
- Количество переходов по ссылкам будет длиной кода Хаффмана.
Составление кода[править | править код]
- Расположим элементы в лексикографическом порядке.
- Составим таблицу, состоящую из блоков, начиная с самой большой длины кода. Каждый блок будет содержать элементы с одинаковой длиной кода.
- Самый первый символ таблицы кодируется нулями.
- В каждом блоке символы будут находиться в лексикографическом порядке.
- Коды в блоке будут иметь двоичный вид и различаться на 1.
- При переходе в следующий блок биты кода самого последнего символа отсекаются и добавляется 1.
Биграммная модель[править | править код]
Существует разновидность алгоритма Хаффмана, использующая контекст. В данном случае размер контекста равен единице (биграммный — два символа, триграммный — три и так далее). Это метод построения префиксного кода для моделей высших порядков, уже не источника без памяти. Он использует результат (предыдущей операции) операции над предыдущей буквой совместно с текущей буквой. Строится на основе цепи Маркова с глубиной зависимости 
Алгоритм
- Строится таблица в виде квадрата — распределение вероятностей на биграммах. Сразу вычисляется стартовая схема, с помощью которой будет кодироваться только первая буква. Строками в таблице, например, являются предыдущие буквы, а столбцами текущие.
- Вычисляются вероятности для кодовых деревьев для контекстов.
- По контекстам длины
строятся остальные кодовые деревья, с помощью которых будут кодироваться все остальные символы (кроме первого).
- Выполняется кодирование, первый символ кодируется согласно стартовой схеме, все последующие — исходя из кодовых деревьев для контекстов (предыдущего символа).
Декодирование выполняется аналогично: из стартовой кодовой схемы получаем первый контекст, а затем переходим к соответствующему кодовому дереву. Более того, декодеру необходима таблица распределения вероятностей.
Пример
Допустим, сообщение, которое надо закодировать «abcabcabc». Нам заранее известна таблица частотностей символов (на основе других данных, например, статистических данных по словарю).
| a | b | c | Сумма | |
|---|---|---|---|---|
| a | 
|

|

|

|
| b | 
|

|

|

|
| c | 
|

|

|

|
Имеем стартовую схему: 

Для контекста «a» имеем:
,
,
.
Для контекста «b» имеем:
,
,
.
Для контекста «c» имеем:
,
,
.
Примечание: здесь p(x, y) не равно p(y, x).
Строим кодовые деревья для каждого контекста. Выполняем кодирование и имеем закодированное сообщение: (00, 10, 01, 11, 10, 01, 11, 10, 01).
- 00 — из кода буквы «a» для стартовой схемы,
- 10 — из кода буквы «b» для контекста «a»,
- 01 — из кода буквы «c» для контекста «b»,
- 11 — из кода буквы «a» для контекста «c».
Переполнение[править | править код]
В процессе работы алгоритма сжатия вес узлов в дереве кодирования Хаффмана неуклонно растет. Первая проблема возникает тогда, когда вес корня дерева начинает превосходить вместимость ячейки, в которой он хранится. Как правило, это 16-битовое значение и, следовательно, не может быть больше, чем 65535. Вторая проблема, заслуживающая ещё большего внимания, может возникнуть значительно раньше, когда размер самого длинного кода Хаффмана превосходит вместимость ячейки, которая используется для того, чтобы передать его в выходной поток. Декодеру все равно, какой длины код он декодирует, поскольку он движется сверху вниз по дереву кодирования, выбирая из входного потока по одному биту. Кодер же должен начинать от листа дерева и двигаться вверх к корню, собирая биты, которые нужно передать. Обычно это происходит с переменной типа «целое», и, когда длина кода Хаффмана превосходит размер типа «целое» в битах, наступает переполнение.
Можно доказать, что максимальную длину код Хаффмана для сообщений с одним и тем же входным алфавитом будет иметь, если частотности символов образует последовательность Фибоначчи. Сообщение с частотностями символов, равными числам Фибоначчи до Fib (18), — это отличный способ протестировать работу программы сжатия по Хаффману.
Масштабирование весов узлов дерева Хаффмана[править | править код]
Принимая во внимание сказанное выше, алгоритм обновления дерева Хаффмана должен быть изменен следующим образом: при увеличении веса нужно проверять его на достижение допустимого максимума. Если мы достигли максимума, то необходимо «масштабировать» вес, обычно разделив вес листьев на целое число, например, 2, а потом пересчитав вес всех остальных узлов.
Однако при делении веса пополам возникает проблема, связанная с тем, что после выполнения этой операции дерево может изменить свою форму. Объясняется это тем, что при делении целых чисел отбрасывается дробная часть.
Правильно организованное дерево Хаффмана после масштабирования может иметь форму, значительно отличающуюся от исходной. Это происходит потому, что масштабирование приводит к потере точности статистики. Но со сбором новой статистики последствия этих «ошибок» практически сходят на нет. Масштабирование веса — довольно дорогостоящая операция, так как она приводит к необходимости заново строить все дерево кодирования. Но, так как необходимость в ней возникает относительно редко, то с этим можно смириться.
Выигрыш от масштабирования[править | править код]
Масштабирование веса узлов дерева через определенные интервалы дает неожиданный результат. Несмотря на то, что при масштабировании происходит потеря точности статистики, тесты показывают, что оно приводит к лучшим показателям сжатия, чем если бы масштабирование откладывалось. Это можно объяснить тем, что текущие символы сжимаемого потока больше «похожи» на своих близких предшественников, чем на тех, которые встречались намного раньше. Масштабирование приводит к уменьшению влияния «давних» символов на статистику и к увеличению влияния на неё «недавних» символов. Это очень сложно измерить количественно, но, в принципе, масштабирование оказывает положительное влияние на степень сжатия информации. Эксперименты с масштабированием в различных точках процесса сжатия показывают, что степень сжатия сильно зависит от момента масштабирования веса, но не существует правила выбора оптимального момента масштабирования для программы, ориентированной на сжатие любых типов информации.
Применение[править | править код]
Кодирование Хаффмана широко применяется при сжатии данных, в том числе при сжатии фото- и видеоизображений (JPEG, MPEG), в популярных архиваторах (PKZIP, LZH и др.), в протоколах передачи данных HTTP (Deflate), MNP5 и MNP7 и других.
Модификации[править | править код]
В 2013 году была предложена модификация алгоритма Хаффмана, позволяющая кодировать символы дробным количеством бит — ANS[5][6]. На базе данной модификации реализованы алгоритмы сжатия Zstandard (Zstd, Facebook, 2015—2016)[7] и LZFSE[fr] (Apple, OS X 10.11, iOS 9, 2016)[8][9][10][11].
Примечания[править | править код]
- ↑ Huffman, D. (1952). “A Method for the Construction of Minimum-Redundancy Codes” (PDF). Proceedings of the IRE. 40 (9): 1098—1101. DOI:10.1109/JRPROC.1952.273898. Архивировано (PDF) из оригинала 2010-12-15. Дата обращения 2022-12-04.
- ↑ Д. Мастрюков. Монитор 7-8.93 Архивная копия от 17 мая 2018 на Wayback Machine
- ↑ Подробнее с примерами алгоритм расписан в Managing Gigabytes авторов Witten, Мoffat, Bell на 68-й странице.
- ↑ Shmuel T. Klein and Dana Shapira. Huffman Coding with Non-Sorted Frequencies (2008). Дата обращения: 2 января 2016. Архивировано 4 марта 2016 года.
- ↑ Архивированная копия. Дата обращения: 2 января 2016. Архивировано 5 марта 2016 года.
- ↑ Архивированная копия. Дата обращения: 2 января 2016. Архивировано 11 сентября 2016 года.
- ↑ Facebook опубликовал реализацию алгоритма сжатия Zstandard 1.0 Архивная копия от 2 сентября 2016 на Wayback Machine / Opennet.ru, 01.09.2016
- ↑ Компания Apple открыла реализацию алгоритма сжатия без потерь LZFSE Архивная копия от 11 сентября 2016 на Wayback Machine / Opennet.ru, 07.07.2016
- ↑ Apple Open-Sources its New Compression Algorithm LZFSE. Дата обращения: 1 сентября 2016. Архивировано 11 сентября 2016 года.
- ↑ Data Compression
- ↑ GitHub — lzfse/lzfse: LZFSE compression library and command line tool. Дата обращения: 1 сентября 2016. Архивировано 28 ноября 2020 года.
Литература[править | править код]
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-е изд. — М.: Вильямс, 2006. — 1296 с. — ISBN 0-07-013151-1.
- Д. Сэломон. Сжатие данных, изображения и звука. — М.: Техносфера, 2004. — 368 с. — 3000 экз. — ISBN 5-94836-027-X.
- Ian H. Witten, Alistair Moffat, Timothy C. Bell. Managing Gigabytes: Compressing and Indexing Documents and Images. — 1999. — 551 с. — ISBN 1558605703.
- Левитин А. В. Глава 9. Жадные методы: Алгоритм Хаффмана // Алгоритмы. Введение в разработку и анализ — М.: Вильямс, 2006. — С. 392—398. — 576 с. — ISBN 978-5-8459-0987-9
- Марков А. А. Введение в теорию кодирования. — М.: Наука, 1982. — 192 с.
Ссылки[править | править код]
- Код Хаффмана (WebArchive)
- Визуализатор построения дерева для m2=2
- Визуализатор кодирования букв русского алфавита
- Сжатие по алгоритму Хаффмана на algolist.manual.ru
- Хабрахабр: Алгоритм Хаффмана на пальцах
- Хабрахабр: Алгоритмы используемые при сжатии данных
- Хабрахабр: Сжатие информации без потерь. Часть первая
4. Изучение алгоритма сжатия Хаффмана
4.1. Цель работы
Изучить алгоритм оптимального префиксного кодирования Хаффмана и его использование для сжатия сообщений.
4.2. Теоретические сведения
Алгоритм Хаффмана — адаптивный жадный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью. Был разработан в 1952 году аспирантом Массачусетского технологического института Дэвидом Хаффманом.
Сжатие данных по Хаффману применяется при сжатии фото- и видеоизображений (JPEG, стандарты сжатия MPEG), в архиваторах (PKZIP, LZH и др.), в протоколах передачи данных MNP5 и MNP7.
Жадный алгоритм (Greedy algorithm) — алгоритм, заключающийся в принятии локально оптимальных решений на каждом этапе, допуская, что конечное решение также окажется оптимальным.
Идея алгоритма Хаффмана состоит в следующем: зная вероятности символов в сообщении, можно описать процедуру построения кодов переменной длины, состоящих из целого количества битов. Символам с большей вероятностью ставятся в соответствие более короткие коды. Коды Хаффмана обладают свойством префиксности (то есть ни одно кодовое слово не является префиксом другого), что позволяет однозначно их декодировать.
Этот метод кодирования состоит из двух основных этапов:
1.Построение оптимального кодового дерева.
2.Построение отображения код-символ на основе построенного дере-
ва.
Классический алгоритм Хаффмана на входе получает таблицу частот встречаемости символов в сообщении. Далее на основании этой таблицы строится дерево кодирования Хаффмана (Н-дерево).
1.Символы входного алфавита образуют список свободных узлов. Каждый лист имеет вес, который может быть равен либо вероятности, либо количеству вхождений символа в сжимаемое сообщение.
2.Выбираются два свободных узла дерева с наименьшими весами.
3.Создается их родитель с весом, равным их суммарному весу.
4.Родитель добавляется в список свободных узлов, а два его потомка удаляются из этого списка.
5.Одной дуге, выходящей из родителя, ставится в соответствие бит 1, другой — бит 0.
20
6. Шаги, начиная со второго, повторяются до тех пор, пока в списке свободных узлов не останется только один свободный узел. Он и будет считаться корнем дерева.
Для примера рассмотрим кодирование фразы
пупкин василий кириллович
Можно видеть, что фраза состоит из L = 25 символов.
Первоначально необходимо сформировать алфавит фразы и построить таблицу количества вхождений и вероятности символов. Она представлена в табл. 4.1.
Таблица 4.1
Алфавит фразы и вероятности символов
|
Алфавит |
п |
у |
к |
и |
н |
« » |
в |
|
Кол. вх. |
2 |
1 |
2 |
6 |
1 |
2 |
2 |
|
Вероятн. |
0.08 |
0.04 |
0.08 |
0.24 |
0.04 |
0.08 |
0.08 |
|
Алфавит |
а |
с |
л |
й |
р |
о |
ч |
|
Кол. вх. |
1 |
1 |
3 |
1 |
1 |
1 |
1 |
|
Вероятн. |
0.04 |
0.04 |
0.12 |
0.04 |
0.04 |
0.04 |
0.04 |
Алфавит составляют NA = 14 символов, включая знак пробела (« »). Далее сортируем алфавит в порядке убывания вероятности появления
символов (табл. 4.2).
Таблица 4.2 Алфавит фразы, отсортированный по вероятности (количеству вхождений)
|
Алфавит |
и |
л |
п |
к |
« » |
в |
у |
|
Кол. вх. |
6 |
3 |
2 |
2 |
2 |
2 |
1 |
|
Вероятн. |
0.24 |
0.12 |
0.08 |
0.08 |
0.08 |
0.08 |
0.04 |
|
Алфавит |
н |
а |
с |
й |
р |
о |
ч |
|
Кол. вх. |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Вероятн. |
0.04 |
0.04 |
0.04 |
0.04 |
0.04 |
0.04 |
0.04 |
Последовательно строим дерево кодирования, начиная с символов с наименьшими весами (вероятностями), пока не достигнем корня, который будет иметь вес равный 1 (по вероятности). Построение дерева показано на рис. 4.1.
Для удобства перерисуем построенное дерево, упорядочив его слеванаправо, начиная с корня. Каждой ветви дерева присвоим свой код. При этом, ветвь, идущая выше, будет иметь код «0», а ветвь, идущая ниже — «1». Упорядоченное дерево показано на рис. 4.2.
21

|
и/6 |
л/3 |
п/2 |
к/2 |
/2 |
в/2 |
у/1 |
н/1 |
а/1 |
с/1 |
й/1 |
р/1 |
о/1 |
ч/1 |
|
0.24 |
0.12 |
0.08 |
0.08 |
0.08 |
0.08 |
0.04 |
0.04 |
0.04 |
0.04 |
0.04 |
0.04 |
0.04 |
0.04 |
|
4 |
4 |
2 |
2 |
2 |
2 |
||||||||
|
0.16 |
0.16 |
0.08 |
0.08 |
0.08 |
0.08 |
||||||||
|
7 |
4 |
4 |
|||||||||||
|
0.28 |
0.16 |
0.16 |
|||||||||||
|
10 |
8 |
||||||||||||
|
0.40 |
0.32 |
||||||||||||
|
15 |
|||||||||||||
|
0.60 |
25
1.00
Рис. 4.1. Дерево кодирования Хаффмана
|
0 |
1 |
0 |
и |
00 |
|
0 |
010 |
|||
|
1 |
1 |
в |
011 |
|
|
0 |
1 |
0 |
л |
100 |
|
0 |
п |
1010 |
||
|
1 |
1 |
к |
1011 |
|
|
0 |
0 |
0 |
у |
11000 |
|
1 |
1 |
н |
||
|
11001 |
||||
|
1 |
0 |
а |
11010 |
|
|
1 |
с |
|||
|
11011 |
||||
|
0 |
0 |
й |
11100 |
|
|
1 |
1 |
р |
||
|
11101 |
||||
|
0 |
о |
11110 |
||
|
1 |
ч |
|||
|
11111 |
Рис. 4.2. Упорядоченное дерево кодирования Хаффмана
В итоге получается, что символам с большей вероятностью появления соответствуют более короткие коды.
Теперь можно закодировать исходную строку. Она будет иметь вид:
22

п у п к и н ¾ ¿ в а с и л и й
1010 11000 1010 1011 00 11001 010 011 11010 11011 00 100 00 11100
¾ ¿ к и р и л л о в и ч
010 1011 00 11101 00 100 100 11110 011 00 11111
Для декодирования кодовой строки достаточно идти по упорядоченному дереву на рис. 4.2, до получения символа. Затем производится возврат к корню и определяется следующий символ.
Рассчитаем коэффициент сжатия относительно использования кодировки ASCII (8 бит/символ).
LASCII = 8 25 = 200 бит.
LHuff = 6 2 + 3 3 + 2 2 3 + 2 2 4 + 8 5 = 89 бит. Следовательно, коэффициент сжатия будет равен
Kсж = LASCII 2:247
LHuff
Коэффициент сжатия относительно равномерного кода (5 бит/символ, т. к. у нас всего 25 символов) будет равен
Kсж = 5 25 = 125 1:404
LHuff 89
Рассчитаем среднюю длину полученного кода по формуле
lср = åps ls;
s
где s — множество символов алфавита; ps — вероятность появления символа; ls — количество бит в коде символа.
Для полученного кода средняя длина будет равна
lср = 0:24 2 + 0:12 3 + 2 0:08 3 + 2 0:08 4 + 8 0:04 5 = 2:36 бит/символ:
Поскольку при построении дерева кода Хаффмана может возникнуть некоторый произвол, для выбора оптимального варианта кода используют дисперсию. Дисперсия показывает насколько сильно отклоняются длины индивидуальных кодов от их средней величины. Лучшим будет код с наименьшей дисперсией.
Дисперсия рассчитывается по формуле
d = åps(ls lср)2:
s
Для полученного кода дисперсия будет равна
d= 0:24 (2 2:36)2 + 0:12 (3 2:36)2 + 2 0:08 (3 2:36)2+ +2 0:08 (4 2:36)2 + 8 0:01 (5 2:36)2 = 1:1337
23
Кодирование Хаффмана (часть 1 и 2)
| Редактировалось 10 янв 2018
Кодирование Хаффмана. Часть 1.
Вступление
Здравствуй, дорогой читатель! В данной статье будет рассмотрен один из способов сжатия данных. Этот способ является достаточно широко распространённым и заслуживает определённого внимания. Данный материал рассчитан по объёму на три статьи, первая из которых будет посвящена алгоритму сжатия, вторая – программной реализации алгоритма, а третья ― декомпрессии. Алгоритм сжатия будет написан на языке C++, алгоритм декомпрессии ― на языке Assembler.
Однако, перед тем, как приступить к самому алгоритму, следует включить в статью немного теории.
Немного теории
Компрессия (сжатие) ― способ уменьшения объёма данных с целью дальнейшей их передачи и хранения.
Декомпрессия ― это способ восстановления сжатых данных в исходные.
Компрессия и декомпрессия могут быть как без потери качества (когда передаваемая/хранимая информация в сжатом виде после декомпрессии абсолютно идентична исходной), так и с потерей качества (когда данные после декомпрессии отличаются от оригинальных). Например, текстовые документы, базы данных, программы могут быть сжаты только способом без потери качества, в то время как картинки, видеоролики и аудиофайлы сжимаются именно за счёт потери качества исходных данных (характерный пример алгоритмов ― JPEG, MPEG, ADPCM), при порой незаметной потере качества даже при сжатии 1:4 или 1:10.
Выделяются основные виды упаковки:
- Десятичная упаковка предназначена для упаковки символьных данных, состоящих только из чисел. Вместо используемых 8 бит под символ можно вполне рационально использовать всего лишь 4 бита для десятичных и шестнадцатеричных цифр, 3 бита для восьмеричных и так далее. При подобном подходе уже ощущается сжатие минимум 1:2.
- Относительное кодирование является кодированием с потерей качества. Оно основано на том, что последующий элемент данных отличается от предыдущего на величину, занимающую в памяти меньше места, чем сам элемент. Характерным примером является аудиосжатие ADPCM (Adaptive Differencial Pulse Code Modulation), широко применяемое в цифровой телефонии и позволяющее сжимать звуковые данные в соотношении 1:2 с практически незаметной потерей качества.
- Символьное подавление – способ сжатия информации, при котором длинные последовательности из идентичных данных заменяются более короткими.
- Статистическое кодирование основано на том, что не все элементы данных встречаются с одинаковой частотой (или вероятностью). При таком подходе коды выбираются так, чтобы наиболее часто встречающемуся элементу соответствовал код с наименьшей длиной, а наименее частому ― с наибольшей.
Кроме этого, коды подбираются таким образом, чтобы при декодировании можно было однозначно определить элемент исходных данных. При таком подходе возможно только бит-ориентированное кодирование, при котором выделяются разрешённые и запрещённые коды. Если при декодировании битовой последовательности код оказался запрещённым, то к нему необходимо добавить ещё один бит исходной последовательности и повторить операцию декодирования. Примерами такого кодирования являются алгоритмы Шеннона и Хаффмана, последний из которых мы и будем рассматривать.
Конкретнее об алгоритме
Как уже известно из предыдущего подраздела, алгоритм Хафмана основан на статистическом кодировании. Разберёмся поподробнее в его реализации.
Пусть имеется источник данных, который передаёт символы [math](a_1, a_2, …, a_n)[/math] с разной степенью вероятности, то есть каждому [math]a_i[/math] соответствует своя вероятность (или частота) [math]P_i(a_i)[/math], при чём существует хотя бы одна пара [math]a_i[/math] и [math]a_j[/math] ,[math]ine j[/math], такие, что [math]P_i(a_i)[/math] и [math]P_j(a_j)[/math] не равны. Таким образом образуется набор частот [math]{P_1(a_1), P_2(a_2),…,P_n(a_n)}[/math], при чём [math]displaystyle sum_{i=1}^{n} P_i(a_i)=1[/math], так как передатчик не передаёт больше никаких символов кроме как [math]{a_1,a_2,…,a_n}[/math].
Наша задача ― подобрать такие кодовые символы [math]{b_1, b_2,…,b_n}[/math] с длинами [math]{L_1(b_1),L_2(b_2),…,L_n(b_n)}[/math], чтобы средняя длина кодового символа не превышала средней длины исходного символа. При этом нужно учитывать условие, что если [math]P_i(a_i)>P_j(a_j)[/math] и [math]ine j[/math], то [math]L_i(b_i)le L_j(b_j)[/math].
Хафман предложил строить дерево, в котором узлы с наибольшей вероятностью наименее удалены от корня. Отсюда и вытекает сам способ построения дерева:
1. Выбрать два символа [math]a_i[/math] и [math]a_j[/math], [math]ine j[/math], такие, что [math]P_i(a_i)[/math] и [math]P_j(a_j)[/math] из всего списка [math]{P_1(a_1),P_2,…,P_n(a_n)}[/math] являются минимальными.
2. Свести ветки дерева от этих двух элементов в одну точку с вероятностью [math]P=P_i(a_i)+P_j(a_j)[/math], пометив одну ветку нулём, а другую ― единицей (по собственному усмотрению).
3. Повторить пункт 1 с учётом новой точки вместо [math]a_i[/math] и [math]a_j[/math], если количество получившихся точек больше единицы. В противном случае мы достигли корня дерева.
Теперь попробуем воспользоваться полученной теорией и закодировать информацию, передаваемую источником, на примере семи символов.
Разберём подробно первый цикл. На рисунке изображена таблица, в которой каждому символу [math]a_i[/math] соответствует своя вероятность (частота) [math]P_i(a_i)[/math]. Согласно пункту 1 мы выбираем два символа из таблицы с наименьшей вероятностью. В нашем случае это [math]a_1[/math] и [math]a_4[/math]. Согласно пункту 2 сводим ветки дерева от [math]a_1[/math] и [math]a_4[/math] в одну точку и помечаем ветку, ведущую к [math]a_1[/math], единицей, а ветку, ведущую к [math]a_4[/math],― нулём. Над новой точкой приписываем её вероятность (в данном случае ― 0.03) В дальнейшем действия повторяются уже с учётом новой точки и без учёта [math]a_1[/math] и [math]a_4[/math].
После многократного повторения изложенных действий выстраивается следующее дерево:
По построенному дереву можно определить значение кодов [math]{b_1,b_2,…,b_n}[/math], осуществляя спуск от корня к соответствующему элементу [math]a_i[/math], при этом приписывая к получаемой последовательности при прохождении каждой ветки ноль или единицу (в зависимости от того, как именуется конкретная ветка). Таким образом таблица кодов выглядит следующим образом:
i bi Li(bi) 1 011111 6 2 1 1 3 0110 4 4 011110 6 5 010 3 6 00 2 7 01110 5 Теперь попробуем закодировать последовательность из символов.
Пусть символу [math]a_i[/math] соответствует (в качестве примера) число [math]i[/math]. Пусть имеется последовательность 12672262. Нужно получить результирующий двоичный код.
Для кодирования можно использовать уже имеющуюся таблицу кодовых символов [math]b_i[/math] при учёте, что [math]b_i[/math] соответствует символу [math]a_i[/math]. В таком случае код для цифры 1 будет представлять собой последовательность 011111, для цифры 2 ― 1, а для цифры 6 ― 00. Таким образом, получаем следующий результат:
Данные 1 2 6 7 2 2 6 2 Длина кода Исходные 001 010 110 111 010 010 110 010 24 бит Кодированные 011111 1 00 01110 1 1 00 1 19 бит В результате кодирования мы выиграли 5 бит и записали последовательность 19 битами вместо 24.
Однако это не даёт полной оценки сжатия данных. Вернёмся к математике и оценим степень сжатия кода. Для этого понадобится энтропийная оценка.
Энтропия ― мера неопределённости ситуации (случайной величины) с конечным или с чётным числом исходов. Математически энтропия формулируется как сумма произведений вероятностей различных состояний системы на логарифмы этих вероятностей, взятых с обратным знаком:[math]H(X)=-displaystyle sum_{i=1}^{n}P_icdot log_d (P_i)[/math].Где [math]X[/math] ― дискретная случайная величина (в нашем случае ― кодовый символ), а [math]d[/math] ― произвольное основание, большее единицы. Выбор основания равносилен выбору определённой единицы измерения энтропии. Так как мы имеем дело с двоичными цифрами, то в качестве основания рационально выбрать [math]d=2[/math].
Таким образом, энтропию для нашего случая можно представить в виде:[math]H(b)=-displaystyle sum_{i=1}^{n}P_i(a_i)cdot log_2 (P_i(a_i))[/math].Энтропия обладает замечательным свойством: она равна минимальной допустимой средней длине кодового символа [math]overline{L_{min}}[/math] в битах. Сама же средняя длина кодового символа вычисляется по формуле
[math]overline{L(b)}=displaystyle sum_{i=1}^{n}P_i(a_i)cdot L_i(b_i)[/math].Подставляя значения в формулы [math]H(b)[/math] и [math]overline{L(b)}[/math], получаем следующий результат: [math]H(b)=2,048[/math], [math]overline{L(b)}=2,100[/math].
Величины [math]H(b)[/math] и [math]overline{L(b)}[/math] очень близки, что говорит о реальном выигрыше в выборе алгоритма. Теперь сравним среднюю длину исходного символа и среднюю длину кодового символа через отношение:[math]frac{overline{L_{src}}}{L(b)}=frac{3}{2,1}=1,429[/math].Таким образом, мы получили сжатие в соотношении 1:1,429, что очень неплохо.
И напоследок, решим последнюю задачу: дешифровка последовательности битов.
Пусть для нашей ситуации имеется последовательность битов:001101100001110001000111111Необходимо определить исходный код, то есть декодировать эту последовательность.
Конечно, в такой ситуации можно воспользоваться таблицей кодов, но это достаточно неудобно, так как длина кодовых символов непостоянна. Гораздо удобнее осуществить спуск по дереву (начиная с корня) по следующему правилу:
1. Исходная точка ― корень дерева.
2. Прочитать новый бит. Если он ноль, то пройти по ветке, помеченной нулём, в противном случае ― единицей.
3. Если точка, в которую мы попали, конечная, то мы определили кодовый символ, который следует записать и вернуться к пункту 1. В противном случае следует повторить пункт 2.
Рассмотрим пример декодирования первого символа. Мы находимся в точке с вероятностью 1,00 (корень дерева), считываем первый бит последовательности и отправляемся по ветке, помеченной нулём, в точку с вероятностью 0,60. Так как эта точка не является конечной в дереве, то считываем следующий бит, который тоже равен нулю, и отправляемся по ветке, помеченной нулём, в точку [math]a_6[/math], которая является конечной. Мы дешифровали символ ― это число 6. Записываем его и возвращаемся в исходное состояние (перемещаемся в корень).
Таким образом декодированная последовательность принимает вид.
Данные 001101100001110001000111111 Длина кода Кодированные 00 1 1 0110 00 01110 00 1 00 011111 1 27 бит Исходные 6 2 2 3 6 7 6 2 6 1 2 33 бит В данном случае выигрыш составил 6 бит при достаточно небольшой длине последовательности.
Вывод напрашивается сам собой: алгоритм прост. Однако следует сделать замечание: данный алгоритм хорош для сжатия текстовой информации (действительно, реально мы используем при набивке текста примерно 60 символов из доступных 256, то есть вероятность встретить иные символы близка к нулю), но достаточно плох для сжатия программ (так как в программе все символы практически равновероятны). Так что эффективность алгоритма очень сильно зависит от типа сжимаемых данных.
Постскриптум
В этой статье мы рассмотрели алгоритм кодирования по методу Хаффмана, который базируется на неравномерном кодировании. Он позволяет уменьшить размер передаваемых или хранимых данных. Алгоритм прост для понимания и может давать реальный выигрыш. Кроме этого, он обладает ещё одним замечательным свойством: возможность кодировать и декодировать информацию “на лету” при условии того, что вероятности кодовых слов правильно определены. Хотя существует модификация алгоритма, позволяющая изменять структуру дерева в реальном времени.
В следующей части статьи мы рассмотрим байт-ориентированное сжатие файлов с использованием алгоритма Хаффмана, реализованное на C++.
Кодирование Хаффмана. Часть 2
Вступление
В прошлой части мы рассмотрели алгоритм кодирования, описали его математическую модель, произвели кодирование и декодирование на конкретном примере, рассчитали среднюю длину кодового слова, а также определили коэффициент сжатия. Кроме этого, были сделаны выводы о преимуществах и недостатках данного алгоритма.
Однако, помимо этого неразрешёнными остались ещё два вопроса: реализация программы, сжимающей файл данных, и программы, распаковывающей сжатый файл. Первому вопросу и посвящена настоящая статья. Поэтому следует заняться проектированием.
Проектирование
Первым делом необходимо посчитать частоты вхождения символов в файл. Для этого опишем следующую структуру:
Эта структура будет описывать каждый символ из 256. ch ― сам ASCII-символ, freq ― количество вхождений символа в файл. Поле table ― указатель на структуру:
Как видно, TTable ― это описатель узла с разветвлением по нулю и единице. При помощи этих структур в дальнейшем и будет осуществляться построение дерева компрессии. Теперь объявим для каждого символа свою частоту и свой узел:
Попробуем разобраться, каким образом будет осуществляться построение дерева. На начальной стадии программа должна осуществить проход по всему файлу и подсчитать количество вхождений символов в него. Помимо этого, для каждого найденного символа программа должна создать описатель узла. После этого из созданных узлов с учётом частоты символов программа строит дерево, размещая узлы в определённом порядке и устанавливая между ними связи.
Построенное дерево хорошо для декодирования файла. Но для кодирования файла оно неудобно, потому что неизвестно, в каком направлении следует идти от корня, чтобы добраться до необходимого символа. Для этого удобнее построить таблицу преобразования символов в код. Поэтому определим ещё одну структуру:
Здесь opcode ― кодовая комбинация символа, а len – её длина (в битах). И объявим таблицу из 256 таких структур:
Зная кодируемый символ, можно определить его кодовое слово по таблице. Теперь перейдём непосредственно к подсчёту частот символов (и не только).
Подсчёт частот символов
В принципе, это действие не составляет труда. Достаточно открыть файл и подсчитать в нём число символов, заполнив соответствующие структуры. Посмотрим реализацию этого действия.
Для этого объявим глобальные дескрипторы файлов:in ― файл, из которого осуществляется чтение несжатых данных.
out ― файл, в который осуществляется запись сжатых данных.
assemb ― файл, в который будет сохранено дерево в удобном для распаковки виде. Так как распаковщик будет написан на ассемблере, то вполне рационально дерево сделать частью распаковщика, то есть представить его в виде инструкций на Ассемблере.
Первым делом необходимо проинициализировать все структуры нулевыми значениями:
После этого мы подсчитываем число вхождений символа в файл и размер файла (конечно, не самым идеальным способом, но в примере нужна наглядность):
Так как код неравномерный, то распаковщику будет проблематично узнать число считываемых символов. Поэтому в таблице распаковки необходимо зафиксировать его размер:
После этого все используемые символы смещаются в начало массива, а неиспользуемые затираются (путём перестановок).
И только после такой “сортировки” выделяется память под узлы (для некоторой экономии).
Таким образом, мы написали функцию первоначальной иницализации системы, или, если смотреть на алгоритм в первой части статьи, “записали используемые символы в столбик и приписали к ним вероятности”, а также для каждого символа создали “отправную точку” ― узел ― и проинициализировали её. В поля left и right записали нули. Таким образом, если узел будет в дереве последним, то это будет легко увидеть по left и right, равным нулю.
Создание дерева
Итак, в предыдущем разделе мы “записали используемые символы в столбик и приписали к ним вероятности”. На самом деле, мы приписали к ним не вероятности, а числители дроби (то есть количество вхождений символов в файл). Теперь надо построить дерево. Но для того, чтобы это сделать, необходимо найти минимальный элемент в списке. Для этого вводим функцию, в которую передаём два параметра ― количество элементов в списке и элемент, который следует исключить (потому что искать будем парами, и будет очень неприятно, если мы от функции дважды получим один и тот же элемент):
Поиск реализован несложно: сначала выбираем “минимальный” элемент массива. Если исключаемый элемент ― 0, то берём в качестве минимума первый элемент, в противном случае минимумом считаем нулевой. По мере прохождения по массиву сравниваем текущий элемент с “минимальным”, и если он окажется меньше, то его помечаем как минимальный.
Теперь, собственно говоря, сама функция построения дерева:
Таблица кодовых символов
Итак, дерево в памяти мы построили: попарно брали два узла, создавали новый узел, в который записывали на них указатели, после чего второй узел удаляли из списка, а вместо первого узла писали новый с разветвлением.
Теперь возникает ещё одна проблема: кодировать по дереву неудобно, потому что необходимо точно знать, по какому пути находится тот или иной символ. Однако проблема решается довольно просто: создаётся ещё одна таблица ― таблица кодовых символов ― в неё и записываются битовые комбинации всех используемых символов. Для этого достаточно однократно рекурсивно обойти дерево. Заодно, чтобы повторно его не обходить, можно в функцию обхода добавить генерацию ассемблерного файла для дальнейшего декодирования сжатых данных (см. раздел “Проектирование“).
Собственно, сама функция не сложна. Она должна приписывать к кодовой комбинации 0 или 1, если узел не конечный, в противном случае добавить кодовый символ в таблицу. Помимо всего этого, сгенерировать ассемблерный файл. Рассмотрим эту функцию:
Помимо всего прочего, после прохождения узла функция удаляет его (освобождает указатель). Теперь разберёмся, что за параметры передаются в функцию.
- tbl ― узел, который надо обойти.
- opcode ― текущее кодовое слово. Старший бит должен быть всегда свободен.
- len ― длина кодового слова.
В принципе, функция не сложнее “классического факториала” и не должна вызывать трудностей.
Битовый вывод
Вот мы и добрались до не самой приятной части нашего архиватора, а именно ― до вывода кодовых символов в файл. Проблема состоит в том, что кодовые символы имеют неравномерную длину и вывод приходится осуществлять побитовый. В этом поможет функция PutCode. Но для начала объявим две переменные ― счётчик битов в байте и выводимый байт:OutBits увеличивается на один при каждом выводе бита, OutBits==8 сигнализирует о том, что OutChar следует сохранить в файл.
Помимо этого, нужно организовать что-то вроде “fflush”, то есть после вывода последнего кодового слова OutChar не поместится в выходной файл, так как OutBits!=8. Отсюда появляется ещё одна небольшая функция:
Вызываем помощников
Все рассмотренные ранее функции не являются основными. Но с их помощью можно проиллюстрировать простой порядок действий:
1. Выписать все элементы в столбик и приписать вероятности.
2. Построить дерево по полученному столбику.
3. Записать кодовую таблицу символов.
4. По кодовой таблице закодировать исходные данные.
Собственно говоря, вот и функция, которая выполняет эти действия:
Мейн
Всё, все функции готовы. Осталось только реализовать функцию main. Необходимо определить, какие она должна получить аргументы. А всё очень просто ― имя исходного файла, имя закодированного файла, а также имя файла, в который будет помещена таблица. Лично я всю операцию по открытию/закрытию файлов решил возложить на main. И вот как это выглядит:
Постскриптум
Вот и эта статья подошла к своему логическому завершению. В принципе, здесь представлен вполне рабочий код. Однако стоит заметить, что этот код не всегда способен работать. Например, если частоты символов обладают следующей закономерностью: 0.5, 0.25, 0.125, 0.0625, то есть у каждого символа вероятность его появления обратнопропорциональна степени двойки. В таком случае максимальная длина символа составит 255 бит, что никак не поместится в переменную типа DWORD. Поэтому для таких особых случаев придётся немного поднапрячься и усложнить генерацию кодовой таблицы.
Да, чуть не забыл. Провёл бенчмарк, сжав эту статью. Получил отношение 1:1.41, что довольно-таки неплохо.
P.P.S.
Позволю себе немного пофилософствовать. Сначала я не знал C++ и говорил: “C++ это – язык программирования”. Потом, когда стал его изучать, я всячески его хвалил: “он может то, может это, а вот это – вообще класс, это супер язык”. Но помере набора опыта С++ стал для меня “просто языком программирования”. Почувствуйте разницу между этими тремя утверждениями.
Скачать исходный код к статье
SadKo
Владимир Садовников
- Регистрация:
- 4 июн 2007
- Публикаций:
- 8
Комментарии


Huffman tree generated from the exact frequencies of the text “this is an example of a huffman tree”. The frequencies and codes of each character are below. Encoding the sentence with this code requires 135 (or 147) bits, as opposed to 288 (or 180) bits if 36 characters of 8 (or 5) bits were used. (This assumes that the code tree structure is known to the decoder and thus does not need to be counted as part of the transmitted information.)
| Char | Freq | Code |
|---|---|---|
| space | 7 | 111 |
| a | 4 | 010 |
| e | 4 | 000 |
| f | 3 | 1101 |
| h | 2 | 1010 |
| i | 2 | 1000 |
| m | 2 | 0111 |
| n | 2 | 0010 |
| s | 2 | 1011 |
| t | 2 | 0110 |
| l | 1 | 11001 |
| o | 1 | 00110 |
| p | 1 | 10011 |
| r | 1 | 11000 |
| u | 1 | 00111 |
| x | 1 | 10010 |
In computer science and information theory, a Huffman code is a particular type of optimal prefix code that is commonly used for lossless data compression. The process of finding or using such a code proceeds by means of Huffman coding, an algorithm developed by David A. Huffman while he was a Sc.D. student at MIT, and published in the 1952 paper “A Method for the Construction of Minimum-Redundancy Codes”.[1]
The output from Huffman’s algorithm can be viewed as a variable-length code table for encoding a source symbol (such as a character in a file). The algorithm derives this table from the estimated probability or frequency of occurrence (weight) for each possible value of the source symbol. As in other entropy encoding methods, more common symbols are generally represented using fewer bits than less common symbols. Huffman’s method can be efficiently implemented, finding a code in time linear to the number of input weights if these weights are sorted.[2] However, although optimal among methods encoding symbols separately, Huffman coding is not always optimal among all compression methods – it is replaced with arithmetic coding[3] or asymmetric numeral systems[4] if a better compression ratio is required.
History[edit]
In 1951, David A. Huffman and his MIT information theory classmates were given the choice of a term paper or a final exam. The professor, Robert M. Fano, assigned a term paper on the problem of finding the most efficient binary code. Huffman, unable to prove any codes were the most efficient, was about to give up and start studying for the final when he hit upon the idea of using a frequency-sorted binary tree and quickly proved this method the most efficient.[5]
In doing so, Huffman outdid Fano, who had worked with Claude Shannon to develop a similar code. Building the tree from the bottom up guaranteed optimality, unlike the top-down approach of Shannon–Fano coding.
Terminology[edit]
Huffman coding uses a specific method for choosing the representation for each symbol, resulting in a prefix code (sometimes called “prefix-free codes”, that is, the bit string representing some particular symbol is never a prefix of the bit string representing any other symbol). Huffman coding is such a widespread method for creating prefix codes that the term “Huffman code” is widely used as a synonym for “prefix code” even when such a code is not produced by Huffman’s algorithm.
Problem definition[edit]

Constructing a Huffman Tree
Informal description[edit]
- Given
- A set of symbols and their weights (usually proportional to probabilities).
- Find
- A prefix-free binary code (a set of codewords) with minimum expected codeword length (equivalently, a tree with minimum weighted path length from the root).
Formalized description[edit]
Example[edit]
We give an example of the result of Huffman coding for a code with five characters and given weights. We will not verify that it minimizes L over all codes, but we will compute L and compare it to the Shannon entropy H of the given set of weights; the result is nearly optimal.
| Input (A, W) | Symbol (ai) | a | b | c | d | e | Sum |
|---|---|---|---|---|---|---|---|
| Weights (wi) | 0.10 | 0.15 | 0.30 | 0.16 | 0.29 | = 1 | |
| Output C | Codewords (ci) | 010
|
011
|
11
|
00
|
10
|
|
| Codeword length (in bits) (li) |
3 | 3 | 2 | 2 | 2 | ||
| Contribution to weighted path length (li wi ) |
0.30 | 0.45 | 0.60 | 0.32 | 0.58 | L(C) = 2.25 | |
| Optimality | Probability budget (2−li) |
1/8 | 1/8 | 1/4 | 1/4 | 1/4 | = 1.00 |
| Information content (in bits) (−log2 wi) ≈ |
3.32 | 2.74 | 1.74 | 2.64 | 1.79 | ||
| Contribution to entropy (–wi log2 wi) |
0.332 | 0.411 | 0.521 | 0.423 | 0.518 | H(A) = 2.205 |
For any code that is biunique, meaning that the code is uniquely decodeable, the sum of the probability budgets across all symbols is always less than or equal to one. In this example, the sum is strictly equal to one; as a result, the code is termed a complete code. If this is not the case, one can always derive an equivalent code by adding extra symbols (with associated null probabilities), to make the code complete while keeping it biunique.
As defined by Shannon (1948), the information content h (in bits) of each symbol ai with non-null probability is
The entropy H (in bits) is the weighted sum, across all symbols ai with non-zero probability wi, of the information content of each symbol:
(Note: A symbol with zero probability has zero contribution to the entropy, since 
As a consequence of Shannon’s source coding theorem, the entropy is a measure of the smallest codeword length that is theoretically possible for the given alphabet with associated weights. In this example, the weighted average codeword length is 2.25 bits per symbol, only slightly larger than the calculated entropy of 2.205 bits per symbol. So not only is this code optimal in the sense that no other feasible code performs better, but it is very close to the theoretical limit established by Shannon.
In general, a Huffman code need not be unique. Thus the set of Huffman codes for a given probability distribution is a non-empty subset of the codes minimizing 
Basic technique[edit]
Compression[edit]
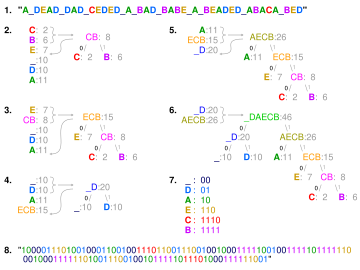
Visualisation of the use of Huffman coding to encode the message “A_DEAD_DAD_CEDED_A_BAD_BABE_A_BEADED_ABACA_
BED”. In steps 2 to 6, the letters are sorted by increasing frequency, and the least frequent two at each step are combined and reinserted into the list, and a partial tree is constructed. The final tree in step 6 is traversed to generate the dictionary in step 7. Step 8 uses it to encode the message.

A source generates 4 different symbols 

| Symbol | Code |
|---|---|
| a1 | 0 |
| a2 | 10 |
| a3 | 110 |
| a4 | 111 |
The standard way to represent a signal made of 4 symbols is by using 2 bits/symbol, but the entropy of the source is 1.74 bits/symbol. If this Huffman code is used to represent the signal, then the average length is lowered to 1.85 bits/symbol; it is still far from the theoretical limit because the probabilities of the symbols are different from negative powers of two.
The technique works by creating a binary tree of nodes. These can be stored in a regular array, the size of which depends on the number of symbols, 


The process begins with the leaf nodes containing the probabilities of the symbol they represent. Then, the process takes the two nodes with smallest probability, and creates a new internal node having these two nodes as children. The weight of the new node is set to the sum of the weight of the children. We then apply the process again, on the new internal node and on the remaining nodes (i.e., we exclude the two leaf nodes), we repeat this process until only one node remains, which is the root of the Huffman tree.
The simplest construction algorithm uses a priority queue where the node with lowest probability is given highest priority:
- Create a leaf node for each symbol and add it to the priority queue.
- While there is more than one node in the queue:
- Remove the two nodes of highest priority (lowest probability) from the queue
- Create a new internal node with these two nodes as children and with probability equal to the sum of the two nodes’ probabilities.
- Add the new node to the queue.
- The remaining node is the root node and the tree is complete.
Since efficient priority queue data structures require O(log n) time per insertion, and a tree with n leaves has 2n−1 nodes, this algorithm operates in O(n log n) time, where n is the number of symbols.
If the symbols are sorted by probability, there is a linear-time (O(n)) method to create a Huffman tree using two queues, the first one containing the initial weights (along with pointers to the associated leaves), and combined weights (along with pointers to the trees) being put in the back of the second queue. This assures that the lowest weight is always kept at the front of one of the two queues:
- Start with as many leaves as there are symbols.
- Enqueue all leaf nodes into the first queue (by probability in increasing order so that the least likely item is in the head of the queue).
- While there is more than one node in the queues:
- Dequeue the two nodes with the lowest weight by examining the fronts of both queues.
- Create a new internal node, with the two just-removed nodes as children (either node can be either child) and the sum of their weights as the new weight.
- Enqueue the new node into the rear of the second queue.
- The remaining node is the root node; the tree has now been generated.
Once the Huffman tree has been generated, it is traversed to generate a dictionary which maps the symbols to binary codes as follows:
- Start with current node set to the root.
- If node is not a leaf node, label the edge to the left child as 0 and the edge to the right child as 1. Repeat the process at both the left child and the right child.
The final encoding of any symbol is then read by a concatenation of the labels on the edges along the path from the root node to the symbol.
In many cases, time complexity is not very important in the choice of algorithm here, since n here is the number of symbols in the alphabet, which is typically a very small number (compared to the length of the message to be encoded); whereas complexity analysis concerns the behavior when n grows to be very large.
It is generally beneficial to minimize the variance of codeword length. For example, a communication buffer receiving Huffman-encoded data may need to be larger to deal with especially long symbols if the tree is especially unbalanced. To minimize variance, simply break ties between queues by choosing the item in the first queue. This modification will retain the mathematical optimality of the Huffman coding while both minimizing variance and minimizing the length of the longest character code.
Decompression[edit]
Generally speaking, the process of decompression is simply a matter of translating the stream of prefix codes to individual byte values, usually by traversing the Huffman tree node by node as each bit is read from the input stream (reaching a leaf node necessarily terminates the search for that particular byte value). Before this can take place, however, the Huffman tree must be somehow reconstructed. In the simplest case, where character frequencies are fairly predictable, the tree can be preconstructed (and even statistically adjusted on each compression cycle) and thus reused every time, at the expense of at least some measure of compression efficiency. Otherwise, the information to reconstruct the tree must be sent a priori. A naive approach might be to prepend the frequency count of each character to the compression stream. Unfortunately, the overhead in such a case could amount to several kilobytes, so this method has little practical use. If the data is compressed using canonical encoding, the compression model can be precisely reconstructed with just 
Main properties[edit]
The probabilities used can be generic ones for the application domain that are based on average experience, or they can be the actual frequencies found in the text being compressed.
This requires that a frequency table must be stored with the compressed text. See the Decompression section above for more information about the various techniques employed for this purpose.
Optimality[edit]
Huffman’s original algorithm is optimal for a symbol-by-symbol coding with a known input probability distribution, i.e., separately encoding unrelated symbols in such a data stream. However, it is not optimal when the symbol-by-symbol restriction is dropped, or when the probability mass functions are unknown. Also, if symbols are not independent and identically distributed, a single code may be insufficient for optimality. Other methods such as arithmetic coding often have better compression capability.
Although both aforementioned methods can combine an arbitrary number of symbols for more efficient coding and generally adapt to the actual input statistics, arithmetic coding does so without significantly increasing its computational or algorithmic complexities (though the simplest version is slower and more complex than Huffman coding). Such flexibility is especially useful when input probabilities are not precisely known or vary significantly within the stream. However, Huffman coding is usually faster and arithmetic coding was historically a subject of some concern over patent issues. Thus many technologies have historically avoided arithmetic coding in favor of Huffman and other prefix coding techniques. As of mid-2010, the most commonly used techniques for this alternative to Huffman coding have passed into the public domain as the early patents have expired.
For a set of symbols with a uniform probability distribution and a number of members which is a power of two, Huffman coding is equivalent to simple binary block encoding, e.g., ASCII coding. This reflects the fact that compression is not possible with such an input, no matter what the compression method, i.e., doing nothing to the data is the optimal thing to do.
Huffman coding is optimal among all methods in any case where each input symbol is a known independent and identically distributed random variable having a probability that is dyadic. Prefix codes, and thus Huffman coding in particular, tend to have inefficiency on small alphabets, where probabilities often fall between these optimal (dyadic) points. The worst case for Huffman coding can happen when the probability of the most likely symbol far exceeds 2−1 = 0.5, making the upper limit of inefficiency unbounded.
There are two related approaches for getting around this particular inefficiency while still using Huffman coding. Combining a fixed number of symbols together (“blocking”) often increases (and never decreases) compression. As the size of the block approaches infinity, Huffman coding theoretically approaches the entropy limit, i.e., optimal compression.[6] However, blocking arbitrarily large groups of symbols is impractical, as the complexity of a Huffman code is linear in the number of possibilities to be encoded, a number that is exponential in the size of a block. This limits the amount of blocking that is done in practice.
A practical alternative, in widespread use, is run-length encoding. This technique adds one step in advance of entropy coding, specifically counting (runs) of repeated symbols, which are then encoded. For the simple case of Bernoulli processes, Golomb coding is optimal among prefix codes for coding run length, a fact proved via the techniques of Huffman coding.[7] A similar approach is taken by fax machines using modified Huffman coding. However, run-length coding is not as adaptable to as many input types as other compression technologies.
Variations[edit]
Many variations of Huffman coding exist,[8] some of which use a Huffman-like algorithm, and others of which find optimal prefix codes (while, for example, putting different restrictions on the output). Note that, in the latter case, the method need not be Huffman-like, and, indeed, need not even be polynomial time.
n-ary Huffman coding[edit]
The n-ary Huffman algorithm uses the {0, 1,…, n − 1} alphabet to encode message and build an n-ary tree. This approach was considered by Huffman in his original paper. The same algorithm applies as for binary (
Adaptive Huffman coding[edit]
A variation called adaptive Huffman coding involves calculating the probabilities dynamically based on recent actual frequencies in the sequence of source symbols, and changing the coding tree structure to match the updated probability estimates. It is used rarely in practice, since the cost of updating the tree makes it slower than optimized adaptive arithmetic coding, which is more flexible and has better compression.
Huffman template algorithm[edit]
Most often, the weights used in implementations of Huffman coding represent numeric probabilities, but the algorithm given above does not require this; it requires only that the weights form a totally ordered commutative monoid, meaning a way to order weights and to add them. The Huffman template algorithm enables one to use any kind of weights (costs, frequencies, pairs of weights, non-numerical weights) and one of many combining methods (not just addition). Such algorithms can solve other minimization problems, such as minimizing ![max _{i}left[w_{i}+mathrm {length} left(c_{i}right)right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a80c0b460cf854976824c251037db43d7ed1810)
Length-limited Huffman coding/minimum variance Huffman coding[edit]
Length-limited Huffman coding is a variant where the goal is still to achieve a minimum weighted path length, but there is an additional restriction that the length of each codeword must be less than a given constant. The package-merge algorithm solves this problem with a simple greedy approach very similar to that used by Huffman’s algorithm. Its time complexity is 



Huffman coding with unequal letter costs[edit]
In the standard Huffman coding problem, it is assumed that each symbol in the set that the code words are constructed from has an equal cost to transmit: a code word whose length is N digits will always have a cost of N, no matter how many of those digits are 0s, how many are 1s, etc. When working under this assumption, minimizing the total cost of the message and minimizing the total number of digits are the same thing.
Huffman coding with unequal letter costs is the generalization without this assumption: the letters of the encoding alphabet may have non-uniform lengths, due to characteristics of the transmission medium. An example is the encoding alphabet of Morse code, where a ‘dash’ takes longer to send than a ‘dot’, and therefore the cost of a dash in transmission time is higher. The goal is still to minimize the weighted average codeword length, but it is no longer sufficient just to minimize the number of symbols used by the message. No algorithm is known to solve this in the same manner or with the same efficiency as conventional Huffman coding, though it has been solved by Karp whose solution has been refined for the case of integer costs by Golin.
Optimal alphabetic binary trees (Hu–Tucker coding)[edit]
In the standard Huffman coding problem, it is assumed that any codeword can correspond to any input symbol. In the alphabetic version, the alphabetic order of inputs and outputs must be identical. Thus, for example, 




The canonical Huffman code[edit]
If weights corresponding to the alphabetically ordered inputs are in numerical order, the Huffman code has the same lengths as the optimal alphabetic code, which can be found from calculating these lengths, rendering Hu–Tucker coding unnecessary. The code resulting from numerically (re-)ordered input is sometimes called the canonical Huffman code and is often the code used in practice, due to ease of encoding/decoding. The technique for finding this code is sometimes called Huffman–Shannon–Fano coding, since it is optimal like Huffman coding, but alphabetic in weight probability, like Shannon–Fano coding. The Huffman–Shannon–Fano code corresponding to the example is 

Applications[edit]
Arithmetic coding and Huffman coding produce equivalent results — achieving entropy — when every symbol has a probability of the form 1/2k. In other circumstances, arithmetic coding can offer better compression than Huffman coding because — intuitively — its “code words” can have effectively non-integer bit lengths, whereas code words in prefix codes such as Huffman codes can only have an integer number of bits. Therefore, a code word of length k only optimally matches a symbol of probability 1/2k and other probabilities are not represented optimally; whereas the code word length in arithmetic coding can be made to exactly match the true probability of the symbol. This difference is especially striking for small alphabet sizes.[citation needed]
Prefix codes nevertheless remain in wide use because of their simplicity, high speed, and lack of patent coverage. They are often used as a “back-end” to other compression methods. Deflate (PKZIP’s algorithm) and multimedia codecs such as JPEG and MP3 have a front-end model and quantization followed by the use of prefix codes; these are often called “Huffman codes” even though most applications use pre-defined variable-length codes rather than codes designed using Huffman’s algorithm.
References[edit]
- ^ Huffman, D. (1952). “A Method for the Construction of Minimum-Redundancy Codes” (PDF). Proceedings of the IRE. 40 (9): 1098–1101. doi:10.1109/JRPROC.1952.273898.
- ^ Van Leeuwen, Jan (1976). “On the construction of Huffman trees” (PDF). ICALP: 382–410. Retrieved 2014-02-20.
- ^ Ze-Nian Li; Mark S. Drew; Jiangchuan Liu (2014-04-09). Fundamentals of Multimedia. Springer Science & Business Media. ISBN 978-3-319-05290-8.
- ^ J. Duda, K. Tahboub, N. J. Gadil, E. J. Delp, The use of asymmetric numeral systems as an accurate replacement for Huffman coding, Picture Coding Symposium, 2015.
- ^ Huffman, Ken (1991). “Profile: David A. Huffman: Encoding the “Neatness” of Ones and Zeroes”. Scientific American: 54–58.
- ^ Gribov, Alexander (2017-04-10). “Optimal Compression of a Polyline with Segments and Arcs”. arXiv:1604.07476 [cs.CG].
- ^ Gallager, R.G.; van Voorhis, D.C. (1975). “Optimal source codes for geometrically distributed integer alphabets”. IEEE Transactions on Information Theory. 21 (2): 228–230. doi:10.1109/TIT.1975.1055357.
- ^ Abrahams, J. (1997-06-11). Written at Arlington, VA, USA. Division of Mathematics, Computer & Information Sciences, Office of Naval Research (ONR). “Code and Parse Trees for Lossless Source Encoding”. Compression and Complexity of Sequences 1997 Proceedings. Salerno: IEEE: 145–171. CiteSeerX 10.1.1.589.4726. doi:10.1109/SEQUEN.1997.666911. ISBN 0-8186-8132-2. S2CID 124587565.
- ^ Hu, T. C.; Tucker, A. C. (1971). “Optimal Computer Search Trees and Variable-Length Alphabetical Codes”. SIAM Journal on Applied Mathematics. 21 (4): 514. doi:10.1137/0121057. JSTOR 2099603.
- ^ Knuth, Donald E. (1998), “Algorithm G (Garsia–Wachs algorithm for optimum binary trees)”, The Art of Computer Programming, Vol. 3: Sorting and Searching (2nd ed.), Addison–Wesley, pp. 451–453. See also History and bibliography, pp. 453–454.
Bibliography[edit]
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 16.3, pp. 385–392.
External links[edit]
- Huffman coding in various languages on Rosetta Code
- Huffman codes (python implementation)
- A visualization of Huffman coding


