Как найти коэффициент сжимаемости газа - Сайт, где вы сможете решить свои вопросы

In thermodynamics, the compressibility factor (Z), also known as the compression factor or the gas deviation factor, describes the deviation of a real gas from ideal gas behaviour. It is simply defined as the ratio of the molar volume of a gas to the molar volume of an ideal gas at the same temperature and pressure. It is a useful thermodynamic property for modifying the ideal gas law to account for the real gas behaviour.^[1] In general, deviation from ideal behaviour becomes more significant the closer a gas is to a phase change, the lower the temperature or the larger the pressure. Compressibility factor values are usually obtained by calculation from equations of state (EOS), such as the virial equation which take compound-specific empirical constants as input. For a gas that is a mixture of two or more pure gases (air or natural gas, for example), the gas composition must be known before compressibility can be calculated.
Alternatively, the compressibility factor for specific gases can be read from generalized compressibility charts^[1] that plot as a function of pressure at constant temperature.

The compressibility factor should not be confused with the compressibility (also known as coefficient of compressibility or isothermal compressibility) of a material, which is the measure of the relative volume change of a fluid or solid in response to a pressure change.

Definition and physical significance[edit]

A graphical representation of the behavior of gases and how that behavior relates to compressibility factor.

The compressibility factor is defined in thermodynamics and engineering frequently as:

${displaystyle Z={frac {p}{rho R_{text{specific}}T}},}$

where p is the pressure, rho is the density of the gas and ${textstyle R_{text{specific}}={frac {R}{M}}}$ is the specific gas constant,^[2] being the molar mass, and the is the absolute temperature (kelvin or Rankine scale).

In statistical mechanics the description is:

${displaystyle Z={frac {pV}{nRT}}}$

where p is the pressure, n is the number of moles of gas, is the absolute temperature, and is the gas constant.

For an ideal gas the compressibility factor is Z=1 per definition. In many real world applications requirements for accuracy demand that deviations from ideal gas behaviour, i.e., real gas behaviour, be taken into account. The value of generally increases with pressure and decreases with temperature. At high pressures molecules are colliding more often. This allows repulsive forces between molecules to have a noticeable effect, making the molar volume of the real gas ( $V_{{{mathrm {m}}}}$ ) greater than the molar volume of the corresponding ideal gas ( $(V_{{{mathrm {m}}}})_{{{text{ideal gas}}}}=RT/p$ ), which causes to exceed one.^[3] When pressures are lower, the molecules are free to move. In this case attractive forces dominate, making Z<1 . The closer the gas is to its critical point or its boiling point, the more deviates from the ideal case.

Fugacity[edit]

The compressibility factor is linked to the fugacity by the relation:^{[citation needed]}

${displaystyle f=Pexp left(int {frac {Z-1}{P}}dPright)}$

Generalized compressibility factor graphs for pure gases[edit]

Generalized compressibility factor diagram.

The unique relationship between the compressibility factor and the reduced temperature, T_r , and the reduced pressure, $P_{r}$ , was first recognized by Johannes Diderik van der Waals in 1873 and is known as the two-parameter principle of corresponding states. The principle of corresponding states expresses the generalization that the properties of a gas which are dependent on intermolecular forces are related to the critical properties of the gas in a universal way. That provides a most important basis for developing correlations of molecular properties.

As for the compressibility of gases, the principle of corresponding states indicates that any pure gas at the same reduced temperature, T_r , and reduced pressure, $P_{r}$ , should have the same compressibility factor.

The reduced temperature and pressure are defined by

$T_r = frac{T}{T_c}$

and $P_{r}={frac {P}{P_{c}}}.$

Here $T_{c}$ and $P_{c}$ are known as the critical temperature and critical pressure of a gas. They are characteristics of each specific gas with $T_{c}$ being the temperature above which it is not possible to liquify a given gas and $P_{c}$ is the minimum pressure required to liquify a given gas at its critical temperature. Together they define the critical point of a fluid above which distinct liquid and gas phases of a given fluid do not exist.

The pressure-volume-temperature (PVT) data for real gases varies from one pure gas to another. However, when the compressibility factors of various single-component gases are graphed versus pressure along with temperature isotherms many of the graphs exhibit similar isotherm shapes.

In order to obtain a generalized graph that can be used for many different gases, the reduced pressure and temperature, $P_{r}$ and T_r , are used to normalize the compressibility factor data. Figure 2 is an example of a generalized compressibility factor graph derived from hundreds of experimental PVT data points of 10 pure gases, namely methane, ethane, ethylene, propane, n-butane, i-pentane, n-hexane, nitrogen, carbon dioxide and steam.

There are more detailed generalized compressibility factor graphs based on as many as 25 or more different pure gases, such as the Nelson-Obert graphs. Such graphs are said to have an accuracy within 1–2 percent for values greater than 0.6 and within 4–6 percent for values of 0.3–0.6.

The generalized compressibility factor graphs may be considerably in error for strongly polar gases which are gases for which the centers of positive and negative charge do not coincide. In such cases the estimate for may be in error by as much as 15–20 percent.

The quantum gases hydrogen, helium, and neon do not conform to the corresponding-states behavior and the reduced pressure and temperature for those three gases should be redefined in the following manner to improve the accuracy of predicting their compressibility factors when using the generalized graphs:

${displaystyle T_{r}={frac {T}{T_{c}+8}}}$

and $P_{r}={frac {P}{P_{c}+8}}$

where the temperatures are in kelvins and the pressures are in atmospheres.^[4]

Reading a generalized compressibility chart[edit]

In order to read a compressibility chart, the reduced pressure and temperature must be known. If either the reduced pressure or temperature is unknown, the reduced specific volume must be found. Unlike the reduced pressure and temperature, the reduced specific volume is not found by using the critical volume. The reduced specific volume is defined by,

${displaystyle nu _{R}={frac {nu _{text{actual}}}{RT_{text{cr}}/P_{text{cr}}}}}$

where ${displaystyle nu _{text{actual}}}$ is the specific volume.^[5]

Once two of the three reduced properties are found, the compressibility chart can be used. In a compressibility chart, reduced pressure is on the x-axis and Z is on the y-axis. When given the reduced pressure and temperature, find the given pressure on the x-axis. From there, move up on the chart until the given reduced temperature is found. Z is found by looking where those two points intersect. the same process can be followed if reduced specific volume is given with either reduced pressure or temperature.

Observations made from a generalized compressibility chart[edit]

There are three observations that can be made when looking at a generalized compressibility chart. These observations are:

Gases behave as an ideal gas regardless of temperature when the reduced pressure is much less than one (P_R ≪ 1).
When reduced temperature is greater than two (T_R > 2), ideal-gas behavior can be assumed regardless of pressure, unless pressure is much greater than one (P_R ≫ 1).
Gases deviate from ideal-gas behavior the most in the vicinity of the critical point.^[6]

Theoretical models[edit]

The virial equation is especially useful to describe the causes of non-ideality at a molecular level (very few gases are mono-atomic) as it is derived directly from statistical mechanics:

${displaystyle Z=1+{frac {B}{V_{mathrm {m} }}}+{frac {C}{V_{mathrm {m} }^{2}}}+{frac {D}{V_{mathrm {m} }^{3}}}+dots }$

Where the coefficients in the numerator are known as virial coefficients and are functions of temperature.

The virial coefficients account for interactions between successively larger groups of molecules. For example, accounts for interactions between pairs, for interactions between three gas molecules, and so on. Because interactions between large numbers of molecules are rare, the virial equation is usually truncated after the third term.^[7]

When this truncation is assumed, the compressibility factor is linked to the intermolecular-force potential φ by:

${displaystyle Z=1+2pi {frac {N_{text{A}}}{V_{text{m}}}}int _{0}^{infty }left(1-exp left({frac {varphi }{kT}}right)right)r^{2}dr}$

The Real gas article features more theoretical methods to compute compressibility factors.

Physical mechanism of temperature and pressure dependence[edit]

Deviations of the compressibility factor, Z, from unity are due to attractive and repulsive intermolecular forces. At a given temperature and pressure, repulsive forces tend to make the volume larger than for an ideal gas; when these forces dominate Z is greater than unity. When attractive forces dominate, Z is less than unity. The relative importance of attractive forces decreases as temperature increases (see effect on gases).

As seen above, the behavior of Z is qualitatively similar for all gases. Molecular nitrogen, N₂, is used here to further describe and understand that behavior. All data used in this section were obtained from the NIST Chemistry WebBook.^[8] It is useful to note that for N₂ the normal boiling point of the liquid is 77.4 K and the critical point is at 126.2 K and 34.0 bar.

Overview of the temperature and pressure dependence of the compressibility factor for N₂.

The figure on the right shows an overview covering a wide temperature range. At low temperature (100 K), the curve has a characteristic check-mark shape, the rising portion of the curve is very nearly directly proportional to pressure. At intermediate temperature (160 K), there is a smooth curve with a broad minimum; although the high pressure portion is again nearly linear, it is no longer directly proportional to pressure. Finally, at high temperature (400 K), Z is above unity at all pressures. For all curves, Z approaches the ideal gas value of unity at low pressure and exceeds that value at very high pressure.

The pressure dependence of the compressibility factor for N₂ at low temperatures. The dashed line shows the gas-liquid coexistence curve.

To better understand these curves, a closer look at the behavior for low temperature and pressure is given in the second figure. All of the curves start out with Z equal to unity at zero pressure and Z initially decreases as pressure increases. N₂ is a gas under these conditions, so the distance between molecules is large, but becomes smaller as pressure increases. This increases the attractive interactions between molecules, pulling the molecules closer together and causing the volume to be less than for an ideal gas at the same temperature and pressure. Higher temperature reduces the effect of the attractive interactions and the gas behaves in a more nearly ideal manner.

As the pressure increases, the gas eventually reaches the gas-liquid coexistence curve, shown by the dashed line in the figure. When that happens, the attractive interactions have become strong enough to overcome the tendency of thermal motion to cause the molecules to spread out; so the gas condenses to form a liquid. Points on the vertical portions of the curves correspond to N₂ being partly gas and partly liquid. On the coexistence curve, there are then two possible values for Z, a larger one corresponding to the gas and a smaller value corresponding to the liquid. Once all the gas has been converted to liquid, the volume decreases only slightly with further increases in pressure; then Z is very nearly proportional to pressure.

As temperature and pressure increase along the coexistence curve, the gas becomes more like a liquid and the liquid becomes more like a gas. At the critical point, the two are the same. So for temperatures above the critical temperature (126.2 K), there is no phase transition; as pressure increases the gas gradually transforms into something more like a liquid. Just above the critical point there is a range of pressure for which Z drops quite rapidly (see the 130 K curve), but at higher temperatures the process is entirely gradual.

The pressure dependence of the compressibility factor for N₂ at high temperatures, compared with that for an ideal gas.

The final figures shows the behavior at temperatures well above the critical temperatures. The repulsive interactions are essentially unaffected by temperature, but the attractive interaction have less and less influence. Thus, at sufficiently high temperature, the repulsive interactions dominate at all pressures.

This can be seen in the graph showing the high temperature behavior. As temperature increases, the initial slope becomes less negative, the pressure at which Z is a minimum gets smaller, and the pressure at which repulsive interactions start to dominate, i.e. where Z goes from less than unity to greater than unity, gets smaller. At the Boyle temperature (327 K for N₂), the attractive and repulsive effects cancel each other at low pressure. Then Z remains at the ideal gas value of unity up to pressures of several tens of bar. Above the Boyle temperature, the compressibility factor is always greater than unity and increases slowly but steadily as pressure increases.

Experimental values[edit]

It is extremely difficult to generalize at what pressures or temperatures the deviation from the ideal gas becomes important. As a rule of thumb, the ideal gas law is reasonably accurate up to a pressure of about 2 atm, and even higher for small non-associating molecules. For example, methyl chloride, a highly polar molecule and therefore with significant intermolecular forces, the experimental value for the compressibility factor is at a pressure of 10 atm and temperature of 100 °C.^[9] For air (small non-polar molecules) at approximately the same conditions, the compressibility factor is only (see table below for 10 bars, 400 K).

Compressibility of air[edit]

Normal air comprises in crude numbers 80 percent nitrogen N
₂ and 20 percent oxygen O
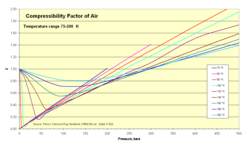
₂. Both molecules are small and non-polar (and therefore non-associating). We can therefore expect that the behaviour of air within broad temperature and pressure ranges can be approximated as an ideal gas with reasonable accuracy. Experimental values for the compressibility factor confirm this.

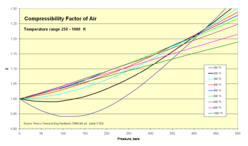
Z for air as function of pressure 1–500 bar
75–200 K isotherms
250–1000 K isotherms

Compressibility factor for air (experimental values)^[10]

Temp. (K)	Pressure, absolute (bar)
1	5	10	20	40	60	80	100	150	200	250	300	400	500
75	0.0052	0.0260	0.0519	0.1036	0.2063	0.3082	0.4094	0.5099	0.7581	1.0125
80		0.0250	0.0499	0.0995	0.1981	0.2958	0.3927	0.4887	0.7258	0.9588	1.1931	1.4139
90	0.9764	0.0236	0.0453	0.0940	0.1866	0.2781	0.3686	0.4681	0.6779	0.8929	1.1098	1.3110	1.7161	2.1105
100	0.9797	0.8872	0.0453	0.0900	0.1782	0.2635	0.3498	0.4337	0.6386	0.8377	1.0395	1.2227	1.5937	1.9536
120	0.9880	0.9373	0.8860	0.6730	0.1778	0.2557	0.3371	0.4132	0.5964	0.7720	0.9530	1.1076	1.5091	1.7366
140	0.9927	0.9614	0.9205	0.8297	0.5856	0.3313	0.3737	0.4340	0.5909	0.7699	0.9114	1.0393	1.3202	1.5903
160	0.9951	0.9748	0.9489	0.8954	0.7803	0.6603	0.5696	0.5489	0.6340	0.7564	0.8840	1.0105	1.2585	1.4970
180	0.9967	0.9832	0.9660	0.9314	0.8625	0.7977	0.7432	0.7084	0.7180	0.7986	0.9000	1.0068	1.2232	1.4361
200	0.9978	0.9886	0.9767	0.9539	0.9100	0.8701	0.8374	0.8142	0.8061	0.8549	0.9311	1.0185	1.2054	1.3944
250	0.9992	0.9957	0.9911	0.9822	0.9671	0.9549	0.9463	0.9411	0.9450	0.9713	1.0152	1.0702	1.1990	1.3392
300	0.9999	0.9987	0.9974	0.9950	0.9917	0.9901	0.9903	0.9930	1.0074	1.0326	1.0669	1.1089	1.2073	1.3163
350	1.0000	1.0002	1.0004	1.0014	1.0038	1.0075	1.0121	1.0183	1.0377	1.0635	1.0947	1.1303	1.2116	1.3015
400	1.0002	1.0012	1.0025	1.0046	1.0100	1.0159	1.0229	1.0312	1.0533	1.0795	1.1087	1.1411	1.2117	1.2890
450	1.0003	1.0016	1.0034	1.0063	1.0133	1.0210	1.0287	1.0374	1.0614	1.0913	1.1183	1.1463	1.2090	1.2778
500	1.0003	1.0020	1.0034	1.0074	1.0151	1.0234	1.0323	1.0410	1.0650	1.0913	1.1183	1.1463	1.2051	1.2667
600	1.0004	1.0022	1.0039	1.0081	1.0164	1.0253	1.0340	1.0434	1.0678	1.0920	1.1172	1.1427	1.1947	1.2475
800	1.0004	1.0020	1.0038	1.0077	1.0157	1.0240	1.0321	1.0408	1.0621	1.0844	1.1061	1.1283	1.1720	1.2150
1000	1.0004	1.0018	1.0037	1.0068	1.0142	1.0215	1.0290	1.0365	1.0556	1.0744	1.0948	1.1131	1.1515	1.1889

values are calculated from values of pressure, volume (or density), and temperature in Vasserman, Kazavchinskii, and Rabinovich, “Thermophysical Properties of Air and Air Components;’ Moscow, Nauka, 1966, and NBS-NSF Trans. TT 70-50095, 1971: and Vasserman and Rabinovich, “Thermophysical Properties of Liquid Air and Its Component, “Moscow, 1968, and NBS-NSF Trans. 69-55092, 1970.

References[edit]

^ ^a ^b Properties of Natural Gases Archived 2011-02-06 at the Wayback Machine. Includes a chart of compressibility factors versus reduced pressure and reduced temperature (on last page of the PDF document)
^ Zucker, Robert D.; Biblarz, Oscar (2002). Fundamentals of Gas Dynamics (2nd ed.). Wiley Books. ISBN 0-471-05967-6. page 327
^ McQuarrie, Donald A.; Simon, John D. (1999). Molecular Thermodynamics. University Science Books. ISBN 1-891389-05-X. page 55
^ Y.V.C. Rao (1997). Chemical Engineering Thermodynamics. Universities Press (India). ISBN 81-7371-048-1.
^ Cengel, Yunus A.; Boles, Michael A. (2015). Thermodynamics: An Engineering Approach, Eighth Edition. McGraw-Hill Education. ISBN 978-0-07-339817-4. page 140
^ Cengel, Yunus A.; Boles, Michael A. (2015). Thermodynamics: An Engineering Approach, Eighth Edition. McGraw-Hill Education. ISBN 978-0-07-339817-4. page 139
^ Smith, J.M.; et al. (2005). Introduction to Chemical Engineering Thermodynamics (Seventh ed.). McGraw Hill. ISBN 0-07-310445-0. page73
^ NIST Chemistry WebBook
^ Perry’s chemical engineers’ handbook (6 ed.). MCGraw-Hill. 1984. ISBN 0-07-049479-7. page 3-268
^
Perry’s chemical engineers’ handbook (6 ed.). MCGraw-Hill. 1984. p. 3-162. ISBN 0-07-049479-7.

External links[edit]

Compressibility factor (gases) A Citizendium article.
Real Gases includes a discussion of compressibility factors.

Источник

1 Назначение и область применения
2 Нормативные ссылки
3 Определение коэффициента сжимаемости
4 Влияние погрешности исходных данных на погрешность расчета коэффициента сжимаемости
5 Программная и техническая реализация расчета коэффициента сжимаемости
Таблицы констант и параметров уравнения состояния AGA8-92DC
Таблицы коэффициентов и параметров уравнения состояния ВНИЦ СМВ
Листинг программы расчета коэффициента сжимаемости природного газа
Примеры расчета коэффициента сжимаемости природного газа
Влияние погрешности исходных данных на погрешность расчета коэффициента сжимаемости природного газа (примеры расчета)
Библиография

ГОСТ 30319.2-96

МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ

ГАЗ ПРИРОДНЫЙ

МЕТОДЫ РАСЧЕТА ФИЗИЧЕСКИХ СВОЙСТВ

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА СЖИМАЕМОСТИ

МЕЖГОСУДАРСТВЕННЫЙ СОВЕТ ПО СТАНДАРТИЗАЦИИ, МЕТРОЛОГИИ И СЕРТИФИКАЦИИ

Минск

Предисловие

1 РАЗРАБОТАН Всероссийским научно-исследовательским центром стандартизации, информации и сертификации сырья, материалов и веществ (ВНИЦ СМВ) Госстандарта России; фирмой «Газприборавтоматика» акционерного общества «Газавтоматика» РАО «Газпром»

ВНЕСЕН Госстандартом Российской Федерации

2 ПРИНЯТ Межгосударственным Советом по стандартизации, метрологии и сертификации (протокол № 9-96 от 12 апреля 1996 г.)

За принятие проголосовали:

Наименование государства	Наименование национального органа по стандартизации
Азербайджанская Республика	Азгосстандарт
Республика Армения	Армгосстандарт
Республика Беларусь	Госстандарт Беларуси
Республика Грузия	Грузстандарт
Республика Казахстан	Госстандарт Республики Казахстан
Киргизская Республика	Киргизстандарт
Республика Молдова	Молдовастандарт
Российская Федерация	Госстандарт России
Республика Таджикистан	Таджикгосстандарт
Туркменистан	Главная государственная инспекция Туркменистана
Украина	Госстандарт Украины

3 ПОСТАНОВЛЕНИЕМ Государственного комитета Российской Федерации по стандартизации, метрологии и сертификации от 30 декабря 1996 г. № 723 межгосударственный стандарт ГОСТ 30319.2-96 введен в действие непосредственно в качестве государственного стандарта Российской Федерации с 1 июля 1997 г.

4 ВВЕДЕН ВПЕРВЫЕ

5 ПЕРЕИЗДАНИЕ

ГОСТ 30319.2-96

МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ

Газ природный

МЕТОДЫ РАСЧЕТА ФИЗИЧЕСКИХ СВОЙСТВ

Определение коэффициента сжимаемости

Natural gas. Methods of calculation of physical properties. Definition of compressibility coefficient

Дата введения 1997-07-01

Настоящий стандарт устанавливает четыре метода определения коэффициента сжимаемости природного газа: при неизвестном полном компонентном составе природного газа (два метода) и известном компонентном составе.

Стандарт устанавливает предпочтительные области применения каждого метода по измеряемым параметрам (давление, температура, плотность природного газа при стандартных условиях и компонентный состав природного газа), однако не запрещает использование любого из методов и в других областях.

Допускается применять любые другие методы расчета коэффициента сжимаемости, однако погрешность расчета коэффициента сжимаемости по этим методам не должна превышать погрешностей, приведенных в настоящем стандарте (см. 3.2.1).

Используемые в настоящем стандарте определения и обозначения приведены в соответствующих разделах ГОСТ 30319.0.

В настоящем стандарте использованы ссылки на следующие стандарты:

ГОСТ 30319.0-96 Газ природный. Методы расчета физических свойств. Общие положения

ГОСТ 30319.1-96 Газ природный. Методы расчета физических свойств. Определение физических свойств природного газа, его компонентов и продуктов его переработки

3.1 Общие положения

Коэффициент сжимаемости вычисляют по формуле

К = z/zc, (1)

где z и zc – фактор сжимаемости соответственно при рабочих и стандартных условиях.

Рабочие условия характеризуются такими давлениями и температурами, которые определяются измерениями в процессе добычи, переработки и транспортирования природного газа. Давление pc и температура Tc при стандартных условиях приведены в ГОСТ 30319.0.

3.2 Методы расчета коэффициента сжимаемости

3.2.1 Пределы применимости методов расчета и погрешности расчета коэффициента сжимаемости

В таблице 1 приведены общие результаты апробации методов расчета и область их применения. Апробация проведена на обширном массиве высокоточных экспериментальных данных о факторе сжимаемости природного газа [1-12].

Погрешность данных не превышает 0,1 %.

Таблица 1 – Результаты апробации и область применения методов расчета коэффициента сжимаемости природного газа

Метод расчета	Область применения и погрешность метода расчета	Отклонения от экспериментальных данных
Область применения	rс, кг/м3	r, МПа	Погрешность d, %	dсист, %	diмакс, %
NX19 мод.	32fНс.в, МДж/м3f40	<0,70	<3	0,12	-0,02	+0,07	-0,09
3-7	0,18	-0,01	+0,37	-0,10
>7	0,41	0,17	+0,59	-0,08
0,66frс, кг/м3f1,05	0,70 – 0,75	<3	0,13	0,01	+0,14	-0,13
0fxа, мол.%f15	3-7	0,29	0,12	+0,46	-0,15
0fxy, мол.%f15	>7	0,42	0,27	+0,66	-0,12
250fТ, Кf340	>0,75	<3	0,20	0,05	+0,41	-0,13
0,1fр, МПаf12,0	3-7	0,57	0,24	+1,06	-0,25
	>7	1,09	0,34	+1,65	-0,40
	0,74-1,00 (смеси с H2S)	0,1-11	0,15	-0,02	+0,09	-0,10
УС GERG-91 мод.	20fНс.в, МДж/м3f48	<0,70	<3	0,11	0,01	+0,13	-0,04
3-7	0,15	0,02	+0,51	-0,06
>7	0,20	0,03	+0,63	-0,06
0,66frс, кг/м3f1,05	0,70 – 0,75	<3	0,12	-0,01	+0,08	-0,17
0fxа, мол.%f15	3-7	0,15	-0,02	+0,11	-0,43
0fxy, мол.%f15	>7	0,19	0,02	+0,16	-0,34
250fТ, Кf340	>0,75	<3	0,13	0,01	+0,26	-0,12
0,1fр, МПаf12,0	3-7	0,15	-0,01	+0,15	-0,30
	>7	0,19	0,01	+0,65	-0,31
	0,74-1,00 (смеси с H2S)	0,1-11	2,10	-0,66	+0,06	-3,10
УС AGA8-92DC	20fНс.в, МДж/м3f48	<0,70	<3	0,10	-0,01	+0,03	-0,06
3-7	0,11	-0,01	+0,15	-0,06
>7	0,12	0,02	+0,19	-0,04
0,66frс, кг/м3f1,05	0,70 – 0,75	<3	0,12	-0,01	+0,08	-0,18
0fxа, мол.%f15	3-7	0,15	-0,03	+0,11	-0,43
0fxy, мол.%f15	>7	0,19	0,01	+0,16	-0,37
250fТ, Кf340	>0,75	<3	0,12	0,01	+0,25	-0,11
0,1fр, МПаf12,0	3-7	0,15	-0,02	+0,24	-0,24
	>7	0,17	0,01	+0,31	-0,17
	0,74-1,00 (смеси с H2S)	0,1-11	1,30	-0,38	+0,06	-1,88
УС ВНИЦСМВ	20fНс.в, МДж/м3f48	<0,70	<3	0,11	-0,04	+0,01	-0,10
	3-7	0,12	-0,04	+0,05	-0,11
	>7	0,12	-0,01	+0,06	-0,14
0,66frс, кг/м3f1,05	0,70 – 0,75	<3	0,12	-0,03	+0,08	-0,17
0fxа, мол.%f15	3-7	0,15	-0,02	+0,11	-0,33
0fxy, мол.%f15	>7	0,18	0,02	+0,13	-0,27
250fТ, Кf340	>0,75	<3	0,13	-0,01	+0,25	-0,11
0,1fр, МПаf12,0	3-7	0,15	-0,01	+0,18	-0,25
	>7	0,24	-0,01	+0,28	-0,33
	0,74-1,00 (смеси с H2S)	0,1-11	0,36	0,10	+0,54	-0,24
Примечания: 1 При использовании методов расчета NX19 мод. и УС GERG-91 мод. высшую удельную теплоту сгорания (Нс.в.) вычисляют по формуле (52) ГОСТ 30319.1. 2 При использовании методов расчета УС AGA8-92DC и УС ВНИЦ СМВ плотность газа при стандартных условиях (rс) вычисляют по формуле (16) ГОСТ 30319.1, а высшую удельную теплоту сгорания (Нс.в.) – по 7.2 ГОСТ 30319.1 (допускается вычислять Нс.в по формуле (52) ГОСТ 30319.1).

Для расчета коэффициента сжимаемости природного газа при определении его расхода и количества рекомендуется применять:

1) модифицированный метод NX19 мод.- при распределении газа потребителям;

2) модифицированное уравнение состояния (УС) GERG-91 мод. [13, 14] и УС AGA8-92DC [15] – при транспортировании газа по магистральным газопроводам;

3) уравнение состояния ВНИЦСМВ – при добыче и переработке газа». Погрешность расчета коэффициента сжимаемости d приведена в таблице 1 без учета погрешности исходных данных.

Метод NX19 мод. и уравнение состояния GERG-91 мод. могут быть использованы при неизвестном полном компонентном составе природного газа, расчет по этим методам не требует применения ЭВМ.

Расчет по уравнениям состояния AGA8-92DC и ВНИЦ СМВ может быть осуществлен только при наличии ЭВМ и известном полном компонентном составе природного газа, при этом должны быть выдержаны следующие диапазоны концентраций компонентов (в мол. %):

метан 65 – 100 этан f 15

пропан f 3,5 бутаны f 1,5

азот f 15 диоксид углерода f 15

сероводород f 30 (УС ВНИЦ СМВ) и f 0,02 (УС AGA8-92DC)

остальные f 1

В области давлений (12 – 30) МПа и температур (260 – 340) К для расчета коэффициента сжимаемости допускается применять уравнения состояния GERG-91 мод. и AGA8-92DC. Погрешность расчета коэффициента сжимаемости природного газа в указанной области давлений и температур составляет: для уравнения GERG-91 мод. – 3,0 % [14], для уравнения AGA8-92DC – 0,5 % [15].

Выбор конкретного метода расчета коэффициента сжимаемости допускается определять в контракте между потребителем природного газа и его поставщиком с учетом требований настоящего стандарта.

В таблице 1 приняты следующие обозначения:

1) dсист – систематическое отклонение от экспериментальных данных

, (2)

2) diмакс – максимальное отклонение в i-й точке экспериментальных данных

, (3)

где Красч и Кэксп – соответственно расчетный и экспериментальный коэффициенты сжимаемости;

3) d – погрешность расчета коэффициента сжимаемости по ИСО 5168 [16]

, (4)

где dст – стандартное отклонение, которое вычисляется из выражения

, (5)

dэксп – погрешность экспериментальных данных (0,1 %).

(Измененная редакция, Изм. № 1).

3.2.2 Модифицированный метод NX19 мод.

В соответствии с требованиями стандарта Германии [17] расчет фактора сжимаемости по модифицированному методу NX19 мод. основан на использовании уравнения следующего вида

, (6)

где , (7)

, (8)

, (9)

, (10)

, (11)

Корректирующий множитель F в зависимости от интервалов параметров ра и DТа вычисляют по формулам:

при 0 f ра f 2 и 0 f DТа f 0,3

, (12)

при 0 f ра< 1,3 и -0,25 f DТа < 0

, (13)

при 1,3 f ра< 2 и -0,21 f DТа < 0

, (14)

где DTa = Ta – 1,09.

Параметры рa и Тa определяются по следующим соотношениям:

, (15)

, (16)

где рпк и Тпк – псевдокритические значения давления и температуры, определяемые по формулам (48) и (49) ГОСТ 30319.1, а именно:

, (17)

. (18)

В формулах (17), (18) вместо молярных долей диоксида углерода и азота допускается применять их объемные доли (ry и ra).

Коэффициент сжимаемости природного газа вычисляют по формуле (1), при этом фактор сжимаемости при рабочих условиях рассчитывают по формулам (6) – (18) настоящего стандарта, а фактор сжимаемости при стандартных условиях – по формуле (24) ГОСТ 30319.1

(Измененная редакция, Изм. № 1).

3.2.3 Модифицированное уравнение состояния GERG-91 мод.

Европейская группа газовых исследований на базе экспериментальных данных, собранных в [12], и уравнения состояния вириального типа [18], разработала и опубликовала в [13, 14] УС

, (19)

где Вm и Сm – коэффициенты УС;

rм – молярная плотность, кмоль/м3.

Коэффициенты уравнения состояния определяют из следующих выражений:

, (20)

, (21)

где хэ – молярная доля эквивалентного углеводорода

хэ = 1 – ха – ху, (22)

, (23)

, (24)

, (25)

, (26)

, (27)

, (28)

, (29)

, (30)

, (31)

, (32)

. (33)

В формулах (23), (27) Н рассчитывают по выражению

, (34)

где Мэ – молярная масса эквивалентного углеводорода, значение которой определяется из выражения

, (35)

В выражении (35) молярную долю эквивалентного углеводорода (xэ) рассчитывают с использованием формулы (22), а фактор сжимаемости при стандартных условиях (zс) рассчитывают по формуле (24) ГОСТ 30319.1, а именно

, (36)

После определения коэффициентов уравнения состояния (19) Вm и Сm рассчитывают фактор сжимаемости при заданных давлении (р, МПа) и температуре (Т, К) по формуле

, (37)

где

, (38)

, (39)

, (40)

, (41)

С0 = b2Cm, (42)

, (43)

Коэффициент сжимаемости природного газа рассчитывают по формуле (1), а именно

, (44)

Фактор сжимаемости при стандартных условиях zс рассчитывают по формуле (36).

(Измененная редакция, Изм. № 1).

3.2.4 Уравнение состояния AGA8-92DC

В проекте стандарта ISO/TC 193 SC1 № 62 [15] Американской Газовой Ассоциацией для расчета фактора сжимаемости предложено использовать уравнение состояния

, (45)

где В и Сn* – коэффициенты УС;

rм – молярная плотность, кмоль/м3.

Константы {bn, cn, kn} УС (45) приведены в таблице A.1.

Если состав газа задан в объемных долях, то молярные доли рассчитываются по формуле (12) ГОСТ 30319.1.

Приведенную плотность определяют по формуле

, (46)

Параметр Кт вычисляют по формуле (53).

Коэффициенты УС рассчитывают из следующих соотношений:

, (47)

, (48)

где N – количество компонентов в природном газе.

Константы {an, un, gn, qn, fn} и характерные параметры компонентов {Еi, Кi, Gi, Qi, Fi} в формулах (47), (48) приведены соответственно в таблицах А.1 и А.2.

Бинарные параметры {Eij, Gij} и параметры {U, G, Km, Q, F} рассчитывают с использованием следующих уравнений:

, (49)

(i ¹ j)

, (50)

(i ¹ j)

, (51)

, (52)

, (53)

, (54)

, (55)

где {Eij*, Gij*, Uij*, Kij*} – параметры бинарного взаимодействия, которые даны в таблице А.3.

Параметры бинарного взаимодействия, которые не приведены в этой таблице, а также при i=j, равны единице.

Для расчета фактора сжимаемости по уравнению состояния (45) необходимо определить плотность rм при заданных давлении (р, МПа) и температуре (Т, К).

Плотность rм из УС (45) определяют по методу Ньютона в следующем итерационном процессе:

1) начальную плотность определяют по формуле

, (56)

где приведенное давление вычисляют из выражения

, (57)

2) плотность на k-м итерационном шаге определяют из выражений

. (58)

, (59)

где z(k-1) – рассчитывают из УС (45) при плотности на итерационном шаге (k-1), т.е. при rм(k-1), а безразмерный комплекс А1 определяют из выражения

,(60)

при этом rп = Кт3rм(k-1);

4) критерий завершения итерационного процесса

, (61)

если критерий (61) не выполняется, то необходимо продолжить итерационный процесс, начиная с пункта 2) алгоритма.

После определения фактора сжимаемости при рабочих и стандартных условиях по формуле (1) рассчитывают коэффициент сжимаемости.

(Измененная редакция, Изм. № 1).

3.2.5 Уравнение состояния ВНИЦ СМВ

Во Всероссийском научно-исследовательском центре стандартизации, информации и сертификации сырья, материалов и веществ (ВНИЦ СМВ) для расчета фактора сжимаемости природного газа разработано уравнение состояния

, (62)

где ckl – коэффициенты УС;

rп = rм/rпк – приведенная плотность;

Тп = Т/Тпк – приведенная температура;

rм – молярная плотность, кмоль/м3;

rпк и Тпк – псевдокритические параметры природного газа.

Коэффициенты УС определяют по формуле

, (63)

где {akl, bkl} – обобщенные коэффициенты УС, которые приведены в таблице Б.1.

Псевдокритические параметры природного газа и его фактор Питцера вычисляют по формулам:

– псевдокритическую плотность

, (64)

где , (65)

(; )

– псевдокритическую температуру

, (66)

где , (67)

; (68)

(; )

– фактор Питцера

, (69)

где , (70)

В соотношениях (64) – (70) N – число основных компонентов природного газа (метана, этана, пропана, н-бутана, и-бутана, азота, диоксида углерода, сероводорода).

Критические параметры компонентов {rкi, rкj, Ткj, Ткj}, их молярная масса {Мi, Мj,} и факторы Питцера {Wi, Wj} приведены в таблице Б.2, а параметры бинарного взаимодействия {xij, lij} – в таблицах Б.3 и Б.4.

Если заданный компонентный состав природного газа включает, кроме основных, другие компоненты (но не более 1 % в сумме), то молярные доли этих компонентов прибавляют к соответствующим долям основных компонентов следующим образом:

– ацетилен и этилен к этану;

– пропилен к пропану;

– углеводороды от н-пентана и выше к н-бутану;

– прочие компоненты к азоту.

Если состав газа задан в объемных долях, то молярные доли рассчитывают по формуле (12) ГОСТ 30319.1.

Для расчета фактора сжимаемости по уравнению состояния (62) необходимо определить плотность rм при заданных давлении (р, МПа) и температуре (Т, К).

Плотность rм из УС (62) определяют по методу Ньютона в следующем итерационном процессе:

1) начальную плотность определяют по формуле

, (75)

где приведенное давление вычисляют из выражений

, (76)

, (77)

а псевдокритические плотность (rпк), температуру (Тпк) и фактор Питцера (W) рассчитывают по формулам (64), (66) и (69);

2) плотность на k-м итерационном шаге определяется из выражений

, (78)

, (79)

где z(k-1) рассчитывают из УС (62) при плотности на итерационном шаге (k-1), т.е. при rм(k-1), a безразмерный комплекс A1 определяют из выражения

, (80)

4) критерий завершения итерационного процесса.

, (81)

если критерий (81) не выполняется, то необходимо продолжить итерационный процесс, начиная с пункта 2) алгоритма.

(Измененная редакция, Изм. № 1).

При измерении расхода и количества природного газа, транспортируемого в газопроводах, давление (р), температуру (T), плотность при стандартных условиях (rc) и состав (хi) измеряют с определенной погрешностью. Перечисленные параметры являются исходными данными для расчета коэффициента сжимаемости.

В соответствии с рекомендациями ИСО 5168 [16] погрешность расчета коэффициента сжимаемости, которая появляется в связи с погрешностью измерения исходных данных, определяют по формуле

, (82)

где dид – погрешность расчета коэффициента сжимаемости, связанная с погрешностью измерения исходных данных;

dqk – погрешность измерения параметра исходных данных;

, (83)

, (84)

В формулах (82) – (84):

qk – условное обозначение k-го параметра исходных данных (р. Т, rc, хi,);

`qk – среднее значение k-го параметра в определенный промежуток времени (сутки, месяц, год и т.д.);

qkмакс и qkмин – максимальное и минимальное значения k-го параметра в определенный промежуток времени;

Nq – количество параметров исходных данных.

При вычислении частных производных по формуле (83) коэффициенты сжимаемости Кqk+ и Кqk- – рассчитывают при средних параметрах и параметрах и соответственно. Рекомендуется выбирать

Коэффициент сжимаемости `К (среднее значение) рассчитывают по выбранному рекомендуемому методу расчета при средних параметрах qk.

Для методов:

1) NX 19 мод. и УС GERG-91 мод. – Nq = 5 и параметрами исходных данных являются давление, температура, плотность при стандартных условиях, молярные доли азота и диоксида углерода;

2) УС AGA8-92DC и УС ВНИЦ СМВ – Nq = 2 + N (N – количество компонентов) и параметрами исходных данных являются давление, температура и молярные доли компонентов природного газа, причем для УС ВНИЦ СМВ учитываются молярные доли только основных компонентов газа.

Общую погрешность расчета коэффициента сжимаемости определяют по формуле

, (85)

где d – погрешность расчета коэффициента сжимаемости, которая для каждого метода приведена в 3.2.1.

Для методов NX19 мод. и УС GERG-91 мод. допускается рассчитывать погрешность dи.д по формуле

, (86)

где dТ, dp, drc, dxa и dxy – погрешности измеряемых параметров, соответственно, температуры, давления, плотности природного газа при стандартных условиях, содержания азота и диоксида углерода в нем.

Коэффициенты КT, Кр, Кrc, Кxa и Кxу в зависимости от метода, используемого для расчета коэффициента сжимаемости K, определяются по следующим выражениям (см. формулы (34) – (38) или (39) – (43) ГОСТ 30319.1):

– при расчете К по методу NX19 мод.

, (87)

, (88)

, (89)

, (90)

, (91)

– при расчете К по методу GERG-91

, (92)

, (93)

, (94)

, (95)

. (96)

(Измененная редакция, Изм. № 1).

Расчет коэффициента сжимаемости природного газа по указанным в стандарте методам реализован на ПЭВМ, совместимых с IBM PC/AT/XT, на языке программирования ФОРТРАН-77. Листинг программы приведен в приложении В.

В приложениях Г и Д приведены примеры расчета соответственно коэффициента сжимаемости и погрешности вычисления коэффициента сжимаемости, которая вызвана погрешностью определения исходных данных.

ПРИЛОЖЕНИЕ А

(обязательное)

Таблица А.1 – Константы уравнения состояния AGA8-92DC

п	ап	bn	cn	kn	un	gn	qn	fn
1	0,153832600	1	0	0	0,0	0	0	0
2	1,341953000	1	0	0	0,5	0	0	0
3	-2,998583000	1	0	0	1,0	0	0	0
4	-0,048312280	1	0	0	3,5	0	0	0
5	0,375796500	1	0	0	-0,5	1	0	0
6	-1,589575000	1	0	0	4,5	1	0	0
7	-0,053588470	1	0	0	0,5	0	1	0
8	2,29129Е-9	1	1	3	-6,0	0	0	1
9	0,157672400	1	1	2	2,0	0	0	0
10	-0,436386400	1	1	2	3,0	0	0	0
11	-0,044081590	1	1	2	2,0	0	1	0
12	-0,003433888	1	1	4	2,0	0	0	0
13	0,032059050	1	1	4	11,0	0	0	0
14	0,024873550	2	0	0	-0,5	0	0	0
15	0,073322790	2	0	0	0,5	0	0	0
16	-0,001600573	2	1	2	0,0	0	0	0
17	0,642470600	2	1	2	4,0	0	0	0
18	-0,416260100	2	1	2	6,0	0	0	0
19	-0,066899570	2	1	4	21,0	0	0	0
20	0,279179500	2	1	4	23,0	1	0	0
21	-0,696605100	2	1	4	22,0	0	1	0
22	-0,002860589	2	1	4	-1,0	0	0	1
23	-0,008098836	3	0	0	-0,5	0	1	0
24	3,150547000	3	1	1	7,0	1	0	0
25	0,007224479	3	1	1	-1,0	0	0	1
26	-0,705752900	3	1	2	6,0	0	0	0
27	0,534979200	3	1	2	4,0	1	0	0
28	-0,079314910	3	1	3	1,0	1	0	0
29	-1,418465000	3	1	3	9,0	1	0	0
30	-5,99905Е-17	3	1	4	-13,0	0	0	1
31	0,105840200	3	1	4	21,0	0	0	0
32	0,034317290	3	1	4	8,0	0	1	0
33	-0,007022847	4	0	0	-0,5	0	0	0
34	0,024955870	4	0	0	0,0	0	0	0
35	0,042968180	4	1	2	2,0	0	0	0
36	0,746545300	4	1	2	7,0	0	0	0
37	-0,291961300	4	1	2	9,0	0	1	0
38	7,294616000	4	1	4	22,0	0	0	0
39	-9,936757000	4	1	4	23,0	0	0	0
40	-0,005399808	5	0	0	1,0	0	0	0
41	-0,243256700	5	1	2	9,0	0	0	0
42	0,049870160	5	1	2	3,0	0	1	0
43	0,003733797	5	1	4	8,0	0	0	0
44	1,874951000	5	1	4	23,0	0	1	0
45	0,002168144	6	0	0	1,5	0	0	0
46	-0,658716400	6	1	2	5,0	1	0	0
47	0,000205518	7	0	0	-0,5	0	1	0
48	0,009776195	7	1	2	4,0	0	0	0
49	-0,020487080	8	1	1	7,0	1	0	0
50	0,015573220	8	1	2	3,0	0	0	0
51	0,006862415	8	1	2	0,0	1	0	0
52	-0,001226752	9	1	2	1,0	0	0	0
53	0,002850906	9	1	2	0,0	0	1	0

Таблица А.2 – Характерные параметры компонентов

Компонент	Молярная масса	Характерные параметры
Е, К	К, м3/кмоль	G	Q	F
Метан	16,0430	151,3183	0,4619255	0,0	0,0	0,0
Этан	30,0700	244,1667	0,5279209	0,079300	0,0	0,0
Пропан	44,0970	298,1183	0,5837490	0,141239	0,0	0,0
н-Бутан	58,1230	337,6389	0,6341423	0,281835	0,0	0,0
и-Бутан	58,1230	324,0689	0,6406937	0,256692	0,0	0,0
Азот	28,0135	99,73778	0,4479153	0,027815	0,0	0,0
Диоксид углерода	44,0100	241,9606	0,4557489	0,189065	0,69	0,0
Сероводород	34,0820	296,3550	0,4618263	0,088500	0,0	0,0
н-Пентан	72,1500	370,6823	0,6798307	0,366911	0,0	0,0
и-Пентан	72,1500	365,5999	0,6738577	0,332267	0,0	0,0
н-Гексан	86,1770	402,8429	0,7139987	0,432254	0,0	0,0
н-Гептан	100,2040	427,5391	0,7503628	0,512507	0,0	0,0
н-Октан	114,2310	450,6472	0,7851933	0,576242	0,0	0,0
Гелий	4,0026	2,610111	0,3589888	0,0	0,0	0,0
Моноксид углерода	28,0100	105,5348	0,4533894	0,038953	0,0	0,0
Кислород	31,9988	122,7667	0,4186954	0,021000	0,0	0,0
Аргон	39,9480	119,6299	0,4216551	0,0	0,0	0,0
Вода	18,0153	514,0156	0,3825868	0,332500	0,0	0,0

Таблица А.3 – Параметры бинарного взаимодействия

Компоненты	Параметры бинарного взаимодействия
i	J	Eij*	Uij	Kij	Gij*
Метан	Азот	0,971640	0,886106	1,003630
Диоксид углерода	0,960644	0,963827	0,995933	0,807653
Пропан	0,996050	1,023960
Моноксид углерода	0,990126
и-Бутан	1,019530
н-Бутан	0,995474	1,021280
и-Пентан	1,002350
н-Пентан	1,003050
н-Гексан	1,012930
Н-Гептан	0,999758
н-Октан	0,988563
Азот	Диоксид углерода	1,022740	0,835058	0,982361	0,982746
Этан	0,970120	0,816431	1,007960
Пропан	0,945939	0,915502
Моноксид углерода	1,005710
и-Бутан	0,946914
н-Бутан	0,973384	0,993556
и-Пентан	0,959340
н-Пентан	0,945520
н-Гексан	0,937880
н-Гептан	0,935977
н-Октан	0,933269
Диоксид углерода	Этан	0,925053	0,969870	1,008510	0,370296
Пропан	0,960237
Моноксид углерода	1,500000	0,900000
и-Бутан	0,906849
н-Бутан	0,897362
и-Пентан	0,726255
н-Пентан	0,859764
н-Гексан	0,766923
н-Гептан	0,782718
н-Октан	0,805823
Этан	Пропан	1,035020	1,080500	1,000460
и-Бутан		1,250000
н-Бутан	1,013060	1,250000
и-Пентан		1,250000
н-Пентан	1,005320	1,250000
Пропан	н-Бутан	1,004900

ПРИЛОЖЕНИЕ Б

(обязательное)

Таблица Б.1 – Обобщенные коэффициенты уравнения состояния ВНИЦ СМВ

k	l	akl	bkl	k	l	akl	bkl
1	0	6,087766 – 10-1	-7,187864 – 10-1	8	2	4,015072 -10-1	-9,576900 – 100
2	0	-4,596885 -10-1	1,067179 – 101	9	2	-1,016264 – 10-1	2,419650 – 100
3	0	1,149340 – 100	-2,576870 – 101	10	2	-9,129047 – 10-3	2,275036 – 10-1
4	0	-6,075010 – 10-1	1,713395 – 101	1	3	-2,837908 – 100	1,571955 – 101
5	0	-8,940940 – 10-1	1,617303 – 101	2	3	1,534274 – 101	-3,020599 – 102
6	0	1,144404 – 100	-2,438953 – 101	3	3	-2,771885 – 101	6,845968 – 102
7	0	-3,457900 – 10-1	7,156029 – 100	4	3	3,511413 – 101	-8,281484 – 102
8	0	-1,235682 – 10-1	3,350294 – 100	5	3	-2,348500 – 101	5,600892 – 102
9	0	1,098875 – 10-1	-2,806204 – 100	6	3	7,767802 – 100	-1,859581 – 102
10	0	-2,193060 – 10-2	5,728541 – 10-1	7	3	-1,677977 – 100	3,991057 – 101
1	1	-1,832916 – 100	6,057018 – 100	8	3	3,157961 – 10-1	-7,567516 – 100
2	1	4,175759 – 100	-7,947685 – 101	9	3	4,008579 – 10-3	-1,062596 – 10-1
3	1	-9,404549 – 100	2,167887 – 102	1	4	2,606878 – 100	-1,375957 – 101
4	1	1,062713 – 101	-2,447320 – 102	2	4	-1,106722 – 101	2,055410 – 102
5	1	-3,080591 – 100	7,804753 – 101	3	4	1,279987 – 101	-3,252751 – 102
6	1	-2,122525 – 100	4,870601 – 101	4	4	-1,211554 – 101	2,846518 – 102
7	1	1,781466 – 100	-4,192715 – 101	5	4	7,580666 – 100	-1,808168 – 102
8	1	-4,303578 – 10-1	1,000706 – 101	6	4	-1,894086 – 100	4,605637 – 101
9	1	-4,963321 – 10-2	1,237872 – 100	1	5	-1,155750 – 100	6,466081 – 100
10	1	3,474960 – 10-2	-8,610273 – 10-1	2	5	3,601316 – 100	-5,739220 – 101
1	2	1,317145 – 100	-1,295347 – 101	3	5	-7,326041 – 10-1	3,694793 – 101
2	2	-1,073657 – 101	2,208390 – 102	4	5	-1,151685 – 100	2,077675 – 101
3	2	2,395808 – 101	-5,864596 – 102	5	5	5,403439 – 10-1	-1,256783 – 101
4	2	-3,147929 – 101	7,444021 – 102	1	6	9,060572 – 10-2	-9,775244 – 10-1
5	2	1,842846 – 101	-4,470704 – 102	2	6	-5,151915 – 10-1	2,612338 – 100
6	2	-4,092685 – 100	9,965370 – 101	3	6	7,622076 – 10-2	-4,059629 – 10-1
7	2	-1,906595 – 10-1	5,136013 – 100	1	7	4,507142 – 10-2	-2,298833 – 10-1

Таблица Б.2 – Физические свойства компонентов природного газа, используемые в уравнении состояния ВНИЦ СМВ

Компоненты	Химическая формула	Молярная масса Мi	Критические параметры	rci, кг/м3	Фактор Питцера Wi
pki, МПа	rki, кг/м3	Tki, K	zki,
Метан	СН4	16,043	4,5988	163,03	190,67	0,2862	0,6682	0,0006467
Этан	С2Н6	30,070	4,88	205,53	305,57	0,2822	1,2601	0,1103
Пропан	С3Н8	44,097	4,25	218,54	369,96	0,2787	1,8641	0,1764
н-Бутан	н-С4Н10	58,123	3,784	226,69	425,40	0,2761	2,4956	0,2213
и-Бутан	и-С4Н10	58,123	3,648	225,64	407,96	0,2769	2,488	0,2162
Азот	N2	28,0135	3,390	315,36	125,65	0,2850	1,16490	0,04185
Диоксид углерода	СО2	44,010	7,386	466,74	304,11	0,2744	1,8393	0,2203
Сероводород	H2S	34,082	8,940	349,37	373,18	0,2810	1,4311	0,042686
Примечания 1 Плотность (rki), температура (Tki) в критической точке и фактор Питцера (Wi) отличаются от литературных данных и применимы только для уравнения состояния ВНИЦ СМВ. 2 rci – плотность i-го компонента при стандартных условиях

Таблица Б.3 – Параметры бинарного взаимодействия xij

j	i
СН4	C2H6	С3Н8	н-C4H10	и-С4Н10	N2	CO2	H2S
СН4	0,0	0,036	0,076	0,121	0,129	0,060	0,074	0,089
C2H6	–	0,0	0,0	0,0	0,0	0,106	0,093	0,079
С3Н8	–	–	0,0	0,0	0,0	0,0	0,0	0,0
н-C4Н10	–	–	–	0,0	0,0	0,0	0,0	0,0
и-С4Н10	–	–	–	–	0,0	0,0	0,0	0,0
N2	–	–	–	–	–	0,0	0,022	0,211
CO2	–	–	–	–	–	–	0,0	0,089
H2S	–	–	–	–	–	–	–	0,0

Таблица Б.4 – Параметры бинарного взаимодействия lij

j	i
СН4	С2Н6	С3Н8	н-С4Н10	и-C4H10	N2	СО2	H2S
СН4	0,0	-0,074	-0,146	-0,258	-0,222	-0,023	-0,086	0,0
С2Н6	–	0,0	0,0	0,0	0,0	0,0	0,0	0,0
С3Н8	–	–	0,0	0,0	0,0	0,0	0,0	0,0
н-C4H10	–	–	–	0,0	0,0	0,0	0,0	0,0
и-С4Н10	–	–	–	–	0,0	0,0	0,0	0,0
N2	–	–	–	–	–	0,0	-0,064	0,0
СО2	–	–	–	–	–	–	0,0	-0,062
H2S	–	–	–	–	–	–	–	0,0

ПРИЛОЖЕНИЕ В

(рекомендуемое)

C **********************************************************

C * *

С * Программа расчета коэффициента сжимаемости природного газа *

С * (основной модуль) *

С * *

C **********************************************************

IMPLICIT REAL*8(A-H,O-Z)

CHARACTER*26 AR(25)

DIMENSION PI(100),TI(100),ZP(100,100)

COMMON/P/P/T/T/RON/RON/YI/YC(25)/Z/Z/NPR/NPR

DATA AR/’ метана (СН4)’,’ этана (С2Н6)’,’ пропана (С3Н8)’,

*’ н-бутана (н-С4Н10)’,’ и-бутана (и-С4Н10)’,’ азота (N2)’,

*’ диоксида углерода (СO2)’,’ сероводорода (H2S)’,

*’ ацетилена (С2Н2)’,’ этилена (С2Н4)’,’ пропилена (С3Н6)’,

*’ н-пентана (н-С5Н12)’,’ и-пентана (и-C5H12)’,

*’ нео-пентана (нео-С5Н12)’,’ н-гексана (н-С6Н14)’,

*’ бензола (С6Н6)’,’ н-гептана (н-С7Н16)’,’ толуола (С7Н8)’,

*’ н-октана (н-С8Н18)’,’ н-нонана (н-С9Н20)’,

*’ н-декана (н-С10Н22)’,’ гелия (Не)’,’ водорода (Н2)’,

*’ моноксида углерода (СО)’,’ кислорода (О2)’/

200 WRITE(*,100)

CALL VAR(NVAR)

IF(NVAR.EQ.5) GO TO 134

WRITE(*,l00)

100 FORMAT(25(/))

WRITE(*,1)

1 FORMAT(’ Введите исходные данные для расчета.’/)

IF(NVAR.LE.2) THEN

WRITE(*,’(A)’)

*’ Плотность при 293.15 К и 101.325 кПа, в кг/куб.м ’

READ(*,*)RON

WRITE(*,53)

53 FORMAT(’ Введите 0, если состав азота и диоксида углерода’,

*’ задан в молярных долях’/

*’ или 1, если состав этих компонентов задан’,

*’ в объемных долях ’)

READ(*,*)NPR

IF(NPR.EQ.0) WRITE(*,3)

3 FORMAT (’ Значение молярной доли, в мол. %’)

IF(NPR.EQ.l) WRITE(*,33)

33 FORMAT(’ Значение объемной доли, в об. %’)

WRITE(*,’(A)’) ’ азота (N2)

READ(*,*)YA

YA = YA/100.

WRITE(*,’(A)’) ’ диоксида углерода (С02) ’

READ(*,*)YY

YY = YY/100.

ELSE

WRITE(*,35)

35 FORMAT(’ Введите 0, если состав задан в молярных долях’/

*’ или 1, если состав задан в объемных долях ’)

READ(*,*)NPR

IF(NPR.EQ.0) WRITE(*,3)

IF(NPR.EQ.l) WRITE(*,33)

DO 5 I=1,25

WRITE(*,’(A)’) AR(I)

READ(*,*)YC(I)

5 YC(I) = YC(I)/100.

ENDIF

WRITE(*,’(A)’)

*’ Введите количество точек по давлению: ’

READ(*,*)NP

WRITE(*,’(A)’)

*’ Введите количество точек по температуре: ’

READ(*,*)NT

WRITE(*,’(A)’)

*’ Введите значения давлений в МПа: ’

READ(*,*)(PI(I),I=1,NP)

WRITE(*,’(A)’)

*’ Введите значения температур в К: ’

READ(*,*)(TI(I),I=1,NT)

WRITE(*,’(A)’)

*’ Ввод исходных данных завершен. ’

P=.101325D0

T=293.15D0

ICALC=1

GO TO (10,20,30,40) NVAR

10 CALL NX19(YA,YY)

ZN=Z

GO TO 50

20 CALL GERG2(ICALC,YA,YY)

ZN=Z

GO TO 50

30 CALL AGA8DC(ICALC)

ZN=Z

GO TO 50

40 CALL VNIC(ICALC)

ZN=Z

50 CONTINUE

IF(Z.EQ.0D0) THEN

CALL RANGE(NRANGE)

IF(NRANGE) 134,134,200

ENDIF

ICALC=2

NTS=0

DO 7 I=1,NP

P=PI(I)

D07 J=1,NT

T=TI(J)

IF(NVAR.EQ.l) CALL NX19(YA,YY)

IF(NVAR.EQ.2) CALL GERG2(ICALC,YA,YY)

IF(NVAR.EQ.3) CALL AGA8DC(ICALC)

IF(NVAR.EQ.4) CALL VNIC(ICALC)

IF(Z.NE.0D0) NTS=NTS+1

ZP(I,J)=Z/ZN

7 CONTINUE

IF(NTS.EQ.0) THEN

CALL RANGE(NRANGE)

IF (NRANGE) 134,134,200

ELSE

I=1

9 IС=0

DO 11 J=1,NT

IF(ZP(I,J).EQ.0D0)

IC=IC+1

11 CONTINUE

IF(IC.EQ.NT) THEN

IF(I.NE.NP) THEN

DO 13 J=I,NP-1

PI(J)=PI(J+1)

DO 13 K=1,NT

13 ZP(J,K)=ZP(J+1,K)

ENDIF

NP=NP-1

ELSE

I=I+1

ENDIF

IF(I.LE.NP) GO TO 9

J=l

15 JS=0

DO 17 I=1,NP

IF(ZP(I,J).EQ.0D0) JS=JS+1

17 CONTINUE

IF(JS.EQ.NP) THEN

IF(J.NE.NT) THEN

DO 19 I=J,NT-1

ТI(I)=ТI(I+1)

DO 19 K=1,NP

19 ZP(K,I)=ZP(K,I+1)

ENDIF

NT=NT-1

ELSE

J=J+1

ENDIF

IF(J.LE.NT) GO TO 15

CALL TABL(YA,YY,PI,TI,ZP,NP,NT,NVAR,AR)

ENDIF

GO TO 200

134 STOP

END

SUBROUTINE VAR(NVAR)

WRITE(*,1)

1 FORMAT(//

*10X,’ Расчет коэффициента сжимаемости природного газа’//

*10Х,’ —————-Метод расчета—————– ’/

*10Х,’ ’/

*10Х,’ 1. Модифицированный метод NX 19 ’/

*10Х,’ ’/

*10Х,’ 2. Уравнение состояния GERG-91 ’/

*10Х,’ ’/

*10Х,’ 3. Уравнение состояния AGA8-92DC ’/

*10Х,’ ’/

*10Х,’ 4. Уравнение состояния ВНИЦ СМВ ’/

*10Х,’ ’/

*10Х,’—————————————————’/)

WRITE(*,5)

5 FORMAT(/,3X,

*’Введите порядковый номер метода расчета или 5 для выхода в ДОС’,

READ(*,*)NVAR

RETURN

END

SUBROUTINE RANGE(NRANGE)

IMPLICIT REAL*8(A-H,О-Z)

COMMON/Z/Z

WRITE(*,1)

1 FORMAT(//

*’ Выбранная Вами методика при заданных параметрах «не работает»’/

*’ Продолжить работу программы ? 0 – нет, 1 – да ’)

READ(*,*)NRANGE

RETURN

END

SUBROUTINE TABL(YA,YY,PI,TI,ZP,NP,NT,NVAR,AR)

IMPLICIT REAL*8(A-H,О-Z)

CHARACTER*26 AR(25), FNAME

CHARACTER METH(4)*31,A*6,LIN1(5)*9,LIN2(5)*9,LIN3(6)*9,LIN4*9,

*AT(06)*28

CHARACTER*70 F,FZ(11,2)

DIMENSION PI(100),TI(100),ZP(100,100),ZPP(6)

COMMON/RON/RON/YI/YC(25)/NPR/NPR

DATA METH/

*’(модифицированный метод NX19)’,

*’(уравнение состояния GERG-91)’,

*’(уравнение состояния AGA8-92DC)’,

*’(уравнение состояния ВНИЦ СМВ)’/

DATA LIN1/5*’——’/,LIN2/5*’——’/,LIN3/6*’——’/,

*LIN4/’——’/,A/’ – ’/

DATA AT/

*’ T, K’,’ T, K’,’ T, K’,’ T,K’,

*’ T, K’,’ T, K’/

DATA FZ/

*’(3X,F5.2,2X,6(3X,F6.4))’,’(3X,F5.2,5X,A6,5(3X,F6.4))’,

*’(3X,F5.2,2X,2(3X,A6),4(3X,F6.4))’,’(3X,F5.2,2X,3(3X,A6),

*3(3X,F6.4))’,

*’(3X,F5.2,2X,4(3X,A6),2(3X,F6.4))’,’(3X,F5.2,2X,5(3X,A6),

*3X,F6.4)’,

*’(3X,F5.2,2X,5(3X,F6.4),3X,A6)’,’(3X,F5.2,2X,4(3X,F6.4),

*2(3X,A6))’,

*’(3X,F5.2,2X,3(3X,F6.4),3(3X,A6))’,’(3X,F5.2,2X,2(3X,F6.4),

*4(3X,A6))’,

*’(3X,F5.2,5X,F6.4,5(3X,A6))’,’(3X,F9.6,1X,F6.4,5(3X,F6.4))’,

*’(ЗX,F9.6,lX,A6,5(3X,F6.4))’,’(3X,F9.б,lX,A6,3X,A6,4(3X,F6.4))’,

*’(3X,F9.6,1X,A6,2(3X,A6),3(3X,F6.4))’,’(3X,F9.6,1X,A6,3(3X,A6),

*2(3X,F6.4))’,

*’(3X,F9.6,1X,A6,4(3X,A6),3X,F6.4)’,’(3X,F9.6,1X,F6.4,4(3X,F6.4),

*3X,A6)’,

*’(3X,F9.6,1X,F6.4,3(3X,F6.4),2(3X,A6))’,’(3X,F9.6,1X,F6.4),

*2(3X,F6.4),3(3X,A6))’,

*’(3X,F9.6,1X,F6.4,3X,F6.4,4(3X,A6))’,’(3X,F9.6,1X,F6.4,5(3X,A6))’/

22 WRITE(*,44)

44 FORMAT(//’ Устройство вывода результатов расчета ?,’)

WRITE(*,’(A)’)

*’ 0 – дисплей, 1 – принтер, 2 – файл на диске ’

READ(*,*)NYST

IF(NYST.EQ.0) OPEN(1,FILE=’CON’)

IF(NYST.EQ.l) OPEN(1,FILE=’PRN’)

IF(NYST.EQ.2) WRITE(*,’(A)’) ’ Введите имя файла ’

IF(NYST.EQ.2) READ(*,’(A)’)FNAME

IF(NYST.EQ.2) OPEN(1,FILE=FNAME)

IF(NYST.EQ.0) WRITE(*,100)

100 FORMAT(25(/))

IF(NYST.EQ.l) PAUSE

*’ Включите принтер, вставьте бумагу и нажмите ’

WRITE(1,88)METH(NVAR)

88 FORMAT(

*13X,’Коэффициент сжимаемости природного газа.’/

*18Х,А31/)

NW=3

IF(NVAR.LE.2) THEN

WRITE(1,1)RON

1 FORMAT(’ Плотность при 293.15 К и 101.325 кПа ’,F6.4,’ кг/куб.м’)

NW=NW+1

IF(YA.NE.0D0.OR.YY.NE.0D0) THEN

IF(NPR.EQ.0) WRITE(1,3)

3 FORMAT(’ Содержание в мол. %’)

IF(NPR.EQ.l) WRITE(1,33)

33 FORMAT(’ Содержание в об.%’)

NW=NW+1

IF(YA.NE.0D0) THEN

WRITE(1,5)AR(6),YA* 100.

5 FORMAT(2(A26,F7.4))

NW=NW+1

ENDIF

IF(YY.NE.0D0) THEN

WRITE(1,5)AR(7),YY*100.

NW=NW+1

ENDIF

ELSE

IF(NPR.EQ.0) WRITE(1,3)

IF(NPR.EQ.l) WRITE(1,33)

NW=NW+1

I=1

9 J=I+1

13 CONTINUE

IF(YC(J).NE.0D0) THEN

WRITE(1,5)AR(I),YC(I)*100.,AR(J),YC(J)*100.

NW=NW+1

DO 11 I=J+1,25

IF(YC(I).NE.0D0.AND.I.NE.25) GO TO 9

IF(YC(I).NE.0D0.AND.I.EQ.25) THEN

WRITE(1,5)AR(I),YC(I)*100.

nw=nw+1

GO TO 99

ENDIF

11 CONTINUE

ELSE

J=J+1

IF(J.LE.25) THEN

GO TO 13

ELSE

WRITE(1,5)AR(I),YC(I)*100.

NW=NW+1

ENDIF

99 CONTINUE

IF(NW.GT.12.AND.NYST.EQ.0) THEN

WRITE(*,7)

7 FORMAT(/)

PAUSE ’ Для продолжения вывода нажмите ’

WRITE(*,100)

NW=0

ENDIF

DO 15 I=1,NT,6

IF(NW.GT.12.AND.NYST.EQ.0) THEN

WRITE(*,7)

PAUSE ’ Для продолжения вывода нажмите ’

WRITE(*,100)

NW=0

ENDIF

IF(NW.GT.46.AND.NYST.NE.O) THEN

WRITE(1,7)

WRITE(*,7)

IF(NYST.EQ.l)

PAUSE

*’ Для продолжения вывода вставьте бумагу и нажмите ’

NW=0

ENDIF

IF(I+5.LE.NT) THEN

NL=6

ELSE

NL=NT-I+1

ENDIF

WRITE(1,7)

IF(NL.GT.1) WRITE(1,17)LIN2(1),(LIN1(K),K=1,NL-1)

IF(NL.EQ.l) WRITE(1,17)LIN2(1)

17 FORMAT(’ ——’,6A9)

WRITE(1,19)AT(NL)

19 FORMAT(’ ——’,A28)

IF(NL.GT.1)WRITE(1,21)LIN4,(LIN2(K),K=1,NL-1)

IF(NL.EQ.l) WRITE(1,21)LIN4

21 FORMAT(’ p, МПа ’,6А9)

WRITE(1,23)(TI(K),K=I,I+NL-1)

23 FORMAT(10X,6(:,’|’,F6.2))

WRITE(1,17)(LIN3(K),K=1,NL)

NW=NW+6

DO 25 J=1,NP

JP=1

IF(PI(J).EQ.0.101325D0) JP=2

NL1=0

NLN=0

DO 27K=I,I+NL-1

NL1=NL1+1

IF(ZP(J,K).EQ.0D0) THEN

ZPP(NL1)=A

NLN=NLN+1

ELSE

ZPP(NL1)=ZP(J,K)

ENDIF

27 CONTINUE

IF(NLN.EQ.NL) GO TO 133

IF(NLN.EQ.0) THEN

F=FZ(1,JP)

ELSE

IF(ZP(J,I).EQ.0D0) F=FZ(NLN+1,JP)

IF(ZP(J,I+NL-1).EQ.0D0) F=FZ(NLN+12-NL,JP)

ENDIF

IF(NLI.EQ.1)WRITE(1,F)PI(J),ZPP(1)

IF(NL1.EQ.2)WRITE(1,F)PI(J),ZPP(1),ZPP(2)

IF(NL1.EQ.3)WRITE(1,F)PI(J),ZPP(1),ZPP(2),ZPP(3)

IF(NL1.EQ.4)WRITE(1,F)PI(J),ZPP(1),ZPP(2),ZPP(3),ZPP(4)

IF(NL1.EQ.5)

*WRITE(1,F)PI(J),ZPP(1),ZPP(2),ZPP(3),ZPP(4),ZPP(5)

IF(NL1.EQ.6)

*WRITE(1,F)PI(J),ZPP(1),ZPP(2),ZPP(3),ZPP(4),ZPP(5),ZPP(6)

NW=NW+1

133 CONTINUE

IF(NW.EQ.20.AND.NYST.EQ.0) THEN

IF(J.EQ.NP.AND.I+NL-1.EQ.NT) GO TO 29

WRITE(*,7)

PAUSE ’ Для продолжения вывода нажмите ’

WRITE(*,100)

NW=0

WRITE(1,7)

IF(NL.GT.1)WRITE(1,17)LIN2(1),(LIN1(K),K=1,NL-1)

IF(NL.EQ.l) WRITE(1,17)LIN2(1)

WRITE(1,19)AT(NL)

IF(NL.GT.1)WRITE(1,21)LIN4,(LIN2(K),K=1,NL-1)

IF(NL.EQ.l) WRITE(1,21)LIN4

WRITE(1,23)(TI(K),K=I,I+NL-1)

WRITE(1,17)(LIN3(K),K=1,NL)

NW=NW+6

ENDIF

IF(NW.EQ.54.AND.NYST.NE.0) THEN

IF(J.EQ.NP.AND.I+NL-1.EQ.NT) GO TO 29

WRITE(1,7)

WRITE(*,7)

IF(NYST.EQ.l) PAUSE

*’ Для продолжения вывода вставьте бумагу и нажмите ’

NW=0

IF(NL.GT.1) WRITE(1,17)LIN2(1),(LIN1(K),K=1,NL-1)

IF(NL.EQ.l) WRITE(1,17)LIN2(1)

WRITE(1,19)AT(NL)

IF(NL.GT.1) WRITE(1,21)LIN4,(LIN2(K),K=1,NL-1)

IF(NL.EQ.l) WRITE(1,21)LIN4

WRITE(1,23)(TI(K),K=I,I+NL-1)

WRITE(1,17)(LIN3(K),K=1,NL)

NW=NW+6

ENDIF

25 CONTINUE

15 CONTINUE

29 CLOSE(l)

WRITE(*,7)

PAUSE ’ Вывод завершен, для продолжения работы нажмите ’

WRITE(*,66)

66 FORMAT(/’ Назначить другое устройство вывода ?’,

*’, 0 – нет, 1 – да ’)

READ(*,*)NBOLB

IF(NBOLB.EQ.l) GO TO 22

RETURN

END

C **********************************************************

С * *

С * Подпрограмма расчета коэффициента сжимаемости природного *

С * газа по модифицированному методу NX19. *

C **********************************************************

SUBROUTINE NX19(YA,YY)

IMPLICIT REAL*8(A-H,O-Z)

COMMON/NCONT/NCONT/YA/Y(2)/RON/RON

Y(1)=YA

Y(2)=YY

CALL PTCONT

IF(NCONT.EQ.l) GO TO 134

CALL EA

CALL PHASEA

134 RETURN

END

SUBROUTINE PTCONT

IMPLICIT REAL*8(A-H,O-Z)

COMMON/NCONT/NCONT/Z/Z/P/P/T/T/YA/Y(2)/RON/RON

NCONT=0

IF(RON.LT.0.66D0.OR.RON.GT.1D0) NCONT=1

IF(Y(1).GT.0.2D0.OR.Y(2).GT.0.15D0) NCONT=l

IF(P.LE.0.D0.OR.T.LE.0.D0) NCONT=1

IF(T.LT.250.D0.OR.T.GT.340.D0) NCONT=1

IF(P.GT.12.D0) NCONT=1

IF(NCONT.EQ.1) Z=0D0

RETURN

END

SUBROUTINE EA

IMPLICIT REAL*8(A-H,O-Z)

COMMON/T/T/YA/Y(2)/RON/RON/P/P/PT/PA,TA/BI/B1,B2/T0/T0

PCM=2.9585*(1.608D0-0.05994*RON+Y(2)-.392*Y(1))

TCM=88.25*(0.9915D0+1.759*RON-Y(2)-1.681*Y(1))

PA=0.6714*P/PCM+0.0147

TA=0.71892*T/TCM+0.0007

DTA=TA-1.09D0

F=0D0

IF(PA.GE.0D0.AND.PA.LT.2D0.AND.DTA.GE.0D0.AND.DTA.LT.0.3D0)

F=75D-5*PA**2.3/DEXP(20.*DTA)+

*11D-4*DTA**0.5*(PA*(2.17D0-PA+1.4*DTA**0.5))**2

IF(PA.GE.0D0.AND.PA.LT.1.3D0.AND.DTA.GE.-0.25D0.AND.DTA.LT.0D0)

*F=75D-5*PA**2.3*(2D0-DEXP(20.*DTA))+

*1.317*PA*(1.69D0-PA**2)*DTA**4

IF(PA.GE.1.3D0.AND.PA.LT.2D0.AND.DTA.GE.-0.21D0.AND.DTA.LT.0D0)

*F=75D-5*PA**2.3*(2D0-DEXP(20.*DTA))+

*0.455*(1.3D0-PA)*(1.69*2.D0**1.25-PA**2)*(DTA*(0.03249D0+

*18.028*DTA**2)+DTA**2*(2.0167D0+DTA**2*(42.844D0+200.*DTA**2)))

T1=:TA**5/(TA**2*(6.60756*TA-4.42646D0)+3.22706D0)

T0=(TA**2*(1.77218D0-0.8879*TA)+0.305131D0)*T1/TA**4

B1=2.*T1/3.-TO**2

B0=T0*(T1-T0**2)+0.1*T1*PA*(F-1D0)

B2=(B0+(B0**2+B1**3)**0.5)**(1D0/3D0)

RETURN

END

SUBROUTINE PHASEA

IMPLICIT REAL*8(A-H,O-Z)

COMMON/Z/Z/PT/PA,TA/BI/B1,B2/T0/T0

Z=(1D0+0.00132/TA**3.25)**2*0.1*PA/(B1/B2-B2+T0)

RETURN

END

C *************************************************************

С * *

С * Подпрограмма расчета коэффициента сжимаемости природного *

С * газа по модифицированному уравнению состояния GERG-91. *

С * *

C *************************************************************

$NOTRUNCATE

SUBROUTINE GERG2(ICALC,YA,YY)

IMPLICIT REAL*8(A-H,O-Z)

COMMON/T/T1/P/PRESS/RON/RON/Z/Z

COMMON/XBLOK/X1,X2,X3,X11,X12,X13,X22,X23,X33

COMMON/MBLOK/GM2,GM3,FA,FB,TO,R

DATABMO/.0838137D0/,BM1/-.00851644D0/,WD0/134.2153D0/,

*WD1/1067.943D0/

Z=-1D0

IF(ICALC.EQ.2) GO TO 3

X2=YA

X3=YY

IF(RON.LT.0.66D0.OR.RON.GT.1D0)Z=0D0

IF(X2.LT.0D0.OR.X2.GT.0.2D0)Z=0D0

IF(X3.LT.0D0.OR.X3.GT.0.15D0) Z=0D0

IF(Z.EQ.0D0) GO TO 133

X1=1D0-X2-X3

Х11=Х1*Х1

X12=X1*X2

X13=X1*X3

X22=X2*X2

X23=X2*X3

X33=X3*X3

Z=1D0-(.0741*RON-.006D0-.063*YA-.0575*YY)**2

BMNG=24.05525*Z*RON

Y1=1D0-YA-YY

BMY=(BMNG-28.0135*YA-44.01*YY)/Y1

С Расчет теплоты сгорания эквивалентного углеводорода (Н)

H=47.479*BMY+128.64D0

RETURN

3 Т=Т1

ТС=Т1-Т0

P=PRESS

IF(PRESS.LE.0D0.OR.PRESS.GT.12D0)Z=0D0

IF(T1.LT.250D0.OR.T1.GT.340D0)Z=0D0

IF(Z.EQ.0D0) GO TO 133

CALL B11BER(T,H,B11)

CALL BBER(T,B11,B,Z)

IF(Z.EQ.0D0) GO TO 133

CALL CBER(T,H,C,Z)

IF(Z.EQ.0D0) GO TO 133

CALL ITER2(P,T,B,C,Z)

133 RETURN

END

SUBROUTINE B11BER(T,H,B11)

IMPLICIT REAL*8(A-H,O-Z)

COMMON/BBLOK/BR11H0(3),BR11H1(3),BR11H2(3),BR22(3),BR23(3),BR33(3)

T2=T*T

B11=BR11H0(1)+BR11H0(2)*T+BR11H0(3)*T2+

*(BR11H1(1)+BR11H1(2)*T+BR11H1(3)*T2)*H+

*(BR11H2(1)+BR11H2(2)*T+BR11H2(3)*T2)*H*H

END

SUBROUTINE BBER(T,B11,BEFF,Z)

IMPLICIT REAL*8(A-H,O-Z)

COMMON/BBLOK/BR11H0(3),BR11H1(3),BR11H2(3),BR22(3),BR23(3),BR33(3)

COMMON/ZETA/Z12,Z13,Y12,Y13,Y123

COMMON/XBLOK/X1,X2,X3,X11,X12,X13,X22,X23,X33

T2=T*T

B22=BR22(1)+BR22(2)*T+BR22(3)*T2

B23=BR23(1)+BR23(2)*T+BR23(3)*T2

B33=BR33(1)+BR33(2)*T+BR33(3)*T2

BA13=B11*B33

IF(BA13.LT.0D0) THEN

Z=0D0

RETURN

ENDIF

ZZZ=Z12+(320D0-T)**2*1.875D-5

BEFF=X11*B11+X12*ZZZ*(B11+B22)+2.*X13*Z13*DSQRT(BA13)+

*X22*B22+2.*X23*B23+X33*B33

END

SUBROUTINE CBER(T,H,CEFF,Z)

IMPLICIT REAL*8(A-H,O-Z)

COMMON/CBLOK/CR111H0(3),CR111H1(3),CR111H2(3),CR222(3),CR223(3),

*CR233(3),CR333(3)

COMMON/ZETA/Z12,Z13,Y12,Y13,Y123

COMMON/XBLOK/X1,X2,X3,X11,X12,X13,X22,X23,X33

T2=T*T

C111=CR111 H0(1)+CR111H0(2)*T+CR111H0(3)*T2+

*(CR111H1(1)+CR111H1(2)*T+CR111H1(3)*T2)*H+

*(CR111H2(1)+CR111H2(2)*T+CR111H2(3)*T2)H*H

C222=CR222(1)+CR222(2)*T+CR222(3)*T2

C223=CR223(1)+CR223(2)*T+CR223(3)*T2

C233=CR233(1)+CR233(2)*T+CR233(3)*T2

C333=CR333(1)+CR333(2)*T+CR333(3)*T2

CA112=C111*C111*C222

CA113=C111*C111*C333

CA122=C111*C222*C222

CA123=C111*C222*C333

CA133=C111<C333*C333

IF(CA112.LT.0D0.OR.CA113.LT.0D0.OR.CA122.LT.0DO0.OR.

*CA123.LT.0D0.OR.CA133.LT.0D0)THEN

Z=0D0

RETURN

ENDIF

D3REP=1D0/3D0

CEFF=X1*X11*C111+3D0*X11*X2*(CA112)**D3REP*(Y12+(T-270D0)*.0013D0)

*+3.*X11*X3*(CA113)**D3REP*Y13+

*3.*X1*X22*(CA122)**D3REP*(Y12+(T-270D0)*.0013D0)+

*6.*X1*X2*X3*(CA123)**D3REP*Y123+3.*X1*X33*(CA133)**D3REP*Y13+

*X22*X2*C222+3.*X22*X3*C223+3.*X2*X33*C233+X3*X33*C333

END

С Подпрограмма, реализующая схему Кардано для определения

С фактора сжимаемости из уравнения состояния

SUBROUTINE ITER2(P,T,Bm,Cm,Z)

IMPLICIT REAL*8(A-H,O-Z)

B1=1D3*P/2.7715/T

B0=Bl*Bm

C0=Bl**2*Cm

A1=1D0+B0

A0=1D0+1.5*(B0+C0)

A01=A0**2-A1**3

IF(A01.LE.0D0) THEN

Z=0D0

RETURN

ENDIF

A=A0-A01**0.5

A2=DABS(A)**(1D0/3D0)

IF(A-LT.0D0) A2=-A2

Z=(1D0+A2+A1/A2)/3.

END

BLOCK DATA BDGRG2

IMPLICIT REAL*8(A-H,O-Z)

COMMON/BBLOK/BR11H0(3),BR11H1(3),BR11H2(3),BR22(3),BR23(3),

*BR33(3)/CBLOK/CR111H0(3),CR111H1(3),CR111H2(3),CR222(3),

*CR223(3),CR233(3),CR333(3)

COMMON/ZETA/Z12,Z13,Y12,Y13,Y123

COMMON/MBLOK/GM2,GM3,FA,FB,TO,R

DATA BR11H0/-.425468D0,.2865D-2,-.462073D-5/,

* BR11H1/.877118D-3,-.556281D-5,.881514D-8/,

* BR11H2/-.824747D-6,.431436D-8,-.608319D-11/,

* BR22/-.1446D0,.74091D-3,-.91195D-6/,

* BR23/-.339693D0,.161176D-2,-.204429D-5/,

* BR33/-.86834D0,.40376D-2,-.51657D-5/

DATA CR111H0/-.302488D0,.195861D-2,-.316302D-5/,

* CR111 H1/.646422D-3,-.422876D-5,.688157D-8/,

* CR111H2/-.332805D-6,.22316D-8,-.367713D-11/,

* CR222/.78498D-2,-.39895D-4,.61187D-7/,

* CR223/.552066D-2,-.168609D-4,.157169D-7/,

* CR233/.358783D-2,.806674D-5,-.325798D-7/,

* CR333/.20513D-2,.34888D-4,-.83703D-7/

DATA Z12/.72D0/,Z13/-.865D0/,Y12/.92D0/,Y13/.92D0/,Y123/1.1D0/

DATA GM2/28.0135D0/,GM3/44.01D0/,

* FA/22.414097D0/,FB/22.710811D0/,

* TO/273.15D0/,R/.0831451D0/

END 46

C **********************************************************

С * *

С * Подпрограмма расчета коэффициента сжимаемости природного *

С * газа по уравнению состояния AGA8-92DC. *

C * *

C **********************************************************

SUBROUTINE AGA8DC(ICALC)

IMPLICIT REAL*8(A-H,O-Z)

REAL*8 KI,KIJ,KD

COMMON/RM/RM/Y1/Y(19)/NC1/NC/NI1/NI(19)/EFI/EI(19),KI(19),

*GI(19),QI(19),FI(19)

*/INTER1/EIJ(19,19),UIJ(19,19),KIJ(19,19),GIJ(19,19)

*/EFD/ED(19),KD(19),GD(19),QD(19),FD(19)/Z/Z

RM=8.31448D0

IF(ICALC.NE.l) GO TO 3

CALL COMPO1

IF(Z.EQ.0D0) GO TO 133

CALL PARIN1

DO 75 I=1,NC

EI(I)=ED(NI(I))

KI(I)=KD(NI(I))

GI(I)=GD(NI(I))

QI(I)=QD(NI(I))

FI(I)=FD(NI(I))

DO 123 J=1,NC

IF(I.GE.J) GO TO 123

EIJ(I,J)=EIJ(NI(I),NI(J))

UIJ(I,J)=UIJ(NI(I),NI(J))

KIJ(I,J)=KIJ(NI(I),NI(J))

GIJ(I,J)=GIJ(NI(I),NI(J))

123 CONTINUE

75 CONTINUE

CALL PARMI1

3 CALL PHASE1

133 RETURN

END

SUBROUTINE COMPO1

IMPLICIT REAL*8(A-h,O-Z)

DIMENSION ZNI(25),YI(25)

COMMON/YI/Y(19)/YI/YC(25)/NC1/NC/NT1/NI(19)/NPR/NPR

DATA ZNI/.9981D0,.992D0,.9834D0,.9682D0,.971D0,.9997D0,.9947D0,

*.99D0,.993D0,.994D0,985D0,.945D0,.953D0,1D0,.919D0,

*.936D0,.876D0,.892D0,3*1D0,1.0005D0,1.0006D0,.9996D0,.9993D0/

DO 100 I=1,25

100 YI(I)=YC(I)

YI(13)=YI(13)+YI(14)

YI(14)=0D0

IF(NPR.EQ.0D0) GO TO 5

YI(17)=YI(17)+YI(19)+YI(20)+YI(21)

YI(19)=0D0

YI(20)=0D0

YI(21)=0D0

SUM=0D0

DO 7 I=1,25

7 SUM=SUM+YI(I)/ZNI(I)

DO 9 I=1,25

9 YI(I)=YI(I)/ZNI(I)/SUM

5 YI(2)=YI(2)+YI(9)+YI(10)

YI(9)=0D0

YI(10)=O0D0

YI(3)=YI(3)+YI(11)

YI(11)=0D0

YI(15)=YI(15)+YI(16)

YI(16)=0D0

YI(17)=YI(17)+YI(18)

YI(18)=0D0

NC=0

ИС=0

YSUM=0D0

DO 11 1=1,25

IF((I.GE.9.AND.I.LE.11).OR.I.EQ.14.0R.I.EQ.16.0R.I.EQ.18)

*ИС=ИС+1

IF(YI(I).EQ.0D0) GO TO 11

NC=NC+1

NI(NC)=I-ИC

Y(NC)=YI(I)

YSUM=YSUM+Y(NC)

11 CONTINUE

CALL MOLDOl(YI)

DO 13 I=1,NC

13 Y(I)=Y(I)/YSUM

RETURN

END

SUBROUTINE MOLDO1(YI)

IMPLICIT REAL*8(A-H,O-Z)

DIMENSION YI(25)

COMMON/Z/Z

Z=-1D0

YS=0D0

DO 1 I=9,25

1 YS=YS+YI(I)

1F(YI(1).LT.0.65D0.OR.YI(2).GT.0.15D0.OR.YI(3).GT.0.035D0.OR.

*YI(4).GT.0.015D0.OR.YI(5).GT.0.015D0.OR.YS.GT.0.01D0) Z=0D0

IF(YI(6).GT.0.2D0.OR.YI(7).GT.0.15D0.OR.Y1(8).GT.5D-5) Z=O0D0

RETURN

END

SUBROUTINE PARIN1

IMPLICIT REAL*8(A-H,O-Z)

REAL*8 KIJ

COMMON/INTER1/EIJ(19,19),UIJ(19,19),KIJ(19,19),GIJ(19,19)

DO 1 I=1,19

DO 1 J=1,19

EIJ(I,J)=1D0

UIJ(I,J)=1D0

KIJ(I,J)=1D0

1 GIJ(I,J)=1D0

EIJ(1,6)=0.97164D0

UIJ(1,6)=0.886106D0

KIJ(1,6)=1.00363D0

EIJ(1,7)=0.960644D0

UIJ(1,7)=0.963827D0

KIJ(1,7)=0.995933D0

GIJ(1,7)=0.807653D0

EIJ(1,3)=0.99605D0

UIJ(1,3)=1.02396D0

EU(1,17)=1.17052D0

UIJ(1,17)=1.15639D0

KIJ(1,17)=1.02326D0

GIJ(1,17)=1.95731D0

EIJ(1,18)=0.990126D0

EIJ(1,5)=1.01953D0

EIJ(1,4)=0.995474D0

UIJ(1,4)=1.02128D0

EIJ(1,10)=1.00235D0

EIJ(1,9)=1.00305D0

EIJ(1,11)=1.01293D0

EIJ(1,12)=0.999758D0

EIJ(1,13)=0.988563D0

EIJ(6,7)=1.02274D0

UIJ(6,7)=0.835058D0

KIJ(6,7)=0.982361D0

GIJ(6,7)=0.982746D0

EIJ(2,6)=0.97012D0

UIJ(2,6)=0.816431D0

KIJ(2,6)=1.00796D0

EIJ(3,6)=0.945939D0

UIJ(3,6)=0.915502D0

EIJ(6,17)=1.08632D0

UIJ(6,17)=0.408838D0

KIJ(6,17)=1.03227D0

EIJ(6,18)=1.00571D0

EIJ(5,6)=0.946914D0

EIJ(4,6)=0.973384D0

UIJ(4,6)=0.993556D0

EIJ(6,10)=0.95934D0

EIJ(6,9)=0.94552D0

EIJ(6,11)=0.93788D0

EIJ(6,12)=0.935977D0

EIJ(6,13)=0.933269D0

EIJ(2,7)=0.925053D0

UIJ(2,7)=0.96987D0

KIJ(2,7)=1.00851D0

GIJ(2,7)=0.370296D0

EIJ(3,7)=0.960237D0

EIJ(7,17)=1.28179D0

EIJ(7,18)=1.5D0

UIJ(7,18)=0.9D0

EIJ(5,7)=0.906849D0

EIJ(4,7)=0.897362D0

EIJ(7,10)=0.726255D0

EIJ(7,9)=0.859764D0

EIJ(7,11)=0.766923D0

EIJ(7,12)=0.782718D0

EIJ(7,13)=0.805823D0

EIJ(2,3)=1.03502D0

UIJ(2,3)=1.0805D0

KIJ(2,3)=1.00046D0

EIJ(2,17)=1.16446D0

UIJ(2,17)=1.61666D0

KIJ(2,17)=1.02034D0

UIJ(2,5)=1.25D0

EIJ(2,4)=1.01306D0

UIJ(2,4)=1.25D0

UIJ(2,10)=1.25D0

EIJ(2,9)=1.00532D0

UIJ(2,9)=1.25D0

EIJ(3,17)=1.034787D0

EIJ(3,4)=1.0049D0

EIJ(17,18)=1.1D0

EIJ(5,17)=1.3D0

EIJ(4,17)=1.3D0

RETURN

END

SUBROUTINE PARMI1

IMPLICIT REAL*8(A-H,O-Z)

REAL*8 KI,KIJ,KM

INTEGER GN,QN,FN

DIMENSION EIJM(19,19),GIJM(19,19)

COMMON/Y1/Y(19)/NC1/NC/EFI/EI(19),KI(19),GI(19),QI(19),FI(19)

*/INTER1/EIJ(19,19),UIJ(19,19),KIJ(19,19),GIJ(19,19)

*/KM/KM/COEF1/B1(13),C1(53)/AN/AN(53)

*/GQFN/GN(53),QN(53),FN(53)/UN/UN(53)

DO 1 I=1,NC

EIJM(I,I)=EI(I)

GIJM(I,I)=GI(I)

DO 1 J=1,NC

IF(I.GE.J) GO TO 1

EIJM(I,J)=EIJ(I,J)*(EI(I)*EI(J))**.5

GIJM(I,J)=GIJ(I,J)*(GI(I)+GI(J))/2.

1 CONTINUE

KM=0D0

UM=0D0

KM=0D0

UM=0D0

GM=0D0

QM=0D0

FM=0D0

DO 3 I=1,NC

KM=KM+Y(I)*KI(I)**2.5

UM=UM+Y(I)*EI(I)**2.5

GM=GM+Y(I)*GI(I)

QM=QM+Y(I)*QI(I)

3 FM=FM+Y(I)**2*FI(I)

KM=KM*KM

UM=UM*UM

DO 5 I=1,NC-1

DO 5 J=I+1,NC

UM=UM+2.*Y(I)*Y(J)*(UIJ(I,J)**5-1D0)*(EI(I)*EI(J))**2.5

GM=GM+2.*Y(I)*Y(J)*(GIJ(I,J)-1D0)*(GI(I)+GI(J))

5 KM=KM+2.*Y(I)*Y(J)*(KIJ(I,J)**5-1D0)*(KI(I)*KI(J))**2.5

KM=KM**.6

UM=UM**.2

DO 7 N=1,13

B1(N)=0D0

DO 9 I=1,NC

9 В1(N)=B1(N)+Y(I)*Y(I)(GIJM(I,I)+ 1D0-GN(N))**GN(N)*

*(QI(I)*QI(I)+1D0-QN(N))**QN(N)*(FI(I)+1D0-FN(N))*FN(N)*

*EIJM(I,I)”UN(N)*KI(I)*KI(I)*KI(I)

DO 11 I=1,NC-1

DO 11 J=I+1,NC

11 В1(N)=B1(N)+2.*Y(I)*Y(J)(GIJМ(I,J)+1D0-GN(N))**GN(N)*

*(QI(I)*QI(J)+1D0-QN(N))**QN(N)*((FI(I)*FI(J))**.5+

1D0-FN(N))**FN(N)*EIJM(I,J)**UN(N)*(KI(I)*KI(J)**1.5

7 CONTINUE

DO 13 N=8,53

13 C1(N)=AN(N)*(GM+1D0-GN(N))**GN(N)*(QM**2+1D0-QN(N))**

*QN(N)*(FM+1D0-FN(N))**FN(N)*UM**UN(N)

RETURN

END

SUBROUTINE PHASE1

IMPLICIT REAL*8(A-H,O-Z)

COMMON/Z/Z/RM/RM/T/T/P/P/AI1/AO,A1/AN/AN(53)

*/COEF1/B1(13),C1(53)/COEF2/B,C(53)/UN/UN(53)

CALL PCONT1(P,T)

IF(Z.EQ.0D0) GO TO 134

B=0D0

DO 1 N=1,13

1 B=B+AN(N)/T**UN(N)*B1(N)

DO 3 N=8,53

3 C(N)=C1(N)/T**UN(N)

PR=P/5.

RO=9D3*P/(RM*T*(1.1*PR+0.7D0))

CALL FUN1(RO)

Z=1D0+AO

134 RETURN

END

С Подпрограмма, реализующая итерационный процесс определения

С плотности из уравнения состояния (метод Ньютона)

SUBROUTINE FUN1(X)

IMPLICIT REAL*8(A-H,O-Z)

COMMON/P/P/RM/RM/T/T/AI1/AO,A1

ITER=1

1 CONTINUE

CALL COMPL1(X)

Z=1.D0+AO

FX= 1 .D6*(P-(1.D-3*RM*T*Z*X))

F= 1 .D3*RM*(1.D0+A1)

DR=FX/F

X=X+DR

IF(ITER.GT.10) GO TO 4

ITER=ITER+1

IF(DABS(DR/X).GT.1.D-6) GO TO 1

4 CALL COMPL1(X)

RETURN

END

SUBROUTINE PCONT1(P,T)

IMPLICIT REAL*8(A-H,O-Z)

COMMON/Z/Z

Z=-1D0

IF(T.LT.250D0.OR.T.GT.340D0)Z=0D0

IF(P.LE.0D0.OR.P.GT.12D0) Z=0D0

RETURN

END

SUBROUTINE COMPL1(RO)

IMPLICIT REAL*8(A-H,O-Z)

REAL*8 KM

INTEGER BN,CN

COMMON/KM/KM/COEF2/B,C(53)/BCKN/BN(53),CN(53),KN(53)/AI1/AO,A1

ROR=KM*RO

S1=0D0

S2=0D0

S3=0D0

DO 1 N=8,53

EXP=DEXP(-CN(N)*ROR**KN(N))

IF(N.LE.13) S1=S1+C(N)

S2=S2+C(N)*(BN(N)-CN(N)*KN(N)*ROR**KN(N))*ROR**BN(N)*EXP 1

S3=S3+C(N)*(-CN(N)*KN(N)**2*KM*ROR**(KN(N)-1)*ROR**BN(N)*

*EXP+(BN(N)-CN(N)*KN(N)*ROR**KN(N))*BN(N)*KM*ROR**(BN(N)-1)*

*EXP-(BN(N)-CN(N)*KN(N)*ROR**KN(N))*ROR**BN(N)*EXP*CN(N)*KN(N)*

*KM*ROR**(KN(N)-1))AO1=B*RO-ROR*S1

AO=AO1+S2

A1=AO+AO1+RO*S3

RETURN

END

BLOCK DATA DCAGA8

IMPLICIT REAL*8(A-H,O-Z)

REAL*8 KD

INTEGER BN,CN,GN,QN,FN

COMMON/EFD/ED(19),KD(19),GD(19),QD(19),FD(19)

*/BCKN/BN(53),CN(53),KN(53)/UN/UN(53)

*/AN/AN(53)/GQFN/GN(53),QN(53),FN(53)

DATA ED/151.3183D0,244.1667D0,298.1183D0,337.6389D0,324.0689D0,

*99.73778D0,241.9606D0,296.355D0,370.6823D0,365.5999D0,

*402.8429D0,427.5391D0,450.6472D0,472.1194D0:488.7633D0,

*2.610111D0,26.95794D0,105.5348D0,122.7667D0/

DATA KD/.4619255D0,.5279209D0,.583749D0,.6341423D0,.6406937D0,

*.4479153D0,.4557489D0,.4618263D0,.6798307D0,.6738577D0,

*.7139987D0,.7503628D0,.7851933D0,.8157596D0,.8389542D0,

*.3589888D0,.3514916D0,.4533894D0,.4186954D0/

DATA GD/0D0,.0793D0,.141239D0,.281835D0,.256692D0,.027815D0,

*.189065D0,.0885D0,.366911D0,.332267D0,.432254D0,.512507D0,

*.576242D0,.648601D0,.716574D0,0D0,.034369D0,.038953D0,.021D0/

DATA QD/6*0D0,.69D0,12*0D0/,FD/16*0D0,1D0,2*0D0/

DATA AN/.1538326D0,1.341953D0,-2.998583D0,-.04831228D0,

*.3757965D0,-1.589575D0,-.05358847D0,2.29129D-9,1576724D0,

*-.4363864D0,-.04408159D0,-.003433888D0,.03205905D0,.02487355D0, –

*.07332279D0,-.001600573D0,.6424706D0,-.4162601D0,-.06689957D0,

*.2791795D0,-.6966051D0,-.002860589D0,-.008098836D0,3.150547D0,

*.007224479D0,-.7057529D0,.5349792D0,-.07931491D0-1.418465D0,

*-5.99905D-17,.1058402D0,.03431729D0,-.007022847D0,.02495587D0,

*.04296818D0,.7465453D0,-.2919613D0,7.294616D0,-9.936757D0,

*-.005399808D0,-.2432567D0,.04987016D0,.003733797D0,1.874951D0,

*.002168144D0,-.6587164D0,.000205518D0,.009776195D0,-.02048708D0,

*.01557322D0,.006862415D0,-.001226752D0,.002850906D0/

DATA BN/13*1,9*2,10*3,7*4,5*5,2*6,2*7,3*8,2*9/

DATA CN/7*0,6*1,2*0,7*1,0,9*1,2*0,5*1,0,4*1,0,1,0,6*1/

DATA KN/7*0,3,3*2,2*4,2*0,3*2,4*4,0,2*1,2*2,2*3,3*4,2*0,3*2,

*2*4,0,2*2,2*4,0,2,0,2,1,4*2/

DATA UN/0D0,.5D0,1D0,3.5D0,-.5D0,4.5D0,.5D0,-6D0,2D0,3D0,2*2D0,

*11D0,-.5D0,.5D0,0D0,4D0,6D0,21D0,23D0,22D0,-1D0,-.5D0,7D0,-1D0,

*6D0,4D0,1D0,9D0,-13D0,21D0,8D0,-.5D0,0D0,2D0,7D0,9D0,22D0,23D0,

*1D0,9D0,3D0,8D0,23D0,1.5D0,5D0,-.5D0,4D0,7D0,3D0,0D0,1D0,0D0/

DATA GN/4*0,2*1,13*0,1,3*0,1,2*0,3*1,16*0,1,2*0,1,0,1,2*0/

DATA QN/6*0,1,3*0,1,9*0,1,0,1,8*0,1,4*0,1,4*0,1,0,1,2*0,1,5*0,1/

DATA FN/7*0,1,13*0,1,2*0,1,4*0,1,23*0/

END

C ***********************************************************

С * *

С * Подпрограмма расчета коэффициента сжимаемости природного *

С * газа по уравнению состояния ВНИЦ СМВ. *

С * *

C ***********************************************************

SUBROUTINE VNIC(ICALC)

IMPLICIT REAL*8(A-H,O-Z)

REAL*8 LIJ(8,8)

DIMENSION VC(8),TC(8),PII(8),DIJ(8,8)

COMMON/PARCD/VCD(8),TCD(8),PIID(8)/ABIJ/AIJ(10,8),BIJ(10,8)

*/B/B(10,8)/RM/RM/Y/Y(8)/BM/BM(8)/NI/NI(8)/NC/NC/Z/Z

RM=8.31451DO

IF(ICALC.NE.1) GO TO 1

CALL COMPON

IF(Z.EQ.0D0) GO TO 133

CALL DDIJ(DIJ,LIJ)

DO 75 I=1,NC

TC(I)=TCD(NI(I))

VC(I)=BM(I)/VCD(NI(I))

PII(I)=PIID(NI(I))

DO 123 J=1,NC

IF(I.GE.J) GO TO 123

DIJ(I,J)=DIJ(NI(I),NI(J))

LIJ(I,J)=LIJ(NI(I),NI(J))

123 CONTINUE

75 CONTINUE

CALL PARMIX(DIJ,LIJ,TC,VC,PII,PIM)

DO 27 I=1,10

DO 27 J=l,8

27 B(I,J)=AIJ(I,J)+BIJ(I,J)*PIM

1 CALL PHASE

133 RETURN

END

SUBROUTINE COMPON

IMPLICIT REAL*8(A-H,O-Z)

DIMENSION BMI(25),ROI(8),GI(8),YI(25)

COMMON/Y/Y(8)/BMM/BMM/BM/BM(8)/YI/YC(25)/NI/NI(8)/NC/NC/NPR/NPR

DATA BMI/16.043D0,30.07D0,44.097D0,2*58.123D0,28.0135D0,

*44.01D0,34.082D0,26.038D0,28.054D0,42.081D0,3*72.15D0,

*86.177D0,78.114D0,100.204D0,92.141D0,114.231D0,128.259D0,

*142.286D0,4.0026D0,2.0159D0,28.01D0,31.9988D0/

DATAR0I/0.6682D0,1.2601D0,1.8641D0,2.4956D0,2.488D0,

*1.1649D0,1.8393D0,1.4311D0/

DO 100 I=1,25

100 YI(I)=YC(I)

IF(NPR.EQ.1) GO TO 333

BMM=0D0

DO 3333 I=1,25

3333 ВММ=ВММ+YI(I)*ВМI(I)

333 YS=0D0

DO 55 I=9,25

YS=YS+YI(I)

55 CONTINUE

YS1=0D0

DO 67 I=12,21

67 YS1=YS1+YI(I)

YS2=0D0

DO 69 1=22,25

69 YS2=YS2+YI(I)

YI(2)=YI(2)+YI(9)+YI(10)

YI(3)=YI(3)+YI(11)

YI(4)=YI(4)+YS1

YS3=YI(4)+YI(5)

IF(NPR.EQ.1.AND.YI(5).LT.0.01D0.AND.YS3.LT.0.03D0) YI(4)=YS3

IF(NPR.EQ.1.AND.YI(5).LT.0.01D0.AND.YS3.LT.0.03D0) YI(5)=0D0

IF(NPR.EQ.0.AND.Y1(5).LT.0.01D0.AND.YS3.LE.0.03D0) YI(4)=YS3

IF(NPR.EQ.0.AND.YI(5).LT.0.01D0.AND.YS3.LE.0.03D0)YI(5)=0D0

YI(6)=YI(6)+YS2

IF(NPR.EQ.0) GO TO 555

ROM=0D0

DO 7 I=1,8

7 ROM=ROM+YI(I)*ROI(I)

DO 9 I=1,8

9 GI(I)=YI(I)*ROI(I)/ROM

SUM=0D0

DO 11 1=1,8

11 SUM=SUM+GI(I)/BMI(I)

SUM=1./SUM

DO 13 I=1,8

13 YI(I)=GI(I)*SUM/BMI(I)

555 NC=0

YSUM=0D0

DO 155 I=1,8

IF(YI(I).EQ.0D0) GO TO 155

NC=NC+1

NI(NC)=I

Y(NC)=YI(I)

YSUM=YSUM+Y(NC)

BM(NC)=BMI(I)

155 CONTINUE

CALL MOLDOL(YI,YS)

DO 551 I=1,NC

551 Y(I)=Y(I)/YSUM

RETURN

END

SUBROUTINE MOLDOL(YI,YS)

IMPLICIT REAL*8(A-H,O-Z)

DIMENSION YI(25)

COMMON/Z/Z

Z=-1D0

IF(YI(1).LT.0.65D0.OR.YI(2).GT.0.15D0.OR.YI(3).GT.0.035D0.OR.

*YI(4).GT.0.015D0.OR.YI(5).GT.0.015D0.OR.YS.GT.0.01D0)Z=0D0

IF(YI(6).GT.0.2D0.OR.YI(7).GT.0.15D0.OR.YI(8).GT.0.3D0)Z=0D0

RETURN

END

SUBROUTINE DDIJ(DIJ,LIJ)

IMPLICIT REAL-8(A-H,O-Z)

REAL*8 LIJ(8,8)

DIMENSION DIJ(8,8)

DO 1 I=1,8

DO 1 J=l,8

LIJ(I,J)=0.D0

1 DIJ(I,J)=0.D0

DIJ(1,2)=0.036D0

DIJ(1,3)=0.076D0

DIJ(1,4)=0.121D0

DIJ(1,5)=0.129D0

DIJ(1,6)=0.06D0

DIJ(1,7)=0.074D0

DIJ(2,6)=0.106D0

DIJ(2,7)=0.093D0

DIJ(6,7)=0.022D0

DIJ(1,8)=0.089D0

DIJ(2,8)=0.079D0

DU(6,8)=0.211D0

DIJ(7,8)=0.089D0

LIJ(1,2)=-0.074D0

LIJ(1,3)=-0.146D0

LIJ(1,4)=-0.258D0

LIJ(1,5)=-0.222D0

LIJ(1,6)=-0.023D0

LIJ(1,7)=-0.086D0

LIJ(6,7)=-0.064D0

LIJ(7,8)=-0.062D0

RETURN

END

SUBROUTINE PARMIX(DIJ,LIJ,TC,VC,PII,PIM)

IMPLICIT REAL*8(A-H,O-Z)

REAL*8 LIJ(8,8)

DIMENSION Y(8),DIJ(8,8),VCIJ(8,8),TCIJ(8,8),V13(8),TC(8),VC(8),

*PII(8),PIIJ(8,8)

COMMON/PARCM/TCM,VCM/Y/Y/NC/NC/PCM/PCM

DO 1 I=1,NC

1 V13(I)=VC(I)**(1.DO/3.DO)

DO 3 I=1,NC

VCIJ(I,I)=VC(I)

PIIJ(I,I)=PII(I)

TCIJ(I,I)=TC(I)

DO 3 J=1,NC

IF(I.GE.J) GO TO 3

VCIJ(I,J)=(1.DO-LIJ(I,J))*((V13(I)+V13(J))/2.)**3

PIIJ(I,J)=(VC(I)*PII(I)+VC(J)*PII(J))/(VC(I)+VC(J))

TCU(I,J)=(1.D0-DIJ(I,J))*(TC(I)*TC(J))**0.5

VCIJ(J,I)=VCIJ(I,J)

PIIJ(J,I)=PIIJ(I,J)

TCIJ(J,I)=TCIJ(I,J)

3 CONTINUE

VCM=0.D0

PIM=0.D0

TCM=0.D0

DO 5 I=1,NC

DO 5 J=1,NC

VCM=VCM+Y(I)*Y(J)*VCIJ(I,J)

PIM=PIM+Y(I)*Y(J)*VCIJ(I,J)*PIIJ(I,J)

5 TCM=TCM+Y(I)*Y(J)*VCIJ(I,J)*TCIJ(I,J)**2

PIM=PIM/VCM

TCM=(TCM/VCM)**0.5

PCM=8.31451D-3*(0.28707D0-0.05559*PIM)*TCM/VCM

RETURN

END

SUBROUTINE PHASE

IMPLICIT REAL*8(A-H,O-Z)

COMMON/Z/Z/RM/RM/T/T/P/P/PCM/PCM/AI/AO,A1

IF(T.LT.250D0.OR.T.GT.340D0.OR.P.LE.0D0.OR.P.GT.12D0) THEN

Z=0D0

GO TO 134

ENDIF

PR=P/PCM

RO=9D3*P/(RM*T*(1.1*PR+0.7D0))

CALL FUN(RO)

CALL OMTAU(RO,T)

IF(Z.EQ.0D0) GO TO 134

Z=1.D0+AO

134 RETURN

END

С Подпрограмма, реализующая итерационный процесс определения

С плотности из уравнения состояния (метод Ньютона)

SUBROUTINE FUN(X)

IMPLICIT REAL*8(A-H,О-Z)

COMMON/P/P/RM/RM/T/T/AI/AO,A1

ITER=1

1 CONTINUE

NPRIZ=0

IF(ITER.NE.l) NPRIZ=1

CALL COMPL(X,T,NPRIZ)

Z=1.D0+AO

FX=1.D6*(P-(1.D-3*RM*T*Z*X))

F=1.D3*RM*T*(1.D0+A1)

DR=FX/F

X=X+DR

IF(ITER.GT.10) GO TO 4

ITER=ITER+1

IF(DABS(DR/X).GT.1.D-6) GO TO 1

4 CALL COMPL(X,T,NPRIZ)

RETURN

END

SUBROUTINE OMTAU(RO,T)

IMPLICIT REAL*8(A-H,O-Z)

COMMON/PARCM/TCM,VCM/Z/Z

Z=-1D0

TR=T/TCM

ROR=RO*VCM

IF(TR.LT.1.05D0) Z=0D0

IF(ROR.LT.0.D0.OR.ROR.GT.3.D0) Z=0D0

RETURN

END

SUBROUTINE COMPL(RO,T,NPRIZ)

IMPLICIT REAL*8(A-H,O-Z)

DIMENSION B(10,8),BK(10)

COMMON/PARCM/TCM,VCM/B/B/AI/AO,A1

IF(NPRIZ.NE.0) GO TO 7

TR=T/TCM

DO 1 I=1,10

BK(I)=0

DO 1 J=1,8

1 BK(I)=BK(I)+B(I,J)/TR**(J-1)

7 ROR=RO*VCM

AO=0.D0

A1=0.D0

DO 33 I=1,10

D=BK(I)*ROR**I

AO=AO+D

33 A1=A1+(I+1)*D

RETURN

END

BLOCK DATA BDVNIC

IMPLICIT REAL*8(A-H,O-Z)

COMMON/PARCD/VCD(8),TCD(8),PIID(8)/ABIJ/AIJ(10,8),BIJ(10,8)

DATA TCD/190.67D0,305.57D0,369.96D0,425.4D0,407.96D0,

*125.65D0,304.11D0,373.18D0/

DATA VCD/163.03D0,205.53D0,218.54D0,226.69D0,225.64D0,

*315.36D0,466.74D0,349.37D0/

DATA PIID/0.0006467D0,0.1103D0,0.1764D0,0.2213D0,0.2162D0,

*0.04185D0,0.2203D0,0.042686D0/

DATA AIJ/.6087766D0,-.4596885D0,1.14934D0,-.607501D0,

*-.894094D0,1.144404D0,-.34579D0,-.1235682D0,.1098875D0,

*-.219306D-1,-1.832916D0,4.175759D0,-9.404549D0,10.62713D0,

*-3.080591D0,-2.122525D0,1.781466D0,-.4303578D0,-.4963321D-1,

*.347496D-1,1.317145D0,-10.73657D0,23.95808 D0,-31.47929D0,

* 18.42846D0,-4.092685D0,-. 1906595D0,.4015072D0,-.1016264D0,

*-.9129047D-2,-2.837908D0,15.34274D0,-27.71885D0,35.11413D0,

*-23.485D0,7.767802D0,-1.677977D0,.3157961D0,.4008579D-2,0.D0,

*2.606878D0,-11.06722D0,12.79987D0,-12.11554D0,7.580666D0,

*-1.894086D0,4*0.D0,

*-1.15575D0,3.601316D0,-.7326041D0,-1.151685D0,.5403439D0,

*5*0.D0,.9060572D-1,-.5151915D0,.7622076D-1,7*0.D0,

*.4507142D-1,9*0.D0/

DATA BIJ/-.7187864D0,10.67179D0,-25.7687D0,17.13395D0,

*16.17303D0,-24.38953D0,7.156029D0,3.350294D0,-2.806204D0,

*.5728541D0,6.057018D0,-79.47685D0,216.7887D0,-244.732D0,

*78.04753D0,48.70601D0,-41.92715D0,10.00706D0,1.237872D0,

*-.8610273D0,-12.95347D0,220.839D0,-586.4596D0,744.4021D0,

*-447.0704D0,99.6537D0,5.136013D0,-9.5769D0,2.41965D0,

*.2275036D0,15.71955D0,-302.0599D0,684.5968D0,-828.1484D0,

*560.0892D0,-185.9581D0,39.91057D0,-7.567516D0,-.1062596D0,

*0.D0,-13.75957D0,205.541D0,-325.2751D0,284.6518D0,

*-180.8168D0,46.05637D0,4*0.D0,

*6.466081D0,-57.3922D0,36.94793D0,20.77675D0,-12.56783D0,

*5*0.D0,-.9775244D0,2.612338D0,-.4059629D0,7*0.D0,

*-.2298833D0,9*0.D0/

END

ПРИЛОЖЕНИЕ Г

(обязательное)

Г.1 Модифицированный метод NX19

Плотность при 0,101325 МПа и 293,15 К: 0,6799 кг/м3

Содержание:

азота ………………………………………………………………………………………….. 0,8858 мол. %

диоксида углерода ……………………………………………………………………… 0,0668 мол. %

Давление ……………………………………………………………………………………. 2,001 МПа

Температура ………………………………………………………………………………. 270,00 К

Коэффициент сжимаемости ……………………………………………………….. 0,9520

Давление ……………………………………………………………………………………. 2,494 МПа

Температура ………………………………………………………………………………. 280,00 К

Коэффициент сжимаемости ……………………………………………………….. 0,9473

Давление ……………………………………………………………………………………. 0,900 МПа

Температура ………………………………………………………………………………. 290,00 К

Коэффициент сжимаемости ……………………………………………………….. 0,9844

Г.2 Уравнение состояния GERG-91

Плотность при 0,101325 МПа и 293,15 К: 0,6799 кг/м3

Содержание:

азота ………………………………………………………………………………………….. 0,8858 мол. %

диоксида углерода ……………………………………………………………………… 0,0668 мол. %

Давление ……………………………………………………………………………………. 2,001 МПа

Температура ………………………………………………………………………………. 270,00 К

Коэффициент сжимаемости ……………………………………………………….. 0,9521

Давление ……………………………………………………………………………………. 3,997 МПа

Температура ………………………………………………………………………………. 290,00 К

Коэффициент сжимаемости ……………………………………………………….. 0,9262

Давление ……………………………………………………………………………………. 7,503 МПа

Температура ………………………………………………………………………………. 330,00 К

Коэффициент сжимаемости ……………………………………………………….. 0,9244

Г.3 Уравнение состояния AGA8-92DC

Состав природного газа в молярных процентах:

метан …………………………………………………………………………………………. 98,2722

этан …………………………………………………………………………………………… 0,5159

пропан ……………………………………………………………………………………….. 0,1607

н-бутан ………………………………………………………………………………………. 0,0592

азот ……………………………………………………………………………………………. 0,8858

диоксид углерода ……………………………………………………………………….. 0,0668

н-пентан …………………………………………………………………………………….. 0,0157

н-гексан …………………………………………………………………………………….. 0,0055

н-гептан …………………………………………………………………………………….. 0,0016

н-октан ………………………………………………………………………………………. 0,0009

гелий …………………………………………………………………………………………. 0,0157

Плотность при 0,101325 МПа и 293,15 К: 0,6799 кг/м3

Давление ……………………………………………………………………………………. 2,001 МПа

Температура ………………………………………………………………………………. 270,00 К

Коэффициент сжимаемости ……………………………………………………….. 0,9520

Давление ……………………………………………………………………………………. 3,997 МПа

Температура ………………………………………………………………………………. 290,00 К

Коэффициент сжимаемости ……………………………………………………….. 0,9262

Давление ……………………………………………………………………………………. 7,503 МПа

Температура ………………………………………………………………………………. 330,00 К

Коэффициент сжимаемости ……………………………………………………….. 0,9246

Г.4 Уравнение состояния ВНИЦ СМВ

Состав природного газа в молярных процентах:

метан …………………………………………………………………………………………. 89,2700

этан …………………………………………………………………………………………… 2,2600

пропан ……………………………………………………………………………………….. 1,0600

и-бутан ………………………………………………………………………………………. 0,0100

азот ……………………………………………………………………………………………. 0,0400

диоксид углерода ……………………………………………………………………….. 4,3000

сероводород ……………………………………………………………………………….. 3,0500

пропилен …………………………………………………………………………………… 0,0100

Плотность при 0,101325 МПа и 293,15 К: 0,7675 кг/м3

Давление ……………………………………………………………………………………. 1,081 МПа

Температура ………………………………………………………………………………. 323,15 К

Коэффициент сжимаемости ……………………………………………………….. 0,9853

Давление ……………………………………………………………………………………. 4,869 МПа

Температура ………………………………………………………………………………. 323,15 К

Коэффициент сжимаемости ……………………………………………………….. 0,9302

Давление ……………………………………………………………………………………. 9,950 МПа

Температура ………………………………………………………………………………. 323,15 К

Коэффициент сжимаемости ……………………………………………………….. 0,8709

ПРИЛОЖЕНИЕ Д

(обязательное)

Д.1 Модифицированный метод NX19

Исходные данные (заданные параметры)	Значение
минимальное	максимальное	погрешности, %
Давление, МПа	1,991	2,011	1,00
Температура, К	269,50	270,50	0,35
Плотность, кг/м3 (0,101325 МПа, 293,15 К)	0,6790	0,6808	0,25
Содержание, мол. %:
азота (N2)	0,8769	0,8947	2,00
диоксида углерода (СО2)	0,0661	0,0675	2,00

Коэффициент сжимаемости (среднее значение) – 0,9520

Погрешность расчета: по формуле (82) – 0,09 %; по формуле (86) – 0,07 %.

Д.2 Уравнение состояния GERG-91

Исходные данные (заданные параметры)	Значение
минимальное	максимальное	погрешности, %
Давление, МПа	1,991	2,011	1,00
Температура, К	269,50	270,50	0,35
Плотность, кг/м3 (0,101325 МПа, 293,15 К)	0,6790	0,6808	0,25
Содержание, мол. %:
азота (N2)	0,8769	0,8947	2,00
диоксида углерода (СО2)	0,0661	0,0675	2,00

Коэффициент сжимаемости (среднее значение) – 0,9521

Погрешность расчета: по формуле (82) – 0,09 %; по формуле (86) – 0,09 %.

Д.3 Уравнение состояния AGA8-92DC

Исходные данные (заданные параметры)	Значение
минимальное	максимальное	погрешности, %
Давление, МПа	1,991	2,011	1,00
Температура, К	269,50	270,50	0,35
Содержание, мол. %:
метана (СН4)	97,2722	99,2722	2,00
этана (С2Н6)	0,5030	0,5288	5,00
пропана (С3Н8)	0,1607	0,1607	–
н-бутана (н-С4Д10)	0,0592	0,0592	–
азота (N2)	0,8769	0,8947	2,00
диоксида углерода (СО2)	0,0661	0,0675	2,00
н-пентана (н-С5Н12)	0,0157	0,0157	–
н-гексана (н-С6Н14)	0,0055	0,0055	–
н-гептана (н-С7Н16)	0,0016	0,0016	–
н-октана (н-C8H18)	0,0009	0,0009	–
гелия (Не)	0,0157	0,0157	–

Коэффициент сжимаемости (среднее значение) – 0,9520

Погрешность расчета – 0,08 %

Д.4 Уравнение состояния ВНИЦ СМВ

Исходные данные (заданные параметры)	Значение
минимальное	максимальное	погрешности, %
Давление, МПа	1,076	1,086	1,00
Температура, К	322,65	323,65	0,31
Содержание, мол. %:
метана (СН4)	88,3700	90,1700	2,00
этана (С2Н6)	2,2030	2,3170	5,00
пропана (C3H8)	1,0600	1,0600	–
и-бутана (и-С4Н10)	0,0100	0,0100	–
азота (N2)	0,0396	0,0404	2,00
диоксида углерода (СО2)	4,2570	4,3430	2,00
сероводорода (H2S)	3,0500	3,0500	–
пропилена (С3Н6)	0,0100	0,0100	–

Коэффициент сжимаемости (среднее значение) – 0,9853

Погрешность расчета – 0,03 %

ПРИЛОЖЕНИЕ Е

(справочное)

[1] Сычев В.В. и др. Термодинамические свойства метана. – М., Изд-во стандартов, 1979, 348 с

[2] Kleinrahm R., Duschek W., Wagner W. Measurement and correlation of the (pressure, density, temperature) relation of methane in the temperature range from 273.15 К to 323.15 К at pressures up to 8 MPa. – J. Chem. Thermodynamics, 1988, v.20, p.621-631

[3] Robinson R.L., Jacoby R.H. Better compressibility factors. – Hydrocarbon Processing, 1965,v.44,No.4,p.141-145

[4] Achtermann H.-J., Klobasa F.,Rogener H. Realgasfaktoren von Erdgasen. Teil I: Bestimmung von Realgasfaktoren aus Brechungsindex-Messungen. – Brennstoff-Warme-Kraft, 1982, Bd.34, No.5, s.266-271

[5] Achtermann H.-J., Klobasa F.,Rogener H. Realgasfaktoren von Erdgasen. Teil II: Bestimmung von Realgasfaktoren mit eener Burnett-Apparatur. – Brennstoff-Warme-Kraft, 1982, Bd.34, No.6, s.311-314

[6] Eubank Ph.T., Scheloske J., Hall K.R., Holste J.C. Densities and mixture virial coefficients for wet natural gas mixtures. – Journal of Chemical and Engineering Data, 1987, v.32, No.2, p.230-233

[7] Jaeschke М., JulicherH.P. Realgasfaktoren von Erdgasen. Bestimmung von Realgasfaktoren nach der Expansionsmethode. – Brennstoff-Warme-Kraft, 1984, Bd.36, No.11, s.445-451

[8] Jaeschke М. Realgasverhalten Einheitliche Berechnungsmoglichkeiten von Erdgas L und H. – Gas und Wasserfach. Gas/Erdgas, 1988, v.129, No.l, s.30-37

[9] Blanke W., Weiss R. pvT-Eigenschaften und Adsorptions- verhalten von Erdgas bei Temperaturen zwischen 260 К und 330 К mit Drucken bis 3 MPa. – Erdol-Erdgas-Kohle, 1988, Bd.104, H.10, s.412-417

[10] Samirendra N.B. et al Compressibility Isotherms of Simulated Natural Gases. – J. Chem. Eng. Data, 1990, v.35, No.l, p.35-38

[11] Fitzgerald M.P., Sutton C.M. Measurements of Kapuni and Maui natural gas compressibility factors and comparison with calculated values. – New Zealand Journal of Technology, 1987, v.3, No.4, p.215-218

[12] Jaeschke М., Humphreys A.E. The GERG Databank of High Accuracy Compressibility Factor Measurements. GERG TM4 1990. – GERG Technical Monograph, 1990, 477 p

[13] Jaeschke М., Humphreys A.E. Standard GERG Virial Equation for Field Use. Simplification of the Input Data Requirements for the GERG Virial Equation – an Alternative Means of Compressibility Factor Calculation for Natural Gases and Similar Mixtures. GERG TM5 1991. – GERG Technical Monograph, 1991, 173 p

[14] ISO/TC 193 SC1 № 63. Natural gas – calculation of compression factor. Part 3: Calculation using measured physical properties

[15] ISO/TC 193 SC1 № 62. Natural gas – calculation of compression factor. Part 2: Calculation using a molar composition analysis

[16] ISO 5168:1978 International Standard. Measurement of fluid flow – Estimation of uncertainty of a flow-rate measurement

[17] VDI/VDE 2040, part 2, 1987. Calculation principles for measurement of fluid flow using orifice plates, nozzles and venturi tubes. Equations and formulas

[18] Jaeschke М. et al. High Accuracy Compressibility Factor Calculation for Natural Gases and Similar Mixtures by Use of a Truncated Virial Equation. GERG TM2 1988. – GERG Technical Monograph, 1988, 163 p

Источник

При
относительно высоких температурах и
небольших давлениях реальные газы ведут
себя почти так же, как идеальные. С
повышением давления и понижением
температуры в уравнения, описывающие
их поведение, приходится вводить
различные поправочные коэффициенты.
Так, необходимо вводить поправочный
коэффициент в уравнения при расчете
объема паров, константы фазового
равновесия, теплоемкости. Этот коэффициент
Z
получил название коэффициента (фактора)
сжимаемости. Коэффициент сжимаемости
зависит от величин приведенных параметров

Z
= f(T_пр,
P_пр)
(32)

Коэффициент
сжимаемости зависит от природы вещества,
температуры, давления и может быть
найден экспериментально или при помощи
графиков (1-5). Зная приведенные значения
давления (Р_пр)
и температуры (Т_пр),
можно найти Z
по графику (рис. 7). Для идеальных газов
Z
= 1. При определении коэффициента
сжимаемости для нефтяных фракций и
газовых смесей в формулы (30) и (31) вместо
критических параметров Т_кр
и Р_крследует
подставлять значения псевдокритических
параметров (Т_п.кр
и Р_п.

кр).

Псевдокритические параметры для смеси
газообразных индивидуальных углеводородов,
если неизвестен состав этой смеси, можно
с достаточной для практических расчетов
точностью определить по правилу
аддитивности или по графику (рис. 8); на
графике представлена зависимость этих
параметров от относительной (по отношению
к воздуху) плотности газовой смеси. В
соответствии с правилом аддитивности
можно использовать формулы

(33)

где
y_i
— мольная доля компонентов смеси.

Рис. 7. График для
определения коэффициента сжимаемости
Z

Рис. 8. Зависимость
псевдокритических параметров смеси

углеводородных
газов от ее относительной плотности

9. Фугитивность

Фугитивность – это давление реального
газа, свойства которого выражены
уравнением состояния идеального газа.
Фугитивностью пользуются при расчетах
равновесных паровой и жидкой фаз и
числовых значений констант фазового
равновесия.

Для равновесной
системы, согласно законам Рауля и
Дальтона,

(34)

откуда

где
Р
– давление насыщенных паров чистого
компонента, Па; х’
– мольная концентрация компонента в
жидкой фазе, %, мол; П
– давление в системе, Па; у’
– мольная концентрация компонента в
паровой фазе, %, мол; k
– константа фазового равновесия
(Приложения
10 и 11).

Для
идеальной системы значение k
равно отношению давления насыщенных
паров данного компонента к давлению в
системе и характеризует распределение
данного компонента между паровой и
жидкой фазами. Для реальных систем
константа фазового равновесия, вычисленная
этим методом, не дает вполне
удовлетворительных результатов.

Для
реальных газов и растворов давление
насыщенных паров Р
и давление в системе П
заменяют соответственно фугитивностью
жидкости
и паров .
Уравнение (34) приобретает вид

а константа фазового
равновесия равна

(35)

Фугитивность
характеризует степень отклонения
свойств реального газа от идеального
в случае изотермического процесса. При
низких давлениях и высоких температурах
реальный газ приближается к состоянию
идеального газа, а величина f
– к величине Р.
Фугитивность имеет ту же размерность,
что и давление. Отношение фугитивности
к давлению называется коэффициентом
активности

(36)

Для
идеального газа .

Установлено,
что коэффициент активности является
функцией приведенных температуры и
давления. Поэтому значение фугитивности
можно определить, пользуясь графиком
(рис. 9). По приведенной температуре Т_при приведенному
давлению Р_пр
находят коэффициент активности. Затем,
подставляя в уравнение (36) давление
насыщенных паров Р
или давление системы П,
получают соответственно фугитивность
жидкости или паров.

Для
точных расчетов константы фазового
равновесия, когда жидкий компонент
находится не под давлением Р
своих насыщенных паров, а под любым
другим давлением, фугитивность этого
компонента в жидкой фазе находят по
формуле

(37)

где
– фугитивность
жидкости при давлении в системе П
и давлении насыщенных паров Р
соответственно, Па; V_ж
– мольный объем компонента, л/моль,
м³/кмоль;
П
– давление в системе, Па; Р
– давление насыщенных паров чистого
компонента, Па; R
– универсальная газовая постоянная,
КДж/(кмольК);
Т
– температура системы, К.

Пример 15.Определить
фугитивность паров узкой бензиновой
фракции (М = 100), находящейся при 400°С
и 4,55 МПа. Критические параметры фракцииt_кр= 321°С иР_кр= 3,72 МПа.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

КОЭФФИЦИЕНТ СЖИМАЕМОСТИ ГАЗОВ И ГАЗОКОНДЕНСАТНЫХ СМЕСЕЙ: ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ И РАСЧЕТЫ

В.И. Лапшин, А.Н. Волков, И.М. Шафиев (ООО «Газпром ВНИИГАЗ»)

Коэффициент сжимаемости (Z) характеризует отличие реальных газов от идеальных.

Для идеальных газов, в которых отсутствует взаимодействие между молекулами, справедлив закон Клайперона, который обобщает законы Бойля – Мариотта и Гей-Люссака: (P • V) / T = (P0 • V0) / T0 = R, где R – универсальная газовая постоянная.

Для реальных газов произведение объема на давление (P • V) при постоянной температуре не является постоянной величиной. С ростом давления это произведение вначале уменьшается до определенного предела, а затем с увеличением давления увеличивается.

При практических расчетах для оценки степени указанных отклонений в уравнение Клайперона вводится поправочный коэффициент (Z) [1,

2, 3]. Уравнение Клайперона – Менделеева с учетом коэффициента сжимаемости имеет вид PV = ZNRT, где Р – абсолютное давление; V – объем, занимаемый газом (газоконденсатной смесью) при определенных давлении и температуре; R – универсальная газовая постоянная; N – число молей газа.

Это уравнение можно записать в виде

N = —. (1)

ZRT

Учитывая, что определение коэффициента сжимаемости проводится без изменения числа молей газа (N = const),

N = ^Z^, (2)

Zo RTo

f 3 Л

где V0 – объем газа при Р0 = 0,1013 МПа, м3; Т0 = 293 К; R = 24,01 МПа м

V К

Z0 = 1.

Экспериментальное определение коэффициента сжимаемости газов и газоконденсатных смесей, особенно с высоким содержанием Н28 и СО2, рекомендуется проводить на установках типа Маgra-РVT, АСФ-PVT или дру-

гих большеобъемных установках PVT [2, 4, 5]. Схема соединения технологических узлов установки Magra-PVT для изучения коэффициента сжимаемости газов и газоконденсатных смесей приведена на рис. 1. Для более точного определения объемов газа при различных давлениях рекомендуется проведение специального комплекса тарировочных исследований, которые включают определение объемов камер PVT, а также поправок на их термическое расширение и механическую деформацию.

Проведенные авторами настоящей статьи исследования [4, 5] показали, что наиболее технологичным способом определения коэффициента сжимаемости является сжатие определенного объема газа в камере PVT за счет изменения ее объема нагнетанием ртути или введением поршня.

Определение объемов камер PVT и насосов осуществлялось методом замера объема тарировочной жидкости (ртути) после ее слива из полностью заполненных камер при нормальных условиях: Ркам = 0,1013 МПа; Ткам = 293 К; количество замеров 15. Результаты определения объемов камер PVT и насосов по 15 замерам приведены в табл. 1.

Рис. 1. Схема установки для исследования коэффициента сжимаемости газов и газоконденсатных смесей: 1, 2 – ртутный насос; 3 – датчик объема; 4 – контейнер с газом; 5 – контейнер с конденсатом; 6 – камера PVT (0,7 л); 7 – кран высокого давления; 8 – датчик давления и температуры; 9 – камера PVT (3,8 л);

10 – сепаратор-термостат; 11 – газовый счетчик

Таблица 1

Результаты определения объемов камер PVT и насосов установки

Magra-PVT

3 Объем камер PVT и насосов, см

Камеры PVT Насосы

0,7 л 3,8 л 1 2

705,0 3604,0 489,2 489,2

+0,3 +3,0 ±0,1 ±0,1

Для расчета истинного объема газа в камерах PVT использовалось следующее выражение:

Vг = Vkom ± AVKcm(t) ± АVкам(р) – V рт(с) – AVpm(t) + A Vpm(p), (3)

где VKam – объем камеры PVT при нормальных условиях; AVKam(t) – поправка на термическое расширение камеры PVT; AVKam(p) – поправка на механическую деформацию камеры PVT; Урт(с) – объем закачанной в камеру PVT ртути (по счетчику); AVpm(t) – поправка на термическое расширение закачанной в камеру PVT ртути (по счетчику); AVpm(p) – поправка на механическую деформацию ртути.

Исходя из уравнения состояния для индивидуальных газов и газовых смесей, коэффициент сжимаемости рассчитывается по формуле PVT

Z = (4)

PVT

Определение коэффициента сжимаемости сухих газов начинается с заправки газа в камеру PVT, которая проводится следующим образом. В камеру PVT емкостью 0,7 л (см. рис. 1) из галонного контейнера передавливают газ в объеме, равном 50 или 100 л. Ориентировочно объем газа оценивается по давлению заправки, которое рассчитывается по формуле р = Р0Z Тт Qs (5)

, Ту ’ К }

0 кам

где Р0 – нормальное давление (0,1013 МПа); Тт – температура термостата, К; Qz – объем газа (100 л), загруженного в камеру при Т0; Т0 – нормальная температура, 293 К; VKam – объем камеры (0,7) с учетом поправок согласно формуле (1); Z – коэффициент сжимаемости.

Коэффициент сжимаемости газа при этом определяется ориентировочно – расчетным или экспериментальным путем. Далее в рабочей камере создают необходимую температуру и поэтапно повышают давление до 70-80 МПа. В конце каждого этапа после стабилизации давления опреде-

ляют объем сжатого газа. Объем газа при Р0 = 0,1013 МПа и Т0 = 293 К замеряют, пропуская газ через термостат и газовый счетчик.

Вычисляют коэффициент сжимаемости при давлении Р по формуле 2 = РУТ0 / °0°0Т, з (6)

где V – объем газа при давлении Р и температуре Т, м ; У0 – объем газа при Р0 = 0,1013 МПа и Т0 = 293 К, м3.

Для оценки точности определения коэффициентов сжимаемости газа сепарации Карачаганакского НГКМ проведен цикл экспериментов с использованием газовой смеси одного состава. Всего проведено 17 экспериментов, в каждом из которых определялись объем газовой смеси и давление и рассчитывался коэффициент сжимаемости (Т = Т0 = 293 К) (табл. 2). В табл. 2 приведены результаты определения коэффициента сжимаемости газа сепарации Карачаганакского НГКМ (состав газа приведен ниже).

Таблица 2

Результаты определения коэффициента сжимаемости газа сепарации

Карачаганакского НГКМ

№ п/п Р0, МПа У0, л Объем смеси ^ з с поправкой, см Давление в камере, МПа ^ с^° II N

1 2 3 4 5 6

1 0,1013 99,387 306,09 29,97 0,9114

2 – // – – // – 306,04 29,92 0,9112

3 – // – – // – 306,09 30,02 0,9113

4 – // – – // – 306,09 29,97 0,9115

5 – // – – // – 306,14 29,96 0,9113

6 – // – – // – 306,14 30,03 0,9140

7 – // – – // – 305,59 29,92 0,9080

8 – // – – // – 306,04 30,02 0,9110

9 – // – – // – 306,20 30,02 0,9130

10 – // – – // – 306,20 30,02 0,9090

11 – // – – // – 306,14 29,97 0,9110

12 – // – – // – 306,14 29,92 0,9090

13 – // – – // – 306,02 29,92 0,9080

14 – // – – // – 306,14 29,92 0,9080

15 – // – – // – 306,14 29,99 0,9110

16 – // – – // – 306,09 29,97 0,9114

17 – // – – // – 306,14 30,30 0,9115

Среднее – // – – // – У = 306,09 Р = 29,97 2 = 0,9112

Исходя из данных, приведенных в табл. 2, определены значения давления и объема газа сепарации с учетом погрешности измерения:

Рг.с = PC + АР = 29,97 ± 0,05 МПа; (7)

V = V~ + AV = 306,09 ± 0,55 см3. (8)

г .с г .с 5 5 V /

Среднее значение коэффициента сжимаемости равно

PV 29 97 ■ 306 09

Z = PVc = 29,97 306,09 = 0,9112. (9)

P0V0 0,1013 ■ 993,87

Коэффициент сжимаемости с учетом среднеквадратичного отклонения равен

Z = Z+AZ = 0,9112+ 0,0021. (10)

Относительная погрешность косвенных измерений находилась следующим образом:

-=о^ = 0,0021 = 0,0023; (11)

Z 0,9112

d~z = 0,0023 ■ 100 % = 0,23 % .

Анализ полученных данных позволяет говорить о высокой точности определения коэффициента сжимаемости газов и газовых смесей на установке Magra-PVT, т.к. относительная погрешность составляет доли процента.

При определении коэффициента сжимаемости газоконденсатных смесей делаются следующие допущения [2, 6]:

■ коэффициент сжимаемости определяется при давлении выше Рнк;

■ объем смеси при Р0 = 0,1013 МПа и Т0 = 293 К принимается равным сумме объемов сухого газа V0 и газового эквивалента V^ (Уг.э – объем паров, получаемых после испарения жидких углеводородов, растворенных в газе).

Определение коэффициента сжимаемости газоконденсатной смеси начинается с ее рекомбинации в камере PVT (6) (см. рис.1). Основные исследования проводят, используя газоконденсатную смесь в газообразном состоянии. Для этого поэтапно изотермически снижают давление в камере и в конце каждого этапа определяют объем газоконденсатной смеси

VCM при давлении Рсм. Снижение давления и определение объема исследуемой смеси проводят до достижения давления начала конденсации.

Затем давление в камере (6) снижается до минимально возможного и она охлаждается до комнатной температуры, при этом смесь разделяется на газ и конденсат. Газ пропускается через термостат (10) при Т = 293 К и счетчик (11), в котором замеряется объем У0. Весь выпавший конденсат собирается в сепараторе и камере, замеряется его объем qк и определяется плотность рк.

Расчет коэффициента сжимаемости проводится по формуле

Z =

V„ =

PVT 0

см см 0

(P0V0 + VK )Тс

24,040 • q к9к Тт 293 -М„

(12)

(13)

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

где Рсм, Тсм , VCM – давление, температура и объем смеси в камере; V0 -объем газа, замеренного счетчиком при Р0; VK – объем паров, получаемых после испарения выпавших жидких углеводородов (конденсата); qK – ко-

3 3

личество выпавшего конденсата, см ; рк – плотность конденсата, г/см ; Тт – температура термостата, К; Мк – молярная масса конденсата, г/моль.

Оценка точности разработанной методики проводилась путем сопоставления результатов определения коэффициентов сжимаемости индивидуальных газов (метана, углекислого газа, сероводорода) экспериментальным путем на установке PVT с данными, приведенными в [7, 8] (рис. 2).

Рис. 2. Экспериментальные и эталонные кривые коэффициента сжимаемости для метана (а); углекислого газа (б); сероводорода (в) при температурах: 423 К (1); 383 К (2); 293 К (4):

———- эталонные; • экспериментальные

Отклонение экспериментальных данных от эталонных практически во всех интервалах давлений и температур не превышает 0,2-1,3 %, что свидетельствует о достаточно высокой точности разработанной методики.

Для выявления влияния углекислого газа на сжимаемость проведены исследования смесей, состоящих из 75 % метана, 25 % углекислого газа (% мол.) и разного содержания С5+ при различных давлениях и температурах. Результаты проведенных экспериментов показали, что растворение в метане углекислого газа (рис. 3) существенно изменяет конфигурацию кривых коэффициентов сжимаемости.

Результаты, полученные в ходе экспериментальных работ, позволяют решать задачи, связанные с разработкой, добычей и транспортом газа. Так, например, разработаны графики для определения коэффициентов сжимаемости газов сепарации Астраханского ГКМ и Карачаганакского НГКМ в интервале давлений от 0,1013 до 70.0 МПа и температур от 293 до 383 К [7, 10].

20 40 60 80 20 40 60 20 40 60

Давление. МПа Давление, МПа Давление, МПа

а б в

Рис. 3. Экспериментальные зависимости коэффициента сжимаемости

3 3

газовой (а) и газоконденсатных (б – С5+ = 200 г/м ; в – С5+ = 800 г/м ) смесей от давления и температуры: 1 – 423 К; 2 – 293 К

Для Астраханского ГКМ графики построены по результатам исследования газа сепарации следующего состава: Ы28 – 24,52; СО2 – 14,68; С1 -55,43; С2 – 2,63; С3 – 1,09; С4 – 0,56; С5+ – 0,41; N2 – 0,67 % мол. (рис. 4). Этот состав газа сепарации близок к среднему составу по месторождению.

Для Карачаганакского НГКМ графики построены по результатам исследования газа сепарации следующего состава: Ы28 – 3,2; СО2 – 6,72; С1 – 80,61; С2 – 5,20; С3 – 2,11; С4 – 0,79; С5+ – 0,15; N2 – 1,29 % мол. (рис. 5).

Сопоставление расчетных значений коэффициентов сжимаемости различными методами с экспериментальными данными показало [2, 9], что отклонение в различных интервалах давлений и температур доходит до 27,7 %.

Наиболее близкие к экспериментальным аналитические значения коэффициентов сжимаемости для газа сепарации Астраханского ГКМ получены при использовании:

■ метода определения коэффициентов сжимаемости по Вичерту -Азизу – Кей – Брауну в диапазоне давлений 30-70 МПа и температур 293-348 К. Рассчитанные по этому методу значения в среднем завышены на + 5,8 %;

■ методов определения коэффициентов сжимаемости по Кей -Брауну и Кей – Питцеру в диапазоне давлений 50-70 МПа и температур 293-383 К. Отклонение расчетных коэффициентов сжимаемости от экспериментальных колеблется в пределах 0,8-5,4 %.

Из анализа расчетов коэффициентов сжимаемости с помощью уравнения состояния Пенга – Робинсона [2] следует, что при давлениях до 30 МПа с наименьшей погрешностью коэффициенты сжимаемости рассчитываются с помощью вышеупомянутого уравнения. С увеличением давления погрешность расчета возрастает.

Исследование коэффициента сжимаемости газоконденсатных смесей показало, что растворение в метане жидкой фазы (конденсата) приводит к его увеличению (рис. 6).

Так, при растворении 200 г/м углеводородов С5+ увеличение коэффициента сжимаемости составляет 2-5 %, при растворении порядка 800 г/м – 17-32 % в зависимости от температуры.

Особый интерес представляют впервые экспериментально определенные коэффициенты сжимаемости реальных газоконденсатных смесей Карачаганакского НГКМ с высоким содержанием конденсата (рис. 7).

Коэффициент сжимаемости

Температура, К

Рис. 4. График для определения коэффициента сжимаемости газа сепарации Астраханского ГКМ при различных давлениях и температурах

Коэффициент сжимаемости

Температура, К

Рис. 5. График для определения коэффициента сжимаемости газа сепарации Карачаганакского НГКМ при различных давлениях и температурах

Коэффициент сжимаемости

200 400 6 00 800 0

Конденсатосодержание, г/м” б

200 4 00 600 800

Конденсатосодержание, г/м3

Рис. 6. Зависимость коэффициента сжимаемости газоконденсатной смеси от содержания конденсата при различных давлениях и температурах:

1 – 50 МПа; 2 – 60 МПа; 3 – 70 МПа; 4 – 80 МПа: а – 293 К; б – 343 К; в – 383 К

Рис. 7. График для определения коэффициентов сжимаемости газоконденсатных смесей Карачаганакского НГКМ

Список литературы

1. Гуревич Г.Р. Справочное пособие по расчету фазового состояния и свойств газоконденсатных смесей / Г.Р. Гуревич, А.И. Брусиловский. -М.: Недра, 1984. – 264 с.

2. Гуревич Г.Р. Коэффициенты сжимаемости природных газов с высоким содержанием сероводорода и двуокиси углеводорода / Г. Р. Гуревич, В.И. Лапшин, А.И. Брусиловский, А.П. Желтов // Изв. вузов. Сер. Нефть и газ. – 1989. – № 7. – С. 61-64.

3. Ширковский А.И. Разработка и эксплуатация газовых и газоконденсатных месторождений: учебник для вузов. – 2-е изд. – М.: Недра, 1987. -309 с.

4. Лапшин В.И. Методика и результаты исследования коэффициентов сверхсжимаемости природных газов с высоким содержанием сероводорода и углекислого газа / В.И. Лапшин, А.П. Желтов, Г.Р. Гуревич // Геология нефти и газа. – 1989. – № 7. – С. 38-40.

5. Лапшин В.И. Экспериментальное определение коэффициента сверхсжимаемости газовых смесей с высоким содержанием Н28, С02 / В.И. Лапшин, Ю.Ю. Круглов, А.П. Желтов // Экспрес. информ. Сер. Разработка и эксплуатация газовых и газоконденсатных месторождений. -1988. – № 1. – С. 7-12.

6. Лапшин В. И. Природные газы сложного состава. Результаты исследования сверхсжимаемости / В.И. Лапшин // Газовая промышленность. -1991. – № 2. – С. 32-33.

7. Динков В. А. Расчет коэффициентов сжимаемости углеводородных газов и смесей: справочное пособие / В.А. Динков, З.Т. Галиуллин, А.П. Подкопаев. – М.: Недра, 1984. – С. 118.

8. Катц Д. Л. Руководство по добыче, транспорту и переработке природного газа / Д. Л. Катц, Д. Корнелл, Р. Кобаяши и др. – М.: Недра, 1965. -676 с.

9. Лапшин В.И. Аналитическое определение коэффициента сверхсжимаемости газов Астраханского месторождения. Совершенствование технологии строительства глубоких разведочных скважин в аномальных условиях Прикаспийской впадины / В.И. Лапшин, В.В. Томилкин, А.П. Желтов; под ред. П.С. Шмелева. – Саратов, 1989. – С. 121-128.

Источник

Коэффициент сжимаемости: как рассчитать, примеры и упражнения

Коэффициент сжимаемости: как рассчитать, примеры и упражнения – Наука

Содержание:

В коэффициент сжимаемости Z, или коэффициент сжатия для газов, представляет собой безразмерное значение (без единиц измерения), которое вводится как поправка в уравнение состояния идеальных газов. Таким образом, математическая модель больше напоминает наблюдаемое поведение газа.

В идеальном газе уравнение состояния, связанное с переменными P (давление), V (объем) и T (температура), выглядит следующим образом: П.В. _{идеальный} = n.R.T где n = число молей и R = постоянная идеального газа. Добавляя поправку на коэффициент сжимаемости Z, это уравнение принимает вид:

Как рассчитать коэффициент сжимаемости?

Учитывая, что молярный объем равен V_{прохладно} = В / п, имеем реальный молярный объем:

Поскольку коэффициент сжимаемости Z зависит от условий газа, он выражается как функция давления и температуры:

Сравнивая первые два уравнения, можно увидеть, что если число молей n равно 1, молярный объем реального газа связан с объемом идеального газа следующим образом:

Когда давление превышает 3 атмосферы, большинство газов перестают вести себя как идеальные газы, и фактический объем значительно отличается от идеального.

Это было реализовано в его экспериментах голландского физика Йоханнеса Ван дер Ваальса (1837-1923), которые привели его к созданию модели, которая лучше подходила для практических результатов, чем уравнение идеального газа: уравнение состояния Вана. дер Ваальс.

Примеры

Согласно уравнению П.В._{настоящий}= Z.n.RT, для идеального газа Z = 1. Однако в реальных газах с увеличением давления увеличивается и значение Z. Это имеет смысл, потому что чем выше давление, молекулы газа имеют больше возможностей для столкновения, поэтому силы отталкивания увеличиваются, а вместе с ними и объем.

С другой стороны, при более низких давлениях молекулы движутся более свободно и силы отталкивания уменьшаются. Поэтому ожидается меньшая громкость. Что касается температуры, то при повышении Z уменьшается.

Как заметил Ван-дер-Ваальс, вблизи так называемой критической точки поведение газа сильно отличается от поведения идеального газа.

Критическая точка (T_c, П_c) любого вещества являются значениями давления и температуры, определяющими его поведение до фазового перехода:

-T_c это температура, выше которой рассматриваемый газ не сжижается.

-П_c– минимальное давление, необходимое для сжижения газа при температуре T_c

Однако у каждого газа есть своя критическая точка, определяющая температуру и пониженное давление T_р И п_р следующим образом:

Замечено, что ограниченный газ с идентичным V_р Y Т_р оказывает такое же давление п_р. По этой причине, если Z отображается как функция п_р себе Т_р, каждая точка на этой кривой одинакова для любого газа. Это называется принцип соответствующих состояний.

Коэффициент сжимаемости в идеальных газах, воздухе, водороде и воде

Ниже представлена кривая сжимаемости для различных газов при различных пониженных температурах. Вот несколько примеров Z для некоторых газов и процедура определения Z с помощью кривой.

Идеальные газы

У идеальных газов Z = 1, как объяснялось в начале.

Воздух

Для воздуха Z составляет приблизительно 1 в широком диапазоне температур и давлений (см. Рисунок 1), где модель идеального газа дает очень хорошие результаты.

Водород

Z> 1 для всех давлений.

вода

Чтобы найти Z для воды, вам нужны значения критических точек. Критическая точка воды: P_c = 22,09 МПа и T_c= 374,14 ° С (647,3 К). Снова необходимо учитывать, что коэффициент сжимаемости Z зависит от температуры и давления.

Например, предположим, что вы хотите найти Z воды при 500 ºC и 12 МПа. Итак, первое, что нужно сделать, это вычислить приведенную температуру, для которой градусы Цельсия необходимо преобразовать в Кельвина: 50 ºC = 773 K:

Этими значениями поместим на график рисунка кривую, соответствующую T_р = 1,2, обозначено красной стрелкой. Затем смотрим на горизонтальную ось значение P_р ближе к 0,54, отмечен синим цветом. Теперь рисуем вертикаль, пока не перехватим кривую T_р = 1,2 и, наконец, он проецируется из этой точки на вертикальную ось, где мы читаем приблизительное значение Z = 0,89.

Решенные упражнения

Упражнение 1

Это образец газа с температурой 350 К и давлением 12 атмосфер с молярным объемом на 12% больше, чем предсказывается законом идеального газа. Рассчитать:

а) Коэффициент сжатия Z.

б) Молярный объем газа.

c) На основании предыдущих результатов укажите, какие силы преобладают в данной пробе газа.

Данные: R = 0,082 л атм / моль К

Решение для

Зная, что V _{настоящий} на 12% больше, чем V_{идеальный} :

Решение б

П. V_{настоящий} = Z. R. T → V_{настоящий} = (1,12 x 0,082 x 350/12) л / моль = 2,14 л / моль.

Решение c

Силы отталкивания преобладают, так как объем образца увеличился.

Упражнение 2.

В объеме 4,86 л при 27 ° C содержится 10 моль этана. Найдите давление этана по формулам:

а) Модель идеального газа

б) Уравнение Ван-дер-Ваальса

c) Найдите коэффициент сжатия из предыдущих результатов.

Данные для этана

а = 5,489 дм 6 . атм. моль -2 и b = 0,06380 дм 3 . моль -1 .

Критическое давление: 49 атм. Критическая температура: 305 К

Решение для

Температура переводится в Кельвин: 27 º C = 27 + 273 K = 300 K, также помните, что 1 литр = 1 л = 1 дм 3 .

Затем предоставленные данные подставляются в уравнение идеального газа:

P.V = n.R.T → P = (10 x 0,082 x 300 / 4,86 л) атм = 50,6 атм

Решение б

Уравнение состояния Ван-дер-Ваальса:

Где a и b – коэффициенты, указанные в заявлении. При очистке P:

Решение c

Рассчитываем пониженное давление и температуру:

С этими значениями мы ищем значение Z на графике на рисунке 2, обнаруживая, что Z составляет приблизительно 0,7.

Ссылки

Аткинс, П. 1999. Физическая химия. Издания Омега.
Ценгель, Ю. 2012. Термодинамика. 7 ма Издание. Макгроу Хилл.
Энгель, Т. 2007. Введение в физико-химию: термодинамика. Пирсон.
Левин, И. 2014. Основы физико-химии. 6-е. Издание. Макгроу Хилл.
Википедия. Фактор сжимаемости. Получено с: en.wikipedia.org.

Значение символа медицины

Морская звезда: характеристика, виды, среда обитания, дыхание

Уравнение состояния газов

Состояние газов характеризуется давлением Р, температурой 7, и объемом V. Связь между этими величинами определяется законами газового состояния.

Нефтяные и природные газы имеют значительные отклонения от законов идеальных газов вследствие взаимодействия между собой молекул, которое возникает при сжатии реальных газов. Степень отклонения сжимаемости реальных газов от идеальных характеризуется коэффициентом сжимаемости z, показывающим отношение объема реального газа к объму идеального при одних и тех же условиях.

В пласте углеводородные газы могут находиться в самых различных условиях. С увеличением давления от О до 3-4 МПа объем газов уменьшается. При этом молекулы углеводородного газа сближаются и силы притяжения между ними помогают внешним силам, сжимающим газ. Когда углеводородный газ сильно сжат, межмолекулярные расстояния оказываются настолько малыми, что отталкивающие силы начинают оказывать сопротивление дальнейшему уменьшению объема и сжимаемость газа уменьшается.

На практике состояние реальных углеводородных газов при различных температурах и давлениях можно описывать на основании уравнения Клапейрона:

где Р – давление гз. Па; V’ – объем, занимаемый газом при заданном давлении, м 3 ; т – масса газа, кг; R –газовая постоянная, Дж/(кг-К); Т- температура, К; г – коэффициент сжимаемости.

Коэффициент сжимаемости определяют по графикам, построенным по экспериментальным данным.

Состояние углеводородных газожидкостных систем при изменении давления и температуры.

При движении нефти и газа в пласте, стволе скважины, системах сбора и подготовки меняются давление и температура, что обусловливает изменение фазового состояния углеводородов — переход из жидкого в газообразное состояние и наоборот. Так как нефть и газ состоят из большого числа разнообразных по своим свойствам компонентов, то при определенных условиях часть этих компонентов может находиться в жидкой фазе, а другая — в паровой (газовой) фазе. Очевидно, что закономерности движения однофазной системы в пласте и стволе скважины значительно отличаются от закономерностей многофазного движения. Условия дальнего транспорта нефти и газа и последующей переработки требуют отделения легко испаряющихся компонентов от жидкой конденсированной фракции. Поэтому выбор технологии разработки месторождения, системы внутрипромысловой подготовки нефти и газа во многом связан с изучением фазового состояния углеводородов в меняющихся термодинамических условиях.

Фазовые превращения углеводородных систем иллюстрируются диаграммами фазовых состояний, показывающими связь между давлением, температурой и удельным объемом вещества.

На рис. 2.2, а приведена диаграмма состояния чистого газа, (этана). Сплошными линиями на диаграмме показана связь между давлением и удельным объемом вещества при постоянных температурах. Линии, проходящие через область, ограниченную пунктирной кривой, имеют три характерных участка. Если рассматривать одну из линий области высоких давлений, то сначала рост давления сопровождается небольшим увеличением удельного объема вещества, которое обладает сжимаемостью и в этой области находится в жидком состоянии.

Рис. 2.2. Диаграмма состояния чистого газа

При некотором давлении изотерма резко изламывается и имеет вид горизонтальной линии. При постоянном давлении происходит непрерывное увеличение объема вещества. В этой области жидкость испаряется и переходит в паровую фазу. Испарение заканчивается в точке второго излома изотермы, после которого изменение объема сопровождается почти пропорциональным уменьшением давления. В этой области все вещество находится в газообразном

состоянии (в паровой фазе). Пунктирной линией, соединяющей точки излома изотерм, ограничена область перехода вещества из жидкого в паровое состояние или наоборот (в сторону уменьшения удельных объемов). Эта область соответствует условиям, при которых вещество находится одновременно в двух состояниях жидком и газообразном (область двухфазного состояния вещества). Пунктирная линия, расположенная влево от точки С, называется кривой точек парообразования. Координаты точек данной линии — давление и температура, при которых начинается кипение вещества. Вправо от точки С лежит пунктирная линия, называемая кривой точек конденсации или точек росы. Она показывает при каких давлениях и температурах начинается конденсация пара – переход вещества в жидкое состояние. Точка С, лежащая в вершине двухфазной области, называется критической точкой. При давлении и температуре, соответствующей этой точке, свойства паровой и жидкой фаз одинаковы. Кроме того, для чистого вещества критическая точка определяет наивысшие значения давления и температуры, при которых вещество может одновременно находиться в двухфазном состоянии. При рассмотрении изотермы, не пересекающей двухфазную область видно, что свойства вещества изменяются непрерывно и переход вещества из жидкого состояния в газообразное или наоборот происходит, минуя двухфазное состояние.

На рис. 2.2, б приведена диаграмма состояния этана, перестроенная в координатах давление-температура. Так как чистое вещество из одного фазового состояния в другое переходит при постоянном давлении, то кривые точек испарения и конденсации на этой диаграмме совпадают и заканчиваются критической точкой С. полученная линия разграничивает области жидкого и парообразного вещества. В двухфазном состоянии вещество может находиться только при давлениях и температурах соответствующих координатам этой линии.

Коэффициент сжимаемости природного газа

Большая Энциклопедия Нефти и Газа

Коэффициент сжимаемости природного газа определяется по температуре и давлению газа на входе в нагнетатель. График зависимости Z / ( рн, Ts, А) показан на рис. П-12. Значение газовой постоянной принимается по величине относительного удельного веса ( по воздуху) или данным химического анализа. [2]

Коэффициент сжимаемости природного газа определяется по температуре и давлению газа на входе в нагнетатель. График зависимости Z — f ( ри, Тл, А) показан на рис. П-12. Значение газовой постоянной принимается по величине относительного удельного веса ( по воздуху) или данным химического анализа. [3]

Коэффициент сжимаемости природных газов приближенно может быть определен по критическим параметрам. [4]

Коэффициенты сжимаемости природных газов в диапазоне давлений до 2 5 МПа и содержащих не более 2 % группы Cs высшие или ароматических углеводородов и не более 5 % полярных или кислых компонентов можно находить по графикам Брауна с соавторами или графикам Максвелла. [5]

Рассчитываякоэффициенты сжимаемости природных газов, обычно применяют методы, в основу которых положен принцип соответственных состояний. Согласно этому принципу значения коэффициентов сжимаемости различных УВ при одинаковых приведенных температуре ТПР и давлении рпр приблизительно равны. Это позволяет использовать для определения объема газа его зависимость от приведенных параметров. [6]

Значениякоэффициента сжимаемости природного газа указаны в табл. 3 для приведенных давления и температуры. [7]

А правильно ли мы определяемкоэффициент сжимаемости природного газа. [8]

На рис. 6 показана зависимостькоэффициента сжимаемости природного газа от приведенных параметров, а на рис. 7 и 8 та же величина, в первом случае, для паров углеводородов с молекулярным весом от 20 до 40 и, во втором случае, для паров. [10]

Все упомянутые выше методы определениякоэффициента сжимаемости природного газа применяются для расчета z газовых смесей, не содержащих пары воды. Для определения z газовых смесей с парами воды следует найти молярную долю паров воды в смеси и пересчитать ее состав. [11]

Нижеследующие три таблицы представляют некоторые результаты расчетовкоэффициента сжимаемости природного газа по методу AGA8, полученные с помощью пакета Гаэпак, в котором обе методики используются как рабочие. [12]

Метод 4 основан на применении псевдоприведенных свойств и диаграммыкоэффициента сжимаемости природных газов. [13]

И в свой кабинет и задал вопрос, который для нас был неожиданным: А правильно ли мы определяемкоэффициент сжимаемости природного газа. [14]

Сравнение рекомендованных справочных ( таблицы ГСССД 81 — 84) и расчетных данных ( по модифицированному уравнению состояния) длякоэффициентов сжимаемости природного газа, состав которого регламентирован ГОСТ 2319 — 83: 98 63 мол. [15]

ПОИСК

Для метана в пределах давления от 1 до 350 бар коэффициент сжимаемости меньше единицы, т. е. за счет действия межмолеку-лярных сил притяжения метан сжимается сильнее, чем идеальный газ.

Минимальное значение коэффициента сжимаемости метана соответствует давлению 140—160 бар. При давлении выше 350 бар при сжатии газа начинают влиять на его объем размеры молекул и коэффициент сжимаемости становится больше единицы. [c.

Значения коэффициента сжимаемости газа, являющегося смесью различных газов, принимают в приближенных расчетах по его ОСНОВНОМ компоненту в частности, для природного и попутного газов — по метану (см. табл.

3), а в точных расчетах — в зависимости от коэффициента сжимаемости отдельных составляющих газов и их содержания в смеси. [c.8]

Вещество сравнения. Одним из методов, применяемых для нормализации или приведения уравнений, является соотнесение свойств рассматриваемого вещества со свойствами вещества сравнения, которые хорошо известны.

Так, в ходе многолетней работы Отмер [536] разработал линейную зависимость между рядом свойств и некоторым другим свойством, например давлением паров иолы при постоянной температуре. Питцер и др. [555] определили коэффициент сжимаемости как отклонение от значения коэффициента сжимаемости такой жидкости сравнения, как аргон.

Ли и Кеслер [425] соотносят свойства со свойствами двух хорошо изученных жидкостей — простой жидкости и н-октана. Авторы работы [684] в некоторых случаях применяют в качестве жидкостей сравнения метан и н-октан. [c.29]

В табл. 33 приведено содержание воды в газовой фазе системы метан — вода, полученное пересчетом данных из [Olds R. H., Sage В. H., La ey W. N., 1942 r.], при этом коэффициент сжимаемости газового раствора г) принимался рав- [c.51]

Поэтому, несмотря на доступность воспроизведения и измерения в широких пределах температуры и давления, изучение объемного поведения всей совокупности смесей практически не осуш ествимо.

Тем не менее необходимость точной интерполяции влияния состава на поведение системы требует экспериментального изучения достаточного числа различных смесей в широком диапазоне, изменения составов. На рис. 2.

3 показано влияние состава на коэффициент сжимаемости смеси метан — этан для ряда давлений при температуре 71,1° С. [c.21]

Смотреть страницы где упоминается термин Метан коэффициент сжимаемости: [c.29] [c.245] [c.28] [c.1015] Технология связанного азота Издание 2 (1974) — [ c.101 ]

Коэффициент сжимаемости

Метан коэффициенты

Сжимаемость

© 2019 chem21.info Реклама на сайте

Способ оперативного определения коэффициента сжимаемости газов и их смесей

Изобретение относится к измерительной технике и может быть использовано на замерных узлах газодобывающих и газотранспортных предприятий, при проведении исследований физических свойств газов и их смесей (в частности, топливных природных и попутных нефтяных) и в других случаях, где необходимо знание величины отступления поведения газа от идеального.

Одним из основных показателей работы газодобывающего или газотранспортного предприятия является количество добываемого или передаваемого газа в единицу времени — его объемный расход Q0.

Наиболее распространенным способом измерения объемного расхода, принятым на сегодня, является способ определения переменного перепада давления на сужающем устройстве (СУ) — сопле или диафрагме.

При этом основным расчетным соотношениям для определения величины Qo является следующее 1:

где ΔР — перепад давления на СУ, ρ — плотность газа в рабочих условиях (р.у.) (при давлении Р и температуре газа в трубопроводе 7), Q0 — объемный расход (в р.у.), А — интегральный коэффициент, учитывающий форму СУ (коэффициент расхода), поправочный множитель на расширение газа, площадь минимального проходного отверстия СУ и др.

Плотность газа в рабочих условиях р на предприятиях газовой промышленности не измеряется (из-за отсутствия надежных и сравнительно недорогих средств измерения). Как правило, поступают одним из следующих образов:

— либо в лаборатории взвешивают представительную пробу газа в особом сосуде известного объема (пикнометре) при комнатной температуре, определяют плотность, затем измеряют температуру и атмосферное давление, вносят поправку на отличие давления и температуры газа от стандартных, т.е. приводят плотность к стандартным условиям, иными словами, получают ее значение ρс при давлении Рс=1,0131·105 Па и температуре Тс=293,15K (наиболее распространенный способ);

— либо на хроматографе определяют компонентный состав (с соответствующей высокой точностью) и, уже исходя из него, вычисляют значение ρс (более редкий способ).

Для расчета состояния реальных газов и их свойств используют полуэмпирические формулы или уравнения, построенные на основе обработки реальных зависимостей, полученных из эксперимента [4].

В инженерных расчетах чаще всего пользуются обобщенным уравнением Менделеева-Клапейрона (2), в которое вводится некоторый безразмерный коэффициент Z, получивший название фактора сжимаемости; он учитывает отклонение поведения реального газа от идеального:

здесь Р — давление газа, Т — его температура, V — занимаемый газом объем, R — универсальная газовая постоянная, m — масса газа, М — его молярный вес.

Зная температуру и давление, из уравнения состояния (2) вычисляют плотность ρ газа как в рабочих, так и в стандартных условиях:

а из соотношениядалее находят ρ через ρс:

здесь Zc и Z — значения факторов сжимаемости при стандартных (Рс, Тс) и рабочих (Р, Т) условиях. При этом уравнение (1) примет вид

где коэффициент- отношение факторов сжимаемости получил название коэффициента сжимаемости.

Как видно из (5), коэффициент сжимаемости прямо входит в формулу, по которой рассчитывается расход, и его погрешность входит в погрешность определения расхода.

Наиболее точно факторы сжимаемости любых газов — чистых попутных нефтяных либо природных газов определяются экспериментально.

На специальном физическом оборудовании в лаборатории в некоторой области температур и давлений получают совокупность экспериментальных точек [Рi, Vi, Ti, или [Рi, ρi, Ti], или [Zi, ρi, Ti], где Рi, Vi, ρi, Тi, Zi — соответственно давление, удельный объем, плотность, температура и фактор сжимаемости в точке i.

Обрабатывая эти данные, получают зависимости Z(P, Т), по которым можно найти значения Z в промежуточных точках.

Техника для экспериментального определения зависимостей Z(P, Т) достаточно сложна и не может быть сегодня воспроизведена в заводской лаборатории газового предприятия или в ЦНИПРе. Кроме того, такие измерения (по существу исследования) требуют значительного труда и времени. Поэтому на практике используют графические и аналитические способы определения коэффициентов Z и K.

ГОСТ 30319.2-96 [4] рекомендует использовать один из 4-х расчетных способов определения Z и K, а именно: NX19 мод., УС GERG, УС AGA8-92DC и УС ВНИЦ СМВ.

Исходными данными для первых двух являются давление, температура, плотность в стандартных условиях ρс и молярные доли азота и углекислого газа.

Для последних двух способов исходными являются давление, температура и молярные доли всех компонентов природного газа.

Погрешность вычисления величины Z-δZ зависит от того, какой расчетный способ используется, а также от точности измерения вводимых исходных данных и термобарических параметров (рабочих условий).

Действительно, обратившись к таблице 1 ГОСТ 30319.2-96, увидим, что для способа NX19 мод.

при ρс>0,75 кг/м3 и Р>7 МПа погрешность расчета составляет 1,09%, а отклонение от экспериментальных данных — 1,65%.

Для способа GERG-91 мод.: при ρ=0,74-1,00 кг/м2 (смеси с H2S) при Р — 0,1-11 МПа погрешность расчета составляет 2,1% отклонение от экспериментальных данных 3,1%.

Для способа АGА8-92ДС: при ρ=0,74-1,00 (смеси с H2S) и Р=0,1-11 МПа погрешность расчета — 1,3%, отклонение экспериментального значения — 1,88% и т.д.

Примем далее за прототип один из способов, например, GERG-91 мод.

Таким образом, для природных газов только погрешности расчета (в отдельных областях рабочих условий) доходят до 2%. Экспериментальные данные дадут, по-видимому, расхождение с истинными еще больше.

На уровне погрешностей измерения других параметров расхода — температуры, давления, перепада давления, лежащих в диапазоне 0,1…0,5%, такие большие погрешности при установлении величины Z становятся определяющими.

Важным моментом является также то обстоятельство, что расчетная величина Z выступает как средняя за период между измерениями величин, входящими в исходные расчетные данные при подсчете, изменении компонентного состава в течение этого промежутка времени, неконтролируемая погрешность может выходить за границы погрешности расчетной величины Z.

Таким образом, недостатком существующего способа определения коэффициента сжимаемостиявляется необходимость проведения предварительного хроматографического анализа с целью получения данных о компонентном составе и высокая погрешность расчетов величины К в отдельных термобарических областях. Кроме того, полученное значение коэффициента сжимаемости относится к определенному моменту времени — времени взятия пробы для анализа tо, т.е. К=K(tо). Невозможность непрерывного слежения за величиной К=K(t) является следующим недостатком способа определения К.

Техническим результатом предлагаемого способа определения коэффициента сжимаемости К является возможность оперативно измерять этот коэффициент, т.е.

находить функцию K(t) с погрешностью не выше погрешности измерения других входящих в формулу расхода (5) физических величин (Р, ΔР, Т, ρс) в любом диапазоне термобарических параметров и, как следствие этого, понижение погрешности измерения расхода при использовании расходомеров на сужающих устройствах.

Технический результат достигается тем, что в способе оперативного определения коэффициента сжимаемости используют объемный резонатор, выполненный из металла с малым коэффициентом температурного расширения и с известной собственной частотой в вакууме ω0, заполняют газом при стандартном давлении и температуре и измеряют значение резонансной частоты ωс, затем заполняют его газом при рабочих давлениях Р и температуре Т и измеряют значение собственной частоты ωр, после чего коэффициент сжимаемости К рассчитывают по соотношению:

На фиг.1 изображена схема устройства, реализующего предложенный способ. Она включает в себя СВЧ генератор 3 см диапазона длин волн на диоде Ганна 1, два объемных резонатора, изготовленных из металла с малым температурным коэффициентом расширения — измерительный 2 и опорный 3, детектор измерительного канала 4, детектор опорного канала 5.

Электронная часть устройства состоит из блока управления 8, блока измерения частоты 9 и стабилизированного блока питания 10. Газовый тракт включает трубку подвода газа 11, редуктор 12, входной 13 и выходной 14 газовые вентили, манометр 15, термометр 16, выкидную трубку 17. Измерительный резонатор помещен в термостат 18.

Работа устройства происходит следующим образом.

В блоке 8 вырабатывается пилообразное напряжение, управляющее частотой генератора 1.

Более точно — «пила» состоит из 256 ступенек, так что номер ступеньки («код») однозначно определяет напряжение и, следовательно, частоту генератора: таким образом, осуществляется взаимнооднозначное соответствие между кодом и частотой. Код, соответствующий резонансной частоте резонатора 2, высвечивается на передней панели прибора.

Опорный канал, на основе резонатора 3 и детектора 5, служит для стабилизации начальной частоты генератора 1; электроника блока управления 8 устроена таким образом, что резонансная частота резонатора 3 всегда соответствует одному и тому же коду; в случае отклонения от заданного значения кода вырабатывается напряжение, подаваемое на диод Ганна, генератора 1, которое корректирует уход частоты.

Выходным параметром схемы регистрации является резонансная частота резонатора. В отсутствие газа (в вакууме) частота резонатора равна ωо; при заполнении резонатора газом с диэлектрической постоянной ε частота его понижается и становится равной ω.

Используем соотношение между диэлектрической проницаемостью и плотностью газа, основанное на соотношении Клаузиуса-Мосотти, которое связывает микроскопические параметры вещества газа — его поляризуемость α и молярную массу М — с макроскопическими, измеряемыми параметрами — плотностью вещества ρ и его относительной диэлектрической проницаемостью (ДП) ε 6:

где NA — число Авогадро; εо=8,854·10-12 ф/м — электрическая постоянная.

Разрешив (5) относительно ρ, получим:

Поскольку для всех газов при небольших и умеренных давлениях (P≤10 МПа) ε-1

Коэффициент сжимаемости газов и газоконденсатных смесей: экспериментальное определение и расчеты — PDF

1 120 Коэффициент сжимаемости газов и газоконденсатных смесей: экспериментальное определение и расчеты КОЭФФИЦИЕНТ СЖИМАЕМОСТИ ГАЗОВ И ГАЗОКОНДЕНСАТНЫХ СМЕСЕЙ: ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ И РАСЧЕТЫ В.И. Лапшин, А.Н. Волков, И.М.

Шафиев (ООО «Газпром ВНИИГАЗ») Коэффициент сжимаемости (Z) характеризует отличие реальных газов от идеальных. Для идеальных газов, в которых отсутствует взаимодействие между молекулами, справедлив закон Клайперона, который обобщает законы Бойля Мариотта и Гей-Люссака: (P V) / T = (P 0 V 0 ) / T 0 = R, где R универсальная газовая постоянная.

Для реальных газов произведение объема на давление (P V) при постоянной температуре не является постоянной величиной. С ростом давления это произведение вначале уменьшается до определенного предела, а затем с увеличением давления увеличивается.

При практических расчетах для оценки степени указанных отклонений в уравнение Клайперона вводится поправочный коэффициент (Z) [1, 2, 3].

Уравнение Клайперона Менделеева с учетом коэффициента сжимаемости имеет вид PV = ZNRT, где Р абсолютное давление; V объем, занимаемый газом (газоконденсатной смесью) при определенных давлении и температуре; R универсальная газовая постоянная; N число молей газа. Это уравнение можно записать в виде PV N =.

(1) ZRT Учитывая, что определение коэффициента сжимаемости проводится без изменения числа молей газа (N г = const), PV 0 0 N г =, (2) Z RT 0 0 где V 0 объем газа при Р 0 = 0,1013 МПа, м 3 ; Т 0 = 293 К; R = 24,01 МПа К Z 0 = 1. Экспериментальное определение коэффициента сжимаемости газов и газоконденсатных смесей, особенно с высоким содержанием Н 2 S и СО 2, рекомендуется проводить на установках типа Маgra-РVT, АСФ-PVT или дру- м 3 ;

2 Актуальные вопросы исследований пластовых систем месторождений углеводородов. Часть I 121 гих большеобъемных установках PVТ [2, 4, 5]. Схема соединения технологических узлов установки Маgra-РVT для изучения коэффициента сжимаемости газов и газоконденсатных смесей приведена на рис. 1.

Для более точного определения объемов газа при различных давлениях рекомендуется проведение специального комплекса тарировочных исследований, которые включают определение объемов камер PVT, а также поправок на их термическое расширение и механическую деформацию.

Проведенные авторами настоящей статьи исследования [4, 5] показали, что наиболее технологичным способом определения коэффициента сжимаемости является сжатие определенного объема газа в камере PVT за счет изменения ее объема нагнетанием ртути или введением поршня.

Определение объемов камер PVT и насосов осуществлялось методом замера объема тарировочной жидкости (ртути) после ее слива из полностью заполненных камер при нормальных условиях: Р кам = 0,1013 МПа; Т кам = 293 К; количество замеров 15. Результаты определения объемов камер PVT и насосов по 15 замерам приведены в табл. 1. Рис. 1.

Схема установки для исследования коэффициента сжимаемости газов и газоконденсатных смесей: 1, 2 ртутный насос; 3 датчик объема; 4 контейнер с газом; 5 контейнер с конденсатом; 6 камера PVT (0,7 л); 7 кран высокого давления; 8 датчик давления и температуры; 9 камера PVT (3,8 л); 10 сепаратор-термостат; 11 газовый счетчик

3 122 Коэффициент сжимаемости газов и газоконденсатных смесей: экспериментальное определение и расчеты Таблица 1 Результаты определения объемов камер PVT и насосов установки Magra-PVT Объем камер PVT и насосов, см 3 Камеры PVT Насосы 0,7 л 3,8 л ,0 3604,0 489,2 489,2 +0,3 +3,0 +0,1 +0,1 Для расчета истинного объема газа в камерах PVT использовалось следующее выражение: V г = V кам + ΔV кам (t) + ΔV кам (р) V рт (с) ΔV рт (t) + ΔV рт (р), (3) где V кам объем камеры PVT при нормальных условиях; ΔV кам (t) поправка на термическое расширение камеры PVT; ΔV кам (р) поправка на механическую деформацию камеры PVT; V рт (с) объем закачанной в камеру PVT ртути (по счетчику); ΔV pт (t) поправка на термическое расширение закачанной в камеру PVT ртути (по счетчику); ΔV рт (р) поправка на механическую деформацию ртути. Исходя из уравнения состояния для индивидуальных газов и газовых смесей, коэффициент сжимаемости рассчитывается по формуле PVT Z = 0. (4) PV 0 0T Определение коэффициента сжимаемости сухих газов начинается с заправки газа в камеру PVT, которая проводится следующим образом. В камеру PVT емкостью 0,7 л (см. рис. 1) из галонного контейнера передавливают газ в объеме, равном 50 или 100 л. Ориентировочно объем газа оценивается по давлению заправки, которое рассчитывается по формуле Р0Z тqг Р = Т з, (5) Т 0Vкам где Р 0 нормальное давление (0,1013 МПа); Т т температура термостата, К; Q г объем газа (100 л), загруженного в камеру при Т 0 ; Т 0 нормальная температура, 293 К; V кам объем камеры (0,7) с учетом поправок согласно формуле (1); Z коэффициент сжимаемости. Коэффициент сжимаемости газа при этом определяется ориентировочно расчетным или экспериментальным путем. Далее в рабочей камере создают необходимую температуру и поэтапно повышают давление до МПа. В конце каждого этапа после стабилизации давления опреде-

4 Актуальные вопросы исследований пластовых систем месторождений углеводородов. Часть I 123 ляют объем сжатого газа. Объем газа при Р 0 = 0,1013 МПа и Т 0 = 293 К замеряют, пропуская газ через термостат и газовый счетчик.

Вычисляют коэффициент сжимаемости при давлении Р по формуле Z = PVT 0 / P 0 V 0 T, (6) где V объем газа при давлении Р и температуре Т, м 3 ; V 0 объем газа при P 0 = 0,1013 МПа и Т 0 = 293 К, м 3.

Для оценки точности определения коэффициентов сжимаемости газа сепарации Карачаганакского НГКМ проведен цикл экспериментов с использованием газовой смеси одного состава.

Всего проведено 17 экспериментов, в каждом из которых определялись объем газовой смеси и давление и рассчитывался коэффициент сжимаемости (Т = Т 0 = 293 К) (табл. 2). В табл. 2 приведены результаты определения коэффициента сжимаемости газа сепарации Карачаганакского НГКМ (состав газа приведен ниже).

Таблица 2 Результаты определения коэффициента сжимаемости газа сепарации Карачаганакского НГКМ п/п Р 0, МПа V 0, л Объем смеси с поправкой, см з Давление в камере, МПа , , ,09 29,97 0, // — — // — 306,04 29,92 0, // — — // — 306,09 30,02 0, // — — // — 306,09 29,97 0, // — — // — 306,14 29,96 0, // — — // — 306,14 30,03 0, // — — // — 305,59 29,92 0, // — — // — 306,04 30,02 0, // — — // — 306,20 30,02 0, // — — // — 306,20 30,02 0, // — — // — 306,14 29,97 0, // — — // — 306,14 29,92 0, // — — // — 306,02 29,92 0, // — — // — 306,14 29,92 0, // — — // — 306,14 29,99 0, // — — // — 306,09 29,97 0, // — — // — 306,14 30,30 0,9115 Среднее — // — — // — V = 306,09 P = 29,97 Z = 0,9112 Z = PV P 0 V 0

5 124 Коэффициент сжимаемости газов и газоконденсатных смесей: экспериментальное определение и расчеты Исходя из данных, приведенных в табл. 2, определены значения давления и объема газа сепарации с учетом погрешности измерения: Р г.с = P с г. + ΔР = 29,97 ± 0,05 МПа; (7) 3 V = V + ΔV = 306,09 0,55 cм. (8) г с г ±..

с Среднее значение коэффициента сжимаемости равно PV Z = г. с 29,97 306,09 = = 0, (9) PV 0 0 0, ,87 Коэффициент сжимаемости с учетом среднеквадратичного отклонения равен Z = Z + ΔZ = 0, ,0021. (10) Относительная погрешность косвенных измерений находилась следующим образом: σz 0,0021 σ = = = 0,0023; (11) Z 0,9112 d = 0, % = 0,23 %.

Z Анализ полученных данных позволяет говорить о высокой точности определения коэффициента сжимаемости газов и газовых смесей на установке Magra-PVT, т.к. относительная погрешность составляет доли процента.

При определении коэффициента сжимаемости газоконденсатных смесей делаются следующие допущения [2, 6]: коэффициент сжимаемости определяется при давлении выше Р нк ; объем смеси при Р 0 = 0,1013 МПа и Т 0 = 293 К принимается равным сумме объемов сухого газа V 0 и газового эквивалента V г.э (V г.

э объем паров, получаемых после испарения жидких углеводородов, растворенных в газе). Определение коэффициента сжимаемости газоконденсатной смеси начинается с ее рекомбинации в камере PVT (6) (см. рис.1). Основные исследования проводят, используя газоконденсатную смесь в газообразном состоянии.

Для этого поэтапно изотермически снижают давление в камере и в конце каждого этапа определяют объем газоконденсатной смеси V см при давлении Р см. Снижение давления и определение объема исследуемой смеси проводят до достижения давления начала конденсации.

6 Актуальные вопросы исследований пластовых систем месторождений углеводородов. Часть I 125 Затем давление в камере (6) снижается до минимально возможного и она охлаждается до комнатной температуры, при этом смесь разделяется на газ и конденсат. Газ пропускается через термостат (10) при Т = 293 К и счетчик (11), в котором замеряется объем V 0.

Весь выпавший конденсат собирается в сепараторе и камере, замеряется его объем q к и определяется плотность ρ к.

Расчет коэффициента сжимаемости проводится по формуле Z = V кр Р V см ( 0 0 V Т см 0, (12) + Vк ) Т q ρ кт кк24,040 = 293 М см т, (13) где Р см, Т см, V cм давление, температура и объем смеси в камере; V 0 объем газа, замеренного счетчиком при Р 0 ; V к объем паров, получаемых после испарения выпавших жидких углеводородов (конденсата); q к количество выпавшего конденсата, см 3 ; ρ к плотность конденсата, г/см 3 ; Т т температура термостата, К; М к молярная масса конденсата, г/моль. Оценка точности разработанной методики проводилась путем сопоставления результатов определения коэффициентов сжимаемости индивидуальных газов (метана, углекислого газа, сероводорода) экспериментальным путем на установке PVT с данными, приведенными в [7, 8] (рис. 2). Рис. 2. Экспериментальные и эталонные кривые коэффициента сжимаемости для метана (а); углекислого газа (б); сероводорода (в) при температурах: 423 К (1); 383 К (2); 293 К (4): эталонные; экспериментальные

7 126 Коэффициент сжимаемости газов и газоконденсатных смесей: экспериментальное определение и расчеты Отклонение экспериментальных данных от эталонных практически во всех интервалах давлений и температур не превышает 0,2 1,3 %, что свидетельствует о достаточно высокой точности разработанной методики.

Для выявления влияния углекислого газа на сжимаемость проведены исследования смесей, состоящих из 75 % метана, 25 % углекислого газа (% мол.) и разного содержания C 5+ при различных давлениях и температурах. Результаты проведенных экспериментов показали, что растворение в метане углекислого газа (рис.

3) существенно изменяет конфигурацию кривых коэффициентов сжимаемости. Результаты, полученные в ходе экспериментальных работ, позволяют решать задачи, связанные с разработкой, добычей и транспортом газа.

Так, например, разработаны графики для определения коэффициентов сжимаемости газов сепарации Астраханского ГКМ и Карачаганакского НГКМ в интервале давлений от 0,1013 до 70.0 МПа и температур от 293 до 383 К [7, 10]. Рис. 3.

Экспериментальные зависимости коэффициента сжимаемости газовой (а) и газоконденсатных (б С 5+ = 200 г/м 3 ; в С 5+ = 800 г/м 3 ) смесей от давления и температуры: К; К Для Астраханского ГКМ графики построены по результатам исследования газа сепарации следующего состава: H 2 S 24,52; СО 2 14,68; С 1 55,43; С 2 2,63; С 3 1,09; С 4 0,56; С 5+ 0,41; N 2 0,67 % мол. (рис. 4). Этот состав газа сепарации близок к среднему составу по месторождению.

8 Актуальные вопросы исследований пластовых систем месторождений углеводородов. Часть I 127 Для Карачаганакского НГКМ графики построены по результатам исследования газа сепарации следующего состава: H 2 S 3,2; CО 2 6,72; С 1 80,61; С 2 5,20; С 3 2,11; С 4 0,79; С 5+ 0,15; N 2 1,29 % мол. (рис. 5).

Сопоставление расчетных значений коэффициентов сжимаемости различными методами с экспериментальными данными показало [2, 9], что отклонение в различных интервалах давлений и температур доходит до 27,7 %.

Наиболее близкие к экспериментальным аналитические значения коэффициентов сжимаемости для газа сепарации Астраханского ГКМ получены при использовании: метода определения коэффициентов сжимаемости по Вичерту Азизу Кей Брауну в диапазоне давлений МПа и температур К.

Рассчитанные по этому методу значения в среднем завышены на + 5,8 %; методов определения коэффициентов сжимаемости по Кей Брауну и Кей Питцеру в диапазоне давлений МПа и температур К. Отклонение расчетных коэффициентов сжимаемости от экспериментальных колеблется в пределах 0,8 5,4 %.

Из анализа расчетов коэффициентов сжимаемости с помощью уравнения состояния Пенга Робинсона [2] следует, что при давлениях до 30 МПа с наименьшей погрешностью коэффициенты сжимаемости рассчитываются с помощью вышеупомянутого уравнения. С увеличением давления погрешность расчета возрастает.

Исследование коэффициента сжимаемости газоконденсатных смесей показало, что растворение в метане жидкой фазы (конденсата) приводит к его увеличению (рис. 6). Так, при растворении 200 г/м 3 углеводородов С 5+ увеличение коэффициента сжимаемости составляет 2 5 %, при растворении порядка 800 г/м % в зависимости от температуры. Особый интерес представляют впервые экспериментально определенные коэффициенты сжимаемости реальных газоконденсатных смесей Карачаганакского НГКМ с высоким содержанием конденсата (рис. 7).

9 128 Коэффициент сжимаемости газов и газоконденсатных смесей: экспериментальное определение и расчеты Рис. 4. График для определения коэффициента сжимаемости газа сепарации Астраханского ГКМ при различных давлениях и температурах

10 Актуальные вопросы исследований пластовых систем месторождений углеводородов. Часть I 129 Рис. 5. График для определения коэффициента сжимаемости газа сепарации Карачаганакского НГКМ при различных давлениях и температурах

11 130 Коэффициент сжимаемости газов и газоконденсатных смесей: экспериментальное определение и расчеты Рис. 6.

Зависимость коэффициента сжимаемости газоконденсатной смеси от содержания конденсата при различных давлениях и температурах: 1 50 МПа; 2 60 МПа; 3 70 МПа; 4 80 МПа: а 293 К; б 343 К; в 383 К Рис. 7.

График для определения коэффициентов сжимаемости газоконденсатных смесей Карачаганакского НГКМ

12 Актуальные вопросы исследований пластовых систем месторождений углеводородов. Часть I 131 Список литературы 1. Гуревич Г.Р. Справочное пособие по расчету фазового состояния и свойств газоконденсатных смесей / Г.Р. Гуревич, А.И. Брусиловский. М.: Недра, с. 2. Гуревич Г.Р.

Коэффициенты сжимаемости природных газов с высоким содержанием сероводорода и двуокиси углеводорода / Г.Р. Гуревич, В.И. Лапшин, А.И. Брусиловский, А.П. Желтов // Изв. вузов. Сер. Нефть и газ С Ширковский А.И. Разработка и эксплуатация газовых и газоконденсатных месторождений: учебник для вузов. 2-е изд. М.: Недра, с. 4. Лапшин В.И.

Методика и результаты исследования коэффициентов сверхсжимаемости природных газов с высоким содержанием сероводорода и углекислого газа / В.И. Лапшин, А.П. Желтов, Г.Р. Гуревич // Геология нефти и газа С Лапшин В.И. Экспериментальное определение коэффициента сверхсжимаемости газовых смесей с высоким содержанием Н 2 S, CO 2 / В.И. Лапшин, Ю.Ю. Круглов, A.

П. Желтов // Экспрес. информ. Сер. Разработка и эксплуатация газовых и газоконденсатных месторождений С Лапшин В.И. Природные газы сложного состава. Результаты исследования сверхсжимаемости / В.И. Лапшин // Газовая промышленность С Динков В.А. Расчет коэффициентов сжимаемости углеводородных газов и смесей: справочное пособие / В.А. Динков, З.Т.

Галиуллин, А.П. Подкопаев. М.: Недра, С Катц Д.Л. Руководство по добыче, транспорту и переработке природного газа / Д.Л. Катц, Д. Корнелл, Р. Кобаяши и др. М.: Недра, с. 9. Лапшин В.И. Аналитическое определение коэффициента сверхсжимаемости газов Астраханского месторождения.

Совершенствование технологии строительства глубоких разведочных скважин в аномальных условиях Прикаспийской впадины / В.И. Лапшин, В.В. Томилкин, A.П. Желтов; под ред. П.С. Шмелева. Саратов, С

[spoiler title=”источники:”]

http://megaobuchalka.ru/9/19776.html

http://istra-gaz.ru/gazoprovod/koeffitsient-szhimaemosti-prirodnogo-gaza.html

[/spoiler]

Источник

Definition and physical significance[edit]

Fugacity[edit]

Generalized compressibility factor graphs for pure gases[edit]

Reading a generalized compressibility chart[edit]

Observations made from a generalized compressibility chart[edit]

Theoretical models[edit]

Physical mechanism of temperature and pressure dependence[edit]

Experimental values[edit]

Compressibility of air[edit]

See also[edit]

References[edit]

External links[edit]

3.1 Общие положения

3.2 Методы расчета коэффициента сжимаемости

3.2.1 Пределы применимости методов расчета и погрешности расчета коэффициента сжимаемости

3.2.2 Модифицированный метод NX19 мод.

3.2.3 Модифицированное уравнение состояния GERG-91 мод.

3.2.4 Уравнение состояния AGA8-92DC

3.2.5 Уравнение состояния ВНИЦ СМВ

9. Фугитивность

Коэффициент сжимаемости: как рассчитать, примеры и упражнения

Содержание:

Как рассчитать коэффициент сжимаемости?

Примеры

Коэффициент сжимаемости в идеальных газах, воздухе, водороде и воде

Идеальные газы

Воздух

Водород

вода

Решенные упражнения

Упражнение 1

Решение для

Решение б

Решение c

Упражнение 2.

Решение для

Решение б

Решение c

Ссылки

Уравнение состояния газов

Коэффициент сжимаемости природного газа

Большая Энциклопедия Нефти и Газа

ПОИСК

Способ оперативного определения коэффициента сжимаемости газов и их смесей

Коэффициент сжимаемости газов и газоконденсатных смесей: экспериментальное определение и расчеты — PDF

Вам также может понравиться

Как найти похожий звук в тик токе

Как найти работу на автокаде

Как найти адрес больницы по номеру телефона

Добавить комментарий Отменить ответ