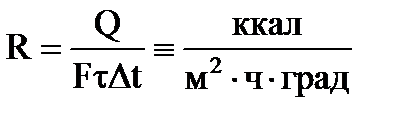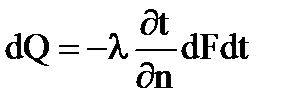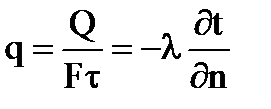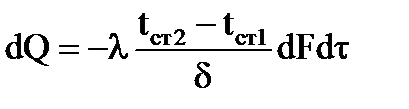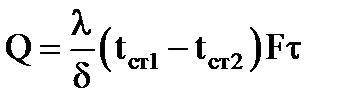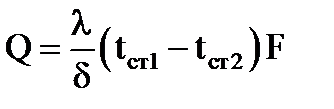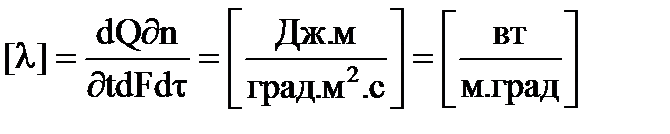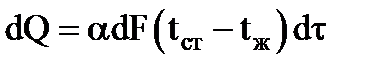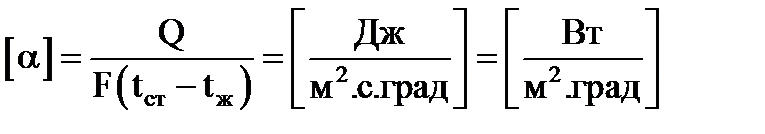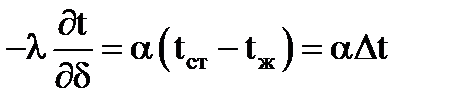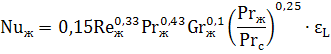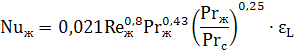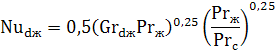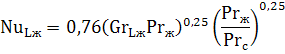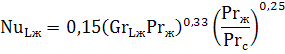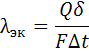Как найти коэффициент теплообмена

Во многих инженерных задачах, связанных с теплопередачей, например, при проектировании теплообменных аппаратов и радиаторов охлаждения, важное значение имеет расчет коэффициента теплоотдачи. Коэффициент теплоотдачи, который чаще всего рассчитывается с помощью эмпирических формул, характеризует интенсивность теплообмена на поверхности твердого тела. В этой статье мы расскажем и покажем, как рассчитать коэффициент теплоотдачи на плоской поверхности с помощью среды численного моделирования COMSOL Multiphysics®.

Что такое коэффициент теплоотдачи?

Рассмотрим нагретую стенку или поверхность, находящуюся в контакте с потоком жидкости. Перенос теплоты в жидкости определяется преимущественно конвекцией. Аналогично, конвекцией определяется перенос теплоты через твердую стенку, омываемую с двух сторон двумя разными жидкостями, например, в теплообменных аппаратах. Интенсивность теплопередачи в обоих случаях пропорциональна разности температур, а коэффициент пропорциональности, собственно, и является коэффициентом теплоотдачи. Коэффициент теплоотдачи характеризует теплообмен между поверхностью твердого тела и жидкостью.

В математическом смысле h— это отношение плотности теплового потока на стенке к разности температур стенки и жидкости; таким образом,

(1)

где q^{prime prime}— плотность теплового потока, T_w— температура стенки, а T_infty— характерная температура жидкости.

В качестве характерной температуры жидкости могут выступать температура жидкости вдали от стенки или среднемассовая температура в трубе.

Если объект находится в неограниченно большом объеме воздуха, можно предположить, что температура воздуха вдали от поверхности объекта является постоянной и известной величиной. Такие задачи теплообмена называются внешними.

Рассмотрим пристеночную область (пусть плоскость стенки расположена по нормали к оси y, и y = 0 соответствует поверхности стенки). С учетом сделанного выше допущения очевидно, что при выполнении условия прилипания на стенке (то есть отсутствия проскальзывания) вблизи стенки образуется тонкая пленка почти неподвижной жидкости. Следовательно, перенос теплоты в этой пленке осуществляется исключительно за счет теплопроводности.

Математически этот процесс описывается уравнением [1]:

(2)

Здесь k— коэффициент теплопроводности жидкости, а производная от T рассчитывается в области жидкости.

Из уравнений (1) и (2) следует, что коэффициент теплоотдачи можно определить следующим образом:

(3)

h=dfrac{-k bigg(dfrac{partial T} {partial y}
bigg)_{y=0}}{T_w {-} T_infty}

Расчет коэффициента теплоотдачи в COMSOL Multiphysics®

На практике измерить градиент температуры на стенке довольно затруднительно. Кроме того, хотелось бы эффективно анализировать процессы теплообмена вблизи твердой поверхности без привлечения значительных вычислительных ресурсов. Поэтому для расчета коэффициента теплоотдачи, как правило, используются неаналитические методы.

Широко признанным методом расчета коэффициента теплоотдачи является использование уравнений подобия для безразмерного числа Нуссельта. Эти уравнения позволяют быстро рассчитать коэффициент теплоотдачи для разных условий теплообмена, в том числе при свободной и вынужденной конвекции в задачах внешнего обтекания и при течении в каналах. Однако этот подход можно использовать только для объектов правильной геометрической формы: для горизонтальных и вертикальных плоских поверхностей, цилиндров и сфер.

Если поверхность теплообмена в задаче имеет более сложную форму, коэффициент теплоотдачи можно рассчитать с помощью моделирования сопряженного теплообмена.

Рассмотрим эти два варианта решения задачи:

1. Расчет коэффициента теплоотдачи на поверхностях простой геометрической формы (например, на плоской пластине):
   • Моделирование сопряженного теплообмена
   • Расчетные формулы; область течения не моделируется
2. Вычисление коэффициента теплоотдачи на поверхностях сложной геометрической формы (например, на гофрированной пластине)

Отметим, что очень важно принимать во внимание режим течения жидкости, поскольку коэффициент теплоотдачи зависит от механизмов переноса теплоты в жидкости. В обоих случаях рассмотрим наиболее реалистичный вариант быстрого течения, например, в системе вентиляции или устройстве охлаждения электронной микросхемы. Таким образом, модель должна учитывать дополнительные механизмы переноса теплоты, обусловленные турбулентностью.

Пример 1. Теплообмен при вынужденном обтекании плоской горизонтальной пластины

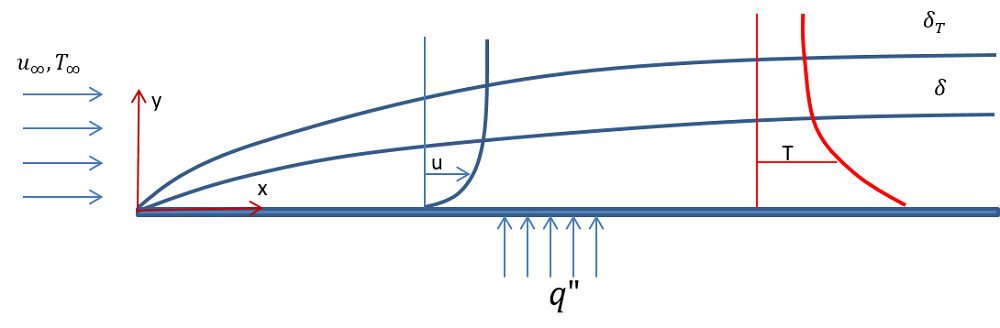
Рассмотрим задачу об обтекании горизонтальной плоской пластины длиной 5 м, на которой задана постоянная плотность теплового потока 10 Вт/м². Пластина обдувается воздухом со средней скоростью 0,5 м/с и температурой 283 K. На рисунке ниже представлена схема области течения и показаны профили скорости и температуры в пределах динамического (delta ) и температурного (delta {T}) пограничных слоев при ламинарном режиме обтекания.

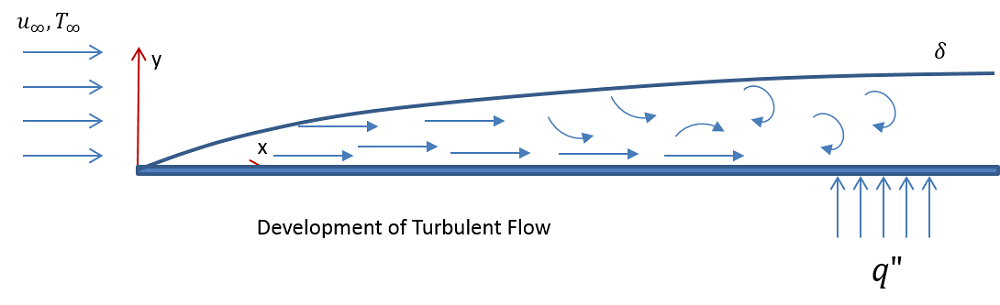
Схематическое изображение ламинарного (сверху) и турбулентного (снизу) пограничных слоев на горизонтальной пластине.

Моделирование сопряженного теплообмена

В COMSOL Multiphysics поставленную задачу можно решить численно, если воспользоваться интерфейсом Conjugate Heat Transfer (Сопряженный теплообмен), который позволяет рассчитать поля течения и температуры в жидкости. Поля скорости и давления рассчитываются в области, занятой воздухом, а поле температуры ещё и в самой пластине.

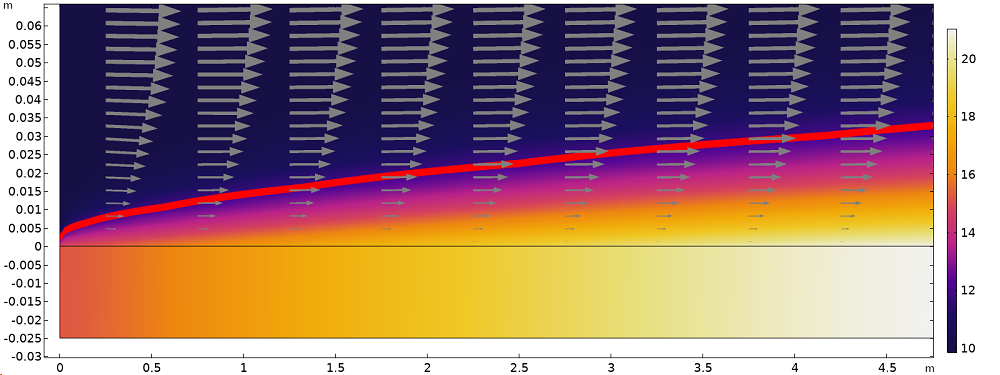
На следующем рисунке показано распределение температуры в пределах расчетной области, включающей пластину и воздух. В области течения формируются температурный и динамический погранслои, которые занимают область над пластиной толщиной около 2 см.

Распределение температуры (график скалярного поля), изотерма на 11 °C (красная линия) и поле скорости (стрелки), показывающие температурный и динамический погранслои у поверхности пластины (масштабы осей не совпадают).

По результатам моделирования можно рассчитать плотность теплового потока, если обратиться к соответствующей встроенной переменной постобработки. Если разделить найденное значение на разность температур (T_w-T_infty), получим коэффициент теплоотдачи (уравнение 3). На графике ниже показано, как изменяется рассчитанное значение коэффициента теплоотдачи вдоль пластины.

Расчет коэффициента теплоотдачи по формулам для числа Нуссельта

Уравнение для расчета числа Нуссельта при вынужденном обтекании плоской пластины можно найти в литературных источниках (например, в [1]).

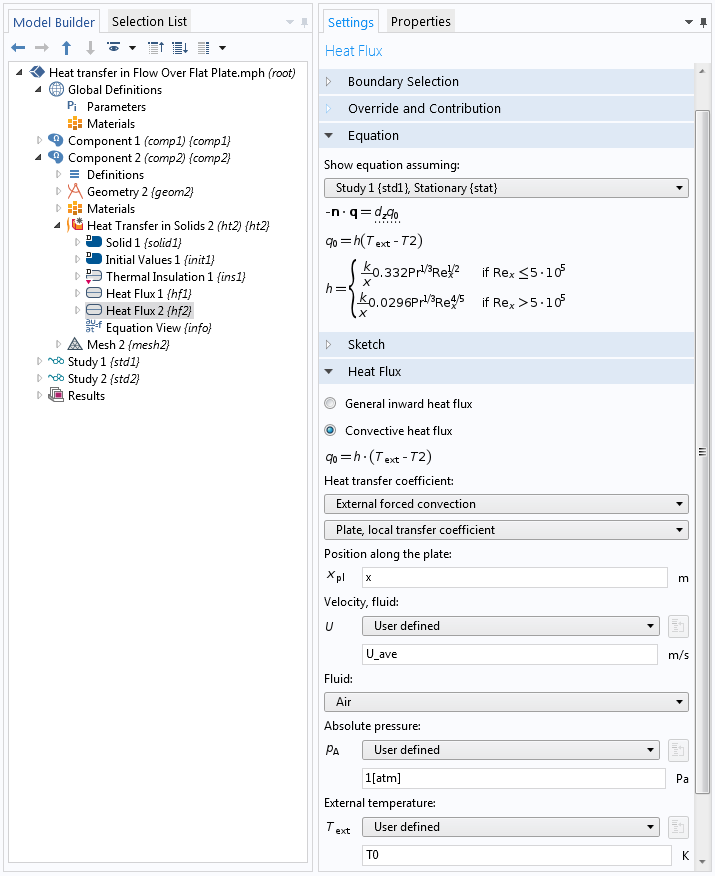
Во втором варианте расчета мы решим ту же задачу, но без моделирования области течения; то есть мы воспользуемся формулами для расчета коэффициента теплоотдачи. В этом случае расчетная область включает в себя только твердое тело (пластину). Плотность теплового потока, передаваемая с поверхности нагретой пластины холодной жидкости, задается с помощью граничного условия Heat Flux (Тепловой поток). В настройках этого граничного условия предусмотрен вариант, позволяющий задать коэффициент теплоотдачи на границе с помощью встроенных формул для расчета числа Нуссельта, как показано ниже. Еще раз отметим, что эти формулы уже имеются в COMSOL Multiphysics.

Настройки граничного условия Heat Flux (Тепловой поток).

С помощью этого условия можно рассчитать поле температуры в пластине. Зная коэффициент теплоотдачи на поверхности пластины, заданный в граничном условии Heat Flux (Тепловой поток), можно рассчитать плотность теплового потока: q=hcdot(T_infty-T).

Расчет коэффициента теплоотдачи

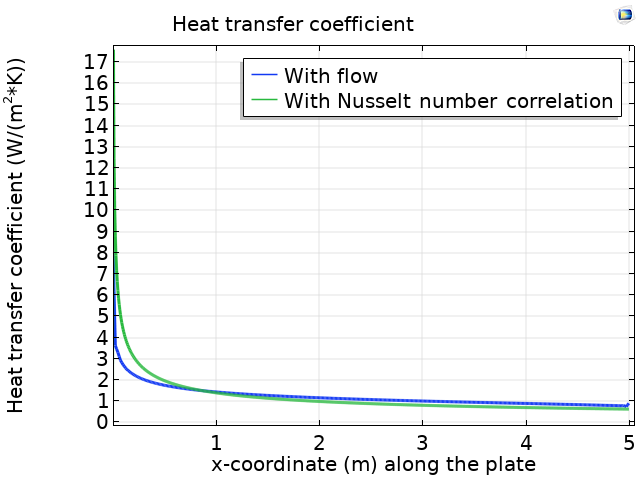
Рассчитать, как изменяется коэффициент теплоотдачи по длине пластины, можно с помощью любого из двух описанных выше методов. На рисунке ниже показано сравнение результатов расчета коэффициента теплоотдачи двумя методами.

Сравнение значений коэффициента теплоотдачи на плоской пластине, рассчитанных методом моделирования сопряженного теплообмена (синяя линия) и с помощью уравнений для числа Нуссельта (зеленая линия).

Как видно на графике, значения, полученные с помощью уравнений для числа Нуссельта, и значения, рассчитанные на основе численного моделирования сопряженного теплообмена, почти идентичны.

Интерес представляет интенсивность теплообмена на пластине, рассчитанная этими двумя методами:

1. Формула для расчета числа Нуссельта: 50 Вт/м
2. Сопряженный теплообмен: 49,884 Вт/м

В некоторых задачах эмпирические формулы для числа Нуссельта позволяют рассчитать плотность теплового потока с достаточно высокой точностью. Теперь рассмотрим ситуацию, когда теплообмен происходит на поверхностии сложной формы, для которой нет формул расчета числа Нуссельта, и решить задачу можно только численно.

Пример 2. Течение у гофрированной поверхности горизонтальной пластины

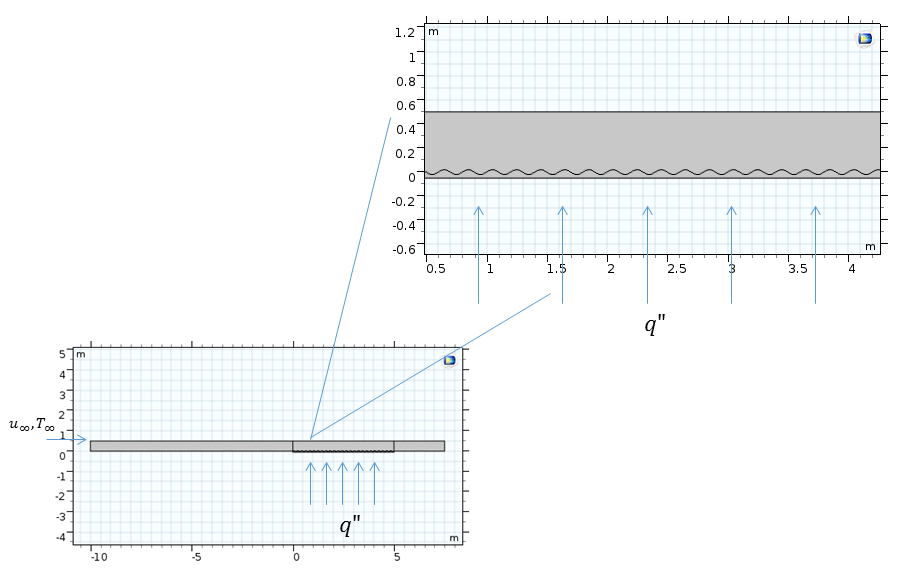
Рассмотрим задачу с теми же исходными условиями, что и в первом случае, но только теперь верхняя поверхность пластины пусть будет гофрированной. На рисунке ниже представлена схема, иллюстрирующая постановку задачи. В этой модели одна из секций верхней поверхности пластины гофрирована. Остальные части пластины плоские.

Схема течения на горизонтальной пластине.

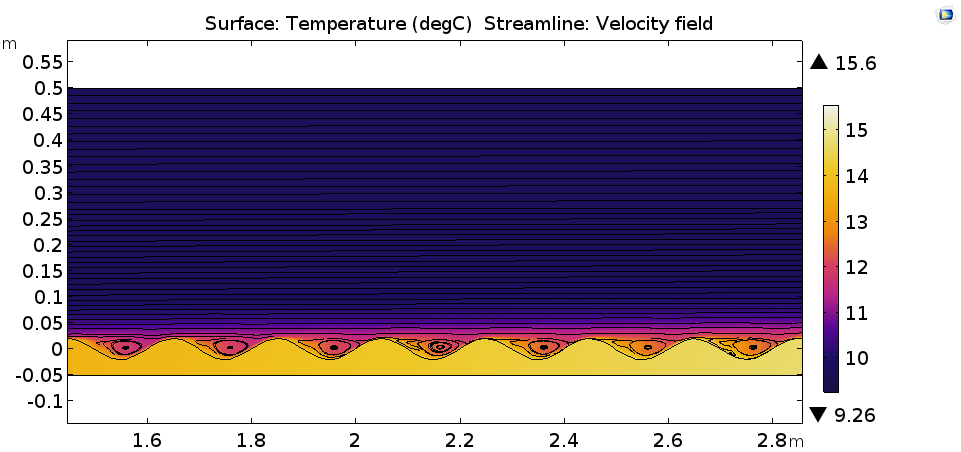
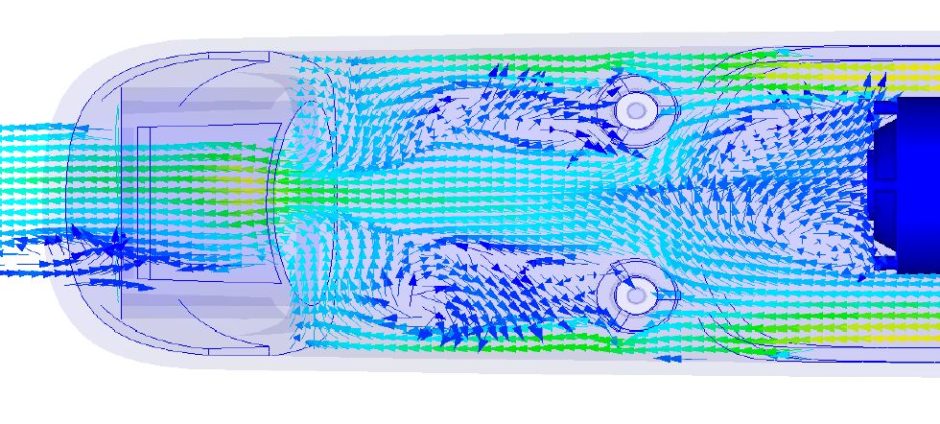
При такой форме поверхности стенки в пристеночной области появляются зоны рециркуляции, в результате чего интенсивность теплообмена повышается. На рисунке ниже представлено распределение температуры и линии тока.

Распределение температуры в градусах Цельсия (поверхность) и поле скорости (линии тока).

На графике слева показано изменение коэффициента теплоотдачи вдоль гофрированной пластины. В задачах со сложной формой поверхности теплообмена, как например при обтекании гофрированной пластины, коэффициент теплоотдачи зависит от нескольких факторов: поля температуры, поля скорости и геометрических параметров поверхности теплообмена (например, высоты гофры). Таким образом, коэффициент теплоотдачи оказывается выше, чем в случае плоской пластины (см. рисунок справа).

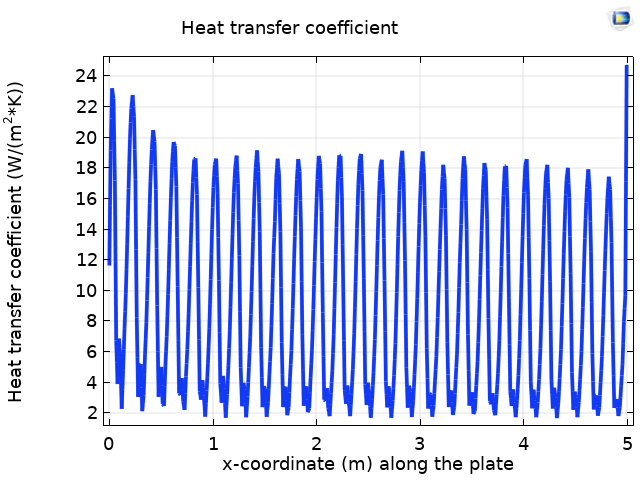
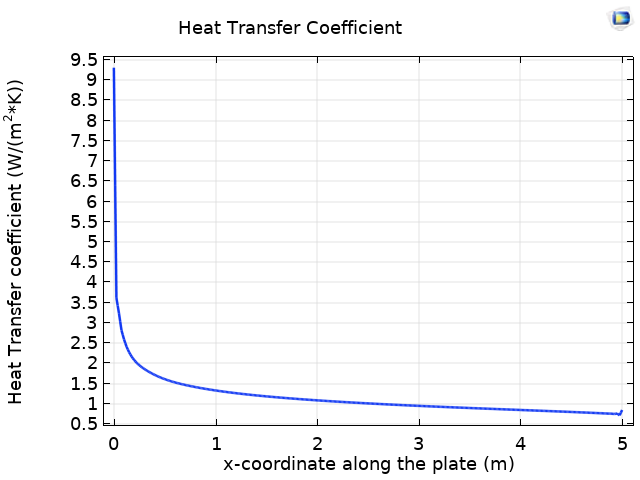
Изменение коэффициента теплоотдачи вдоль гофрированной пластины (слева) и вдоль плоской пластины (справа).

Для моделирования сопряженного теплообмена в моделях со сложной формой поверхностей могут потребоваться значительные вычислительные ресурсы, поэтому иногда предпочтение отдается альтернативным методам решения задачи. Хорошим вариантом решения является замена поверхности сложной формы на простую и подстановка значений коэффициента теплоотдачи, полученных на поверхности сложной формы с учетом геометрических параметров, поля скорости и разности температур. Следует отметить, что, даже если поверхность не является изотермической или если плотность теплового потока не постоянна, значение коэффициента теплоотдачи все равно представляет интерес для некоторых конфигураций, не слишком сильно отличающихся от исходной модели.

Для проверки рассмотрим простой вариант задачи о расчете коэффициента теплоотдачи на омываемой потоком гофрированной поверхности пластины. На основе полученных данных можно определить средний коэффициент теплоотдачи, который затем легко использовать в модели с плоской поверхностью пластины. Корректность такого приближенного подхода можно проверить, если проанализировать полный тепловой поток с поверхности или коэффициент теплоотдачи на основе моделирования сопряженного теплообмена.

Заключение

В этой статье мы рассказали о двух методах расчета коэффициента теплоотдачи. При моделировании сопряженного теплообмена можно использовать встроенные переменные COMSOL Multiphysics, содержащие значения плотности теплового потока. Применение граничного условия Heat Flux (Тепловой поток) и формул для расчета числа Нуссельта позволяет решать задачи о теплообмене на поверхностях простой формы. Также мы кратко обсудили, как использовать упрощенную геометрическую модель для получения данных о коэффициенте теплоотдачи на поверхностях сложной формы.

Дальнейшие шаги

Нажмите на кнопку ниже, чтобы получить дополнительную информацию о специализированных функциях моделирования теплообмена в среде численного моделирования COMSOL®.

Опробуйте рассмотренные методы с помощью учебных моделей:

• Свободно-конвективное охлаждение сосуда Дьюара
• Неизотермические турбулентное течение вдоль плоской пластины
• Неизотермическое ламинарное течение в круглой трубе

Список литературы

1. A. Bejan et al., Heat Transfer Handbook (Справочник по теплопередаче), John Wiley & Sons, 2003.

• Что такое коэффициент теплоотдачи, его размерность, как его определить для выполнения расчетов?

α– характеризует интенсивность
конвективного теплообмена и зависит
от скорости теплоносителя, теплоемкости,
вязкости, от формы поверхности и тд.

[Вт/(м²град)].

Коэффициент теплоотдачи численно равен
мощности теплового потока, передаваемому
одному квадратному метру поверхности
при разности температур между
теплоносителем и поверхностью в 1°С.

Основной и наиболее трудной проблемой
в расчётах процессов конвективной
теплоотдачи является нахождение
коэффициента теплоотдачи α.
Современные методы описания процесса
коэф. теплопроводности, основанные на
теориипограничного
слоя,позволяют получить
теоретические (точные или приближённые)
решения для некоторых достаточно простых
ситуаций. В большинстве же встречающихся
на практике случаев коэффициент
теплоотдачи определяют экспериментальным
путём. При этом как результаты теоретических
решений, так и экспериментальные данные
обрабатываются методамитеории
подобия
и представляются обычно в
следующем безразмерном виде:

Nu=f (Re, Pr) — для вынужденной
конвекции и

Nu=f (Gr Re,, Pr) — для свободной
конвекции,

где
—
число Нуссельта,— безразмерный
коэффициент теплоотдачи (L —характерный размер потока,λ—
коэффициент теплопроводности);Re=—число Рейнольдса, характеризующее
соотношение сил инерции и внутреннего
трения в потоке (u —характерная
скорость движения среды, υ — кинематический
коэффициент вязкости);

Pr=—число Прандтля, определяющее
соотношение интенсивностей термодинамических
процессов (α – коэффициент
температуропроводности);

Gr=
— число Грассгофа, характеризующее
соотношение архимедовых сил, сил инерции
и внутреннего трения в потоке (g —ускорение свободного падения,β—
термический коэффициент объёмного
расширения).

• От чего зависит коэффициент теплоотдачи? Порядок его величины для различных случаев теплообмена.

Коэффициент конвективной теплоотдачи
αтем больше, чем больше коэффициент
теплопроводностиλи скорость потокаw,чем меньше
коэффициент динамической вязкости υ и
больше плотностьρи чем меньше
приведенный диаметр каналаd.

Наиболее интересным с точки зрения
технических приложений случаем
конвективного теплопереноса является
конвективная теплоотдача, то есть
процесс двух конвективных теплообменов,
протекающий на границе раздела двух
фаз (твердой и жидкой, твердой и
газообразной, жидкой и газообразной).
При этом задача расчета состоит в
нахождении плотности теплового потока
на границе раздела фаз, то есть величины,
показывающей, какое количество тепла
получает или отдает единица поверхности
раздела фаз за единицу времени. Помимо
указанных выше факторов, влияющих на
процесс конвективного теплообмена,
плотность теплового потока зависит
также от формы и размеров тела, от степени
шероховатости поверхности, а также от
температур поверхности и теплоотдающей
или тепловоспринимающей среды.

Для описания конвективной теплоотдачи
используется формула:

q_cт = α(Т₀—Т_ст),

где q_cт —плотность
теплового потока на поверхности, Вт/м²;
α —коэффициент теплоотдачи,
вт/(м²·°С);T₀иТ_ст— температуры среды (жидкости или газа)
и поверхности соответственно. ВеличинуT₀ —Т_ст
часто обозначают ΔТи называетсятемпературным
напором.Коэффициент
теплоотдачиαхарактеризует
интенсивность процесса теплоотдачи;
он возрастает при увеличении скорости
движения среды и при переходе от
ламинарного режима движения к турбулентному
в связи с интенсификацией конвективного
переноса. Он также всегда больше для
тех сред, у которых выше коэффициент
теплопроводности. Коэффициент теплоотдачи
существенно повышается, если на
поверхности происходит фазовый переход
(например, испарение или конденсация),
всегда сопровождающийся выделением
(поглощением) скрытой теплоты. На значение
коэффициента теплоотдачи сильное
влияние оказываетмассообменна поверхности.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Основные уравнение теплообмена

Основы теории передачи тепла. Классификация теплообменных аппаратов. Конструкции.

Основные понятия

Перенос энергии в форме тепла, происходящий между телами, имеющими различную температуру, называется теплообменом. Движущая сила любого процесса теплообмена — разность температур более и менее нагретого тел. При наличии такой разности тепло самопроизвольно, в соответствии со вторым законом термодинамики, переходит от более нагретого к менее нагретому телу. Теплообмен представляет собой обмен энергией между молекулами, атомами и свободными электронами.

Тела, участвующие в тпелообмене, называются теплоносителями.

Теплопередача — наука о процессах распространения тепла. Различают три элементарных способа передачи тепла.

1) Теплопроводность — перенос тепла вследствие теплового движения микрочастиц, непосредственно соприкасающихся друг с другом. В твердых телах теплопроводность — основной способ распространения тепла.

2) Конвекция — перенос тепла вследствие движения и перемешивания макроскопических объемов газа или жидкости. Различают свободную (естественную) конвекцию, обусловленную разностью плотностей в различных точках объема жидкости или газа за счет разности температур, и вынужденную конвекцию, происходящую при принудительном движении всего объема.

3) Тепловое излучение — распространение электромагнитных колебаний с различной длиной волн, обусловленный тепловым движением атомов или молекул излучающего тела. Все тела способны излучать и поглощать энергию, таким образом осуществляется лучистый теплообмен.

В реальных условиях тепло передается комбинированным путем.

Перенос тепла от стенки к газообразной или жидкой среде или в обратном направлении называется теплоотдачей. Процесс передачи тепла от более нагретой к менее нагретой жидкости или газу через разделяющую их поверхность или твердую стенку называется теплопередачей.

Расчет теплообменной аппаратуры включает:

1) Определение теплового потока — количества тепла Q, которое должно быть передано за определенное время от одного теплоносителя к другому. Тепловой поток вычисляется путем составления и решения тепловых балансов.

2) Определение поверхности теплообмена F аппарата, обеспечивающей передачу требуемого количества тепла в заданное время. Величина поверхности теплообмена определяется скоростью теплопередачи, зависящей от механизмов передачи тепла и их сочетанием друг с другом. Поверхность теплообмена находят из основного уравнения теплопередачи.

Основные уравнение теплообмена

Основное уравнение теплопередачи выражает общую зависимость для процессов теплопередачи, выражающее связь между тепловым потоком Q’ и поверхностью теплообмена F:

K — коэффициент теплопередачи, определяющий среднюю скорость передачи тепла вдоль всей поверхности теплообмена; Dt_ср — средняя разность температур между теплоносителями, определяющая среднюю движущую силу процесса теплопередчи, или температурный напор; t — время.

Физический смысл уравнения: количество тепла, передаваемое от более нагретого к менее нагретому теплоносителю, пропорционально поверхности теплообмена F, среднему температурному напору Dt_ср и времени t.

Для непрерывных процессов теплообмена:

Отсюда коэффициент теплопередачи:

Коэффициент теплопередачи показывает, какое количество тепла (в Дж) переходит за 1 секунду от более нагретого к менее нагретому теплоносителю через поверхность теплообмена 1 м 3 при средней разности температур между теплоносителями 1 градус.

В основе расчета теплопроводности лежит закон Фурье:

То есть, количество тепла dQ, передаваемое посредством теплопроводности через элемент поверхности dF, перпендикулярный тепловому потоку, за время dt прямо порпорционально температурному градиенту ∂t/∂n поверхности dF и времени dt.

Количество тепла, передаваемое через единицу поверхности в единицу времени:

Здесь q — плотность теплового потока. Знак минус указывает на то, что тепло перемещается в сторону падения температуры.

Количество переданного тепла:

Здесь d — толщина стенки, м; t_ст1 – t_ст2 — разность температур поверхностей стенки, град; F — площадь поверхности стенки, м 2 ;  — время, с.

Для непрерывного процесса передачи тепла теплопроводностью при =1:

Коэффициент пропорциональности l называется коэффициентом теплопроводности.

Коэффициент теплопроводности l показывает, какое количество тепла проходит вследствие теплопроводности в единицу времени через единицу поверхности теплообмена при падении температуры на 1 градус на единицу длины нормали к изотермической поверхности. Его величина зависит от природы вещества, его структуры, температуры и некоторых других факторов.

При обычных температурах и давлениях лучшими проводниками тепла являются металлы, худшими — газы.

В основе расчета теплоотдачи лежит закон охлаждения Ньютона:

То есть: количество тепла dQ, отдаваемое за время dt поверхностью стенки dF, имеющей температуур t_ст, к жидкости с температурой t_ж, прямо пропорционально dF и разности температур t_ст – t_ж.

Применительно к поверхности теплообмена всего аппарата F для непрерывного процесса теплоотдачи это уравнение принимает вид:

Коэффициент пропорциональности a называется коэффициентом теплоотдачи. Величина его характеризует интенсивность переноса тепла между поверхностью тела и окружающей средой. Он выражается следующим образом:

То есть, коэффициент теплоотдачи a показывает, какое количество тепла передается от 1 м 2 поверхности стенки к жидкости (или наоборот) в течение 1 секунды при разности температур между стенкой и жидкостью 1 градус.

Вследствие сложной структуры потоков, особенно в условиях турбулентного движения, величина a является сложной функцией многих переменных. Коэффициент теплоотдачи зависит от: — скорости жидкости, ее плотности и вязкости, — тепловых свойств жидкости (удельная теплоемкость, теплопроводность) и коэффициента объемного расширения, — геометрических параметров — формы и определяющих размеров стенки (для труб – от размера и диаметра) и шероховатости стенки.

При сопоставлении уравнений теплопроводности и теплоотдачи получаем следующее выражение для установившегося процесса теплообмена:

После преобразований получим:

Nu — критерий Нуссельта. Равенство критериев Нуссельта характеризует подобие процессов теплопереноса на границе между стенкой и потоком жидкости. Он является мерой соотношения толщины пограничного слоя d и определяющего геометрического размера.

Уравнение теплоотдачи коэффициент теплоотдачи его размерность и физический смысл

1. Конвективный перенос теплоты

Конвекция возможна только в текучей среде, в которой перенос теплоты связан с переносом самой среды. Конвекция теплоты всегда сопровождается теплопроводностью, так как при движении жидкости или газа неизбежно происходит соприкосновение отдельных частиц, имеющих различные температуры. Совместный перенос теплоты путем конвекции и теплопроводности называют конвективным теплообменом.

Теплоотдача – конвективный теплообмен между движущейся средой и поверхностью (стенкой).

Количество теплоты, переданное в процессе теплоотдачи, определяется по уравнению Ньютона-Рихмана:

для установившегося режима

, Вт; (1.1)

для неустановившегося режима

, Дж, (1.2)

где α – коэффициент теплоотдачи, Вт/(м 2 ∙К); t _ж , t _ст – средние температуры жидкости и стенки, °С; F – поверхность стенки, м 2 ; Q ( Q / ) – тепловой поток (количество теплоты), Вт (Дж); τ – время, с.

Коэффициент теплоотдачи α – характеризует интенсивность теплообмена между поверхностью тела и окружающей средой. Коэффициент α показывает, какое количество тепла передается от единицы поверхности стенки к жидкости в единицу времени при разности температур между стенкой и жидкостью в 1 градус (К), .

Установлено, что коэффициент теплоотдачи зависит от многих факторов: вида и режима движения жидкости, ее физических свойств, размеров и формы стенки, шероховатости стенки. Определение α является основной задачей расчета теплообменных аппаратов. Обычно коэффициент теплоотдачи определяют из критериальных уравнений, полученных преобразованием дифференциальных уравнений гидродинамики и конвективного теплообмена методами теории подобия.

Согласно положений теории подобия конвективный теплообмен без изменения агрегатного состояния вещества в стационарных условиях может быть описан критериальным уравнением вида:

, (1.3)

– критерий Нуссельта, характеризующий подобие процессов теплопереноса на границе между стенкой и потоком жидкости;

– критерий Рейнольдса, который характеризует гидродинамический режим потока при вынужденном движении и является мерой соотношения сил инерции и вязкого трения;

– критерий Прандтля, который характеризует физико – химические свойства теплоносителя и является мерой подобия температурных и скоростных полей в потоке;

– критерий Грасгофа, характеризующий соотношение сил вязкого трения и подъемной силы, описывает режим свободного движения теплоносителя;

– безразмерный геометрический симплекс, характеризующий геометрическое подобие системы.

В выражении этих критериев: – кинематический коэффициент вязкости теплоносителя, м 2 /с; w – скорость движения теплоносителя, м/с; – коэффициент температуропроводности, м 2 /с; g – ускорение свободного падения м/с 2 ; l – определяющий размер, м; – характерный размер, м; β – коэффициент температурного расширения, 1/К; ρ – плотность теплоносителя, кг/м 3 ; ∆ t = t _ст – t _ж – температурный напор между стенкой и теплоносителем, 0 С; λ – коэффициент теплопроводности теплоносителя, Вт/(м·К); μ – динамический коэффициент вязкости, Па·с; с – теплоемкость теплоносителя, Дж/(кг·К); τ – время процесса, с.

Критерий Нуссельта, входящий в уравнение (1.3), является определяемым. При известном значении Nu коэффициент теплоотдачи может быть рассчитан по формуле:

. (1.4)

Для расчета числа критерия Нуссельта при вынужденном движении потока в прямых трубах или каналах можно рекомендовать следующие уравнения:

а) для ламинарного режима движения теплоносителя, :

, (1.5)

где – критерий Прандтля для теплоносителя при температуре стенки;

б) для переходного режима движения теплоносителя, :

. (1.6)

Значение коэффициента С определяется из таблицы 1.1 в зависимости от величины критерия Рейнольдса.

Для приближенных расчетов можно пользоваться уравнением:

. (1.7)

Критериальные уравнения теплообмена: расчет теплоотдачи в трубах и каналах

Теплоотдача при вынужденном течении жидкости в трубах и каналах

Теплоотдача в трубах и каналах может происходить при вынужденном или свободном характере конвекционных потоков (возможны также их сочетания в случае существенного влияния гравитационных сил).

При вынужденном течении (вынужденная конвекция) жидкость нагнетается или отводится под действием сил внешнего давления, например, ветра, насоса или вентилятора.

Свободное течение жидкости происходит под действием подъемных (гравитационных) сил за счет изменения ее плотности из-за разницы температуры – слой жидкости с меньшей плотностью стремиться занять верхнее положение относительно холодного слоя (свободная или естественная конвекция).

Интенсивность теплоотдачи, как при вынужденной, так и при свободной конвекции характеризуется коэффициентом теплоотдачи α, имеющим размерность Вт/(м 2 ·град), который определяется по формуле:

Nu – число Нуссельта; λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);

d – эквивалентный диаметр, равный

F – площадь сечения канала, м 2 ; П – периметр канала, м.

Для трубы круглого сечения, эквивалентный диаметр равен внутреннему диаметру трубы.

В целом, расчет коэффициента теплоотдачи сводится к определению числа Нуссельта, значение которого задается соответствующими критериальными уравнениями конвективного теплообмена, зависящими от режима течения жидкости и формы канала.

Течение жидкости в трубах определяется значением числа Рейнольдса Re и в зависимости от его величины может быть ламинарным, переходным или турбулентным.

• Ламинарный режим течения жидкости характеризуется величиной числа Re до 2300.
• При значении числа Re от 2300 до 10000 режим течения в трубах является переходным.
• Турбулентный режим течения в трубах наблюдается при числах Re более 10000.

Число (критерий) Рейнольдса представляет собой безразмерный комплекс, связывающий скоростные и вязкостные характеристики жидкости с определяющим размером канала (для трубы – это ее диаметр).

Число Re определяется по формуле:

w – скорость течения жидкости, м/с; d – эквивалентный диаметр канала, м; ν — кинематическая вязкость жидкости при средней температуре, м 2 /с.

Теплоотдача в трубах и каналах существенно зависит от режима течения жидкости. При ламинарном режиме интенсивность теплоотдачи значительно меньше, чем при развитом турбулентном.

Теплоотдача при ламинарном течении в трубах и каналах

Ламинарный режим течения жидкости обычно характеризуется низкой скоростью потока. При этом в некоторых случаях влиянием конвекции, обусловленной действием гравитационных сил, пренебрегать нельзя.

Для выбора правильного критериального уравнения теплообмена и оценки влияния естественной конвекции на интенсивность теплопередачи при ламинарном режиме служит критерий Грасгофа Gr.

g – ускорение свободного падения, м/с 2 ;

β – температурный коэффициент объемного расширения, град -1 ;

d – эквивалентный диаметр канала, м;

ν — кинематическая вязкость жидкости при средней температуре, м 2 /с;

Δt – средняя разность температур жидкости и стенки, °С.

Теплоотдача при ламинарном течении в трубах и каналах с учетом естественной конвекции. Если величина комплекса GrPr превышает 8·10 5 , то расчет коэффициента теплоотдачи необходимо проводить с учетом влияния естественной конвекции в потоке жидкости по следующему критериальному уравнению:

Индекс «ж» означает, что свойства среды, входящие в критерии подобия Re, Pr и Gr берутся при средней температуре жидкости.

Число Прандтля с индексом «с» Pr_с берется для жидкости при температуре стенки.

ε_L – коэффициент, учитывающий изменение теплоотдачи по длине трубы или канала. Его можно определить с помощью таблицы:

_L

L/d	1	2	5	10	15	20	30	40	50
εL	1,9	1,7	1,44	1,28	1,18	1,13	1,05	1,02	1

Значения коэффициента ε при ламинарном режиме

Теплоотдача при ламинарном течении в трубах и каналах без учета естественной конвекции. При значении GrPr 5 , влияние естественной конвекции на теплоотдачу жидкости пренебрежительно мало, и расчет коэффициента теплоотдачи можно проводить по следующему критериальному уравнению:

d – эквивалентный диаметр канала, м;

L – длина трубы (канала), м.

Представленные критериальные уравнения теплообмена при ламинарном режиме позволяют определить среднее значение числа Нуссельта, по величине которого можно рассчитать средний коэффициент теплоотдачи:

λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);

d – эквивалентный диаметр, м.

Теплоотдача в трубах и каналах при турбулентном режиме

Теплоотдача в трубах и каналах при турбулентном режиме осуществляется путем передачи тепла при интенсивном перемешивании слоев жидкости. Критериальное уравнение теплообмена для расчета средней теплоотдачи в трубах и каналах в этом случае имеет вид:

Критерии подобия Re и Pr берутся при средней температуре жидкости. Число Прандтля с индексом «с» Pr_с берется при температуре стенки.

Представленное критериальное уравнение применяется в диапазоне чисел Re от 1·10 4 до 5·10 6 и Pr от 0,6 до 2500.

ε_L – коэффициент, учитывающий изменение среднего коэффициента теплоотдачи по длине трубы или канала при турбулентном режиме течения. Значения ε_L приведены в следующей таблице при различных числах Рейнольдса и отношениях длины канала к его эквивалентному диаметру:

_L

Reж	L/d
1	2	5	10	15	20	30	40	50
1·10 4	1,65	1,5	1,34	1,23	1,17	1,13	1,07	1,03	1
2·10 4	1,51	1,4	1,27	1,18	1,13	1,1	1,05	1,02	1
5·10 4	1,34	1,27	1,18	1,13	1,1	1,08	1,04	1,02	1
1·10 5	1,28	1,22	1,15	1,1	1,08	1,06	1,03	1,02	1
1·10 6	1,14	1,11	1,08	1,05	1,04	1,03	1,02	1,01	1

Значения коэффициента ε при турбулентном режиме

Расчет теплоотдачи в изогнутых трубах и каналах проводится по тому же критериальному уравнению с добавлением множителя — поправки на действие центробежных сил, которая определяется по формуле:

R — радиус изгиба трубы или канала, м; d – эквивалентный диаметр трубы или канала, м.

Теплоотдача в изогнутых трубах проходит более интенсивно, чем в прямых, за счет большего вихреобразования и лучшего перемешивания жидкости.

Расчет теплоотдачи при вынужденной конвекции

Пример расчета. Рассчитаем средний коэффициент теплоотдачи воды, текущей по трубопроводу длиной 1 м, диаметром d=0,01 м с расходом Q=20 л/мин. Средняя температура воды t_ж=50°С, температура стенки трубы t_с=10°С.

1. Определим физические свойства воды при температуре 50°С:

• Теплопроводность воды λ_ж= 0,648 Вт/(м·град);
• Плотность воды ρ_ж=988 кг/м 3 ;
• Кинематическая вязкость воды ν_ж=0,556·10 -6 , м 2 /с;
• Число Прандтля при температуре жидкости Pr_ж=3,54;
• Число Прандтля при температуре стенки Pr_с=9,52.

2. Рассчитаем среднюю скорость течения воды w по трубе:

3. Определим число Рейнольдса Re:

4. Поскольку число Рейнольдса имеет значение больше 1·10 4 , то режим течения является турбулентным и расчет теплоотдачи необходимо проводить по следующему критериальному уравнению:

Определим коэффициент ε_L по соотношению L/d=1/0,01=100. Поскольку L/d>50, то коэффициент ε_L=1_.

Выполним расчет числа Нуссельта по приведенному критериальному уравнению:

5. Рассчитаем средний коэффициент теплоотдачи от воды к стенке трубы по формуле:

Таким образом, средний коэффициент теплоотдачи от воды к стенке трубы составляет 14,65 кВт/(м 2 ·град).

Теплоотдача при свободной конвекции в трубах и каналах

Теплообмен при свободном движении жидкости (или газа) происходит вследствие разности плотностей нагретых и холодных ее слоев. Интенсивность теплоотдачи жидкости в трубах и каналах при свободной конвекции существенно зависит от их положения в пространстве относительно силы тяжести.

Теплоотдача при свободной конвекции имеет различный характер в случаях свободного течения в неограниченном пространстве и теплообмена в ограниченном объеме (в узкой трубе или канале).

Свободная конвекция в неограниченном пространстве

Конвекция в неограниченном пространстве протекает, например при охлаждении трубопровода центрального отопления, расположенного на улице в безветренную погоду, вблизи от которого отсутствуют препятствия для движения воздушных потоков.

Горизонтальный канал или труба. Интенсивность теплоотдачи при свободной конвекции зависит от величины комплекса GrPr. При значении GrPr от 10 3 до 10 9 критериальное уравнение, описывающее среднюю теплоотдачу от поверхности горизонтальных труб и каналов, имеет вид:

В качестве определяющего размера принимается наружный диаметр d канала или трубы.

Вертикальный канал (труба, пластина). Для вертикальных труб и каналов при значении GrPr от 10 3 до 10 9 критериальное уравнение, описывающее среднюю теплоотдачу, имеет вид:

При GrPr>10 9 :

Примечание: В приведенных критериальных уравнениях теплообмена свойства жидкости, входящие в числа Gr и Pr, определяются при температуре окружающей среды. Число Прандтля с индексом «с» Pr_с берется для жидкости при температуре стенки. В качестве определяющего размера принимается длина L (высота) вертикально стоящей трубы или канала.

Свободная конвекция в ограниченном объеме

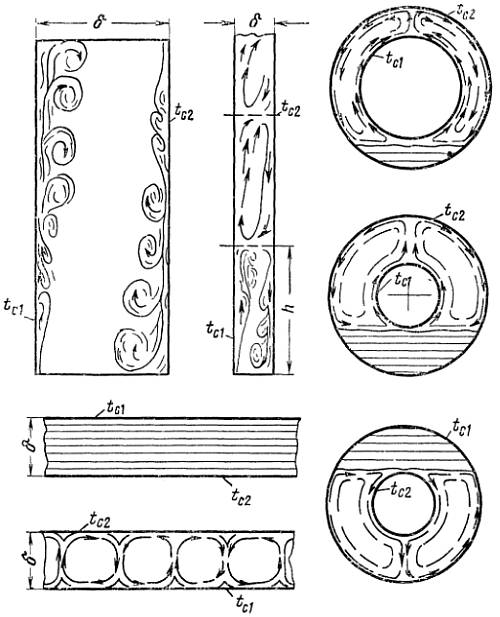
Теплообмен жидкости в ограниченном объеме при свободной конвекции характеризуется совместным протеканием процессов нагрева и охлаждения соседних слоев жидкости (или газа). Эти процессы сопровождаются сложным течением нисходящих и восходящих потоков, зависящих от рода жидкости, разницы температуры, формы канала и его геометрических размеров.

Для упрощения расчета таких сложных процессов конвективного теплообмена принято рассматривать их, как явление теплопроводности в щели толщиной δ с учетом понятия эквивалентного коэффициента теплопроводности λ_эк.

Эквивалентный коэффициент теплопроводности определяется по формуле:

Q — количество переданного тепла, Вт; δ — толщина слоя жидкости (или газа), м; F — площадь теплоотдающей поверхности, м 2 ; Δt=t_c1-t_c2 — температурный напор между нагретой и холодной стенками, °С.

Отношение эквивалентного коэффициента теплопроводности λ_эк к величине теплопроводности окружающей жидкости при средней температуре называется коэффициентом конвекции ε_к, который определяется значением комплекса GrPr.

При малых значениях комплекса GrPr 3 6 :

При 10 6 10 :

Примечание: Числа подобия Gr и Pr рассчитываются при средней температуре жидкости (или газа), равной t_ж=0,5(t_c1+t_c2). В качестве определяющего размера принимается δ — толщина слоя жидкости.

Расчет теплоотдачи при свободной конвекции

Пример расчета. Рассчитаем потери тепла естественной конвекцией от горизонтального трубопровода центрального отопления, находящегося на открытом воздухе. Диаметр трубопровода d=0,15 м, длина L=5 м, средняя температура наружной стенки t_с=80°С. Температура окружающего воздуха t_ж=20°С.

1. Определим физические свойства воздуха при температуре 20°С:

• Теплопроводность воздуха λ_ж= 0,0259 Вт/(м·град);
• Кинематическая вязкость воздуха ν_ж=15,06·10 -6 , м 2 /с;
• Число Прандтля при температуре жидкости Pr_ж=0,703;
• Число Прандтля при температуре стенки Pr_с=0,69;
• Коэффициент объемного расширения β_ж=1/(273+20)=0,00341 град -1 .

2. Вычислим число Грасгофа Gr по формуле:

3. Определим значение комплекса GrPr:

Этому значению комплекса соответствует следующее критериальное уравнение теплообмена при свободной конвекции в случае горизонтальной трубы:

4. Вычислим значение числа Нуссельта Nu:

5. Рассчитаем коэффициент теплоотдачи от трубы α по формуле:

6. Определим потери тепла с боковой поверхности трубопровода по формуле:

Подставляя численные значения, окончательно получаем потерю тепла:

Таким образом, только путем естественной (свободной) конвекции рассмотренный трубопровод отопления отдает воздуху 1681 Вт тепла.

[spoiler title=”источники:”]

http://www.isuct.ru/dept/chemkiber/piaht/metodwork/newmet/1.htm

http://thermalinfo.ru/eto-interesno/kriterialnye-uravneniya-teploobmena-raschet-teplootdachi-v-trubah-i-kanalah

[/spoiler]

Теплоотдача при вынужденном течении жидкости в трубах и каналах

Теплоотдача в трубах и каналах может происходить при вынужденном или свободном характере конвекционных потоков (возможны также их сочетания в случае существенного влияния гравитационных сил).

При вынужденном течении (вынужденная конвекция) жидкость нагнетается или отводится под действием сил внешнего давления, например, ветра, насоса или вентилятора.

Свободное течение жидкости происходит под действием подъемных (гравитационных) сил за счет изменения ее плотности из-за разницы температуры – слой жидкости с меньшей плотностью стремиться занять верхнее положение относительно холодного слоя (свободная или естественная конвекция).

Интенсивность теплоотдачи, как при вынужденной, так и при свободной конвекции характеризуется коэффициентом теплоотдачи α, имеющим размерность Вт/(м²·град), который определяется по формуле:

Nu – число Нуссельта; λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);

d – эквивалентный диаметр, равный

F – площадь сечения канала, м²; П – периметр канала, м.

Для трубы круглого сечения, эквивалентный диаметр равен внутреннему диаметру трубы.

В целом, расчет коэффициента теплоотдачи сводится к определению числа Нуссельта, значение которого задается соответствующими критериальными уравнениями конвективного теплообмена, зависящими от режима течения жидкости и формы канала.

Течение жидкости в трубах определяется значением числа Рейнольдса Re и в зависимости от его величины может быть ламинарным, переходным или турбулентным.

• Ламинарный режим течения жидкости характеризуется величиной числа Re до 2300.
• При значении числа Re от 2300 до 10000 режим течения в трубах является переходным.
• Турбулентный режим течения в трубах наблюдается при числах Re более 10000.

Число (критерий) Рейнольдса представляет собой безразмерный комплекс, связывающий скоростные и вязкостные характеристики жидкости с определяющим размером канала (для трубы – это ее диаметр).

Число Re определяется по формуле:

w – скорость течения жидкости, м/с; d – эквивалентный диаметр канала, м; ν — кинематическая вязкость жидкости при средней температуре, м²/с.

Теплоотдача в трубах и каналах существенно зависит от режима течения жидкости. При ламинарном режиме интенсивность теплоотдачи значительно меньше, чем при развитом турбулентном.

Теплоотдача при ламинарном течении в трубах и каналах

Ламинарный режим течения жидкости обычно характеризуется низкой скоростью потока. При этом в некоторых случаях влиянием конвекции, обусловленной действием гравитационных сил, пренебрегать нельзя.

Для выбора правильного критериального уравнения теплообмена и оценки влияния естественной конвекции на интенсивность теплопередачи при ламинарном режиме служит критерий Грасгофа Gr.

g – ускорение свободного падения, м/с²;

β – температурный коэффициент объемного расширения, град^-1;

d – эквивалентный диаметр канала, м;

ν — кинематическая вязкость жидкости при средней температуре, м²/с;

Δt – средняя разность температур жидкости и стенки, °С.

Теплоотдача при ламинарном течении в трубах и каналах с учетом естественной конвекции. Если величина комплекса GrPr превышает 8·10⁵, то расчет коэффициента теплоотдачи необходимо проводить с учетом влияния естественной конвекции в потоке жидкости по следующему критериальному уравнению:

Индекс «ж» означает, что свойства среды, входящие в критерии подобия Re, Pr и Gr берутся при средней температуре жидкости.

Число Прандтля с индексом «с» Pr_с берется для жидкости при температуре стенки.

ε_L – коэффициент, учитывающий изменение теплоотдачи по длине трубы или канала. Его можно определить с помощью таблицы:

Значения коэффициента ε_L при ламинарном режиме

L/d	1	2	5	10	15	20	30	40	50
εL	1,9	1,7	1,44	1,28	1,18	1,13	1,05	1,02	1

Теплоотдача при ламинарном течении в трубах и каналах без учета естественной конвекции. При значении GrPr<8·10⁵, влияние естественной конвекции на теплоотдачу жидкости пренебрежительно мало, и расчет коэффициента теплоотдачи можно проводить по следующему критериальному уравнению:

d – эквивалентный диаметр канала, м;

L – длина трубы (канала), м.

Представленные критериальные уравнения теплообмена при ламинарном режиме позволяют определить среднее значение числа Нуссельта, по величине которого можно рассчитать средний коэффициент теплоотдачи:

λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);

d – эквивалентный диаметр, м.

Теплоотдача в трубах и каналах при турбулентном режиме

Теплоотдача в трубах и каналах при турбулентном режиме осуществляется путем передачи тепла при интенсивном перемешивании слоев жидкости. Критериальное уравнение теплообмена для расчета средней теплоотдачи в трубах и каналах в этом случае имеет вид:

Критерии подобия Re и Pr берутся при средней температуре жидкости. Число Прандтля с индексом «с» Pr_с берется при температуре стенки.

Представленное критериальное уравнение применяется в диапазоне чисел Re от 1·10⁴ до 5·10⁶ и Pr от 0,6 до 2500.

ε_L – коэффициент, учитывающий изменение среднего коэффициента теплоотдачи по длине трубы или канала при турбулентном режиме течения. Значения ε_L приведены в следующей таблице при различных числах Рейнольдса и отношениях длины канала к его эквивалентному диаметру:

Значения коэффициента ε_L при турбулентном режиме

Reж	L/d
1	2	5	10	15	20	30	40	50
1·104	1,65	1,5	1,34	1,23	1,17	1,13	1,07	1,03	1
2·104	1,51	1,4	1,27	1,18	1,13	1,1	1,05	1,02	1
5·104	1,34	1,27	1,18	1,13	1,1	1,08	1,04	1,02	1
1·105	1,28	1,22	1,15	1,1	1,08	1,06	1,03	1,02	1
1·106	1,14	1,11	1,08	1,05	1,04	1,03	1,02	1,01	1

Расчет теплоотдачи в изогнутых трубах и каналах проводится по тому же критериальному уравнению с добавлением множителя — поправки на действие центробежных сил, которая определяется по формуле:

R — радиус изгиба трубы или канала, м; d – эквивалентный диаметр трубы или канала, м.

Теплоотдача в изогнутых трубах проходит более интенсивно, чем в прямых, за счет большего вихреобразования и лучшего перемешивания жидкости.

Теплоотдача при свободной конвекции в трубах и каналах

Теплообмен при свободном движении жидкости (или газа) происходит вследствие разности плотностей нагретых и холодных ее слоев. Интенсивность теплоотдачи жидкости в трубах и каналах при свободной конвекции существенно зависит от их положения в пространстве относительно силы тяжести.

Теплоотдача при свободной конвекции имеет различный характер в случаях свободного течения в неограниченном пространстве и теплообмена в ограниченном объеме (в узкой трубе или канале).

Свободная конвекция в неограниченном пространстве

Конвекция в неограниченном пространстве протекает, например при охлаждении трубопровода центрального отопления, расположенного на улице в безветренную погоду, вблизи от которого отсутствуют препятствия для движения воздушных потоков.

Горизонтальный канал или труба. Интенсивность теплоотдачи при свободной конвекции зависит от величины комплекса GrPr. При значении GrPr от 10³ до 10⁹ критериальное уравнение, описывающее среднюю теплоотдачу от поверхности горизонтальных труб и каналов, имеет вид:

В качестве определяющего размера принимается наружный диаметр d канала или трубы.

Вертикальный канал (труба, пластина). Для вертикальных труб и каналов при значении GrPr от 10³ до 10⁹ критериальное уравнение, описывающее среднюю теплоотдачу, имеет вид:

При GrPr>10⁹:

Примечание: В приведенных критериальных уравнениях теплообмена свойства жидкости, входящие в числа Gr и Pr, определяются при температуре окружающей среды. Число Прандтля с индексом «с» Pr_с берется для жидкости при температуре стенки. В качестве определяющего размера принимается длина L (высота) вертикально стоящей трубы или канала.

Свободная конвекция в ограниченном объеме

Теплообмен жидкости в ограниченном объеме при свободной конвекции характеризуется совместным протеканием процессов нагрева и охлаждения соседних слоев жидкости (или газа). Эти процессы сопровождаются сложным течением нисходящих и восходящих потоков, зависящих от рода жидкости, разницы температуры, формы канала и его геометрических размеров.

Для упрощения расчета таких сложных процессов конвективного теплообмена принято рассматривать их, как явление теплопроводности в щели толщиной δ с учетом понятия эквивалентного коэффициента теплопроводности λ_эк.

Эквивалентный коэффициент теплопроводности определяется по формуле:

Q — количество переданного тепла, Вт; δ — толщина слоя жидкости (или газа), м; F — площадь теплоотдающей поверхности, м²; Δt=t_c1-t_c2 — температурный напор между нагретой и холодной стенками, °С.

Отношение эквивалентного коэффициента теплопроводности λ_эк к величине теплопроводности окружающей жидкости при средней температуре называется коэффициентом конвекции ε_к, который определяется значением комплекса GrPr.

При малых значениях комплекса GrPr<1000 коэффициент конвекции ε_к=1, то есть теплоотдача просходит только за счет теплопроводности среды (λ_эк=λ).

В случае 10³<GrPr<10⁶:

При 10⁶<GrPr<10¹⁰:

Примечание: Числа подобия Gr и Pr рассчитываются при средней температуре жидкости (или газа), равной t_ж=0,5(t_c1+t_c2). В качестве определяющего размера принимается δ — толщина слоя жидкости.

Источники:

1. Михеев М. А., Михеева И. М. Основы теплопередачи.
2. Исаченко В. П., Осипова В. А., Сукомел А. С. Теплопередача. Учебник для вузов — М.: «Энергия», 1975.