
{mu = dfrac{F_{тр}}{mg}}
Ускорение свободного падения g
Приводим 2 варианта нахождения коэффициента трения – зная силу трения и массу тела или зная угол наклона. Для обоих вариантов вы найдете удобные калькуляторы и формулы для расчета.
Коэффициент трения представляет собой безразмерную скалярную величину, которая равна отношению силы трения между двумя телами и силы, прижимающей их друг к другу, во время или в начале скольжения.
Коэффициент трения чаще всего обозначают греческой буквой µ («мю»).
Следует помнить, что коэффициент трения (μ) величина безразмерная, то есть не имеет единицы измерения.
Коэффициент трения зависит от качества обработки трущихся поверхностей, скорости движения тел относительно друг друга и материала соприкасающихся поверхностей. В большинстве случаев коэффициент трения находится в пределах от 0,1 до 0,5 (см. таблицу).
Содержание:
- калькулятор коэффициента трения
- формула коэффициента трения через силу трения и массу
- формула коэффициента трения через угол наклона
- таблица коэффициентов трения
- примеры задач
Формула коэффициента трения через силу трения и массу

mu = dfrac{F_{тр}}{mg}
Fтр – сила трения
m – масса тела
g – ускорение свободного падения (в большинстве задач можно принять g=9.81 м/с²)
Формула коэффициента трения через угол наклона

mu = tg(alpha)
α – угол наклона
Таблица коэффициентов трения скольжения для разных пар материалов
| Трущиеся материалы (при сухих поверхностях) | Коэффициенты трения | |
|---|---|---|
| покоя | при движении | |
| Резина по сухому асфальту | 0,95-1,0 | 0,5-0,8 |
| Резина по влажному асфальту | 0,25-0,75 | |
| Алюминий по алюминию | 0,94 | |
| Бронза по бронзе | 0,20 | |
| Бронза по чугуну | 0,21 | |
| Дерево по дереву (в среднем) | 0,65 | 0,33 |
| Дерево по камню | 0,46-0,60 | |
| Дуб по дубу (вдоль волокон) | 0,62 | 0,48 |
| Дуб по дубу (перпендикулярно волокнам) | 0,54 | 0,34 |
| Железо по железу | 0,15 | 0,14 |
| Железо по чугуну | 0,19 | 0,18 |
| Железо по бронзе (слабая смазка) | 0,19 | 0,18 |
| Канат пеньковый по деревянному барабану | 0,40 | |
| Канат пеньковый по железному барабану | 0,25 | |
| Каучук по дереву | 0,80 | 0,55 |
| Каучук по металлу | 0,80 | 0,55 |
| Кирпич по кирпичу (гладко отшлифованные) | 0,5-0,7 | |
| Колесо со стальным бандажем по рельсу | 0,16 | |
| Лед по льду | 0,05-0,1 | 0,028 |
| Метал по аботекстолиту | 0,35-0,50 | |
| Метал по дереву (в среднем) | 0,60 | 0,40 |
| Метал по камню (в среднем) | 0,42-0,50 | |
| Метал по металу (в среднем) | 0,18-0,20 | |
| Медь по чугуну | 0,27 | |
| Олово по свинцу | 2,25 | |
| Полозья деревянные по льду | 0,035 | |
| Полозья обитые железом по льду | 0,02 | |
| Резина (шина) по твердому грунту | 0,40-0,60 | |
| Резина (шина) по чугуну | 0,83 | 0,8 |
| Ремень кожаный по деревянному шкиву | 0,50 | 0,30-0,50 |
| Ремень кожаный по чугунному шкиву | 0,30-0,50 | 0,56 |
| Сталь по железу | 0,19 | |
| Сталь(коньки) по льду | 0,02-0,03 | 0,015 |
| Сталь по райбесту | 0,25-0,45 | |
| Сталь по стали | 0,15-0,25 | 0,09 (ν = 3 м/с)
0,03 (ν = 27 м/с) |
| Сталь по феродо | 0,25-0,45 | |
| Точильный камень (мелкозернистый) по железу | 1 | |
| Точильный камень (мелкозернистый) по стали | 0,94 | |
| Точильный камень (мелкозернистый) по чугуну | 0,72 | |
| Чугун по дубу | 0,65 | 0,30-0,50 |
| Чугун по райбесту | 0,25-0,45 | |
| Чугун по стали | 0,33 | 0,13 (ν = 20 м/с) |
| Чугун по феродо | 0,25-0,45 | |
| Чугун по чугуну | 0,15 |
Примеры задач на нахождение коэффициента трения
Задача 1
Найдите коэффициент трения между полом и ящиком массой 20 кг, который равномерно двигают с силой 50 Н.
Решение
Для решения задачи воспользуемся формулой.
mu = dfrac{F_{тр}}{mg} = dfrac{50}{20 cdot 9.81} = dfrac{50}{196.2} approx 0.25484
Ответ: approx 0.25484
С помощью калькулятора удобно проверить ответ.
Задача 2
Найдите коэффициент трения если угол наклона 30°.
Решение
Для решения этой задачи воспользуемся второй формулой.
mu = tg(alpha) = tg(30°) approx 0.57735
Ответ: approx 0.57735
Проверим полученный ответ с помощью калькулятора .
Сила трения. Коэффициент трения
- Причины возникновения трения
- Трение покоя
- Трение скольжения
- Трение качения
- Задачи
- Лабораторная работа №8. Измерение коэффициента трения скольжения
п.1. Причины возникновения трения
При движении одного тела по поверхности другого всегда возникает сила, направленная противоположно направлению скорости и замедляющая движение. Эта сила называется силой трения.
По своей природе сила трения отличается от силы тяготения и силы упругости, которые были рассмотрены в предыдущих параграфах.
Причины возникновения силы трения можно разделить на два класса: 1) шероховатость поверхностей контактирующих тел; 2) взаимное притяжение молекул при контакте.
Неровности поверхностей проявляются на макроуровне и видны невооруженным глазом или в оптический микроскоп. Их влияние можно уменьшить, если отполировать поверхности или нанести смазку.
Взаимное притяжение молекул проявляется на микроуровне и приводит к тому, что даже на идеально отполированных поверхностях не удается избежать трения, когда частицы одного тела перемещаются относительно частиц другого.
Сила трения – это сумма межмолекулярных сил, возникающих при деформациях и изломах контактирующих поверхностей за счет разрыва межмолекулярных связей.
Сила трения направлена вдоль поверхностей контактирующих тел.
Как и сила упругости, сила трения имеет электромагнитную природу и связана с межмолекулярным взаимодействием.
Но в отличие от силы упругости, причиной силы трения является разрыв межмолекулярных связей. Кроме того, если сила упругости всегда направлена перпендикулярно поверхностям контактирующих тел, то сила трения всегда направлена вдоль этих поверхностей.
В зависимости от характера движения контактирующих тел различают трение покоя, трение скольжения и трение качения.
п.2. Трение покоя
Сила трения, возникающая при относительной скорости двух контактирующих тел равной нулю, называется силой трения покоя.
Сила трения покоя равна по модулю приложенной силе и направлена в сторону, противоположную возможному движению тела, параллельно контактирующим поверхностям.
Если параллельно поверхности контакта на тело не действует сила, сила трения покоя равна нулю. Максимальное значение силы трения, при котором тело все ещё неподвижно, называется максимальной силой трения покоя.
Пример изменения силы трения покоя
 |
Сила трения покоя равна приложенной силе, которая все ещё не приводит тело в движение. Допустим, что мы прикладываем к шкафу последовательно силу 100 Н, 200 Н, 300 Н, и он начинает равномерно двигаться только при 300 Н. Как только тело начинает скользить, на него уже действует сила трения скольжения. Получаем: |
||
| Приложенная сила, Н | Движение | Сила трения покоя, Н | Сила трения скольжения, Н |
| 100 | Нет | 100 | – |
| 200 | Нет | 200 | – |
| 300 | Есть, равномерное | – | 300 |
п.3. Трение скольжения
Силу трения, возникающую в результате движения одного тела по поверхности другого, называют силой трения скольжения.
Сила трения скольжения всегда направлена в сторону, противоположную перемещению тела («тормозит» движение).
 |
Если тело расположено на горизонтальной опоре, сила тяжести (mg), действующая на него, равна по величине силе реакции опоры (N) (см. §22 данного справочника). Сила трения направлена противоположно силе тяги. |
Сила трения скольжения прямо пропорциональна силе реакции опоры: $$ F_{text{тр}}=mu N $$ Коэффициент (mu) называют коэффициентом трения скольжения; величина (mu) зависит от материала трущихся тел и состояния их поверхностей.
Значения коэффициентов трения скольжения для различных поверхностей приводятся в справочных таблицах.
При проектировании и разработке машин и механизмов коэффициенты трения скольжения для отдельных узлов определяются в специальных лабораториях.
п.4. Трение качения
Сила трения, возникающая при качении одного тела по поверхности другого, называется силой трения качения.
Сила трения качения значительно меньше силы трения скольжения.
 |
Уменьшение трения за счет качения используется в шариковых и роликовых подшипниках. Первый подшипник качения был установлен в опоре ветряка, построенного в Англии в 1780 г. Этот подшипник состоял из двух литых чугунных дорожек качения, между которыми находилось 40 чугунных шаров. Сегодня подшипники являются незаменимой деталью во всех подвижных конструкциях; они уменьшают износ трущихся деталей и снижают потери энергии на нагрев из-за трения. |
п.5. Задачи
Задача 1. Найдите коэффициент трения между шинами автомобиля и дорогой, если при равномерном движении по прямолинейному участку двигатель развивает силу тяги, равную 30 кН. Масса автомобиля 6 т.
Дано:
(m=6 text{т}=6cdot 10^3 text{кг})
(F_{text{тяги}}=30 text{кН}=3cdot 10^4 text{Н})
(gapprox 10 text{м/с}^2)
__________________
(mu-?)

Коэффициент трения $$ mu=frac{F_{text{тр}}}{N}. $$ При равномерном движении скорость постоянна и ускорение (overrightarrow{a}=0). По второму закону Ньютона, равнодействующая горизонтальных сил равна нулю $$ overrightarrow{F_{text{тр}}}+ overrightarrow{F_{text{тяги}}}=0. $$ Значит, сила трения и сила тяги равны по модулю: $$ F_{text{тр}}=F_{text{тяги}}. $$ Сила реакции горизонтальной опоры равна силе тяжести, действующей на автомобиль: $$ n=mg. $$ Получаем: $$ mu=frac{F_{text{тр}}}{N}= frac{F_{text{тяги}}}{mg}, mu=frac{3cdot 10^4}{6cdot 10^3cdot 10}=0,5. $$ Ответ: 0,5
Задача 2. Деревянный брусок массой 3 кг равномерно тянут по горизонтальной деревянной доске с помощью динамометра. Жесткость пружины динамометра равна 3 Н/см, коэффициент трения дерева об дерево 0,3. На сколько сантиметров растянется пружина?
Дано:
(m=3 text{кг})
(k=3frac{text{Н}}{text{см}}=frac{3 text{Н}}{0,01 text{м}}=300frac{text{Н}}{text{м}})
(mu=0,3)
(gapprox 10 text{м/с}^2)
__________________
(Delta l-?)
Показания динамометра – это сила упругости, равная силе тяги. При равномерном движении сила тяги равна по модулю силе трения. Поэтому begin{gather*} F_{text{упр}}=kDelta l=F_{text{тр}}=mu N=mu mgRightarrow kDelta l=mu mg end{gather*} Получаем: $$ Delta l=frac{mu mg}{k}, Delta l=frac{0,3cdot 3cdot 10}{300}=0,03 (text{м})=3 (text{см}) $$ Ответ: 3 см.
Задача 3. Автомобиль движется по горизонтальному участку дороги со скоростью 72 км/ч. Рассчитайте время торможения и тормозной путь до полной остановки, если коэффициент трения колес о дорогу равен 0,4.
Дано:
(v_1=72frac{text{км}}{text{ч}}=20frac{text{м}}{text{с}})
(mu=0,4)
(v_2=0)
(gapprox 10 text{м/с}^2)
__________________
(t, s-?)
Автомобиль тормозит за счет силы трения. По второму закону Ньютона begin{gather*} F_{text{тр}}=ma. end{gather*} С другой стороны на горизонтальной дороге $$ F_{text{тр}}=mu N=mu mg. $$ Получаем: $$ ma=mu mgRightarrow a=mu g. $$ По определению ускорения $$ a=frac{v_2-v_1}{t}. $$ Т.к. (v_2=0), ускорение отрицательное.
Модуль ускорения $$ |a|=frac{v_1}{t}=mu gRightarrow t=frac{v_1}{mu g} $$ Время торможения прямо пропорционально скорости и обратно пропорционально коэффициенту трения. $$ t=frac{20}{0,4cdot 10}=5 (text{с}) $$ Найдем тормозной путь $$ s=v_1t+frac{at^2}{2}=v_1t+ left(frac{overbrace{v_2}^{=0}-v_1}{t}right)frac{t^2}{2}=v_1t -frac{v_1t}{2}=frac{v_1t}{2}=frac{v_1t}{2}cdot frac{v_1}{mu g}=frac{v_1^2}{2mu g} $$ Тормозной путь прямо пропорционален квадрату(!) скорости и обратно пропорционален коэффициенту трения. $$ s=frac{20^2}{2cdot 0,4cdot 10}=50 (text{м}) $$ Ответ: 5 с; 50 м.
п.6. Лабораторная работа №8. Измерение коэффициента трения скольжения
Цель работы
Научиться измерять силу трения скольжения и определять коэффициент трения скольжения. Изучить зависимость коэффициента трения скольжения от материалов соприкасающихся тел и от площади опоры движущегося тела.
Теоретические сведения
 |
При (v=const) (равномерное движение) получаем По вертикали (moverrightarrow{g}=-overrightarrow{N}). Модули этих сил равны По горизонтали (overrightarrow{F_{text{тр}}}=-overrightarrow{F_{text{тяги}}}). Модули этих сил равны $$ F_{text{тяги}}=F_{text{тр}}=mu N=mu mg $$ |
Если тело перемещать с помощью динамометра, то сила упругости, возникающая в пружине, будет равна силе тяги. Т.е., сила тяги непосредственно измеряется динамометром.
В работе используются стандартные лабораторные грузики массой 100 г.
Измерив силу тяги и зная массу перемещаемого тела, рассчитываем коэффициент трения: $$ mu=frac{F_{text{тяги}}}{mg} $$
Для расчетов используем стандартное значение (g=9,80665 text{м/с}^2).
Погрешность для прямых измерений (F_{text{тяги}}) определяется как половина цены деления динамометра. Погрешность для массы определяется по маркировке грузиков и бруска, (Delta m=2 text{г}) для (m=100 text{г}), т.е. (delta_m=2text{%}).
Погрешность эксперимента (delta_e) рассчитывается как средняя арифметическая по результатам измерений и вычислений.
Приборы и материалы
Лабораторный динамометр на 5 Н; набор грузиков по 100 г; деревянный брусок с крючком 100 г; деревянная доска; наждачная бумага.
Ход работы
1. Прикрепите динамометр к бруску, положите доску горизонтально, поставьте брусок самой большой по площади гранью слева на доску.
2. Перемещая брусок слева направо по доске, добейтесь равномерного скольжения (со стабильными показаниями динамометра). Снимите показания динамометра и запишите.
3. Повторите эксперимент, нагружая брусок одним, двумя, тремя и четырьмя грузиками.
4. Рассчитайте коэффициент трения дерева об дерево, определите относительную и абсолютную погрешности эксперимента.
5. Повторите эксперимент, перемещая брусок по доске, обмотанной наждачной бумагой. Найдите коэффициент трения дерева об наждак, определите относительную и абсолютную погрешности эксперимента.
6. Снимите наждачную бумагу и повторите эксперимент для трения дерева об дерево. Однако на этот раз брусок должен опираться на меньшую по площади грань. Рассчитайте коэффициент трения дерева об дерево в этом случае.
7. Сравните полученные коэффициенты трения, сделайте выводы о зависимости коэффициента трения от материала соприкасающихся поверхностей и от площади опоры движущегося тела.
Результаты измерений и вычислений
Цена деления динамометра (d=0,1 text{Н}).
Таблица для расчета коэффициента трения скольжения дерева об дерево
| Опыт | (m, text{кг}) | (F_{text{тяги}}, text{Н}) | (mu=frac{F_{text{тяги}}}{mg}) | (Delta=|mu-mu_{text{ср}}|) | |
| 1 | Брусок | 0,1 | 0,3 | 0,306 | 0,026 |
| 2 | Брусок + 1 грузик | 0,2 | 0,7 | 0,357 | 0,025 |
| 3 | Брусок + 2 грузика | 0,3 | 1,0 | 0,340 | 0,008 |
| 4 | Брусок + 3 грузика | 0,4 | 1,3 | 0,331 | 0,001 |
| 5 | Брусок + 4 грузика | 0,5 | 1,6 | 0,326 | 0,006 |
| Всего | – | – | 1,660 | 0,065 |
Среднее значение коэффициента трения $$ mu_{text{ср}}=frac{1,660}{5}=0,332 $$ Среднее значение абсолютного отклонения $$ Delta =frac{0,065}{5}=0,013 $$ Относительная погрешность begin{gather*} delta=frac{0,013}{0,332}cdot 100text{%}approx 3,9text{%}\[7pt] mu_{text{дд}}=(0,332pm 0,013), delta_mu=3,9text{%} end{gather*}
Таблица для расчета коэффициента трения скольжения дерева об наждак
| Опыт | (m, text{кг}) | (F_{text{тяги}}, text{Н}) | (mu=frac{F_{text{тяги}}}{mg}) | (Delta=|mu-mu_{text{ср}}|) | |
| 1 | Брусок | 0,1 | 0,6 | 0,612 | 0,039 |
| 2 | Брусок + 1 грузик | 0,2 | 1,1 | 0,561 | 0,012 |
| 3 | Брусок + 2 грузика | 0,3 | 1,7 | 0,578 | 0,005 |
| 4 | Брусок + 3 грузика | 0,4 | 2,2 | 0,561 | 0,012 |
| 5 | Брусок + 4 грузика | 0,5 | 2,7 | 0,551 | 0,022 |
| Всего | – | – | 2,862 | 0,090 |
Среднее значение коэффициента трения $$ mu_{text{ср}}=frac{2,862}{5}approx 0,572 $$ Среднее значение абсолютного отклонения $$ Delta =frac{0,090}{5}=0,018 $$ Относительная погрешность begin{gather*} delta=frac{0,018}{0,572}cdot 100text{%}approx 3,1text{%}\[7pt] mu_{text{дн}}=(0,572pm 0,018), delta_mu=3,1text{%} end{gather*}
Таблица для расчета коэффициента трения скольжения дерева об дерево (узкая грань)
| Опыт | (m, text{кг}) | (F_{text{тяги}}, text{Н}) | (mu=frac{F_{text{тяги}}}{mg}) | (Delta=|mu-mu_{text{ср}}|) | |
| 1 | Брусок | 0,1 | 0,35 | 0,357 | 0,011 |
| 2 | Брусок + 1 грузик | 0,2 | 0,7 | 0,357 | 0,011 |
| 3 | Брусок + 2 грузика | 0,3 | 1,0 | 0,340 | 0,006 |
| 4 | Брусок + 3 грузика | 0,4 | 1,3 | 0,331 | 0,015 |
| 5 | Брусок + 4 грузика | 0,5 | 1,7 | 0,347 | 0,000 |
| Всего | – | – | 1,732 | 0,043 |
Среднее значение коэффициента трения $$ mu_{text{ср}}=frac{1,732}{5}approx 0,346 $$ Среднее значение абсолютного отклонения $$ Delta =frac{0,043}{5}approx 0,009 $$ Относительная погрешность begin{gather*} delta=frac{0,009}{0,346}cdot 100text{%}approx 2,5text{%}\[7pt] mu ‘_{text{дд}}=(0,346pm 0,009), delta_mu=2,5text{%} end{gather*}
Выводы
На основании проделанной работы можно сделать следующие выводы.
В работе исследовалась зависимость коэффициента трения скольжения от поверхностей, из которых изготовлены соприкасающиеся тела.
Для скольжения дерева об дерево был получен коэффициент begin{gather*} mu_{text{дд}}=(0,332pm 0,013), delta_mu=3,9text{%} end{gather*}
Для скольжения дерева об наждак был получен коэффициент begin{gather*} mu_{text{дн}}=(0,572pm 0,018), delta_mu=3,1text{%}\[7px] mu_{text{дн}}gt mu_{text{дд}} end{gather*}
Наждак является более шероховатой поверхностью и сила трения на ней больше.
Коэффициент трения скольжения сильно зависит от материалов соприкасающихся поверхностей.
Также в работе исследовалась зависимость коэффициента трения скольжения от площади опоры движущегося тела. Брусок выставлялся на более узкую грань, и изучалось скольжение дерева об дерево в этом случае. Был получен коэффициент begin{gather*} mu’_{text{дд}}=(0,346pm 0,009), delta_mu=2,5text{%} end{gather*} Поскольку begin{gather*} 0,319le mu_{text{дд}}le 0,345 0,337le mu’_{text{дд}}le 0,355 end{gather*} Полученные отрезки значений перекрываются.
Таким образом, в рамках погрешности эксперимента коэффициент трения скольжения не зависит от площади опоры движущегося тела.
Трение — вариант взаимодействия двух тел. Оно возникает при движении одного тела по поверхности другого. При этом тела действуют друг на друга с силой, которая называется силой трения. Сила трения имеет электромагнитную природу.
Сила трения — сила, возникающая между телами при их движении или при попытке их сдвинуть. Обозначается как Fтр. Единица измерения — Н (Ньютон).
Трение бывает сухим и жидким. В школьном курсе физике изучается сухое трение.
Виды сухого трения:
- трение скольжения;
- трение качения;
- трение покоя.
Трение скольжения
Трение скольжения — трение, возникающее при скольжении одного тела по поверхности другого. Сила трения скольжения направлена противоположно направлению движения тела: Fтр↑↓v.
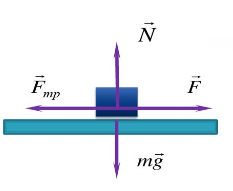
Сила трения скольжения определяется формулой:
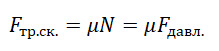
μ — коэффициент трения, N — сила реакции опоры, Fдавл. — сила нормального давления
Сила реакции опоры и сила нормального давления — равные по модулю, но противоположные по направлению силы. Если тело не перемещается с ускорением относительно оси ОУ, модули силы реакции опоры и силы нормального давления равны модулю силы тяжести, действующей на это тело.
Силу трения скольжения зависит от степени неровности (шероховатости) поверхности. Поэтому ее можно легко менять.
Чтобы увеличить силу трения скольжения, нужно сделать поверхность тела более шероховатой. Так, чтобы зимой автомобили не скользили по голому льду, автомобилисты используют зимние шины. От летних они отличаются глубоким протектором и наличием шипов, создающих дополнительную неровность.
Чтобы уменьшить силу трения скольжения, нужно сделать поверхность более ровной. Ее можно отшлифовать или смазать. Так, чтобы лыжи скользили по снегу лучше, их смазывают специальными мазями или парафинами.
Полезные факты
- Если тело движется по гладкой поверхности, сила трения между ними отсутствует.
- Сила трения скольжения не зависит от площади соприкосновения тел.
- Сила трения качения обычно в несколько раз меньше силы трения скольжения. Поэтому тяжелые грузы перемещают не волоком, а с помощью тележек на колесах.
Пример №1. Конькобежец массой 70 кг скользит по льду. Какова сила трения, действующая на конькобежца, если коэффициент трения скольжения коньков по льду равен 0,002?
Сила реакции опоры по модулю равна силе тяжести, действующей на конькобежца. Отсюда:
Трение покоя
Трение покоя возникает при попытке сдвинуть предмет с места. Трение покоя противоположно направлено приложенной к телу силе (в сторону возможного движения).
Сила трения покоя всегда больше нуля, но всегда меньше силы трения скольжения:
0 < Fтр.пок. < Fтр. ск.
Способы определения вида силы трения, возникающей между телами, и ее модуля:
- Когда к телу прикладывается сила F , модуль которой меньше силы трения скольжения, возникает сила трения покоя. Тело продолжает покоиться. При этом модуль силы трения покоя равен модулю прикладываемой к телу силы. Если F < Fтр. ск., Fтр.пок. = F.
- Когда к телу прикладывается сила, модуль которой равен силе трения скольжения или превышает ее, возникает сила трения скольжения. Тело при этом начинает двигаться. Сила трения определяется формулой силы трения скольжения. Если F ≥ Fтр. ск., Fтр. = Fтр.ск.
Графически это можно изобразить так:
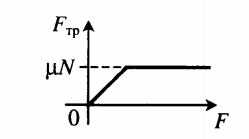
Пример №2. На горизонтальном полу стоит ящик массой 20 кг. Коэффициент трения между полом и ящиком равен 0,3. К ящику в горизонтальном направлении прикладывают силу 36 Н. Какова сила трения между ящиком и полом?
Чтобы определить вид трения, возникающего между ящиком и полом, нужно найти силу трения скольжения и сравнить с ней приложенную к ящику силу.
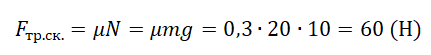
Сила, приложенная к ящику, меньше силы трения скольжения. Значит, между ящиком и полом возникает сила трения покоя. Модуль силы трения покоя равен модулю приложенной силы:
Fтр.пок. = F = 36 (Н).
Описание движения тел с учетом сил трения
Тело может двигаться по горизонтальной, наклонной или вертикальной плоскости. Оно может покоиться, двигаться равномерно или с ускорением, а сила тяги, под действием которой движется тело, может быть направлена, как в сторону движения тела, так и под углом к плоскости. Поэтому применение законов Ньютона к каждому из случаев имеет свои особенности.
Движение тела по горизонтальной плоскости
Равноускоренное движение по горизонтали, сила тяги параллельная плоскости |
|
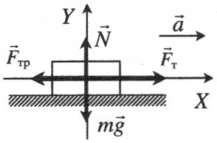 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fт – Fтр = ma Проекция на ось ОУ: N – mg = 0 |
Равнозамедленное движение по горизонтали, сила тяги параллельная плоскости |
|
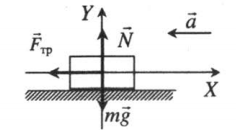 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: – Fтр = –ma Проекция на ось ОУ: N – mg = 0 |
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вверх) |
|
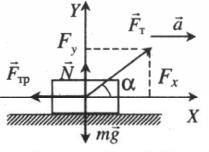 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fтcosα – Fтр = ma Проекция на ось ОУ: Fтsinα + N – mg = 0 |
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вниз) |
|
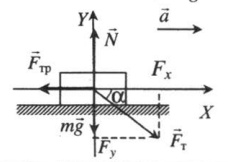 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fтcosα – Fтр = ma Проекция на ось ОУ: N – Fтsinα – mg = 0 |
Внимание! В случаях, когда сила тяги Fт направлена под углом к плоскости движения, сила реакции опоры не равна силе тяжести: N ≠ mg.
Пример №3. Брусок массой 1 кг движется равноускоренно по горизонтальной поверхности под действием силы 10 Н, как показано на рисунке. Коэффициент трения скольжения равен 0,4, а угол наклона α — 30 градусов. Чему равен модуль силы трения?
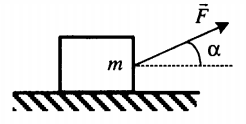
Сила трения равна произведению коэффициента трения скольжения на силу реакции опоры:
Fтр = μN
Проекция сил на ось ОУ выглядит так:
N – Fтsinα – mg = 0
Отсюда силы реакции опоры равна:
N = Fтsinα + mg
Подставим ее в формулу для вычисления силы трения и получим:
Fтр = μN = μ (Fтsinα + mg) = 0,4(10∙0,5 + 1∙10) = 6 (Н)
Движение тела по вертикальной плоскости
Тело прижали к вертикальной плоскости и удерживают |
|
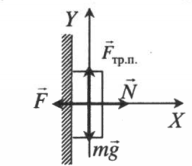 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: N – F = 0 Проекция на ось ОУ: Fт.п. – mg = 0 |
Тело поднимается под действием силы тяги, направленной под углом к вертикали |
|
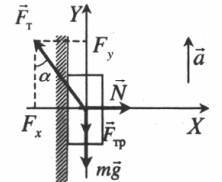 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: N – Fтsinα = 0 Проекция на ось ОУ: Fтcosα – Fтр – mg = 0 |
Пример №4. Груз массой 50 кг удерживают на вертикальной плоскости, коэффициент трения которой равен 0,4. Определить, какую силу нужно приложить, чтобы груз оставался в состоянии покоя.
Проекция на ось ОХ:
N – F = 0
Отсюда следует, что сила должна быть равна силе реакции опоры.
Проекция на ось ОУ:
Fт.п. – mg = 0
Перепишем, выразив силу трения через силу реакции опоры:
μN – mg = 0
Отсюда выразим силу реакции опоры:
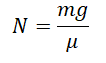
Следовательно:
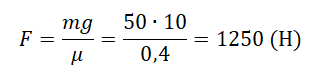
Движение тела по наклонной плоскости
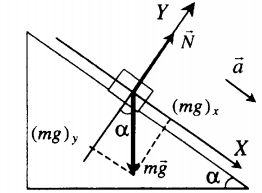
Движение вниз без трения |
|
 |
Второй закон Ньютона в векторной форме: |
|
mg + N = ma |
|
| Проекция на ось ОХ: | |
|
mg sinα = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
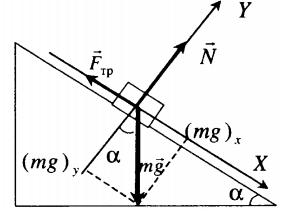
Тело покоится на наклонной плоскости |
|
 |
Второй закон Ньютона в векторной форме: |
|
mg + N + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
mg sinα – Fтр.п. = 0 |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
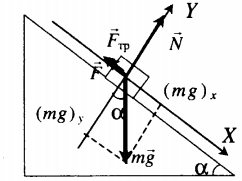
Тело удерживают на наклонной плоскости |
|
 |
Второй закон Ньютона в векторной форме: |
|
mg + N + F + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
F + Fтр. – mg sinα = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Равноускоренное движение вверх с учетом силы трения |
|
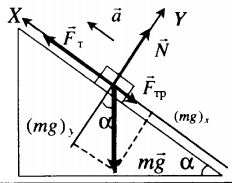 |
Второй закон Ньютона в векторной форме: |
|
mg + N + Fт + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
Fт – mg sinα – Fтр. = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Равномерное движение вверх с учетом силы трения |
|
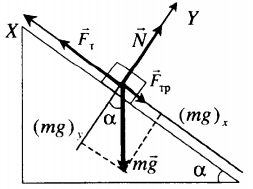 |
Второй закон Ньютона в векторной форме: |
|
mg + N + F + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
Fт – mg sinα – Fтр. = 0 |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
Пример №5. Брусок массой 200 г покоится на наклонной плоскости. Коэффициент трения между поверхностью бруска и плоскостью равен 0,6. Определите величину силы трения, если угол наклона плоскости к горизонту равен 30 градусам.
Переведем массу в килограммы: 200 г = 0,2 кг.
Проекция сил, действующих на тело, на ось ОХ:
mg sinα – Fтр.п. = 0
Отсюда сила трения равна:
Fтр.п. = mg sin α
Подставляем известные данные и вычисляем:
Fтр.п. = 0,2∙10∙sin30o = 2∙0,5 = 1 (Н)
Полезная информация
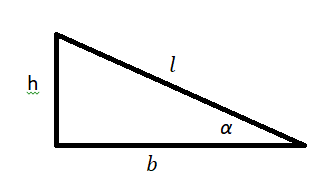
Задание EF18204
При исследовании зависимости силы трения скольжения Fтр от силы нормального давления Fд были получены следующие данные:
|
Fтр, Н |
1,0 |
2,0 |
3,0 |
4,0 |
|
Fд, Н |
2,0 |
4,0 |
6,0 |
8,0 |
Из результатов исследования можно сделать вывод, что коэффициент трения скольжения равен:
а) 0,2
б) 2
в) 0,5
г) 5
Алгоритм решения
1.Записать формулу, связывающую силу трения с силой нормального давления.
2.Выразить из нее коэффициент трения.
3.Взять значения силы трения и силы нормального давления из любого опыта (из любого столбца таблицы).
4.Вычислить коэффициент трения на основании табличных данных.
Решение
Силу трения и силу нормального давления связывает формула:
Fтр = μN
Отсюда коэффициент трения равен:
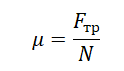
Сделаем расчет коэффициента трения на основании данных первого опыта (1 столбца):
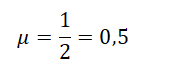
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17513
Полый конус с углом при вершине 2α вращается с угловой скоростью ω вокруг вертикальной оси, совпадающей с его осью симметрии. Вершина конуса обращена вверх. На внешней поверхности конуса находится небольшая шайба, коэффициент трения которой о поверхность конуса равен μ. При каком максимальном расстоянии L от вершины шайба будет неподвижна относительно конуса? Сделайте схематический рисунок с указанием сил, действующих на шайбу.
Алгоритм решения
1.Построить чертеж. Указать все силы, действующие на шайбу. Выбрать систему координат.
2.Записать второй закон Ньютона для описания движения шайбы в векторном виде.
3.Записать второй закон Ньютона в виде проекций на оси.
4.Через систему уравнений вывести искомую величину.
Решение
Так как шайба вращается, покоясь на поверхности конуса, на нее действуют четыре силы: сила трения, сила тяжести, сила реакции опоры и центростремительная сила. Изобразим их на чертеже. Выберем систему координат, параллельную оси вращения.
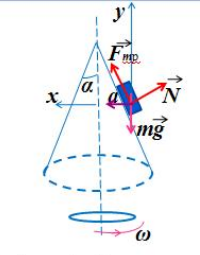
Второй закон Ньютона в векторном виде выглядит следующим образом:
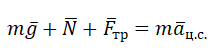
Теперь запишем этот закон в проекциях на оси ОХ и ОУ соответственно:
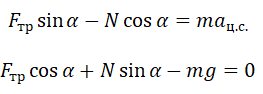
Так как шайба покоится относительно поверхности конуса, сила трения равна силе трения покоя:
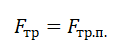
Максимальное значение силы трения равно:
![]()
Принимая в учет силу трения покоя, проекции на оси ОХ и ОУ примут следующий вид:
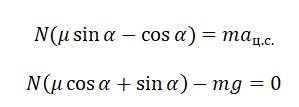
Запишем систему уравнение в следующем виде:
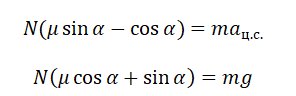
Поделим первое уравнение на второе и получим:
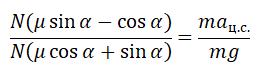
Сделаем сокращения и получим:
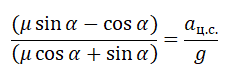
Отсюда центростремительное ускорение равно:
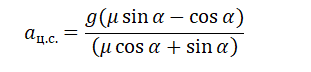
Но также известно, что центростремительное ускорение равно произведению квадрата угловой скорости на радиус окружности:
![]()
Радиус окружности, по которой вращается шайба вместе с конусом, можно вычислить по формуле:
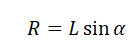
Отсюда центростремительное ускорение равно:
![]()
Выразим искомую величину L:
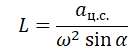
Подставим в это выражение выведенную для центростремительного ускорения формулу и получим:
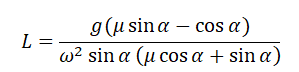
Поделим числитель на синус угла α, чтобы упростить выражение, и получим:
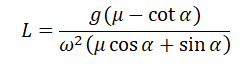
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18051
Грузовик массой m, движущийся по прямолинейному горизонтальному участку дороги со скоростью υ, совершает торможение до полной остановки. При торможении колёса грузовика не вращаются. Коэффициент трения между колёсами и дорогой равен μ. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

Алгоритм решения
1.Записать исходные данные.
2.Сделать чертеж. Указать все силы, действующие на грузовик во время торможения. Выбрать систему координат.
3.Записать второй закон Ньютона в векторной форме.
4.Записать второй закон Ньютона в виде проекций на оси ОХ и ОУ.
5.Записать формулу для нахождения силы трения скольжения.
6.Записать формулу для расчета перемещения при движении с постоянным ускорением.
7.Использовать второй закон Ньютона для определения тормозного пути.
Решение
Из условий задачи нам известны следующие величины:
• Начальная скорость грузовика (до начала торможения) v0 = v.
• Коэффициент трения между колесами и дорогой μ.
Выполним чертеж. Выберем такую систему координат, в которой направление движения грузовика во время торможения совпадает с направлением оси ОХ:
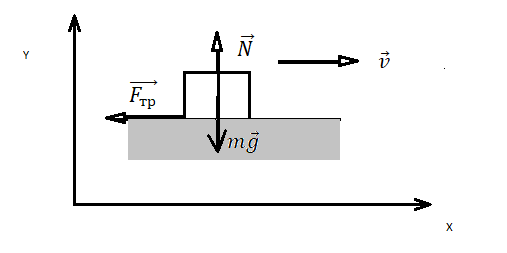
Запишем второй закон Ньютона в векторной форме:
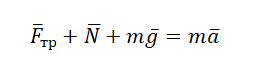
Запишем второй закон Ньютона в проекциях на оси:
Fтр = ma
N – mg = 0
Известно, что сила трения скольжения определяется формулой:
Fтр = μN = μmg
Значит, в первую ячейку таблицы мы должны поставить «1».
Перемещение при равнозамедленном движении определяется формулой (учтем, что конечная скорость равна 0, так как грузовик остановился):
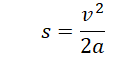
Выразим ускорение через проекцию сил на ось ОХ:
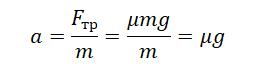
Подставим найденное ускорение в формулу тормозного пути и получим:
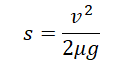
Следовательно, во вторую ячейку таблицы мы должны поставить «4».
Полный ответ: «14».
Ответ: 14
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 14.4k
(Занятие каникулярной школы для учащихся 8–9 кл.)
Цель:
- Активизация мыслительной деятельности учащихся.
- Формирование обобщенного умения проводить физические измерения.
- Формирование обобщенного умения проводить экспериментальную проверку
физических закономерностей. - Формирование умения систематизировать полученные результаты в виде
таблицы, умение делать вывод на основе эксперимента.
Организация проведения практикума: Все учащиеся принимающие участие в
работе практикума делятся на группы. Каждая группа учащихся получает задание с
кратким описанием работы.
По окончании выполнения работы учащимся необходимо составить отчет. Отчет
состоит из таблицы, вычисления искомой величины и ее погрешности, вывода по
работе.
Ход работы
I. Вступительное слово учителя:
Если положить на горизонтальную поверхность брусок и подействовать на него с
достаточной силой в горизонтальном направлении, то брусок станет двигаться.
Нетрудно убедиться, что в этом случае на брусок действуют четыре силы: в
вертикальном направлении – сила тяжести P и сила реакции опоры Q, равные по
модулю противоположные по направлению; в горизонтальном направлении – сила тяги
F и
противоположная по направлению сила трения Fmp.
Чтобы брусок двигался равномерно и прямолинейно, нужно, чтобы
модуль силы тяги был равен модулю силы трения.
На этом основан метод измерения силы трения. Следует приложить к бруску силу
тяги, которая будет поддерживать равномерное прямолинейное движение этого тела.
По этой силе тяги определяют модуль силы трения.
II. Практикум.
Задание группе I.
Определите коэффициент трения скольжения при движении бруска по
горизонтальной поверхности стола.
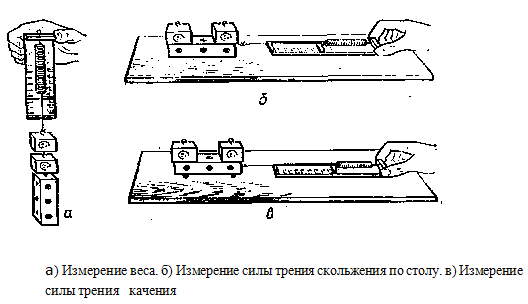
Оборудование: трибометр, деревянная
линейка, деревянный бруска с тремя отверстиями; динамометр; набор грузов по
механике.
Порядок выполнения работы.
- Вычислите цену деления шкалы динамометра.
- Измерьте вес бруска при помощи динамометра. Результат измерения веса
запишите в таблицу. - Измерьте силу трения скольжения бруска с грузами по столу. Для этого
перемещайте брусок с грузами равномерно по столу при помощи динамометра. - Результат измерения запишите в таблицу.
- Нагружая брусок одним, двумя и тремя грузами, измерьте в каждом случае
силу трения. Данные занесите в таблицу. - Вычислите коэффициент трения скольжения
- Определите инструментальную погрешность коэффициента трения.
- Сделайте вывод.
Легко убедиться, что в случае движения тела по горизонтальной поверхности
сила нормального давления равна силе тяжести, действующей на это тело:
N = P.
Это позволяет вычислить коэффициент трения:
![]()
Цена деления шкалы динамометра, ц.д
= 0,1 Н.
1. Определили вес бруска и груза с помощью динамометра, записали в таблицу.
2. Двигая брусок равномерно по деревянной линейке, определили силу тяги,
которая равна силе трения. Записали ее значение в таблицу.
| Количество грузов | Fтр, H |
P, H |
µ |
| Без груза | 0,6 ± 0,1 | ||
| Один груз | 0,3 ± 0,1 | 1,6 ± 0,1 | 0,18 ± 0,06 |
| Два груза | 0,5 ± 0,1 | 2,6 ± 0,1 | 0,19 ± 0,04 |
| Три груза | 0,7 ± 0,1 | 3,6 ± 0,1 | 0,19 ± 0,03 |
3. Определили коэффициент трения для каждого измерения силы трения, занесли
их в таблицу.
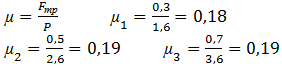
4. Определили погрешность измерения для каждого значения коэффициента
силы трения.
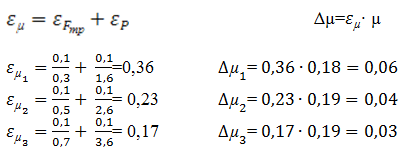
Вывод:
1. Коэффициент трения равен 0,2.
2. Инструментальная погрешность измерения равна 0,06.
3. Коэффициент трения скольжения при взаимном движении тела по поверхности стола
является величиной постоянной не зависящей от силы нормального давления.
2. Сравните коэффициент трения покоя, скольжения и качения. Сделайте вывод.
Оборудование: динамометр, брусок деревянный, грузы с двумя
крючками – 2 шт., карандаши круглые – 2 шт.
Порядок выполнения работы.
1. Вычислите цену деления шкалы динамометра.
2. Измерьте вес бруска с двумя грузами при помощи динамометра. Результат
измерения веса запишите в тетрадь.
3. Измерьте максимальную силу трения покоя бруска по столу. Для этого
положите брусок на стол, а на брусок два груза; к бруску прицепите динамометр и
приведите брусок с грузами в движение. Запишите показания динамометра,
соответствующее началу движения бруска.
4. Измерьте силу трения скольжения бруска с грузами по столу. Для этого
перемещайте брусок с грузами равномерно по столу при помощи динамометра.
Результат измерения силы запишите в тетрадь.
5. Измерьте силу трения качения бруска по столу. Для этого положите
брусок с двумя грузами на два круглых карандаша и перемещайте равномерно брусок
по столу при помощи динамометра. Результат измерения силы запишите в тетрадь.
6. Сделайте вывод о том, какая сила больше:
а) вес тела или максимальная сила трения покоя?
б) максимальная сила трения покоя или сила трения скольжения?
в) сила трения скольжения или сила трения качения?
7. Сравните коэффициент трения покоя, трения скольжения и трения качения.
Цена деления шкалы динамометра, ц.д = 0,1 Н.
| Вид трения | Fтр, H |
P, H |
µ |
| Трение покоя | 0,9 ± 0,1 | 2,6 ± 0,1 | 0,35 |
| Трение скольжения | 0,5 ± 0,1 | 2,6 ± 0,1 | 0,19 |
| Трение качения | 0,1 ± 0,1 | 2,6 ± 0,1 | 0,04 |
Вывод:
а) Вес тела больше чем максимальная сила трения покоя.
б) Максимальная сила трения покоя больше чем сила трения скольжения.
в) Сила трения скольжения больше чем сила трения качения.
г) При неизменном весе тела, наименьшее значение коэффициент трения имеет при
качении тела, а наибольшее в случае покоя.
3. Определите коэффициент трения скольжения при движении бруска вдоль
поверхности резины, нешлифованной деревянной рейки, наждачной бумаги.
Оборудование: динамометр, брусок деревянный, грузы с двумя
крючками – 2 шт., отрез линолеума, деревянная нешлифованная рейка, наждачная
бумага.
Порядок выполнения работы.
1. Вычислите цену деления шкалы динамометра.
2. Измерьте вес бруска при помощи динамометра. Результат измерения веса запишите
в таблицу.
3. Измерьте силу трения скольжения бруска с грузами по поверхности резины,
деревянной нешлифованной линейки и по поверхности наждачной бумаги. Для этого
перемещайте брусок с грузами равномерно по столу при помощи динамометра.
Результат измерения запишите в таблицу.
4. Вычислите коэффициент трения скольжения.
5. Сделайте вывод.
Цена деления шкалы динамометра, ц.д = 0,1 Н.
| Виды трущихся поверхностей | Fтр, H |
P, H |
µ |
| Дерево по дереву (гладкая поверхность) | 0,5 ± 0,1 | 2,6 ± 0,1 | 0,19 |
| Дерево по дереву (нешлифованная деревянная рейка) |
0,9 ± 0,1 | 2,6 ± 0,1 | 0, 35 |
| Дерево по линолеуму | 1,1 ± 0,1 | 2,6 ± 0,1 | 0, 42 |
| Дерево по наждачной бумаге | 2,6 ± 0,1 |
Вывод:
1. Сила трения:
а) зависит от рода трущихся поверхностей.
б) зависит от шероховатости трущихся поверхностей.
в) чем больше шероховатости поверхности, тем коэффициент трения больше.
2. Способы увеличения или уменьшения силы трения скольжения:
Увеличить: увеличить шероховатость трущихся поверхностей, насыпать между
трущихся поверхностей частицы (стружку, опилки, песок).
Уменьшить: шлифовка, полировка трущихся поверхностей, нанесение смазки.
Задание группе II.
Измерение коэффициент трения скольжения, используя наклонную плоскость
Оборудование: линейка деревянная от трибометра, брусок деревянный,
линейка измерительная, штатив.
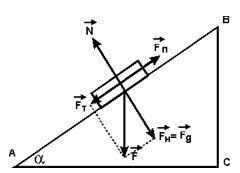
Порядок выполнения работы.
1. Используя штатив, закрепите линейку под углом к столу.
2. Положите брусок на закрепленную под углом деревянную линейку.
3. Меняя угол наклона линейки, найдите такой максимальный угол, при котором
брусок еще покоится.
4. Измерьте длину основания линейки и высоту подъема линейки.
5. Рассчитайте значение коэффициента трения скольжения дерева о дерево по
формуле:
![]()
6. Рассчитайте погрешность измерения.
7. Вывод.

Экспериментальные данные.
Измерили высоту подъема и длину основания линейки.
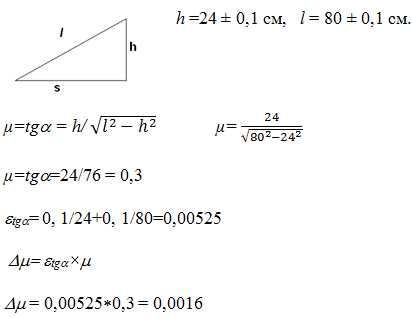
Вывод:
1. Коэффициент трения равен 0,3.
2. Погрешность измерения равна 0,0016.
2. Измерение коэффициента трения скольжения, через опрокидывание
бруска
Оборудование: брусок деревянный, линейка деревянная от
трибометра, нить, линейка ученическая.
Порядок выполнения работы.
Теоретическое обоснование: Брусок с привязанной к длинной грани нитью
поставьте торцом на горизонтальную поверхность стола и тяните за нить. Если нить
закреплена невысоко над поверхностью стола, то брусок будет скользить. При
определенной высоте h точки А крепления нити сила натяжения нити F опрокидывает
брусок.
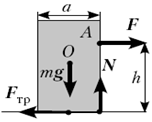
Условия равновесия для этого случая относительно точки – угла опрокидывания:
Fh – mga/2
= 0;
Согласно II закону Ньютона:
F – Fтр
= 0;
N – mg =
0.
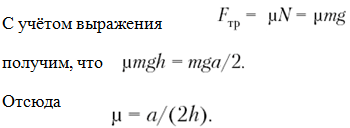
Обработка результатов.
1. Рассчитайте по формуле значение коэффициента трения скольжения дерева о
дерево.
2. Определите погрешность измерений.
3. Запишите полученный ответ с учетом допущенных погрешностей измерений.
4. Сделайте вывод.
Экспериментальный расчет.
a = 45 ± 1 мм, h
= 80 ± 1 мм.
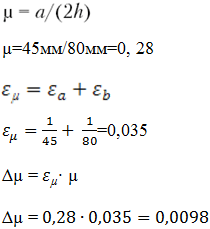
Вывод:
1. Коэффициент трения равен 0,28.
2. Инструментальная погрешность измерения равна 0,0098.
3. Измерение коэффициента трения скольжения с помощью карандаша.
Оборудование: карандаш, линейка деревянная от трибометра, линейка
ученическая.
Порядок выполнения работы.
Теоретическое обоснование: Поставьте карандаш на стол вертикально,
нажмите на него, наклоните и наблюдайте характер его падения. При небольших
углах наклона к вертикали карандаш не проскальзывает относительно поверхности
стола при любой величине силы, прижимающей его к столу. Проскальзывание
начинается с некоторого критического угла, зависящего от силы трения.
Записываем второй закон Ньютона в проекциях на координатные оси при угле
наклона, равном критическому. (Силой тяжести mg, действующей на карандаш, по
сравнению с большой силой F пренебрегаем).
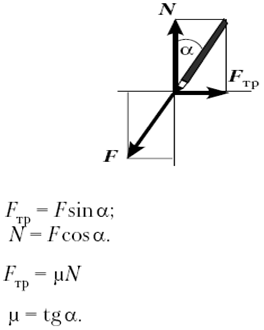
Обработка результатов:
1. Рассчитайте по формуле значение коэффициента трения скольжения дерева о
дерево.
2. Определите погрешность измерений.
3. Запишите полученный ответ с учетом допущенных погрешностей измерений.
4. Сделайте вывод.
Экспериментальный расчет.
1. Обработка результатов
α =
300,
µ= tgα
= sina /cosa
µ = 0,58
Вывод:
1. Коэффициент трения равен 0,58.
III. Подведение итогов практикума:
Сила трения скольжения зависит:
а) От рода трущихся поверхностей.
б) От шероховатости трущихся поверхностей.
в) Прямо пропорционально от силы давления.
г) Коэффициент трения скольжения при взаимном движении тела по поверхности
является величиной постоянной не зависящей от силы нормального давления.
д) Чем больше шероховатости поверхности, тем коэффициент трения больше.
Приложение.
Явление трения в жизни человека играет как положительную, так и отрицательную роль. С одной стороны, без его присутствия было бы невозможным движение, с другой же стороны, из-за трения происходят огромные потери энергии и рабочих материалов. В статье рассмотрим с точки зрения физики, что собой представляет трение, а также как найти коэффициент трения.
Явление трения
Трение – это контактное явление, которое возникает в зоне соприкосновения различных тел, и которое оказывает противодействие любому их взаимному движению.
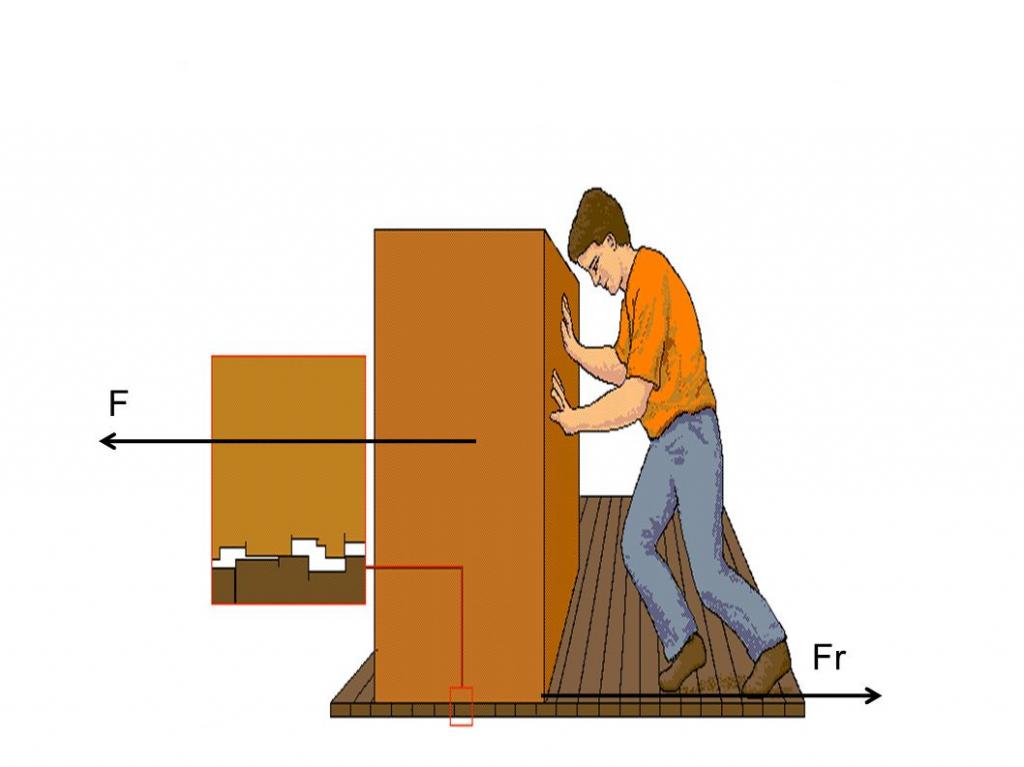
В механике движения твердых тел выделяют три вида трения:
- действующее в покое;
- действующее во время скольжения поверхностей друг по другу;
- возникающее при качении тел.
Трение покоя возникает, когда мы прикладываем внешнюю касательную к поверхности силу к телу, чтобы сдвинуть его с места. Яркими примерами трения скольжения является скольжение лыж по снегу. Наконец, трение во время качения проявляет себя, когда колесо транспортного средства катится по дороге.
Формула для определения силы трения
В физике перечисленные виды трения описываются одной и той же формулой при расчете действующих сил. Эта формула имеет следующий вид:
Ft = µ * N.
Сила трения Ft равна произведению коэффицента трения µ на реакцию опоры N. При рассмотрении соответствующего вида трения меняется только значение коэффициента µ, который является величиной безразмерной.
В случае сил трения покоя и скольжения величина µ составляет порядка десятых долей единицы. Зависит µ от контактирующих материалов, от шероховатости их поверхности, и не зависит от площади контакта или скорости скольжения.
Для трения качения коэффициент µ (его принято обозначать CR) зависит от характеристик упругости катящегося тела, от его твердости, от радиуса качения и некоторых других факторов. Для большинства материалов величина этого коэффициента для качения составляет сотые и тысячные доли от единицы.
Поскольку влияющих на величину µ факторов много, то определенной математической формулы для его расчета не существует. Отвечая на вопрос, как найти трения коэффициент, следует сказать, что его измеряют экспериментально.
Определение коэффициента µ
В этом пункте рассмотрим два способа практического определения величины µ на примере трения скольжения и покоя.
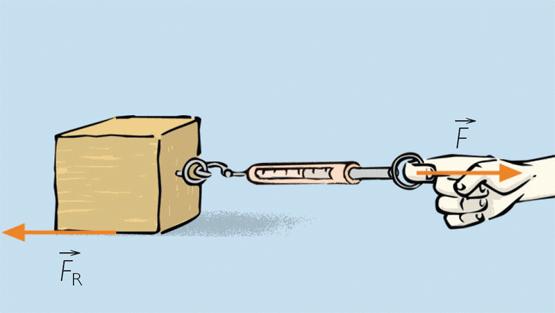
Первый способ, дающий ответ на вопрос, как найти коэффициент трения, заключается в помещении на горизонтальную плоскость бруска, к которому прикреплен динамометр. Брусок и плоскость изготовлены из исследуемой пары материалов, например, из стекла и дерева. Перемещая равномерно брусок, взявшись за динамометр, можно определить силу скольжения Ft. Зная массу m бруска, коэффициент µ рассчитывают так:
µ = Ft / (m * g).
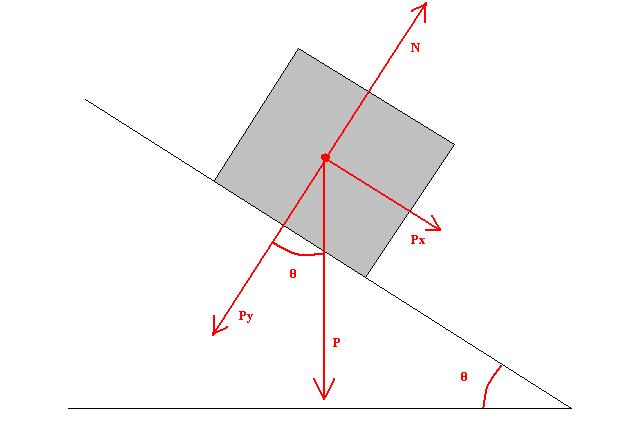
Второй способ удобен для определения µ для трения покоя. Для этого необходимо поместить на горизонтальную плоскость брусок. Затем, следует медленно поднимать один конец плоскости, наклоняя ее на некоторый угол к горизонту. При определенном угле θ брусок начнет соскальзывать с поверхности. Измерив этот угол, коэффициент трения µ можно определить из равенства:
µ = tg(θ).
Измерение µ для трения качения предполагает использование более сложной установки, которая называется наклонным маятником. Расчет µ в этом случае выполняется при помощи исследования уравнений динамики движения.
