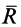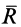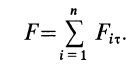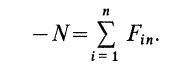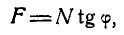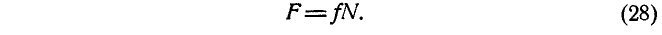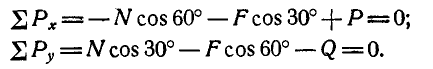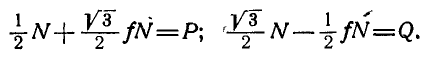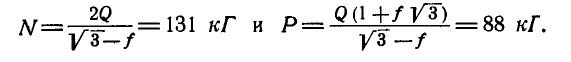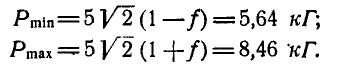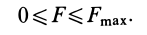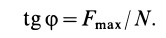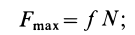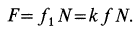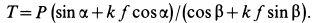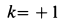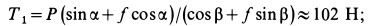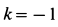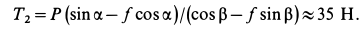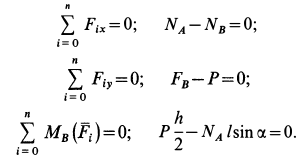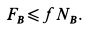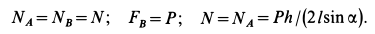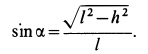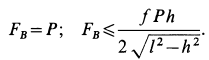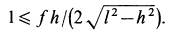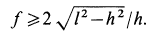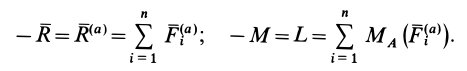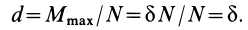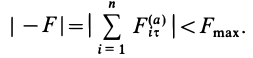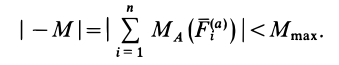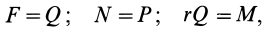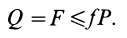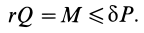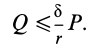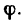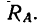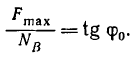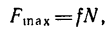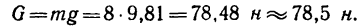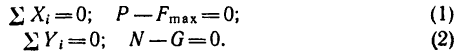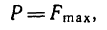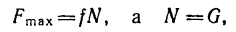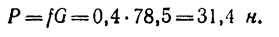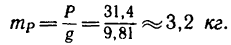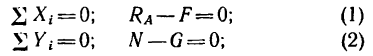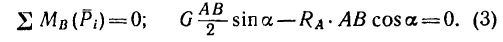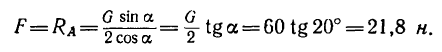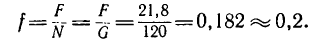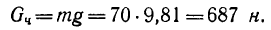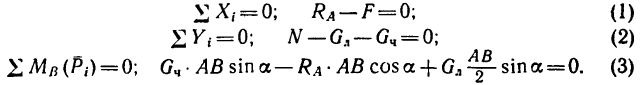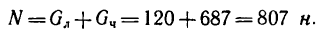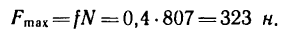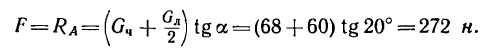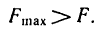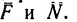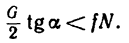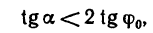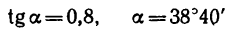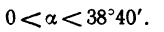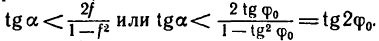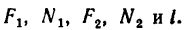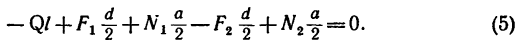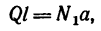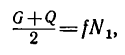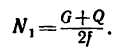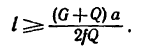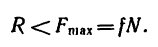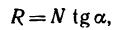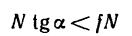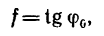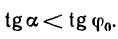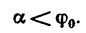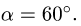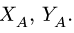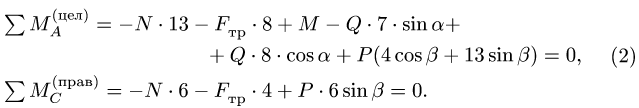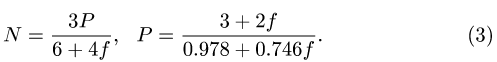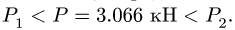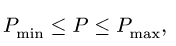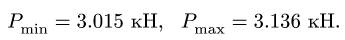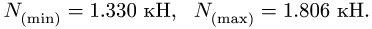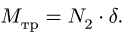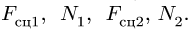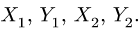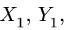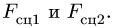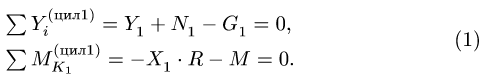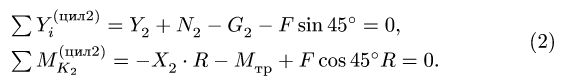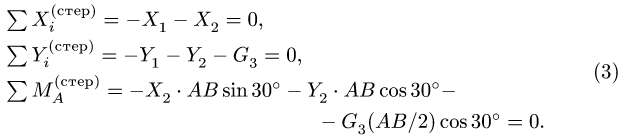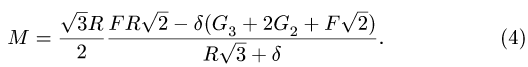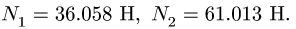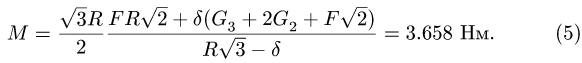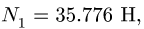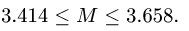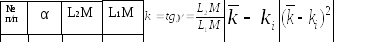{mu = dfrac{F_{тр}}{mg}}
Ускорение свободного падения g
Приводим 2 варианта нахождения коэффициента трения – зная силу трения и массу тела или зная угол наклона. Для обоих вариантов вы найдете удобные калькуляторы и формулы для расчета.
Коэффициент трения представляет собой безразмерную скалярную величину, которая равна отношению силы трения между двумя телами и силы, прижимающей их друг к другу, во время или в начале скольжения.
Коэффициент трения чаще всего обозначают греческой буквой µ («мю»).
Следует помнить, что коэффициент трения (μ) величина безразмерная, то есть не имеет единицы измерения.
Коэффициент трения зависит от качества обработки трущихся поверхностей, скорости движения тел относительно друг друга и материала соприкасающихся поверхностей. В большинстве случаев коэффициент трения находится в пределах от 0,1 до 0,5 (см. таблицу).
Содержание:
- калькулятор коэффициента трения
- формула коэффициента трения через силу трения и массу
- формула коэффициента трения через угол наклона
- таблица коэффициентов трения
- примеры задач
Формула коэффициента трения через силу трения и массу
mu = dfrac{F_{тр}}{mg}
Fтр – сила трения
m – масса тела
g – ускорение свободного падения (в большинстве задач можно принять g=9.81 м/с²)
Формула коэффициента трения через угол наклона
mu = tg(alpha)
α – угол наклона
Таблица коэффициентов трения скольжения для разных пар материалов
| Трущиеся материалы (при сухих поверхностях) | Коэффициенты трения | |
|---|---|---|
| покоя | при движении | |
| Резина по сухому асфальту | 0,95-1,0 | 0,5-0,8 |
| Резина по влажному асфальту | 0,25-0,75 | |
| Алюминий по алюминию | 0,94 | |
| Бронза по бронзе | 0,20 | |
| Бронза по чугуну | 0,21 | |
| Дерево по дереву (в среднем) | 0,65 | 0,33 |
| Дерево по камню | 0,46-0,60 | |
| Дуб по дубу (вдоль волокон) | 0,62 | 0,48 |
| Дуб по дубу (перпендикулярно волокнам) | 0,54 | 0,34 |
| Железо по железу | 0,15 | 0,14 |
| Железо по чугуну | 0,19 | 0,18 |
| Железо по бронзе (слабая смазка) | 0,19 | 0,18 |
| Канат пеньковый по деревянному барабану | 0,40 | |
| Канат пеньковый по железному барабану | 0,25 | |
| Каучук по дереву | 0,80 | 0,55 |
| Каучук по металлу | 0,80 | 0,55 |
| Кирпич по кирпичу (гладко отшлифованные) | 0,5-0,7 | |
| Колесо со стальным бандажем по рельсу | 0,16 | |
| Лед по льду | 0,05-0,1 | 0,028 |
| Метал по аботекстолиту | 0,35-0,50 | |
| Метал по дереву (в среднем) | 0,60 | 0,40 |
| Метал по камню (в среднем) | 0,42-0,50 | |
| Метал по металу (в среднем) | 0,18-0,20 | |
| Медь по чугуну | 0,27 | |
| Олово по свинцу | 2,25 | |
| Полозья деревянные по льду | 0,035 | |
| Полозья обитые железом по льду | 0,02 | |
| Резина (шина) по твердому грунту | 0,40-0,60 | |
| Резина (шина) по чугуну | 0,83 | 0,8 |
| Ремень кожаный по деревянному шкиву | 0,50 | 0,30-0,50 |
| Ремень кожаный по чугунному шкиву | 0,30-0,50 | 0,56 |
| Сталь по железу | 0,19 | |
| Сталь(коньки) по льду | 0,02-0,03 | 0,015 |
| Сталь по райбесту | 0,25-0,45 | |
| Сталь по стали | 0,15-0,25 | 0,09 (ν = 3 м/с)
0,03 (ν = 27 м/с) |
| Сталь по феродо | 0,25-0,45 | |
| Точильный камень (мелкозернистый) по железу | 1 | |
| Точильный камень (мелкозернистый) по стали | 0,94 | |
| Точильный камень (мелкозернистый) по чугуну | 0,72 | |
| Чугун по дубу | 0,65 | 0,30-0,50 |
| Чугун по райбесту | 0,25-0,45 | |
| Чугун по стали | 0,33 | 0,13 (ν = 20 м/с) |
| Чугун по феродо | 0,25-0,45 | |
| Чугун по чугуну | 0,15 |
Примеры задач на нахождение коэффициента трения
Задача 1
Найдите коэффициент трения между полом и ящиком массой 20 кг, который равномерно двигают с силой 50 Н.
Решение
Для решения задачи воспользуемся формулой.
mu = dfrac{F_{тр}}{mg} = dfrac{50}{20 cdot 9.81} = dfrac{50}{196.2} approx 0.25484
Ответ: approx 0.25484
С помощью калькулятора удобно проверить ответ.
Задача 2
Найдите коэффициент трения если угол наклона 30°.
Решение
Для решения этой задачи воспользуемся второй формулой.
mu = tg(alpha) = tg(30°) approx 0.57735
Ответ: approx 0.57735
Проверим полученный ответ с помощью калькулятора .
Содержание:
Трение:
При движении или стремлении двигать одно тело по поверхности другого в касательной плоскости поверхностей соприкосновения возникает сила трения скольжения.
Если одно тело, например цилиндрический каток, катить или стремиться катить по поверхности другого тела, то кроме силы трения скольжения из-за деформации поверхностей тел дополнительно возникает пара сил, препятствующая качению катка. Возникновение силы трения, препятствующей скольжению, иногда называют трением первого рода, а возникновение пары сил, препятствующей качению,— трением второго рода.
Трение скольжения
Пусть на тело действует плоская система активных сил и тело находится в равновесии, соприкасаясь с поверхностью другого тела, являющегося связью для рассматриваемого тела. Если поверхности соприкасающихся тел абсолютно гладкие и тела абсолютно твердые, то реакция поверхности связи направлена по нормали к общей касательной в точке соприкосновения и направление реакции в этом случае не зависит от действующих на тело активных сил. От активных сил зависит только числовое значение силы реакции. В действительности абсолютно гладких поверхностей и абсолютно твердых тел не бывает. Все поверхности тел в той или иной степени шероховаты и все тела деформируемы. В связи с этим и сила реакции
Если силу реакции
В теоретической механике обычно рассматривается только сухое трение между поверхностями тел, т. е. такое трение, когда между ними нет смазывающего вещества. Для сухого трения надо различать трение скольжения при покое или равновесии тела и трение скольжения при движении одного тела по поверхности другого с некоторой относительной скоростью.
При покое сила трения зависит только от активных сил. При выбранном направлении касательной в точке соприкосновения поверхностей тел сила трения вычисляется по формуле
Аналогично, при выбранном направлении нормали нормальная реакция выражается через заданные силы
В 1781 г. Кулон установил основные приближенные законы для сухого трения скольжения. В дальнейшем законы Кулона многократно проверялись другими исследователями. Но эти законы подтверждались в случае, когда поверхности тел не вдавливались друг в друга и шероховатость была не очень велика.
Законы Кулона можно установить на приборе, схема которого дана рис. 59. На этом приборе изменяя вес гири, можно изменять нормальное давление 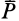
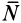
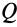
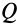
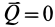
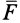
Если силу 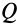
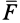
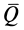
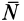
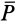
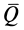
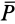
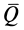
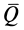
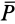
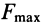
Рис. 59
Трение скольжения:
При решении многих технических вопросов приходится принимать в расчет силы трения. Остановимся на рассмотрении сил трения 1-го рода (скольжения).
Рис. 31.
Пусть на тело А (рис. 31), лежащее на горизонтальной негладкой плоскости, действует сила Р под углом а к вертикали. Раскладывая силу Р на две составляющие 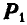
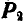
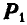
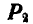
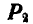
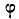

где 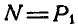
Угол 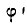
Формула (28) выражает первый закон трения, который формулируется так:
Первый закон трения
1. Сила трения прямо пропорциональна нормальному давлению или реакции связи и направлена в сторону, противоположную относительному перемещению трущихся тел.
Этот закон был установлен опытным путем. Амонтоном-Кулоном и другими исследователями были установлены еще следующие законы:
2. Коэффициент трения зависит от материала и состояния трущихся поверхностей.
3. Коэффициент трения в покое больше коэффициента трения в движении.
4. Коэффициент трения не зависит от величины трущихся поверхностей (можно считать правильным лишь в первом приближении).
5. Коэффициент трения зависит от скорости движения трущихся поверхностей и с увеличением этой скорости уменьшается, приближаясь к некоторой предельной величине.
Обращаясь к рисунку 31, замечаем, что тело А находится в равновесии, если сила Р проходит внутри конуса с углом при вершине С, равным двойному углу трения 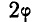
Когда тело А находится еще в покое (рис. 31), то по мере увеличения угла 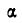
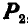
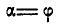
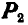
Рис. 32.
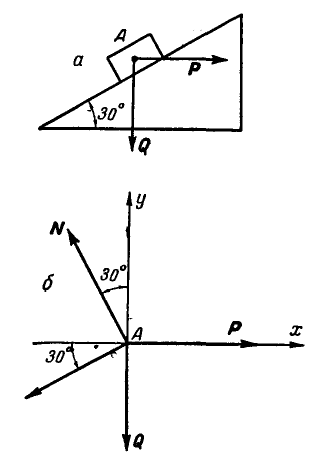
Задача №1
Тело А весом Q=100кГ лежит на шероховатой наклонной плоскости (рис. 32,а). Какую наименьшую горизонтальную силу Р ладо приложить к телу, чтобы оно начало двигаться, если коэффициент трения тела о плоскость f=0,2.
Решение. Рассмотрим равновесие тела А. Помимо горизонтальной силы Р на тело действует сила Q, нормальная реакция N плоскости и сила трения F, направленная параллельно плоскости в обратную сторону движения тела (рис. 32,6).
Составляя уравнения равновесия (27), имеем:
В двух уравнениях имеются три неизвестные величины: Р, N и F. Для получения третьего уравнения по формуле (28) имеем > зависимость: 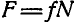
Выражая в уравнениях равновесия F через N, получим:
Оторда находим:
Задача №2
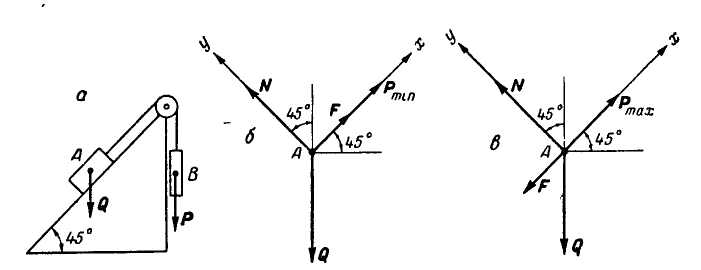
Определить наибольший и наименьший груз Р, при котором груз Q = 10 кГ не будет двигаться (рис» 33, а). Коэффициент трения груза Q о плоскость f=0,2.
Рис. 33.
Указание: при наименьшем грузе 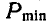
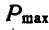
Составляя для каждого из случаев (рис. 33, б и 33, в) по два уравнения равновесия и принимая во внимание формулу (28), получим:
32
Законы Кулона
1. Сила трения скольжения находится в общей касательной плоскости соприкасающихся поверхностей тел и направлена в сторону, противоположную направлению возможного или реального скольжения тела под действием приложенных сил. Сила трения при покое зависит от активных сил и ее модуль заключен между нулем и максимальным значением, которое достигается в момент выхода тела из положения равновесия, т. е.
2. Максимальная сила трения скольжения при прочих равных условиях не зависит от площади соприкосновения трущихся поверхностей. Из этого закона следует, что для того, чтобы сдвинуть, например, кирпич, надо приложить одну и ту же силу независимо от того, какой гранью он положен на поверхность, широкой или узкой.
3. Максимальная сила трения скольжения пропорциональна нормальному давлению (нормальной реакции), т. е.
где безразмерный коэффициент 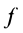
4. Коэффициент трения скольжения зависит от материала и физического состояния трущихся поверхностей, т. е. от величины и характера шероховатости, влажности, температуры и других условий. Коэффициент трения скольжения в зависимости от различных условий устанавливается экспериментально. Так, коэффициент трения для кирпича по бетону равен 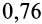
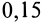
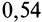
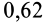
Опыты показывают, что при скольжении одного тела по поверхности другого с некоторой относительной скоростью возникает сила трения скольжения, равная максимальной, только при этом коэффициент трения скольжения незначительно изменяется в зависимости от скорости скольжения. Для большинства материалов он уменьшается с увеличением скорости скольжения, но для некоторых материалов, наоборот, увеличивается (трение кожи о металл).
В приближенных технических расчетах обычно считают, что коэффициент трения скольжения не зависит от относительной скорости скольжения.
В отличие от сухого трения трение при наличии смазывающего слоя между поверхностями определяется распределением относительной скорости скольжения в этом слое. В этом случае трение происходит не между поверхностями тел, а между слоями смазывающего вещества. Теория трения в смазывающем слое жидкости рассматривается в гидродинамике.
Угол и конус трения
Многие задачи на равновесие тела на шероховатой поверхности, т. е. при наличии силы трения, удобно решать геометрически. Для этой цели введем понятия угла и конуса трения.
Пусть твердое тело под действием активных сил находится на шероховатой поверхности в предельном состоянии равновесия, т. е. таком состоянии, когда сила трения достигает своего наибольшего значения при данном значении нормальной реакции (рис. 60). В этом случае полная реакция шероховатой поверхности 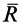
Этот наибольший угол 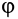
Угол трения 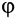
Но по третьему закону Кулона,
следовательно,
т. е. тангенс угла трения равен коэффициенту трения.
Рис. 60
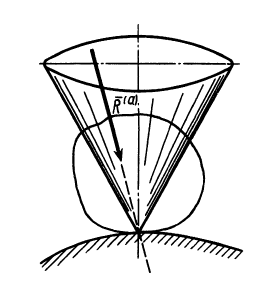
Конусом трения называют конус, описанный полной реакцией, построенной на максимальной силе трения, вокруг направления нормальной реакции. Его можно получить изменяя активные силы так, чтобы тело на шероховатой поверхности находилось в предельных положениях равновесия, стремясь выйти из равновесия по всем возможным направлениям, лежащим в общей касательной плоскости соприкасающихся поверхностей.
Если коэффициент трения во всех направлениях одинаков, то конус трения круговой. Если не одинаков, то конус трения не круговой, например в случае, когда свойства соприкасающихся поверхностей различны (вследствие определенного направления волокон или в зависимости от направления обработки поверхности тел, если обработка происходит на строгальном станке и т. п.).
Равновесие тела на шероховатой поверхности
При равновесии сил, действующих на твердое тело, находящееся в равновесии на шероховатой поверхности, возникает дополнительно неизвестная сила реакции шероховатой поверхности— сила трения. В случае предельного равновесия сила трения достигает своего максимального значения и по формуле (1) выражается через нормальную реакцию. В общем случае равновесия сила трения находится между нулем и ее максимальным значением. Поэтому соответствующие условия равновесия, в которые входит сила трения после замены ее максимальным значением, становятся неравенствами. После этого неизвестные находят путем совместного решения уравнений и неравенств. Для всех неизвестных или для их части получают решения в виде неравенств.
Некоторые задачи на равновесие с учетом сил трения удобно решать геометрически с помощью конуса трения.
Можно сформулировать условия равновесия тела на шероховатой поверхности используя конус трения. Если активные силы, действующие на тело, приводятся к равнодействующей силе 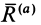
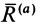
Очевидно, при изменении равнодействующей активных сил тело находится в равновесии до тех пор, пока составляющая 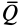
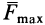
Рис. 61
Рис. 62
Предельным положением равновесия тела является случай, когда сила 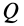
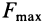
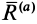
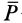
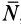
Тело нельзя вывести из равновесия любой по модулю активной силой, если ее линия действия проходит внутри конуса трения.
Если линия действия равнодействующей активных сил не проходит внутри конуса трения или по его образующей, то тело на шероховатой поверхности не может находиться в равновесии (рис. 63).
Рис. 63
Рис. 64
Пример 1.
Тело, сила тяжести которого 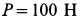
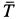
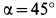
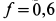
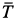
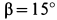
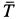
Решение. К телу приложены силы 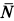
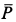
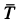
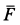
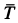
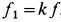
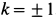
Составляем условия равновесия в виде суммы проекций сил на координатные оси для обоих предельных случаев. Имеем
По закону Кулона,
Решая эти уравнения относительно 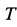
Отсюда при
при
Таким образом, сила 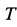
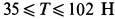
Пример 2.
Однородный тяжелый стержень 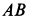
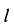
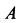
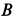
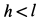
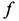
Рис. 65
Решение. Рассмотрим случай, когда точка 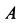
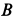
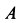
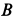
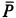
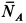
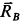
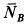
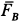
Составим условия равновесия плоской системы сил:
К этим условиям следует добавить неравенство для силы трения
Из уравнений равновесия находим
Из геометрических условий задачи имеем
Итак, для силы трения 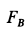
Исключая из них силу трения 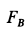
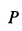
Искомое условие для коэффициента трения 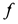
Трение качения
Если рассматриваемое тело имеет форму катка и под действием приложенных активных сил может катиться по поверхности другого тела, то из-за деформации поверхностей этих тел в месте соприкосновения могут возникнуть силы реакции, препятствующие не только скольжению, но и качению. Примерами таких катков являются различные колеса, как, например, у электровозов, вагонов, автомашин, шарики и ролики в шариковых и роликовых подшипниках и т. п.
Пусть цилиндрический каток находится на горизонтальной плоскости под действием активных сил. Соприкосновение катка с плоскостью из-за деформации фактически происходит не вдоль одной образующей, как в случае абсолютно твердых тел, а по некоторой площадке. Если активные силы приложены симметрично относительно среднего сечения катка, т. е. вызывают одинаковые деформации вдоль всей его образующей, то можно изучать только одно среднее сечение катка. Этот случай рассмотрен ниже.
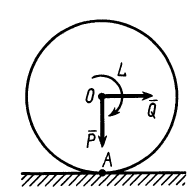
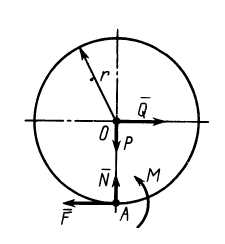
Активные силы, действующие на катки в виде колес (рис. 66), кроме силы тяжести 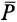
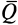
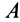
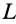
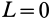
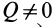
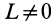
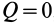
Если активные силы, действующие на колесо, привести к точке 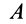
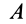
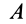
Рис. 66
Рис. 67
Рис. 68
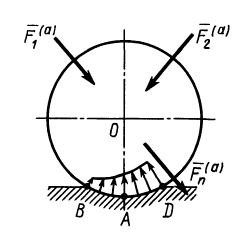
Соприкосновение среднего сечения колеса с неподвижной плоскостью из-за деформации колеса и плоскости происходит по некоторой линии 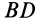
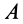
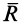
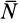
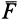
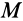
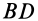
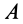
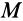
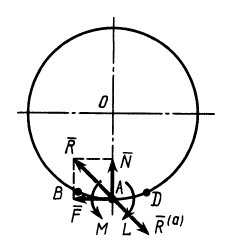
Приведем активные силы 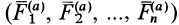
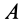
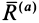
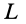
При равновесии катка, т. е. когда каток не катится и не скользит по плоскости, активные силы уравновешиваются силами реакций связи и, следовательно,
Изменив активные силы, приложенные к катку так, чтобы увеличивался момент 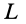
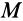
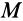
Установлены следующие приближенные законы для наибольшего момента пары сил, препятствующей качению:
1. Наибольший момент пары сил, препятствующей качению, в довольно широких пределах не зависит от радиуса катка.
2. Предельное значение момента 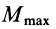
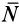
Коэффициент пропорциональности 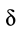
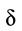
3. Коэффициент трения качения 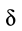
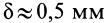
Законы трения качения, как и законы трения скольжения, справедливы для не очень больших нормальных давлений и не слишком легко деформирующихся материалов катка и плоскости.
Эти законы позволяют не рассматривать деформации катка и плоскости, считая их абсолютно твердыми телами, касающимися в одной точке. В этой точке соприкосновения в среднем сечении катка кроме нормальной реакции и силы трения надо приложить еще и пару сил, препятствующую качению.
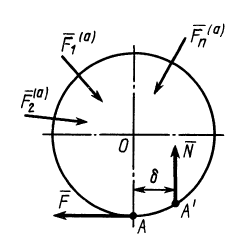
Коэффициент трения качения равен длине 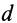
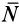
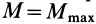
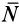
В предельном случае равновесия катка 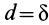
Для того чтобы каток не скользил, необходимо выполнение условия
Для заданных активных сил соответственно
Для того чтобы каток не катился, должно выполняться условие
Для активных сил оно имеет вид
Рис. 69
Рис. 70
Для примера рассмотрим случай ведомого колеса, к которому кроме силы тяжести 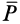
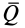
Если каток находится в равновесии, то из условий равновесия плоской системы сил, приложенных к катку, получаем
где за моментную точку взята точка 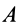
В случае отсутствия скольжения по формуле (4) с учетом условий равновесия
Аналогично, при отсутствии качения по формуле (5) имеем
Таким образом, при отсутствии скольжения сила 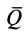
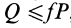
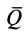
Если 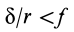
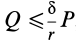
Если 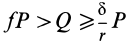
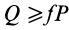
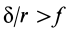
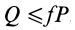
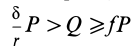
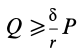
В том случае, если 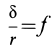
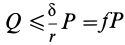
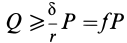
Обычно 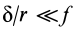
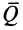
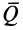
С точки зрения затраты энергии выгодно заменять скольжение качением. Этим объясняется преимущество шариковых и роликовых подшипников по сравнению с подшипниками скольжения, если даже в них трение и не уменьшается введением смазывающего вещества.
Аналогично трению качения можно рассмотреть и явление возникновения так называемого трения верчения, т.е. случая, когда активные силы стремятся вращать тело, например в форме шара, вокруг нормали к общей касательной поверхности соприкосновения.
В этом случае возникает пара сил, препятствующая верчению, причем наибольший ее момент, возникающий в момент начала верчения, также прямо пропорционален нормальной реакции. Коэффициент пропорциональности, т. е. коэффициент трения верчения, обычно значительно меньше коэффициента трения качения.
Равновесие с учетом сил трения
Задачи, приведенные в этом параграфе, отличаются от предыдущих тем, что в них рассматривается равновесие тел, имеющих, кроме идеальных, еще и реальные связи, т. е. связи с трением.
При свободном опирании тела на поверхность идеальной связи реакция такой связи 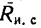
Если же тело опирается на поверхность реальной связи (в отличие от идеальных связей реальные связи условимся отмечать двойной штриховкой), то ее реакция 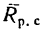
Поясним это общее положение следующим примером.
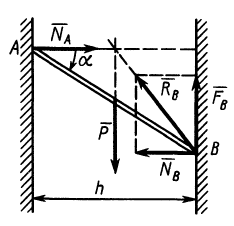
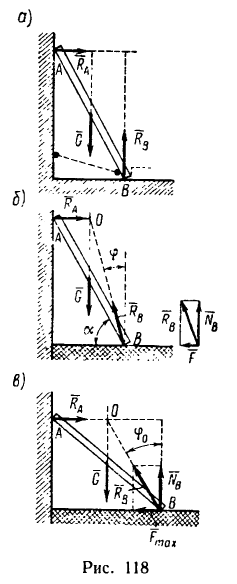
Наклонный брус (рис. 118, а), вес которого G, опирается в двух
точках А и В соответственно на вертикальную и горизонтальную поверхности идеальных связей. Этот брус не может находиться в равновесии, потому что три силы —вес бруса G и реакции 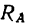
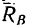
Чтобы брус, показанный на рис. 118, а, находился в равновесии, необходимо наложить еще одну связь, например, удержать брус шнуром или упереть в выступ на горизонтальной плоскости (обе возможные связи показаны пунктиром).
Теперь представим, что в точке В брус опирается не на идеально гладкую, а на шероховатую (реальную) поверхность (рис 118, б). В этом случае брус может находиться в равновесии без дополнительной связи (шнура или упорной планки). Значит три силы — вес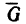
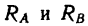
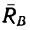
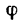
Если реакцию 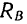
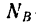
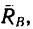
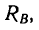
При увеличении угла а, характеризующего наклон бруса относительно горизонтальной поверхности, угол 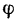
Если же уменьшать угол а, то угол ф, характеризующий отклонение реакции 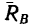
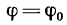
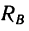
У гол 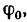
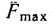
Для случая предельного равновесия между силой трения и углом трения имеем такую зависимость;
Постоянное для данной пары соприкасающихся тел значение 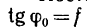
Таким образом,
При решении задач необходимо учитывать, что сила трения направлена всегда в сторону, противоположную той, при которой точка может скользить по идеальной поверхности.
Если в число реакций связей, обеспечивающих равновесие тела, входит сила трения, то такое состояние равновесия называется самоторможением. Во всех приведенных ниже задачах рассмотрены различные случаи самоторможения (равновесия при наличии силы трения) и условия, при которых возможно самоторможение.
Задача №3
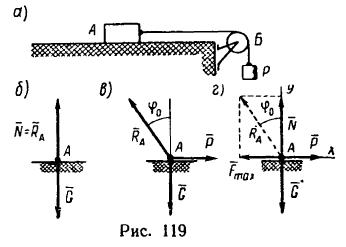
Тело А массой 8 кг поставлено на шероховатую горизонтальную поверхность стола. К телу привязана нить, перекинутая через блок Б (рис. 119, а). Какой груз Р можно подвязать к концу нити, свешивающейся с блока, чтобы не нарушить равновесия тела А? Коэффициент трения f = 0,4. Трением на блоке пренебречь.
Решение.
1. Если масса тела А m = 8 кг, то его вес
2. Пренебрегая размерами тела, будем считать, что все силы приложены к точке А.
3. Когда тело поставлено на горизонтальную поверхность, то на него действуют только две силы: вес 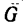
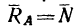
4. Если же приложить некоторую силу 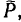
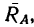
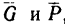
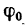
5. Разложив реакцию 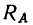
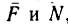
Спроектировав эту систему сил на оси хну, получим два уравнения равновесия:
Решаем полученную систему уравнений:
но
поэтому
Таким образом, равновесие тела А сохраняется при условии, что к концу нити, перекинутой через блок, подвешен груз, не превышающий по весу 31,4 н.
При этом масса груза Р
Задача №4
При каком минимальном коэффициенте трения между полом и лестницей последняя может находиться в равновесии, опираясь верхним концом о гладкую стену, как показано на рис. 120, а? Вес лестницы G = 120 н.
Решение.
1. На лестницу действует только одна нагрузка — ее собственный вес, приложенный в точке С посредине длины лестницы АВ.
2. Вес лестницы уравновешен реакцией 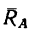
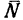
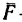
3. Составим три уравнения равновесия:
4. Из уравнений (1) и (3)
А так как N = G [из уравнения (2)[, то минимальный коэффициент трения, обеспечивающий равновесие лестницы.
Таким образом, при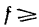
Задача №5
В месте соприкосновения пола и лестницы в предыдущей задаче коэффициент трения f= 0,4. Сможет ли человек, масса которого 70 кг, подняться по лестнице до самого верха и чтобы лестница при этом не скользила по полу?
Решение.
1. К силам 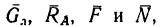
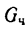
2. Вес человека
3. Человек сможет подняться до самого верха лестницы лишь в том случае, если горизонтальная составляющая реакции пола (сила 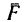
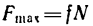
4. Составим уравнения равновесия:
5. Из уравнения (2)
Максимальная сила трения, которая может возникнуть в данном случае
Из уравнений (1) и (3) находим силу F—горизонтальную составляющую реакции пола, которая может обеспечить равновесие лестницы с человеком, стоящим наверху:
Таким образом,
Следовательно, человек сможет подняться по лестнице до самого верха.
- Заказать решение задач по теоретической механике
Задача №6
При каких значениях угла а, образуемого с гладкой вертикальной стеной, лестница, опирающаяся нижним концом о шероховатый горизонтальный пол, будет находиться в равновесии, если, кроме собственного веса, она ничем не нагружена и известно, что коэффициент трения при соприкосновении лестницы с полом f?
Решение.
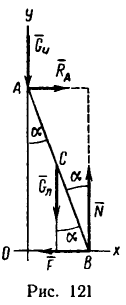
1. Для решения этой задачи воспользуемся рис. 120, б, так как на лестницу действуют те же четыре силы: вес лестницы 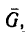
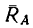
2. Лестница не выйдет из состояния равновесия (не начнет скользить) до тех пор, пока
т. е. пока горизонтальная составляющая реакции пола остается меньше максимальной силы трения, возникающей при опирании лестницы о пол в данном случае.
3. Из уравнений (1) и (3), составленных при решении задачи 90-15, найдено, что
Сопоставляем уравнения (а) и (б):
А так как в данном случае G =N, то лестница находится равновесии до тех пор, пока выполняется неравенство
или
где 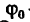
Следовательно, лестница находится в равновесии до тех пор, пока тангенс угла, образуемого лестницей с вертикальной гладкой стеной, остается меньше удвоенного коэффициента трения между лестницей и полом. Например, при f=0,4
и неравенство (в) соблюдается при значениях углов
Следовательно, при f=0,4 лестница не будет скользить по полу при любом значении угла a от 0 до 38°40′.
Следующую задачу рекомендуется решить самостоятельно.
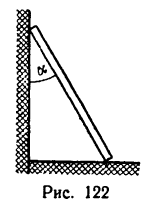
Задача №7
При каких значениях угла a однородная лестница, опирающаяся на шероховатые стену и пол (рис. 122), будет находиться в равновесии? Коэффициенты трения при опирании лестницы о стену и о пол считать одинаковыми и равными f.
Ответ.
Указание. В данной задаче в системе сил, действующих на лестницу, образуется пять неизвестных: четыре реакции и угол а. Поэтому при решении задачи нужно к трем уравнениям равновесия добавить еще два уравнения, выражающих зависимость сил трения от нормального давления.
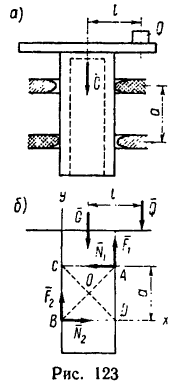
Задача №8
Цилиндр с горизонтальной площадкой наверху (рис. 123, а), находясь в двух кольцевых направляющих, скользит вниз, так как между поверхностью цилиндра и поверхностями направляющих имеется незначительный зазор. Вес цилиндра 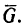
Решение.
1. На цилиндр в состоянии равновесия действуют две нагрузки: вес 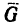
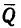
2. Груз Q, помещенный на горизонтальную площадку, прижимает цилиндр к верхнему направляющему кольцу в точке А, а к нижнему — в точке В. Благодаря зазору в точках С и D цилиндр не касается направляющих колец. В точках А и В возникают две реакции, которые заменим их составляющими 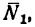
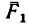
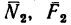
3. Образовалось пять неизвестных величин:
Если спроектировать все силы на ось х, то получим
откуда
Так как и
и
также, имея в виду равенство (1а), находим что
Скоректировав все силы на ось у, получим четвертое уравнение:
откуда с учетом (За)
Приняв за центр моментов точку О, лежащую на оси цилиндра и на середине расстояния а, составим пятое уравнение — уравнение моментов, в котором d- диаметр цилиндра (d = CA = BD):
Имея в виду равенства (1а) и (За), уравнение (5) можно упростить так:
откуда
Если теперь в уравнение (2) подставить значение 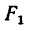
откуда
И теперь выражение (5а) принимает окончательный вид:
При значениях /, удовлетворяющих полученному неравенству, цилиндр не скользит вниз.
Задача №9
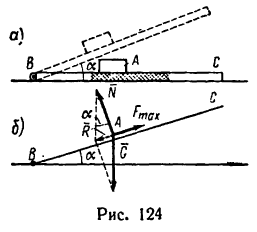
Тело А поставлено на негладкую пластину ВС, которую можно поворачивать около шарнира В. Коэффициент трения f между телом А и пластиной ВС известен. Определить, при каких значениях угла а (рис. 124, а) тело А будет оставаться на пластине в покое? Решение.
1. Представим, что пластина ВС наклонена к горизонту на некоторый угол а (рис. 124, б).
При этом положении пластины на тело А действуют три силы: его собственный вес 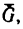
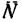
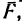
2. Тело А будет находиться в покое до тех пор, пока равнодействующая сил 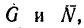
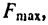
но
поэтому
или
Следовательно, пока тангенс угла наклона пластины к горизонту меньше коэффициента трения, тело А остается в покое.
Это положение выражает так называемое условие самоторможения тела по наклонной плоскости.
3. Учитывая, что
где 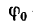
Так как углы 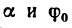
Тело А находится в покое на наклонной плоскости до тех пор, пока угол наклона плоскости меньше угла трения.
Следующую задачу рекомендуется решить самостоятельно.
Равновесие при наличии трения
Постановка Задачи. Конструкция состоит из двух шарнирно соединенных между собой тел. Одна из опор конструкции представляет собой одностороннюю связь и допускает проскальзывание с трением. Коэффициент трения, размеры конструкции и часть внешних нагрузок заданы. Найти пределы изменения одной из внешних нагрузок, действующей на конструкцию в условии равновесия.
План решения:
1. Задаем направление возможного движения подвижной опоры, скользящей с трением. Прикладываем к этой опоре силу трения, направляя ее в сторону противоположную возможному движению. Предельное значение силы трения связываем с величиной нормальной реакции опоры N по формуле Кулона 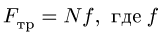
2. Решаем задачу о равновесии системы тел. Для этого разбиваем систему на две отдельные части, для которых составляем и решаем уравнения равновесия. Из решения определяем предельное значение нагрузки д.чя заданного направления скольжения опоры.
3. Меняем направление возможного движения системы и направление предельной силы трения. Предыдущий пункт плана выполняем заново и определяем другое предельное значение нагрузки. Два найденных значения нагрузки определяют ту область ее изменения, при которой конструкция находится в равновесии.
Задача №10
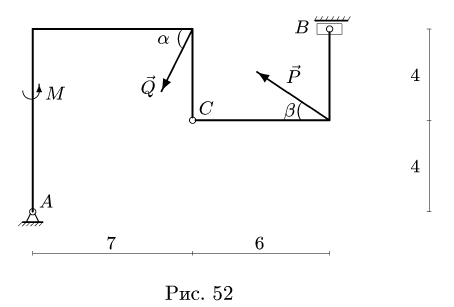
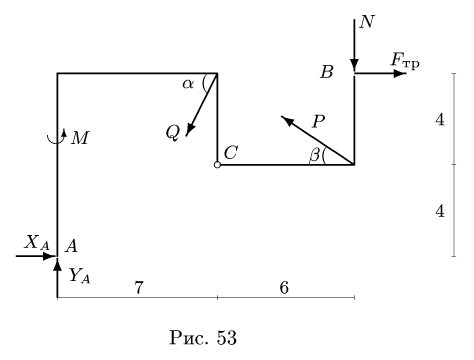
Конструкция состоит из двух частей, шарнирно соединенных в точке С (рис. 52). Опора В представляет собой одностороннюю связь и допускает проскальзывание с коэффициентом трения 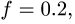
Размеры даны в метрах. Найти продолы изменения нагрузки Р, действующей под углом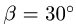
Решение
1. Задаем направление возможного движения подвижной опоры, скользящей с трением Предполагая возможное движение ползуна В влево, силу трения 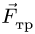
где 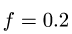
2. Решаем задачу о равновесии системы тел. Для этого систему разбиваем по шарниру С на две отдельные части — АС и СВ. Реакции шарнира С 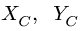
Действие ползуна заменяем нормальной реакцией N, направленной вниз, так как ползун по условию задачи является односторонней связью, и силой трения 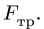
Уравнения (2) вместе с законом Кулона (1) образуют замкнутую систему трех линейных уравнений с тремя неизвестными 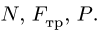
При 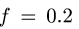
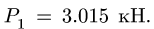
3. Меняем направление возможного движения системы и направление предельной силы трения. Пусть ползун В движется вправо. Силу 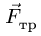
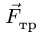
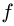
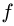
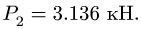
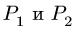
Чтобы убедиться, что равновесие соответствует значениям нагрузки между этими числами, определим Р при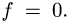
Из выражения (3) для N также следует, что при 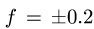
где
Этим нагрузкам соответствуют следующие значения нормальной реакции:
Замечание. Неравенство 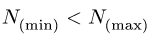
Трение качения
Постановка задачи. Система состоит из двух цилиндров, соединенных стержнем. Цилиндры могут кататься без проскальзывания, один цилиндр без сопротивления, другой — с трением качения. В каких пределах меняется внешний момент, приложенный к одному из цилиндров, в условии равновесия системы?
Трение качения происходит за счет деформации цилиндра и опорной поверхности в месте контакта. В результате реакция опоры смещается в сторону возможного движения на половину длины площадки контакта и создает момент сопротивления. Плечо этого момента принимают за коэффициент трения качения. Таким образом, 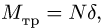
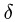
в теле мала, а глубиной продавливания цилиндра в поверхность (или величиной смятия цилиндра) пренебрегают. Коэффициент трения качения зависит не только от свойств материала цилиндра и поверхности, но и от радиуса цилиндра.
План решения:
1. Задаем направление возможного движения при достижении условия предельного равновесия. К катящемуся телу (цилиндру, колесу) прикладываем момент трения качения, направляя его в сторону, противоположную возможному движению. Не забываем про силу сцепления в точке контакта, направленную вдоль плоскости.
2. Решаем задачу о равновесии системы тел. Используем метод разбиения системы на отдельные тела. Внешние и внутренние связи заменяем их реакциями. Составляем и решаем уравнения равновесия. Оси координат для уравнения проекций для цилиндрических тел выбираем вдоль нормальной реакции, а уравнение моментов составляем относительно точки касания. Из решения системы уравнений равновесия определяем условие предельного равновесия.
3. Меняем направление возможного движения системы и направление момента трения качения. Решаем задачу заново, определяем второе условие предельного равновесия.
Задача №11
Система состоит из двух цилиндров весом 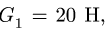
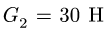
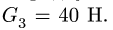
Коэффициент трения качения 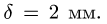
Решение
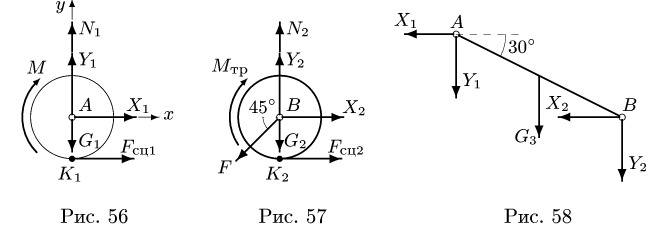
1. Задаем направление возможного движения при достижении условия предельного равновесия. Пусть за счет достаточно большой, по сравнению с моментом М, силы F произойдет движение системы влево. Тогда момент трения качения, приложенный к цилиндру 2, будет направлен по часовой стрелке (рис. 57). Его величину находим по формуле
2. Решаем задачу о равновесии системы двух цилиндров и стержня. Разбиваем систему на три тела (рис. 56, 57, 58). Внешние связи заменяем реакциями
Реакции 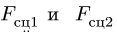
При составлении системы семи уравнений с неизвестными 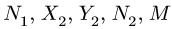
Составляем уравнения равновесия для цилиндра 1 (рис. 56):
Уравнения равновесия цилиндра 2 (рис. 57) имеют вид
3.2.Трения качения
Уравнения равновесия стержня АВ (рис. 58) имеют вид
Из решения системы уравнений (1-3) определяем
Радиус и коэффициент трения качения переводим в метры R = 0.5 м, 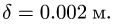
Убеждаемся, что 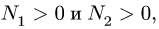
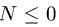
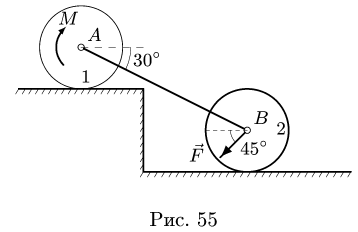
3. Меняем направление возможного движения системы. Пусть за счет действия момента М произойдет движение системы вправо. Момент трения качения направим против часовой стрелки (рис. 59). Составляя уравнения равновесия для новой системы сил, заметим, что отличие от прежней системы проявляется только в знаке 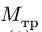
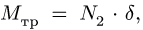
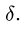
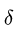
Точно так же находим нормальные реакции опор: 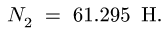
цилиндру 1, изменяется в пределах (в Нм)
- Пространственная система сил
- Центр тяжести
- Кинематика точки
- Плоское движение твердого тела
- Теория пар сил
- Приведение системы сил к простейшей системе
- Условия равновесия системы сил
- Плоская система сил
Как найти коэффициент трения
На данной странице калькулятор поможет рассчитать коэффициент трения онлайн. Для расчета задайте угол наклона.
Коэффициент трения – количественная характеристика силы, необходимой для скольжения или движения одного материала по поверхности другого.
По углу наклона
Угол α:
Результат
Ответы:
Формула для нахождения средней скорости, зная расстояние и время:
α – угол наклона.
Пусть имеем линейку, тело и наклонную плоскость, угол наклона которой можно изменять.
Задача.
Определить коэффициент трения скольжения тела по наклонной плоскости с использованием данных нам объектов.
Как известно, любую физическую величину можно либо измерить с помощью прибора, либо рассчитать по формуле.
Мы, конечно, помним формулу, по которой можно рассчитать коэффициент трения µ = Fтр/N. Но, значения сил, входящих в формулу нам не известны. Вспомним, что прибор для измерения силы называется динамометр, а по условию задания у нас есть только линейка.
Решение.
Пусть тело находится на наклонной плоскости. При увеличении угла наклона плоскости до определенного значения βmax тело ещё покоится на месте. Именно этот предельный угол βmax для нас имеет значение. Выполним чертёж к этой задаче. Изобразим на чертеже все силы, действующие на тело в этом случае. Такими силами будут: со стороны Земли – сила тяжести mg, со стороны опоры – сила реакции опоры N и сила трения Fтр.
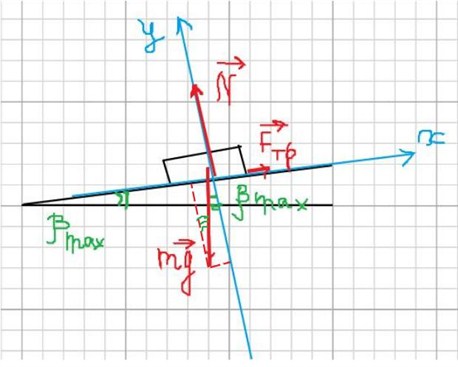
Запишем II закон Ньютона в векторном виде для этого случая:
ma->= mg->+ N->+ Fтр->
Запишем теперь этот же закон в проекциях на оси, помня о выражении (*):
OX: 0 = -mgSIN β + 0 + Fтр => mgSIN β = Fтр (1)
OY: 0 = -mgCOS β + N + 0 => mgCOS β = N (2)
Вспомним о том, что /Fтр/ = /µN/ и перепишем выражение (1) в другом виде (выражение (2 )оставим без изменения):
mgSIN β = µN (3)
mgCOS β = N (2)
Разделим выражение (3) на выражение (2)
mgSIN β / mgCOS β = µN/N,
tg β = µ.
Формула для расчёта коэффициента трения выведена, осталось вспомнить определение тангенса угла βmax в прямоугольном треугольнике АВС. Смотрим внимательно на чертёж ниже.
Итак, µ = tg β = ВС/AC.
Длины ВС и AC измеряем линейкой. Задание выполнено!
А если Вы знаете другие способы определения коэффициента трения при помощи исходного оборудования, то напишите нам в блог.
Остались вопросы? Не знаете, как подготовиться к лабораторной работе по физике?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Работа 2
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ СИЛ ТРЕНИЯ
СКОЛЬЖЕНИЯ
Принадлежности: прибор, прямоугольный
прозрачный треугольник с миллиметровыми
делениями.
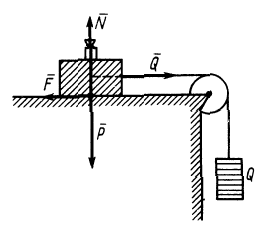
Введение. Если к телу (бруску),
лежащему на горизонтальной плоскости,
приложить небольшую силу F
(рис. I), оно будет покоиться,
так как внешняя сила F
будет уравновешена силой трения покоя
fтр.
С увеличением силы F будет
в такой же степени расти и сила трения.
Последняя, однако не может расти
беспредельно.
К
она достигнет максимальной величины,
брусок начнёт скользить по плоскости.
В этом случае сила трения покоя сменяется
силой трения скольжения, которая
несколько меньше силы трения покоя (на
10-20%). Опыт показывает, что сила трения
скольжения Рис. I
пропорциональна силе N,
с которой тела прижимаются друг к другу,
и не зависит от площади соприкосновения
тел:
fтр
= kN,
где k – коэффициент силы
трения скольжения. Величина его зависит
только от свойств трущихся поверхностей
и в общем случае от скорости их
относительного движения.
Известен простой способ измерения
коэффициента силы трения. Для этого
наклоняют плоскость с лежащим на ней
бруском до тех пор, пока брусок не начнёт
скользить. В этом случае сила тяжести
бруска раскладывается на две составляющие
– “скатывающую силу” F
и силу давления N. Для
определения коэффициента силы трения
достаточно измерить предельный угол
наклона плоскости к горизонту, при
котором тело начинает скользить по
плоскости, при этом F =
fтр.
Тогда коэффициент силы трения можно
вычислить по формуле:
,
где φ – предельный угол наклона плоскости.
В
данной работе предлагается несколько
видоизменённый метод определения
коэффициента трения. Сущность его можно
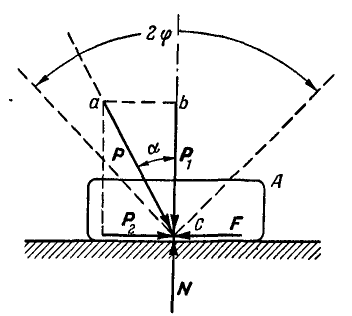
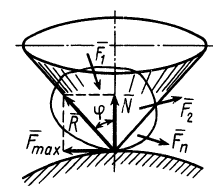
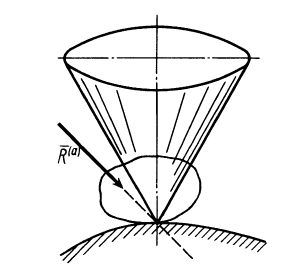
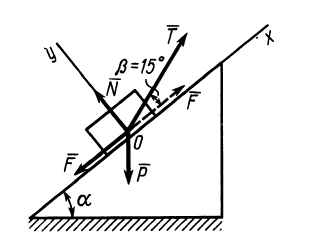
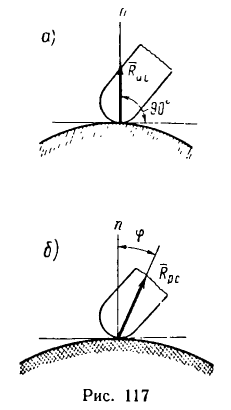
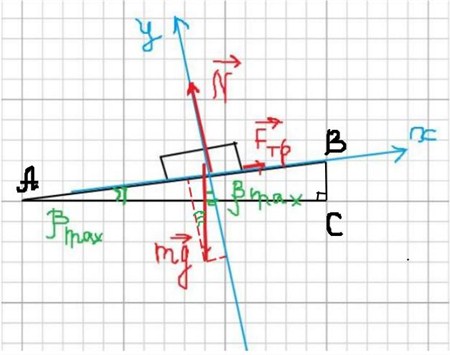
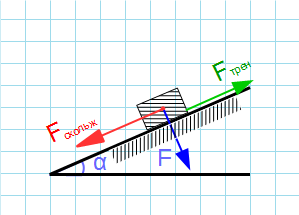
пояснить с помощью рис. 2. Тело (брусок)
1 помещают на горизонтальную плоскость
2, по которой равномерно движется
прямоугольный треугольник 3 со скоростью
υ вдоль одного из своих катетов и
гипотенузой толкает брусок 1. Если сила
трения между бруском и гипотенузой
треугольника достаточно велика, брусок
будет двигаться в ту же сторону, что и
треугольник. При достаточно больших
углах α брусок начнёт скользить по
гипотенузе треугольника и сила трения
покоя между ними сменится силой трения
скольжения. Брусок начнёт двигаться
вдоль равнодействующей F
двух сил: силы трения скольжения Fтр
между бруском и горизонтальной
плоскостью. Сила N всегда
направлена нормально к гипотенузе
треугольника. Направление силы F
можно определить по направлению движения
бруска. Тангенс угла γ между силами N
и F даёт значение коэффициента
силы трения скольжения бруска о линейку:
.
(1)
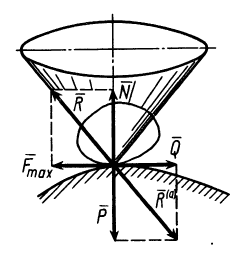
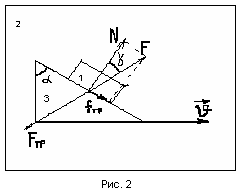
Описание прибора. Установка (рис.
3) состоит из горизонтальной доски 1 с
зажимом 2 и “рейсшины”, имеющей
металлическую линейку 3 (которая выполняет
роль гипотенузы прямоугольного
треугольника в рассматриваемой теории),
ползушку 4 и винт 5, которым линейка может
закрепляться на ползушке под разными
углами α. Движущимся телом является
пластинка 6.
Линейка рейсшины закрепляется на
ползушке под углом α не менее 45 градусов.
Пластинка помещается на доске справа
от линейки, соприкасаясь с ней. При
перемещении рейсшины слева направо
наблюдается движение пластинки по
линейке в сторону её свободного конца.
Пусть центр масс пластинки переместился
по доске на расстояние L1L2.
Проекция перемещения на нормаль к
линейке будет L1M.
Сравнивая рисунки 2 и 3, видим, что
коэффициент силы трения скольжения
пластинки по линейке может быть определён
по формуле (1).
Рис. 3
Для отметок начального и конечного
положения центра масс пластинка имеет
отверстие в своём геометрическом центре.
Отметка производится карандашом через
это отверстие на листе бумаги, положенном
на доску и закреплённом зажимом 2. Линейка
рейсшины сделана из уголкового дюраля,
а пластинки – из разных материалов.
Измерения. 1. На плоскость доски
накладывается и закрепляется зажимом
2 лист бумаги.
2. На бумагу помещается линейка рейсшины,
ползушка которой до упора сдвинута
влево. К поверхности линейки прикладывается
брусок. Очень осторожно, придерживая
левой рукой рейсшину и брусок, отмечают
остро отточенным карандашом начальное
положение центра масс бруска (точка
L1).
3. Плавно и равномерно, прижимая ползушку
к ребру доски, перемещают рейсшину до
предела вправо. Осторожно, не сдвигая
при этом бруска, отмечают новое положение
центра масс (точка L2).
4. Через точки L1
и L2
проводят карандашом прямую, которая
является траекторией движения бруска.
Смещают линейку влево и с помощью
прозрачного прямоугольного треугольника
проводят карандашом нормаль к линейке
из точки пересечения её с траекторией.
Тангенс угла между этими прямыми будет
равен коэффициенту трения скольжения.
Тангенс угла γ определяют из соотношения
катетов прямоугольного треугольника,
который получается путём пересечения
этих прямых нормалью к одной из них.
5.Описанные в пунктах 3-4 операции повторяют
для каждой пластинки не менее пяти раз,
варьируя в небольших пределах угол α.
Все результаты измерений заносят в
таблицу. После их обработки записывают
окончательный результат в виде:
где
6. Вычисляют относительную погрешность
.
7. Убедиться, что изменение величины
силы трения между нижней поверхностью
пластинки и поверхностью доски не
изменяет величину коэффициента трения.
Для этого проводят ещё одно измерение,
положив на пластинку гирьку 200г. В этом
случае необходимо быть особенно
осторожным, чтобы при наложении и снятии
гирьки и отметке карандашом точек центра
масс, не сдвинуть пластинку. Сопоставляют
вычисленный для этого случая коэффициент
трения с ранее полученной величиной.
Контрольные вопросы.
1. Что такое коэффициент трения?
2. Как зависит сила трения скольжения
от скорости?
3. Чем отличается сухое трение от
вязкого?
4. Нарисуйте схематически экспериментальную
установку.
Литература
Матвеев А.Н. Механика и теория
относительности. – М.: Высшая школа,
1976, гл.12, §53.
Стрелков С.П. Механика. – М.: Наука,
1975, гл 5, § 38, 41, 42.
Савельев И.В. Курс общей физики. Т.1.
– М.: Наука, 1977, гл. 2, § 15.
Соседние файлы в папке Методички (мех)
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #