Лабораторная
работа № 21
ОПРЕДЕЛЕНИЕ
КОЭФФИЦИЕНТА ВНУТРЕННЕГО ТРЕНИЯ
ВОЗДУХА
ПРИ РАЗЛИЧНЫХ ТЕМПЕРАТУРАХ.
Принадлежности:
лабораторная
установка.
Цель
работы:
1.
Определение коэффициента внутреннего
трения воздуха при различных температурах.
2.
Определение средней длины свободного
пробега молекул в воздухе.
Введение.
Если
в текущей жидкости (газе) соседние слои
имеют различную
скорость,
то между ними возникает сила внутреннего
(вязкого) трения,
определяемая
законом Ньютона
где
– коэффициент внутреннего трения (или
коэффициент вязкости),
– градиент
скорости – это вектор, который направлен
в сторону
наибыстрейшего
возрастания скорости слоев текущей
жидкости,

–
элементарная площадка на поверхности
соприкосновения слоев,
перпендикулярная
градиенту скорости. Коэффициент
внутреннего трения является важной
характеристикой жидкости(газа), зависящей
от ее природы, так и от температуры.
Коэффициент
внутреннего трения газа измеряют
различными способами.
В
данной работе применяется метод,
основанный на использовании закона
Пуазейля,
сущность которого заключается в
следующем. При ламинарном
течении
жидкости по трубе круглого сечения, как
показали Пуазейль и Стокс, объем протекшей
жидкости за время τ
равен
(1)
где
p1
– p2
= B
g
(h1
– h2)
– разность давлений воздуха на входе
и выходе из капилляра,
(h1
– h2)
– разность уровней воды в манометре;
r
–
радиус капилляра;
L
– длина капилляра;
V
– объём воздуха, протекающего через
капилляр за время
при данной температуре.
B
–
плотность воды при температуре и давлении
в лаборатории.
Эта
формула справедлива не только для
капельных жидкостей, но и для
плотных
газов
(когда λ
<<
r
–
радиуса трубки), если им обеспечен
ламинарный режим течения. Предполагается,
что в трубке достаточной длины и малого
радиуса (капилляре) при условиях близких
к нормальным, газ течет ламинарно.
Средней
длиной пробега
молекул в газе `
называется среднее
расстояние,
которое пролетает молекула от одного
столкновения до
следующего.
Она зависит от условий, при которых
находится газ, и от свойств молекул
следующим образом

(2)
эфф
– эффективное сечение молекул; n
–
число молекул газа в единице объёма
(концентрация). Площадь сечения сферы
ограждения молекул по большому кругу
называется эффективным
сечением молекулы
при рассеянии ее на других молекулах.
Эффективное сечение

где d
–
диаметр молекулы.
Согласно
молекулярно-кинетической теории газа
тепловое хаотическое
движение
молекул газа является причиной так
называемых явлений
переноса,
к которым, в частности, относится
внутреннее
трение (или вязкость).
Дальнейшие
рассуждения и выводы относятся к плотным
газам,
в которых
длина
свободного пробега молекул намного
меньше характерного размера
сосуда,
в нашем случае длина пробега меньше
радиуса капилляра. Из теории
получается
не только ньютоновский закон внутреннего
трения, но и
коэффициент
внутреннего трения h,
который
выражается следующей
формулой:
(3)
где

средняя длина свободного пробега молекул
в газе,
– средняя
скорость теплового движения молекул,
ρ
–
плотность
газа при данных условиях.
Формула
(2) дает возможность определить длину
свободного пробега
молекул
газа, если предварительно измерен
коэффициент внутреннего трения и
рассчитана средняя скорость молекул и
плотность по известным формулам
молекулярно-кинетической теории
идеального газа.

(4)
где
R
–
универсальная газовая постоянная, Т
–
абсолютная температура,
р
–
давление, µ – молярная масса газа. В
этом случае
(5)
Из
соотношений (2)-(3) следует
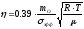
(6)
Если
в данном диапазоне температур и давлений
воздух можно приближённо считать
идеальным газом, то эффективное сечение
молекул остаётся постоянной величиной
и
, следовательно, можно записать

(7)
В
работе предлагается проверить
зависимость(7) .
Описание экспериментальной установки.
На
Рис.1 и Рис.2 представлена передняя панель
и схема экспериментальной установки
для измерения коэффициента внутреннего
трения воздуха.
Микрокомпрессор
1 прокачивает воздух через ротаметр 2
и затем направляется в медный термостат
(цилиндрическая трубка) 3, внутри которой
находится капилляр 4. Внутри медного
термостата находится спай термопары
5, измеряющей температуру воздуха
протекающего через капилляр 4 в атмосферу.
Термоэлектроды 7 соединены с измерителем
температуры 8. Перепад давления на
капилляре измеряется U
– манометром 6. Медный термостат 3
находится в керамическом цилиндре, на
внешней поверхности которого находится
электрический нагреватель 9, соединённый
с регулятором мощности 10.
На
передней панели находится тумблер
включения питания установки 11, тумблер
12 включения нагревателя 9, регулятор
температуры воздуха 10, протекающего
через капилляр 4, измеритель температуры
нагретого воздуха 13, измеритель объёмного
расхода воздуха 2, протекающего через
капилляр 4 (ротаметр), U
– манометр 6. для измерения перепада
давления воздуха на капилляре, тумблер
14 включения компрессора 1, тумблер 15
включения вентилятора.
Внимание!
Перед
выполнением работы тщательно ознакомьтесь
с порядком работы. Заранее подготовьте
таблицу. Конструктивные особенности
лабораторной установки не позволяют
быстро охладить воздух в баллоне.
ИЗМЕРЕНИЯ МОЖНО ПРОВЕСТИ ТОЛЬКО ОДИН
РАЗ ЗА ЗАНЯТИЕ!
Измерения.
1.
Включить электропитание установки
тумблером 11рис.1.
2.
Включить компрессор 1 рис.2 тумблером
14, измеритель температуры 8 тумблером
13.
3.
Включить питание регулятора температуры
10 тумблером 12 и нажатием клавиши 16.
4.
Повернуть со щелчком ручку 17 регулятора
температуры по часовой стрелке и
установить до красной метки.
5.
По показаниям температуры 8 наблюдать
ее увеличение до 2000С.
6.
Записать в таблицу показания ротаметра
2 в столбец « деление шкалы ротаметра»
при температуре 2000С.
Тщательно по нижним точкам менисков
уровня жидкости отсчитать величины
положений уровней жидкости h1
в
правом
колене манометра 6 и h2
–
в левом колене. Записать показания
температур 8 (красные цифры).
8.
Выключить регулятор температур. Включить
вентилятор 15 .Внимательно следить за
показаниями ротаметра 2 , когда показания
ротаметра изменятся на одно деление,
записать в таблицу значения h1
,
h2
при соответствующей температуре t0C.
9.
Повторить пункт 8 при каждом изменении
показаний ротаметра на одно деление
(не менее 6-7 измерений).
10.
По окончании эксперимента выключить
вентилятор, измеритель температур.
Обработка результатов измерений
1.Для
каждой температуры рассчитать разность
давлений

кг/м3–
плотность воды, значение
записать в системе СИ.
2.
Используя градуировочный график
ротаметра определить расход воздуха G
,данные записать в соответствующую
колонку таблицы №1.
3.
Из формулы (1) определить коэффициент
внутреннего трения воздуха

с табличным значением.
4.
Построить график зависимости
от
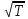
перевести в Кельвины.
5.
Из формулы (5) определить эффективное
сечение соударения молекул, величину

найти
из графика. Молярная масса воздуха
µ=29∙10-3кг/моль,
универсальная газовая постоянная
R=8,31Дж/моль∙К,
масса молекулы m=
постоянная Авогадро NА=6,02
∙1023моль-1.Определить
диаметр молекулы .
6.
По формуле (3) определить среднюю скорость
теплового движения молекул.
7.Определить
плотность воздуха в лаборатории по
формуле

Р- атмосферное давление воздуха.
8.
Определить длину свободного пробега
молекул
9.Написать
заключение о проведенной работе.
Таблица
№1
Длина
капилляра L=40
мм.
Диаметр
капилляра d=1м.
Начальная
температура t=
|
№ |
h1,см |
h2,см |
h1,-h2,м |
t0,С |
Деления |
G, 10-6 м3/с |
Па |
Таблица
№2
|
№ |
Т,К |
|
|
Контрольные
вопросы.
1.
Напишите
формулу Ньютона для силы вязкого трения
и поясните
значение
всех входящих в нее величин. Дайте
определение коэффициента
вязкости,
выведите его размерность.
2.
Что называется коэффициентом вязкости,
каков его физический смысл?
3.
При каких условиях выполняется закон
Пуазейля?
4.Что
называют средней длиной свободного
пробега. Как зависит средняя длина
свободного пробега молекул от температуры
газа, давления?
5.Как
зависит коэффициент внутреннего трения
в газах от температуры.
6.
Поясните формулы (4).
7.
Что называют эффективным сечением
молекулы? Как определить диаметр
молекулы?
8.
Каков механизм внутреннего трения в
жидкостях, чем он отличается от газов?
9.
Что показывает ротаметр? Почему при
понижении температуры показания
ротаметра увеличиваются?
10.
Какую роль играет микропроцессор?
11.
Поясните метод измерения температуры
Соседние файлы в папке Методички (мол)
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Unit Converter
Enter the density of the fluid (kg/m^3), the speed of the object (m/s), cross-sectional air (m^2), and the air resistance coefficient into the calculator to determine the Air Friction.
- All Friction Calculators
- Work Done By Friction Calculator
- Coefficient of Friction W/ Angle Calculator
- Friction Calculator
Air Friction Formula
The following formula is used to calculate the Air Friction.
Fair = .5 * p * V^2 * C * A
- Where Fair is the Air Friction (N)
- p is the density of the fluid (kg/m^3)
- V is the speed of the object (m/s)
- C is the air resistance coefficient
- A is the cross-sectional area (m^2)
How to Calculate Air Friction?
The following example problems outline how to calculate the Air Friction.
Example Problem #1
- First, determine the density of the fluid (kg/m^3). In this example, the density of the fluid (kg/m^3) is given as 124 .
- Next, determine the speed of the object (m/s). For this problem, the speed of the object (m/s) is given as 35 .
- Next, determine the air resistance coefficient. In this case, the air resistance coefficient is found to be .6.
- Next, determine the cross-sectional area. In this example, this is .25m^2.
- Finally, calculate the Air Friction using the formula above:
Fair = .5 * p * V^2 * C * A
Inserting the values from above yields:
Fair = .5 * 124 * 35^2 * .6 * .25 = 11,392.5 (N)
Example Problem #2
Using the same method as above, determine the variables required by the equation. For this example problem, these are as follows:
density of the fluid (kg/m^3) = 145
speed of the object (m/s) = 5
air resistance coefficient = .80
cross-sectional area (m^2) = .34
Entering these given values and solving gives:
Fair = .5 * 145 * 5^2 * .8 * .34 = 493 (N)
Пример 6.1. Найти длину трубопровода L , эквивалентного распределительному золотнику, у которого = 60-10- (dy = 15 мм) коэффициент трения воздуха в трубе X = 0,03. [c.150]
Газовая постоянная 20, 23 График коэффициента трения воздуха в трубе 146 [c.266]
Коэффициент трения воздуха в трубе 143 [c.267]
Средняя плотность дымовых газов Рх = 0,6 кг/м II окружающего атмосферного воздуха = 1,2 кг/м. Коэффициент сопротивления трения в трубе принять Я =- 0,03. [c.250]
Средняя плотность дымовых газов pi = 0,6 кг/м и окружающего атмосферного воздуха рг = 1,2 кг/м . Коэффициент сопротивления трения в трубе принять X = 0,03. [c.251]
В гл. 6 показано, что для длинных волн излучение распространяется в форме плоской волны, возбуждаемой суммарной объемной пульсацией, даваемой мембраной, и не зависит от формы ее колебаний. Собственный импеданс колеблющейся пластинки или мембраны, представляющей распределенную систему, можно условно отнести к центру системы, движение которого характеризуется некоторой скоростью щ. Учитывая кинетическую, потенциальную и рассеянную в системе энергию, введем некоторые эквивалентные параметры М Е и / , характеризующие массу, упругость и трение для системы, приведенной к центру . Таким образом, мы заменяем распределенную систему системой с одной степенью свободы с эквивалентными массой М упругостью Е и коэффициентом трения / . Кроме того, силу, действующую на систему по всей ее площади, придется заменить эквивалентной силой действующей в центре и производящей ту же самую работу. Кроме объемной пульсации, порождающей плоскую волну, мембрана или пластинка дает дополнительные колебания в окружающей среде, вызываемые высшими модами колебания поверхности. При длинных волнах высшие моды не порождают волн, распространяющихся в трубе, и возбуждают колебательный процесс лишь в ближней зоне. Это приводит к возникновению дополнительной энергии, связанной с этими колебаниями, и формально может быть выражено как появление добавочной или присоединенной массы, как бы движущейся в целом со скоростью По, Для колебаний в воздухе [c.180]
Значения коэффициентов местных сопротивлений зависят от конфигурации местного сопротивления и режима потока, подходящего к сопротивлению этот режим определяется коэффициентом гидравлического трения Л подходящего потока [1], т. е. числом Рейнольдса и относительной шероховатостью. При движении воды и воздуха влияние числа Рейнольдса на значения коэффициентов местных сопротивлений проявляется не всегда и в практических расчетах его часто можно не учитывать. Более заметным становится влияние чисел Рейнольдса при малых их значениях, а также при постепенном изменении величины ила направления скорости (закругленный поворот, плавный вход в трубу и пр.). Приводимые ниже значения коэффициентов сопротивления относятся к квадратичной области сопротивления. [c.73]
Величина А, при этом зависит от числа Рейнольдса и от относительной шероховатости трубы. При турбулентном движении берут значение с запасом 0,25. При этом коэффициент относительной шероховатости не отличается от числа Рейнольдса при дальнейшем его возрастании значение постоянно и нри этом тем больше, чем больше шероховатость трубы. Подобные же явления наблюдаются при прохождении потока через каналы между ребрами. Данные различных авторов в количественном отношении сильно разнятся друг от друга, что указывает на различные условия проведения опытов. Поэтому при выборе параметров из таблиц следует критически оценивать условия проведения экспериментов. Во всяком случае всегда следует учитывать потери на трение воздуха о стенки каналов. [c.536]
Здесь К — коэффициент сопротивления трению I — постоянная конусность внутренней поверхности верхнего участка трубы Ра—плотность атмосферного воздуха при расчетном режиме, кг/м Ло — динамический напор, создаваемый продуктами сгорания в выходном отверстии трубы, Па р — плотность продуктов сгорания при расчетном режиме, кг/м . [c.354]
Средний удельный вес дымовых газов Y, = 0, кГ1м и окружающе-А/ го атмосферного воздуха Yj = -Рв —1,2 кГ м Коэффициент сопротивления трения в трубе принять К задаче 9-20. Я =0,03. [c.250]
Определить расход воздуха, засасываемого двигателем вутреннего сгорания из атмосферы, при котором, вакуум в горловине ди( узора составляет Рвак 15 кПа, если диаметр трубы Z) = 40 мм, диаметр диффузора d = 20 мм, коэффициенты сопротивления воздухоочистителя t,i = б, колена = 0,3, воздушной заслонки 3 = 0,5 отнесены к скорости в трубе, а коэффициент сопротивления диффузора 4 = 0,04 отнесен к скорости движения воздуха в его горловине (рис. 4.6). Плотность воздуха р = 1,23 кг/м . Потерями напора на трение пренебречь. [c.45]
Исследование трения в вакууме 10 —мм рт. ст. проводилось на установке, созданной на базе печи ТГВ-1М, а на воздухе — в специально оборудованной криптоловой печи. Была принята схема трения с коэффициентом взаимного перекрытия, равным единице (рис. 1). Трубчатые образцы соприкасаются торцами, выполненными по сфере большого радиуса (выпуклой для верхнего образца и вогнутой для нижнего). Такой контакт (по сфере) обеспечивает возможность самоустановки образцов, что позволяет компенсировать возможные неточности изготовления и сборки узла трения. Нижний образец установлен на трубе, приводимой во вращение от расположенного вне вакуумной камеры привода. Верхний образец, установленный на концентрично расположенном в трубе стержне, неподвижный. Нагрузка на образцы передается через этот стержень, нижний конец которого связан с пружинным нагрузочно-измерительным устройством. Приложенная нагрузка и возникающий момент трения регистрируются датчиками, наклеенными на соответствующие пружины динамометра [1]. Испытания проводились при нагрузке —5 кГ и скорости скольжения 0,5 mImuh. [c.49]
Большинство опытов по изучению влияния шерохо ватости на теплообмен, а также аналитические исследо вания проведены при числах Прандтля, близких к 1 Типичными являются опытные данные Нуннера при те чении воздуха (Рг = 0,7) в шероховатых трубах [Л. 27]. Зависимость числа Нуссельта от коэффициента трения согласно данным Нуннера приближенно коррелируется уравнением [c.239]
Остается рассмотреть еще один существенный момент. Когда отношение рЫ между частотой вынужденных и собственных колебаний отклоняется в ту или другую сторону от единицы, величина потерь уменьшается но сравнению с максимальным значением тем быстрее, чем меньше значение коэффициента трения Ь. Другими словами, чем интенсивнее резонанс в случае точного совпадения частот, тем уже область, в которой величина колебаний остается близкой к максимальному значению. Например, для того, чтобы заметным образом возбудить камертон, — даже если он снабжен резонансным ящикоаг, — колебаниями другого камертона, расположенного поблизости, требуется очень точная настройка, тогда как столб воздуха в почти полностью закрытом сосуде (например, в колбе или в органной трубе) сильно реагирует на колебания в значительно более широком диапазоне частот. Для уяснения этого вопроса заметим, что выражение для рассеяния энергии (20) в 12 можно переписать в следующем виде [c.51]
Пример 5.19. Определить длину пе(рфо1рированного стального воздухочода с непрерывной раздачей по длине, если диаметр его =0,1 м и расход воздуха в начале трубы С = 0,05 м /с. Избыточное давление воздуха на входе в перфорированный трубопровод р=200 Па. Температура воздуха 20°С. Сравнить о расчетом в предположении наличия квадратичного закона сопротивления и постоянства коэффициента гидравлического трения по длине трубопровода. [c.127]
Результаты, приведенные в этом и предыдущих параграфах, справедливы только для капельных жидкостей. В случае течения газа при больших температурных напорах необходимо учитывать не только зависимость ц от Т, но и зависимость р, Я и Ср от Т. Некоторые расчеты теплообмена и трения для воздуха в условиях охлаждения вдали от входа в трубу при 7с = onst проведены в Л. 10]. Они показывают, что если 1к в выражении для числа NUoo Bbi6paTb при средней массовой температуре Т, то с уменьшением TdT от 1 до 0,25 число Nu , при переменных физических свойствах возрастает. Однако это возрастание невелико и не превышает 6% от значения Nu при постоянных физических свойствах. Коэффициент сопротивления в этих условиях изменяется в зависимости от Тс/Т приблизительно так же, как и в случае с = onst (см. 9-4). [c.137]
Воздух плотностью р = 1,2 кг/м подается в помещение по всасывающей трубе вентилятора (рис. 11.39) длиной / = 4 м,. Гидравлический коэфс )ициент трения к = 0,02 коэффициенты потерь на плавном входе Zm == 0,3 и на повороте Спов = 0,35. Определить а) разрежение (вакуум) Рван перед вентилятором, если его производительность Q = 1300 м /ч, а диаметр всасывающей трубы D — [c.63]
В 1955 г. было опубликовано краткое сообщение [Л. 574] о докторской диссертации Р. Тренса, посвященной исследованию теплообмена в слое, псевдоожиженном воздухом. Трене экспериментально определял коэффициенты теплообмена псевдоожиженного слоя стеклянных шариков (d =0,15-f-1,10 мм) с погруженным в него аксиально высоким нагревателем (/=500 мм), выступавшим за пределы плотной фазы псевдоожиженного слоя. Шарики загружались на газораспределительную решетку в вертикальную трубу (0т = 100л1л) слоем, имевшим до псевдоожижения толщину 76—455 мм. Весовая скорость фильтрации воздуха составляла от 470 до 19 ООО кг/ж ч. Коэффициенты теплообмена варьировали от 34 до Q1 ккал м -ч-град. Трене предложил эмпирическую формулу для увязки своих опытных данных. Сами опытные данные в публикации отсутствуют. [c.366]
Для случая турбулентного движения воздуха Блязиусом, Ни-курадзе и другими предложены экспериментальные формулы определения коэффициента сопротивления трению X для гладких и Мизесом — для шероховатых труб. По этим формулам значе- ния гладких труб устанавливаются в зависимости от числа Re, а шероховатых — от шероховатости стенок трубы и числа Re. Недостатком формул является их сложность [70]. [c.30]

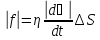













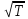
 ,Па∙с
,Па∙с