Как найти коэффициент треугольника паскаля

Основная формула

Строки треугольника обычно нумеруются, начиная со строки n = 0 в верхней части. Записи в каждой строке целочисленные и нумеруются слева, начиная с k = 0, обычно располагаются в шахматном порядке относительно чисел в соседних строчках. Построить фигуру можно следующим образом:

• В центре верхней части листа ставится цифра “1”.
• В следующем ряду — две единицы слева и справа от центра (получается треугольная форма).
• В каждой последующей строке ряд будет начинаться и заканчиваться числом “1”. Внутренние члены вычисляются путём суммирования двух цифр над ним.

Запись в n строке и k столбце паскалевской фигуры обозначается (n k). Например, уникальная ненулевая запись в самой верхней строке (0 0) = 1. С помощью этого конструкция предыдущего абзаца может быть записана следующим образом, образуя формулу треугольника Паскаля (n k) = (n – 1 k-1) + (n – 1 k), для любого неотрицательного целого числа n и любого целого числа k от 0 до n включительно. Трёхмерная версия называется пирамидой или тетраэдром, а общие — симплексами.

История открытия

Паскаль ввёл в действие многие ранее недостаточно проверенные способы использования чисел треугольника, и он подробно описал их в, пожалуй, самом раннем из известных математических трактатов, специально посвящённых этому вопросу, в труде об арифметике Traité du triangle (1665). За столетия до того обсуждение чисел возникло в контексте индийских исследований комбинаторики и биномиальных чисел, а у греков были работы по «фигурным числам».

Из более поздних источников видно, что биномиальные коэффициенты и аддитивная формула для их генерации были известны ещё до II века до нашей эры по работам Пингала. К сожалению, бо́льшая часть трудов была утеряна. Варахамихира около 505 года дал чёткое описание аддитивной формулы, а более подробное объяснение того же правила было дано Халаюдхой (около 975 года). Он также объяснил неясные ссылки на Меру-прастаара, лестницы у горы Меру, дав первое сохранившееся определение расположению этих чисел, представленных в виде треугольника.

Примерно в 850 году джайнский математик Махавира вывел другую формулу для биномиальных коэффициентов, используя умножение, эквивалентное современной формуле. В 1068 году Бхаттотпала во время своей исследовательской деятельности вычислил четыре столбца первых шестнадцати строк. Он был первым признанным математиком, который уравнял аддитивные и мультипликативные формулы для этих чисел.

Примерно в то же время персидский учёный Аль-Караджи (953–1029) написал книгу (на данный момент утраченную), в которой содержалось первое описание треугольника Паскаля. Позднее работа была переписана персидским поэтом, астрономом и математиком Омаром Хайямом (1048–1131). Таким образом, в Иране фигура упоминается как треугольник Хайяма.

Известно несколько теорем, связанных с этой темой, включая биномы. Хайям использовал метод нахождения n-x корней, основанный на биномиальном разложении и, следовательно, на одноимённых коэффициентах. Треугольник был известен в Китае в начале XI века благодаря работе китайского математика Цзя Сианя (1010–1070). В XIII веке Ян Хуэй (1238–1298) представил этот способ, и поэтому в Китае он до сих пор называется треугольником Ян Хуэя.

На западе биномиальные коэффициенты были рассчитаны Жерсонидом в начале XIV века, он использовал мультипликативную формулу. Петрус Апиан (1495–1552) опубликовал полный треугольник на обложке своей книги примерно в 1527 году. Это была первая печатная версия фигуры в Европе. Майкл Стифель представил эту тему как таблицу фигурных тел в 1544 году.

В Италии паскалевский треугольник зовут другим именем, в честь итальянского алгебраиста Никколо Фонтана Тарталья (1500–1577). Вообще, современное имя фигура приобрела благодаря Пьеру Раймонду до Монтрмору (1708), который назвал треугольник «Таблица Паскаля для сочетаний» (дословно: Таблица мистера Паскаля для комбинаций) и Абрахамом Муавром (1730).

Отличительные черты

Треугольник Паскаля и его свойства — тема довольно обширная. Главное, в нём содержится множество моделей чисел. Обзор следует начать с простого — ряды:

• Сумма элементов одной строки в два раза больше суммы строки, предшествующей ей. Например, строка 0 (самая верхняя) имеет значение 1, строчка 1–2, а 2 имеет значение 4 и т. д. Это потому что каждый элемент в строке производит два элемента в следующем ряду: один слева и один справа. Сумма элементов строки n равна 2 ⁿ.
• Принимая произведение элементов в каждой строке, последовательность продуктов можно связать с основанием натурального логарифма.
• В треугольнике Паскаля через бесконечный ряд Нилаканты можно найти число Пи.
• Значение строки, если каждая запись считается десятичным знаком (имеется в виду, что числа больше 9 переносятся соответственно), является степенью 11 (11ⁿ для строки n). Таким образом, в строке 2 ⟨1, 2, 1⟩ становится 11², равно как ⟨1, 5, 10, 10, 5, 1⟩ в строке пять становится (после переноса) 161, 051, что составляет 11⁵. Это свойство объясняется установкой x = 10 в биномиальном разложении (x + 1) ⁿ и корректировкой значений в десятичной системе.
• Некоторые числа в треугольнике Паскаля соотносятся с числами в треугольнике Лозанича.
• Сумма квадратов элементов строки n равна среднему элементу строки 2 n. Например, 1 ² + 4 ² + 6 ² + 4 ² + 1 ² = 70.
• В любой строчке n, где n является чётным, средний член за вычетом члена в двух точках слева равен каталонскому числу (n / 2 + 1).
• В строчке р, где р представляет собой простое число, все члены в этой строке, за исключением 1s, являются кратными р.
• Чётность. Для измерения нечётных терминов в строке n необходимо преобразовать n в двоичную форму. Пусть x будет числом 1s в двоичном представлении. Тогда количество нечётных членов будет 2 ^х. Эти числа являются значениями в последовательности Гулда.
• Каждая запись в строке 2 ⁿ-1, n ≥ 0, является нечётной.
• Полярность. Когда элементы строки треугольника Паскаля складываются и вычитаются вместе последовательно, каждая строка со средним числом, означающим строки с нечётным числом целых чисел, даёт 0 в качестве результата.

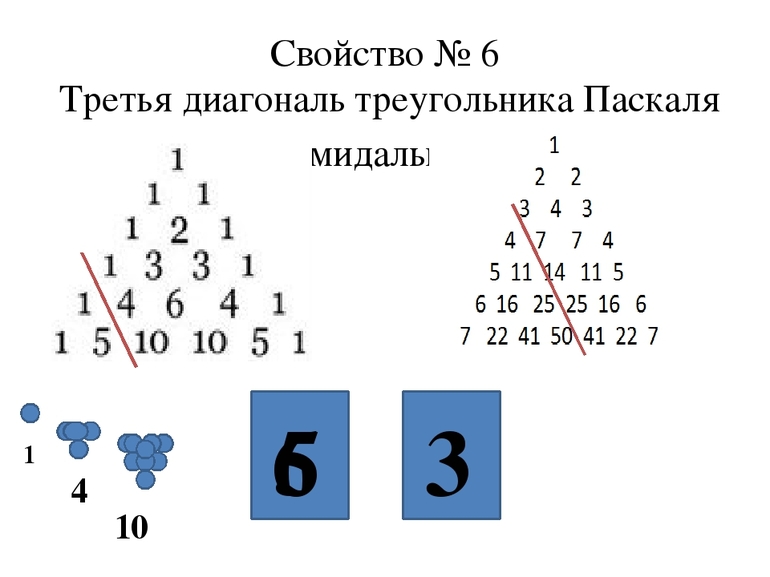
Диагонали треугольника содержат фигурные числа симплексов. Например:

• Идущие вдоль левого и правого краёв диагонали содержат только 1.
• Рядом с рёбрами диагонали содержат натуральные числа по порядку.
• Двигаясь внутрь, следующая пара содержит треугольные числа по порядку.
• Следующая пара — тетраэдрические, а следующая пара — числа пятиугольника.

Существуют простые алгоритмы для вычисления всех элементов в строке или диагонали без вычисления других элементов или факториалов.

Общие свойства

Образец, полученный путём раскраски только нечётных чисел, очень похож на фрактал, называемый треугольником Серпинского. Это сходство становится всё более точным, так как рассматривается больше строк в пределе, когда число рядов приближается к бесконечности, получающийся в результате шаблон представляет собой фигуру, предполагающую фиксированный периметр. В целом числа могут быть окрашены по-разному в зависимости от того, являются ли они кратными 3, 4 и т. д.

В треугольной части сетки количество кратчайших путей от заданного до верхнего угла треугольника является соответствующей записью в паскалевском треугольнике. На треугольной игровой доске Плинко это распределение должно давать вероятности выигрыша различных призов. Если строки треугольника выровнены по левому краю, диагональные полосы суммируются с числами Фибоначчи.

Благодаря простому построению факториалами можно дать очень простое представление фигуры Паскаля в терминах экспоненциальной матрицы: треугольник — это экспонента матрицы, которая имеет последовательность 1, 2, 3, 4… на её субдиагонали, а все другие точки – 0.

Количество элементов симплексов фигуры можно использовать в качестве справочной таблицы для количества элементов (рёбра и углы) в многогранниках (треугольник, тетраэдр, квадрат и куб).

Шаблон, созданный элементарным клеточным автоматом с использованием правила 60, является в точности паскалевским треугольником с биномиальными коэффициентами, приведёнными по модулю 2. Правило 102 также создаёт этот шаблон, когда завершающие нули опущены. Правило 90 создаёт тот же шаблон, но с пустой ячейкой, разделяющей каждую запись в строках. Фигура может быть расширена до отрицательных номеров строк.

Секреты треугольника

Конечно, сейчас большинство расчётов для решения задач не в классе можно сделать с помощью онлайн-калькулятора. Как пользоваться треугольником Паскаля и для чего он нужен, обычно рассказывают в школьном курсе математики. Однако его применение может быть гораздо шире, чем принято думать.

Начать следует со скрытых последовательностей. Первые два столбца фигуры не слишком интересны — это только цифры и натуральные числа. Следующий столбец — треугольные числа. Можно думать о них, как о серии точек, необходимых для создания групп треугольников разных размеров.

Точно так же четвёртый столбец — это тетраэдрические числа или треугольные пирамидальные. Как следует из их названия, они представляют собой раскладку точек, необходимых для создания пирамид с треугольными основаниями.

Столбцы строят таким образом, чтобы описывать «симплексы», которые являются просто экстраполяциями идеи тетраэдра в произвольные измерения. Следующий столбец — это 5-симплексные числа, затем 6-симплексные числа и так далее.

Полномочия двойки

Если суммировать каждую строку, получатся степени основания 2 начиная с 2⁰ = 1. Если изобразить это в таблице, то получится следующее:

1
1	+	1	=	2
1	+	2	+	1	=	4
1	+	3	+	3	+	1	=	8
1	+	4	+	6	+	4	+	1	=	16
1	+	5	+	10	+	10	+	5	+	1	=	32
1	+	6	+	15	+	20	+	15	+	6	+	1	=	64

Суммирование строк показывает силы базы 2.

Силы одиннадцати

Треугольник также показывает силы основания 11. Всё, что нужно сделать, это сложить числа в каждом ряду вместе. Как показывает исследовательский опыт, этого достаточно только для первых пяти строк. Сложности начинаются, когда записи состоят из двузначных чисел. Например:

1	=	11°
11	=	11¹
121	=	11²
1331	=	11³

Оказывается, всё, что нужно сделать — перенести десятки на одно число слева.

Совершенные квадраты

Если утверждать, что 4² – это 6 + 10 = 16, то можно найти идеальные квадраты натуральных чисел в столбце 2, суммируя число справа с числом ниже. Например:

• 2² → 1 + 3 = 4
• 3² → 3 + 6
• 4² → 6 + 10 = 16 и так далее.

Комбинаторные варианты

Чтобы раскрыть скрытую последовательность Фибоначчи, которая на первый взгляд может отсутствовать, нужно суммировать диагонали лево-выровненного паскалевского треугольника. Первые 7 чисел в последовательности Фибоначчи: 1, 1, 2, 3, 5, 8, 13… найдены. Используя исходную ориентацию, следует заштриховать все нечётные числа, и получится изображение, похожее на знаменитый фрактальный треугольник Серпинского.

Возможно, самое интересное соотношение, найденное в треугольнике — это то, как можно использовать его для поиска комбинаторных чисел, поскольку его первые шесть строк написаны с помощью комбинаторной записи. Поэтому, если нужно рассчитать 4, стоит выбрать 2, затем максимально внимательно посмотреть на пятую строку, третью запись (поскольку счёт с нуля), и будет найден ответ.

Действия с биномами

Например, есть бином (x + y), и стоит задача повысить его до степени, такой как 2 или 3. Обычно нужно пройти долгий процесс умножения (x + y)² = (x + y)(x + y) и т. д. Если воспользоваться треугольником, решение будет найдено гораздо быстрее. К примеру, нужно расширить (x + y)³. Поскольку следует повышать (x + y) до третьей степени, то необходимо использовать значения в четвёртом ряду фигуры Паскаля (в качестве коэффициентов расширения). Затем заполнить значения x и y. Получится следующее: 1 x³ + 3 x²y + 3 xy² + 1 y³. Степень каждого члена соответствует степени, до которой возводится (x + y).

В виде более удобной формулы этот процесс представлен в теореме бинома. Как известно, всё лучше разбирать на примерах. Итак – (2x – 3)³. Пусть x будет первым слагаемым, а y – вторым. Тогда x = 2x, y = –3, n = 3 и k – целые числа от 0 до n = 3, в этом случае k = {0, 1, 2, 3}. Следует внести эти значения в формулу. Затем заполнить значения для k, которое имеет 4 разные версии, их нужно сложить вместе. Лучше упростить условия с показателями от нуля до единицы.

Как известно, комбинаторные числа взяты из треугольника, поэтому можно просто найти четвёртую строку и подставить в значения 1, 3, 3, 1 соответственно, используя соответствующие цифры Паскаля 1, 3, 3, 1. Последнее — необходимо завершить умножение и упрощение, в итоге должно получиться: 8 x³ – 36 x² + 54x – 27. С помощью этой теоремы можно расширить любой бином до любой степени, не тратя время на умножение.

Биномиальное распределение описывает распределение вероятностей на основе экспериментов, которые можно разделить на группы с двумя возможными исходами. Самый классический пример этого — бросание монеты. Например, есть задача выбросить «решку» — успех с вероятностью p. Тогда выпадение «орла» является случаем «неудачи» и имеет вероятность дополнения 1 – p.

Если спроектировать этот эксперимент с тремя испытаниями, с условием, что нужно узнать вероятность выпадения «решки», можно использовать функцию вероятности массы (pmf) для биномиального распределения, где n – это количество испытаний, а k – это число успехов. Предполагаемая вероятность удачи – 0,5 (р = 0,5). Самое время обратиться к треугольнику, используя комбинаторные числа: 1, 3, 3, 1. Вероятность получить ноль или три «решки» составляет 12,5%, в то время как переворот монеты один или два раза на сторону «орла» — 37,5%. Вот так математика может применяться в жизни.

Треугольник Паскаля (арифметический треугольник) — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля. Числа, составляющие треугольник Паскаля, возникают естественным образом в алгебре, комбинаторике, теории вероятностей, математическом анализе, теории чисел^[1].

История[править | править код]

Первое упоминание треугольной последовательности биномиальных коэффициентов под названием meru-prastaara встречается в комментарии индийского математика X века Халаюдхи^[en] к трудам другого математика, Пингалы. Треугольник исследуется также Омаром Хайямом около 1100 года, поэтому в Иране эту схему называют треугольником Хайяма. В 1303 году была выпущена книга «Яшмовое зеркало четырёх элементов» китайского математика Чжу Шицзе, в которой был изображен треугольник Паскаля на одной из иллюстраций; считается, что изобрёл его другой китайский математик, Ян Хуэй (поэтому китайцы называют его треугольником Яна Хуэя).

В Италии треугольник Паскаля иногда называют «треугольником Тартальи», поскольку Никколо Тарталья описал эту таблицу на сто лет раньше Паскаля. На титульном листе учебника арифметики, написанном в 1529 году Петером Апианом, астрономом из Ингольштадтского университета, также изображён треугольник Паскаля. А в 1665 году^[2] вышла книга Блеза Паскаля «Трактат об арифметическом треугольнике»^[3], которая была специально посвящена данной таблице и по содержательности опережала своих предшественников.

Обозначения и свойства[править | править код]

Биномиальные коэффициенты часто обозначаются или и читаются как «число сочетаний из n элементов по k»^[1].

• Числа треугольника симметричны (равны) относительно вертикальной оси.
• В строке с номером n (нумерация начинается с 0):
• Сумма чисел восходящей диагонали, начинающейся с первого элемента (n − 1)-й строки, есть n-е число Фибоначчи:

  

• Если вычесть из центрального числа в строке с чётным номером соседнее число из той же строки, то получится число Каталана.
• Сумма чисел n-й строки треугольника Паскаля равна .
• Все числа в n-й строке, кроме единиц, делятся на число n тогда и только тогда, когда n является простым числом^[4] (следствие теоремы Люка).
• Если в строке с нечётным номером сложить все числа с порядковыми номерами вида 3n, 3n + 1, 3n + 2, то первые две суммы будут равны, а третья на 1 меньше.
• Каждое число в треугольнике равно количеству способов добраться до него из вершины, перемещаясь либо вправо-вниз, либо влево-вниз.

Цитаты[править | править код]

См. также[править | править код]

• Треугольник Серпинского
• Гипотеза Сингмастера
• Треугольник Хосойя

Примечания[править | править код]

Литература[править | править код]

• Паскаля треугольник // Энциклопедический словарь юного математика / Сост. А. П. Савин. — М.: Педагогика, 1985. — С. 230-232. — 352 с.
• Фукс Д., Фукс М. Арифметика биномиальных коэффициентов // Квант. — 1970. — № 6. — С. 17—25.
• Успенский В. А. Треугольник Паскаля. — М.: Наука, 1979. — 48 с. — (Популярные лекции по математике). — 200 000 экз.

Ссылки[править | править код]

• Weisstein, Eric W. Pascal’s Triangle (англ.) на сайте Wolfram MathWorld.
• Построение треугольника Паскаля

Бином Ньютона и треугольник Паскаля

18 декабря 2021

Сегодня мы детально разберём Бином Ньютона. Это формула, по которой можно раскрыть скобки ${{left( a+b right)}^{n}}$ и получить готовый многочлен. Сама формула выглядит так:

[{{left( a+b right)}^{n}}=sumlimits_{k=0}^{n}{C_{n}^{k}cdot {{a}^{n-k}}{{b}^{k}}}]

где $C_{n}^{k}$ — биноминальные коэффициенты (они же — «число сочетаний из $n$ по $k$»), которые считаются по формуле

[C_{n}^{k}=frac{n!}{k!left( n-k right)!}]

Вот и всё. На этом можно было бы закончить, но есть одно но: большинство начинающих учеников не понимают эту формулу, не умеют пользоваться её, а уж чтобы доказать её — об этом даже речи не идёт.

Сегодня мы всё это исправим. Вы узнаете буквально всё, что нужно знать про Бином Ньютона:

1. Постановка задачи — в чём вообще проблема?
2. Формула бинома Ньютона — что значат все эти значки?
3. Знак суммы — чрезвычайно полезный материал для всех, кто хочет понять математику.
4. Биноминальные коэффициенты — минутка комбинаторики.
5. Треугольник Паскаля — лайфхак для быстрых вычислений.
6. Доказательство Бинома Ньютона — для тех, кто хочет познать Истину.:)

Материала много, но всё будет максимально понятно и — главное — чрезвычайно полезно. Погнали!

1. Постановка задачи

Итак, мы хотим быстро раскрывать скобки в конструкциях вида ${{left( a+b right)}^{n}}$. Начнём с того, что мы и так знаем. Например:

[{{left( a+b right)}^{1}}=a+b]

Спасибо, кэп. Теперь вспомним формулы сокращённого умножения. Квадрат суммы:

[{{left( a+b right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}]

И куб суммы:

[{{left( a+b right)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}]

Видим, что с ростом степени растёт и количество слагаемых-одночленов: их всегда на одно больше, чем степень. Но это не проблема. Проблема в другом: у этих одночленов появляются некие коэффициенты, принцип вычисления которых не ясен. Пока не ясен…

Именно для нахождения этих коэффициентов придумали бином Ньютона.

2. Бином Ньютона

Пусть $nin mathbb{N}$. Тогда верно равенство

[{{left( a+b right)}^{n}}=sumlimits_{k=0}^{n}{C_{n}^{k}cdot {{a}^{n-k}}{{b}^{k}}}]

где $sum{left( … right)}$ — краткая запись суммы, $C_{n}^{k}$ — биноминальный коэффициент, который считается по формуле

[C_{n}^{k}=frac{n!}{k!left( n-k right)!}]

В этой формуле прекрасно всё. Одних пугает знак суммы. Другие не понимают, что за $C_{n}^{k}$ такое (ещё раз: это объект из мира комбинаторики, читается «число сочетаний из $n$ по $k$»). Третьи более-менее понимают, о чём речь, но применить эту формулу на практике не могут.

Сегодня мы решим все эти проблемы. Начнём со знака суммы.

3. Знак суммы

Знак суммы — это краткая запись суммы нескольких однотипных слагаемых:

[sumlimits_{k=a}^{k=b}{fleft( k right)}]

Формула $fleft( k right)$ задаёт общий вид однотипных слагаемых, а нижний и верхний индексы $k=a$ и $k=b$ (сверху вместо $k=b$ обычно пишут просто $b$) определяют диапазон значений, которые «пробегает» $k$ и которые нужно подставить в $fleft( k right)$. Например:

[sumlimits_{k=3}^{5}{2k}=2cdot 3+2cdot 4+2cdot 5]

Более привычный формат:

[sumlimits_{k=1}^{n}{fleft( k right)=fleft( 1 right)+fleft( 2 right)+…+fleft( n right)}]

То же самое с индексами:

[sumlimits_{k=1}^{n}{{{a}_{k}}={{a}_{1}}+{{a}_{2}}+…+{{a}_{n}}}]

Обратите внимание: если $k$ пробегает значения от $k=a$ до $k=b$, то всего таких слагаемых будет ровно $b-a+1$:

[sumlimits_{k=a}^{b}{fleft( k right)=underbrace{fleft( a right)+fleft( a+1 right)+ldots +fleft( b right)}_{b-a+1text{ слагаемых!}}}]

Кроме того, полезно потренироваться и с обратным переходом — от полной записи к краткой:

[frac{1}{1}+frac{1}{3}+frac{1}{5}+frac{1}{7}+frac{1}{9}=sumlimits_{n=1}^{5}{frac{1}{2n-1}}]

[frac{2}{3}+frac{4}{9}+frac{6}{27}+frac{8}{81}=sumlimits_{n=1}^{4}{frac{2n}{{{3}^{n}}}}]

В приложении к уроку — куча задач для самостоятельной тренировки.

Но вернёмся к биному Ньютона. Распишем его без знака суммы:

[begin{align} {{left( a+b right)}^{n}} & =C_{n}^{0}cdot {{a}^{n}}{{b}^{0}}+C_{n}^{1}cdot {{a}^{n-1}}{{b}^{1}}+ \ & +ldots +C_{n}^{k}cdot {{a}^{n-k}}{{b}^{k}}+ldots + \ & +C_{n}^{n-1}cdot {{a}^{1}}{{b}^{n-1}}+C_{n}^{n}cdot {{a}^{0}}{{b}^{n}} end{align}]

В целом, всё понятно: степени буквы $a$ уменьшаются с ${{a}^{n}}$ до ${{a}^{0}}$; одновременно степени буквы $b$ растут с ${{b}^{0}}$ до ${{b}^{n}}$. Сумма степеней этих букв в каждом одночлене равна $n$. Но что такое $C_{n}^{k}$?

4. Биноминальные коэффициенты

Немного комбинаторики.

Определение. Число сочетаний из $n$ по $k$ — это число способов, которыми можно выбрать $k$ элементов среди $n$ элементов, если порядок выбора не имеет значения. Обозначается $C_{n}^{k}$ и считается по формуле

[C_{n}^{k}=frac{n!}{k!left( n-k right)!}]

Обратите внимание: в числителе и знаменателе стоят факториалы. Стандартное определение: $n!$ — это произведение всех чисел от единицы до $n$:

[n!=1cdot 2cdot 3cdot …cdot n]

У факториалов много интересных свойств. Чуть позже мы рассмотрим их и даже введём более корректное определение самого факториала. А пока просто потренируемся считать биноминальные коэффициенты.

Пример. На пруду плавают 5 уток. Сколькими способами можно выбрать 2 из них, чтобы покормить?

Очевидно, порядок кормления уток неважен. Покормить сначала утку №1, а затем №2 — это то же самое, что покормить сначала утку №2, затем №1. Результат один и тот же: накормлены лишь эти две утки, а остальные три — нет. Поэтому считаем $C_{5}^{2}$:

[begin{align} C_{5}^{2} & =frac{5!}{2!cdot 3!} \ & =frac{5cdot 4cdot 3cdot 2cdot 1}{2cdot 1cdot 3cdot 2cdot 1}= \ & =10 end{align}]

Вот и всё. Однако при больших $n$ и $k$ посчитать число сочетаний напрямую становится затруднительно. Тут на помощь приходит сокращение дробей.

Пример. На пруду 150 уток. Сколькими способами можно выбрать 2 из них, чтобы покормить?

Порядок вновь неважен, просто уток стало больше. Поэтому считаем $C_{150}^{2}$:

[begin{align} C_{150}^{2} & =frac{150!}{2!cdot 148!}= \ & =frac{150cdot 149cdot 148cdot …cdot 1}{2cdot 1cdot 148cdot …cdot 1}= \ & =frac{150cdot 149}{2cdot 1}= \ & =11175 end{align}]

Видим, что факториалы образуют «длинные хвосты» в числителе и знаменателе, которые легко сокращаются. Однако для корректной работы с биномом Ньютона нам потребуется расширить определение факториала.

4.1. Новое определение факториала

Стандартное определение мы уже привели выше:

[n!=1cdot 2cdot 3cdot …cdot n,quad nin mathbb{N}]

Но как посчитать, например, факториал нуля? И как сокращать «длинные хвосты», не расписывая факториалы? Здесь нам поможет более грамотное определение.

Определение. Пусть $nin mathbb{N}bigcup left{ 0 right}$ — целое неотрицательное число. Тогда факториал считается по формуле:

[n!=left{ begin{align} & 1,quad n=0 \ & ncdot left( n-1 right)!,quad n gt 0 \ end{align} right.]

В частности, $0!=1$ по определению.

Простейшие коэффициенты:

[begin{align} C_{n}^{0} & =frac{n!}{0!left( n-0 right)!}=frac{n!}{1cdot n!}=1; \ C_{n}^{1} & =frac{n!}{1!left( n-1 right)!}=frac{ncdot left( n-1 right)!}{1cdot left( n-1 right)!}=n; \ end{align}]

А вот ещё парочка весёлых примеров:

[begin{align} C_{7}^{3} & =frac{7cdot 6cdot 5cdot 4cdot ldots cdot 1}{3cdot 2cdot 1cdot 4cdot ldots cdot 1}=35 \ C_{8}^{2} & =frac{8cdot 7cdot 6cdot ldots cdot 1}{2cdot 1cdot 6cdot ldots cdot 1}=28 \ C_{64}^{3} & =frac{64cdot 63cdot 62cdot 61cdot ldots cdot 1}{3cdot 2cdot 1cdot 61cdot ldots cdot 1}= \ & =41664 end{align}]

5. Треугольник Паскаля

Посчитаем бином Ньютона для $n=0$, $n=1$, $n=2$, $n=3$:

[begin{align} & {{left( a+b right)}^{0}}=1 \ & {{left( a+b right)}^{1}}=1cdot a+1cdot b \ & {{left( a+b right)}^{2}}=1cdot {{a}^{2}}+2cdot ab+1cdot {{b}^{2}} \ & {{left( a+b right)}^{3}}=1cdot {{a}^{3}}+3cdot {{a}^{2}}b+3cdot a{{b}^{2}}+1cdot {{b}^{3}} \ end{align}]

Составим таблицу:

[begin{matrix} 1 \ 1quad 1 \ 1quad 2quad 1 \ 1quad 3quad 3quad 1 \ 1quad 4quad 6quad 4quad 1 \ end{matrix}]

Получили треугольник, который в народе называют «Треугольник Паскаля»: по бокам единицы, а внутри каждое число равно сумме двух ближайших, стоящих этажом выше:

[begin{align} & 3=1+2 \ & 4=1+3 \ & 6=3+3 \ end{align}]

И это не случайность. Перед нами важнейшее свойство биноминальных коэффициентов, которое мы оформим в виде теоремы и докажем.

Теорема. Биноминальные коэффициенты вычисляются по формуле

[C_{n}^{k}+C_{n}^{k+1}=C_{n+1}^{k+1}]

Доказывается напролом.

Распишем доказательство детально:

[C_{n}^{k}+C_{n}^{k+1}=frac{n!}{k!left( n-k right)!}+frac{n!}{left( k+1 right)!left( n-k-1 right)!}]

[begin{align} & C_{n}^{k}+C_{n}^{k+1}= \ = & frac{n!}{k!left( n-k right)!}+frac{n!}{left( k+1 right)!left( n-k-1 right)!} \ end{align}]

Заметим, что по определению факториала

[begin{align} & left( k+1 right)!=left( k+1 right)cdot k! \ & left( n-k right)!=left( n-k right)cdot left( n-k-1 right)! end{align}]

Поэтому знаменатели биноминальных коэффициентов можно переписать:

[C_{n}^{k}+C_{n}^{k+1}=frac{n!}{k!left( n-k right)left( n-k-1 right)!}+frac{n!}{left( k+1 right)k!left( n-k-1 right)!}]

[begin{align} C_{n}^{k}+C_{n}^{k+1} & =frac{n!}{k!left( n-k right)left( n-k-1 right)!}+ \ & +frac{n!}{left( k+1 right)k!left( n-k-1 right)!} end{align}]

Приведём к общему знаменателю:

[begin{align} C_{n}^{k}+C_{n}^{k+1} & =frac{left( k+1 right)cdot n!}{left( k+1 right)!left( n-k right)!}+frac{left( n-k right)cdot n!}{left( k+1 right)!left( n-k right)!}= \ & =frac{left( k+1+n-k right)cdot n!}{left( k+1 right)!left( n-k right)!}= \ & =frac{left( n+1 right)cdot n!}{left( k+1 right)!left( n-k right)!} end{align}]

[begin{align} & C_{n}^{k}+C_{n}^{k+1}= \ = & frac{left( k+1 right)cdot n!}{left( k+1 right)!left( n-k right)!}+frac{left( n-k right)cdot n!}{left( k+1 right)!left( n-k right)!}= \ = & frac{left( k+1+n-k right)cdot n!}{left( k+1 right)!left( n-k right)!}=frac{left( n+1 right)cdot n!}{left( k+1 right)!left( n-k right)!} \ end{align}]

Окончательно получим:

[begin{align} C_{n}^{k}+C_{n}^{k+1} & =frac{left( n+1 right)!}{left( k+1 right)!left( n-k right)!}= \ & =frac{left( n+1 right)!}{left( k+1 right)!left( n+1-left( k+1 right) right)!}= \ & = C_{n+1}^{k+1} end{align}]

Теорема доказана. Теперь мы знаем, как формируется треугольник Паскаля. Осталось доказать сам Бином Ньютона.

6. Доказательство Бинома Ньютона

Итак, нужно доказать, что

[{{left( a+b right)}^{n}}=sumlimits_{k=0}^{n}{C_{n}^{k}cdot {{a}^{n-k}}{{b}^{k}}}]

где $C_{n}^{k}$ — биноминальные коэффициенты с теми чудесными свойствами, которые мы рассмотрели и доказали выше.

Будем доказывать по индукции.

6.1. База индукции

Рассмотрим $n=1$. Формула Бинома Ньютона для него:

[begin{align} {{left( a+b right)}^{1}} & =sumlimits_{k=0}^{1}{C_{1}^{k}{{a}^{1-k}}{{b}^{k}}}= \ & =C_{1}^{0}{{a}^{1}}{{b}^{0}}+C_{1}^{1}{{a}^{0}}{{b}^{1}}= \ & =a+bend{align}]

Очевидно, для $n=1$ формула верна. Переходим к индуктивному предположению.

6.2. Индуктивное предположение

Пусть Бином Ньютона верен для некоторого $n=t$:

[{{left( a+b right)}^{t}}=sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}]

Используя этот факт, докажем верность и для $n=t+1$, т.е. выполним индуктивный переход.

6.3. Индуктивный переход

Докажем, что бином Ньютона верен для $n=t+1$:

[{{left( a+b right)}^{t+1}}=sumlimits_{k=0}^{t+1}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}]

Для этого сначала заметим, что

[{{left( a+b right)}^{t+1}}={{left( a+b right)}^{t}}cdot left( a+b right)]

Однако согласно индуктивному предположению, ${{left( a+b right)}^{t}}$ допускает разложение по Биному Ньютона, поэтому

[begin{align} left( a+b right)cdot {{left( a+b right)}^{t}} & =left( a+b right)cdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}= \ & =acdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}+bcdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}= \ & =sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}} end{align}]

[begin{align} & left( a+b right)cdot {{left( a+b right)}^{t}}= \ = & left( a+b right)cdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}= \ = & acdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}+bcdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}= \ = & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}} \ end{align}]

Запишем отдельно первое слагаемое первой суммы и учтём, что $C_{t}^{0}=C_{t+1}^{0}=1$:

[begin{align} sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} & = C_{t}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} \ & = C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} end{align}]

[begin{align} & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}= \ = & C_{t}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} \ = & C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} \ end{align}]

И последнее слагаемое последней второй суммы и учтём, что $C_{t}^{t}=C_{t+1}^{t+1}=1$:

[begin{align} sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}} & =sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t}^{t}cdot {{b}^{t+1}} \ & =sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} end{align}]

[begin{align} & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}= \ = & sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t}^{t}cdot {{b}^{t+1}} \ = & sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]

Сейчас будет самая нетривиальная операция. Меняем индекс суммирования в последней сумме: выполняем подстановку $k=m-1$. При этом меняются и пределы суммирования:

[left[ begin{align} k & =m-1 \ k & =0Rightarrow m=1 \ k & =t-1Rightarrow m=t \ k+1 & =m \ t-k & =t+1-m \ end{align} right]]

В итоге последняя сумма перепишется так:

[sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}=sumlimits_{m=1}^{t}{C_{t}^{m-1}cdot {{a}^{t+1-m}}{{b}^{m}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}]

[begin{align} & sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}= \ = & sumlimits_{m=1}^{t}{C_{t}^{m-1}cdot {{a}^{t+1-m}}{{b}^{m}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]

Объединяем суммы вместе:

[begin{align} & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}= \ = & C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{m=1}^{t}{C_{t}^{m-1}cdot {{a}^{t+1-m}}{{b}^{m}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]

[begin{align} & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}= \ = & C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+ \ + & sumlimits_{m=1}^{t}{C_{t}^{m-1}cdot {{a}^{t+1-m}}{{b}^{m}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]

Заметим, что два знака суммы различаются лишь названием индекса и биноминальными коэффициентами. Всё остальное — диапазоны суммирования, степени буквы $a$ и буквы $b$ — всё идеально совпадает и никак не меняется, если написать вместо $k$ индекс $m$ или наоборот.

Такие суммы можно записать под единым знаком:

[C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{left( C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}+C_{t}^{k-1}cdot {{a}^{t+1-k}}{{b}^{k}} right)}+C_{t+1}^{t+1}cdot {{b}^{t+1}}]

[begin{align} & C_{t+1}^{0}cdot {{a}^{t+1}}+ \ + & sumlimits_{k=1}^{t}{left( C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}+C_{t}^{k-1}cdot {{a}^{t+1-k}}{{b}^{k}} right)}+ \ + & C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]

Выражение под знаком суммы легко раскладывается на множители:

[begin{align} C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}+C_{t}^{k-1}cdot {{a}^{t+1-k}}{{b}^{k}} & =left( C_{t}^{k}+C_{t}^{k-1} right)cdot {{a}^{t+1-k}}{{b}^{k}}= \ & =C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}} end{align}]

[begin{align} & C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}+C_{t}^{k-1}cdot {{a}^{t+1-k}}{{b}^{k}}= \ = & left( C_{t}^{k}+C_{t}^{k-1} right)cdot {{a}^{t+1-k}}{{b}^{k}}= \ = & C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}} \ end{align}]

Здесь в последнем шаге мы использовали свойство биноминальных коэффициентов, доказанное выше:

[C_{n}^{k}+C_{n}^{k+1}=C_{n+1}^{k+1}]

Или, что то же самое

[C_{n}^{k-1}+C_{n}^{k}=C_{n+1}^{k}]

Таким образом, всю сумму можно переписать более компактно, а затем внести под знак суммы первое и последнее слагаемое:

[ C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}=sumlimits_{k=0}^{t+1}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}]

[begin{align} C_{t+1}^{0}cdot {{a}^{t+1}} & +sumlimits_{k=1}^{t}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}= \ & =sumlimits_{k=0}^{t+1}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} \ end{align}]

Сопоставляя исходное выражение и конечное, получим

[{{left( a+b right)}^{t+1}}=sumlimits_{k=0}^{t+1}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}]

Именно это и требовалось доказать. Следовательно, исходная формула Бинома Ньютона верна.

Смотрите также:

1. Схема Горнера
2. Теорема Безу и корни многочленов
3. Знаки тригонометрических функций
4. Уравнение касательной к графику функции
5. Как представить обычную дробь в виде десятичной
6. Сложные задачи B2 на проценты: вычисление полной стоимости

In mathematics, Pascal’s triangle is a triangular array of the binomial coefficients that arises in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Blaise Pascal, although other mathematicians studied it centuries before him in Persia,^[1] India,^[2] China, Germany, and Italy.^[3]

The rows of Pascal’s triangle are conventionally enumerated starting with row at the top (the 0th row). The entries in each row are numbered from the left beginning with and are usually staggered relative to the numbers in the adjacent rows. The triangle may be constructed in the following manner: In row 0 (the topmost row), there is a unique nonzero entry 1. Each entry of each subsequent row is constructed by adding the number above and to the left with the number above and to the right, treating blank entries as 0. For example, the initial number of row 1 (or any other row) is 1 (the sum of 0 and 1), whereas the numbers 1 and 3 in row 3 are added to produce the number 4 in row 4.

Formula[edit]

The entry in the th row and th column of Pascal’s triangle is denoted . For example, the unique nonzero entry in the topmost row is . With this notation, the construction of the previous paragraph may be written as follows:

,

for any non-negative integer and any integer .^[4] This recurrence for the binomial coefficients is known as Pascal’s rule.

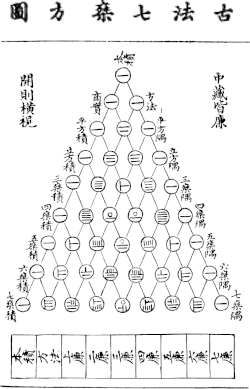
History[edit]

The pattern of numbers that forms Pascal’s triangle was known well before Pascal’s time. The Persian mathematician Al-Karaji (953–1029) wrote a now-lost book which contained the first formulation of the binomial coefficients and the first description of Pascal’s triangle.^[5][6][7] It was later repeated by Omar Khayyám (1048–1131), another Persian mathematician; thus the triangle is also referred to as the Khayyam triangle (مثلث خیام) in Iran.^[8] Several theorems related to the triangle were known, including the binomial theorem. Khayyam used a method of finding nth roots based on the binomial expansion, and therefore on the binomial coefficients.^[1]

Pascal’s triangle was known in China during the early 11th century as a result of the work of the Chinese mathematician Jia Xian (1010–1070). During the 13th century, Yang Hui (1238–1298) presented the triangle and hence it is still known as Yang Hui’s triangle (杨辉三角; 楊輝三角) in China.^[9]

In Europe, Pascal’s triangle appeared for the first time in the Arithmetic of Jordanus de Nemore (13th century).^[10]
The binomial coefficients were calculated by Gersonides during the early 14th century, using the multiplicative formula for them.^[11] Petrus Apianus (1495–1552) published the full triangle on the frontispiece of his book on business calculations in 1527.^[12] Michael Stifel published a portion of the triangle (from the second to the middle column in each row) in 1544, describing it as a table of figurate numbers.^[11] In Italy, Pascal’s triangle is referred to as Tartaglia’s triangle, named for the Italian algebraist Niccolò Fontana Tartaglia (1500–1577), who published six rows of the triangle in 1556.^[11] Gerolamo Cardano, also, published the triangle as well as the additive and multiplicative rules for constructing it in 1570.^[11]

Pascal’s Traité du triangle arithmétique (Treatise on Arithmetical Triangle) was published posthumously in 1665.^[13] In this, Pascal collected several results then known about the triangle, and employed them to solve problems in probability theory. The triangle was later named for Pascal by Pierre Raymond de Montmort (1708) who called it “Table de M. Pascal pour les combinaisons” (French: Table of Mr. Pascal for combinations) and Abraham de Moivre (1730) who called it “Triangulum Arithmeticum PASCALIANUM” (Latin: Pascal’s Arithmetic Triangle), which became the basis of the modern Western name.^[14]

Binomial expansions[edit]

Pascal’s triangle determines the coefficients which arise in binomial expansions. For example, consider the expansion

.

The coefficients are the numbers in the second row of Pascal’s triangle: , , .

In general, when a binomial like is raised to a positive integer power of , we have:

,

where the coefficients in this expansion are precisely the numbers on row of Pascal’s triangle. In other words,

.

This is the binomial theorem.

The entire right diagonal of Pascal’s triangle corresponds to the coefficient of in these binomial expansions, while the next diagonal corresponds to the coefficient of and so on.

To see how the binomial theorem relates to the simple construction of Pascal’s triangle, consider the problem of calculating the coefficients of the expansion of in terms of the corresponding coefficients of (setting for simplicity). Suppose then that

.

Now

The two summations can be reorganized as follows:

(because of how raising a polynomial to a power works, ).

We now have an expression for the polynomial in terms of the coefficients of (these are the s), which is what we need if we want to express a line in terms of the line above it. Recall that all the terms in a diagonal going from the upper-left to the lower-right correspond to the same power of , and that the -terms are the coefficients of the polynomial , and we are determining the coefficients of . Now, for any given , the coefficient of the term in the polynomial is equal to . This is indeed the simple rule for constructing Pascal’s triangle row-by-row.

It is not difficult to turn this argument into a proof (by mathematical induction) of the binomial theorem.

Since , the coefficients are identical in the expansion of the general case.

An interesting consequence of the binomial theorem is obtained by setting both variables and equal to one. In this case, we know that , and so

In other words, the sum of the entries in the th row of Pascal’s triangle is the th power of 2. This is equivalent to the statement that the number of subsets (the cardinality of the power set) of an -element set is , as can be seen by observing that the number of subsets is the sum of the number of combinations of each of the possible lengths, which range from zero through to .

Combinations[edit]

A second useful application of Pascal’s triangle is in the calculation of combinations. For example, the number of combinations of items taken at a time (pronounced n choose k) can be found by the equation

.

But this is also the formula for a cell of Pascal’s triangle. Rather than performing the calculation, one can simply look up the appropriate entry in the triangle. Provided we have the first row and the first entry in a row numbered 0, the answer will be located at entry in row . For example, suppose 8 jobs need to be filled but there are 10 candidates; the selection committee wants to know how many ways there are of selecting 8 from the 10. The answer is entry 8 in row 10, which is 45; that is, 10 choose 8 is 45.

Relation to binomial distribution and convolutions[edit]

When divided by , the th row of Pascal’s triangle becomes the binomial distribution in the symmetric case where . By the central limit theorem, this distribution approaches the normal distribution as increases. This can also be seen by applying Stirling’s formula to the factorials involved in the formula for combinations.

This is related to the operation of discrete convolution in two ways. First, polynomial multiplication corresponds exactly to discrete convolution, so that repeatedly convolving the sequence with itself corresponds to taking powers of , and hence to generating the rows of the triangle. Second, repeatedly convolving the distribution function for a random variable with itself corresponds to calculating the distribution function for a sum of n independent copies of that variable; this is exactly the situation to which the central limit theorem applies, and hence results in the normal distribution in the limit.

Patterns and properties[edit]

Pascal’s triangle has many properties and contains many patterns of numbers.

Rows[edit]

• The sum of the elements of a single row is twice the sum of the row preceding it. For example, row 0 (the topmost row) has a value of 1, row 1 has a value of 2, row 2 has a value of 4, and so forth. This is because every item in a row produces two items in the next row: one left and one right. The sum of the elements of row  equals to .
• Taking the product of the elements in each row, the sequence of products (sequence A001142 in the OEIS) is related to the base of the natural logarithm, e.^[15][16] Specifically, define the sequence for all as follows: Then, the ratio of successive row products is

  

  and the ratio of these ratios is

  

  The right-hand side of the above equation takes the form of the limit definition of

  

  .

• can be found in Pascal’s triangle by use of the Nilakantha infinite series.^[17]

  

• The value of a row, if each entry is considered a decimal place (and numbers larger than 9 carried over accordingly), is a power of 11 ( 11ⁿ, for row n). Thus, in row 2, ⟨1, 2, 1⟩ becomes 11², while ⟨1, 5, 10, 10, 5, 1⟩ in row five becomes (after carrying) 161,051, which is 11⁵. This property is explained by setting x = 10 in the binomial expansion of (x + 1)ⁿ, and adjusting values to the decimal system. But the variable term can be chosen to allow rows to represent values in any base x (more generally, if y = x + 1 for y < 0, then the corresponding base is x mod 2y = {y – 1, -(y + 1)}, with odd values of n yielding negative row values).
  • In base 3: 1 2 1₃ = 4² (16)
  • ⟨1, 3, 3, 1⟩ → 2 1 0 1₃ = 4³ (64)
  • In base 9: 1 2 1₉ = 10² (100)
  •               1 3 3 1₉ = 10³ (1000)
  • ⟨1, 5, 10, 10, 5, 1⟩ → 1 6 2 1 5 1₉ = 10⁵ (100000)

  In particular (see previous property), for x = 1 place value remains constant (1^place=1). Thus entries can simply be added in interpreting the value of a row.

• Some of the numbers in Pascal’s triangle correlate to numbers in Lozanić’s triangle.
• The sum of the squares of the elements of row n equals the middle element of row 2n. For example, 1² + 4² + 6² + 4² + 1² = 70. In general form:

  

• On any row n, where n is even, the middle term minus the term two spots to the left equals a Catalan number, specifically the (n/2 + 1)th Catalan number. For example: on row 4, 6 − 1 = 5, which is the 3rd Catalan number, and 4/2 + 1 = 3.
• In a row p where p is a prime number, all the terms in that row except the 1s are multiples of p. This can be proven easily, since if , then p has no factors save for 1 and itself. Every entry in the triangle is an integer, so therefore by definition and are factors of . However, there is no possible way p itself can show up in the denominator, so therefore p (or some multiple of it) must be left in the numerator, making the entire entry a multiple of p.
• Parity: To count odd terms in row n, convert n to binary. Let x be the number of 1s in the binary representation. Then the number of odd terms will be 2^x. These numbers are the values in Gould’s sequence.^[18]
• Every entry in row 2ⁿ−1, n ≥ 0, is odd.^[19]
• Polarity: When the elements of a row of Pascal’s triangle are added and subtracted together sequentially, every row with a middle number, meaning rows that have an odd number of integers, gives 0 as the result. As examples, row 4 is 1 4 6 4 1, so the formula would be 6 – (4+4) + (1+1) = 0; and row 6 is 1 6 15 20 15 6 1, so the formula would be 20 – (15+15) + (6+6) – (1+1) = 0. So every even row of the Pascal triangle equals 0 when you take the middle number, then subtract the integers directly next to the center, then add the next integers, then subtract, so on and so forth until you reach the end of the row.

Diagonals[edit]

The diagonals of Pascal’s triangle contain the figurate numbers of simplices:

• The diagonals going along the left and right edges contain only 1’s.
• The diagonals next to the edge diagonals contain the natural numbers in order. The 1-dimensional simplex numbers increment by 1 as the line segments extend to the next whole number along the number line.
• Moving inwards, the next pair of diagonals contain the triangular numbers in order.
• The next pair of diagonals contain the tetrahedral numbers in order, and the next pair give pentatope numbers.

The symmetry of the triangle implies that the n^th d-dimensional number is equal to the d^th n-dimensional number.

An alternative formula that does not involve recursion is

where n^(d) is the rising factorial.

The geometric meaning of a function P_d is: P_d(1) = 1 for all d. Construct a d-dimensional triangle (a 3-dimensional triangle is a tetrahedron) by placing additional dots below an initial dot, corresponding to P_d(1) = 1. Place these dots in a manner analogous to the placement of numbers in Pascal’s triangle. To find P_d(x), have a total of x dots composing the target shape. P_d(x) then equals the total number of dots in the shape. A 0-dimensional triangle is a point and a 1-dimensional triangle is simply a line, and therefore P₀(x) = 1 and P₁(x) = x, which is the sequence of natural numbers. The number of dots in each layer corresponds to P_d − 1(x).

Calculating a row or diagonal by itself[edit]

There are simple algorithms to compute all the elements in a row or diagonal without computing other elements or factorials.

To compute row with the elements , , …, , begin with . For each subsequent element, the value is determined by multiplying the previous value by a fraction with slowly changing numerator and denominator:

For example, to calculate row 5, the fractions are  ,  ,  ,  and , and hence the elements are  ,   ,   , etc. (The remaining elements are most easily obtained by symmetry.)

To compute the diagonal containing the elements , , , …, we again begin with and obtain subsequent elements by multiplication by certain fractions:

By symmetry, this same process can be used to compute the diagonal , , … .

For example, to calculate the diagonal beginning at , the fractions are  ,  ,  , …, and the elements are ,   ,   , etc. By symmetry, these elements are equal to , , , etc.

Overall patterns and properties[edit]

• The pattern obtained by coloring only the odd numbers in Pascal’s triangle closely resembles the fractal known as the Sierpinski triangle. This resemblance becomes increasingly accurate as more rows are considered; in the limit, as the number of rows approaches infinity, the resulting pattern is the Sierpinski triangle, assuming a fixed perimeter. More generally, numbers could be colored differently according to whether or not they are multiples of 3, 4, etc.; this results in other similar patterns.

• In a triangular portion of a grid (as in the images below), the number of shortest grid paths from a given node to the top node of the triangle is the corresponding entry in Pascal’s triangle. On a Plinko game board shaped like a triangle, this distribution should give the probabilities of winning the various prizes.

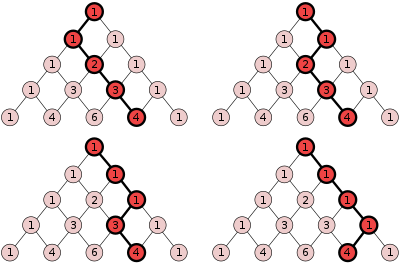
• If the rows of Pascal’s triangle are left-justified, the diagonal bands (colour-coded below) sum to the Fibonacci numbers.

1
1	1
1	2	1
1	3	3	1
1	4	6	4	1
1	5	10	10	5	1
1	6	15	20	15	6	1
1	7	21	35	35	21	7	1

Construction as matrix exponential[edit]

Due to its simple construction by factorials, a very basic representation of Pascal’s triangle in terms of the matrix exponential can be given: Pascal’s triangle is the exponential of the matrix which has the sequence 1, 2, 3, 4, … on its subdiagonal and zero everywhere else.

Relation to geometry of polytopes[edit]

Pascal’s triangle can be used as a lookup table for the number of elements (such as edges and corners) within a polytope (such as a triangle, a tetrahedron, a square, or a cube).

Number of elements of simplices[edit]

Let’s begin by considering the 3rd line of Pascal’s triangle, with values 1, 3, 3, 1. A 2-dimensional triangle has one 2-dimensional element (itself), three 1-dimensional elements (lines, or edges), and three 0-dimensional elements (vertices, or corners). The meaning of the final number (1) is more difficult to explain (but see below). Continuing with our example, a tetrahedron has one 3-dimensional element (itself), four 2-dimensional elements (faces), six 1-dimensional elements (edges), and four 0-dimensional elements (vertices). Adding the final 1 again, these values correspond to the 4th row of the triangle (1, 4, 6, 4, 1). Line 1 corresponds to a point, and Line 2 corresponds to a line segment (dyad). This pattern continues to arbitrarily high-dimensioned hyper-tetrahedrons (known as simplices).

To understand why this pattern exists, one must first understand that the process of building an n-simplex from an (n − 1)-simplex consists of simply adding a new vertex to the latter, positioned such that this new vertex lies outside of the space of the original simplex, and connecting it to all original vertices. As an example, consider the case of building a tetrahedron from a triangle, the latter of whose elements are enumerated by row 3 of Pascal’s triangle: 1 face, 3 edges, and 3 vertices. To build a tetrahedron from a triangle, we position a new vertex above the plane of the triangle and connect this vertex to all three vertices of the original triangle.

The number of a given dimensional element in the tetrahedron is now the sum of two numbers: first the number of that element found in the original triangle, plus the number of new elements, each of which is built upon elements of one fewer dimension from the original triangle. Thus, in the tetrahedron, the number of cells (polyhedral elements) is 0 + 1 = 1; the number of faces is 1 + 3 = 4; the number of edges is 3 + 3 = 6; the number of new vertices is 3 + 1 = 4. This process of summing the number of elements of a given dimension to those of one fewer dimension to arrive at the number of the former found in the next higher simplex is equivalent to the process of summing two adjacent numbers in a row of Pascal’s triangle to yield the number below. Thus, the meaning of the final number (1) in a row of Pascal’s triangle becomes understood as representing the new vertex that is to be added to the simplex represented by that row to yield the next higher simplex represented by the next row. This new vertex is joined to every element in the original simplex to yield a new element of one higher dimension in the new simplex, and this is the origin of the pattern found to be identical to that seen in Pascal’s triangle.

Number of elements of hypercubes[edit]

A similar pattern is observed relating to squares, as opposed to triangles. To find the pattern, one must construct an analog to Pascal’s triangle, whose entries are the coefficients of (x + 2)^{Row Number}, instead of (x + 1)^{Row Number}. There are a couple ways to do this. The simpler is to begin with Row 0 = 1 and Row 1 = 1, 2. Proceed to construct the analog triangles according to the following rule:

That is, choose a pair of numbers according to the rules of Pascal’s triangle, but double the one on the left before adding. This results in:

The other way of producing this triangle is to start with Pascal’s triangle and multiply each entry by 2^k, where k is the position in the row of the given number. For example, the 2nd value in row 4 of Pascal’s triangle is 6 (the slope of 1s corresponds to the zeroth entry in each row). To get the value that resides in the corresponding position in the analog triangle, multiply 6 by 2^{Position Number} = 6 × 2² = 6 × 4 = 24. Now that the analog triangle has been constructed, the number of elements of any dimension that compose an arbitrarily dimensioned cube (called a hypercube) can be read from the table in a way analogous to Pascal’s triangle. For example, the number of 2-dimensional elements in a 2-dimensional cube (a square) is one, the number of 1-dimensional elements (sides, or lines) is 4, and the number of 0-dimensional elements (points, or vertices) is 4. This matches the 2nd row of the table (1, 4, 4). A cube has 1 cube, 6 faces, 12 edges, and 8 vertices, which corresponds to the next line of the analog triangle (1, 6, 12, 8). This pattern continues indefinitely.

To understand why this pattern exists, first recognize that the construction of an n-cube from an (n − 1)-cube is done by simply duplicating the original figure and displacing it some distance (for a regular n-cube, the edge length) orthogonal to the space of the original figure, then connecting each vertex of the new figure to its corresponding vertex of the original. This initial duplication process is the reason why, to enumerate the dimensional elements of an n-cube, one must double the first of a pair of numbers in a row of this analog of Pascal’s triangle before summing to yield the number below. The initial doubling thus yields the number of “original” elements to be found in the next higher n-cube and, as before, new elements are built upon those of one fewer dimension (edges upon vertices, faces upon edges, etc.). Again, the last number of a row represents the number of new vertices to be added to generate the next higher n-cube.

In this triangle, the sum of the elements of row m is equal to 3^m. Again, to use the elements of row 4 as an example: 1 + 8 + 24 + 32 + 16 = 81, which is equal to .

Counting vertices in a cube by distance[edit]

Each row of Pascal’s triangle gives the number of vertices at each distance from a fixed vertex in an n-dimensional cube. For example, in three dimensions, the third row (1 3 3 1) corresponds to the usual three-dimensional cube: fixing a vertex V, there is one vertex at distance 0 from V (that is, V itself), three vertices at distance 1, three vertices at distance √2 and one vertex at distance √3 (the vertex opposite V). The second row corresponds to a square, while larger-numbered rows correspond to hypercubes in each dimension.

Fourier transform of sin(x)ⁿ⁺¹/x[edit]

As stated previously, the coefficients of (x + 1)ⁿ are the nth row of the triangle. Now the coefficients of (x − 1)ⁿ are the same, except that the sign alternates from +1 to −1 and back again. After suitable normalization, the same pattern of numbers occurs in the Fourier transform of sin(x)ⁿ⁺¹/x. More precisely: if n is even, take the real part of the transform, and if n is odd, take the imaginary part. Then the result is a step function, whose values (suitably normalized) are given by the nth row of the triangle with alternating signs.^[20] For example, the values of the step function that results from:

compose the 4th row of the triangle, with alternating signs. This is a generalization of the following basic result (often used in electrical engineering):

is the boxcar function.^[21] The corresponding row of the triangle is row 0, which consists of just the number 1.

If n is congruent to 2 or to 3 mod 4, then the signs start with −1. In fact, the sequence of the (normalized) first terms corresponds to the powers of i, which cycle around the intersection of the axes with the unit circle in the complex plane:

Extensions[edit]

To higher dimensions[edit]

Pascal’s triangle has higher dimensional generalizations. The three-dimensional version is known as Pascal’s pyramid or Pascal’s tetrahedron, while the general versions are known as Pascal’s simplices.

Negative-numbered rows[edit]

Pascal’s triangle can be extended to negative row numbers.

First write the triangle in the following form:

m n	0	1	2	3	4	5	…
0	1	0	0	0	0	0	…
1	1	1	0	0	0	0	…
2	1	2	1	0	0	0	…
3	1	3	3	1	0	0	…
4	1	4	6	4	1	0	…

Next, extend the column of 1s upwards:

m n	0	1	2	3	4	5	…
−4	1						…
−3	1						…
−2	1						…
−1	1						…
0	1	0	0	0	0	0	…
1	1	1	0	0	0	0	…
2	1	2	1	0	0	0	…
3	1	3	3	1	0	0	…
4	1	4	6	4	1	0	…

Now the rule:

can be rearranged to:

which allows calculation of the other entries for negative rows:

m n	0	1	2	3	4	5	…
−4	1	−4	10	−20	35	−56	…
−3	1	−3	6	−10	15	−21	…
−2	1	−2	3	−4	5	−6	…
−1	1	−1	1	−1	1	−1	…
0	1	0	0	0	0	0	…
1	1	1	0	0	0	0	…
2	1	2	1	0	0	0	…
3	1	3	3	1	0	0	…
4	1	4	6	4	1	0	…

This extension preserves the property that the values in the mth column viewed as a function of n are fit by an order m polynomial, namely

.

This extension also preserves the property that the values in the nth row correspond to the coefficients of (1 + x)ⁿ:

For example:

When viewed as a series, the rows of negative n diverge. However, they are still Abel summable, which summation gives the standard values of 2ⁿ. (In fact, the n = -1 row results in Grandi’s series which “sums” to 1/2, and the n = -2 row results in another well-known series which has an Abel sum of 1/4.)

Another option for extending Pascal’s triangle to negative rows comes from extending the other line of 1s:

m n	−4	−3	−2	−1	0	1	2	3	4	5	…
−4	1	0	0	0	0	0	0	0	0	0	…
−3		1	0	0	0	0	0	0	0	0	…
−2			1	0	0	0	0	0	0	0	…
−1				1	0	0	0	0	0	0	…
0	0	0	0	0	1	0	0	0	0	0	…
1	0	0	0	0	1	1	0	0	0	0	…
2	0	0	0	0	1	2	1	0	0	0	…
3	0	0	0	0	1	3	3	1	0	0	…
4	0	0	0	0	1	4	6	4	1	0	…

Applying the same rule as before leads to

m n	−4	−3	−2	−1	0	1	2	3	4	5	…
−4	1	0	0	0	0	0	0	0	0	0	…
−3	−3	1	0	0	0	0	0	0	0	0	…
−2	3	−2	1	0	0	0	0	0	0	0	…
−1	−1	1	−1	1	0	0	0	0	0	0	..
0	0	0	0	0	1	0	0	0	0	0	…
1	0	0	0	0	1	1	0	0	0	0	…
2	0	0	0	0	1	2	1	0	0	0	…
3	0	0	0	0	1	3	3	1	0	0	…
4	0	0	0	0	1	4	6	4	1	0	…

This extension also has the properties that just as

we have

Also, just as summing along the lower-left to upper-right diagonals of the Pascal matrix yields the Fibonacci numbers, this second type of extension still sums to the Fibonacci numbers for negative index.

Either of these extensions can be reached if we define

and take certain limits of the gamma function, .

See also[edit]

References[edit]

External links[edit]

• “Pascal triangle”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Weisstein, Eric W. “Pascal’s triangle”. MathWorld.
• The Old Method Chart of the Seven Multiplying Squares (from the Ssu Yuan Yü Chien of Chu Shi-Chieh, 1303, depicting the first nine rows of Pascal’s triangle)
• Pascal’s Treatise on the Arithmetic Triangle (page images of Pascal’s treatise, 1654; summary)

Треугольник Паскаля – формула, свойства и применение

Основная формула

Строки треугольника обычно нумеруются, начиная со строки n = 0 в верхней части. Записи в каждой строке целочисленные и нумеруются слева, начиная с k = 0, обычно располагаются в шахматном порядке относительно чисел в соседних строчках. Построить фигуру можно следующим образом:

• В центре верхней части листа ставится цифра “1”.
• В следующем ряду — две единицы слева и справа от центра (получается треугольная форма).
• В каждой последующей строке ряд будет начинаться и заканчиваться числом “1”. Внутренние члены вычисляются путём суммирования двух цифр над ним.

Запись в n строке и k столбце паскалевской фигуры обозначается (n k). Например, уникальная ненулевая запись в самой верхней строке (0 0) = 1. С помощью этого конструкция предыдущего абзаца может быть записана следующим образом, образуя формулу треугольника Паскаля (n k) = (n – 1 k-1) + (n – 1 k), для любого неотрицательного целого числа n и любого целого числа k от 0 до n включительно. Трёхмерная версия называется пирамидой или тетраэдром, а общие — симплексами.

История открытия

Паскаль ввёл в действие многие ранее недостаточно проверенные способы использования чисел треугольника, и он подробно описал их в, пожалуй, самом раннем из известных математических трактатов, специально посвящённых этому вопросу, в труде об арифметике Traité du triangle (1665). За столетия до того обсуждение чисел возникло в контексте индийских исследований комбинаторики и биномиальных чисел, а у греков были работы по «фигурным числам».

Из более поздних источников видно, что биномиальные коэффициенты и аддитивная формула для их генерации были известны ещё до II века до нашей эры по работам Пингала. К сожалению, бо́льшая часть трудов была утеряна. Варахамихира около 505 года дал чёткое описание аддитивной формулы, а более подробное объяснение того же правила было дано Халаюдхой (около 975 года). Он также объяснил неясные ссылки на Меру-прастаара, лестницы у горы Меру, дав первое сохранившееся определение расположению этих чисел, представленных в виде треугольника.

Примерно в 850 году джайнский математик Махавира вывел другую формулу для биномиальных коэффициентов, используя умножение, эквивалентное современной формуле. В 1068 году Бхаттотпала во время своей исследовательской деятельности вычислил четыре столбца первых шестнадцати строк. Он был первым признанным математиком, который уравнял аддитивные и мультипликативные формулы для этих чисел.

Примерно в то же время персидский учёный Аль-Караджи (953–1029) написал книгу (на данный момент утраченную), в которой содержалось первое описание треугольника Паскаля. Позднее работа была переписана персидским поэтом, астрономом и математиком Омаром Хайямом (1048–1131). Таким образом, в Иране фигура упоминается как треугольник Хайяма.

Известно несколько теорем, связанных с этой темой, включая биномы. Хайям использовал метод нахождения n-x корней, основанный на биномиальном разложении и, следовательно, на одноимённых коэффициентах. Треугольник был известен в Китае в начале XI века благодаря работе китайского математика Цзя Сианя (1010–1070). В XIII веке Ян Хуэй (1238–1298) представил этот способ, и поэтому в Китае он до сих пор называется треугольником Ян Хуэя.

На западе биномиальные коэффициенты были рассчитаны Жерсонидом в начале XIV века, он использовал мультипликативную формулу. Петрус Апиан (1495–1552) опубликовал полный треугольник на обложке своей книги примерно в 1527 году. Это была первая печатная версия фигуры в Европе. Майкл Стифель представил эту тему как таблицу фигурных тел в 1544 году.

В Италии паскалевский треугольник зовут другим именем, в честь итальянского алгебраиста Никколо Фонтана Тарталья (1500–1577). Вообще, современное имя фигура приобрела благодаря Пьеру Раймонду до Монтрмору (1708), который назвал треугольник «Таблица Паскаля для сочетаний» (дословно: Таблица мистера Паскаля для комбинаций) и Абрахамом Муавром (1730).

Отличительные черты

Треугольник Паскаля и его свойства — тема довольно обширная. Главное, в нём содержится множество моделей чисел. Обзор следует начать с простого — ряды:

• Сумма элементов одной строки в два раза больше суммы строки, предшествующей ей. Например, строка 0 (самая верхняя) имеет значение 1, строчка 1–2, а 2 имеет значение 4 и т. д. Это потому что каждый элемент в строке производит два элемента в следующем ряду: один слева и один справа. Сумма элементов строки n равна 2 n .
• Принимая произведение элементов в каждой строке, последовательность продуктов можно связать с основанием натурального логарифма.
• В треугольнике Паскаля через бесконечный ряд Нилаканты можно найти число Пи.
• Значение строки, если каждая запись считается десятичным знаком (имеется в виду, что числа больше 9 переносятся соответственно), является степенью 11 (11 n для строки n). Таким образом, в строке 2 ⟨1, 2, 1⟩ становится 11 2 , равно как ⟨1, 5, 10, 10, 5, 1⟩ в строке пять становится (после переноса) 161, 051, что составляет 11 5 . Это свойство объясняется установкой x = 10 в биномиальном разложении (x + 1) n и корректировкой значений в десятичной системе.
• Некоторые числа в треугольнике Паскаля соотносятся с числами в треугольнике Лозанича.
• Сумма квадратов элементов строки n равна среднему элементу строки 2 n. Например, 1 2 + 4 2 + 6 2 + 4 2 + 1 2 = 70.
• В любой строчке n, где n является чётным, средний член за вычетом члена в двух точках слева равен каталонскому числу (n / 2 + 1).
• В строчке р, где р представляет собой простое число, все члены в этой строке, за исключением 1s, являются кратными р.
• Чётность. Для измерения нечётных терминов в строке n необходимо преобразовать n в двоичную форму. Пусть x будет числом 1s в двоичном представлении. Тогда количество нечётных членов будет 2 х . Эти числа являются значениями в последовательности Гулда.
• Каждая запись в строке 2 n -1, n ≥ 0, является нечётной.
• Полярность. Когда элементы строки треугольника Паскаля складываются и вычитаются вместе последовательно, каждая строка со средним числом, означающим строки с нечётным числом целых чисел, даёт 0 в качестве результата.

Диагонали треугольника содержат фигурные числа симплексов. Например:

• Идущие вдоль левого и правого краёв диагонали содержат только 1.
• Рядом с рёбрами диагонали содержат натуральные числа по порядку.
• Двигаясь внутрь, следующая пара содержит треугольные числа по порядку.
• Следующая пара — тетраэдрические, а следующая пара — числа пятиугольника.

Существуют простые алгоритмы для вычисления всех элементов в строке или диагонали без вычисления других элементов или факториалов.

Общие свойства

Образец, полученный путём раскраски только нечётных чисел, очень похож на фрактал, называемый треугольником Серпинского. Это сходство становится всё более точным, так как рассматривается больше строк в пределе, когда число рядов приближается к бесконечности, получающийся в результате шаблон представляет собой фигуру, предполагающую фиксированный периметр. В целом числа могут быть окрашены по-разному в зависимости от того, являются ли они кратными 3, 4 и т. д.

В треугольной части сетки количество кратчайших путей от заданного до верхнего угла треугольника является соответствующей записью в паскалевском треугольнике. На треугольной игровой доске Плинко это распределение должно давать вероятности выигрыша различных призов. Если строки треугольника выровнены по левому краю, диагональные полосы суммируются с числами Фибоначчи.

Благодаря простому построению факториалами можно дать очень простое представление фигуры Паскаля в терминах экспоненциальной матрицы: треугольник — это экспонента матрицы, которая имеет последовательность 1, 2, 3, 4… на её субдиагонали, а все другие точки – 0.

Количество элементов симплексов фигуры можно использовать в качестве справочной таблицы для количества элементов (рёбра и углы) в многогранниках (треугольник, тетраэдр, квадрат и куб).

Шаблон, созданный элементарным клеточным автоматом с использованием правила 60, является в точности паскалевским треугольником с биномиальными коэффициентами, приведёнными по модулю 2. Правило 102 также создаёт этот шаблон, когда завершающие нули опущены. Правило 90 создаёт тот же шаблон, но с пустой ячейкой, разделяющей каждую запись в строках. Фигура может быть расширена до отрицательных номеров строк.

Секреты треугольника

Конечно, сейчас большинство расчётов для решения задач не в классе можно сделать с помощью онлайн-калькулятора. Как пользоваться треугольником Паскаля и для чего он нужен, обычно рассказывают в школьном курсе математики. Однако его применение может быть гораздо шире, чем принято думать.

Начать следует со скрытых последовательностей. Первые два столбца фигуры не слишком интересны — это только цифры и натуральные числа. Следующий столбец — треугольные числа. Можно думать о них, как о серии точек, необходимых для создания групп треугольников разных размеров.

Точно так же четвёртый столбец — это тетраэдрические числа или треугольные пирамидальные. Как следует из их названия, они представляют собой раскладку точек, необходимых для создания пирамид с треугольными основаниями.

Столбцы строят таким образом, чтобы описывать «симплексы», которые являются просто экстраполяциями идеи тетраэдра в произвольные измерения. Следующий столбец — это 5-симплексные числа, затем 6-симплексные числа и так далее.

Полномочия двойки

Если суммировать каждую строку, получатся степени основания 2 начиная с 2⁰ = 1. Если изобразить это в таблице, то получится следующее:

1
1	+	1	=	2
1	+	2	+	1	=	4
1	+	3	+	3	+	1	=	8
1	+	4	+	6	+	4	+	1	=	16
1	+	5	+	10	+	10	+	5	+	1	=	32
1	+	6	+	15	+	20	+	15	+	6	+	1	=	64

Суммирование строк показывает силы базы 2.

Силы одиннадцати

Треугольник также показывает силы основания 11. Всё, что нужно сделать, это сложить числа в каждом ряду вместе. Как показывает исследовательский опыт, этого достаточно только для первых пяти строк. Сложности начинаются, когда записи состоят из двузначных чисел. Например:

1	=	11°
11	=	11¹
121	=	11²
1331	=	11³

Оказывается, всё, что нужно сделать — перенести десятки на одно число слева.

Совершенные квадраты

Если утверждать, что 4² – это 6 + 10 = 16, то можно найти идеальные квадраты натуральных чисел в столбце 2, суммируя число справа с числом ниже. Например:

• 2² → 1 + 3 = 4
• 3² → 3 + 6
• 4² → 6 + 10 = 16 и так далее.

Комбинаторные варианты

Чтобы раскрыть скрытую последовательность Фибоначчи, которая на первый взгляд может отсутствовать, нужно суммировать диагонали лево-выровненного паскалевского треугольника. Первые 7 чисел в последовательности Фибоначчи: 1, 1, 2, 3, 5, 8, 13… найдены. Используя исходную ориентацию, следует заштриховать все нечётные числа, и получится изображение, похожее на знаменитый фрактальный треугольник Серпинского.

Возможно, самое интересное соотношение, найденное в треугольнике — это то, как можно использовать его для поиска комбинаторных чисел, поскольку его первые шесть строк написаны с помощью комбинаторной записи. Поэтому, если нужно рассчитать 4, стоит выбрать 2, затем максимально внимательно посмотреть на пятую строку, третью запись (поскольку счёт с нуля), и будет найден ответ.

Действия с биномами

Например, есть бином (x + y), и стоит задача повысить его до степени, такой как 2 или 3. Обычно нужно пройти долгий процесс умножения (x + y)² = (x + y)(x + y) и т. д. Если воспользоваться треугольником, решение будет найдено гораздо быстрее. К примеру, нужно расширить (x + y)³. Поскольку следует повышать (x + y) до третьей степени, то необходимо использовать значения в четвёртом ряду фигуры Паскаля (в качестве коэффициентов расширения). Затем заполнить значения x и y. Получится следующее: 1 x³ + 3 x²y + 3 xy² + 1 y³. Степень каждого члена соответствует степени, до которой возводится (x + y).

В виде более удобной формулы этот процесс представлен в теореме бинома. Как известно, всё лучше разбирать на примерах. Итак – (2x – 3)³. Пусть x будет первым слагаемым, а y – вторым. Тогда x = 2x, y = –3, n = 3 и k – целые числа от 0 до n = 3, в этом случае k = <0, 1, 2, 3>. Следует внести эти значения в формулу. Затем заполнить значения для k, которое имеет 4 разные версии, их нужно сложить вместе. Лучше упростить условия с показателями от нуля до единицы.

Как известно, комбинаторные числа взяты из треугольника, поэтому можно просто найти четвёртую строку и подставить в значения 1, 3, 3, 1 соответственно, используя соответствующие цифры Паскаля 1, 3, 3, 1. Последнее — необходимо завершить умножение и упрощение, в итоге должно получиться: 8 x³ – 36 x² + 54x – 27. С помощью этой теоремы можно расширить любой бином до любой степени, не тратя время на умножение.

Биномиальное распределение описывает распределение вероятностей на основе экспериментов, которые можно разделить на группы с двумя возможными исходами. Самый классический пример этого — бросание монеты. Например, есть задача выбросить «решку» — успех с вероятностью p. Тогда выпадение «орла» является случаем «неудачи» и имеет вероятность дополнения 1 – p.

Если спроектировать этот эксперимент с тремя испытаниями, с условием, что нужно узнать вероятность выпадения «решки», можно использовать функцию вероятности массы (pmf) для биномиального распределения, где n – это количество испытаний, а k – это число успехов. Предполагаемая вероятность удачи – 0,5 (р = 0,5). Самое время обратиться к треугольнику, используя комбинаторные числа: 1, 3, 3, 1. Вероятность получить ноль или три «решки» составляет 12,5%, в то время как переворот монеты один или два раза на сторону «орла» — 37,5%. Вот так математика может применяться в жизни.

Бином Ньютона

Биноминальное разложение с использованием треугольника Паскаля

Рассмотрим следующие выражения со степенями (a + b) n , где a + b есть любой бином, а n – целое число.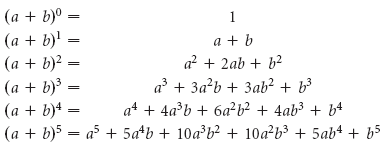

Каждое выражение – это полином. Во всех выражениях можно заметить особенности.

1. В каждом выражении на одно слагаемое больше, чем показатель степени n.

2. В каждом слагаемом сумма степеней равна n, т.е. степени, в которую возводится бином.

3. Степени начинаются со степени бинома n и уменьшаются к 0. Последний член не имеет множителя a. Первый член не имеет множителя b, т.е. степени b начинаются с 0 и увеличиваются до n.

4. Коэффициенты начинаются с 1 и увеличиваются на определенные значения до “половины пути”, а потом уменьшаются на те же значения обратно к 1.

Давайте рассмотрим коэффициенты подробнее. Предположим, что мы хотим найти значение (a + b) 6 . Согласно особенности, которую мы только что заметили, здесь должно быть 7 членов
a 6 + c₁a 5 b + c₂a 4 b 2 + c₃a 3 b 3 + c₄a 2 b 4 + c₅ab 5 + b 6 .
Но как мы можем определить значение каждого коэффициента, c_i? Мы можем сделать это двумя путями. Первый метод включает в себя написание коэффициентов треугольником, как показано ниже. Это известно как Треугольник Паскаля: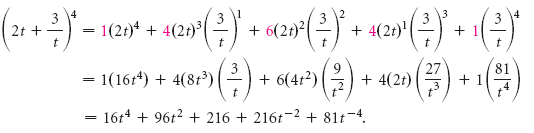

Есть много особенностей в треугольнике. Найдите столько, сколько сможете.
Возможно вы нашли путь, как записать следующую строку чисел, используя числа в строке выше. Единицы всегда расположены по сторонам. Каждое оставшееся число это сумма двух чисел, расположенных выше этого числа. Давайте попробуем отыскать значение выражения (a + b) 6 путем добавления следующей строки, используя особенности, которые мы нашли:

Мы видим, что в последней строке

первой и последнее числа 1;
второе число равно 1 + 5, или 6;
третье число это 5 + 10, или 15;
четвертое число это 10 + 10, или 20;
пятое число это 10 + 5, или 15; и
шестое число это 5 + 1, или 6.

Таким образом, выражение (a + b) 6 будет равно
(a + b) 6 = 1a 6 + 6a 5 b + 15a 4 b 2 + 20a 3 b 3 + 15a 2 b 4 + 6ab 5 + 1b 6 .

Для того, чтобы возвести в степень (a + b) 8 , мы дополняем две строки к треугольнику Паскаля: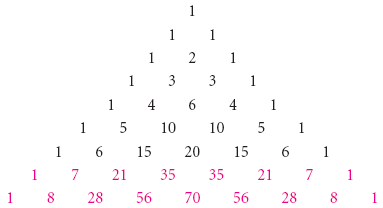

Тогда
(a + b) 8 = a 8 + 8a 7 b + 28a 6 b 2 + 56a 5 b 3 + 70a 4 b 4 + 56a 3 b 5 + 28a 2 b 6 + 8ab 7 + b 8 .

Мы можем обобщить наши результаты следующим образом.

Бином Ньютона с использованием треугольника Паскаля

Для любого бинома a+ b и любого натурального числа n,
(a + b) n = c₀a n b 0 + c₁a n-1 b 1 + c₂a n-2 b 2 + . + c_n-1a 1 b n-1 + c_na 0 b n ,
где числа c₀, c₁, c₂. c_n-1, c_n взяты с (n + 1) ряда треугольника Паскаля.

Пример 1 Возведите в степень: (u – v) 5 .

Решение У нас есть (a + b) n , где a = u, b = -v, и n = 5. Мы используем 6-й ряд треугольника Паскаля:
1 5 10 10 5 1
Тогда у нас есть
(u – v) 5 = [u + (-v)] 5 = 1(u) 5 + 5(u) 4 (-v) 1 + 10(u) 3 (-v) 2 + 10(u) 2 (-v) 3 + 5(u)(-v) 4 + 1(-v) 5 = u 5 – 5u 4 v + 10u 3 v 2 – 10u 2 v 3 + 5uv 4 – v 5 .
Обратите внимание, что знаки членов колеблются между + и -. Когда степень -v есть нечетным числом, знак -.

Пример 2 Возведите в степень: (2t + 3/t) 4 .

Решение У нас есть (a + b) n , где a = 2t, b = 3/t, и n = 4. Мы используем 5-й ряд треугольника Паскаля:
1 4 6 4 1
Тогда мы имеем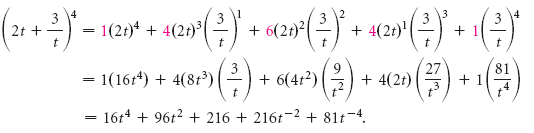

Разложение бинома используя значения факториала

Предположим, что мы хотим найти значение (a + b) 11 . Недостаток в использовании треугольника Паскаля в том, что мы должны вычислить все предыдущие строки треугольника, чтобы получить необходимый ряд. Следующий метод позволяет избежать этого. Он также позволяет найти определенную строку – скажем, 8-ю строку – без вычисления всех других строк. Этот метод полезен в вычислениях, статистике и он использует биномиальное обозначение коэффициента .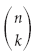
Мы можем сформулировать бином Ньютона следующим образом.

Бином Ньютона с использованием обозначение факториала

Для любого бинома (a + b) и любого натурального числа n,
.

Бином Ньютона может быть доказан методом математической индукции. Она показывает почему 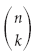называется биноминальным коэффициентом.

Пример 3 Возведите в степень: (x 2 – 2y) 5 .

Решение У нас есть (a + b) n , где a = x 2 , b = -2y, и n = 5. Тогда, используя бином Ньютона, мы имеем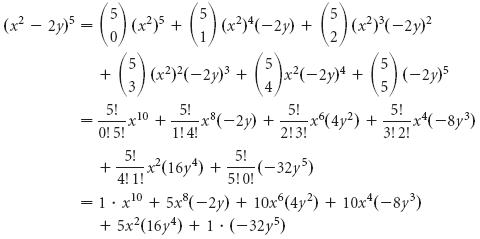

Наконец, (x 2 – 2y) 5 = x 10 – 10x 8 y + 40x 6 y 2 – 80x 4 y 3 + 80x 2 y 4 – 35y 5 .

Пример 4 Возведите в степень: (2/x + 3√ x ) 4 .

Решение У нас есть (a + b) n , где a = 2/x, b = 3√ x , и n = 4. Тогда, используя бином Ньютона, мы получим

Finally (2/x + 3√ x ) 4 = 16/x 4 + 96/x 5/2 + 216/x + 216x 1/2 + 81x 2 .

Нахождение определенного члена

Предположим, что мы хотим определить тот или иной член термин из выражения. Метод, который мы разработали, позволит нам найти этот член без вычисления всех строк треугольника Паскаля или всех предыдущих коэффициентов.

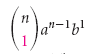Обратите внимание, что в биноме Ньютона дает нам 1-й член, дает нам 2-й член, дает нам 3-й член и так далее. Это может быть обощено следующим образом.

Нахождение (k + 1) члена

(k + 1) член выражения (a + b) n есть .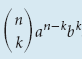

Пример 5 Найдите 5-й член в выражении (2x – 5y) 6 .

Решение Во-первых, отмечаем, что 5 = 4 + 1. Тогда k = 4, a = 2x, b = -5y, и n = 6. Тогда 5-й член выражения будет

Пример 6 Найдите 8-й член в выражении (3x – 2) 10 .

Решение Во-первых, отмечаем, что 8 = 7 + 1. Тогда k = 7, a = 3x, b = -2 и n = 10. Тогда 8-й член выражения будет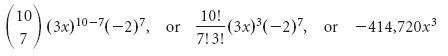

Общее число подмножеств

Предположим, что множество имеет n объектов. Число подмножеств, содержащих k элементов есть 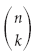. Общее число подмножеств множества есть число подмножеств с 0 элементами, а также число подмножеств с 1 элементом, а также число подмножеств с 2-мя элементами и так далее. Общее число подмножеств множества с n элементами есть
.
Теперь давайте рассмотрим возведение в степень (1 + 1) n :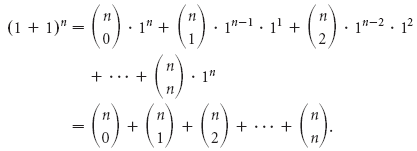
.
Так. общее количество подмножеств (1 + 1) n , или 2 n . Мы доказали следующее.

Полное число подмножеств

Полное число подмножеств множества с n элементами равно 2 n .

Пример 7 Сколько подмножеств имеет множество ?

Решение Множество имеет 5 элементов, тогда число подмножеств равно 2 5 , или 32.

Пример 8 Сеть ресторанов Венди предлагает следующую начинку для гамбургеров:
<кетчуп, горчица, майонез, помидоры, салат, лук, грибы, оливки, сыр>.
Сколько разных видов гамбургеров может предложить Венди, исключая размеры гамбургеров или их количество?

Решение Начинки на каждый гамбургер являются элементами подмножества множества всех возможных начинок, а пустое множество это просто гамбургер. Общее число возможных гамбургеров будет равно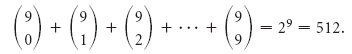

. Таким образом, Венди может предложить 512 различных гамбургеров.

Бином Ньютона

Бином Ньютона – формула

С натуральным n формула Бинома Ньютона принимает вид a + b n = C n 0 · a n + C n 1 · a n – 1 · b + C n 2 · a n – 2 · b 2 + . . . + C n n – 1 · a · b n – 1 + C n n · b n , где имеем, что C n k = ( n ) ! ( k ) ! · ( n – k ) ! = n ( n – 1 ) · ( n – 2 ) · . . . · ( n – ( k – 1 ) ) ( k ) ! – биномиальные коэффициенты, где есть n по k , k = 0 , 1 , 2 , … , n , а ” ! ” является знаком факториала.

В формуле сокращенного умножения a + b 2 = C 2 0 · a 2 + C 2 1 · a 1 · b + C 2 2 · b 2 = a 2 + 2 a b + b 2
просматривается формула бинома Ньютона, так как при n = 2 является его частным случаем.

Первая часть бинома называют разложением ( a + b ) n , а С n k · a n – k · b k – ( k + 1 ) -ым членом разложения, где k = 0 , 1 , 2 , … , n .

Коэффициенты бинома Ньютона, свойства биномиальных коэффициентов, треугольник Паскаля

Представление биномиальных коэффициентов для различных n осуществляется при помощи таблицы, которая имеет название арифметического треугольника Паскаля. Общий вид таблицы:

Показатель степени	Биноминальные коэффициенты
0	C 0 0
1	C 1 0	C 1 1
2	C 2 0	C 2 1	C 2 2
3	C 3 0	C 3 1	C 3 2	C 3 3
⋮	…	…	…	…	…	…	…	…	…
n	C n 0	C n 1	…	…	…	…	…	C n n – 1	C n n

При натуральных n такой треугольник Паскаля состоит из значений коэффициентов бинома:

Показатель степени	Биноминальные коэффициенты
0	1
1	1	1
2	1	2	1
3	1	3	3	1
4	1	4	6	4	1
5	1	5	10	10	5	1
⋮	…	…	…	…	…	…	…	…	…	…	…	…	…
n	C n 0	C n 1	…	…	…	…	…	…	…	…	…	C n n – 1	C n n

Боковые стороны треугольника имеют значение единиц. Внутри располагаются числа, которые получаются при сложении двух чисел соседних сторон. Значения, которые выделены красным, получают как сумму четверки, а синим – шестерки. Правило применимо для всех внутренних чисел, которые входят в состав треугольника. Свойства коэффициентов объясняются при помощи бинома Ньютона.

Доказательство формулы бинома Ньютона

Имеются равенства, которые справедливы для коэффициентов бинома Ньютона:

• коэффициента располагаются равноудалено от начала и конца, причем равны, что видно по формуле C n p = C n n – p , где р = 0 , 1 , 2 , … , n ;
• C n p = C n p + 1 = C n + 1 p + 1 ;
• биномиальные коэффициенты в сумме дают 2 в степени показателя степени бинома, то есть C n 0 + C n 1 + C n 2 + . . . + C n n = 2 n ;
• при четном расположении биноминальных коэффициентов их сумма равняется сумме биномиальных коэффициентов, расположенных в нечетных местах.

Равенство вида a + b n = C n 0 · a n + C n 1 · a n – 1 · b + C n 2 · a n – 2 · b 2 + . . . + C n n – 1 · a · b n – 1 + C n n · b n считается справедливым. Докажем его существование.

Для этого необходимо применить метод математической индукции.

Для доказательства необходимо выполнить несколько пунктов:

1. Проверка справедливости разложения при n = 3 . Имеем, что
   a + b 3 = a + b a + b a + b = a 2 + a b + b a + b 2 a + b = = a 2 + 2 a b + b 2 a + b = a 3 + 2 a 2 b + a b 2 + a 2 b + 2 a b + b 3 = = a 3 + 3 a 2 b + 3 a b 2 + b 3 = C 3 0 a 3 + C 3 1 a 2 b + C 3 2 a b 2 + C 3 3 b 3
2. Если неравенство верно при n – 1 , тогда выражение вида a + b n – 1 = C n – 1 0 · a n – 1 · C n – 1 1 · a n – 2 · b · C n – 1 2 · a n – 3 · b 2 + . . . + C n – 1 n – 2 · a · b n – 2 + C n – 1 n – 1 · b n – 1

1. Доказательство равенства a + b n – 1 = C n – 1 0 · a n – 1 · C n – 1 1 · a n – 2 · b · C n – 1 2 · a n – 3 · b 2 + . . . + C n – 1 n – 2 · a · b n – 2 + C n – 1 n – 1 · b n – 1 , основываясь на 2 пункте.

Доказательство 1

a + b n = a + b a + b n – 1 = = ( a + b ) C n – 1 0 · a n – 1 · C n – 1 1 · a n – 2 · b · C n – 1 2 · a n – 3 · b 2 + . . . + C n – 1 n – 2 · a · b n – 2 + C n – 1 n – 1 · b n – 1

Необходимо раскрыть скобки, тогда получим a + b n = C n – 1 0 · a n + C n – 1 1 · a n – 1 · b + C n – 1 2 · a n – 2 · b 2 + . . . + C n – 1 n – 2 · a 2 · b n – 2 + + C n – 1 n – 1 · a · b n – 1 + C n – 1 0 · a n – 1 · b + C n – 1 1 · a n – 2 · b 2 + C n – 1 2 · a n – 3 · b 3 + . . . + C n – 1 n – 2 · a · b n – 1 + C n – 1 n – 1 · b n

Производим группировку слагаемых

a + b n = = C n – 1 0 · a n + C n – 1 1 + C n – 1 0 · a n – 1 · b + C n – 1 2 + C n – 1 1 · a n – 2 · b 2 + . . . + + C n – 1 n – 1 + C n – 1 n – 2 · a · b n – 1 + C n – 1 n – 1 · b n

Имеем, что C n – 1 0 = 1 и C n 0 = 1 , тогда C n – 1 0 = C n 0 . Если C n – 1 n – 1 = 1 и C n n = 1 , тогда C n – 1 n – 1 = C n n . При применении свойства сочетаний C n p + C n p + 1 = C n + 1 p + 1 , получаем выражение вида

C n – 1 1 + C n – 1 0 = C n 1 C n – 1 2 + C n – 1 1 = C n 2 ⋮ C n – 1 n – 1 + C n – 1 n – 2 = C n n – 1

Произведем подстановку в полученное равенство. Получим, что

a + b n = = C n – 1 0 · a n + C n – 1 1 + C n – 1 0 · a n – 1 · b + C n – 1 2 + C n – 1 1 · a n – 2 · b 2 + . . . + + C n – 1 n – 1 + C n – 1 n – 2 · a · b n – 1 = C n – 1 n – 1 · b n

После чего можно переходить к биному Ньютона, тогда a + b n = C n 0 · a n + C n 1 · a n – 1 · b + C n 2 · a n – 2 · b 2 + . . . + C n n – 1 · a · b n – 1 + C n n · b n .

[spoiler title=”источники:”]

http://www.math10.com/ru/algebra/veroiatnosti/binominalnaya-teorema/binominalnaya-teorema.html

http://zaochnik.com/spravochnik/matematika/vyrazhenija/binom-njutona/

[/spoiler]