Рано или поздно при изучении курса физики ученики и студенты сталкиваются с задачами на силу упругости и закон Гука, в которых фигурирует коэффициент жесткости пружины. Что же это за величина, и как она связана с деформацией тел и законом Гука?
Содержание:
- Сила упругости и закон Гука
- Определение коэффициента жесткости
- Расчет жесткости системы
- Последовательное соединение системы пружин
- Параллельное соединение системы пружин
- Вычисление коэффициента жесткости опытным методом
- Примеры задач на нахождение жесткости
- Видео
Сила упругости и закон Гука
Для начала определим основные термины, которые будут использоваться в данной статье. Известно, если воздействовать на тело извне, оно либо приобретет ускорение, либо деформируется. Деформация — это изменение размеров или формы тела под влиянием внешних сил. Если объект полностью восстанавливается после прекращения нагрузки, то такая деформация считается упругой; если же тело остается в измененном состоянии (например, согнутом, растянутом, сжатым и т. д. ), то деформация пластическая.
Примерами пластических деформаций являются:
- лепка из глины;
- погнутая алюминиевая ложка.
В свою очередь, упругими деформациями будут считаться:
- резинка (можно растянуть ее, после чего она вернется в исходное состояние);
- пружина (после сжатия снова распрямляется).
В результате упругой деформации тела (в частности, пружины) в нем возникает сила упругости, равная по модулю приложенной силе, но направленная в противоположную сторону. Сила упругости для пружины будет пропорциональна ее удлинению. Математически это можно записать таким образом:
F = – k·x;
где F — сила упругости, x — расстояние, на которое изменилась длина тела в результате растяжения, k — необходимый для нас коэффициент жесткости. Указанная выше формула также является частным случаем закона Гука для тонкого растяжимого стержня. В общей форме этот закон формулируется так: «Деформация, возникшая в упругом теле, будет пропорциональна силе, которая приложена к данному телу». Он справедлив только в тех случаях, когда речь идет о малых деформациях (растяжение или сжатие намного меньше длины исходного тела).

Определение коэффициента жесткости
Коэффициент жесткости (он также имеет названия коэффициента упругости или пропорциональности) чаще всего записывается буквой k, но иногда можно встретить обозначение D или c. Численно жесткость будет равна величине силы, которая растягивает пружину на единицу длины (в случае СИ — на 1 метр). Формула для нахождения коэффициента упругости выводится из частного случая закона Гука:
k = F/x.
Чем больше величина жесткости, тем больше будет сопротивление тела к его деформации. Также коэффициент Гука показывает, насколько устойчиво тело к действию внешней нагрузки. Зависит этот параметр от геометрических параметров (диаметра проволоки, числа витков и диаметра намотки от оси проволоки) и от материала, из которого она изготовлена.
Единица измерения жесткости в СИ — Н/м.
Расчет жесткости системы
Встречаются более сложные задачи, в которых необходим расчет общей жесткости. В таких заданиях пружины соединены последовательно или параллельно.
Последовательное соединение системы пружин
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
1/k = 1/k1 + 1/k2 + … + 1/ki,
где k — общая жесткость системы, k1, k2, …, ki — отдельные жесткости каждого элемента, i — общее количество всех пружин, задействованных в системе.

Параллельное соединение системы пружин
В случае когда пружины соединены параллельно, величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
k = k1 + k2 + … + ki.
Измерение жесткости пружины опытным путем – в этом видео.
Вычисление коэффициента жесткости опытным методом
С помощью несложного опыта можно самостоятельно рассчитать, чему будет равен коэффициент Гука. Для проведения эксперимента понадобятся:
- линейка;
- пружина;
- груз с известной массой.
Последовательность действий для опыта такова:
- Необходимо закрепить пружину вертикально, подвесив ее к любой удобной опоре. Нижний край должен остаться свободным.
- При помощи линейки измеряется ее длина и записывается как величина x1.
- На свободный конец нужно подвесить груз с известной массой m.
- Длина пружины измеряется в нагруженном состоянии. Обозначается величиной x2.
- Подсчитывается абсолютное удлинение: x = x2-x1. Для того чтобы получить результат в международной системе единиц, лучше сразу перевести его из сантиметров или миллиметров в метры.
- Сила, которая вызвала деформацию, — это сила тяжести тела. Формула для ее расчета — F = mg, где m — это масса используемого в эксперименте груза (переводится в кг), а g — величина свободного ускорения, равная приблизительно 9,8.
- После проведенных расчетов остается найти только сам коэффициент жесткости, формула которого была указана выше: k = F/x.
Примеры задач на нахождение жесткости
Задача 1
На пружину длиной 10 см действует сила F = 100 Н. Длина растянутой пружины составила 14 см. Найти коэффициент жесткости.
- Рассчитываем длину абсолютного удлинения: x = 14—10 = 4 см = 0,04 м.
- По формуле находим коэффициент жесткости: k = F/x = 100 / 0,04 = 2500 Н/м.
Ответ: жесткость пружины составит 2500 Н/м.
Задача 2
Груз массой 10 кг при подвешивании на пружину растянул ее на 4 см. Рассчитать, на какую длину растянет ее другой груз массой 25 кг.
- Найдем силу тяжести, деформирующей пружину: F = mg = 10 · 9.8 = 98 Н.
- Определим коэффициент упругости: k = F/x = 98 / 0.04 = 2450 Н/м.
- Рассчитаем, с какой силой действует второй груз: F = mg = 25 · 9.8 = 245 Н.
- По закону Гука запишем формулу для абсолютного удлинения: x = F/k.
- Для второго случая подсчитаем длину растяжения: x = 245 / 2450 = 0,1 м.
Ответ: во втором случае пружина растянется на 10 см.
Видео
Из этого видео вы узнаете, как определить жесткость пружины.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 30 августа 2021 года; проверки требуют 9 правок.
Коэффицие́нт упру́гости, иногда также коэффицие́нт Гу́ка, жёсткость пружи́ны, — коэффициент, связывающий в законе Гука удлинение упругого тела и возникающую вследствие этого удлинения силу упругости. Применяется в механике твердого тела в разделе упругости. Обозначается буквой k[1], иногда D[2] или c[3]. Имеет единицу измерения Н/м или кг/с2 (в СИ), дин/см или г/с2 (в СГС).
Коэффициент упругости численно равен силе, которую надо приложить к пружине, чтобы её длина изменилась на единицу расстояния.
Определение и свойства[править | править код]
Коэффициент упругости по определению равен силе упругости, делённой на изменение длины пружины:

Коэффициент упругости зависит как от свойств материала, так и от размеров упругого тела. Так, для упругого стержня можно выделить зависимость от размеров стержня (площади поперечного сечения 



Жёсткость деформируемых тел при их соединении[править | править код]

Параллельное соединение пружин.

Последовательное соединение пружин.
При соединении нескольких упруго деформируемых тел (далее для краткости — пружин) общая жёсткость системы будет меняться. При параллельном соединении жёсткость увеличивается, при последовательном — уменьшается.
Параллельное соединение[править | править код]
При параллельном соединении 


Последовательное соединение[править | править код]
При последовательном соединении 


Жёсткость некоторых деформируемых тел[править | править код]
Стержень постоянного сечения[править | править код]
Однородный стержень постоянного сечения, упруго деформируемый вдоль оси, имеет коэффициент жёсткости
где
- Е — модуль Юнга, зависящий только от материала, из которого выполнен стержень;
- S — площадь поперечного сечения;
- L0 — длина стержня.
Цилиндрическая витая пружина[править | править код]

Витая цилиндрическая пружина сжатия.
Витая цилиндрическая пружина сжатия или растяжения, намотанная из цилиндрической проволоки и упруго деформируемая вдоль оси, имеет коэффициент жёсткости
где
- dD — диаметр проволоки;
- dF — диаметр намотки (измеряемый от оси проволоки);
- n — число витков;
- G — модуль сдвига (для обычной стали G ≈ 80 ГПа, для пружинной стали G ≈ 78.5 ГПа, для меди ~ 45 ГПа).
См. также[править | править код]
- Закон Гука
- Сила упругости
- Роберт Гук
- Модуль Юнга
- Пружина
Источники и примечания[править | править код]
- ↑ Упругая деформация. Архивировано 30 июня 2012 года.
- ↑ Dieter Meschede, Christian Gerthsen. Physik. — Springer, 2004. — P. 181 ..
- ↑
Bruno Assmann. Technische Mechanik: Kinematik und Kinetik. — Oldenbourg, 2004. — P. 11 .. - ↑ Динамика, Сила упругости. Дата обращения: 22 мая 2012. Архивировано из оригинала 13 октября 2012 года.
- ↑ Механические свойства тел. Дата обращения: 22 мая 2012. Архивировано 15 февраля 2013 года.
Сила упругости
Любое тело, когда его деформируют и оказывают внешнее воздействие, сопротивляется и стремиться восстановить прежние форму и размеры. Это происходит по причине электромагнитного взаимодействия в теле на молекулярном уровне.
Деформация – изменение положения частиц тела друг относительно друга. Результат деформации – изменение межатомных расстояний и перегруппировка блоков атомов.
Сила упругости – сила, возникающая при деформации в теле и стремящаяся вернуть тело в начальное состояние.
Рассмотрим простейшие деформации – растяжение и сжатие
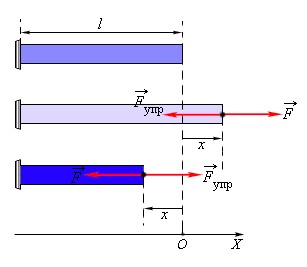
На рисунке показано, как действует сила упругости, когда мы сжимаем или растягиваем стержень.
Закон Гука
Для малых деформаций x≪ l справедлив закон Гука.
Деформация, возникающая в упругом теле, пропорциональна приложенной к телу силе.
Fупр=-kx
Здесь k – коэффициент пропорциональности, называемый жесткостью. Единица измерения жесткости системе СИ Ньютон на метр. Жесткость зависит от материала тела, его формы и размеров.
Знак минус показывает, что сила упругости противодействует внешней силе и стремится вернуть тело в первоначальное состояние.
Существуют и другие формы записи закона Гука. Относительной деформацией тела называется отношение ε=xl. Напряжением в теле называется отношение σ=-FупрS. Здесь S – площадь поперечного сечения деформированного тела. Вторая формулировка закона Гука: относительная деформация пропорциональна напряжению.
ε=σE.
Здесь E – так называемый модуль Юнга, который не зависит от формы и размеров тела, а зависит только от свойств материала. Значение модуля Юнга для различных материалов широко варьируется. Например, для стали E≈2·1011 Нм2, а для резины E≈2·106 Нм2
Закон Гука можно обобщить для случая сложных деформаций. Рассмотрим деформацию изгиба стержня. При такой деформации изгиба сила упругости пропорциональна прогибу стержня.
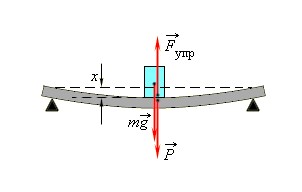
Концы стержня лежат на двух опорах, которые действуют на тело с силой N→, называемой силой нормальной реакции опоры. Почему нормальной? Потому что эта сила направлена перпендикулярно (нормально) поверхности соприкосновения.
Если стержень лежит на столе, сила нормальной реакции опоры направлена вертикально вверх, противоположно силе тяжести, которую она уравновешивает.
Вес тела – это сила, с которой оно действует на опору.
Силу упругости часто рассматривают в контексте растяжения или сжатия пружины. Это распространенный пример, который часто встречается не только в теории, но и на практике. Пружины используются для измерения величины сил. Прибор, предназначенный для этого – динамаметр.
Динамометр – пружина, растяжение которой проградуированно в единицах силы. Характерное свойство пружин заключается в том, что закон Гука для них применим при достаточно большом изменении длины.
При сжатии и растяжении пружины действует закон Гука, возникают упругие силы, пропорциональные изменению длины пружины и ее жесткости (коэффициента k).
В отличие от пружин стержни и проволоки подчиняются закону Гука в очень узких пределах. Так, при относительной дефомации больше 1% в материале возникают необратимые именения – текучесть и разрушения.
Формула жесткости пружины в физике
Формула жесткости пружины
Определение и формула жесткости пружины
Определение
Силу, которая возникает в результате деформации тела и пытающаяся вернуть его в исходное состояние, называют силой упругости.
Чаще всего ее обозначают ${overline{F}}_{upr}$. Сила упругости появляется только при деформации тела и исчезает, если пропадает деформация. Если после снятия внешней нагрузки тело восстанавливает свои размеры и форму полностью, то такая деформация называется упругой.
Современник И. Ньютона Р. Гук установил зависимость силы упругости от величины деформации. Гук долго сомневался в справедливости своих выводов. В одной из своих книг он привел зашифрованную формулировку своего закона. Которая означала: «Ut tensio, sic vis» в переводе с латыни: каково растяжение, такова сила.
Рассмотрим пружину, на которую действует растягивающая сила ($overline{F}$), которая направлена вертикально вниз (рис.1).
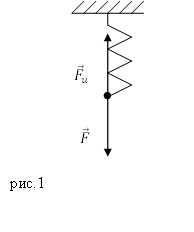
Силу $overline{F }$ назовем деформирующей силой. От воздействия деформирующей силы длина пружины увеличивается. В результате в пружине появляется сила упругости (${overline{F}}_u$), уравновешивающая силу $overline{F }$. Если деформация является небольшой и упругой, то удлинение пружины ($Delta l$) прямо пропорционально деформирующей силе:
[overline{F}=kDelta lleft(1right),]
где в коэффициент пропорциональности называется жесткостью пружины (коэффициентом упругости) $k$.
Жесткость (как свойство) – это характеристика упругих свойств тела, которое деформируют. Жесткость считают возможностью тела оказать противодействие внешней силе, способность сохранять свои геометрические параметры. Чем больше жесткость пружины, тем меньше она изменяет свою длину под воздействием заданной силы. Коэффициент жесткости – это основная характеристика жесткости (как свойства тела).
Коэффициент жесткости пружины зависит от материала, из которого сделана пружина и ее геометрических характеристик. Например, коэффициент жесткости витой цилиндрической пружины, которая намотана из проволоки круглого сечения, подвергаемая упругой деформации вдоль своей оси может быть вычислена как:
[k=frac{Gd^4}{8d^3_pn}left(2right),]
где $G$ – модуль сдвига (величина, зависящая от материала); $d$ – диаметр проволоки; $d_p$ – диаметр витка пружины; $n$ – количество витков пружины.
Единицей измерения коэффициента жесткости в Международной системе единиц (Си) является ньютон, деленный на метр:
[left[kright]=left[frac{F_{upr }}{x}right]=frac{left[F_{upr }right]}{left[xright]}=frac{Н}{м}.]
Коэффициент жесткости равен величине силы, которую следует приложить к пружине для изменения ее длины на единицу расстояния.
Формула жесткости соединений пружин
Пусть $N$ пружин соединены последовательно. Тогда жесткость всего соединения равна:
[frac{1}{k}=frac{1}{k_1}+frac{1}{k_2}+dots =sumlimits^N_{ i=1}{frac{1}{k_i}left(3right),}]
где $k_i$ – жесткость $i-ой$ пружины.
При последовательном соединении пружин жесткость системы определяют как:
[k=k_1+k_2+dots +sumlimits^N_{i=1}{k_i}left(4right).]
Примеры задач с решением
Пример 1
Задание. Пружина в отсутствии нагрузки имеет длину $l=0,01$ м и жесткость равную 10 $frac{Н}{м}. $Чему будет равна жесткость пружины и ее длина, если на пружину действовать силой $F$= 2 Н? Считайте деформацию пружины малой и упругой.
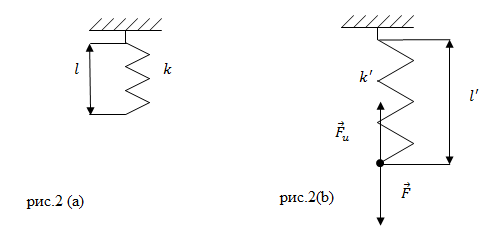
Решение. Жесткость пружины при упругих деформациях является постоянной величиной, значит, в нашей задаче:
[k=k’left(1.1right).]
При упругих деформациях выполняется закон Гука:
[F=kDelta l left(1.2right).]
Из (1.2) найдем удлинение пружины:
[Delta l=frac{F}{k}left(1.3right).]
Длина растянутой пружины равна:
[l’=l+Delta l=l+frac{F}{k}.]
Вычислим новую длину пружины:
[l’=0,01+frac{2}{10}=0,21 left(мright).]
Ответ. 1) $k’=10 frac{Н}{м}$; 2) $l’=0,21$ м
Пример 2
Задание. Две пружины, имеющие жесткости $k_1$ и $k_2$ соединили последовательно. Какой будет удлинение первой пружины (рис.3), если длина второй пружины увеличилась на величину $Delta l_2$?
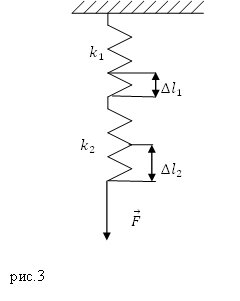
Решение. Если пружины соединены последовательно, то деформирующая сила ($overline{F}$), действующая на каждую из пружин одинакова, то есть можно записать для первой пружины:
[F=k_1Delta l_1left(2.1right).]
Для второй пружины запишем:
[F=k_2Delta l_2left(2.2right).]
Если равны левые части выражений (2.1) и (2.2), то можно приравнять и правые части:
[k_1Delta l_1=k_2Delta l_2left(2.3right).]
Из равенства (2.3) получим удлинение первой пружины:
[Delta l_1=frac{k_2Delta l_2}{k_1}.]
Ответ. $Delta l_1=frac{k_2Delta l_2}{k_1}$
Читать дальше: формула закона Архимеда.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Примеры задач с решением
Задание. Пружина в отсутствии нагрузки имеет длину $l=0,01$ м и жесткость равную 10 $frac. $Чему будет равна жесткость пружины и ее длина, если на пружину действовать силой $F$= 2 Н? Считайте деформацию пружины малой и упругой.

Решение. Жесткость пружины при упругих деформациях является постоянной величиной, значит, в нашей задаче:
При упругих деформациях выполняется закон Гука:
[F=kDelta l left(1.2right).]
Из (1.2) найдем удлинение пружины:
Длина растянутой пружины равна:
Вычислим новую длину пружины:
Ответ. 1) $k’=10 frac$; 2) $l’=0,21$ м
Задание. Две пружины, имеющие жесткости $k_1$ и $k_2$ соединили последовательно. Какой будет удлинение первой пружины (рис.3), если длина второй пружины увеличилась на величину $Delta l_2$?
Решение. Если пружины соединены последовательно, то деформирующая сила ($overline$), действующая на каждую из пружин одинакова, то есть можно записать для первой пружины:
Для второй пружины запишем:
Если равны левые части выражений (2.1) и (2.2), то можно приравнять и правые части:
[k_1Delta l_1=k_2Delta l_2left(2.3right).]
Из равенства (2.3) получим удлинение первой пружины:
Ответ. $Delta l_1=frac$
Как появился первый вариант формулы
Формула для расчета жесткости пружины, которая получила название закона Гука, была установлена экспериментально. В процессе опытов с подвешенными на упругом элементе грузами разной массы замерялась величина его растяжения. Так и выяснилось, что одна и та же испытуемая деталь под разными нагрузками претерпевает различные деформации. Причем подвешивание определенного количества гирек, одинаковых по массе, показало, что каждая добавленная/снятая гирька увеличивает/уменьшает длину упругого элемента на одинаковую величину.
В итоге этих экспериментов появилась такая формула: kx=mg, где k – некий постоянный для данной пружины коэффициент, x – изменение длины пружины, m – ее масса, а g – ускорение свободного падения (примерное значение – 9,8 м/с²).
Так было открыто свойство жесткости, которое, как и формула для определения коэффициента упругости, находит самое широкое применение в любой отрасли промышленности.
Сила упругости.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: силы в механике, сила упругости, закон Гука.
Как мы знаем, в правой части второго закона Ньютона стоит равнодействующая (то есть векторная сумма) всех сил, приложенных к телу. Теперь нам предстоит изучить силы взаимодействия тел в механике. Их три вида: сила упругости, гравитационная сила и сила трения. Начинаем с силы упругости.
Особенности расчета жесткости соединений пружин
Важный моментом является расчет нескольких упругих элементов, соединенных последовательно или параллельно.
При параллельном расположении нескольких деталей общая жесткость этой системы определяется простой суммой коэффициентов отдельных комплектующих. Как нетрудно заметить, жесткость системы больше, чем отдельной детали.
При последовательном расположении формула более сложная: величина, обратная суммарной жесткости, равна сумме величин, обратных к жесткости каждой комплектующей. В этом варианте сумма меньше слагаемых.
Используя эти зависимости, легко определиться с правильным выбором упругих комплектующих для конкретного случая.
Определение коэффициента жесткости
Коэффициент жесткости (он также имеет названия коэффициента упругости или пропорциональности) чаще всего записывается буквой k, но иногда можно встретить обозначение D или c. Численно жесткость будет равна величине силы, которая растягивает пружину на единицу длины (в случае СИ — на 1 метр). Формула для нахождения коэффициента упругости выводится из частного случая закона Гука:
Чем больше величина жесткости, тем больше будет сопротивление тела к его деформации. Также коэффициент Гука показывает, насколько устойчиво тело к действию внешней нагрузки. Зависит этот параметр от геометрических параметров (диаметра проволоки, числа витков и диаметра намотки от оси проволоки) и от материала, из которого она изготовлена.
Единица измерения жесткости в СИ — Н/м.
Как найти удлинение пружины?
Эта формула, а точнее закон Гука, выглядит так: F=|kx|, где k – это коэффициент упругости пружины, x – это удлинение пружины или же, как её ещё называют, величина деформации пружины.
Интересные материалы:
Что происходит с внутренней энергией воды при нагревании? Что происходит с водой при нагревании и при охлаждении? Что происходит с водой в ночь на 19 января? Что стало причиной уменьшения стока воды в Аральское море? Что такое мутить воду? Что такое нерастворимые в воде вещества? Что такое пудровая туалетная вода? Что такое тестер туалетная вода? Что такое вода для 2 класса? Что такое вода для инъекций?
Деформация.
Силы упругости возникают при деформациях тел. Деформация — это изменение формы и размеров тела. К деформациям относятся растяжение, сжатие, кручение, сдвиг и изгиб. Деформации бывают упругими и пластическими. Упругая деформация полностью исчезает после прекращения действия вызывающих её внешних сил, так что тело полностью восстанавливает форму и размеры. Пластическая деформация сохраняется (быть может, частично) после снятия внешней нагрузки, и тело уже не возвращается к прежним размерам и форме.
Частицы тела (молекулы или атомы) взаимодействуют друг с другом силами притяжения и отталкивания, имеющими электромагнитное происхождение (это силы, действующие между ядрами и электронами соседних атомов). Силы взаимодействия зависят о расстояний между частицами. Если деформации нет, то силы притяжения компенсируются силами отталкивания. При деформации изменяются расстояния между частицами, и баланс сил взаимодействия нарушается.
Например, при растяжении стержня расстояния между его частицами увеличиваются, и начинают преобладать силы притяжения. Наоборот, при сжатии стержня расстояния между частицами уменьшаются, и начинают преобладать силы отталкивания. В любом случае возникает сила, которая направлена в сторону, противоположную деформации, и стремится восстановить первоначальную конфигурацию тела.
Сила упругости — это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации. Сила упругости:
1. действует между соседними слоями деформированного тела и приложена к каждому слою; 2. действует со стороны деформированного тела на соприкасающееся с ним тело, вызывающее деформацию, и приложена в месте контакта данных тел перпендикулярно их поверхностям (типичный пример — сила реакции опоры).
Силы, возникающие при пластических деформациях, не относятся к силам упругости. Эти силы зависят не от величины деформации, а от скорости её возникновения. Изучение таких сил выходит далеко за рамки школьной программы.
В школьной физике рассматриваются растяжения нитей и тросов, а также растяжения и сжатия пружин и стержней. Во всех этих случаях силы упругости направлены вдоль осей данных тел.
Закон Гука.
Деформация называется малой, если изменение размеров тела много меньше его первоначальных размеров. При малых деформациях зависимость силы упругости от величины деформации оказывается линейной.
Закон Гука. Абсолютная величина силы упругости прямо пропорциональна величине деформации. В частности, для пружины, сжатой или растянутой на величину , сила упругости даётся формулой:
где — коэффициент жёсткости пружины.
Коэффициент жёсткости зависит не только от материала пружины, но также от её формы и размеров.
Из формулы (1) следует, что график зависимости силы упругости от (малой) деформации является прямой линией (рис. 1 ):
Коэффициент жёсткости — о угловой коэффициент в уравнении прямой . Поэтому справедливо равенство:
где — угол наклона данной прямой к оси абсцисс. Это равенство удобно использовать при экспериментальном нахождении величины .
Подчеркнём ещё раз, что закон Гука о линейной зависимости силы упругости от величины деформации справедлив лишь при малых деформациях тела. Когда деформации перестают быть малыми, эта зависимость перестаёт быть линейной и приобретает более сложный вид. Соответственно, прямая линия на рис. 1 — это лишь небольшой начальный участок криволинейного графика, описывающего зависимость от при всех значениях деформации .
Понятие жесткости
Жесткость как физическая величина характеризует силу, которую нужно приложить к пружине для достижения определенной степени растяжения или сжатия.
Коэффициент жесткости рассчитывается по формуле Гука:
где $F$ — сила, развиваемая пружиной, $k$ — коэффициент жесткости, зависящий от ее характеристик (см. выше) и измеряемый в ньютонах на метр, $x$ — абсолютное приращение расстояния, на которое изменилась длина пружины после приложения внешней силы. Знак минус в правой части формулы свидетельствует о том, что сила, порождаемая пружиной, действует в противоположном по отношению к нагрузке направлении.
Коэффициент жесткости можно вычислить экспериментально, подвешивая на расположенную вертикально и закрепленную за верхний конец пружину грузы с известной массой. В этом случае имеет место зависимость
$m cdot g — k cdot x = 0$,
где $m$ — масса, $g$ — ускорение свободного падения. Отсюда


