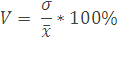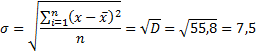Как найти коэффициент вариации что это

Простое объяснение коэффициента вариации на примере оценок студентов. Дисперсии и станд. отклонения разные, коэффициент вариации первого меньше второго (первый учится ровнее).

нет определения

Определение[править | править код]

Коэффициент вариации определяется как отношение стандартного отклонения σ к среднему μ:

${displaystyle {c_{rm {v}}}={frac {sigma }{mu }}}$

^[1]

Он показывает степень изменчивости по отношению к среднему показателю выборки. Коэффициент вариации следует вычислять только для данных, измеренных на шкале отношений, то есть шкал, которые имеют значимый нуль и, следовательно, допускают относительное сравнение двух измерений. Коэффициент вариации может не иметь никакого значения для данных интервальной шкалы. Например, большинство температурных шкал (например, Цельсий, Фаренгейт и т. д.) являются интервальными шкалами с произвольными нулями, поэтому вычисленный коэффициент вариации будет отличаться в зависимости от используемой шкалы. С другой стороны, температура Кельвина имеет значимый нуль, полное отсутствие тепловой энергии, и, таким образом, является шкалой отношения. Говоря простым языком, имеет смысл сказать, что 20 кельвинов в два раза горячее, чем 10 кельвинов, но только в этой шкале с истинным абсолютным нулем. Хотя стандартное отклонение может быть измерено в Кельвинах, градусах Цельсия или Фаренгейта, вычисленное значение применимо только к этой шкале. Только шкала Кельвина может быть использована для вычисления действительного коэффициента вариации.

Измерения, которые распределены логнормально, демонстрируют стационарный КВ; напротив, КОО изменяется в зависимости от ожидаемого значения измерений.

Более надежной возможностью является квартильный коэффициент дисперсии, половина межквартильного диапазона делится на среднее значение квартилей . В большинстве случаев КВ вычисляется для одной независимой переменной (например, для одного фабричного продукта) с многочисленными повторяющимися измерениями зависимой переменной (например, ошибка в производственном процессе). Однако данные, которые являются линейными или даже логарифмически нелинейными и включают непрерывный диапазон для независимой переменной с разреженными измерениями по каждому значению (например, точечная диаграмма), могут поддаваться одиночному вычислению КВ с использованием подхода оценки максимального правдоподобия.

Примеры[править | править код]

Набор данных [100, 100, 100] имеет постоянные значения. Его выборочное стандартное отклонение равно 0, а среднее — 100, что дает коэффициент вариации:

${displaystyle {frac {0}{100}}=0}$

Набор данных [90, 100, 110] имеет бóльшую вариабельность. Его выборочное стандартное отклонение равно 10, а среднее — 100, что дает коэффициент вариации:

${displaystyle {frac {10}{100}}=0.1}$

Набор данных [1, 5, 6, 8, 10, 40, 65, 88] имеет еще бóльшую изменчивость. Его выборочное стандартное отклонение составляет 32,9, а среднее — 27,9, что дает коэффициент вариации:

${displaystyle {frac {32.9}{27.9}}=1.18}$

Примеры неправильного использования[править | править код]

Сравнение коэффициентов вариации между параметрами с использованием относительных единиц может привести к различиям, которые могут быть нереальными. Если мы сравним один и тот же набор температур в градусах Цельсия и Фаренгейта (обе относительные единицы, где Кельвин и шкала Ранкина являются их соответствующими абсолютными значениями):

По Цельсию: [0, 10, 20, 30, 40]

По Фаренгейту: [32, 50, 68, 86, 104]

Стандартные отклонения составляют 15,81 и 28,46 соответственно. КВ первого набора составляет 15,81 / 20 = 79 %.

Для второго набора (при тех же температурах) он составляет 28,46/68 = 42 %.

Если, например, наборы данных — это показания температуры от двух разных датчиков (датчика со шкалой Цельсия и датчика со шкалой Фаренгейта), и вы хотите знать, какой датчик лучше, выбирая тот, который имеет наименьшее отклонение, то вы будете введены в заблуждение, если используете КВ. Проблема здесь в том, что вы разделили на относительную величину, а не на абсолютную.

Сравнение одного и того же набора данных, теперь в абсолютных единицах:

По Кельвину: [273.15, 283.15, 293.15, 303.15, 313.15]

По Ранкину: [491.67, 509.67, 527.67, 545.67, 563.67]

Стандартные отклонения выборок по-прежнему составляют 15,81 и 28,46 соответственно, поскольку на стандартное отклонение не влияет постоянное смещение. Однако, коэффициенты вариации теперь равны 5,39 %.

С математической точки зрения коэффициент вариации не является полностью линейным. То есть для случайной величины Х, коэффициент вариации aX + b равен коэффициенту вариации X только если b = 0. В приведенном выше примере градусы Цельсия могут быть преобразованы в градусы Фаренгейта только с помощью линейного преобразования формы ax + b с b ≠ 0, в то время как градусы Кельвина можно преобразовать в градусы Ранкина через линейное преобразование ax.

Оценка[править | править код]

Когда доступна только выборка данных из популяции, коэффициент вариации в популяции можно оценить, используя отношение стандартного отклонения выборки s к выборочному среднему значению x:

${displaystyle {c_{rm {v}}}={frac {s}{bar {x}}}}$

Но эта оценка, применяемая к небольшой или средней выборке, имеет тенденцию быть слишком не точной: это смещённая оценка. Для нормально распределенных данных несмещенной оценкой для выборки размером n является:

${displaystyle {displaystyle {widehat {c_{rm {v}}}}^{*}={bigg (}1+{frac {1}{4n}}{bigg )}{widehat {c_{rm {v}}}}}}$

Логнормальные данные[править | править код]

Во многих приложениях можно предположить, что данные распределены логарифмически нормально (об этом свидетельствует наличие асимметрии в выборке данных). В таких случаях более точна оценка, полученная из свойств логнормального распределения, которая определяется как:

${displaystyle {displaystyle {widehat {cv}}_{rm {raw}}={sqrt {mathrm {e} ^{s_{rm {ln}}^{2}}-1}}}}$

где ${displaystyle {displaystyle {s_{rm {ln}}}}}$ — выборочное стандартное отклонение данных после преобразования натурального логарифма.

Сравнение со стандартным отклонением[править | править код]

Преимущества[править | править код]

Коэффициент вариации полезен, поскольку стандартное отклонение данных всегда должно пониматься в контексте среднего значения данных. В отличие от этого, фактическое значение КВ не зависит от единицы измерения, поэтому оно является безразмерным числом. Для сравнения наборов данных с различными единицами измерения или сильно отличающимися средними величинами следует использовать коэффициент вариации вместо стандартного отклонения.

Недостатки[править | править код]

Когда среднее значение близко к нулю, коэффициент вариации приближается к бесконечности и поэтому чувствителен к небольшим изменениям среднего. Это часто происходит, если значения не исходят из шкалы отношений
В отличие от стандартного отклонения, его нельзя использовать непосредственно для построения доверительных интервалов для среднего значения.

Приложения[править | править код]

Коэффициент вариации также распространен в прикладных областях вероятности, таких как теория обновления, теория массового обслуживания и теория надежности. В этих областях экспоненциальное распределение часто важнее нормального распределения. Стандартное отклонение экспоненциального распределения равно его среднему значению, поэтому коэффициент вариации равен 1. Распределения с КВ< 1 (например, распределение Эрланга) считаются с низкой дисперсией, в то время как распределения с КВ > 1 (например, гиперэкспоненциальное распределение) считаются с высокой дисперсией. Некоторые формулы в этих полях выражаются с помощью квадратного коэффициента вариации, часто сокращенного ККВ. По существу, КВ заменяет термин стандартного отклонения на среднеквадратичное отклонение. В то время как многие естественные процессы действительно показывают корреляцию между средним значением и величиной вариации вокруг него, точные сенсорные устройства должны быть сконструированы таким образом, чтобы коэффициент вариации был близок к нулю, то есть давал постоянную абсолютную ошибку в их рабочем диапазоне.

В актуарных расчётах КВ известен как унифицированный риск.

При промышленной переработке твердых частиц КВ особенно важен для измерения степени однородности порошковой смеси. Сравнение рассчитанного КВ со спецификацией позволит определить, достигнута ли достаточная степень смешивания.

Как мера экономического неравенства[править | править код]

Коэффициент вариации удовлетворяет требованиям для измерения экономического неравенства. Если x (с элементами x_i) — это список значений экономического показателя (например, богатство), а x_i -богатство агента i, то выполняются следующие требования:

1. Анонимность — c_v не зависит от упорядоченности списка x. Это следует из того, что дисперсия и среднее значение не зависят от упорядоченности списка x.

2. c_v(x)=c_v(αx), где α-действительное число.

3. Если {x, x} является списком x, присоединенным к самому себе, то c_v ({x, x})=c_v (x).

4. Принцип переноса Пигу-Дальтона: когда богатство передается от более богатого агента i к более бедному агенту j (то есть x_i > x_j) без изменения их ранга, то c_v уменьшается и наоборот.

c_v принимает свое минимальное значение равное нулю для полного равенства (все x_i равны). Наиболее заметным недостатком является то, что он не ограничен сверху, поэтому он не может быть нормализован, чтобы быть в пределах фиксированного диапазона (например, как коэффициент Джини, который ограничен между 0 и 1). Однако он лучше поддается анализу, в отличие от коэффициента Джини.

Распределение[править | править код]

При условии, что отрицательные и малые положительные значения выборочного среднего встречаются с пренебрежимо малой частотой, распределение вероятности коэффициента вариации для выборки размера n было показано Хендриксом и Роби:

${displaystyle mathrm {d} F_{c_{rm {v}}}={frac {2}{pi ^{1/2}Gamma left({frac {n-1}{2}}right)}};mathrm {e} ^{-{frac {n}{2left({frac {sigma }{mu }}right)^{2}}}{frac {{c_{rm {v}}}^{2}}{1+{c_{rm {v}}}^{2}}}}{frac {{c_{rm {v}}}^{n-2}}{(1+{c_{rm {v}}}^{2})^{n/2}}}sideset {}{^{prime }}sum _{i=0}^{n-1}{frac {(n-1)!,Gamma left({frac {n-i}{2}}right)}{(n-1-i)!,i!,}}{frac {n^{i/2}}{2^{i/2}left({frac {sigma }{mu }}right)^{i}}}{frac {1}{(1+{c_{rm {v}}}^{2})^{i/2}}},mathrm {d} c_{rm {v}}}$

где символ ∑ указывает, что суммирование закончено только четными значениями n −1- i, то есть, если n нечетное, сумма над четными значениями i, и если n является четным, сумма только над нечетными значениями i.

Это полезно при построении статистических гипотез или доверительных интервалов. Статистический вывод для коэффициента вариации в нормально распределенных данных часто основан на приближении хи-квадрат Маккея для коэффициента вариации.

См. также[править | править код]

ω — коэффициент
Семплирование (математическая статистика)

Примечания[править | править код]

↑ Brian Everitt. The Cambridge dictionary of statistics : [англ.]. — Cambridge University Press, 1988. — P. 67. — 360 p.

Источник

Коэффициент вариации

Из
всех показателей вариации среднеквадратическое
отклонение в наибольшей степени
используется для проведения других
видов статистического анализа. Однако
среднеквадратическое отклонение дает
абсолютную оценку меры разбросанности
значений и чтобы понять, насколько она
велика относительно самих значений,
требуется относительный показатель.
Такой показатель называется он коэффициент
вариации.

Формула
коэффициента вариации:

Данный
показатель измеряется в процентах (если
умножить на 100%).

В
статистике принято, что, если коэффициент
вариации

меньше
10%, то степень рассеивания данных
считается незначительной,

от
10% до 20% – средней,

больше
20% и меньше или равно 33% – значительной,

значение
коэффициента вариации не превышает
33%, то совокупность считается однородной,

если
больше 33%, то – неоднородной.

Средние,
рассчитанные для однородной совокупности
– значимы, т.е. действительно характеризуют
эту совокупность, для неоднородной
совокупности – незначимы, не характеризуют
совокупность из-за значительного
разброса значений признака в совокупности.

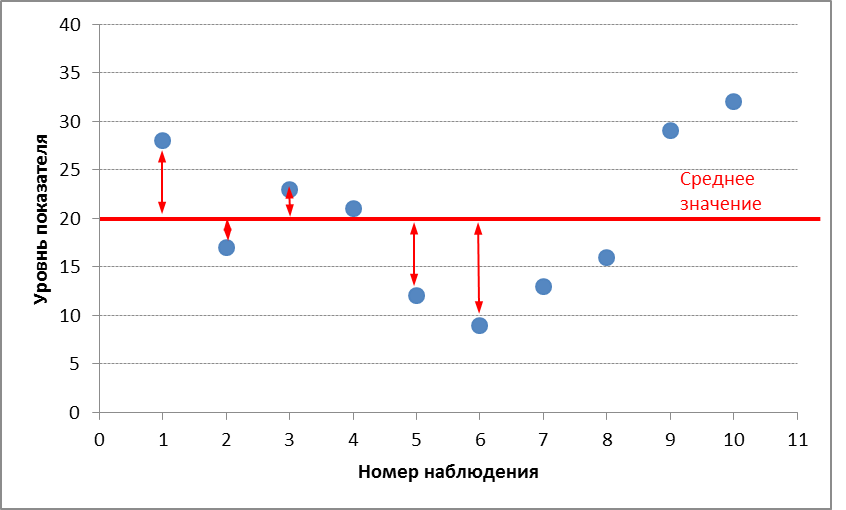
Возьмем
пример с расчетом среднего линейного
отклонения.

И
график для напоминания

По
этим данным рассчитаем: среднее значение,
размах вариации, среднее линейное
отклонение, дисперсию и стандартное
отклонение.

Среднее
значение – это обычная средняя
арифметическая.

Размах
вариации – разница между максимумом и
минимумом:

Среднее
линейное отклонение считается по
формуле:

Дисперсия
считается по формуле:

Среднеквадратическое
отклонение – квадратный корень из
дисперсии:

Расчет
сведем в табличку.

Вариация
показателя отражает изменчивость
процесса или явления. Ее степень может
измеряться с помощью нескольких
показателей.

Размах
вариации –
разница между максимумом и минимумом.
Отражает диапазон возможных значений.
Среднее
линейное отклонение –
отражает среднее из абсолютных (по
модулю) отклонений всех значений
анализируемой совокупности от их
средней величины.
Дисперсия –
средний квадрат отклонений.
Среднеквадратическое
отклонение –
корень из дисперсии (среднего квадрата
отклонений).
Коэффициент
вариации –
наиболее универсальных показатель,
отражающий степень разбросанности
значений независимо от их масштаба и
единиц измерения. Коэффициент вариации
измеряется в процентах и может быть
использован для сравнения вариации
различных процессов и явлений.

Таким
образом, в статистическом анализе
существует система показателей,
отражающих однородность явлений и
устойчивость процессов. Часто показатели
вариации не имеют самостоятельного
смысла и используются для дальнейшего
анализа данных. Исключением является
коэффициент вариации, который характеризует
однородность данных, что является ценной
статистической характеристикой.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Коэффициент вариации – это статистическая метрика, которая может помочь специалистам зарегистрировать изменения в данных с течением времени. Эта метрика также может быть эффективным методом расчета финансового риска и вознаграждения за инвестиционную деятельность. Вы можете рассчитать коэффициент вариации с помощью простой формулы.

В этой статье мы обсудим, что такое коэффициент вариации и как его рассчитать, а также приведем несколько примеров применения этого статистического измерения к различным инвестиционным сценариям.

Основные выводы:

Коэффициент вариации – это эффективная метрика для быстрой оценки относительной дисперсии точек данных вокруг среднего значения выборки.
Финансовые аналитики и инвесторы могут часто оценивать коэффициент вариации для анализа риска и волатильности в зависимости от ожидаемой доходности инвестиций.
Более низкое соотношение между стандартным отклонением и средним значением может указывать на более высокий коэффициент доходности, в то время как более высокое соотношение может указывать на более низкий коэффициент доходности.

Что такое коэффициент вариации?

Коэффициент вариации (CV) измеряет разброс точек данных вокруг среднего значения. Отношение стандартного отклонения к среднему значению делает CV ценным ресурсом при сравнении вариаций одного ряда данных с другим. Он показывает, насколько сильно варьируются данные в выборке по сравнению со средним значением популяции.

Когда вы оцениваете CV, вы можете представить значение в процентах, где более низкий процент может указывать на более низкий CV, а более высокий процент может означать более высокий CV. В финансовом и инвестиционном анализе, где волатильность и риск могут влиять на потенциальную доходность, более низкий CV означает более низкое соотношение риска и доходности, что указывает на лучший компромисс между потенциальной доходностью и риском, присущим конкретному инвестиционному инструменту.

Какова формула для коэффициента вариации?

Формула CV использует стандартное отклонение и среднее значение данных вашей выборки для расчета коэффициента, отражающего дисперсию ваших значений вокруг среднего. В статистическом анализе основной формулой для расчета коэффициента вариации является:

CV = стандартное отклонение выборочного среднего x 100

При применении формулы в бизнесе, например, в финансовых расчетах, многие специалисты упрощают формулу CV, чтобы она соответствовала таким финансовым показателям, как доходность инвестиций, прирост капитала, риск и волатильность инвестиций. Поэтому многие аналитики могут также использовать следующую формулу для расчета CV с точки зрения финансового риска и вознаграждения:

CV = прогнозируемая доходность волатильности x 100

Использование коэффициента вариации

Вы можете использовать КВ для определения соотношения риска и доходности, а также для определения того, превышает ли вознаграждение риск инвестиций. КВ также иногда может привести к неточному или непригодному для использования значению. Например, вычисление отрицательного значения или нуля может указывать на то, что измерение коэффициента неточно отражает ваш коэффициент. Нахождение коэффициента вариации в данных относится не только к сфере бизнеса и финансов.

Например, биологи и исследователи часто используют его в своих наблюдениях для расчета повторяемости результатов данных. Педагоги также могут применять CV для сравнения методик преподавания, выясняя, что приводит к повышению среднего балла. Метеорологи используют его для измерения временной изменчивости осадков. Однако существуют некоторые споры относительно точности CV в этих ситуациях. При широком диапазоне переменных и условий возрастает вероятность неточности.

Как рассчитать коэффициент вариации

Чтобы рассчитать коэффициент вариации, выполните следующие шаги, используя вышеупомянутую формулу:

1. Определите волатильность

Чтобы найти волатильность или стандартное отклонение, вычтите среднюю цену за период из каждой ценовой точки. Чтобы преобразовать разницу в дисперсию, возведите в квадрат, просуммируйте и усредните ответ. Квадратный корень из дисперсии становится приемлемым процентом для волатильности.

2. Определение ожидаемой доходности

Чтобы найти ожидаемую доходность, умножьте потенциальные исходы или доходность на вероятность их наступления. Сумма всех собранных ответов становится ожидаемой доходностью. На данном этапе оба показателя готовы для формулы.

3. Разделить

Рассчитав показатели волатильности и ожидаемой доходности, разделите их друг на друга. Большинство ответов дается в виде десятичных дробей. Вы также можете преобразовать CV в проценты.

4. Умножить на 100

Чтобы перевести в проценты, умножьте десятичные числа на 100. При этом десятичный знак сдвигается на две цифры, создавая либо целое число, либо десятичный процент. Окончательный ответ – коэффициент вариации.

Как рассчитать коэффициент вариации в электронной таблице

Некоторые предприятия и частные лица используют электронные таблицы для записи больших объемов данных за длительные периоды времени. Они выбирают электронные таблицы не только для того, чтобы успевать за огромным количеством собранных данных, но и для того, чтобы легко рассчитать коэффициент вариации в своих данных. Электронные таблицы могут записывать расчеты вместе с данными и продолжать их по мере добавления новых данных. Вы можете рассчитать коэффициент вариации с помощью электронной таблицы, выполнив следующие три шага:

1. Используйте функцию стандартного отклонения для набора данных

Программы для работы с электронными таблицами должны иметь определенную функцию для стандартного отклонения. Для того чтобы расчет работал, набор данных должен содержать эту функцию. Во многих распространенных программах электронных таблиц для вычисления стандартного отклонения можно ввести команду =STDEVP. Введите формулу в пустую ячейку рядом с соответствующим набором данных, который вы оцениваете.

2. Рассчитайте среднее значение

Вычисление среднего значения в электронных таблицах требует специальных формул. Например, в большинстве приложений электронных таблиц вы можете использовать =AVERAGE для применения программной функции. При вводе команды среднего значения поместите его в ячейку рядом с соответствующим набором данных, чтобы легче его увидеть.

3. Разделите стандартное отклонение на среднее значение

Разделите ячейки, содержащие стандартное отклонение и среднее значение. Например, чтобы разделить стандартное отклонение в ячейке A3 и среднее значение в ячейке A5, вы можете использовать функцию =A3A5 в пустой ячейке для вычисления коэффициента и отображения коэффициента вариации.

Некоторые программы обработки электронных таблиц могут вычислять коэффициент вариации с помощью команды =STDEV.P, что устраняет необходимость в нескольких шагах. В зависимости от программы, вы можете просто ввести команду в пустую ячейку и обозначить диапазон данных, которые вы хотите рассчитать. После этого в выбранной ячейке появится значение CV.

Пример расчета

Чтобы принять обоснованное решение между акциями и облигациями, Джамиля применяет формулу коэффициента вариации для определения соотношения риска и доходности для обоих инвестиционных инструментов. Сначала она оценивает инвестиции в акции, волатильность которых составляет 5%, а прогнозируемая доходность – 13%. Используя эти значения в формуле, Джамиля находит:

CV = среднее стандартное отклонение выборки x 100 =
CV = прогнозируемая доходность волатильности x 100 =
CV = (0.05) (0.13) x 100 = 0.38 x 100 = 38%

Чтобы рассчитать коэффициент вариации облигации для сравнения, Джамиля делит волатильность в 3% на прогнозируемую доходность в 15%. Используя формулу, она оценивает:

CV = стандартное отклонение выборочного среднего x 100 =
CV = прогнозируемая доходность волатильности x 100 =
CV = (0.03) (0.15) x 100 = 0.2 = 20%

Джамиля сравнивает инвестиции в облигации и акции и приходит к выводу, что CV инвестиций в облигации в размере 20% указывает на более низкое соотношение риска и доходности, чем CV акций в размере 38%. Теперь, когда Джамиля понимает, какой инвестиционный инструмент представляет наименьшее соотношение риска и доходности, она может выбрать наиболее подходящий вариант для достижения своих финансовых целей.

Источник

Коэффициент вариации и стандартное отклонение: разница

17 авг. 2022 г.
читать 2 мин

Стандартное отклонение набора данных — это способ измерить, насколько среднее значение отличается от среднего.

Чтобы найти стандартное отклонение данного образца , мы можем использовать следующую формулу:

s = √(Σ(x i – x ) 2 / (n-1))

куда:

Σ: символ, означающий «сумма».
x i : значение i -го наблюдения в выборке
x : среднее значение выборки
n: размер выборки

Чем выше значение стандартного отклонения, тем более разбросаны значения в выборке. Однако трудно сказать, является ли заданное значение стандартного отклонения «высоким» или «низким», потому что это зависит от типа данных, с которыми мы работаем.

Например, стандартное отклонение 500 можно считать низким, если речь идет о годовом доходе жителей определенного города. И наоборот, стандартное отклонение 50 можно считать высоким, если мы говорим об экзаменационных баллах студентов по определенному тесту.

Один из способов понять, является ли определенное значение стандартного отклонения высоким или низким, состоит в том, чтобы найти коэффициент вариации , который рассчитывается как:

CV = с / х

куда:

s: Стандартное отклонение выборки
x : Среднее значение выборки

Проще говоря, коэффициент вариации — это отношение между стандартным отклонением и средним значением.

Чем выше коэффициент вариации, тем выше стандартное отклонение выборки относительно среднего значения.

Пример: расчет стандартного отклонения и коэффициента вариации

Предположим, у нас есть следующий набор данных:

Набор данных: 1, 4, 8, 11, 13, 17, 19, 19, 20, 23, 24, 24, 25, 28, 29, 31, 32

Используя калькулятор, мы можем найти следующие показатели для этого набора данных:

Среднее значение выборки ( x ): 19,29
Стандартное отклонение выборки (с): 9,25

Затем мы можем использовать эти значения для расчета коэффициента вариации:

CV = с / х
КВ = 9,25/19,29
КВ = 0,48

Для этого набора данных полезно знать как стандартное отклонение, так и коэффициент вариации.

Стандартное отклонение говорит нам о том, что типичное значение в этом наборе данных отличается от среднего на 9,25 единицы. Затем коэффициент вариации говорит нам, что стандартное отклонение составляет примерно половину среднего значения выборки.

Стандартное отклонение против коэффициента вариации: когда использовать каждый

Стандартное отклонение чаще всего используется, когда мы хотим узнать разброс значений в одном наборе данных.

Однако коэффициент вариации чаще используется, когда мы хотим сравнить вариацию между двумя наборами данных.

Например, в финансах коэффициент вариации используется для сравнения среднего ожидаемого дохода от инвестиций с ожидаемым стандартным отклонением инвестиций.

Например, предположим, что инвестор рассматривает возможность инвестирования в следующие два взаимных фонда:

Взаимный фонд A: среднее = 9%, стандартное отклонение = 12,4%

Взаимный фонд B: среднее = 5%, стандартное отклонение = 8,2%

Инвестор может рассчитать коэффициент вариации для каждого фонда:

CV для взаимного фонда A = 12,4% / 9% = 1,38
CV для взаимного фонда B = 8,2% / 5% = 1,64

Поскольку взаимный фонд А имеет более низкий коэффициент вариации, он предлагает лучшую среднюю доходность по сравнению со стандартным отклонением.

Резюме

Вот краткое изложение основных моментов в этой статье:

И стандартное отклонение, и коэффициент вариации измеряют разброс значений в наборе данных.
Стандартное отклонение измеряет, насколько далеко среднее значение от среднего.
Коэффициент вариации измеряет отношение стандартного отклонения к среднему значению.
Стандартное отклонение используется чаще, когда мы хотим измерить разброс значений в одном наборе данных.
Коэффициент вариации чаще используется, когда мы хотим сравнить вариацию между двумя разными наборами данных.

Дополнительные ресурсы

Как рассчитать среднее и стандартное отклонение в Excel
Как рассчитать коэффициент вариации в Excel

Источник

Определение[править | править код]

Примеры[править | править код]

Примеры неправильного использования[править | править код]

Оценка[править | править код]

Логнормальные данные[править | править код]