Как найти коэффициент вариации
Математическая статистика немыслима без изучения вариации и, в том числе, расчета коэффициента вариации. Он получил самое большое применение на практике благодаря несложному расчету и наглядности результата.

Вам понадобится
- – вариация из нескольких числовых значений;
- – калькулятор.
Инструкция
Сначала найдите выборочную среднюю. Для этого сложите все значения вариационного ряда и разделите их на количество изучаемых единиц. Например, если требуется найти коэффициент вариации трех показателей 85, 88 и 90 для расчета выборочной средней надо прибавить эти значения и поделить на 3: х(ср)=(85+88+90)/3=87,67.
Затем рассчитайте ошибку репрезентативности выборочной средней (среднее квадратическое отклонение). Для этого из каждого значения выборки вычтите среднее значение, найденное в первом шаге. Возведите все разности в квадрат и сложите полученные результаты между собой. Вы получили числитель дроби. В примере расчет будет выглядеть так: (85-87,67)^2+(88-87,67)^2+(90-87,67)^2=(-2,67)^2+0,33^2+2,33^2=7,13+0,11+5,43=12,67.
Чтобы получить знаменатель дроби умножьте количество элементов выборки n на (n-1). В примере это будет выглядеть как 3х(3-1)=3х2=6.
Разделите числитель на знаменатель и из полученного числа выразите дробь, чтобы получить ошибку репрезентативности Sх. У вас получится 12,67/6=2,11. Корень из 2,11 равен 1,45.
Приступайте к самому главному: найдите коэффициент вариации. Для этого разделите полученную ошибку репрезентативности на выборочную среднюю, найденную в первом шаге. В примере 2,11/87,67=0,024. Чтобы получить результат в процентах, умножьте полученное число на 100% (0,024х100%=2,4%). Вы нашли коэффициент вариации, и он равен 2,4%.
Обратите внимание, полученный коэффициент вариации довольно незначительный, поэтому вариация признака считается слабой и изучаемую совокупность вполне можно считать однородной. Если бы коэффициент превышал 0,33 (33%), то среднюю величину нельзя было считать типичной, и изучать по ней совокупность было бы неверно.
Полезный совет
Вы можете проверить результат «на глаз», чтобы убедится в его верности. Оцените примерно элементы выборки, если они почти не отличаются, у вас должен получиться незначительный процент отклонения. Чем сильнее разброс значений показателя, тем больше будет коэффициент вариации.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
17 авг. 2022 г.
читать 2 мин
Коэффициент вариации , часто обозначаемый как CV, представляет собой способ измерения степени разброса значений в наборе данных по отношению к среднему значению. Он рассчитывается как:
CV = σ / μ
куда:
σ = стандартное отклонение набора данных
μ = среднее значение набора данных
Проще говоря, коэффициент вариации — это просто отношение между стандартным отклонением и средним значением.
Когда используется коэффициент вариации?
Коэффициент вариации часто используется для сравнения вариации между двумя разными наборами данных.
В реальном мире он часто используется в финансах для сравнения среднего ожидаемого дохода от инвестиций с ожидаемым стандартным отклонением инвестиций. Это позволяет инвесторам сравнивать соотношение риска и доходности между инвестициями.
Например, предположим, что инвестор рассматривает возможность инвестирования в следующие два взаимных фонда:
Взаимный фонд A: среднее = 7%, стандартное отклонение = 12,4%
Взаимный фонд B: среднее = 5%, стандартное отклонение = 8,2%
При расчете коэффициента вариации для каждого фонда инвестор находит:
CV для взаимного фонда A = 12,4% / 7% = 1,77
CV для взаимного фонда B = 8,2% / 5% = 1,64
Поскольку взаимный фонд B имеет более низкий коэффициент вариации, он предлагает лучшую среднюю доходность по сравнению со стандартным отклонением.
Как рассчитать коэффициент вариации в Excel
В Excel нет встроенной формулы для расчета коэффициента вариации для набора данных, но, к счастью, его относительно легко вычислить, используя пару простых формул. В следующем примере показано, как рассчитать коэффициент вариации для заданного набора данных.
Предположим, у нас есть следующий набор данных, содержащий экзаменационные оценки 20 студентов:
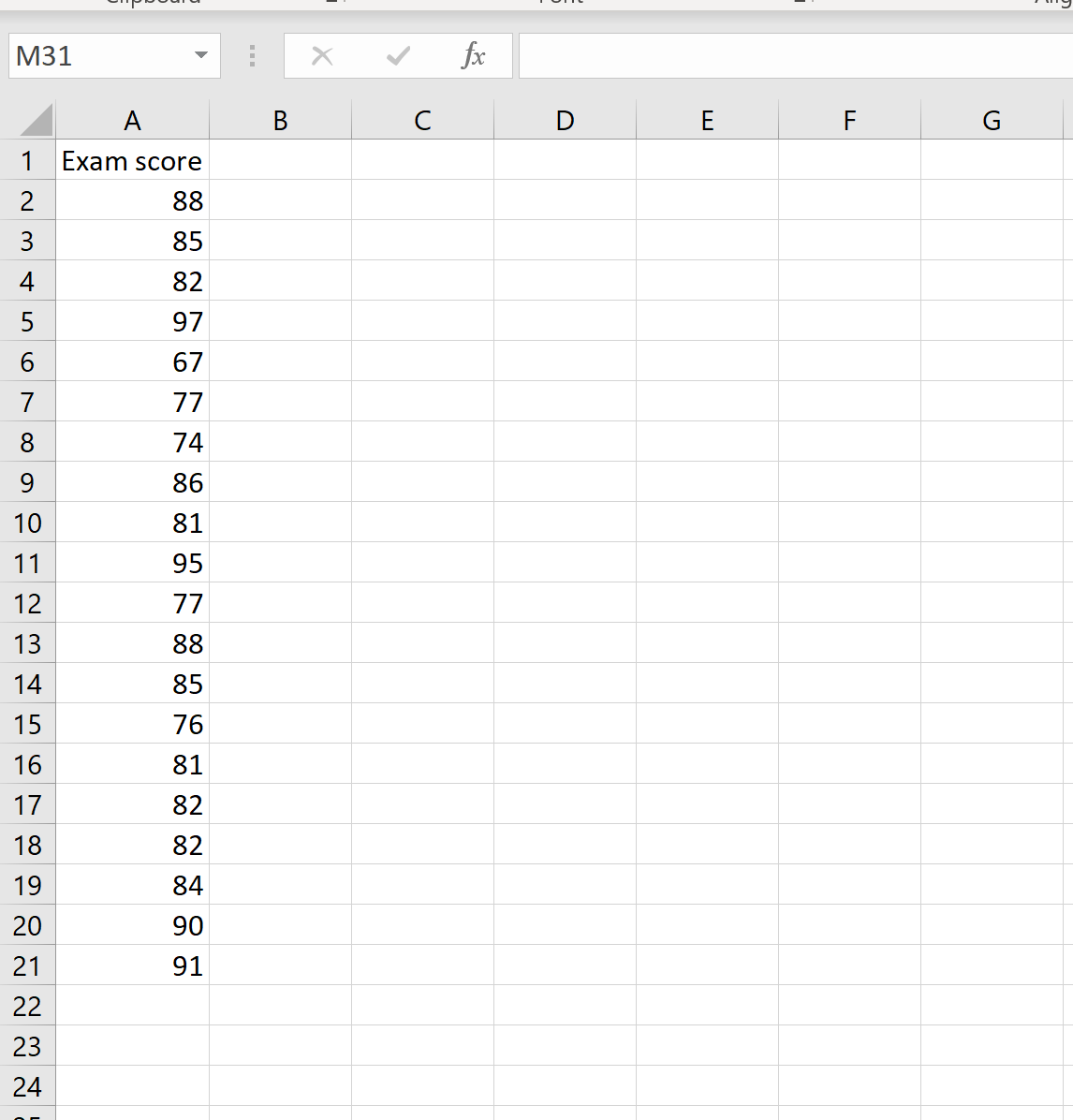
Чтобы рассчитать коэффициент вариации для этого набора данных, нам нужно знать только два числа: среднее значение и стандартное отклонение. Их можно рассчитать по следующим формулам:
Среднее значение: =СРЕДНЕЕ(A2:A21)
Стандартное отклонение: =СТАНДОТКЛОН(A2:A21)
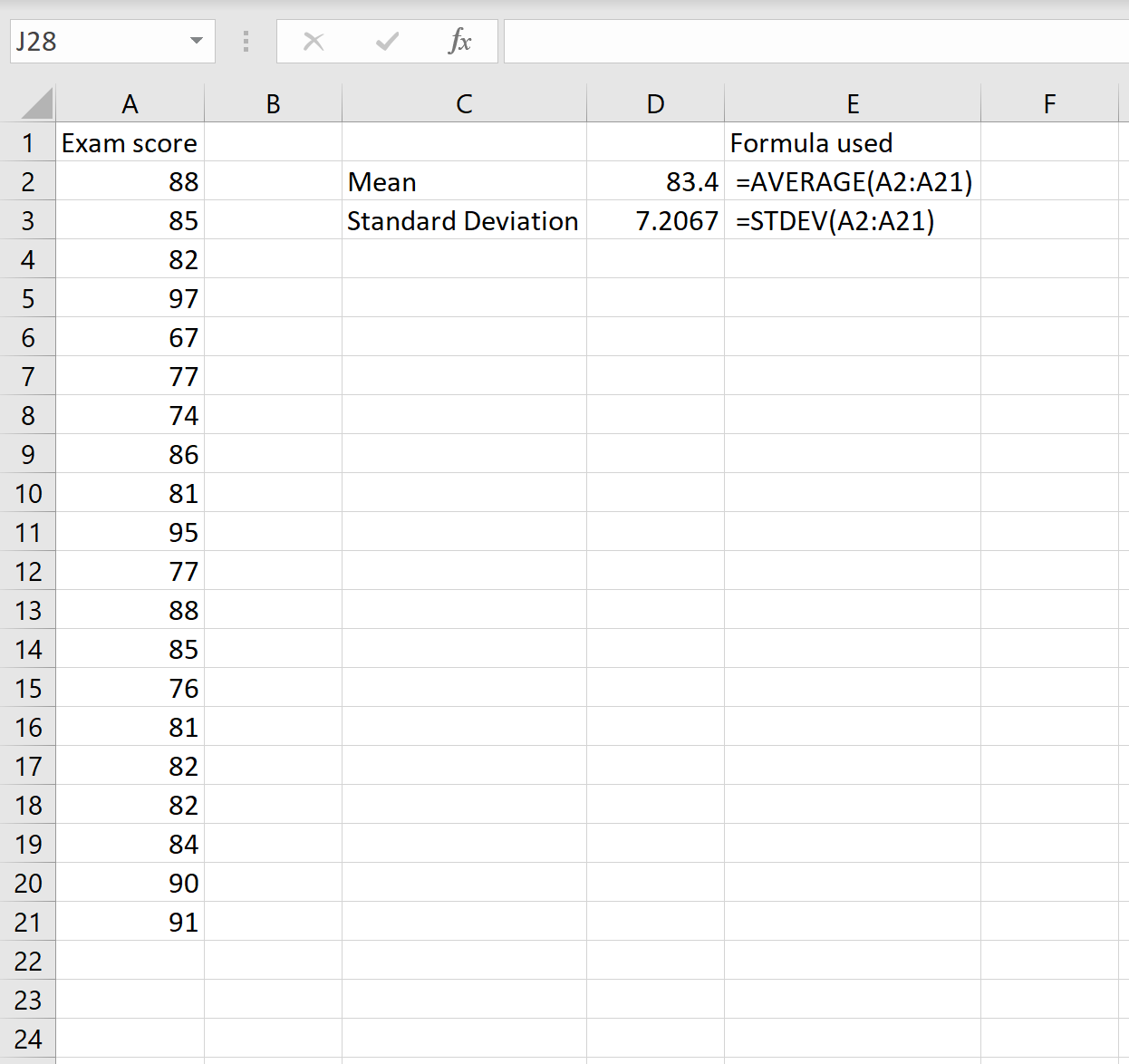
Чтобы вычислить коэффициент вариации, мы затем делим стандартное отклонение на среднее значение:
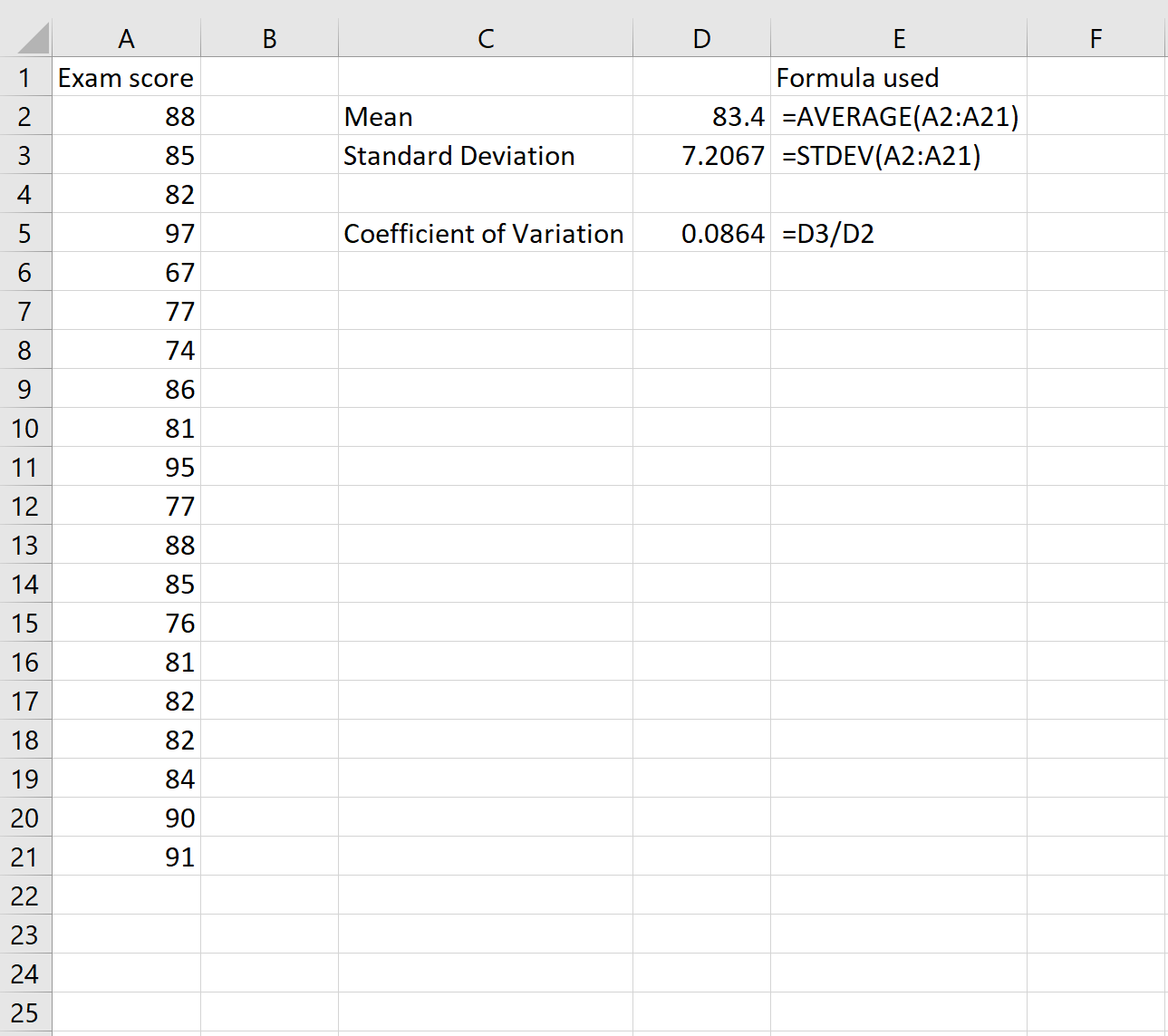
Коэффициент вариации оказывается равным 0,0864 .
Обратите внимание, что мы также могли бы использовать только одну формулу для расчета CV:
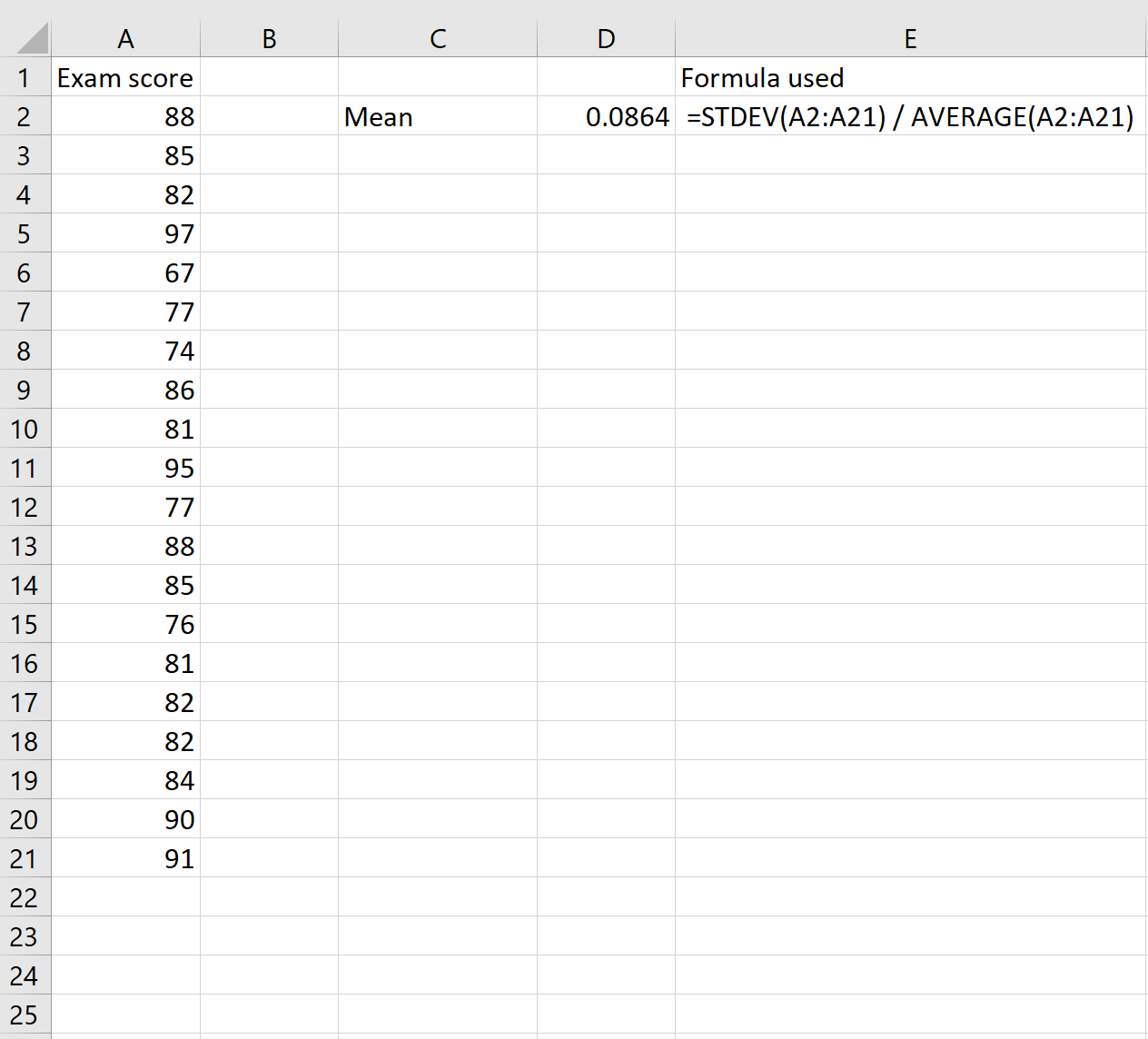
Это приводит к тому же CV 0,0864 .
По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города:
| Размер вклада, руб. | До 400 | 400 – 600 | 600 – 800 | 800 – 1000 | Свыше 1000 |
|---|---|---|---|---|---|
| Число вкладчиков | 32 | 56 | 120 | 104 | 88 |
Определите:
1) размах вариации;
2) средний размер вклада;
3) среднее линейное отклонение;
4) дисперсию;
5) среднее квадратическое отклонение;
6) коэффициент вариации вкладов.
Решение:
Данный ряд распределения содержит открытые интервалы. В таких рядах условно принимается величина интервала первой группы равна величине интервала последующей, а величина интервала последней группы равна величине интервала предыдущей.
Величина интервала второй группы равна 200, следовательно, и величина первой группы также равна 200. Величина интервала предпоследней группы равна 200, значит и последний интервал будет иметь величину, равную 200.
| Размер вклада, руб. | 200 – 400 | 400 – 600 | 600 – 800 | 800 – 1000 | 1000 – 1200 |
|---|---|---|---|---|---|
| Число вкладчиков | 32 | 56 | 120 | 104 | 88 |
1) Определим размах вариации как разность между наибольшим и наименьшим значением признака:
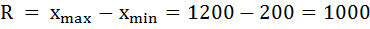
Размах вариации размера вклада равен 1000 рублей.
2) Средний размер вклада определим по формуле средней арифметической взвешенной.
Предварительно определим дискретную величину признака в каждом интервале. Для этого по формуле средней арифметической простой найдём середины интервалов.
Среднее значение первого интервала будет равно:
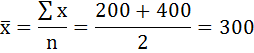
второго – 500 и т. д.
Занесём результаты вычислений в таблицу:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х | xf |
|---|---|---|---|
| 200-400 | 32 | 300 | 9600 |
| 400-600 | 56 | 500 | 28000 |
| 600-800 | 120 | 700 | 84000 |
| 800-1000 | 104 | 900 | 93600 |
| 1000-1200 | 88 | 1100 | 96800 |
| Итого | 400 | – | 312000 |
Средний размер вклада в Сбербанке города будет равен 780 рублей:
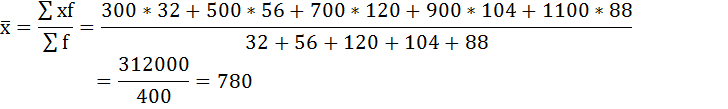
3) Среднее линейное отклонение есть средняя арифметическая из абсолютных отклонений отдельных значений признака от общей средней:
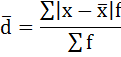
Порядок расчёта среднего линейонго отклонения в интервальном ряду распределения следующий:
1. Вычисляется средняя арифметическая взвешенная, как показано в п. 2).
2. Определяются абсолютные отклонения вариант от средней:
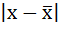
3. Полученные отклонения умножаются на частоты:
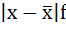
4. Находится сумма взвешенных отклонений без учёта знака:
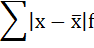
5. Сумма взвешенных отклонений делится на сумму частот:
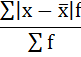
Удобно пользоваться таблицей расчётных данных:
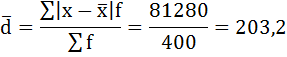
Среднее линейное отклонение размера вклада клиентов Сбербанка составляет 203,2 рубля.
4) Дисперсия – это средняя арифметическая квадратов отклонений каждого значения признака от средней арифметической.
Расчёт дисперсии в интервальных рядах распределения производится по формуле:
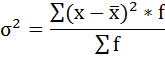
Порядок расчёта дисперсии в этом случае следующий:
1. Определяют среднюю арифметическую взвешенную, как показано в п. 2).
2. Находят отклонения вариант от средней:

3. Возводят в квадрат отклонения каждой варианты от средней:
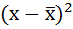
4. Умножают квадраты отклонений на веса (частоты):
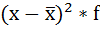
5. Суммируют полученные произведения:
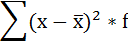
6. Полученная сумма делится на сумму весов (частот):
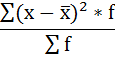
Расчёты оформим в таблицу:
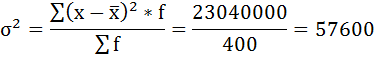
5) Среднее квадратическое отклонение размера вклада определяется как корень квадратный из дисперсии:
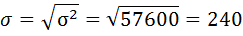
6) Коэффициент вариации – это отношение среднего квадратического отклонения к средней арифметической:
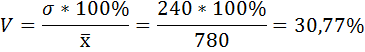
По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значений признаков вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.
Коэффициент вариации в статистике применяется для сравнения разброса двух случайных величин с разными единицами измерения относительно ожидаемого значения. В итоге можно получить сопоставимые результаты. Показатель наглядно иллюстрирует однородность временного ряда.
Коэффициент вариации используется также инвесторами при портфельном анализе в качестве количественного показателя риска, связанного с вложением средств в определенные активы. Особенно эффективен в ситуации, когда у активов разная доходность и различный уровень риска. К примеру, у одного актива высокая ожидаемая доходность, а у другого – низкий уровень риска.
Как рассчитать коэффициент вариации в Excel
Коэффициент вариации представляет собой отношение среднеквадратического отклонения к среднему арифметическому. Для расчета в статистике используется следующая формула:
CV = σ / ǩ,
- CV – коэффициент вариации;
- σ – среднеквадратическое отклонение по выборке;
- ǩ – среднеарифметическое значение разброса значений.
Коэффициент вариации позволяет сравнить риск инвестирования и доходность двух и более портфелей активов. Причем последние могут существенно отличаться. То есть показатель увязывает риск и доходность. Позволяет оценить отношение между среднеквадратическим отклонением и ожидаемой доходностью в относительном выражении. Соответственно, сопоставить полученные результаты.
При принятии инвестиционного решения необходимо учитывать следующий момент: когда ожидаемая доходность актива близка к 0, коэффициент вариации может получиться большим. Причем показатель значительно меняется при незначительном изменении доходности.
В Excel не существует встроенной функции для расчета коэффициента вариации. Но можно найти частное от стандартного отклонения и среднего арифметического значения. Рассмотрим на примере.
Доходность двух ценных бумаг за предыдущие пять лет:

Наглядно это можно продемонстрировать на графике:
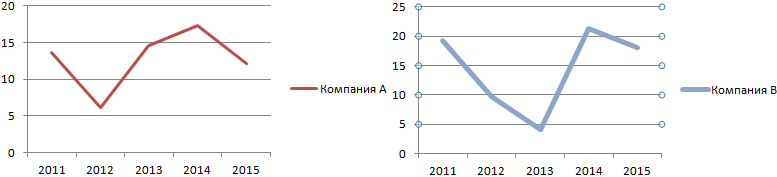
Обычно показатель выражается в процентах. Поэтому для ячеек с результатами установлен процентный формат.
Значение коэффициента для компании А – 33%, что свидетельствует об относительной однородности ряда. Формула расчета коэффициента вариации в Excel:

Сравните: для компании В коэффициент вариации составил 50%: ряд не является однородным, данные значительно разбросаны относительно среднего значения.
Интерпретация результатов
Прежде чем включить в инвестиционный портфель дополнительный актив, финансовый аналитик должен обосновать свое решение. Один из способов – расчет коэффициента вариации.
Ожидаемая доходность ценных бумаг составит:
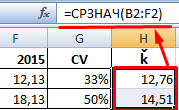
Среднеквадратическое отклонение доходности для активов компании А и В составляет:
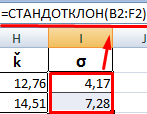
Ценные бумаги компании В имеют более высокую ожидаемую доходность. Они превышают ожидаемую доходность компании А в 1,14 раза. Но и инвестировать в активы предприятия В рискованнее. Риск выше в 1,7 раза. Как сопоставить акции с разной ожидаемой доходностью и различным уровнем риска?
Для сопоставления активов двух компаний рассчитан коэффициент вариации доходности. Показатель для предприятия В – 50%, для предприятия А – 33%. Риск инвестирования в ценные бумаги фирмы В выше в 1,54 раза (50% / 33%). Это означает, что акции компании А имеют лучшее соотношение риск / доходность. Следовательно, предпочтительнее вложить средства именно в них.
Таким образом, коэффициент вариации показывает уровень риска, что может оказаться полезным при включении нового актива в портфель. Показатель позволяет сопоставить ожидаемую доходность и риск. То есть величины с разными единицами измерения.
Коэффициент вариации
Из
всех показателей вариации среднеквадратическое
отклонение в наибольшей степени
используется для проведения других
видов статистического анализа. Однако
среднеквадратическое отклонение дает
абсолютную оценку меры разбросанности
значений и чтобы понять, насколько она
велика относительно самих значений,
требуется относительный показатель.
Такой показатель называется он коэффициент
вариации.
Формула
коэффициента вариации:
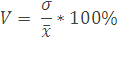
Данный
показатель измеряется в процентах (если
умножить на 100%).
В
статистике принято, что, если коэффициент
вариации
меньше
10%, то степень рассеивания данных
считается незначительной,
от
10% до 20% – средней,
больше
20% и меньше или равно 33% – значительной,
значение
коэффициента вариации не превышает
33%, то совокупность считается однородной,
если
больше 33%, то – неоднородной.
Средние,
рассчитанные для однородной совокупности
– значимы, т.е. действительно характеризуют
эту совокупность, для неоднородной
совокупности – незначимы, не характеризуют
совокупность из-за значительного
разброса значений признака в совокупности.
Возьмем
пример с расчетом среднего линейного
отклонения.

И
график для напоминания
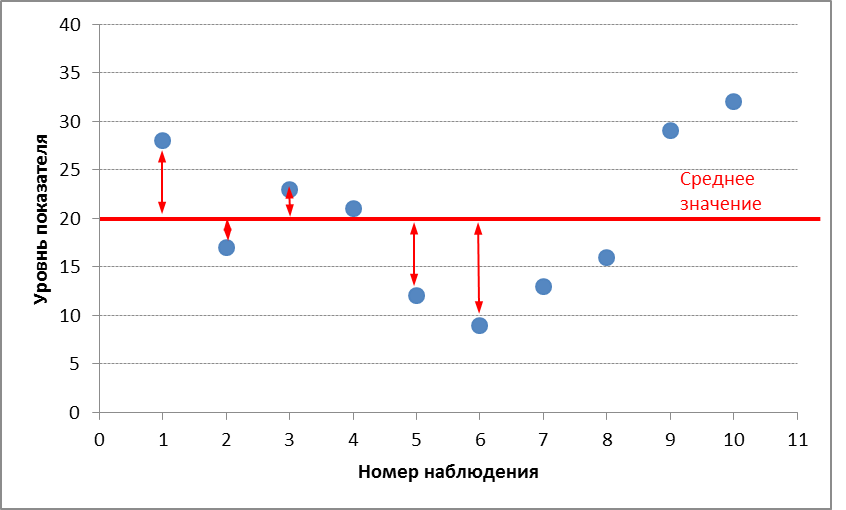
По
этим данным рассчитаем: среднее значение,
размах вариации, среднее линейное
отклонение, дисперсию и стандартное
отклонение.
Среднее
значение – это обычная средняя
арифметическая.
![]()
Размах
вариации – разница между максимумом и
минимумом:
![]()
Среднее
линейное отклонение считается по
формуле:
![]()
Дисперсия
считается по формуле:
![]()
Среднеквадратическое
отклонение – квадратный корень из
дисперсии:
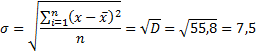
Расчет
сведем в табличку.

Вариация
показателя отражает изменчивость
процесса или явления. Ее степень может
измеряться с помощью нескольких
показателей.
-
Размах
вариации –
разница между максимумом и минимумом.
Отражает диапазон возможных значений. -
Среднее
линейное отклонение –
отражает среднее из абсолютных (по
модулю) отклонений всех значений
анализируемой совокупности от их
средней величины. -
Дисперсия –
средний квадрат отклонений. -
Среднеквадратическое
отклонение –
корень из дисперсии (среднего квадрата
отклонений). -
Коэффициент
вариации –
наиболее универсальных показатель,
отражающий степень разбросанности
значений независимо от их масштаба и
единиц измерения. Коэффициент вариации
измеряется в процентах и может быть
использован для сравнения вариации
различных процессов и явлений.
Таким
образом, в статистическом анализе
существует система показателей,
отражающих однородность явлений и
устойчивость процессов. Часто показатели
вариации не имеют самостоятельного
смысла и используются для дальнейшего
анализа данных. Исключением является
коэффициент вариации, который характеризует
однородность данных, что является ценной
статистической характеристикой.
7
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

