Как найти коэффициент вязкости газа - Сайт, где вы сможете решить свои вопросы

Коэффициент вязкости – это величина, используемая для обозначения силы внутреннего трения текучих веществ. Вязкость – разновидность явлений переноса. Жидкости и газы оказывают сопротивление перемещению двух слоев относительно друг друга. Эта особенность характерна для текучих веществ, связана с движением частиц, из которых и состоят вещества.

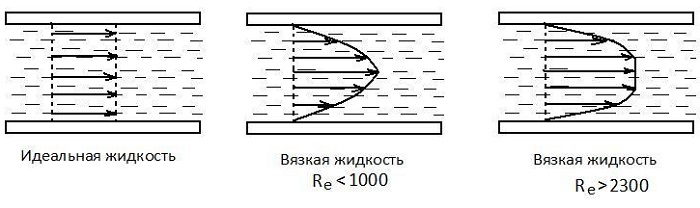
Вязкость называют внутренним трением. В его основе находится хаотическое движение молекул, передающих импульс между слоями. Такие импульсные обмены выравнивают скорости перемещения слоев.

Коэффициент динамической вязкости

Численное обозначение абсолютной вязкости является индексом сопротивляемости испытуемых веществ взаимному перемещению или скольжению их слоев.

Единицей измерения коэффициента в системе СИ приняты паскаль-секунды:

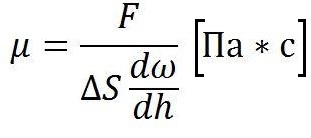
Физическая основа динамического показателя заключается в его соответствии касательному напряжению, которое происходит между слоями вещества, перемещающимися относительно друг друга, при условии расстояния между ними, равного единице длины, и на скорости, равной единице.

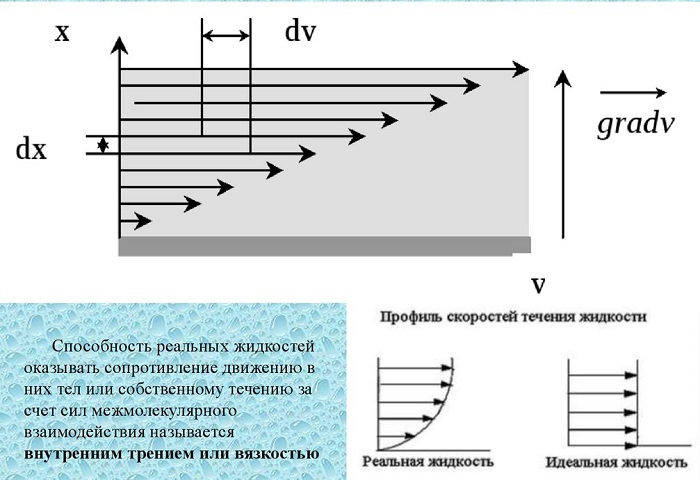
Вязкость жидкости

Вязкость жидкости определяется формулой, в которой динамический коэффициент определяет пропорциональность скорости движения слоев и расстояния между ними:

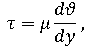
τ – касательное напряжение;
µ – показатель пропорциональности, который является динамическим индексом вещества.

Закон вязкости жидкости был установлен Ньютоном в конце 17 века. Абсолютный показатель зависит от типа газа или жидкости, температуры веществ.

Коэффициент динамической вязкости газа

Для основных газов величины коэффициента при температуре 0 – 600 градусов Цельсия представлены в таблице:

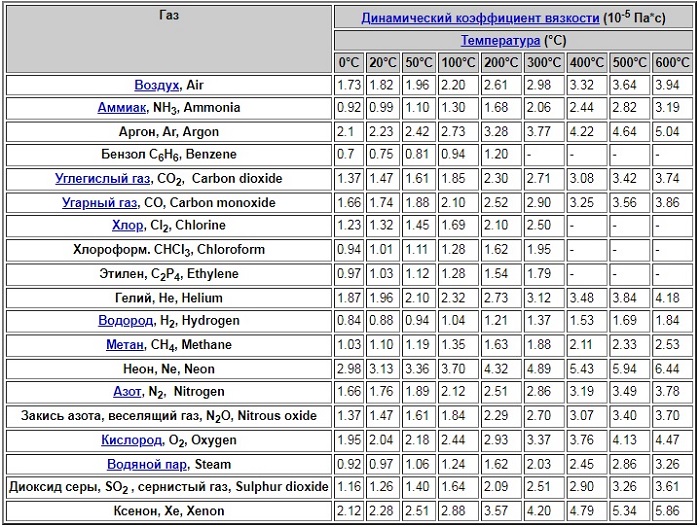
Коэффициент вязкости жидкостей

Для органических жидкостей показания напрямую зависят от температуры. Ниже приведена таблица со значениями абсолютного индекса для веществ при температурах от 0 до 100 градусов Цельсия.

Единица измерения – миллипаскаль-секунды, что соответствует сантипуазам.

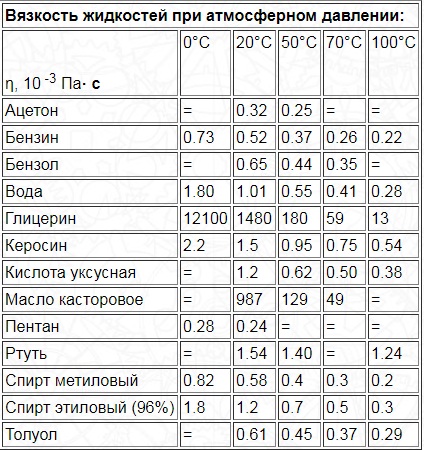
Коэффициент динамической вязкости жидкостей уменьшается при условии нагревания вещества. Другими словами, чем выше температура жидкости, тем менее вязкой она становится.

Связь коэффициента вязкости с числами Рейнольдса и силой трения

Английский механик, физик и инженер Оскар Рейнольдс установил (1876 — 1883 гг.), что характер течения зависит от величины, не имеющей размерностью, и называемой числом Re.

Число Рейнольдса используют для отображения соотношения кинематической энергии вещества к энергопотерям на установленной длине в условиях внутреннего трения.

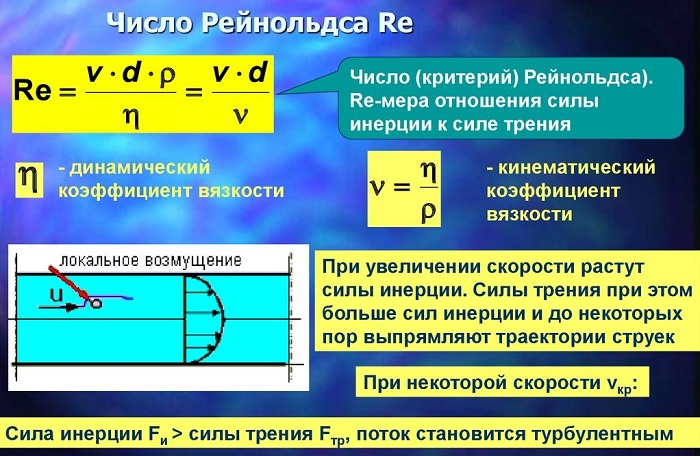
Примеры решения задач

Попробуем решить следующую задачу.

Установить тип движения жидкого вещества по трубам теплообменника, имеющего структуру «труба в трубе». Параметры внутренней трубы – 25*2 мм, внешней – 50*2,5 мм. Массовый расход воды составляет 4000 кг/ч (обозначение G). Плотность жидкости – 1000 кг/м³. Абсолютный индекс составляет 1•10^-3 Па*с.

Действие 1.

Следует узнать эквивалентный диаметр сечения межтрубного пространства:

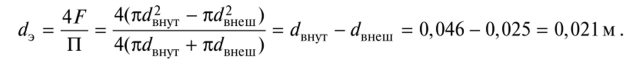
Действие 2.

Определение скорости воды на основе уравнения расхода:

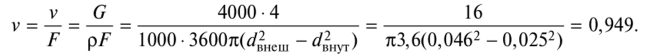
Действие 3.

По формуле Рейнольдса найти число Re:

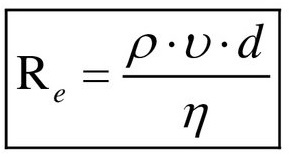
Подставляя значения, получаем:

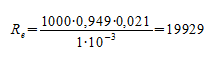
Ответ: режим перемещения воды в межтрубном пространстве является турбулентным.

Коэффициент кинематической вязкости

Кинематическая вязкость – это индекс, который отображает отношение абсолютного показателя вещества к его плотности при установленной температуре.

Физическая формула соотношения выглядит и единицы измерения можно увидеть на картинке:

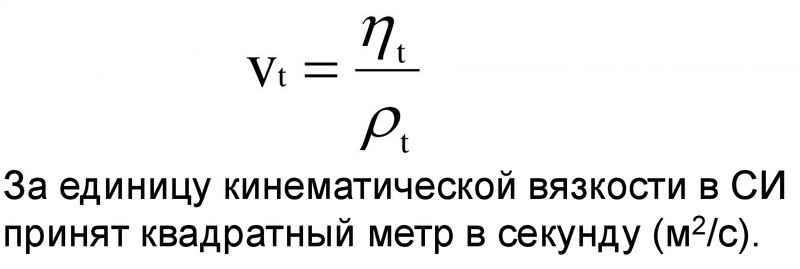
Действие 4. Вычисление кинематического показателя, исходя из формулы:

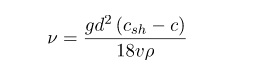
Подставив в уравнение полученные и имеющиеся расчетные данные, получим кинематический индекс вещества.

Заключение

Физический смысл коэффициента вязкости заключается в том, что он демонстрирует, чему равна величина F внутреннего трения, действующая на 1 ед. площади поверхности соприкасающихся слоев при единичном градиенте скорости.

Размерность данной величины и перевод из одних единиц измерения в другие показаны на картинке:

Источник

Механика сплошных сред

Сплошная среда
Классическая механика Закон сохранения массы · Закон сохранения импульса
Теория упругости Напряжение · Тензор · Твёрдые тела · Упругость · Пластичность · Закон Гука · Реология · Вязкоупругость
Гидродинамика Жидкость · Гидростатика · Гидродинамика · Вязкость · Ньютоновская жидкость · Неньютоновская жидкость · Поверхностное натяжение
Основные уравнения Уравнение непрерывности · Уравнение Эйлера · Уравнение Громеки — Лэмба · Уравнение Бернулли · Уравнения Навье — Стокса · Уравнение вихря · Уравнение диффузии · Закон Гука
См. также: Портал:Физика

Поведение жидкости с малой (сверху) и с большой (снизу) вязкостью

Вя́зкость (вну́треннее тре́ние) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате макроскопическая работа, затрачиваемая на это перемещение, рассеивается в виде тепла. Твёрдые тела (стекло, металлы, полупроводники, диэлектрики, ферромагнетики)^[1] также могут обладать вязкостью, но внутреннее трение в твёрдых телах в силу специфики явления обычно рассматривается отдельно в теории упругости и пластичности.

Механизм внутреннего трения в жидкостях и газах заключается в том, что движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.

Вязкость газов и жидкостей характеризуют динамическим коэффициентом вязкости (единица измерения в Международной системе единиц (СИ) — паскаль-секунда, Па·с, в системе СГС — пуаз, П; 1 Па·с = 10 П, 1 сП = 10⁻³ Па·с = 1 мПа·с) или кинематическим коэффициентом вязкости (единица измерения в СИ — м²/c, в СГС — стокс, Ст; 1 Ст = см²/с = 10⁻⁴ м²/с, 1 сСт = 1 мм²/с = 10⁻⁶ м²/с; внесистемная единица — градус Энглера). Кинематический коэффициент вязкости — отношение динамического коэффициента к плотности вещества. Классические методы измерения вязкости включают, например, измерение времени вытекания заданного объёма через калиброванное отверстие под действием силы тяжести. Прибор для измерения вязкости называется вискозиметром.

Переход вещества из жидкого состояния в стеклообразное обычно связывают с достижением вязкости порядка 10¹¹—10¹² Па·с.

Сила вязкого трения[править | править код]

Если параллельные плоские тела площадью S каждое, находящиеся на малом расстоянии h, движутся в той же плоскости со скоростью vec{v} друг относительно друга, а пространство между телами заполнено жидкостью или газом, то на каждое из них действует сила, в простейшем случае пропорциональная относительной скорости vec{v} и площади S и обратно пропорциональная расстоянию между телами h:

${displaystyle {vec {F}}sim -{frac {{vec {v}}cdot S}{h}}.}$

Коэффициент пропорциональности, зависящий от природы жидкости или газа, называют коэффициентом динамической вязкости. Этот закон был предложен Исааком Ньютоном в 1687 году и носит его имя (закон вязкости Ньютона). Экспериментальное подтверждение закона было получено в начале XIX века в опытах Кулона с крутильными весами и в экспериментах Хагена и Пуазёйля с течением воды в капиллярах^[2].

Эта сила называется силой вязкого трения. Её качественное отличие от сухого трения, кроме прочего, в том, что она пропорциональна скорости. Следовательно, при наличии только вязкого трения и сколь угодно малой внешней силы тело обязательно придёт в движение, то есть для вязкого трения не существует трения покоя.

Вторая вязкость[править | править код]

Вторая вязкость, или объёмная вязкость, — внутреннее трение при переносе импульса в направлении движения. Влияет только при учёте сжимаемости и (или) при учёте неоднородности коэффициента второй вязкости по пространству.

Если динамическая (и кинематическая) вязкость характеризует деформацию чистого сдвига, то вторая вязкость характеризует деформацию объёмного сжатия.

Объёмная вязкость играет большую роль в затухании звука и ударных волн и экспериментально определяется путём измерения этого затухания.

Вязкость газов[править | править код]

В кинетической теории газов коэффициент внутреннего трения вычисляется по формуле

${displaystyle eta ={frac {1}{3}}langle urangle langle lambda rangle rho ,}$

где — средняя скорость теплового движения молекул, − средняя длина свободного пробега. Из этого выражения в частности следует, что вязкость не очень разреженных газов практически не зависит от давления, поскольку плотность rho прямо пропорциональна давлению, а длина пробега — обратно пропорциональна. Такой же вывод следует и для других кинетических коэффициентов для газов, например, для коэффициента теплопроводности. Однако этот вывод справедлив только до тех пор, пока разрежение газа не становится столь малым, что отношение длины свободного пробега к линейным размерам сосуда (число Кнудсена) не становится по порядку величины равным единице; в частности, это имеет место в сосудах Дьюара (термосах).

С повышением температуры вязкость большинства газов увеличивается, это объясняется увеличением средней скорости молекул газа , растущей с температурой как .

Влияние температуры на вязкость газов[править | править код]

В отличие от жидкостей, вязкость газов увеличивается с увеличением температуры (у жидкостей она уменьшается при увеличении температуры).

Формула Сазерленда может быть использована для определения вязкости идеального газа в зависимости от температуры:^[3]

${displaystyle mu =mu _{0}{frac {T_{0}+C}{T+C}}left({frac {T}{T_{0}}}right)^{3/2},}$

где

— динамическая вязкость (в Па·с) при заданной температуре

;

$mu _{0}$

— контрольная вязкость (в Па·с) при некоторой контрольной температуре $T_{0}$

;

— заданная температура в кельвинах;

$T_{0}$

— контрольная температура в кельвинах;

— постоянная Сазерленда для того газа, вязкость которого требуется определить.

Эту формулу можно применять для температур в диапазоне 0 < < 555 K и при давлениях менее 3,45 МПа с ошибкой менее 10 %, обусловленной зависимостью вязкости от давления.

Постоянная Сазерленда и контрольные вязкости газов при различных температурах приведены в таблице ниже:

Газ	, K	$T_{0}$ , K	$mu _{0}$ , мкПа·с
Воздух	120	291,15	18,27
Азот	111	300,55	17,81
Кислород	127	292,25	20,18
Углекислый газ	240	293,15	14,8
Угарный газ	118	288,15	17,2
Водород	72	293,85	8,76
Аммиак	370	293,15	9,82
Оксид серы(IV)	416	293,65	12,54
Гелий	79,4^[4]	273	19^[5]

Вязкость жидкостей[править | править код]

Динамическая вязкость[править | править код]

Внутреннее трение жидкостей, как и газов, возникает при движении жидкости вследствие переноса импульса в направлении, перпендикулярном к направлению движения. Для так называемых ньютоновских жидкостей (которых вокруг нас большинство) справедлив общий закон внутреннего трения — закон Ньютона:

${displaystyle tau =-eta {frac {partial v}{partial n}}.}$

Коэффициент вязкости eta (коэффициент динамической вязкости, динамическая вязкость) может быть получен на основе соображений о движениях молекул. Очевидно, что eta будет тем меньше, чем меньше время t «оседлости» молекул. Эти соображения приводят к выражению для коэффициента вязкости, называемому уравнением Френкеля — Андраде:

${displaystyle eta =Ce^{w/kT}.}$

Иная формула, представляющая коэффициент вязкости, была предложена Бачинским^[6]. Как показано, коэффициент вязкости определяется межмолекулярными силами, зависящими от среднего расстояния между молекулами; последнее определяется молярным объёмом вещества ${displaystyle V_{M}}$ . Многочисленные эксперименты показали, что между молярным объёмом и коэффициентом вязкости существует соотношение

${displaystyle eta ={frac {c}{V_{M}-V_{C}}},}$

где:

— константа, характерная для определённой жидкости;

${displaystyle V_{C}}$

— собственный объём, занимаемый частицами жидкости.

Динамическая вязкость жидкостей уменьшается с увеличением температуры и растёт с увеличением давления.

Кинематическая вязкость[править | править код]

В технике, в частности, при расчёте гидроприводов и в триботехнике, часто приходится иметь дело с величиной

$nu ={frac {eta }{rho }},$

и эта величина получила название кинематической вязкости^[7].

Здесь rho — плотность жидкости; eta — коэффициент динамической вязкости.

Кинематическая вязкость в старых источниках часто указана в сантистоксах (сСт). В СИ эта величина переводится следующим образом: 1 сСт = 1 мм²/c = 10⁻⁶ м²/c.

Условная вязкость[править | править код]

Условная вязкость — величина, косвенно характеризующая гидравлическое сопротивление течению, измеряемая временем истечения заданного объёма раствора через вертикальную трубку (определённого диаметра). Измеряют в градусах Энглера (по имени немецкого химика К. О. Энглера), обозначают — °ВУ. Определяется отношением времени истечения 200 мл испытываемой жидкости при данной температуре из специального вискозиметра ко времени истечения 200 мл дистиллированной воды из того же прибора при 20 °С. Условную вязкость до 16 °ВУ переводят в кинематическую по таблице ГОСТ, а условную вязкость, превышающую 16 °ВУ, по формуле

${displaystyle nu =7,4cdot 10^{-6}E_{t},}$

где — кинематическая вязкость (в м²/с), а ${displaystyle E_{t}}$ — условная вязкость (в °ВУ) при температуре t.

Ньютоновские и неньютоновские жидкости[править | править код]

Ньютоновскими называют жидкости, для которых вязкость не зависит от скорости деформации. В уравнении Навье — Стокса для ньютоновской жидкости имеет место аналогичный вышеприведённому закон вязкости (по сути, обобщение закона Ньютона, или закон Навье — Стокса^[8]):

${displaystyle sigma _{ij}=eta left({frac {partial v_{i}}{partial x_{j}}}+{frac {partial v_{j}}{partial x_{i}}}right),}$

где $sigma_{ij}$ — тензор вязких напряжений.

Среди неньютоновских жидкостей по зависимости вязкости от скорости деформации различают псевдопластики и дилатантные жидкости. Моделью с ненулевым напряжением сдвига (действие вязкости подобно сухому трению) является модель Бингама. Если вязкость меняется с течением времени, жидкость называется тиксотропной. Для неньютоновских жидкостей методика измерения вязкости получает первостепенное значение.

С повышением температуры вязкость многих жидкостей падает. Это объясняется тем, что кинетическая энергия каждой молекулы возрастает быстрее, чем потенциальная энергия взаимодействия между ними. Поэтому все смазки всегда стараются охладить, иначе это грозит простой утечкой через узлы.^{[источник не указан 1007 дней]}

Вязкость аморфных материалов[править | править код]

Вязкость аморфных материалов (например, стекла или расплавов) — это термически активизируемый процесс^[9]:

${displaystyle eta (T)=Aexp left({frac {Q}{RT}}right),}$

где

— энергия активации вязкости (Дж/моль);

— температура (К);

— универсальная газовая постоянная (8,31 Дж/моль·К);

— некоторая постоянная.

Вязкое течение в аморфных материалах характеризуется отклонением от закона Аррениуса: энергия активации вязкости изменяется от большой величины $Q_{H}$ при низких температурах (в стеклообразном состоянии) на малую величину $Q_{L}$ при высоких температурах (в жидкообразном состоянии). В зависимости от этого изменения аморфные материалы классифицируются либо как сильные, когда ${displaystyle (Q_{H}-Q_{L})<Q_{L}}$ , или ломкие, когда ${displaystyle (Q_{H}-Q_{L})geqslant Q_{L}}$ . Ломкость аморфных материалов численно характеризуется параметром ломкости Доримуса ${displaystyle R_{D}={frac {Q_{H}}{Q_{L}}}}$ : сильные материалы имеют ${displaystyle R_{D}<2}$ , в то время как ломкие материалы имеют ${displaystyle R_{D}geqslant 2}$ .

Вязкость аморфных материалов весьма точно аппроксимируется двуэкспоненциальным уравнением^[10]

${displaystyle eta (T)=A_{1}Tleft(1+A_{2}exp {frac {B}{RT}}right)left(1+Cexp {frac {D}{RT}}right)}$

с постоянными $A_{1}$ , $A_{2}$ , , и , связанными с термодинамическими параметрами соединительных связей аморфных материалов.

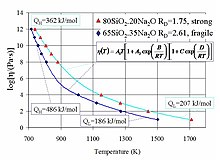
В узких температурных интервалах недалеко от температуры стеклования $T_{g}$ это уравнение аппроксимируется формулами типа VTF или сжатыми экспонентами Кольрауша.

Если температура существенно ниже температуры стеклования, ${displaystyle T<T_{g}}$ , двуэкспоненциальное уравнение вязкости сводится к уравнению типа Аррениуса

${displaystyle eta (T)=A_{L}Texp left({frac {Q_{H}}{RT}}right)}$

с высокой энергией активации $Q_{H}=H_{d}+H_{m}$ , где $H_{d}$ — энтальпия разрыва соединительных связей, то есть создания конфигуронов, а $H_{m}$ — энтальпия их движения. Это связано с тем, что при ${displaystyle T<T_{g}}$ аморфные материалы находятся в стеклообразном состоянии и имеют подавляющее большинство соединительных связей неразрушенными.

При ${displaystyle Tgg T_{g}}$ двуэкспоненциальное уравнение вязкости также сводится к уравнению типа Аррениуса

${displaystyle eta (T)=A_{H}Texp left({frac {Q_{L}}{RT}}right),}$

но с низкой энергией активации $Q_{L}=H_{m}$ . Это связано с тем, что при ${displaystyle Tgg T_{g}}$ аморфные материалы находятся в расправленном состоянии и имеют подавляющее большинство соединительных связей разрушенными, что облегчает текучесть материала.

Относительная вязкость[править | править код]

В технических науках часто пользуются понятием относительной вязкости, под которой понимают отношение коэффициента динамической вязкости (см. выше) раствора к коэффициенту динамической вязкости чистого растворителя:

${displaystyle mu _{r}={frac {mu }{mu _{0}}},}$

где

μ — динамическая вязкость раствора;

μ₀ — динамическая вязкость растворителя.

Вязкость некоторых веществ[править | править код]

Для авиастроения и судостроения наиболее важно знать вязкости воздуха и воды.

Вязкость воздуха[править | править код]

Зависимость вязкости сухого воздуха от давления при температурах 300, 400 и 500 K

Вязкость воздуха зависит в основном от температуры.
При 15,0 °C вязкость воздуха составляет 1,78⋅10⁻⁵ кг/(м·с) = 17,8 мкПа·с = 1,78⋅10⁻⁵ Па·с. Можно найти вязкость воздуха как функцию температуры с помощью программ расчёта вязкостей газов^[11].

Вязкость воды[править | править код]

Зависимость динамической вязкости воды от температуры в жидком состоянии (Liquid Water) и в виде пара (Vapor)

Динамическая вязкость воды составляет 8,90·10⁻⁴ Па·с при температуре около 25 °C. Как функция температуры: T = A × 10^B/(T−C), где A = 2,414·10⁻⁵ Па·с, B = 247,8 K, C = 140 K.

Значения динамической вязкости жидкой воды при разных температурах вплоть до точки кипения приведены в таблице:

Температура, °C	Вязкость, мПа·с
10	1,308
20	1,002
30	0,7978
40	0,6531
50	0,5471
60	0,4668
70	0,4044
80	0,3550
90	0,3150
100	0,2822

Динамическая вязкость разных веществ[править | править код]

Ниже приведены значения коэффициента динамической вязкости некоторых ньютоновских жидкостей:

Вязкость отдельных видов газов

Газ	при 0 °C (273 K), мкПа·с	при 27 °C (300 K), мкПа·с
воздух	17,4	18,6
водород	8,4	9,0
гелий		20,0
аргон		22,9
ксенон	21,2	23,2
углекислый газ		15,0
метан		11,2
этан		9,5

Вязкость жидкостей при 25 °C

Жидкость	Вязкость, Па·с	Вязкость, мПа·с
ацетон	3,06·10⁻⁴	0,306
бензол	6,04·10⁻⁴	0,604
кровь (при 37 °C)	(3—4)·10⁻³	3—4
касторовое масло	0,985	985
кукурузный сироп	1,3806	1380,6
этиловый спирт	1.074·10⁻³	1.074
этиленгликоль	1,61·10⁻²	16,1
глицерин (при 20 °C)	1,49	1490
мазут	2,022	2022
ртуть	1,526·10⁻³	1,526
метиловый спирт	5,44·10⁻⁴	0,544
моторное масло SAE 10 (при 20 °C)	0,065	65
моторное масло SAE 40 (при 20 °C)	0,319	319
нитробензол	1,863·10⁻³	1,863
жидкий азот (при 77K)	1,58·10⁻⁴	0,158
пропанол	1,945·10⁻³	1,945
оливковое масло	0,081	81
пек	2,3·10⁸	2,3·10¹¹
серная кислота	2,42·10⁻²	24,2
вода	8,94·10⁻⁴	0,894

Примечания[править | править код]

↑ Внутреннее трение в металлах, полупроводниках, диэлектриках и ферромагнетиках: Сб. статей / Под ред. Ф. Н. Тавадзе. — М.: Наука, 1978. — 235 с.
↑ О некоторых ошибках в курсах гидродинамики Архивная копия от 22 декабря 2015 на Wayback Machine, с. 3—4.
↑ Alexander J. Smits, Jean-Paul Dussauge Turbulent shear layers in supersonic flow Архивная копия от 17 июля 2017 на Wayback Machine. — Birkhäuser, 2006. — P. 46. — ISBN 0-387-26140-0.
↑ Data constants for Sutherland’s formula Архивная копия от 6 марта 2018 на Wayback Machine.
↑ Viscosity of liquids and gases Архивная копия от 3 октября 2017 на Wayback Machine.
↑ Хмельницкий Р. А. Физическая и коллоидная химия: Учебних для сельскохозяйственных спец. вузов. — М.: Высшая школа, 1988. — С. 40. — 400 с. — ISBN 5-06-001257-3.
↑ Попов Д. Н. Динамика и регулирование гидро- и превмосистем : Учеб. для машиностроительных вузов. — М. : Машиностроение, 176. — С. 175. — 424 с.
↑ Седов Л. И. Механика сплошной среды Архивная копия от 28 ноября 2014 на Wayback Machine. Т. 1. — М.: Наука, 1970. — С. 166.
↑ Френкель Я. И. Кинетическая теория жидкостей. — Ленинград, Наука, 1975. — с. 226.
↑ Ojovan M. Viscous flow and the viscosity of melts and glasses. Physics and Chemistry of Glasses, 53 (4) 143—150 (2012).
↑ Gas Viscosity Calculator Архивная копия от 21 июля 2011 на Wayback Machine.

Литература[править | править код]

R. H. Doremus. J. Appl. Phys., 92, 7619—7629 (2002).
M. I. Ojovan, W. E. Lee. J. Appl. Phys., 95, 3803—3810 (2004).
M. I. Ojovan, K. P. Travis, R. J. Hand. J. Phys.: Condensed Matter, 19, 415107 (2007).
Л. И. Седов. Механика сплошной среды. Т. 1. — М.: Наука, 1970. — 492 с.
П. Н. Гедык, М. И. Калашникова. Смазка металлургического оборудования. — М.: Металлургия, 1976. — 380 с.
И. Ф. Голубев. Вязкость газов и газовых смесей. — М.: Физматлит, 1959.
Ред. Ф. Н. Тавадзе Внутреннее трение в металлах, полупроводниках, диэлектриках и ферромагнетиках. — М., Наука, 1978. — 235 c.

Ссылки[править | править код]

Аринштейн А. Сравнительный вискозиметр Жуковского // Квант, № 9, 1983.
Измерение вязкости нефтепродуктов
Булкин П. С. Попова И. И., Общий физический практикум. Молекулярная физика
Градус условной вязкости // Большой энциклопедический политехнический словарь. — 2004.
Вязкость воды

Источник

Термодинамическая
система.

Термодинамическая
система —
это некая физическая
система,
состоящая из большого количества частиц,
способная обмениваться с окружающей
средой энергией и веществом.
Также обычно полагается, что такая
система подчиняется статистическим
закономерностям. Для термодинамических
систем справедливы законы термодинамики.

Для
описания термодинамической системы
вводят так называемые термодинамические
величины —
набор физических
величин,
значения которых определяют термодинамическое
состояние системы.
Примерами термодинамических величин
являются:

температура
давление
объем
внутренняя
энергия
энтропия
–
в статистической
физике — мера вероятности осуществления
какого-либо макроскопического состояния
энтальпия
– термодинамический
потенциал,
характеризующий состояние системы в
термодинамическом равновесии при
выборе в качестве независимых
переменных давления, энтропии и
числа частиц
свободная
энергия Гельмгольца
– термодинамический
потенциал, убыль которого
в квазистатическомизотермическом
процессе равна работе, совершённой
системой над внешними телами
энергия
Гиббса
– это
величина, показывающая изменение
энергии в ходе химической реакции и
дающая таким образом ответ на
принципиальную возможность протекания
химической реакции

Если
термодинамическое состояние системы
не меняется со временем,
то говорят, что система находится
в состоянии
равновесия.
Строго говоря, термодинамические
величины, приведённые выше, могут быть
определены только в состоянии
термодинамического равновесия.

Термодинамические
системы подразделяются на однородные
по составу (например, газ в
сосуде) и неоднородные (вода и пар или
смесь газов в сосуде).

Выделяют
также изолированные
системы,
то есть системы, которые не обмениваются
с окружающей средой ни энергией, ни
веществом, и закрытые
системы,
которые обмениваются со средой только
энергией, но не обмениваются веществом.
Если же в системе происходят обменные
процессы с окружающей средой, то её
называют открытой.

Состояние
термодинамической системы

В курсе
механики было введено понятие физической
системы (системы тел), для описания
изменений которой используются законы
динамики. Такую систему называют
механической системой. Когда кроме
законов механики требуется применение
законов термодинамики, систему
называют термодинамической
системой.
Необходимость использования этого
понятия возникает, если число элементов
системы (например, число молекул газа)
весьма велико, и движение отдельных её
элементов является микроскопическим
по сравнению с движением самой системы
или ее макроскопических составных
частей. При этом термодинамика описывает
макроскопические движения (изменения
макроскопических состояний)
термодинамической системы.

Параметры,
описывающие такое движение (изменения)
термодинамической системы, принято
разделять на внешние и внутренние.
Это разделение весьма условно и зависит
от конкретной задачи. Так, например, газ
в воздушном шаре с эластичной оболочкой
в качестве внешнего параметра имеет
давление окружающего воздуха, а для
газа в сосуде с жёсткой оболочкой внешним
параметром является объём, ограниченный
этой оболочкой. В термодинамической
системе объём и давление могут изменяться
независимо друг от друга. Для теоретического
описания их изменения необходимо
введение как минимум еще одного параметра
– температуры.

В
большинстве термодинамических задач
трёх параметров достаточно для описания
состояния термодинамической системы.
В этом случае изменения в системе
описываются с помощью трёх термодинамических
координат, связанных с соответствующими
термодинамическими параметрами.

Равновесным
состоянием – состоянием термодинамического
равновесия – называется такое состояния
термодинамической системы, в котором
отсутствуют всякие потоки (энергии,
вещества, импульса и т.д.), а макроскопические
параметры системы являются установившимися
и не изменяются во времени.

Классическая
термодинамика утверждает, что изолированная
термодинамическая система (предоставленная
себе самой) стремится к состоянию
термодинамического равновесия и после
его достижения не может самопроизвольно
из него выйти. Данное
утверждение часто называю нулевым
началом термодинамики.

Системы,
находящиеся в состоянии термодинамического
равновесия, обладают следующими
свойствами:

Если
две термодинамические системы, имеющие
тепловой контакт, находятся в состоянии
термодинамического равновесия, то и
совокупная термодинамическая система
находится в состоянии термодинамического
равновесия.

Если
какая-либо термодинамическая система
находится в термодинамическом равновесии
с двумя другими системами, то и эти две
системы находятся в термодинамическом
равновесии друг с другом.

Далее,
если не будет специально оговорено,
нами будут рассматриваться термодинамические
системы, находящиеся в состоянии
термодинамического равновесия. Описание
систем, находящихся в неравновесном
состоянии, то
есть в состоянии, когда имеют место
макроскопические потоки, занимается
неравновесная термодинамика, краткое
изложение основных положений которой
приведено в четвертой и шестой главах.

Переход
из одного термодинамического состояния
в другое называется термодинамическим
процессом.
Ниже, если не будет особо оговорено,
будут рассматриваться только
квазистатические
процессы или,
что то же самое, квазиравновесные
процессы.
Предельным случаем квазиравновесного
процесса является происходящий бесконечно
медленно равновесный процесс, состоящий
из непрерывно следующих друг за другом
состояний термодинамического равновесия.
Реально такой процесс протекать не
может, однако если макроскопические
изменения в системе происходят достаточно
медленно (за промежутки времени,
значительно превышающие время установления
термодинамического равновесия),
появляется возможность аппроксимировать
реальный процесс квазистатическим
(квазиравновесным). Такая аппроксимация
позволяет проводить вычисления с
достаточно высокой точностью для
большого класса практических задач.
Равновесный процесс является обратимым,
то есть таким, при котором возвращение
к значениям параметров состояния,
имевшим место в предыдущий момент
времени, должно приводить термодинамическую
систему в предыдущее состояние без
каких-либо изменений в окружающих
систему телах.

Практическое
применение квазиравновесных процессов
в каких-либо технических устройствах
малоэффективно. Так, использование в
тепловой машине квазиравновесного
процесса, например, происходящего при
практически постоянной температуре
(см. описание цикла Карно в третьей
главе), неминуемо приводит к тому, что
такая машина будет работать очень
медленно (в пределе – бесконечно медленно)
и иметь очень малую мощность. Поэтому
на практике квазиравновесные процессы
в технических устройствах не используются.
Тем не менее, так как предсказания
равновесной термодинамики для реальных
систем с достаточно высокой точностью
совпадают с экспериментально полученными
для таких систем данными, то она широко
применяется для расчета термодинамических
процессов в различных технических
устройствах.

Если
в ходе термодинамического процесса
система возвращается в исходное
состояние, то такой процесс называется
круговым или циклическим. Круговые
процессы, также как и любые другие
термодинамические процессы, могут быть
как равновесными (а следовательно –
обратимыми), так и неравновесными
(необратимыми). При обратимом круговом
процессе после возвращения термодинамической
системы в исходное состояние в окружающих
ее телах не возникает никаких
термодинамических возмущений, и их
состояния остаются равновесными. В этом
случае внешние параметры системы после
осуществления циклического процесса
возвращаются к своим исходным значениям.
При необратимом круговом процессе после
его завершения окружающие тела переходят
в неравновесные состояния и внешние
параметры термодинамической системы
изменяются.

Первое
начало термодинамики.

Первое
начало термодинамики —
один из трёх основных законов термодинамики,
представляет собой закон
сохранения энергии длятермодинамических
систем.

Первое
начало термодинамики было сформулировано
в середине XIX
века в
результате работ немецкого учёного Ю.
Р. Майера,
английского физика Дж.
П. Джоуля и
немецкого физика Г.
Гельмгольца.
Согласно первому началу термодинамики,
термодинамическая система может
совершать работу только
за счёт своей внутренней
энергии или
каких-либо внешних источников энергии.
Первое начало термодинамики часто
формулируют как невозможность
существования вечного
двигателя первого рода,
который совершал бы работу, не черпая
энергию из какого-либо источника.

Существует
несколько эквивалентных формулировок
первого начала термодинамики

В
любой изолированной системе запас
энергии остаётся постоянным. Это
— формулировка Дж.
П. Джоуля (1842
г.).
Количество
теплоты,
полученное системой, идёт на изменение
её внутренней энергии и совершение
работы против внешних сил
Изменение
внутренней энергии системы при переходе
её из одного состояния в другое равно
сумме работы внешних сил и количества
теплоты, переданного системе, то есть,
оно зависит только от начального и
конечного состояния системы и не зависит
от способа, которым осуществляется
этот переход. Это определение особенно
важно для химической термодинамики (ввиду
сложности рассматриваемых процессов).
Иными словами, внутренняя
энергия является функцией состояния.
В циклическом процессе внутренняя
энергия не изменяется.

Изменение
полной энергии системы в квазистатическом
процессе равно
количеству теплоты Q,
сообщённому системе, в сумме с изменением
энергии, связанной с количеством
вещества N при химическом
потенциале μ,
и работы A‘,
совершённой над системой внешними
силами и полями,
за вычетом работы A,
совершённой самой системой против
внешних сил

ΔU = Q − A +
μΔN + A‘.

Рассмотрим
несколько частных случаев:

Если δQ >
0,
то это означает, что тепло к
системе подводится.
Если δQ <
0,
аналогично — тепло отводится.
Если δQ =
0,
то система не обменивается теплом с
окружающей средой и называется адиабатически
изолированной.

Обобщая:
в конечном процессе
элементарные
количества теплоты могут быть любого
знака. Общее количество теплоты, которое
мы назвали просто Q —
это алгебраическая сумма количеств
теплоты, сообщаемых на всех участках
этого процесса. В ходе процесса теплота
может поступать в систему или уходить
из неё разными способами.

Первое
начало термодинамики:

при
изобарном процессе

при
изохорном процессе (A =
0)

при
изотермическом процессе (ΔU =
0)

Здесь
— масса газа,
— молярная
масса газа,
— молярная
теплоёмкость при
постоянном объёме,
— давление, объём и температура газа
соответственно, причём последнее
равенство верно только для идеального
газа.

Коли́чество
теплоты́ — энергия,
которую получает или теряет тело
при теплопередаче.
Количество теплоты является одной из
основных термодинамических
величин.

Количество
теплоты является функцией процесса,
а не функцией состояния,
то есть количество теплоты, полученное
системой, зависит от способа, которым
она была приведена в текущее состояние.

Единицы
измерения: Джоули Дж

Рассмотрим
систему, состоящую из двух тел A и B.
Предположим, что тело B заключено
почти полностью в жёсткую адиабатическую
оболочку, так что оно не способно
совершать макроскопическую
работу,
а обмениваться теплом (то есть энергией)
посредством микроскопических процессов
может лишь с телом A.
Предположим, что тело A также
заключено в адиабатическую оболочку
почти полностью, так что для него возможен
теплообмен лишь с B,
но не будем предполагать, что оболочка
жёсткая. Количеством
теплоты,
сообщённой телу A в
некотором процессе, будем называть
величину Q_A =
− ΔU_B,
где ΔU_B —
изменение внутренней
энергии тела B.
Согласно закону
сохранения энергии,

ΔA =
ΔU_A +
ΔU_B

где ΔA —
макроскопическая работа внешних сил
над телом A.
Если учесть, что

ΔA =
− A_int

где A_int —
работа, совершённая телом A,
то закону сохранения энергии можно
придать форму первого
начала термодинамики:

ΔQ_A =
ΔU_A + A_int

Из
первого начала термодинамики следует
корректность введённого определения
количества теплоты, то есть независимость
соответствующей величины от выбора
пробного тела B и
способа теплообмена между телами.
Заметим, что для определения количества
теплоты необходимо пробное тело, в
противном случае первое начало теряет
смысл содержательного закона и
превращается в определение количества
теплоты (весьма бесполезное в таком
виде). При определении количества теплоты
независимо от ΔA и ΔU_A первое
начало становится содержательным
законом, допускающим экспериментальную
проверку.

Отметим,
что, как и совершённая работа, количество
переданной теплоты зависит от конкретного
процесса, совершённого над телом.

Вну́тренняя
эне́ргия тела
(обозначается как E или U) —
это сумма энергий молекулярных
взаимодействий и тепловых движений
молекулы. Внутренняя энергия является
однозначной функцией состояния системы.
Это означает, что всякий раз, когда
система оказывается в данном состоянии,
её внутренняя энергия принимает присущее
этому состоянию значение, независимо
от предыстории системы. Следовательно,
изменение внутренней энергии при
переходе из одного состояния в другое
будет всегда равно разности между ее
значениями в конечном и начальном
состояниях, независимо от пути, по
которому совершался переход.

Внутреннюю
энергию тела нельзя измерить напрямую.
Можно определить только изменение
внутренней энергии:

где

—
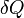
подведённая
к телу теплота,
измеренная в джоулях
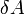
— работа,
совершаемая телом против внешних сил,
измеренная в джоулях

U
= A/q Эта формула является математическим
выражением первого
начала термодинамики

Согласно
закону Джоуля, выведенному эмпирически,
внутренняя энергия идеального
газа не
зависит от давления или объёма. Исходя
из этого факта, можно получить выражение
для изменения внутренней энергии
идеального газа. По определению молярной
теплоёмкости при
постоянном объёме,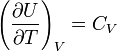
.
Так как внутренняя энергия идеального
газа является функцией только от
температуры, то

Эта
же формула верна и для вычисления
изменения внутренней энергии любого
тела, но только в процессах при постоянном
объёме (изохорных
процессах);
в общем случае C_V(T,V) является
функцией и температуры, и объёма.

Если
пренебречь изменением молярной
теплоёмкости при изменении температуры,
получим:

ΔU =
νC_VΔT,

где ν —
количество вещества, ΔT —
изменение температуры.

Уравнение
состояния идеального
газа (иногда уравнение
Клапейрона или уравнение Клапейрона — Менделеева) —
формула, устанавливающая зависимость
между давлением, молярным
объёмом и абсолютной
температурой идеального
газа.
Уравнение имеет вид:

где

— давление,
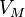
— молярный
объём,
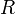
— универсальная
газовая постоянная
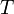
— абсолютная
температура,К.

Так
как
,
где
— количество
вещества,
а
,
где
—
масса,
— молярная
масса,
уравнение состояния можно записать:

Эта
форма записи носит имя уравнения (закона)
Менделеева — Клапейрона.

В
случае постоянной массы газа уравнение
можно записать в виде:

Последнее
уравнение называют объединённым
газовым законом.
Из него получаются законы Бойля —
Мариотта, Шарля и Гей-Люссака:

— закон
Бойля — Мариотта.

— Закон
Гей-Люссака.

— закон Шарля (второй
закон Гей-Люссака, 1808 г.)

Эмиль
Амага обнаружил,
что при высоких давлениях поведение газов отклоняется
от закона Бойля — Мариотта. И это
обстоятельство может быть прояснено
на основании молекулярных представлений.

С
одной стороны, в сильно сжатых газах
размеры самих молекул являются сравнимыми
с расстояниями между молекулами. Таким
образом, свободное пространство, в
котором движутся молекулы, меньше, чем
полный объём газа. Это обстоятельство
увеличивает число ударов молекул в
стенку, так как благодаря ему сокращается
расстояние, которое должна пролететь
молекула, чтобы достигнуть стенки.

С
другой стороны, в сильно сжатом и,
следовательно, более плотном газе
молекулы заметно притягиваются к другим
молекулам гораздо большую часть времени,
чем молекулы в разреженном газе. Это,
наоборот, уменьшает число ударов молекул
в стенку, так как при наличии притяжения
к другим молекулам молекулы газа движутся
по направлению к стенке с меньшей
скоростью, чем при отсутствии притяжения.
При не слишком больших давлениях более
существенным является второе обстоятельство
и произведение
немного
уменьшается. При очень высоких давлениях
большую роль играет первое обстоятельство
и произведение
увеличивается.

Политропические
процессы

Политропный
процесс — термодинамический
процесс,
во время которого удельная
теплоёмкость c газа остаётся
неизменной. Предельными частными
явлениями политропного процесса
являются изотермический
процесс и адиабатный
процесс.
В случае идеального газа изобарный
процесс и изохорный
процесс также
являются политропическими.

Для идеального
газа уравнение
политропы может быть записано в виде:

pVⁿ = const

где
величина
называется
показателем политропы.

В
зависимости от процесса можно определить
значение n:

1.
Изотермический процесс: n =
1,
так как PV¹ = const,
значит PV = const,
значит T = const.

2.
Изобарный процесс: n =
0,
так как PV⁰ = P = const.

3.
Адиабатный процесс: n =
γ,
это следует из уравнения
Пуассона.

Здесь γ — показатель
адиабаты.

4.
Изохорный процесс:
,
так как
,
значит P₁ / P₂ =
(V₂ / V₁)ⁿ,
значит V₂ / V₁ =
(P₁ / P₂)^(1

/ⁿ⁾,
значит, чтобы V₂ / V₁ обратились
в 1, n должна быть бесконечность.

Энтропия

Энтропи́я (от др.-греч. ἐντροπία «поворот»,
«превращение») в естественных
науках —
мера беспорядка системы,
состоящей из многих элементов.
В частности, в статистической
физике — мера вероятности осуществления
какого-либо макроскопического состояния;

Понятие
энтропии впервые было
введено Клаузиусом в термодинамике в 1865
году для
определения меры необратимого рассеивания
энергии,
меры отклонения реального процесса от
идеального. Определённая как сумма
приведённых теплот, она является функцией
состояния и
остаётся постоянной при обратимых
процессах,
тогда как в необратимых —
её изменение всегда положительно.

где dS —
приращение энтропии; δQ —
минимальная теплота, подведенная к
системе; T — абсолютная температура
процесса;

Термодинамическая
энтропия —
термодинамическая функция, характеризующая
меру неупорядоченности термодинамической
системы,
то есть неоднородность расположения
и движения ее частиц.

Дифференциальная
энтропия —
энтропия для непрерывных распределений
Энтропия
динамической системы —
в теории динамических систем мера
хаотичности в поведении траекторий
системы.

Энтропия —
функция состояния системы, равная
в равновесном
процессе количеству
теплоты, сообщённой системе или отведённой
от системы, отнесённому к термодинамической
температуре системы.

Энтропия —
функция, устанавливающая связь между
макро- и микро- состояниями; единственная
функция в физике, которая показывает
направленность процессов. Энтропия —
функция состояния системы, которая не
зависит от перехода из одного состояния
в другое, а зависит только от начального
и конечного положения системы.

Второе
начало термодинамики.

Второе
начало термодинамики —
физический принцип, накладывающий
ограничение на направление процессов
передачи тепла между телами.

Второе
начало термодинамики гласит, что
невозможен самопроизвольный переход
тепла от тела, менее нагретого, к телу,
более нагретому.

Второе
начало термодинамики запрещает так
называемые вечные
двигатели второго рода,
показывая что коэффициент
полезного действия
не может равняться единице, поскольку
для кругового процесса температура
холодильника не может равняться
абсолютному нулю.

Второе
начало термодинамики является постулатом,
не доказываемым в рамках термодинамики.
Оно было создано на основе обобщения
опытных фактов и получило многочисленные
экспериментальные подтверждения.

Существуют
несколько эквивалентных формулировок
второго начала термодинамики:

Постулат Клаузиуса: «Невозможен
процесс, единственным результатом
которого являлась бы передача тепла
от более холодного тела к более
горячему» (такой
процесс называется процессом
Клаузиуса).

Постулат Томсона
(Кельвина): «Невозможен
круговой процесс, единственным
результатом которого было бы производство
работы за счет охлаждения теплового
резервуара» (такой
процесс называется процессом
Томсона).

Эквивалентность
этих формулировок легко показать. В
самом деле, допустим, что постулат
Клаузиуса неверен, то есть существует
процесс, единственным результатом
которого была бы передача тепла от более
холодного тела к более горячему. Тогда
возьмем два тела с различной температурой
(нагреватель и холодильник) и проведем
несколько циклов тепловой
машины,
забрав тепло Q₁ у
нагревателя, отдав Q₂холодильнику
и совершив при этом работу A = Q₁ − Q₂.
После этого воспользуемся процессом
Клаузиуса и вернем тепло Q₂ от
холодильника нагревателю. В результате
получается, что мы совершили работу
только за счет отъёма теплоты от
нагревателя, то есть постулат Томсона
тоже неверен.

С
другой стороны, предположим, что неверен
постулат Томсона. Тогда можно отнять
часть тепла у более холодного тела и
превратить в механическую работу. Эту
работу можно превратить в тепло, например,
с помощью трения, нагрев более горячее
тело. Значит, из неверности постулата
Томсона следует неверность постулата
Клаузиуса.

Таким
образом, постулаты Клаузиуса и Томсона
эквивалентны.

Другая
формулировка второго начала термодинамики
основывается на понятии энтропии:

«Энтропия
изолированной системы не может
уменьшаться» (закон
неубывания энтропии).

Такая
формулировка основывается на представлении
об энтропии как о функции
состояния системы,
что также должно быть постулировано.

Второе
начало термодинамики в аксиоматической
формулировке Рудольфа
Юлиуса Клаузиуса (R.
J. Clausius, 1865) имеет следующий вид:

Для
любой квазиравновесной термодинамической
системы существует однозначная функция
термодинамического состояния S = S(T,x,N),
называемая энтропией, такая, что ее
полный дифференциал dS =
δQ / T.

В
состоянии с максимальной энтропией
макроскопические необратимые процессы
(а процесс передачи тепла всегда является
необратимым из-за постулата Клаузиуса)
невозможны.

С
точки зрения статистической
физики второе
начало термодинамики имеет статистический
характер: оно справедливо для наиболее
вероятного поведения системы.

Барометрическая
формула

При
выводе основного уравнения
молекулярно-кинетической теории газов
и максвелловского распределения молекул
по скоростям делалось предположение,
что внешние силы не действуют на молекулы
газа, поэтому молекулы равномерно
распределены по объему. Но молекулы
любого газа находятся в потенциальном
поле тяготения Земли. Сила тяжести, с
одной стороны, и тепловое движение
молекул — с другой, приводят газ к
некоторому стационарному состоянию,
при котором давление газа с высотой
уменьшается.

Выведем
закон изменения давления с высотой,
предполагая при этом, что масса всех
молекул одинакова, поле тяготения
однородно и температура постоянна.

Если
атмосферное давление на высоте h равно
р , то на высоте h+dh оно равно p+dp (при dh>0
dp<0, так как давление с высотой
уменьшается). Разность давлений р и p+dp
равна весу газа, заключенного в объеме
цилиндра высотой dh с основанием площадью
1 м²:

где
ρ — плотность газа на высоте h (dh настолько
мало, что при изменении высоты в этом
интервале плотность газа можно считать
постоянной). Значит,

(1)

Зная
уравнение состояния идеального газа
pV=(m/M) RT (m — масса газа, М — молярная масса
газа), находим, что

Подставив
это выражение в (1), получим

или

С
изменением высоты от h₁ до
h₂ давление
изменяется от р₁ до
р₂ (рис.
67), т. е.

или

(2)

Выражение
(2) называется барометрической
формулой.
Она позволяет вычислить атмосферное
давление в зависимости от высоты или,
измеряя давление, найти высоту: Так как
высоты считаются относительно уровня
моря, где давление считается нормальным,
то выражение (2) может быть представлено
в виде

(3)

где
р — давление на высоте h.

Прибор
для определения высоты над земной
поверхностью называется высотомером (или альтиметром).
Его работа основана на применении
формулы (3). Из этой формулы следует, что
чем тяжелее газ, тем давление с высотой
убывает тем быстрее.

Барометрическую
формулу (3) можно преобразовать, если
воспользоваться формулой p=nkT:

где
n – концентрация молекул на высоте h,
n₀ –
то же, на высоте h=0. Так как M=m₀N_A (N_A –
постоянная Авогадро, m₀ –
масса одной молекулы), a R=kN_A,
то

(4)

где
m₀gh=P
— потенциальная энергия молекулы в
поле тяготения, т. е.

(5)

Выражение
(5) называется распределением
Больцмана для
внешнего потенциального поля. Из него
видно, что при постоянной температуре
плотность газа больше там, где меньше
потенциальная энергия его молекул.

Если
частицы находятся в состоянии хаотического
теплового движения и имеют одинаковую
массу и , то распределение Больцмана
(5) применимо в любом внешнем потенциальном
поле, а не только в поле сил тяжести.

Вязкость

Вя́зкость (вну́треннее
тре́ние) — одно из явлений переноса,
свойство текучих тел (жидкостей и газов)
оказывать сопротивление перемещению
одной их части относительно другой.
Механизм внутреннего трения в жидкостях
и газах заключается в том, что хаотически
движущиеся молекулы переносят импульс
из одного слоя в другой, что приводит к
выравниванию скоростей — это
описывается введением силы трения.
Вязкость твёрдых тел обладает рядом
специфических особенностей и
рассматривается обычно отдельно.

Различают
динамическую вязкость (единицы
измерения: пуаз,
0,1Па·с) и кинематическую вязкость
(единицы измерения: стокс,
м²/с, внесистемная единица — градус
Энглера).
Кинематическая вязкость может быть
получена как отношение динамической
вязкости к плотности вещества и своим
происхождением обязана классическим
методам измерения вязкости, таким как
измерение времени вытекания заданного
объёма через калиброванное отверстие
под действием силы тяжести.

Прибор
для измерения вязкости называется вискозиметром.

Сила
вязкого трения пропорциональна скорости относительного
движения V тел, пропорциональна площади S
и обратно пропорциональна расстоянию
между плоскостями h.

Коэффициент
пропорциональности, зависящий от сорта
жидкости или газа, называют коэффициентом
динамической вязкости.

Качественно
существенное отличие сил вязкого трения
от сухого
трения,
кроме прочего, то, что тело при наличии
только вязкого трения и сколь угодно
малой внешней силы обязательно придет
в движение, то есть для вязкого трения
не существует трения покоя, и наоборот
– под действием только вязкого трения
тело, вначале двигавшееся, никогда (в
рамках макроскопического приближения,
пренебрегающего броуновским движением)
полностью не остановится, хотя движение
и будет бесконечно замедляться.

Вторая
вязкость, или объёмная вязкость —
внутреннее трение при переносе импульса
в направлении движения. Влияет только
при учёте сжимаемости и/или при учёте
неоднородности коэффициента второй
вязкости по пространству.

Если
динамическая (и кинематическая) вязкость
характеризует деформацию чистого
сдвига, то вторая вязкость характеризует
деформацию объёмного сжатия.

Вязкость газов

В
кинетической теории газов коэффициент
внутреннего трения вычисляется по
формуле

где
—
средняя скорость теплового движения
молекул,
−
средняя длина свободного пробега. Из
этого выражения в частности следует,
что вязкость не очень разреженных газов
практически не зависит от давления,
поскольку плотность ρ прямо
пропорциональна давлению, а
–
обратно пропорциональна. Такой же вывод
следует и для других кинетических
коэффициентов для газов, например,
для коэффициента
теплопроводности.
Однако этот вывод справедлив только до
тех пор, пока разрежение газа не становится
столь малым, что отношение длины
свободного пробега к линейным размерам
сосуда не становится по порядку величины
равным единице;

С
повышением температуры вязкость
большинства газов увеличивается, это
объясняется увеличением средней скорости
молекул газа u,
растущей с температурой как

Влияние температуры на вязкость газов

Формула
Сазерленда может
быть использована для определения
вязкости идеального
газа в
зависимости от температуры:

где:

μ =
динамическая вязкость в (Па·с) при
заданной температуре T,
μ₀ =
контрольная вязкость в (Па·с) при
некоторой контрольной температуре T₀,
T =
заданная температура в Кельвинах,
T₀ =
контрольная температура в Кельвинах,
C =
постоянная Сазерленда для того газа,
вязкость которого требуется определить.

Эту
формулу можно применять для температур
в диапазоне 0 < T <
555 K и при давлениях менее 3,45 МПа с ошибкой
менее 10%, обусловленной зависимостью
вязкости от давления.

Вязкость жидкостей Динамический коэффициент вязкости

Внутреннее
трение жидкостей,
как и газов, возникает при движении
жидкости вследствие переноса импульса
в направлении, перпендикулярном к
направлению движения. Справедлив общий
закон внутреннего трения — закон
Ньютона:

Коэффициент
вязкости η (динамическая
вязкость) может быть получен на основе
соображений о движениях молекул.
Очевидно, что η будет
тем меньше, чем меньше время t «оседлости»
молекул. Эти соображения приводят к
выражению для коэффициента вязкости,
называемому уравнением
Френкеля-Андраде:

η
= Ce^w^/^kT

Иная
формула, представляющая коэффициент
вязкости, была предложена Бачинским.
Как показано, коэффициент вязкости
определяется межмолекулярными силами,
зависящими от среднего расстояния между
молекулами; последнее определяется
молярным объёмом вещества V_M.
Многочисленные эксперименты показали,
что между молярным объёмом и коэффициентом
вязкости существует соотношение

где
с и b — константы. Это эмпирическое
соотношение называется формулой Бачинского.

Динамическая
вязкость жидкостей уменьшается с
увеличением температуры, и растёт с
увеличением давления.

Кинематическая вязкость

В
технике, в частности, при расчёте гидроприводов и
в триботехнике,
часто приходится иметь дело с величиной

и
эта величина получила название
кинематической вязкости.
Здесь ρ — плотность жидкости; η —
динамическая вязкость (см. выше).

Кинематическая
вязкость в старых источниках часто
указана в сантистоксах (сСт). В систему
СИ эта
величина переводится следующим образом:

1
сСт = 1мм² / 1c
= 10 ^−

6 м² / c

Источник

Как рассчитать коэффициент вязкости газов? Как рассчитать коэффициент вязкости газов?

Профи

(637),
на голосовании

12 лет назад

Голосование за лучший ответ

Trooper

Профи

(775)

12 лет назад

В кинетической теории газов коэффициент внутреннего трения вычисляется по формуле

где — средняя скорость теплового движения молекул, − средняя длина свободного пробега. Из этого выражения в частности следует, что вязкость не очень разреженных газов практически не зависит от давления, поскольку плотность ρ прямо пропорциональна давлению, а – обратно пропорциональна. Такой же вывод следует и для других кинетических коэффициентов для газов, например, для коэффициента теплопроводности. Однако этот вывод справедлив только до тех пор, пока разрежение газа не становится столь малым, что отношение длины свободного пробега к линейным размерам сосуда (число Кнудсена) не становится по порядку величины равным единице; в частности, это имеет место в сосудах Дьюара (термосах) .
С повышением температуры вязкость большинства газов увеличивается, это объясняется увеличением средней скорости молекул газа u, растущей с температурой как

Источник

Единица измерения вязкости, теория и онлайн калькуляторы

Единица измерения вязкости

Динамическая вязкость

Вязкость (внутреннее трение) возникает между двумя слоями газа или жидкости, которые перемещаются параллельно друг другу с разными скоростями в результате возникновения сил трения между ними. Вязкость обусловлена переносом молекулами из одного слоя вещества в другой количества движения.

В одномерном случае, когда $v=vleft(xright),$ движение вещества описывают при помощи уравнения Ньютона вида:

[dF=-eta frac{dv}{dx}dS left(1right),]

где $dF$ – сила внутреннего трения, которая действует на площадь ($dS$) поверхностного слоя; $frac{dv}{dx}$ – градиент скорости перемещения слоев по направлению оси X (перпендикулярно поверхностному слою); $eta $ – коэффициент динамической вязкости.

В соответствии с классической кинетической теорией коэффициент вязкости газа равен:

[eta =frac{1}{3}leftlangle lambda rightrangle leftlangle vrightrangle rho left(2right),]

где $leftlangle lambda rightrangle $ – средняя длина свободного пробега молекулы; $leftlangle vrightrangle $ – средняя скорость теплового движения молекул; $rho $ – плотность газа. В более точной теории коэффициент $frac{1}{3}$ , заменяется на параметр ($varphi $), который зависит от характера взаимодействия молекул в веществе. Так, если считают, что молекулы газа сталкиваются как гладкие, твердые шары, то $varphi =0,499.$ При использовании более точных моделей коэффициент $varphi $ является функцией от температуры вещества.

Для жидкостей выражения (2) не является справедливым. Для газов, исходя из (2) $eta sim sqrt{T}$, тогда как, у жидкостей вязкость, с ростом температуры, уменьшается. Вязкость жидкости обратно пропорциональна коэффициенту диффузии (D):

[eta =frac{f}{D}left(3right),]

где $f$ – некоторый постоянный параметр, имеющий размерность силы.

Единица измерения коэффициента динамической вязкости

В Международной системе единиц (СИ) паскаль, умноженный на секунду – единица измерения динамической вязкости. Специального названия единица динамической вязкости не имеет. Единицу измерения коэффициента внутреннего трения легко получить, если использовать выражение (2). Рассмотрим единицы измерения физических величин, которые входят в правую часть формулы (2). Так $left[lambda right]=$м; $left[vright]=frac{м}{с}$; $left[rho right]=frac{кг}{м^3}$, получим:

[left[eta right]=left[frac{1}{3}leftlangle lambda rightrangle leftlangle vrightrangle rho right]=left[lambda right]left[vright]left[rho right]=мcdot frac{м}{с}cdot frac{кг}{м^3}=frac{кг}{мcdot с}=Паcdot с.]

В системе СГС (сантиметр, грамм, секунда) пуаз – единица измерения динамической вязкости. Соотношение между $Паcdot с$ (единица измерения динамической вязкости в СИ) и паузом:

[1 Паcdot с=10 пуаз.]

Кинематическая вязкость

Кинематическая вязкость ($nu $) определяется как отношение динамической вязкости к плотности вещества ($rho $):

[nu =frac{eta }{rho }left(4right).]

Единица измерения коэффициента кинематической вязкости

Из формулы (4) следует, что в системе СИ метр в квадрате, деленный на секунду ($frac{м^2}{с}$) – единица измерения кинематической вязкости:

[left[nu right]=left[frac{eta }{rho }right]=frac{кг}{мcdot с}cdot frac{м^3}{кг}=frac{м^2}{с}.]

Единица измерения кинематической вязкости (как и динамической) является производной в системе СИ.

В системе СГС стокс (Ст) – единица измерения кинематической вязкости:

[nu =1 Ст=1frac{{см}^2}{с}.]

С $frac{м^2}{с} $(единицей измерения кинематической вязкости в СИ) стокс связан как:

[1 Ст={10}^{-4}frac{м^2}{с}.]

Примеры задач с решением

Пример 1

Задание. Получите единицу измерения динамической вязкости жидкости, используя выражение связывающее коэффициент вязкости и коэффициент диффузии.

Решение. В качестве основы для решения задачи (по ее условию) мы будем использовать формулу, которая определяет коэффициент динамической вязкости жидкости:

[eta =frac{f}{D}left(1.1right),]

где $left[fright]=Н$; $left[Dright]=frac{м^2}{с}$. В основных единицах системы СИ, ньютон выражается как:

[Н=frac{кгcdot м}{с^2}.]

Используя выражение (1.1), получаем:

[left[eta right]=frac{left[fright]}{left[Dright]}=frac{кгcdot м}{с^2}cdot frac{с}{м^2}=frac{кг}{сcdot м}=frac{кг}{с^2cdot м}cdot с=Паcdot с.]

Ответ. Мы получили, что $Паcdot с$ – единица измерения динамической вязкости жидкости.

Пример 2

Задание. Маленький шарик, плотность которого $rho $, радиус $r$ всплывает в сосуде, наполненном жидкостью (${rho }_j$ – плотность жидкости). Скорость движения шарика постоянна и равна $v$. Какова динамическая вязкость жидкости ($eta $)? Используя полученную формулу, проверьте, в каких единицах измеряется полученная вязкость.

Решение. Изобразим силы, действующие на шарик при его движении в жидкости. Это сила тяжести ($moverline{g}$); сила Архимеда (${overline{F}}_A$); сила Стокса (сила вязкого трения) ($overline{F}$).

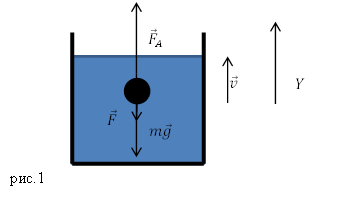
По второму закону Ньютона (учитывая, что шарик движется равномерно) имеем:

[moverline{g}+{overline{F}}_A+overline{F}=0 left(1.1right).]

Запишем проекцию уравнения (1.1) на ось Y:

[-mg-F+F_A=0 left(1.2right),]

где:

[F_A={rho }_jVg=frac{4}{3}pi r^3{rho }_jg;;F=6pi eta rv;;mg=rho frac{4}{3}pi r^3g.]

Следовательно:

[-rho frac{4}{3}pi r^3g-6pi eta rv+frac{4}{3}pi r^3{rho }_jg=0to +rho frac{2}{3}r^2g+3eta v-frac{2}{3}r^2{rho }_jg=0to eta =frac{{2r}^2g}{9v}left({rho }_j-rho right).]

Используя полученное выражение для коэффициента вязкости ($eta =frac{{2r}^2g}{9v}left({rho }_j-rho right)$) определим единицу измерения для $eta $:

[left[eta right]=left[frac{{2r}^2g}{9v}left({rho }_j-rho right)right]=frac{left[r^2right]left[gright]}{left[vright]}left(left[rho right]right)=frac{м^2cdot frac{м}{с^2}}{{м}/{с}}cdot frac{кг}{м^3}=frac{кг}{мcdot с}=Паcdot с.]

Ответ. $eta =frac{{2r}^2g}{9v}left({rho }_j-rho right)$

Читать дальше: единица измерения индуктивности.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

Коэффициент динамической вязкости

Коэффициент динамической вязкости газа

Коэффициент вязкости жидкостей

Связь коэффициента вязкости с числами Рейнольдса и силой трения

Примеры решения задач

Коэффициент кинематической вязкости

Заключение

Сила вязкого трения[править | править код]

Вторая вязкость[править | править код]

Вязкость газов[править | править код]

Влияние температуры на вязкость газов[править | править код]

Вязкость жидкостей[править | править код]

Динамическая вязкость[править | править код]

Кинематическая вязкость[править | править код]

Условная вязкость[править | править код]

Ньютоновские и неньютоновские жидкости[править | править код]

Вязкость аморфных материалов[править | править код]

Относительная вязкость[править | править код]

Вязкость некоторых веществ[править | править код]

Вязкость воздуха[править | править код]

Вязкость воды[править | править код]

Динамическая вязкость разных веществ[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Вязкость газов

Влияние температуры на вязкость газов

Вязкость жидкостей Динамический коэффициент вязкости

Кинематическая вязкость

Как рассчитать коэффициент вязкости газов? Как рассчитать коэффициент вязкости газов?

Единица измерения вязкости

Динамическая вязкость

Единица измерения коэффициента динамической вязкости

Кинематическая вязкость

Единица измерения коэффициента кинематической вязкости

Примеры задач с решением

Вам также может понравиться

Как можно найти время погоды

Почему печень горчит говяжья как исправить

Как найти инвестора для покупки недвижимости

Добавить комментарий Отменить ответ