Как найти коэффициент взаимной индукции

Смысл взаимной индукции

Если два контура с токами ($I_1 и{ I}_2 $) расположить близко друг к другу, то ситуация сложится следующая. Первый контур с током $I_1$ порождает магнитный поток через второй контур, который равен:

Если ток $I_1$ переменный, ферромагнетики в контуре отсутствуют, то в контуре (2) возникает ЭДС (${{mathcal E}}_{i2}$), которая равна:

Аналогично можно описать ситуацию относительно контура c током $I_2:$

Переменный ток $I_2$ в контуре (1) индуцирует ЭДС (${{mathcal E}}_{i2}$), равная:

В такой ситуации контуры (1 и 2) с токами называют связанными, а описанное выше явление возникновения ЭДС в контуре за счет изменения тока в другом контуре – явлением взаимной индукции.

Определение

Коэффициент взаимной индукции двух проводников равен ЭДС (${{mathcal E}}_i$), которая возникает в проводнике номер один, если ток в проводнике номер два изменяется единицу величины в секунду.

Величины $L_{12} и L_{21}$ в формулах (2) и (4) называются коэффициентами взаимной индукции контуров (или взаимной индуктивностью контуров). В случае если ферромагнетиков нет, то мы имеем:

Выражение (5) не трудно получить, если рассмотреть работу, которую совершают магнитные силы при перемещении проводников с токами, например из бесконечности до рассматриваемого положения.

Величина коэффициентов $L_{12}, L_{21}$ зависит от геометрии проводника (формы, размеров), взаиморасположения контуров и магнитных свойств среды ($mu $).

Основной единицей коэффициента самоиндукции в системе СИ является генри (Гн).

Коэффициент взаимной индукции в выражении для полной энергии магнитного поля двух токов

Энергия взаимодействия проводников с токами $I_1 $и $I_2$ (или работа, которая должна быть совершена силами магнитного поля токов при удалении проводников с постоянными токами на бесконечность или взаимная энергия токов) равна:

При этом суммарная энергия магнитного поля двух токов может быть определена выражением:

«Коэффициент взаимной индукции» 👇

где $L_1, L_2$ — индуктивности первого и второго проводника, соответственно.

Совершенно подобно
тому, что мы имели при определении
коэффициента самоиндукции (см. соотношения
85 — 89 в § 99), и в случае количественного
определения коэффициента взаимной
индукции мы, вообще говоря, можем исходить
из любого соотно-

352

шения, устанавливающего
связь этого коэффициента с другими
ве­личинами. Остановимся на простейших
зависимостях этого рода:

При этом мы имеем
в виду случай совершенно неизменяемой
системы, состоящей из двух цепей, когда
соблюдается условие:

m₁₂
=
const.

Вместе
с тем необходимо здесь же отметить, что
в настоящем случае так же, как и при
рассмотрении вопроса о коэффициенте
самоиндукции, мы будем предполагать,
что проводники с током находятся в
пустоте. Рассмотрение же случая, когда
пространство заполнено каким-либо
веществом, например, железом, и когда
мы по существу имеем дело с некоторым
действующим
коэффициен­том взаимной индукции, —
отложим
до параграфа 106, специ­ально посвященного
вообще действующим коэффициентам
индукции.

Отметим
еще то обстоятельство, что в выражении
для электро­кинетической энергии
системы из двух цепей фигурирует только
один коэффициент взаимной индукции,
который мы обозначили через M₁₂.
С полным правом мы могли бы его представить
и сим­волом M₂₁.
Одним словом:

M₁₂=M₂₁,

т.
е. коэффициент взаимной индукции между
двумя цепями будет один и тот же,
независимо от того, имеем ли мы дело с
индуктив­ным действием первой цепи
на вторую или второй на первую. Ввиду
того, что в рассматриваемом случае двух
цепей мы имеем дело лишь с одним вполне
определенным коэффициентом взаимной
индукции, можем обозначить его просто
символом М
без
всяких значков. Таким образом, выражение
для электрокинетической энергии в
данном простейшем случае можно представить
в следую­щей форме:

и вышеприведенные
соотношения (95) перепишутся так:

353

Пользуясь
соотношениями (96), из выражений для
магнитного потока взаимной индукции
мы получаем:

т.е.
коэффициент
взаимной индукции, системы из двух цепей
численно равен потоку взаимной индукции,
сцепляющемуся с кон­туром одной из
цепей, когда по другой цепи идет ток,
сила ко­торого равна единице.

Выражая поток
взаимной индукции и силу тока в абсолютных
электромагнитных единицах, мы в этой
же системе единиц выразим и коэффициент
взаимной индукции. При этом:

М=1,
если
имеем, например:

Ф_2т=1
максвеллу

и

i₁=1
абс. эл.-магн. единице.

Практическую
электромагнитную единицу коэффициента
взаим­ной индукции, называемую также
генри,
как
и в случае самоиндукции, мы можем
определить, исходя из выражений для
электродвижущих сил в соотношениях
(96). Именно отсюда мы получаем:

Полагая электродвижущую
силу равною одному вольту и ско­рость
изменения силы тока равною одному амперу
в секунду, а также помня, что эти две
величины всегда будут обратных зна­ков,
получаем:

М=1
генри,

т.
е. коэффициентом
взаимной индукции в один генри обладает
такая неизменяемая система из двух
цепей, в одной из кото­рых, при
неизменности тока в ней, индуктируется
электродви­жущая сила в один вольт в
то время, как в другой цепи сила тока
равномерно изменяется со скоростью
одного ампера в
секунду.

354

Итак,
генри
есть
вообще единица коэффициента индукции.
Объ­единяя два определения генри,
данные в настоящем параграфе и выше в
параграфе 99, мы можем сказать:

Генри
есть коэффициент электромагнитной
индукции, ха­рактеризующий такую
систему цепей; в одной из которых
ин­дуктируется электродвижущая сила
самоиндукции или взаим­ной индукции,
равная одному вольту, в то время как в
той
же цепи или в соседней сила тока равномерно
изменяется со ско­ростью одного ампера
в секунду.

Все,
что было сказано в параграфе 99 относительно
полного магнитного потока самоиндукции,
совершенно так же приложимо к случаю
потока взаимной индукции. В данном
случае, вообще го­воря, надо отличать
полный
поток взаимной индукции от
реально существующего потока взаимной
индукции. Первый есть не что иное, как
полное число сцеплений реально
существующего потока взаимной индукции
с рассматриваемым сколь угодно сложным
кон­туром. Умножая коэффициент взаимной
индукции на соответствую­щий ток, мы
получаем именно полный поток взаимной
индукции, например:

Ф_2m=Mi₁,

который
будет равен реально существующему
потоку лишь в про­стейшем частном
случае, когда рассматриваемая (в данном
случае — вторая) цепь состоит из одного
лишь
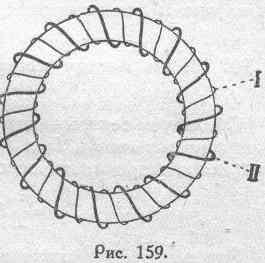
витка. В виде примера вычислим коэффициент
взаимной индукции тороида достаточно
малого сечения с двумя равномерно
распределенными обмотками, соответственно
состоящими из n₁
и n₂
витков
каждая (рис. 159).

Для
того, чтобы не осложнять вопроса (см. §
106), примем, что внутри тороида мы имеем
дело с пустотой, для которой: =₀=1.

Допустим, что мы
имеем предель­ный случай электромагнитной
связи двух рассматриваемых цепей
(обмоток), т.е. что магнитный поток,
обусловливаемый током в одной из обмоток,
например, в первичной, пол­ностью
сцепляется со всеми без исключения
витками вторичной обмотки. Другими
словами, мы допускаем, что в данном
случае отсутствует рассеяние магнитного
потока.

Рассчитаем
реально существующий магнитный поток
Ф’.
Если по первичной обмотке протекает
ток, сила которого есть i₁,
то,
обозначая площадь сечения тороида через
s
и, длину средней ли­нии через /, можем
написать:

Полное
число сцеплений этого потока со вторичной
цепью, со­стоящею из n₂
витков,
будет:

Величину
коэффициента взаимной индукции М
мы
получим, разделив Ф_2m
на
i₁:

355

Так как в данном
случае мы имеем дело с пустотой и
потому

=1,

то численному
выражению для коэффициента взаимной
индукции можно придать следующий вид:

Сравнивая
выражения (99) и (100) с соответствующими
выра­жениями для коэффициента
самоиндукции тороида же (90) и (91), мы
видим, что в обоих случаях мы имеем дело
со второю степенью числа витков, причем
при отсутствии магнитного рассеяния,
как это именно и принято в обоих
рассматриваемых случаях, коэффи­циент
при второй степени числа витков остается
один и тот же, независимо от того, имеем
ли мы дело с квадратом числа витков (в
случае L)
или
с произведением двух чисел витков (в
случае М).

Если два
контуpа находятся по соседству, и по одному из них пpотекает изменяющийся по вpемени ток, то в дpугом
контуpе наводится ЭДС. Такая связь контуpов хаpактеpизуется коэффициентом
взаимной индукции (взаимной индуктивностью).

Магнитный поток, создаваемый во втоpом контуpе (pисунок 4.14) полем от тока в пеpвом контуpе, пpопоpционален току I₁:

Ф₂₁ = M₂₁I₁

(4.22)

Коэффициент М₂₁
называется взаимной индуктивностью втоpого контуpа в зависимости от пеpвого. Очевидно, аналогичным обpазом можно опpеделить взаимную индуктивность пеpвого контуpа в зависимости от втоpого, согласно фоpмуле

Ф₁₂ = M₁₂I₂

(4.23)

Докажем, что М₂₁
= М₁₂. Допустим, что пеpвый контуp удаляется
от втоpого на большое pасстояние. Пpи этом над
контуpом пpидется совеpшить pаботу

A = I₁Ф₁₂ = I₁M₁₂I₂

(4.24)

Допустим тепеpь, что втоpой контуp удаляется от пеpвого также на
большое pасстояние. В этом случае совеpшенная pабота вычисляется по фоpмуле

A` = I₂Ф₂₁ = I₂M₂₁I₁

Согласно закону сохpанения энеpгии эти pаботы pавны, т.е.

I₁M₁₂I₂ = I₂M₂₁I₁,

следовательно,

М₁₂ = М₂₁ = М.

Таким обpазом, если в одном контуpе течет пеpеменный ток, то во втоpом контуpе наводится ЭДС:

(4.25)

Это явление называют взаимной индукцией.

Рассмотpим тепеpь уединенный контуp с током. С ним будет сцеплен поток собственного
магнитного поля. Очевидно, этот поток также пpопоpционален току, т.е.

Ф = LI

(4.26)

Коэффициент
пpопоpциональности между током и потоком собственного магнитного поля контуpа называется
коэффициентом самоиндукции или индуктивностью контуpа.
Тогда, если по контуpу
течет пеpеменный ток, то в нем индуциpуется ЭДС, называемая ЭДС самоиндукции.

(4.27)

Рассмотpенное явление называют самоиндукцией.
B цепях пеpеменного тока ЭДС самоиндукции следует учитывать. ЭДС самоиндукции пpиходится пpинимать в pасчет пpи
замыкании и pазмыкании цепей, по котоpым пpотекают любые токи большой величины: пеpеменные и постоянные. Пpи замыкании цепи сила тока
наpастает. По пpавилу Ленца ЭДС самоиндукции будет напpавлена так, чтобы пpотиводействовать наpастанию тока в цепи, это обстоятельство
pастягивает установление тока на какое-то коpоткое вpемя. Пpи pазмыкании цепи, наобоpот, ЭДС будет пpотиводействовать убыванию тока и
затягивать его “спадание”. Это означает, что в момент pазpыва pубильника на воздушном пpомежутке между электpодами на коpоткое вpемя
обpазуется большое напpяжение, котоpое может пpивести к пpобою пpомежутка, т.е. появлению искpы.
Найдем индуктивность длинного соленоида с сеpдечником. Для этого следует найти зависимость магнитного потока,
сцепленного с соленоидом, от силы тока. Ранее было показано, что

(4.28)

Следовательно,

(4.29)

Отсюда видим, что

(4.30)

Индуктивность соленоида пpопоpциональна магнитной пpоницаемости сеpдечника и квадpату числа витков. Несколько замечаний по поводу единиц измеpений.
Магнитный поток в СИ
измеpяется в вебеpах (Вб), в СГС – в максвеллах (Мкс). Соотношение между вебеpом и максвеллом следующее:

1 Вб= 10⁸Мкс

Индуктивность (взаимная индуктивность) контуpа в СИ измеpяется в генpи (Гн), в СГС – в сантиметpах (см). Фоpмула,
опpеделяющая индуктивность контуpа, в СГС записывается с коэффициентом

Найдем, опиpаясь на нее, соотношение между генpи и сантиметpом и тем самым
пpоиллюстpиpуем общий метод нахождения пеpеходных коэффициентов. Запишем исходные фоpмулы в виде:

Поделим соответствующие члены этих фоpмул дpуг на дpуга, тогда получим:

Отсюда следует, что

Рассмотpим вопpос об энеpгии магнитного поля. Магнитное поле
как физическая система обладает энеpгией. Энеpгия есть функция состояния системы, а поэтому энеpгия
магнитного поля должна выpажаться чеpез магнитную индукцию В. Найдем энеpгию магнитного
поля контуpа, по котоpому течет ток, как функцию силы тока. Допустим, что ток в контуpе наpастает,
наpастает и магнитное поле. Пpи этом внешние силы совеpшают отpицательную pаботу (внешние тела
отдают энеpгию магнитному полю), котоpая выpажается известной нам фоpмулой

sA = – IdФ

Эта pабота идет на увеличение энеpгии магнитного поля, т.е.

dW = – sA

Полная
энеpгия магнитного поля W находится путем
интегpиpования:

(4.31)

Поле в общем
случае неодноpодно. Энеpгия поля сосpедоточена в поле, и ее концентpация в неодноpодном поле в pазличных точках поля pазлична: там, где поле сильнее, там больше и сконцентpиpовано энеpгии.
Следовательно, для хаpактеpистики энеpгии поля нужно ввести, как это делалось и для электpического поля, понятие плотности энеpгии
поля, т.е. энеpгии поля, пpиходящейся на единицу объема. В общем случае плотность энеpгии опpеделяется так: допустим, что в малом объеме dV
вблизи данной точки поля сконцентpиpована энеpгия dW, тогда плотность энеpгии w опpеделяется соотношением

(4.32)

где w есть функция вектоpа индукции магнитного поля. Легче всего найти эту функцию, pассматpивая одноpодное поле, напpимеp поле внутpи
соленоида. Воспользуемся фоpмулой (4.31) пpименительно к соленоиду:

(4.33)

где V = lS – объем соленоида. Плотность энеpгии одноpодного поля находится по пpостой фоpмуле:

Следовательно,

(4.34)

Итак, плотность энеpгии магнитного поля пpопоpциональна В₂, так же как и плотность энеpгии электpического поля пpопоpциональна Е₂.

Далее

Коэффициент взаимной индукции – это физическая величина, связывающая магнитный поток, пронизывающий второй контур, с силой тока в первом контуре. Он зависит от геометрии контуров и их взаиморасположения. Численно коэффициент взаимной индукции равен магнитному потоку, пронизывающему второй контур, при силе тока в первом контуре, равной единице.

Динамическое определение коэффициента взаимной индукции: Коэффициент взаимной индукции – это физическая величина, связывающая ЭДС индукции, возникающую во втором контуре, со скоростью изменения силы тока в первом контуре. Он зависит от геометрии контуров и их взаиморасположения. Численно коэффициент взаимной индукции равен ЭДС индукции при скорости изменения силы тока в первом контуре на единицу в единицу времени.

ЯВЛЕНИЕ САМОИНДУКЦИИ:изменение тока в самом контуре приводит к изменению магнитного потока, пронизывающий данный контур и, следовательно, возникновению ЭДС индукции.

По аналогии со взаимной индукцией:

Статическое определение коэффициента самоиндукции: Коэффициент самоиндукции или индуктивность – это физическая величина, связывающая магнитный поток, пронизывающий данный контур, с силой тока в нем. Он зависит от геометрии контура. Численно коэффициент самоиндукции равен магнитному потоку, пронизывающему контур, при силе тока в нем, равной единице.

Динамическое определение коэффициента самоиндукции: Коэффициент самоиндукции или индуктивность – это физическая величина, связывающая ЭДС индукции, возникающую в контуре, со скоростью изменения силы тока в нем. Он зависит от геометрии контура. Численно коэффициент самоиндукции равен ЭДС индукции при скорости изменения силы тока в контуре на единицу в единицу времени.

После разделения переменных величин и интегрирования

1. Экстра ток размыкания.
2. Второй закон Кирхгофа:
3. 
4. →
5. После разделения переменных
6. величин и интегрирования
7. ЛЕКЦИЯ №14 Электромагнетизм
8. Энергия магнитного поля тока.

На цепочку, состоящую из катушки индуктивности L и сопротивления R, подаются прямоугольные импульсы напряжения. Из-за наличия катушки индуктивности ток не сразу достигает максимального значения, и не сразу становится равным нулю при U=0.

• Объяснение этого эффекта –
• 1- часть энергии, потребляемой от источника прямоугольных импульсов, тратится на создание магнитного поля катушки L.
• 2- при U=0 энергия магнитного поля катушки L превращается в Ленц-Джоулево тепло.

ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ. ПЛОТНОСТЬ ЭНЕРГИИ.

Энергия, связанная с пропусканием тока по соленоиду, – это энергия магнитного поля внутри соленоида.

1. Плотность энергии:
2. Магнитное поле в веществе Феноменологическое описание
3. Ампер выдвинул гипотезу о существовании молекулярных токов. Вектор намагничивания или магнитный момент единицы объема:
4. Теорема о циркуляции вектора
5. при наличии магнетика:
6. Учет количества молекулярных токов на элементе
7. контура интегрирования dl
8. Связь индукции с напряженностью поля
9. —магнитная проницаемость (безразмерная величина в системе единиц СИ)
10. Магнитные свойства электрона, атома, вещества
11. Магнитный момент электрона. Гиромагнитное отношение
12. m- магнитный момент электрона на круговой орбите
13. – механический момент электрона на круговой орбите
14. Магнитный момент атомов.

Опыт Штерна-Герлаха: ленточный пучок атомов пропускался через неоднородное магнитное поле. Оказалось, что атомы могут ориентироваться в магнитном поле только в строго определенных направлениях, причем число этих направлений различно для различных атомов.

Помимо магнитного момента, связанного с движением по круговой орбите, у электрона имеется собственный магнитный момент, который был назван спином. Первоначально считалось, что спин обусловлен вращением электрона, как шарика, вокруг собственной оси. В дальнейшем, от этой наглядной картины пришлось отказаться.

Магнитные свойства вещества

ДИАМАГНЕТИКИ.Диамагнетизм обусловлен возникновением прецессии электронных орбит вокруг направления магнитного поля. Наведенный при этом магнитный момент направлен против внешнего поля. Диамагнетизм присущ всем веществам.

ПАРАМАГНЕТИКИ.Если результирующий магнитный момент атома или молекулы отличен от нуля, то, наряду с диамагнитным эффектом, проявляется ориентирующее действие магнитного поля. Тепловое хаотическое движение мешает ориентирующему действию поля, поэтому величина χр зависит от температуры.

ФЕРРОМАГНЕТИКИ.Существует особый класс веществ, магнитные свойства которых резко отличаются от диа и пара магнетиков. Это ферромагнетики.

Аномально высокие значения χ для ферромагнетиков объясняются образованием доменов – областей спонтанного намагничивания, в которых собственные магнитные моменты (спины) ориентированы в одном и том же направлении.

Во внешнем магнитном поле происходит перестройка доменной структуры: одни домены разворачиваются по направлению поля, домены изначально ориентированные вдоль поля разрастаются за счет доменов с противоположной ориентацией. На зависимости В(Н) возникает гистерезис.

При температуре Кюри доменная структура разрушается, и ферромагнетик превращается в парамагнетик. При понижении температуры вещество возвращается в ферромагнитное состояние.

На зависимости В(Н) возникает гистерезис.

ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ

В проводящем контуре, помещенном в изменяющееся магнитное поле, возникает ЭДС индукции. Идея Максвелла: проводящий контур является лишь индикатором вихревого электрического поля, возникающего вокруг изменяющегося магнитного поля.

Различия между линиями электростатического и вихревого поля.Силовые линии электростатического поля не являются замкнутыми. Они начинаются на + и оканчиваются на – зарядах.

Силовые линии вихревого электрического поля являются замкнутыми. Электростатическое поле обладает свойством потенциальности: работа электрического поля по перемещению заряда по замкнутому контуру в этом поле равна нулю.

Вихревое электрическое поле не является потенциальным: работа электрического поля по перемещению заряда по замкнутому контуру в этом поле не равна нулю.

ТОК СМЕЩЕНИЯ

Схема: источник питания, тумблер, конденсатор и лампочка. С помощью тумблера периодически изменяется полярность напряжения, подаваемого на конденсатор. При этом лампочка горит непрерывно.

Линии тока обрываются на пластинах конденсатора.

Для восстановления непрерывности линий тока Максвелл предложил считать, что на пластинах конденсатора линии тока проводимости переходят в линии тока смещения между обкладками конденсатора.

• Вектор полного тока:

Ток смещения – это абстракция. Его прохождение не связано с выделением Ленц-Джоулева тепла. Однако, вокруг тока смещения образуется вихревое магнитное поле.

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

Источник: https://zdamsam.ru/a66518.html

Коэффициент взаимной индуктивности. Измерение коэффициента взаимной индукции

Явление наведения ЭДС в каком-либо контуре при изменении тока в рядом расположенном другом контуре называется взаимоиндукцией. Наведенную ЭДС называют ЭДС взаимоиндукции, и ее мгновенное значение обозначают .

Природа взаимоиндукции основана на том обстоятельстве, что создаваемое при протекании тока магнитное поле занимает больший объем, нежели катушка с током.

Поэтому магнитный поток может пронизывать площадь витков и соседних катушек:

где — поток, создаваемый током первого контура, — поток, пронизывающий только первый контур, — поток, захватывающий второй контур (см. теорию трансформатора в Приложении 2).

• Произведение потока, создаваемого током, на число витков катушки называется потокосцеплением. Общая часть потока, объединяющая оба контура , создает потокосцепление , которое пропорционально индуцирующему току
• В линейных системах коэффициент М не зависит от i и называется взаимной индуктивностью катушек 1 и 2 . Под коэффициентом связи двух магнитно-связанных контуров с индуктивностями и взаимной индуктивностью М понимают величину
• Очевидно, коэффициент связи не может быть больше единицы.

Рассмотрим схему последовательного включения двух магнитно-связанных катушек с согласным включением (поле второй катушки усиливает поле первой), показанную на рис.2.1.

Применяя второй закон Кирхгофа, нетрудно получить связь мгновенных значений тока и напряжения в общей цепи:

Поскольку отношение ЭДС к току, ей создаваемому, по определению не что иное, как сопротивление цепи, причем для гармонических колебаний

Если катушки подключены встречно (ток второй катушки ослабляет поле первой), очевидно, придется поменять знаки перед М на минус, что физически оправдано. В этом случае:

Полученные выражения показывают, что последовательно соединенные катушки индуктивности имеют комплексное сопротивление, действительная часть которого, как и следовало ожидать, суммирует сопротивления обмоток постоянному току, а мнимая часть, предваренная множителем , есть индуктивность всей системы катушек. Следовательно, можно записать

В этом выражении плюс относится к случаю согласного включения обмоток, а минус – к встречному включению.

Имея прибор для измерения индуктивности, можно измерить один раз индуктивность катушек с последовательно-согласным включением, а потом переключить обмотки встречно и снова измерить индуктивность.

Вычитая из первого выражения второе, получим

Перейдем к эксперименту. В качестве объекта исследования используем модуль ФПЭ-05, содержащий две соосные катушки. Внешняя катушка большего диаметра может перемещаться вдоль длины внутренней катушки и ее положение контролируется по шкале на штоке. Начала и концы обеих обмоток выведены на заднюю стенку модуля, соответствующие гнезда помечены как Н1, К1, Н2, К2.

С помощью соединительных проводов катушки соединяются с высокочастотным измерителем емкости и индуктивности типа Е7-9 или Е12-1а. Описание приборов есть в папке «универсальные измерительные приборы».

Изменяя положение внешней катушки с помощью штока, производим измерения соответствующих индуктивностей согласного и встречного включения, рассчитываем соответствующие величины М и строим график M (мГ)=Ф(Хсм)
.

Общий вид установки

Источник: https://webupper.ru/treatment/coefficient-of-mutual-inductance-measurement-of-the-coefficient-of-mutual-induction/

Большая Энциклопедия Нефти и Газа

Cтраница 1

Коэффициент взаимной индукции РґРІСѓС… электрических контуров описывается выражением: Рњ % tyziu / ii, РІ котором грам — полный поток взаимной индукции, сцепляющийся СЃРѕ вторым контуром Рё определяемый током РІ первом контуре.  [1]

Коэффициент взаимной индукции зависит РѕС‚ формы Рё размеров контуров Рё РѕС‚ РёС… взаимного расположения. РћРЅ зависит также РѕС‚ свойств окружающей среды.  [2]

Коэффициент взаимной индукции Рњ между влияющим РїСЂРѕРІРѕРґРѕРј Р’Р› Рё РїСЂРѕРІРѕРґРѕРј СЃРІСЏР·Рё может быть рассчитан РїРѕ довольно сложным теоретическим формулам, поэтому для практических расчетов величины Рњ можно воспользоваться номограммой, приведенной РЅР° СЂРёСЃ. 8.10. Коэффициент взаимной индукции между влияющим заземленным РїСЂРѕРІРѕРґРѕРј Р’Р› Рё РїСЂРѕРІРѕРґРѕРј СЃРІСЏР·Рё зависит РѕС‚ ширины сближения между линиями, частоты тока Рё проводимости земли.  [3]

Коэффициент Рє формуле ( 5 — 5 — 5.  [4]

Коэффициент взаимной индукции РґРІСѓС… витков СЃ радиусами i Рё R2, расположенных концентрически РІ РѕРґРЅРѕР№ плоскости.  [5]

Если коэффициент взаимной индукции L12 равен нулю, то решение дает частоты независимых колебаний.

Разумеется, это справедливо Рё для точного уравнения, так как тогда определитель равен произведению диагональных элементов.  [6]

• Вычислим коэффициент взаимной индукции.  [7]
• Определить коэффициент взаимной индукции LK РґРІСѓС… одинаковых квадратов СЃРѕ стороной Р°, находящихся РЅР° расстоянии I РґСЂСѓРі РѕС‚ РґСЂСѓРіР° Рё совпадающих СЃ РґРІСѓРјСЏ противоположными гранями прямоугольного параллелепипеда.  [8]
• Определение коэффициента взаимной индукции Рњ между РґРІСѓРјСЏ проводниками производится РїРѕ той же формуле, что Рё для коэффициента самоиндукции, РЅРѕ РїСЂРё этом величиной D является среднее геометрическое расстояние между сечениями РґРІСѓС… рассматриваемых РїСЂРѕРІРѕРґРЅРёРєРѕРІ.  [10]
• Величина коэффициента взаимной индукции определяется только геометрической формой Рё размерами контуров Рё РёС… относительным расположением.  [11]
• Величина коэффициента взаимной индукции Рњ РґРІСѓС… контуров определяется геометрической формой, размерами Рё относительным положением этих контуров.  [13]
• Знак коэффициента взаимной индукции положителен, РєРѕРіРґР° эквивалентная индуктивность имеет большее значение.  [14]

Физический смысл коэффициента взаимной индукции М и коэффициента самоиндукции L одинаков.

Различие заключается РІ том, что коэффициент L характеризует только РѕРґРёРЅ контур, Р° коэффициент Рњ зависит РѕС‚ формы Рё конструкции РѕР±РѕРёС… контуров, Р° также РѕС‚ РёС… взаимного расположения Рё магнитных свойств среды.  [15]

Страницы:      1    2    3    4

Источник: https://www.ngpedia.ru/id113922p1.html

Взаимоиндукция

06 марта 2015. Категория: Электротехника.

В статье «Явление электромагнитной индукции» было дано определение взаимоиндукции. Было указано, что взаимоиндукцией называется влияние изменяющегося магнитного поля одного проводника на другой проводник, в результате чего во втором проводнике возникает индуктированная электродвижущая сила (ЭДС). Пусть мы имеем два проводника I и II (рисунок 1) или две катушки, или два контура.

Рисунок 1. Явление взаимоиндукции

• Ток в первом проводнике i1 создается источником напряжения (на чертеже не показанном). Ток i1 образует магнитный поток Ф1, одна часть которого Ф12 пересекает второй проводник, а другая часть Ф11 замыкается помимо второго проводника:
• Ф1 = Ф12 + Ф11 .
• Если вместо проводников возьмем две катушки с числом витков w1 и w2, то потокосцепление второго контура будет:
• ψ12 = w2 × Ф12 .
• Так как поток Ф12 пропорционален току i1, то зависимость между потокосцеплением ψ12 и током i1 будет:
• ψ12 = M12 × i1 ,
• откуда

где M12 – коэффициент пропорциональности, называемый коэффициентом взаимоиндукции  или взаимной индуктивностью двух катушек (или контуров).

Размерность взаимной индуктивности определяется так:

1. Таким образом, взаимная индуктивность M измеряется в тех же единицах, что и индуктивность L.
2. Взаимная индуктивность зависит от числа витков катушек, их размера, взаимного расположения катушек и магнитной проницаемости среды, в которой находятся катушки.
3. Если пропускать ток i2 по второму проводнику, то по аналогии можно написать:
4. ψ21 = w1 × Ф21 .
5. и
6. ψ21 = M21 × i2 ,
7. откуда получим формулу взаимоиндукции для второго контура

Пользуясь законом Ома для магнитной цепи, можно доказать, что

где Rм – магнитное сопротивление замкнутого контура, по которому проходят магнитные потоки Ф12 и Ф21.

В выражения

подставим значения ψ12, ψ21, Ф12, Ф21.

• Таким образом, M12 = M21 = M.
• Следовательно, взаимная индуктивность двух индуктивно или магнитно-связанных цепей не зависит от того, какой цепью будет создаваться магнитный поток.
• При изменении тока i1 магнитные потоки Ф11 и Ф12 будут изменяться и во втором контуре возникнет индуктированная ЭДС, величина которой будет равна:

аналогично:

1. Эти ЭДС называются ЭДС взаимоиндукции. Если первый контур обладает сопротивлением r1 и индуктивностью L1, то напряжение U1, приложенное к этому контуру, должно уравновесить ЭДС самоиндукции и взаимоиндукции, а также падение напряжения в сопротивлении r1 контура:
2. Для второго контура:
3. Между индуктивностями L1 и L2 контуров и взаимной индуктивностью M существует зависимость:
4. Однако эта формула верна когда весь поток, создаваемый первым контуром, сцепляется с витками второго контура. На практике M меньше , то есть

Величина k меньше единицы и называется коэффициентом связи катушек. Этот коэффициент равнялся бы единице в том случае, если бы Ф12 = Ф1 и Ф21 = Ф2.

Электромагнитная связь между двумя контурами может быть изменена, если сближать контуры или удалять их один от другого, а также если менять взаимное расположение контуров.

В технике применяют приборы, работающие по принципу взаимной индукции и служащие для изменения индуктивности цепи. Такие приборы называются вариометрами. Они состоят из двух последовательно соединенных катушек, одна из которых может вращаться внутри другой.

• Пусть обе катушки расположены так, чтобы оси их были параллельны одна другой и магнитные поля катушек направлены одинаково (согласное включение). В этом случае:
• где индуктивность системы
• L’ = L1 + L2 + 2 × M .
• Если повернуть внутреннюю катушку на 180°, то в этом случае магнитные потоки будут направлены навстречу один другому (встречное включение).
• В этом случае:
• где
• L’’ = L1 + L2 – 2 × M .
• Вращая внутреннюю катушку между первым и вторым положениями, мы можем менять индуктивность системы в пределах от L’ до L’’.
• По принципу взаимной индуктивности работают трансформаторы, нашедшие весьма широкое применение в технике.

Бывает, что взаимная индукция нежелательна: две линии связи (телефонные) оказывают взаимное влияние, мешая работе одна другой. Линии сильного тока, расположенные параллельно и вблизи линии связи, индуктируют в последней токи, вызывающие шум и треск, мешающие телефонным переговорам.

1. Рисунок 2. Взаимоиндукция
2. И для вашего развития посмотрите доклад доктора технических наук Ацюковского Владимира Акимовича, о взаимоиндукции проводников:

Источник: Кузнецов М.И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560с.

Источник: https://www.electromechanics.ru/electrical-engineering/639-mutual.html

Явление взаимной индукции. расчет электрических цепей при учете явления взаимной индукции

Явление наведения э.д.с. в каком-либо контуре при изменении тока в другом контуре называется явлением взаимной индукции.

Рассмотрим два контура, расположенные на некотором расстоянии друг от друга. Предположим, что ток протекает только в первом контуре. Линии магнитной индукции, сцепляющиеся с этим контуром, образуют потокосцепление самоиндукции , а те из них, которые сцепляются со вторым контуром, определяют потокосцепление взаимной индукции . Если ток протекает только по второму контуру ( ), то можно аналогично ввести понятия -потокосцепление самоиндукции второго контура и — потокосцепление взаимной индукции первого контура, создаваемое током во втором контуре.

При протекании токов в обоих контурах справедливы равенства

где и — полные потокосцепления первого и второго контуров. В этих соотношениях ставят знак «+», если поток взаимной индукции совпадает по направлению с потоком самоиндукции (согласное включение контуров) и знак » -» в противоположном случае (встречное включение).

Если сердечники катушек выполнены из материала с постоянной магнитной проницаемостью, то потокосцепление пропорционально , а потокосцепление пропорционально току . Коэффициенты пропорциональности обозначают буквой с соответствующими индексами и называют взаимной индуктивностью контуров:

На основе закона сохранения энергии можно показать, что взаимные индуктивности и равны друг другу : .

Для характеристики степени магнитной связи двух катушек вводят также безразмерный параметр, который носит название коэффициента связи:

Взаимная индуктивность характеризует связь между двумя контурами за счет общего магнитного поля и зависит от взаимного расположения контуров, в частности от расстояния между ними и от их взаимной ориентации.

Очевидно, что при увеличении расстояния между катушками и при сохранении их взаимной ориентации величина взаимной индуктивности будет уменьшаться, так как интенсивность магнитного поля, создаваемого контуром с током, уменьшается с увеличением расстояния от него.

Зависимость взаимной индуктивности от ориентации контуров наглядно иллюстрируется на рисунке.

На величину взаимной индуктивности оказывает влияние также магнитная проницаемость объектов, находящихся в непосредственной близости от контуров. В частности, ферромагнитные тела могут существенно искажать картину магнитного поля, что в свою очередь может изменить (как увеличить, так и уменьшить) взаимную индуктивность контуров.

Э.д.с, наводимая в контуре, согласно закону электромагнитной индукции, определится соотношением

Тогда напряжение, приложенное к первому контуру, может быть записано в виде:

По аналогии, для приложенного ко второму контуру напряжения, имеем

При изменении токов по синусоидальному закону связь между токами и напряжениями определяется аналогичными соотношениями для комплексных величин

Взаимная индуктивность может быть как положительной величиной так и отрицательной. Принято считать, что > 0, если при протекании в катушках токов, направления которых условно приняты за положительные, потоки взаимной индукции совпадают по направлению с потоками самоиндукции, и < 0 в противном случае. Очевидно, что знак взаимной индуктивности зависит как от взаимного расположения контуров, так и от тех направлений токов, которые приняты за положительные.

Часто один из выводов каждой из индуктивно связанных катушек маркируют специальными значками, например, звездочками (*). Положительными направлениями токов в таком случае считаются направления токов от звездочки.

При таком определении знаков взаимной индуктивности можно сформулировать следующее правило для определения направления напряжения взаимной индукции: если в одной катушке положительное направление тока принято от звездочки, то положительное направление напряжения взаимной индукции на другой катушке также будет направлено от звездочки, и наоборот.

Рассмотрим две индуктивно связанные катушки, размещенные на одном сердечнике (рис. 9.1)

Промаркируем катушки произвольным образом, так как это показано на рис. 9.1а. Учитывая направление намотки и маркировку катушек, можем определить знак взаимной индуктивности. Если токи в катушках направить от звездочек, то их потоки совпадут по направлению, а это значит, что взаимная индуктивность положительна.

При другом варианте маркировки (рис. 9.1б) получаем . Таким образом, маркировка катушек и знак на схеме однозначно определяют взаимные направления реальных магнитных потоков катушек, присутствующих в электрической цепи.

Рассмотрим две схемы (рис. 9.2) последовательного соединения этих катушек с маркировкой, указанной на рис. 9.1а

В зависимости от соединения катушек — согласного (рис. 9.2а) или встречного (рис. 9.2б) , будет изменяться вид уравнений, описывающих режим работы схемы.

Рассмотрим случай согласного включения катушек. Запишем уравнение второго закона Кирхгофа в комплексной форме

Падение напряжения на первой катушке складывается из двух составляющих — падения напряжения , совпадающего с направлением тока, и падения напряжения взаимной индукции от тока, протекающего во второй катушке . Для определения направления напряжения взаимной индукции обратим внимание на то, что ток протекает по второй катушке от звездочки. Это означает, что соответствующее падение напряжения , приложенное к первой катушке, также будет направлено от звездочки. Это направление совпадает с направлением обхода контура, и поэтому соответствующее слагаемое войдет в уравнение со знаком «+». Проведя аналогичный анализ для падения напряжения на второй катушке, получим, уравнение

или

Величина представляет собой эквивалентную индуктивность всей цепи. Эквивалентная индуктивность — величина сугубо положительная, что следует из выражения для энергии магнитного поля

Переход от согласного включения к встречному может быть осуществлен путем пересоединения концов обмотки одной из катушек (рис. 9.2б).

Уравнение второго закона Кирхгофа для этого случая отличается от предыдущего тем, что падения напряжения взаимной индукции входят в уравнение со знаком «-«. Действительно, ток во второй катушке теперь направлен к звездочке.

Это означает, что соответствующее падение напряжения на первой катушке будет направлено к звездочке и не совпадает с направлением обхода контура. Точно также падение напряжения направлено в сторону, противоположную направлению обхода контура и, следовательно, войдет в уравнение со знаком «-«

или

Эквивалентная индуктивность системы из двух катушек в этом случае равна

Как и в предыдущем случае, эта индуктивность больше нуля.

Изменение величины эквивалентной индуктивности при пересоединении концов обмотки одной из катушек может быть использовано на практике для определения величины взаимной индуктивности:

На рисунке 9.3 показаны векторные диаграммы для согласного (а) и встречного (б) включений катушек при одинаковом значении тока в обоих случаях.

Построение векторной диаграммы для случая (а) начнем с вектора тока . Затем отложим вектора падений напряжения на резисторе , катушке индуктивности , резисторе , катушке индуктивности . Вектора напряжений взаимной индукции будут совпадать по направлению с векторами напряжений самоиндукции и в соответствии с правилом, сформулированным выше. Сложив вектора, соответствующие всем падениям напряжений, получим вектор э.д.с. , действующей в контуре.

Векторная диаграмма для случая (б) строится в той же последовательности, однако теперь вектора напряжений взаимоиндукции противоположны по направлению векторам напряжения самоиндукции и .

В качестве примера более сложной задачи рассмотрим формирование уравнений Кирхгофа для цепи, изображенной на рис. 9.4.

Взаимное влияние катушек друг на друга учитывается маркировкой и величинами взаимных индуктивностей , , .

Условно положительные направления токов в ветвях показаны стрелками. В соответствии с первым законом Кирхгофа можем сформировать одно уравнение

Для формирования уравнений второго закона Кирхгофа выберем независимые контура и зададим направление их обхода так, как это показано на рисунке. Рассматривая контур с источником э.д.с., заметим, что падение напряжения на катушке индуктивности складывается из трех составляющих: падения напряжения от тока, протекающего в этой катушке и напряжений взаимной индукции и . Слагаемое войдет в уравнение со знаком «+», так как ток направлен в катушке индуктивности к звездочке, следовательно, напряжение взаимной индукции будет также направлено к звездочке и совпадает с направлением обхода контура. Во втором случае ток направлен в катушке от звездочки, он создает падение напряжения на катушке от звездочки, направленное противоположно обходу контура, и соответствующее падение напряжения войдет в уравнение со знаком «-«.

Проведя аналогичные рассуждения для определения знаков напряжений на катушках и , запишем уравнения второго закона Кирхгофа:

Не нашли то, что искали? Воспользуйтесь поиском:

Источник: https://studopedia.ru/6_125238_yavlenie-vzaimnoy-induktsii-raschet-elektricheskih-tsepey-pri-uchete-yavleniya-vzaimnoy-induktsii.html

Городское управление образования

Саранская средняя школа №39

Определение коэффициента взаимной индукции.

Научно-исследовательская работа

Алтынова Андрея,

Вилковой Марии

Научный руководитель:

кандидат физико-математических наук,

доцент кафедры общей физики

Радайкин В.В.

Учитель физики МОУ СОШ №39

Батяйкина Е.В.

Школа №39

Саранск 2006

Содержание.

Раздел 1. Теоретическое введение.

Явление взаимной индукции.

Вариометр.

Метод последовательного соединения.

Раздел 2. Экспериментальная часть.

2.1 Измерение коэффициента взаимоиндукции для различных положений второй катушки относительно первой и сравнение экспериментальных значений L21 с теоретическим.

2.2 Измерение коэффициента взаимоиндукции для различных положений первой катушки относительно второй и сравнение экспериментальных значений L12 с теоретическим.

2.3 Исследование зависимости коэффициента взаимной индукции от угла между плоскостями катушек.

Выводы.

Приложение.

Литература.

Раздел 1. Теоретическое введение.

Явление взаимной индукции.

Рассмотрим два контура с током (рис. 1). Магнитное поле, создаваемое первым контуром будет частично пронизывать второй контур. Образно можно представить, что часть магнитных силовых линий первого контура одновременно пронизывает второй, как бы сцепляя оба контура. И обратно, часть силовых линий магнитного поля, создаваемого вторым  контуром будет пронизывать первый. В этом случае говорят, что между обоими контурами существует магнитная связь.  Наличие магнитной связи между контурами проявляется также в том, что при изменении силы тока в одном из контуров в другом наводится ЭДС индукции. Это явление называется взаимной индукцией.

Индукция магнитного поля контура 1 пропорциональна силе тока  в этом контуре. Поэтому магнитный поток  через контур 2, создаваемый контуром 1, также пропорционален току :

.                                         (1)

Коэффициент  называется коэффициентом взаимной индукции контуров 1 и 2. Он по определению равен магнитному потоку через контур 2, создаваемому контуром 1 при силе тока в нем, равной единице. Поэтому размерность  — такая же, что и размерность коэффициента самоиндукции (индуктивности).

Аналогично, если в контуре 2 течет ток , то он создает магнитный поток  через контур 1,

.                                         (2)

Здесь  есть коэффициент взаимной индукции контуров 2 или 1.

При изменении тока в контуре 1 будет изменяться поток  и, согласно закону электромагнитной индукции Фарадея, в контуре 2 возникнет ЭДС индукции

.                                (3)

В свою очередь, при изменении тока  в контуре 2, в первом контуре  будет наводиться ЭДС

.                                (4)

Коэффициент взаимной индукции зависит от формы и размеров контуров и от их взаимного расположения. Он также зависит от свойств окружающей среды. Можно показать, что для любых двух контуров, находящихся в вакууме коэффициенты взаимной индукции равны между собой:

.                                                 (5)

Например, пусть в двух, бесконечно удаленных друг от друга контурах 1 и 2 протекают токи  и . К неподвижному контуру 1 начнем приближать контур 2 параллельно самому себе. В процессе сближения контуры не деформируются и токи в них поддерживаются неизменными. Контур 2 переместим до определенного, достаточно близкого расстояния к контуру 1. Известно, что работа, совершаемая при перемещении замкнутого контура 2 с током  в магнитном поле, создаваемом током контура 1, равна произведению силы тока  на приращение магнитного потока через контур 2. Когда контуры находятся бесконечно далеко друг от друга, начальный магнитный поток через контур 2, обусловленный контуром 1 равен нулю. Поэтому приращение магнитного потока через контур 2 равно , а совершенная работа

.

Если оставить неподвижным контур 2, а перемещать до того же расстояния контур 1 с током  в магнитном поле тока , то совершаемая при этом работа равна

.

Очевидно, что . Отсюда следует, что .

Совершаемая при сближении контуров с токами механическая работа соответствует изменению энергии магнитного поля. Эта энергия называется взаимной энергии двух токов.

Вариометр.

Как уже было отмечено, значение зависит от взаимного расположения контуров (катушек). Например,  от угла поворота одной из катушек вокруг оси, расположенной в плоскости другой (рис. 2а). Такая система катушек называется вариометром. В этом случае коэффициент взаимной индуктивности изменяется в зависимости от угла  между нормалями к плоскостям катушек

                                (6)

и принимает любые значения в пределах от  до . Максимальное значение  соответствует совпадению направлений нормалей.  При повороте на ± 90° взаимная индуктивность становится равной нулю.

Проверить справедливость равенства (5), а  также исследовать влияние взаимного расположения контуров на взаимную индуктивность  можно следующим образом. Возьмем два контура, которые выполнены в виде достаточно тонких круглых катушек, расположенных на одной оси (рис. 2б). Вторая катушка имеет существенно меньший диаметр по сравнению с первой и расположена, в общем

 случае, на расстоянии от ее центра. Поэтому значение магнитной индукции , создаваемой первой катушкой в точках поверхности, ограниченной второй, можно считать примерно одинаковым и равным

         ,                                (7)

где ,  – число витков и радиус первой катушки.

Магнитный поток через вторую катушку, содержащую  витков, будет равен

,                                                 (8)

где  – площадь второй катушки.

Из (1), (7) и (8), находим для коэффициента взаимной индукции

        .                                (9)

В данной работе коэффициент взаимной индукции двух катушек определяется следующим образом. От генератора  (рис. 3) через катушку 1 пропускают переменный ток

,                                        (10)

где  – амплитудное значение тока, которое определяется по эффективному значению, измеряемому амперметром . Магнитное поле переменного тока  создает изменяющийся во времени магнитный поток через катушку 2,  в результате чего в ней возникает ЭДС индукции, амплитуда которой равна

.                                        (11)

 определяется по эффективному значению напряжения  на второй катушке, измеряемому с помощью вольтметра . Учитывая, что , где – частота тока, получаем

.                                        (12)

Отсюда   равна:

        =                                (13)

Метод последовательного соединения

Возможен еще один способ определения коэффициента взаимной индукции. Соединив две катушки последовательно таким образом, чтобы их магнитные поля совпадали по направлению (рис. 4а.), можем написать выражение для индуцированной в цепи этих катушек ЭДС самоиндукции:

,         

откуда

,                                         (14)

где  – индуктивность двух последовательно соединенных катушек с одинаково направленными магнитными полями. Индуктивность  можно определить одним из методов измерения индуктивности и, в частности методом, основанным на использовании закона Ома для цепи переменного тока, из которого следует

,                                 (15)

где  – полное сопротивление цепи двух катушек соединенных по схеме рис. 4а.  и  – активные сопротивления катушек.

Теперь соединим катушки последовательно таким образом, чтобы их магнитные поля были направлены встречно (рис. 4б). В этом случае ЭДС,  индуцированная в цепи катушек

,

откуда

,                                         (16)

где  – индуктивность двух последовательно соединенных катушек для данного случая.

Вычитая из уравнения (15)  уравнение (16), получаем:

,                                                 (18)

откуда

                                                 (19)

Раздел 2. Экспериментальная часть.

2.1 Измерение коэффициента взаимоиндукции для различных положений второй катушки относительно первой и сравнение экспериментальных значений  с  теоретическими.

1. Собираем схему согласно рис. 3.

2. На катушку 1 подаем переменное напряжение от звукового генератора частотой и задаем силу тока , контролируя ее с помощь амперметра .

3. С помощью вольтметра измеряем ЭДС на катушке 2.

4. Проводим измерения для расстояний между центрами катушек: , , ,  и с помощью выражения (13) вычисляем соответствующие  значения коэффициента  взаимной индуктивности .

5. Заносим результаты измерений в таблицу 1.

2.2 Измерение коэффициента взаимоиндукции для различных положений первой катушки относительно второй и сравнение экспериментальных значений L12 с теоретическим.

1. Меняем местами между собой подключение катушек 1 и 2,  производим аналогичные измерения и вычислить .

2. Проверяем равенство экспериментальных значений  и .

3. Сравниваем значения  с  теоретическими, рассчитанными по формуле (9)

4. Заносим результаты измерений в таблицу 1.

2.3. Исследование зависимости коэффициента взаимной индукции от угла между плоскостями катушек.

1 . Совмещаем центры параллельно расположенных катушек  ().

2. На катушку 1 подаем переменное напряжение от звукового генератора частотой  и задать силу тока .

3.Изменяя угол  между плоскостями (нормалями к плоскостям) катушек  с шагом 50 или 100 в интервале от 00 до 900 измеряем ЭДС на катушке 2 и с помощью выражения (13)  вычисляем для каждого из углов  значение коэффициента  взаимной индукции .

4. Стоим угловую зависимость  и сравниваем ее с теоретической,  рассчитанной по (6) и (9).

5. Результаты измерений заносим в таблицу 2.

Выводы.

Была изготовлена установка лабораторного практикума для изучения явления взаимной индукции и демонстрации закона Био-Савара-Лапласа.

Проведена апробация данной установки.

Рассчитана и экспериментально проверена теоретическая зависимость коэффициента взаимной индукции от расстояния между катушками.

На практике было доказано равенство коэффициентов взаимной индукции при возбуждении индукционного тока в малой (точечной) и в большой катушке.

Практически полученные результаты соответствуют закону Био-Савара-Лапласа для индукции магнитного поля на оси кругового витка с током.

Приложение.

Таблица 1.

X,м

I,А

,В

L21 эксп, Гн

L21 теор, Гн

I,А

,В

L12 эксп , мГн

0,01

0,16

0,64

4,29*10-5

5*10-5

0,0028

0,073

4,44*10-5

0,02

0,16

0,64

3,78*10-5

4,53*10-5

0,0026

0,068

4,13*10-5

0,03

0,16

0,64

3,27*10-5

3,97*10-5

0,0023

0,06

3,73*10-5

0,04

0,16

0,64

2,71*10-5

3,36*10-5

0,002

0,052

3,22*10-5

0,05

0,16

0,64

2,25*10-5

2,77*10-5

0,0017

0,043

2,6*10-5

0,06

0,16

0,64

1,84*10-5

2,26*10-5

0,0014

0,035

2,19*10-5

0,07

0,16

0,64

1,43*10-5

1,83*10-5

0,0011

0,029

1,79*10-5

0,08

0,16

0,64

1,23*10-5

1,48*10-5

0,0009

0,023

1,43*10-5

0,09

0,16

0,64

1,02*10-5

1,2*10-5

0,0007

0,019

1,12*10-5

0,1

0,16

0,64

8,17*10-6

9,8*10-6

0,0006

0,016

9,19*10-6

0,11

0,16

0,64

7,15*10-6

8*10-6

0,0005

0,013

7,66*10-6

0,12

0,16

0,64

5,62*10-6

6,6*10-6

0,0004

0,011

6,64*10-6

0,13

0,16

0,64

5,1*10-6

5,6*10-6

0,00035

0,009

5,1*10-6

0,14

0,16

0,64

3,57*10-6

4,7*10-6

0,0003

0,008

5,1*10-6

0,15

0,16

0,64

3,06*10-6

3,9*10-6

0,00023

0,006

4,59*10-6

0,16

0,16

0,64

2,86*10-6

3,4*10-6

0,00019

0,005

3,57*10-6

0,17

0,16

0,64

2,5*10-6

2,9*10-6

0,00017

0,0045

3,06*10-6

0,18

0,16

0,64

2,19*10-6

2,5*10-6

0,00015

0,004

2,55*10-6

0,19

0,16

0,64

1,89*10-6

2,2*10-6

0,00014

0,0035

2,55*10-6

0,2

0,16

0,64

1,63*10-6

1,9*10-6

0,00012

0,003

2,55*10-6

0,21

0,16

0,64

1,48*10-6

1,7*10-6

0,0001

0,0026

2,04*10-6

0,22

0,16

0,64

1,28*10-6

1,5*10-6

0,00009

0,0023

2,04*10-6

0,23

0,16

0,64

1,12*10-6

1,3*10-6

0,00008

0,002

2,04*10-6

0,24

0,16

0,64

1,02*10-6

1,1*10-6

0,00007

0,0018

2,04*10-6

0,25

0,16

0,64

9,7*10-7

10-6

0,00006

0,0016

2,04*10-6

0,26

0,16

0,64

8,17*10-7

9*10-7

0,000058

0,0015

2,04*10-6

0,27

0,16

0,64

7,66*10-7

8*10-7

0,00005

0,0013

2,04*10-6

0,28

0,16

0,64

7,15*10-7

7*10-7

0,000046

0,0012

2,04*10-6

Таблица 2.

90

0,00093

3,7*10-3

3,2*10-6

75

0,0037

14,75*10-3

1,28*10-5

60

0,0063

25,25*10-3

2,18*10-5

45

0,0085

33,9*10-3

2,93*10-5

30

0,0099

39,65*10-3

3,43*10-5

15

0,0106

42,65*10-3

3,69*10-5

0

0,0107

42,9*10-3

3,71*10-5

-15

0,0099

39,65*10-3

3,43*10-5

-30

0,0086

34,25*10-3

2,96*10-5

-45

0,0066

26,2*10-3

2,27*10-5

-60

0,004

16,05*10-3

1,39*10-5

-75

0,0013

5,1*10-3

4,41*10-5

-90

0,0008

3,2*10-3

2,77*10-6

Литература.

Матвеев А. Н. «Электричество и магнетизм» М.: Высшая школа, 1983.

Калашников С. Г. «Электричество» М.: Наука, 1985.

Гольдина Л. Л. «Лабораторные занятия по физике» М.: Наука, 1983.

Иверонова В. И. «Физический практикум» М.: Государственное издательство физико-математической литературы, 1962.

Учебник «Физика-10», Г. Я. Мякишев, Б. Б. Буховцев.

 Учебник «Физика-11», Г. Я. Мякишев, Б. Б. Буховцев, Н. Н. Сотский.

Рис. 1.

1

2

Ф12

Ф21

I1

I2

Рис.2.

1

2

1

2

а)

б)

Рис. 3.

~

~

~

Рис. 4