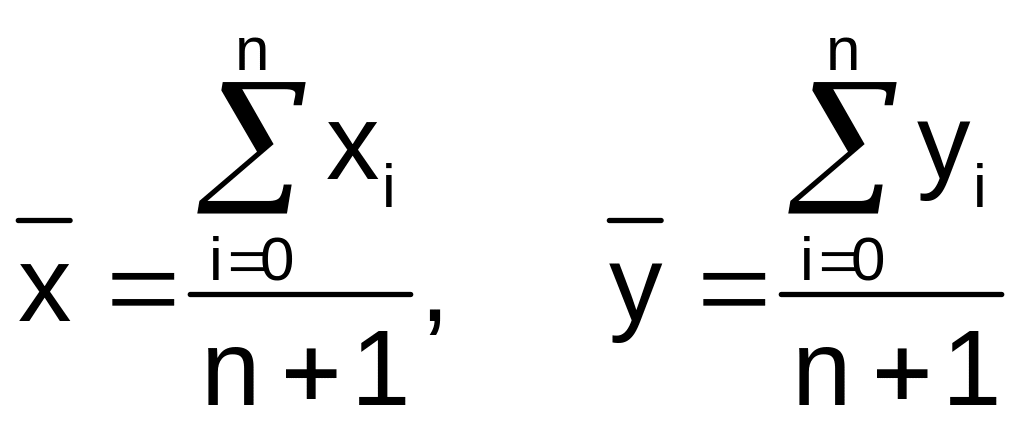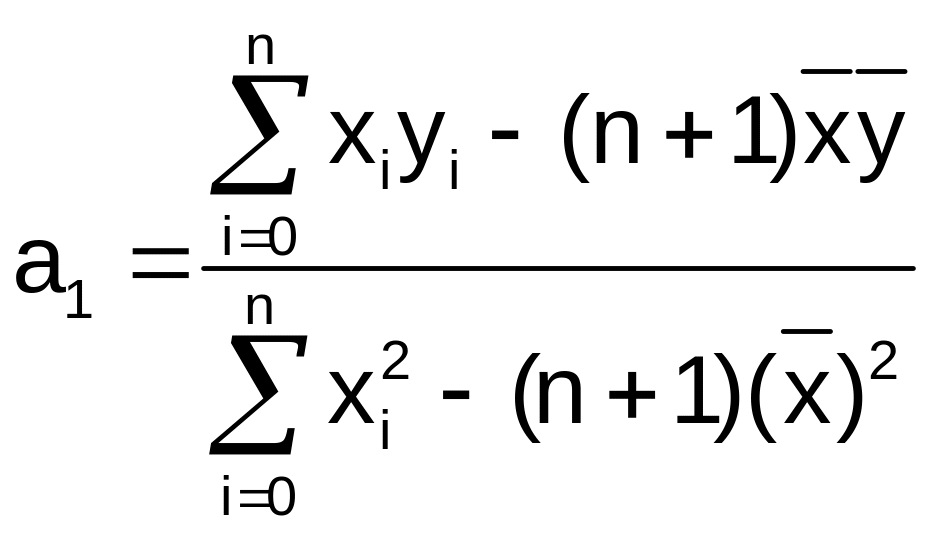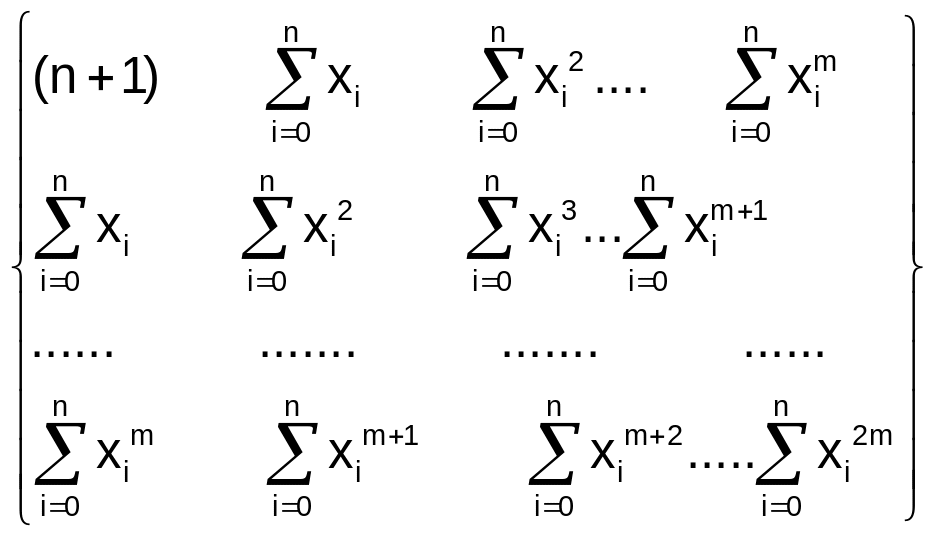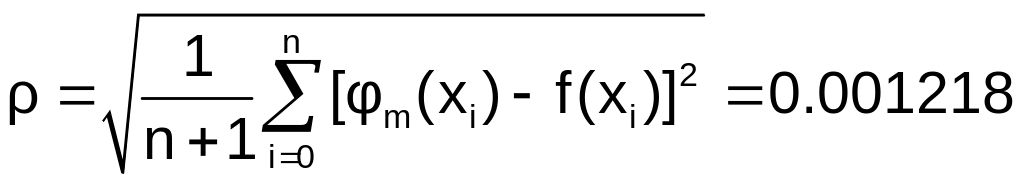Как найти коэффициенты аппроксимирующей функции

7.1. Постановка задачи аппроксимации

Задача аппроксимации
(приближения) функции заключается в
замене некоторой функции y=f(x)
другой функцией g(x, a₀,
a₁,
…, a_n)
таким образом, чтобы отклонение

g(x,
a0, a1, …, an) от f(x)
удовлетворяло в некоторой области (на
множестве Х)
определённому условию. Если множество
Х дискретно (состоит
из отдельных точек), то приближение
называется точечным, если же Х
есть отрезок [a;b],
то приближение называется интегральным.

Если функция
f(x)
задана таблично, то
аппроксимирующая функция

g(x,
a₀,
a₁,
…, a_n)
должна удовлетворять определённому
критерию соответствия ее значений
табличным данным.

Подбор эмпирических
формул состоит из двух этапов – выбора
вида формулы и определения содержащихся
в ней коэффициентов.

Если неизвестен
вид аппроксимирующей зависимости, то
в качестве эмпирической формулы обычно
выбирают один из известных видов функций:
алгебраический многочлен, показательную,
логарифмическую или другую функцию в
зависимости от свойств аппроксимируемой
функции. Поскольку аппроксимирующая
функция, полученная эмпирическим путем,
в ходе последующих исследований, как
правило, подвергается преобразованиям,
то стараются выбирать наиболее простую
формулу, удовлетворяющую требованиям
точности. Часто в качестве эмпирической
формулы выбирают зависимость, описываемую
алгебраическим многочленом невысокого
порядка.

Наиболее распространен
способ выбора функции в виде многочлена:

,

где
φ(x,a₀,a₁,…,a_n)=a₀φ₀(x)+a₁φ₁(x)+…+a_mφ_m(x),
а

φ₀(x),
φ₁(x),
…, φ_m(x)
– базисные функции (m-степень
аппроксимирующего полинома).

Один из возможных
базисов – степенной: φ₀(x)=1,
φ₁(x)=х,
…, φ_m(x)=х^m.

Обычно степень
аппроксимирующего полинома m<<n,
a^T=(a₀,a₁,…,a_m)
– вектор коэффициентов. Если погрешность
исходных данных e,
то количество базисных функций выбирается
так, чтобы

.
Здесь S – численное
значение критерия близости аппроксимирующей
функции φ(x, a₀,
a₁,
…, a_n)
и табличных данных. Отклонения между
опытными данными и значениями эмпирической
функции

e_i
=
φ(x_i,
a₀,
a₁,
…, a_m)
– y_i,
i = 0,1,2,…,n.

Методы определения
коэффициентов выбранной эмпирической
функции различаются критерием минимизации
отклонений.

7.2. Метод наименьших квадратов

Одним из способов
определения параметров эмпирической
формулы является метод наименьших
квадратов. В этом методе параметры a₀,
a₁,
…, a_n
определяются из условия минимума
суммы квадратов отклонений аппроксимирующей
функции от табличных данных.

Вектор коэффициентов
a^T
определяют из условия минимизации

где (n+1)
– количество узловых точек.

Условие минимума
функции Е приводит
к системе линейных уравнений относительно
параметров a₀,
a₁,
…, a_m. Эта
система называется системой нормальных
уравнений, её матрица – матрица Грама.
Элементами матрицы Грама являются
суммы скалярных произведений базисных
функций

Для получения
искомых значений параметров следует
составить и решить систему (m+1)
уравнения

Пусть в качестве
аппроксимирующей функции выбрана
линейная зависимость y=
a₀+a₁x
. Тогда

.

Условия минимума:

Тогда первое
уравнение имеет вид

Раскрывая скобки
и разделив на постоянный коэффициент,
получим

.

Первое уравнение
принимает следующий окончательный вид:

.

Для получения
второго уравнения, приравняем нулю
частную производную по а1:

.

.

Система линейных
уравнений для нахождения коэффициентов
многочлена

(линейная аппроксимация):

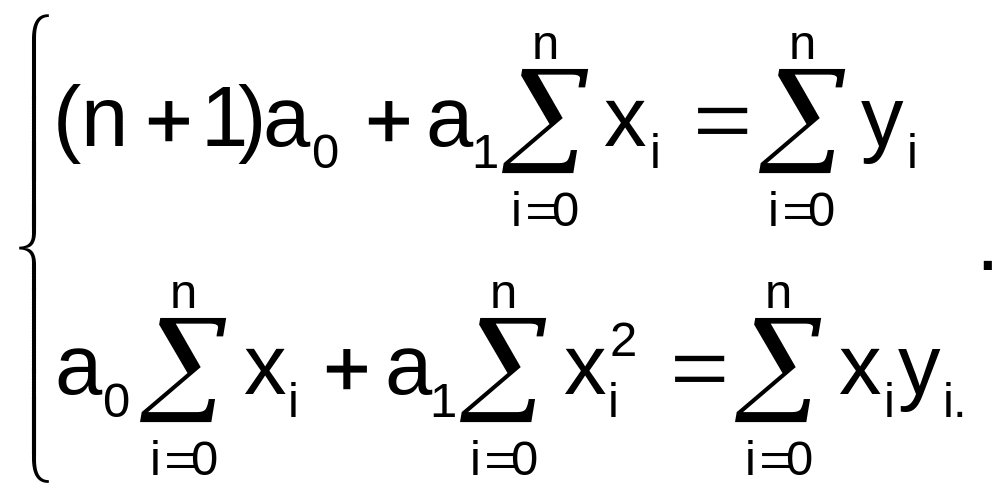
Введем следующие
обозначения

– средние значения исходных данных. Во
введенных обозначениях решениями
системы являются

.

В случае применения
метода наименьших квадратов для
определения коэффициентов аппроксимирующего
многочлена второй степени y=a₀+a₁x+а₂х²
критерий минимизации имеет вид

.

Из условия

получим
следующую систему уравнений:

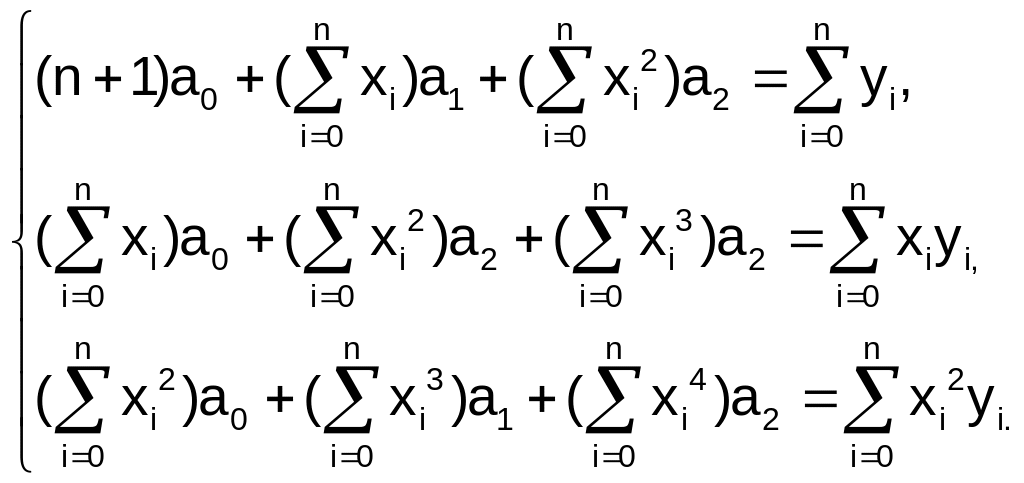
Решение этой
системы уравнений относительно а₀,
а₁,
а₂ позволяет
найти коэффициенты эмпирической формулы

–
аппроксимирующего многочлена 2-го
порядка. При решении системы линейных
уравнений могут быть применены численные
методы.

В случае степенного
базиса (степень аппроксимирующего
полинома равна m)
матрица Грама системы нормальных
уравнений G и столбец
правых частей системы нормальных
уравнений

имеют
вид

G
=

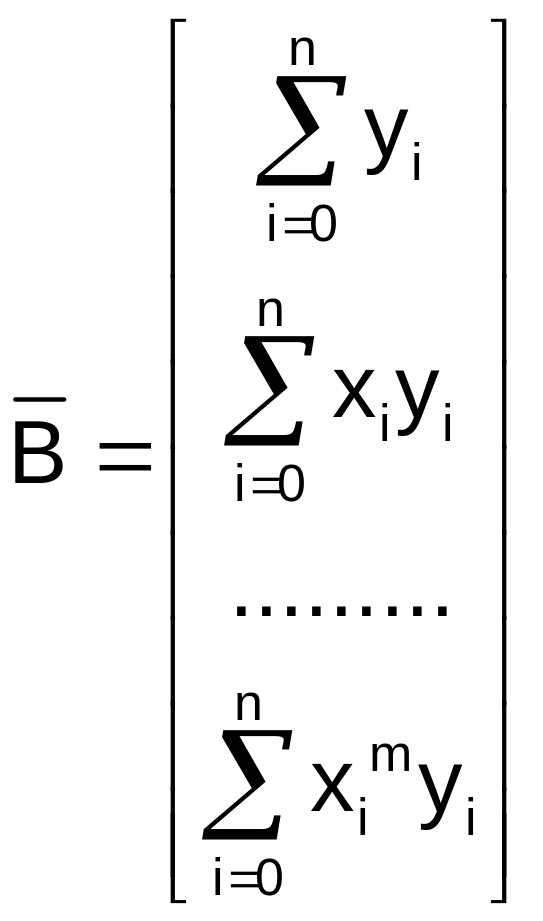
В матричной форме
система нормальных уравнений примет
вид:

.

Решение системы
нормальных уравнений

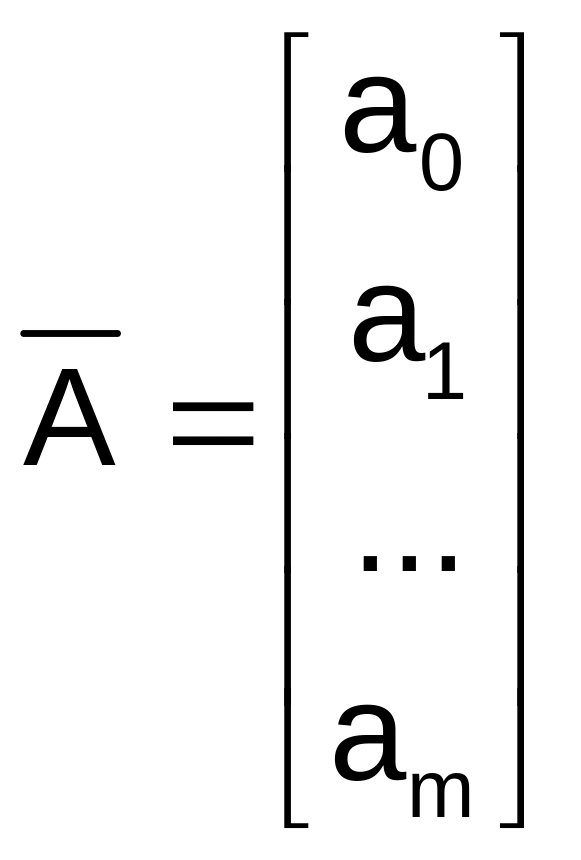
найдется из
выражения

В качестве меры
уклонения заданных значений функции
y₀,
y₁,
…, y_n от
многочлена степени m
– φ(x)=a₀
φ₀(x)+a₁
φ₁(x)+…+a_m
φ_m(x)
,

принимается
величина

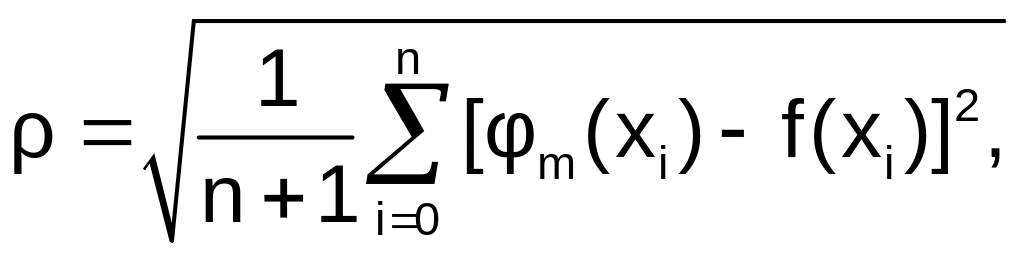
(n+1)
– количество узлов, m
– степень аппроксимирующего многочлена,
n+1>=m.

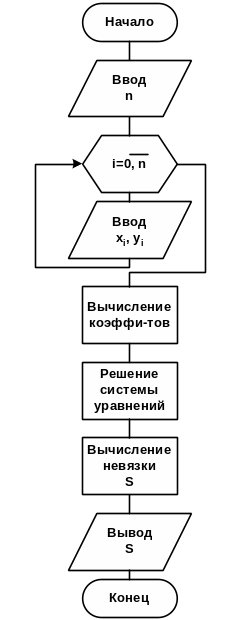
На рис.7.2-1 приведена
укрупненная схема алгоритма метода
наименьших квадратов.

Рис. 7.2-1.
Укрупненная схема алгоритма метода
наименьших квадратов

Данная схема
алгоритма метода наименьших квадратов
является укрупненной и отражает основные
процессы метода, где
n+1
– количество точек, в которых известны
значения х_i,
y_i;
i=0,1,…,
n.

Блок
вычисления коэффициентов предполагает
вычисление коэффициентов при неизвестных
с₀,
с₁,
…, с_m
и
свободных членов системы из m+1
линейных уравнений.

Следующий
блок – блок решения системы уравнений
– предполагает вычисление коэффициентов
аппроксимирующей функции с₀,
с₁,
…, с_m.

Далее вычисляется
невязка

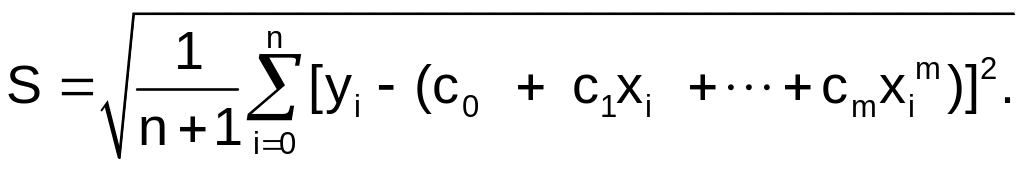
Пример
7.2-1. Аппроксимировать следующие
данные многочленом второй степени,
используя метод наименьших квадратов.

x	0.78	1.56	2.34	3.12	3.81
y	2.50	1.20	1.12	2.25	4.28

Запишем в следующую
таблицу элементы матрицы Грамма и
столбец свободных членов:

i	x	x2	x3	x4	y	xy	x2y
0	0.78	0.608	0.475	0.370	2.50	1.950	1.520
1	1.56	2.434	3.796	5.922	1.20	1.872	2.920
2	2.34	5.476	12.813	29.982	1.12	2.621	6.133
3	3.12	9.734	30.371	94.759	2.25	7.020	21.902
4	3.81	14.516	55.306	210.72	4.28	16.307	62.129
∑	11.61	32.768	102.76	341.75	11.35	29.770	94.604

Система нормальных
уравнений выглядит следующим образом

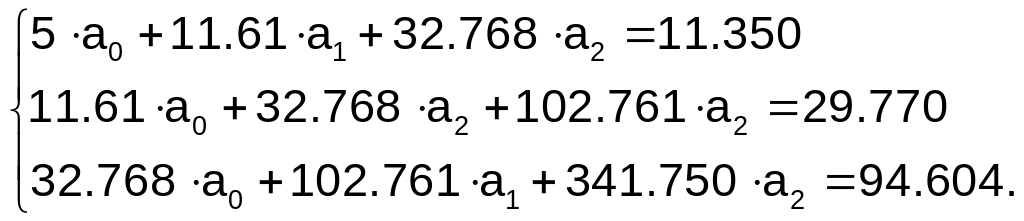
Решением этой
системы являются:

а0
= 5.022; а1 =-4.014; а2=1.002.

Искомая
аппроксимирующая функция

Сравним исходные
значения y со
значениями аппроксимирующего многочлена,
вычисленными в тех же точках:

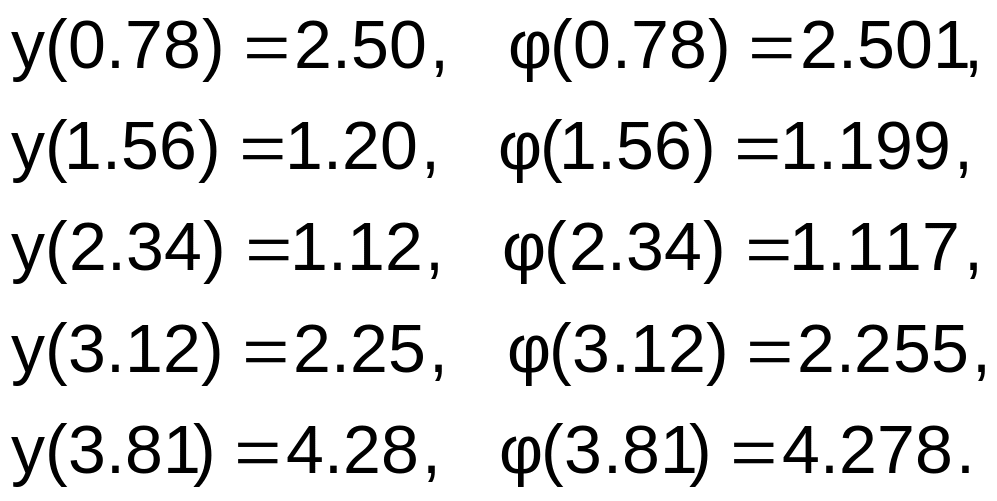
Вычислим
среднеквадратическое отклонение
(невязку)

.

Определение коэффициентов аппроксимирующей функции методом наименьших квадратов без вычисления частных производных.

Автор: Власов Андрей Алексеевич, учитель математики, ГБОУ СОШ №258 с углубленный изучением физики и химии Колпинского района Санкт-Петербурга

Аннотация. В данной статье методом наименьших квадратов определяются коэффициенты аппроксимирующей функции, имеющей два коэффициента. Предлагается способ, не требующий вычисления частных производных, то есть способ, который может применяться школьниками. В качестве формирования функциональной грамотности учащихся на примере  решения задачи высшей школы, показана возможность применения знаний  школьного курса математики.

Ключевые слова: математика; средняя школа; функциональная грамотность; функция двух переменных; метод наименьших квадратов

In this paper, the coefficients of an approximating function with two coefficients are determined by the least squares method. We propose a method that does not require the calculation of partial derivatives, that is, a method that can be used by schoolchildren. As the formation of functional literacy of students on the example of solving the problem of higher school, the possibility of applying the knowledge of the school course of mathematics is shown..

Keywords: mathematics; secondary school; functional literacy; function of two variables; least squares method.

Код УДК: 372.851

Введение.

В статье «Метод наименьших квадратов как пример исследования квадратичной функции в свете формирования функциональной грамотности учащихся» был приведен пример нахождения единственного коэффициента аппроксимирующей функции. Такой функцией является, например, прямая пропорциональность, зависимость от квадратного корня. Развивая данную тему, найдем коэффициенты  функции, зависящей от двух коэффициентов.

Актуальность статьи заключается в новом решении  известной задачи с помощью ограниченных ресурсов.

Цель работы: создать дополнительную мотивацию к изучению математики учащимися на примере решения задачи высшей школы.

Задачи: найти коэффициенты аппроксимирующей функции методами, использующими темы школьного курса математики, сравнить полученный результат с типовым решением, подготовить материал для проектно-исследовательской деятельности учащихся, привести  пример для развития функциональной грамотности учащихся.

Научная новизна работы заключается в предоставлении школьникам математического инструмента обработки экспериментальных данных на профессиональном уровне. Работ с похожей тематикой не было найдено.

Применение метода наименьших квадратов для нахождения коэффициентов линейной функции.

В случае, если зависимость физических параметров описывается  линейной функцией, необходимо найти два коэффициента, то есть сумма разности квадратов зависит от двух переменных.  

Пусть в результате эксперимента получены пары значений x1 и y1,   x2 и y2,…, xn и yn. Предположим, что y зависит от x , и зависимость  описывается функцией y=f(x), имеющей коэффициенты k и b. Для упрощения примем y=kx+b, что не влияет на дальнейший результат.  

z==

=(y1– kx1– b)2+(y2– kx2– b)2+(y3– kx3– b)2+…+(yn – kxn – b)2=

=y12+ k2∙x12+ b2– 2∙ y1∙ k∙x1– 2∙ y1∙ b+2∙ k∙x1∙ b+

+ y22+ k2∙ x22+ b2– 2∙ y2∙ k∙x2– 2∙ y2∙ b+2∙ k∙x2∙ b+…=

= k2∙(x12+ x22+ …+ xn2)+k∙(-2∙ y1∙ x1-2∙ y2∙ x2-…-2∙ yn∙ xn)+

+k ∙ b∙(2∙ x1+2∙x2+…+2∙xn)+ b (- 2∙ y1– 2∙ y2– …- 2∙ yn)+

+n∙ b2 +( y12+ y22+…+ yn2)

Обозначим

x12+ x22+ …+ xn2=A

n=B

-2∙ y1∙ x1-2∙ y2∙ x2-…-2∙ yn∙ xn =C

– 2∙ y1– 2∙ y2– …+2∙xn =D

2∙ x1+2∙x2+…+2∙xn =E

k = x

b= y, тогда формула примет вид

z=A∙x2+B∙y2+C∙x+D∙y+E∙xy                                (1)

В данной формуле x и y  – искомые коэффициенты, а  A, B, C, D, E – некоторые числовые значения, полученные в результате арифметических преобразований экспериментальных данных.

График такой функции будет представлять собой эллиптический параболоид – неограниченную поверхность в трехмерном пространстве, образуемою движением параболы, вершина которой скользит по другой неподвижной параболе, причем оси обеих парабол остаются взаимно перпендикулярными   (Рис.1). Примерами параболоида являются, например,  поверхность отражателя прожектора, поверхность жидкости при вращении сосуда. Наименьшее значение такой функции будет в вершине параболоида. То есть, задача сводится к нахождению ее абсциссы и ординаты.

Рис.1. Поверхность, описываемая формулой x2+y2+x+y+xy=z , и плоскость z=1

Для этого проведем через параболоид плоскость, параллельную плоскости XOY. (Рис. 1) Аппликату выберем с учетом упрощения дальнейших вычислений, например z=1. Получим сечение в виде эллипса, повернутого относительно оси OX на некоторый угол (Рис. 2).

Рис.2 Кривая, описываемая формулой: x2+y2+x+y+xy = 1

Координаты его центра будут искомыми величинами. Каноническое уравнение эллипса

 +  = 1

описывает кривую, большая ось которой совпадает с осью абсцисс, а центр – с началом координат. Если выделить полные квадраты переменных x и y

 +  = 1 ,

то получим уравнение эллипса со смещенным центром, где (x0; y0) – центр, но  в нашем случае слагаемое E∙xy не позволяет выделить полные квадраты, так как эллипс получен не смещением, а поворотом на угол.

Будем называть родительским эллипс, из которого получен исследуемый нами, и систему координат, в которой он находится родительской, исследуемый эллипс и соответствующую систему координат – дочерней. Найдем формулу родительского эллипса в соответствующей системе координат. Для этого рассмотрим не поворот эллипса, а поворот системы координат. Пусть точка с координатами (x;y) в дочерней системе координат (черная на рисунке) имеет в родительской системе (синяя) координаты (x’;y’), и дочерняя система получена из родительской путем поворота на угол  α. (Рис. 3)

	В треугольниках OBG и BAK α=∠X’OX = ∠OBG=∠KAB как углы между взаимно перпендикулярными прямыми, тогда x =OB∙+AB∙=   = y’∙ + x’∙ y = OB∙ – AB∙ =   = y’∙ – x’∙
Рис.3

Заменим в формуле (1 ) x на x’ и y на y’. Получим уравнение дочернего эллипса в родительской системе координат:

A(y’∙ + x’∙)2+B(y’∙ – x’∙)2+

C(y’∙ + x’∙)+D(y’∙ – x’∙) +

E(y’∙ + x’∙)( y’∙ – x’∙) = 1

После раскрытия скобок и приведения подобных получаем:

x’2(Acos2α + Bsin2 – E∙sinα∙cosα) +

 y’2(Asin2α + Bcos2α + E∙sinα∙cosα)+

x’(C∙cosα – D∙sinα) + y’(C∙sinα + D∙cosα) +

 x’∙y’∙(A∙2∙sinα∙cosα – B∙2∙sinα∙cosα+E∙cos2α – E∙sin2α) = 1

Формулу можно привести к каноническому виду эллипса, если коэффициент при x’∙y’ равен нулю, то есть:

A∙2∙sinα∙cosα – B∙2∙sinα∙cosα +E∙cos2α – E∙sin2α = 0

E∙cos2α -sin2α∙(B-A)=0

откуда

tg2α=

Дальнейшее решение в общем виде ввиду громоздкости представляется нецелесообразным. Определив численными методами величину α, следует вычислить коэффициенты при x’2 , y’2 , x’ и  y’ , далее выделить полный квадрат вида

 +  = 1 ,

Таким образом, в родительской системе координат центр эллипса имеет координаты (x’0;y’0). При повороте этой точки на угол α будет получена точка, имеющая в дочерней системе координат координаты (y’0∙ + x’0∙; y’0∙ – x’0∙),

что является решением поставленной задачи.

Для примера возьмем уравнение из рисунка 2: x2+y2+x+y+xy = 1.

tg2α=∞

2 α=90º

α=45º

Acos2α + Bsin2 – E∙sinα∙cosα=1∙()2+1∙(∙-1∙∙ =

Asin2α + Bcos2α + E∙sinα∙cosα =

C∙cosα – D∙sinα = 0

C∙sinα + D∙cosα =

x’2+ y’2+ y’ = 1

+(y’2+2∙ y’+) –  = 1

 +  =

Рис.4 Кривая, описываемая формулой:  +  =

Центр полученного эллипса в родительской системе координат (0; – ), в дочерней системе (- ∙ + 0∙ ; – ∙ – 0∙ ) или (- ∙ ; – )

Рис.5

На рисунке 5 изображены оба эллипса, графически определенный центр совпадает с расчетным значением.

Решение задачи через частные производные.

Проверим полученный ответ через вычисление частных производных.

z=x2+y2+x+y+xy

=2x+y+1

=2y+x+1

Выводы.

В проведенной работе предложен способ, позволяющий определить два коэффициента функции аппроксимации, не прибегая к вычислению частных производных. Использование функции двух переменных и ее графика, формулы эллипса и преобразования графика типа «поворот» служат примером применения школьных знаний математики для решения задач высшей школы, являются дополнительной мотивацией изучения предмета и формируют функциональную грамотность учащихся. Решение задачи через частные производные должно заинтересовать учащихся в дальнейшем изучении математики.

Список использованной литературы.

	Федеральный институт педагогических измерений. Официальный сайт. [Электронный ресурс] – режим доступа: https://fipi.ru – Загр. с экрана.
	Ресурс  для студентов технических, экономических и гуманитарных специальностей [Электронный ресурс] – режим доступа:  http://www.mathprofi.ru – Загр. с экрана.
	Единый федеральный портал дополнительного профессионального педагогического образования. [Электронный ресурс] – режим доступа: https://dppo.edu.ru/ – Загр. с экрана.

Данный калькулятор по введенным данным строит несколько моделей регрессии: линейную, квадратичную, кубическую, степенную, логарифмическую, гиперболическую, показательную, экспоненциальную. Результаты можно сравнить между собой по корреляции, средней ошибке аппроксимации и наглядно на графике. Теория и формулы регрессий под калькулятором.

Если не ввести значения x, калькулятор примет, что значение x меняется от 0 с шагом 1.

Линейная регрессия

Уравнение регрессии:

Коэффициент a:

Коэффициент b:

Коэффициент линейной парной корреляции:

Коэффициент детерминации:

Средняя ошибка аппроксимации:

Квадратичная регрессия

Уравнение регрессии:

Система уравнений для нахождения коэффициентов a, b и c:

Коэффициент корреляции:
,
где

Коэффициент детерминации:

Средняя ошибка аппроксимации:

Кубическая регрессия

Уравнение регрессии:

Система уравнений для нахождения коэффициентов a, b, c и d:

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации – используются те же формулы, что и для квадратичной регрессии.

Степенная регрессия

Уравнение регрессии:

Коэффициент b:

Коэффициент a:

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Показательная регрессия

Уравнение регрессии:

Коэффициент b:

Коэффициент a:

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Гиперболическая регрессия

Уравнение регрессии:

Коэффициент b:

Коэффициент a:

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации – используются те же формулы, что и для квадратичной регрессии.

Логарифмическая регрессия

Уравнение регрессии:

Коэффициент b:

Коэффициент a:

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации – используются те же формулы, что и для квадратичной регрессии.

Экспоненциальная регрессия

Уравнение регрессии:

Коэффициент b:

Коэффициент a:

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации – используются те же формулы, что и для квадратичной регрессии.

Вывод формул

Сначала сформулируем задачу:
Пусть у нас есть неизвестная функция y=f(x), заданная табличными значениями (например, полученными в результате опытных измерений).
Нам необходимо найти функцию заданного вида (линейную, квадратичную и т. п.) y=F(x), которая в соответствующих точках принимает значения, как можно более близкие к табличным.
На практике вид функции чаще всего определяют путем сравнения расположения точек с графиками известных функций.

Полученная формула y=F(x), которую называют эмпирической формулой, или уравнением регрессии y на x, или приближающей (аппроксимирующей) функцией, позволяет находить значения f(x) для нетабличных значений x, сглаживая результаты измерений величины y.

Для того, чтобы получить параметры функции F, используется метод наименьших квадратов. В этом методе в качестве критерия близости приближающей функции к совокупности точек используется суммы квадратов разностей значений табличных значений y и теоретических, рассчитанных по уравнению регрессии.

Таким образом, нам требуется найти функцию F, такую, чтобы сумма квадратов S была наименьшей:

Рассмотрим решение этой задачи на примере получения линейной регрессии F=ax+b.
S является функцией двух переменных, a и b. Чтобы найти ее минимум, используем условие экстремума, а именно, равенства нулю частных производных.

Используя формулу производной сложной функции, получим следующую систему уравнений:

Для функции вида частные производные равны:
,

Подставив производные, получим:

Далее:

Откуда, выразив a и b, можно получить формулы для коэффициентов линейной регрессии, приведенные выше.
Аналогичным образом выводятся формулы для остальных видов регрессий.

Линейная аппроксимация

При обработке экспериментальных данных часто возникает необходимость аппроксимировать их линейной функцией.

Аппроксимацией (приближением) функции f(x) называется нахождение такой функции ( аппроксимирующей функции ) g(x) , которая была бы близка заданной. Критерии близости функций могут быть различные.

В случае если приближение строится на дискретном наборе точек, аппроксимацию называют точечной или дискретной .

В случае если аппроксимация проводится на непрерывном множестве точек (отрезке), аппроксимация называется непрерывной или интегральной . Примером такой аппроксимации может служить разложение функции в ряд Тейлора, то есть замена некоторой функции степенным многочленом.

Наиболее часто встречающим видом точечной аппроксимации является интерполяция – нахождение промежуточных значений величины по имеющемуся дискретному набору известных значений.

Пусть задан дискретный набор точек, называемых узлами интерполяции , а также значения функции в этих точках. Требуется построить функцию g(x) , проходящую наиболее близко ко всем заданным узлам. Таким образом, критерием близости функции является g(xi)=yi .

В качестве функции g(x) обычно выбирается полином, который называют интерполяционным полиномом .

В случае если полином един для всей области интерполяции, говорят, что интерполяция глобальная .

В случае если между различными узлами полиномы различны, говорят о кусочной или локальной интерполяции.

Найдя интерполяционный полином, мы можем вычислить значения функции между узлами, а также определить значение функции даже за пределами заданного интервала (провести экстраполяцию ).

Аппроксимация линейной функцией

Любая линейная функция может быть записана уравнением

Аппроксимация заключается в отыскании коэффициентов a и b уравнения таких, чтобы все экспериментальные точки лежали наиболее близко к аппроксимирующей прямой.

С этой целью чаще всего используется метод наименьших квадратов (МНК), суть которого заключается в следующем: сумма квадратов отклонений значения точки от аппроксимирующей точки принимает минимальное значение:

Решение поставленной задачи сводится к нахождению экстремума указанной функции двух переменных. С этой целью находим частные производные функции функции по коэффициентам a и b и приравниваем их к нулю.

Решаем полученную систему уравнений

Определяем значения коэффициентов

Для вычисления коэффициентов необходимо найти следующие составляющие:

Тогда значения коэффициентов будут определены как

Пример реализации

Для примера реализации воспользуемся набором значений, полученных в соответствии с уравнением прямой

y = 8 · x — 3

Рассчитаем указанные коэффициенты по методу наименьших квадратов.
Результат сохраняем в форме двумерного массива, состоящего из 2 столбцов.
При следующем запуске программы добавим случайную составляющую к указанному набору значений и снова рассчитаем коэффициенты.

Реализация на Си

Построение графика функции

Для наглядности построим график функции, полученный аппроксимацией по методу наименьших квадратов. Подробнее о построении графика функции описано здесь.

Реализация на Си

Аппроксимация с фиксированной точкой пересечения с осью y

В случае если в задаче заранее известна точка пересечения искомой прямой с осью y, в решении задачи останется только одна частная производная для вычисления коэффициента a.

В этом случае текст программы для поиска коэффициента угла наклона аппроксимирующей прямой будет следующий (имя функции getApprox() заменено на getApproxA() во избежание путаницы).

Определение коэффициентов аппроксимирующей функции.

Рассмотрим кратко основные методы определения коэффициентов аппроксимирующей функции. При невысоких требованиях к точности аппроксимации для этой цели используют метод выбранных точек, в соответствии с которым коэффициенты аппроксимирующей функции находят, исходя из совпадения значений этой функции со значениями аппроксимируемой функции в ряде заранее выбранных точек, называемых узлами интерполяции (от лат. interpolare — подновлять). Если для аппроксимации ВАХ, задаваемой множеством точек <х),s,>, выбрана функция

имеющая п + 1 неизвестных постоянных коэффициентов Sj(xj) в произвольном числе точек т, не связанном с числом неизвестных коэффициентов п + 1:

Приравнивая к нулю первые производные о по каждому из коэффициентов, получаем систему из п + 1 уравнений для определения п + 1 неизвестных числовых значений коэффициентов:

Метод наименьших квадратов требует громоздких вычислений и применяется обычно только в тех случаях, когда необходима высокая точность аппроксимации.

Если гипотеза о характере аппроксимирующей функции проверялась методом выравнивания, то неизвестные значения коэффициентов аппроксимирующей функции могут быть определены по известным коэффициентам и К линейного уравнения (5.3), связывающего между собой вспомогательные переменные X и S. Составляя уравнение прямой линии, вдоль которой располагаются точки Sj), и сравнивая его с уравнением, описывающим зависимость между вспомогательными переменными X и У, которое соответствует проверяемой гипотезе о виде функции s(х), например, с уравнениями (5.5), (5.7) или (5.10), находим искомые коэффициенты.

Пример 5.6. Определим коэффициенты экспоненциального полинома i = ае Ьи + с, аппроксимирующего ВАХ полупроводникового диода (см. рис. 5.19, а) в диапазоне напряжений от О до 1 В.

Возможность аппроксимации ВАХ, приведенной на рис. 5.19, экспоненциальным полиномом указанного типа была показана в примере 5.5. Там же было найдено числовое значение коэффициента с. Составим уравнение прямой (см. рис. 5.20), на которой в рассматриваемом диапазоне изменения аргумента располагаются точки :

где <Хуи <Х₂,5*2> — координаты двух любых точек, через которые проходит данная прямая. Выбирая <Х _<= 0,2, S = -0,95> и <Х₂ = 1 ,S₂– -0,42>, получаем уравнение прямой в следующем виде:

Сравнивая это выражение с выражением (5.10), находим соотношения для определения неизвестных значений коэффициентов а и Ь:

откуда а = 0,082, b = 1,52.

Таким образом, в диапазоне от 0 до 1 В данная ВАХ может быть аппроксимирована выражением

На практике для аппроксимации характеристик нелинейных элементов в основном используют степенные полиномы

и кусочно-линейные функции. Аппроксимация с помощью степенного полинома универсальна и позволяет повышать точность расчета путем увеличения степени полинома. Любые аппроксимирующие функции могут быть разложены в степенные ряды и приведены к виду (5.14). Поскольку сложность определения коэффициентов аппроксимирующей функции возрастает с увеличением числа членов полинома, для аппроксимации ВАХ обычно используют полиномы низких степеней.

Аппроксимация с помощью кусочно-линейных функций заключается в разбиении рабочей области аппроксимируемой функции на несколько участков (интервалов) и замене функции на каждом из них отрезком прямой. С увеличением числа интервалов точность аппроксимации возрастает, однако для упрощения анализа цепи желательно использовать кусочно-линейные функции с минимальным числом интервалов. Примеры кусочно-линейной аппроксимации ВАХ представлены на рис. 5.21.

Рис. 5.21. Кусочно-линейная аппроксимация выходных (а) и проходных (б) характеристик полевого транзистора

Аппроксимация

линейный алгебраический численный метод

Часто при анализе экспериментальных данных возникает необходимость найти функциональную зависимость между величинами x и y, которые получены в результате измерений. При аналитическом исследовании взаимосвязи между двумя величинами x и y получается таблица значений, которую также можно представить в графическом виде.

Если же заведомо известен вид аппроксимирующей функции, то задача аппроксимации сводится только к отысканию коэффициентов (a, b, c. ), входящих в функцию. Для нахождения этих коэффициентов используется метод наименьших квадратов, заключающийся в том, что сумма квадратов расстояний по вертикали от точек до графика функции y=f(x, a, b, c. ) наименьшая: S =_i 2 = min, где S_i = y_i – f(x_i, a, b, c. ). Для этого используем необходимое условие экстремума функции нескольких переменных _i – f(x_i, a, b, c. )) 2 : равенство нулю частных производных. В результате получим систему. Таким образом, нахождение коэффициентов сводится только к решению системы:

Линейная регрессия

Линейная функция имеет вид y = ax + b, следовательно, требуется найти два параметра: a и b, с условием, что даны координаты n точек, найденных экспериментально со случайными ошибками («шумом»). Для этого составим функцию _i – (ax_i+b)) 2 , раскроем скобки _i – ax_i – b) 2 и составим систему:

Пусть А = _i , В = _i , С = _ix_i , D = _i 2 , тогда система примет вид:

Решим эту систему линейных алгебраических уравнений методом Крамера и, таким образом, найдем искомые значения параметров a и b:

Таблица. Имеются точки:

Используя способ вычисления параметров линейной функции, получаем:

[spoiler title=”источники:”]

http://studme.org/308641/tehnika/opredelenie_koeffitsientov_approksimiruyuschey_funktsii

http://vuzlit.com/1004359/approksimatsiya

[/spoiler]