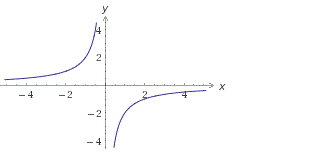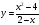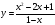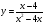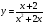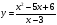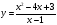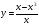Как найти коэффициенты дробно линейной функции - Сайт, где вы сможете решить свои вопросы

1. Дробно-линейная функция и ее график

Функция вида y = P(x) / Q(x), где P(x) и Q(x) – многочлены, называется дробно-рациональной функцией.

С понятием рациональных чисел вы уже наверняка знакомы. Аналогично рациональные функции – это функции, которые можно представить как частное двух многочленов.

Если дробно-рациональная функция представляет собой частное двух линейных функций – многочленов первой степени, т.е. функцию вида

y = (ax + b) / (cx + d), то ее называют дробно-линейной.

Заметим, что в функции y = (ax + b) / (cx + d), c ≠ 0 (иначе функция становится линейной y = ax/d + b/d) и что a/c ≠ b/d (иначе функция константа). Дробно-линейная функция определена при всех действительных числах, кроме x = -d/c. Графики дробно-линейных функций по форме не отличаются от известного вам графика y = 1/x. Кривая, являющаяся графиком функции y = 1/x, называется гиперболой. При неограниченном увеличении x по абсолютной величине функция y = 1/x неограниченно уменьшается по абсолютной величине и обе ветки графика приближаются к оси абсцисс: правая приближается сверху, а левая – снизу. Прямые, к которым приближаются ветки гиперболы, называются ее асимптотами.

Пример 1.

y = (2x + 1) / (x – 3).

Решение.

Выделим целую часть: (2x + 1) / (x – 3) = 2 + 7/(x – 3).

Теперь легко видеть, что график этой функции получается из графика функции y = 1/x следующими преобразованиями: сдвигом на 3 единичных отрезка вправо, растяжением вдоль оси Oy в 7 раз и сдвигом на 2 единичных отрезка вверх.

Любую дробь y = (ax + b) / (cx + d) можно записать аналогичным образом, выделив «целую часть». Следовательно, графики всех дробно-линейных функций есть гиперболы, различным образом сдвинутые вдоль координатных осей и растянутые по оси Oy.

Для построения графика какой-нибудь произвольной дробно-линейной функции совсем не обязательно дробь, задающую эту функцию, преобразовывать. Поскольку мы знаем, что график есть гипербола, будет достаточно найти прямые, к которым приближаются ее ветки – асимптоты гиперболы x = -d/c и y = a/c.

Пример 2.

Найти асимптоты графика функции y = (3x + 5)/(2x + 2).

Решение.

Функция не определена, при x = -1. Значит, прямая x = -1 служит вертикальной асимптотой. Для нахождения горизонтальной асимптоты, выясним, к чему приближаются значения функции y(x), когда аргумент x возрастает по абсолютной величине.

Для этого разделим числитель и знаменатель дроби на x:

y = (3 + 5/x) / (2 + 2/x).

При x → ∞ дробь будет стремиться к 3/2. Значит, горизонтальная асимптота – это прямая y = 3/2.

Пример 3.

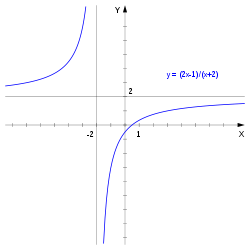
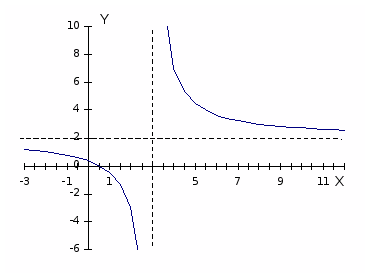
Построить график функции y = (2x + 1)/(x + 1).

Решение.

Выделим у дроби «целую часть»:

(2x + 1) / (x + 1) = (2x + 2 – 1) / (x + 1) = 2(x + 1) / (x + 1) – 1/(x + 1) =

= 2 – 1/(x + 1).

Теперь легко видеть, что график этой функции получается из графика функции y = 1/x следующими преобразованиями: сдвигом на 1 единицу влево, симметричным отображением относительно Ox и сдвигом на 2 единичных отрезка вверх по оси Oy.

Область определения D(y) = (-∞; -1)ᴗ(-1; +∞).

Область значений E(y) = (-∞; 2)ᴗ(2; +∞).

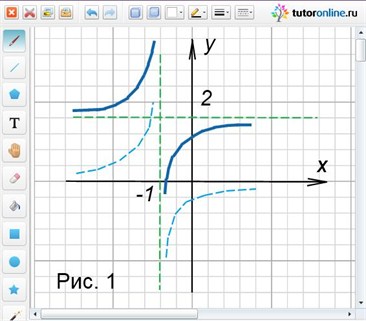
Точки пересечения с осями: c Oy: (0; 1); c Ox: (-1/2; 0). Функция возрастает на каждом из промежутков области определения.

Ответ: рисунок 1.

2. Дробно-рациональная функция

Рассмотрим дробно-рациональную функцию вида y = P(x) / Q(x), где P(x) и Q(x) – многочлены, степени выше первой.

Примеры таких рациональных функций:

y = (x³ – 5x + 6) / (x⁷ – 6) или y = (x – 2)²(x + 1) / (x² + 3).

Если функция y = P(x) / Q(x) представляет собой частное двух многочленов степени выше первой, то ее график будет, как правило, сложнее, и построить его точно, со всеми деталями бывает иногда трудно. Однако, часто достаточно применить приемы, аналогичные тем, с которыми мы уже познакомились выше.

Пусть дробь – правильная (n < m). Известно, что любую несократимую рациональную дробь можно представить, и притом единственным образом, в виде суммы конечного числа элементарных дробей, вид которых определяется разложением знаменателя дроби Q(x) в произведение действительных сомножителей:

P(x)/Q(x) = A₁/(x – K₁)^m1 + A₂/(x – K₁)^m1-1 + … + A_m1/(x – K₁) + …+

+ L₁/(x – K_s)^ms + L₂/(x – K_s)^ms-1 + … + L_ms/(x – K_s) + …+

+ (B₁x + C₁) / (x² +p₁x + q₁)^m1 + … + (B_m1x + C_m1) / (x² +p₁x + q₁) + …+

+ (M₁x + N₁) / (x² +p_tx + q_t)^m1 + … + (M_m1x + N_m1) / (x² +p_tx + q_t).

Очевидно, что график дробно-рациональной функции можно получить как сумму графиков элементарных дробей.

Построение графиков дробно-рациональных функций

Рассмотрим несколько способов построения графиков дробно-рациональной функции.

Пример 4.

Построить график функции y = 1/x².

Решение.

Используем график функции y = x² для построения графика y = 1/x² и воспользуемся приемом «деления» графиков.

Область определения D(y) = (-∞; 0)ᴗ(0; +∞).

Область значений E(y) = (0; +∞).

Точек пересечения с осями нет. Функция четная. Возрастает при все х из интервала (-∞; 0), убывает при x от 0 до +∞.

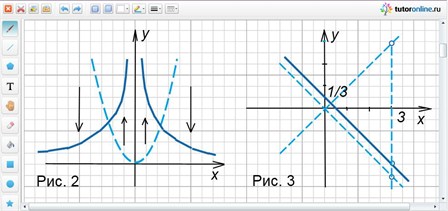
Ответ: рисунок 2.

Пример 5.

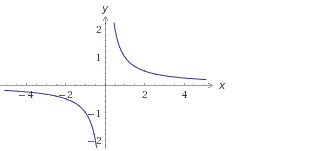
Построить график функции y = (x² – 4x + 3) / (9 – 3x).

Решение.

Область определения D(y) = (-∞; 3)ᴗ(3; +∞).

y = (x² – 4x + 3) / (9 – 3x) = (x – 3)(x – 1) / (-3(x – 3)) = -(x – 1)/3 = -x/3 + 1/3.

Здесь мы использовали прием разложения на множители, сокращения и приведения к линейной функции.

Ответ: рисунок 3.

Пример 6.

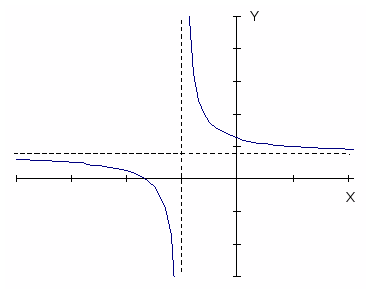
Построить график функции y = (x² – 1)/(x² + 1).

Решение.

Область определения D(y) = R. Так как функция четная, то график симметричен относительно оси ординат. Прежде чем строить график, опять преобразуем выражение, выделив целую часть:

y = (x² – 1)/(x² + 1) = 1 – 2/(x² + 1).

Заметим, что выделение целой части в формуле дробно-рациональной функции является одним из основных при построении графиков.

Если x → ±∞, то y → 1, т.е. прямая y = 1 является горизонтальной асимптотой.

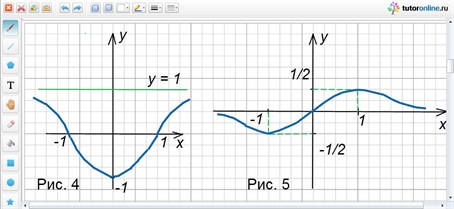
Ответ: рисунок 4.

Пример 7.

Рассмотрим функцию y = x/(x² + 1) и попробуем точно найти наибольшее ее значение, т.е. самую высокую точку правой половины графика. Чтобы точно построить этот график, сегодняшних знаний недостаточно. Очевидно, что наша кривая не может «подняться» очень высоко, т.к. знаменатель довольно быстро начинает «обгонять» числитель. Посмотрим, может ли значение функции равняться 1. Для этого нужно решить уравнение x² + 1 = x, x² – x + 1 = 0. Это уравнение не имеет действительных корней. Значит, наше предположение не верно. Чтобы найти самое большое значение функции, надо узнать, при каком самом большом А уравнение А = x/(x² + 1) будет иметь решение. Заменим исходное уравнение квадратным: Аx² – x + А = 0. Это уравнение имеет решение, когда 1 – 4А² ≥ 0. Отсюда находим наибольшее значение А = 1/2.

Ответ: рисунок 5, max y(x) = ½.

Остались вопросы? Не знаете, как строить графики функций?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

Источник

Дро́бно-лине́йная фу́нкция — это числовая функция, которая может быть представлена в виде дроби, числителем и знаменателем которой являются линейные функции.

Дробно-линейная функция, отображающая в общем случае многомерное числовое пространство в одномерное числовое, представляет собой важный частный случай:

Формальное определение[править | править код]

Дробно-линейная функция — это числовая функция вида

${displaystyle mathbb {U} ^{n}to mathbb {U} :w=L(u_{1},u_{2},dots ,u_{n})={frac {a_{1}u_{1}+a_{2}u_{2}+cdots +a_{n}u_{n}+b}{c_{1}u_{1}+c_{2}u_{2}+cdots +c_{n}u_{n}+d}},}$

где — комплексные () или вещественные () числа, — соответственно комплексные или вещественные переменные, ${displaystyle a_{1},a_{2},dots ,a_{n},}$ ${displaystyle c_{1},c_{2},dots ,c_{n},}$ — соответственно комплексные или вещественные коэффициенты,

${displaystyle |c_{1}|+|c_{2}|+dots +|c_{n}|+|d|>0}$

^[1].

Возможно обобщение на кватернионы^[2].

Вырожденные случаи^[1]:

если

${displaystyle |c_{1}|=|c_{2}|=dots =|c_{n}|=0,}$

то дробно-линейная функция становится целой линейной функций;

если ранг матрицы

${displaystyle left({begin{array}{cccc}a_{1}&a_{2}&ldots &a_{n}&b\c_{1}&c_{2}&ldots &c_{n}&dend{array}}right)}$

равен единице, то дробно-линейная функция вырождается в постоянную.

У собственно (невырожденной) дробно-линейной функции^[1]:

${displaystyle |c_{1}|+|c_{2}|+dots +|c_{n}|>0;}$
равен двум ранг матрицы

${displaystyle left({begin{array}{cccc}a_{1}&a_{2}&ldots &a_{n}&b\c_{1}&c_{2}&ldots &c_{n}&dend{array}}right).}$

Вещественная дробно-линейная функция[править | править код]

Вещественная дробно-линейная функция — это числовая функция вида

${displaystyle mathbb {R} ^{n}to mathbb {R} :y=L(x_{1},x_{2},dots ,x_{n})={frac {a_{1}x_{1}+a_{2}x_{2}+cdots +a_{n}x_{n}+b}{c_{1}x_{1}+c_{2}x_{2}+cdots +c_{n}x_{n}+d}},}$

где — вещественные числа, $x_{1},x_{2},dots ,x_{n}$ — вещественные переменные, ${displaystyle a_{1},a_{2},dots ,a_{n},}$ ${displaystyle c_{1},c_{2},dots ,c_{n},}$ — вещественные коэффициенты,

${displaystyle |c_{1}|+|c_{2}|+dots +|c_{n}|+|d|>0}$

^[1].

Функция одного переменного[править | править код]

В простейшем случае n = 1 и действительных

${displaystyle x_{1}=x,}$

${displaystyle a_{1}=a,}$

${displaystyle c_{1}=c,}$

график дробно-линейной функции — равнобочная гипербола с асимптотами

параллельными осям координат:^[1].

Асимптоты гиперболы[править | править код]

Пусть дробно-линейная функция одного переменного

${displaystyle y={frac {ax+b}{cx+d}}}$

несократима, то есть , и не сводится к целой линейной функции, то есть cneq 0 . Выделим целую часть дроби и вынесем за скобки коэффициент при ^[3]:

${displaystyle y={frac {{frac {a}{c}}x+{frac {b}{c}}}{x+{frac {d}{c}}}}={frac {{frac {a}{c}}left(x+{frac {d}{c}}right)+left({frac {b}{c}}-{frac {ad}{c^{2}}}right)}{x+{frac {d}{c}}}}=}$

${displaystyle ={frac {a}{c}}-{frac {ad-bc}{c^{2}(x+{frac {d}{c}})}}.}$

Теперь ясно, что график функции ${displaystyle {frac {ax+b}{cx+d}}}$ получается из графика ${frac {1}{x}}$ следующими элементарными преобразованиями:

Таким образом, дробно-линейная функция одного переменного ${displaystyle {frac {ax+b}{cx+d}}}$ — это обыкновенная гипербола второго порядка, прямые ${displaystyle x=-{frac {d}{c}}}$ и ${displaystyle y={frac {a}{c}}}$ — асимптоты гиперболы, взаимно перпендикулярные и параллельные осям координат, а точка пересечения асимптот ${displaystyle left(-{frac {d}{c}},{frac {a}{c}}right)}$ , не принадлежащая кривой, — её центр^[3].

Также очевидно, что дробно-линейная функция одного переменного ${displaystyle {frac {ax+b}{cx+d}}}$ ^[3]:

${displaystyle {frac {ax+b}{cx+d}}={frac {a+{frac {b}{x}}}{c+{frac {d}{x}}}}.}$

Производная

${displaystyle left({frac {a}{c}}-{frac {ad-bc}{c^{2}(x+{frac {d}{c}})}}right)'={frac {ad-bc}{c^{2}(x+{frac {d}{c}})^{2}}}.}$

Неопределённый интеграл:

${displaystyle int left({frac {a}{c}}-{frac {ad-bc}{c^{2}(x+{frac {d}{c}})}}right)dx={frac {a}{c}}x-{frac {ad-bc}{c^{2}}}ln left|x+{frac {d}{c}}right|+C.}$

Каноническое уравнение гиперболы[править | править код]

Сначала приведём функцию

${displaystyle y={frac {a}{c}}-{frac {ad-bc}{c^{2}(x+{frac {d}{c}})}}}$

преобразованиями координат к виду

${displaystyle y'={frac {m}{x'}}.}$

Для этого сделаем следующие замены:

${displaystyle x'=x+{frac {d}{c}},}$

${displaystyle y'=y-{frac {a}{c}},}$

${displaystyle m=-{frac {ad-bc}{c^{2}}},}$

получим требуемый вид функции^[4].

Теперь повернём координатные оси на угол ${displaystyle 45^{circ },}$ сделав замену координат

${displaystyle x'=x''cos(45^{circ })-y''sin(45^{circ })={frac {x''-y''}{sqrt {2}}},}$

${displaystyle y'=x''sin(45^{circ })+y''cos(45^{circ })={frac {x''+y''}{sqrt {2}}},}$

получим в новых координатах^[4]:

${displaystyle {frac {x''-y''}{sqrt {2}}}{frac {x''+y''}{sqrt {2}}}=m,}$

${displaystyle {frac {x''^{2}}{2m}}-{frac {y''^{2}}{2m}}=1.}$

Последнее уравнение есть каноническое уравнение равносторонней гиперболы с полуосями ^[4]

Функция двух переменных[править | править код]

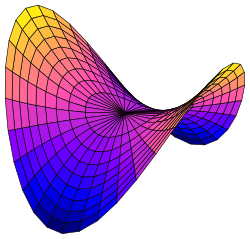
Гиперболический параболоид

В случае n = 2 и действительных ${displaystyle x_{1},}$ ${displaystyle x_{2},}$ ${displaystyle a_{1},}$ ${displaystyle a_{2},}$ ${displaystyle c_{1},}$ ${displaystyle c_{2},}$ график дробно-линейной функции

${displaystyle y={frac {a_{1}x_{1}+a_{2}x_{2}+b}{c_{1}x_{1}+c_{2}x_{2}+d}}}$

представляет собой гиперболический параболоид^[1].

Комплексная дробно-линейная функция[править | править код]

Комплексная дробно-линейная функция — это числовая функция вида

${displaystyle mathbb {C} ^{n}to mathbb {C} :w=L(z_{1},z_{2},dots ,z_{n})={frac {a_{1}z_{1}+a_{2}z_{2}+cdots +a_{n}z_{n}+b}{c_{1}z_{1}+c_{2}z_{2}+cdots +c_{n}z_{n}+d}},}$

где — комплексные числа, ${displaystyle z_{1},z_{2},dots ,z_{n}}$ — комплексные переменные, ${displaystyle a_{1},a_{2},dots ,a_{n},}$ ${displaystyle c_{1},c_{2},dots ,c_{n},}$ — комплексные коэффициенты,

${displaystyle |c_{1}|+|c_{2}|+dots +|c_{n}|+|d|>0}$

^[1].

При n = 1 комплексная дробно-линейная функция

${displaystyle mathbb {C} to mathbb {C} :w=L(z)={frac {az+b}{cz+d}}}$

—

аналитическая функция одной комплексной переменной всюду в расширенной комплексной плоскости , за исключением точки , в которой комплексная дробно-линейная функция имеет простой полюс^[1].

При комплексная дробно-линейная функция

${displaystyle mathbb {C} ^{n}to mathbb {C} :w=L(z_{1},z_{2},dots ,z_{n})={frac {a_{1}z_{1}+a_{2}z_{2}+cdots +a_{n}z_{n}+b}{c_{1}z_{1}+c_{2}z_{2}+cdots +c_{n}z_{n}+d}},}$

—

мероморфная функция в пространстве ${mathbb C}^{n}$ комплексных переменных ${displaystyle z_{1},z_{2},dots ,z_{n}}$ , имеющая полярное множество

${displaystyle {zin mathbb {C} ^{n};c_{1}z_{1}+c_{2}z_{2}+cdots +c_{n}z_{n}+d=0}}$

^[1].

Примечания[править | править код]

↑ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ Математическая энциклопедия, т. 2, 1979, стб. 384.
↑ Alan F. Beardon. The geometry of discrete groups, 1983, p. 56.
↑ ¹ ² ³ Энциклопедия элементарной математики. Книга третья, 1952, с. 56—57.
↑ ¹ ² ³ Ефимов Н. В. Краткий курс аналитической геометрии, 2005, 119, с. 120.

Литература[править | править код]

Ефимов Н. В. Краткий курс аналитической геометрии: Учебн. пособие. 13-е изд., стереот. М.: ФИЗМАТЛИТ, 2005. 238 с., ил. ISBN 5-9221-0252-4.
Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д—Коо. М.: «Советская Энциклопедия», 1979. 1104 стб., ил.
Энциклопедия элементарной математики. Книга третья. Функции и пределы (основы анализа) / Под ред. П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина. М., Л.: Государственное издательство технико-теоретической литературы, 1952. 559 с., ил.
Alan F. Beardon. The geometry of discrete groups. Berlin, Heidelberg, New York: Springer-Verlag, 1983. 337 p., 93 ill.

Источник

Функция у = и её график.

ЦЕЛИ:

1) ввести определение функции у = ;

2) научить строить график функции у = , используя
программу Agrapher;

3) сформировать умение строить эскизы графиков
функции у = ,
используя свойства преобразования графиков
функций;

4) научить читать графики функций у =.

I. Новый материал – развёрнутая беседа.

У: Рассмотрим функции, заданные формулами у = ; у = ; у = .

Что представляют собой выражения, записанные в
правых частях этих формул?

Д: Правые части этих формул имеют вид
рациональной дроби, у которой числитель-двучлен
первой степени или число, отличное от нуля, а
знаменатель-двучлен первой степени.

У: Такие функции принято задавать формулой
вида

у = (1).

Рассмотрите случаи когда а) с = 0 или в) = .

(Если во втором случае учащиеся будут
испытывать затруднения, то нужно попросить их
выра зить с из заданной пропорции и затем
подставить полученное выражение в формулу (1)).

Д1: Если с = 0, то у = х + в – линейная функция.

Д2: Если = , то с = . Подставив
значение с в формулу (1) получим:

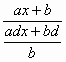
= = = , то есть у = – линейная функция.

У: Функция, которую можно задать формулой
вида у =, где
буквой х обозначена незави-

симая переменная, а буквами а, в, с и d –
произвольные числа, причём с0 и аd – вс 0, называется дробно-линейной
функцией.

Покажем, что графиком дробно-линейной функции
является гипербола.

Пример 1. Построим график функции у = . Выделим из дроби целую часть.

Имеем: = = = 1 + .

График функции у = +1 можно получить из графика функции у = с помощью двух
параллельных переносов: сдвига на 2 единицы
вправо вдоль оси Х и сдвига на 1 единицу вверх в
направлении оси У. При этих сдвигах переместятся
асимптоты гиперболы у = : прямая х = 0 (т. е. ось У) – на 2 единицы
вправо, а прямая у = 0 (т. е. ось Х) – на одну единицу
вверх. Прежде чем строить график, проведём на
координатной плоскости пунктиром асимптоты:
прямые х = 2 и у = 1 (рис. 1а). Учитывая,
что гипербола состоит из двух ветвей, для
построения каждой из них составим, используя
программу Agrapher, две таблицы: одну для х>2, а
другую для х<2.

х	1	0	-1	-2	-4	-10
у	-5	-2	-1	-0,5	0	0,5
х	3	4	5	6	8	12
у	7	4	3	2,5	2	1,6

Отметим (с помощью программы Agrapher) в
координатной плоскости точки, координаты
которых записаны в первой таблице, и соединим их
плавной непрерывной линией. Получим одну ветвь
гиперболы. Аналогично, воспользовавшись второй
таблицей, получим вторую ветвь гиперболы (рис. 1б).

Пример 2. Построим график функции у = –.Выделим из дроби целую часть,
разделив двучлен 2х + 10 на двучлен х + 3. Получим = 2 + . Следовательно, у = –-2.

График функции у = –-2 можно получить из графика функции у = – с помощью двух
параллельных переносов: сдвига на 3 единицы влево
и сдвига на 2 единицы вниз. Асимптоты гиперболы –
прямые х = -3 и у = -2. Составим (с помощью программы
Agrapher) таблицы для х<-3 и для х>-3.

х	-2	-1	1	2	7
у	-6	-4	-3	-2,8	-2,4
х	-4	-5	-7	-8	-11
у	2	0	-1	-1,2	-1,5

Построив (с помощью программы Agrapher) точки в
координатной плоскости и проведя через них ветви
гиперболы, получим график функции у = – (рис. 2).

У: Что является графиком
дробно-линейной функции?

Д: Графиком любой дробно-линейной функции
является гипербола.

У: Как построить график дробно-линейной
функции?

Д: График дробно-линейной функции получается
из графика функции у = с помощью параллельных переносов вдоль
осей координат, ветви гиперболы дробно-линейной
функции симметричны относительно точки (-. Прямая х = – называется
вертикальной асимптотой гиперболы. Прямая у = называется
горизонтальной асимптотой.

У: Какова область определения
дробно-линейной функции?

Д: D(y) =

У: Какова область значений дробно-линейной
функции?

Д: Е(у) = .

У: Есть ли у функции нули?

Д: Если х = 0, то f(0) = , d. То
есть у функции есть нули – точка А.

У: Есть ли у графика дробно-линейной функции
точки пересечения с осью Х?

Д: Если у = 0, то х = –. Значит, если а , то точка пересечения с осью Х имеет
координаты .
Если же а = 0, в , то точек
пересечения с осью абсцисс график
дробно-линейной функции не имеет.

У: Функция убывает на промежутках всей
области определения, если bc-ad > 0 и возрастает на
промежутках всей области определения, если bc-ad <
0. Но это немонотонная функция.

У: Можно ли указать наибольшее и наименьшее
значения функции?

Д: Наибольшего и наименьшего значений
функция не имеет.

У: Какие прямые являются асимптотами графика
дробно-линейной функции?

Д: Вертикальной асимптотой является прямая х
= –; а
горизонтальной асимптотой – прямая y = .

(Все обобщающие выводы-определения и свойства
дробно-линейной функции учащиеся записывают в
тетрадь)

II. Закрепление.

При построении и “чтении” графиков
дробно-линейных функций применяются свойства
программы Agrapher

Постройте график функции: а) у = (рис. 3а); б) у = (рис.
3б).
Найдите область определения и область значений
функции f, если: a) f(x) = (рис. 3в), б) f(x) = (рис. 3г).
Укажите асимптоты гиперболы – графика функции:
а) у = (рис. 4а); б) у =
– (рис.
4б); в) у = .

III. Обучающая самостоятельная работа.

Найдите центр гиперболы, асимптоты и постройте
график функции:

а) у = б) у = в) у = ; г) у = ; д) у = ; е) у = ;

ж) у = з) у = –

Каждый учащийся работает в своём темпе. При
необходимости учитель оказывает помощь, задавая
вопросы, ответы на которые помогут ученику
правильно выполнить задание.

Лабораторно-практическая работа по
исследованию свойств функций у = и у = и особенностей графиков этих
функций.

ЦЕЛИ: 1) продолжить формирование умений
строить графики функций у = и у = , используя программу Agrapher;

2) закрепить навыки “чтения графиков” функций
и способностей “предсказывать” изменения
графиков при различных преобразованиях дробно –
линейных функций.

I. Дифференцированное повторение свойств
дробно–линейной функции.

Каждому учащемуся выдаётся карточка –
распечатка c заданиями. Все построения
выполняются с помощью программы Agrapher. Результаты
выполнения каждого задания обсуждаются сразу же.

Каждый ученик с помощью самоконтроля может
скорректировать результаты, полученные при
выполнении задания и попросить помощи у учителя
или ученика – консультанта.

Постройте график функции у = – Используя график, найдите
значение У, соответствующее значению Х. равному
1,5; 8; -1,5; -2,5.
Постройте график функции f(x) =

Найдите значение аргумента Х, при котором f(x) =6 ;
f(x) =-2.5.

3. Постройте график функции у = Определите, принадлежит ли
графику данной функции точка: а) А(20;0.5); б) В(-30;-); в) С(-4;2.5); г)
Д(25;0,4)?

4. Постройте график функции у = Найдите промежутки в
которых у>0 и в которых у<0.

5. Постройте график функции у = . Найдите область
определения и область значений функции.

6. Укажите асимптоты гиперболы – графика
функции у = –.
Выполните построение графика.

7. Постройте график функции у = . Найдите нули функции.

II.Лабораторно-практическая работа.

Каждому ученику выдаются 2 карточки: карточка
№1 “Инструкция” с планом, по которому выполняется
работа, и текстом с заданием и карточка №2 “Результаты
исследования функции”.

Примерное содержание карточки “Инструкции”:

Постройте график указанной функции.
Найдите область определения функции.
Найдите область значения функции.
Укажите асимптоты гиперболы.
Найдите нули функции (f(x) = 0).
Найдите точку пересечения гиперболы с осью Х (у =
0).

7. Найдите промежутки в которых : а) у<0; б) y>0.

8. Укажите промежутки возрастания (убывания)
функции.

I вариант.

Постройте, используя программу Agrapher, график
функции и исследуйте ей свойства:

а) у = б) у = – в) у = г) у = д) у = е) у = .
-5-

Дополнительное задание.

Найдите точки пересечения графиков, выполнив
построение с помощью программы Agrapher.

Координаты, полученных точек, запишите в
тетрадь:

а) у = – и у = х-7;
б) у = и у = х+2х+3.

I I вариант.

Постройте, используя программу Agrapher, график
функции и исследуйте ей свойства:

а) у = б) у = – в) у = г) у = д) у = е) у = .

Дополнительное задание.

Найдите точки пересечения графиков, выполнив
построение с помощью программы Agrapher.

Координаты, полученных точек, запишите в
тетрадь:

а) у = и у = х+2;
б) у = и у = х-2х+3.

I I I вариант.

Постройте, используя программу Agrapher, график
функции и исследуйте ей свойства:

а) у = б) у = – в) у = г) у = д) у = – е) у = .

Дополнительное задание.

Найдите точки пересечения графиков, выполнив
построение с помощью программы Agrapher.

Координаты, полученных точек, запишите в
тетрадь:

а) у = – и у = -х-1;
б) у = –-2 и у = -х-2х-3.

I V вариант.

1. Постройте, используя программу Agrapher, график
функции и исследуйте ей свойства:

а) у = б) у = – в) у = г) у = – д) у = – е) у = .

Дополнительное задание.

Найдите точки пересечения графиков, выполнив
построение с помощью программы Agrapher.

Координаты, полученных точек, запишите в
тетрадь:

а) у = и у = х+1;
б) у = – и у = – х-2х-5.

Примерное содержание карточки “Результаты
исследования функции” см. “Приложение
1”.

Список литературы.

Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. Алгебра 8
класс: Учебник для школ и классов с углубленным
изучением математики.- М.: Мнемозина, 2001г.
Макарычев Ю.Н., Миндюк Н.Г. Дидактические
материалы по алгебре для 8 класса с углубленным
изучением математики.- М.: Просвещение, 2001г.
Звавич Л. И., Рязановский А. Р. Алгебра 8 класс:
Задачник для класса с углубленным изучением
математики. – М. Мнемозина,2002 г.
Виленкин Н. Я., Сурвилло Г. С., Симонов А.С.,
Кудрявцев А. И. Алгебра для 9 класса : Учебное
пособие для учащихся школ и классов с
углубленным изучением математики. – М.:
Просвещение, 1996г.
Зив Б. Г., Гольдич В. А. Дидактические материалы
по алгебре для 9 класса. С. – П. Черо – на – Неве,
2001г.

Источник

Построение графиков дробно-линейных функций

Рассмотрим специальный класс функций, графиками которых будут гиперболы.

Дробно-линейной называют всякую функцию вида

f(x)=ax+bcx+df(x)=dfrac{ax+b}{cx+d},

где cc и dd одновременно не равны `0`. Поскольку случай c=0c= 0 тривиален, то будем считать с≠0с ≠ 0.

Выполним преобразования:

`f(x)=a/c*(cx+(bc)/a)/(cx+d)=a/c*(cx+d+(bc)/a-d)/(cx+d)=`

`=a/c*((cx+d)/(cx+d)+1/a*(bc-ad)/(cx+d))=a/c+((bc-ad)/c)/(cx+d)`,

то есть

`f(x)=a/c+((bc-ad)/c)/(cx+d)=a/c+((bc-ad)/c^2)/(x+d/c)`.

Будем считать, что bc–ad≠0bc – ad ≠ 0 (иначе коэффициенты в числителе и знаменателе пропорциональны, дробь можно сократить и функция есть постоянная величина на области определения). Это означает, что график дробно-линейной функции можно получить из графика функции `f_0(x) =1/x`, выполнив цепочку преобразований:

1. ПР6: `f_1(x)=1/(x+d/c)`;

2. ПР4: `f_2(x)=((bc-ad)/c^2)/(x+d/c)`;

3. ПР5: `f_3(x)=a/c+((bc-ad)/c^2)/(x+d/c)`.

На первом шаге нужно сдвинуть график y=f0(x)y = f_0(x) на `−d/c` вдоль оси OxOx,

на втором – сжать его или растянуть и, возможно, отразить в зависимости от коэффициента `(bc-ad)/c^2`, а

на третьем – сдвинуть вдоль оси OyOy.

Покажем на примере, как это нужно делать.

Построим график функции f(x)=xx+2f{(x)}=dfrac x{x+2}. Приведём данную функцию к такому виду:

y=x+2-2x+2=1-2x+2y=frac{x+2-2}{x+2}=1-dfrac2{x+2}.

Построим график функции `y=-2/x` (ветви гиперболы лежат во 2-ой и 4-ой четвертях) (рис. 25).

Далее, необходимо, воспользовавшись преобразованием ПР6, сдвинуть график `y=-2/x` на две единицы влево вдоль оси абсцисс (рис. 26). Получим график `y=-2/(x+2)`. Теперь используем преобразование ПР5 и поднимаем график на рис. 26 на единицу вверх. Получим необходимый график функции

y=1−2x+2y=1-frac2{x+2} (рис. 27).

Постройте график функции

y=3x+45x+6y=dfrac{3x+4}{5x+6} .

Будем выполнять построения в таком порядке:

1) Преобразуем данную функцию:

`y=(3x+4)/(5x+6)=(3x+4)/(5x+6)-3/5+3/5=3/5+(2//25)/(x+6//5)`.

2) Построим график функции

`y=1/(x+6//5)` (ПР6, см. рис. 28).

Далее, построим график `y=(2//25)/(x+6//5)`, сжав график относительно оси абсцисс в `2//25` раз (ПР4, см. рис. 29).

3) Осталось сдвинуть график на `3//5` единиц вверх и получим окончательный график (ПР6, см. рис. 30)

`y=3/5+(2//25)/(x+6//5)`.

Построим график функции

y=2x-1y=left|dfrac2{left|xright|-1}right|.

Будем решать данный пример в таком порядке:

1. Построим гиперболу `y=2/x` (рис. 31).

2. Воспользовавшись преобразованием ПР6, сдвинем эту гиперболу на единицу вправо (вдоль оси абсцисс) и получим график функции `y=2/(x-1)` (рис. 32).

3. Теперь воспользуемся преобразованием ПР1 для построенного в п. 2. графика. Получим график функции `y=2/(|x|-1)` (рис. 33).

4. Воспользуемся преобразованием ПР2 и получим график искомой функции `y=|2/(|x|-1)|` (рис. 34).

Источник

Дробно-рациональная функция — это функция вида , где f(x) и g(x) — некоторые функции.
График дробно-рациональной функции представляет собой гиперболу.
Функция имеет две асимптоты — вертикальную и горизонтальную.
Определение.Прямая линия называется асимптотой графика функции, если график функции неограниченно сближается с этой прямой при удалении точки графика в бесконечность:
x=a уравнение вертикальной асимптоты
y=b уравнение горизонтальной асимптоты
y=kx+b уравнение наклонной асимптоты

Дробно-линейная функция представляет собой частный случай дробно-рациональной функции.
Дробно-линейная функция – это такая алгебраическая дробь , у которой числитель и знаменатель представляют собой линейные функции.
Во всякой дробно-линейной функции можно выделить целую часть.
Построим график функции y=1/x:
D(y): х≠0
E(y): у≠0
y = k/x – нечетная

Построим график функции y=k/x:
При k=2 y=-2/x:
ООФ: х≠0
МЗФ: у≠0
y=k/x – нечетная

Пример1 . Построим график функции , т.е. представим ее в виде : выделим целую часть дроби, разделив числитель на знаменатель, мы получим:

Итак, . Мы видим, что график этой функции может быть получен из графика функции у=5/х с помощью двух последовательных сдвигов: сдвига гиперболы у=5/х вправо на 3 единицы, а затем сдвига полученной гиперболы вверх на 2 единицы.

При этих сдвигах асимптоты гиперболы у=5/х также переместятся: ось х на 2 единицы вверх, а ось у на 3 единицы вправо.

Для построения графика проведем в координатной плоскости пунктиром асимптоты: прямую у=2 и прямую х=3. Так как гипербола состоит из двух ветвей, то для построения каждой из них составим две таблицы: одну для х3 (т. е. первую слева от точки пересечения асимптот, а вторую справа от нее):

x	-7	-2	-1	0	1	2	2,5
y	1,5	1	0,75	0,33	-0,5	-3	-8

x	3,5	4	5	6	7	8	13
y	12	7	4,5	3,33	3,25	3	2,52

Отметив в координатной плоскости точки, координаты которых указаны в первой таблице, и соединив их плавной линией, получим одну ветвь гиперболы. Аналогично (используя вторую таблицу) получим вторую ветвь гиперболы. График функции изображен на рисунке 3.

Любую дробь можно записать аналогичным образом, выделив ее целую часть. Следовательно, графики всех дробно-линейных функций являются гиперболами, различным образом сдвинутыми параллельно координатным осям и растянутыми по оси Оу.

Пример 2.

Построим график функции .

Поскольку мы знаем, что график есть гипербола, достаточно найти прямые, к которым приближаются ее ветви (асимптоты), и еще несколько точек.

Найдем сначала вертикальную асимптоту. Функция не определена там, где 2х+2=0, т.е. при х=-1. Стало быть, вертикальной асимптотой служит прямая х=-1.

Чтобы найти горизонтальную асимптоту, надо посмотреть, к чему приближаются значения функций, когда аргумент возрастает (по абсолютной величине), вторые слагаемые в числителе и знаменателе дроби относительно малы. Поэтому

Стало быть, горизонтальная асимптота – прямая у=3/2.

Определим точки пересечения нашей гиперболы с осями координат. При х=0 имеем у=5/2. Функция равна нулю, когда 3х+5=0, т.е. при х=-5/3.

Отметив на чертеже точки (-5/3;0) и (0;5/2) и проведя найденные горизонтальную и вертикальную асимптоты, построим график (рис.4).

Вообще, чтобы найти горизонтальную асимптоту, надо разделить числитель на знаменатель, тогда y=3/2+1/(x+1), y=3/2 – горизонтальная асимптота.

Алгоритм построения графика дробно-рациональной функции, содержащей квадратный трехчлен.

Найти область определения функции.
Разложить на множители квадратный трехчлен.
Сократить дробь.
Построить график (параболу, гиперболу, кубическую параболу).
Исключить из графика точки, не входящие в область определения («выколотые» точки).
Найти значение функции в «выколотых» точках.
Определить, при каких значениях b прямая y=b имеет с графиком ровно одну общую точку.