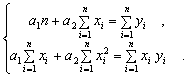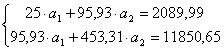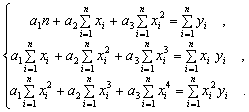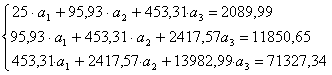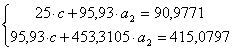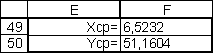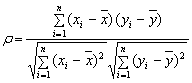Как найти коэффициенты линейной аппроксимации

Как найти коэффициенты линейной аппроксимации

 

При обработке экспериментальных данных часто возникает необходимость аппроксимировать их линейной функцией.

Аппроксимацией (приближением) функции f(x) называется нахождение такой функции (аппроксимирующей функции) g(x), которая была бы близка заданной. Критерии близости функций могут быть различные.

В случае если приближение строится на дискретном наборе точек, аппроксимацию называют точечной или дискретной.

В случае если аппроксимация проводится на непрерывном множестве точек (отрезке), аппроксимация называется непрерывной или интегральной. Примером такой аппроксимации может служить разложение функции в ряд Тейлора, то есть замена некоторой функции степенным многочленом.

Наиболее часто встречающим видом точечной аппроксимации является интерполяция – нахождение промежуточных значений величины по имеющемуся дискретному набору известных значений.

Пусть задан дискретный набор точек, называемых узлами интерполяции, а также значения функции в этих точках. Требуется построить функцию g(x), проходящую наиболее близко ко всем заданным узлам. Таким образом, критерием близости функции является g(xi)=yi.

В качестве функции g(x) обычно выбирается полином, который называют интерполяционным полиномом.

В случае если полином един для всей области интерполяции, говорят, что интерполяция глобальная.

В случае если между различными узлами полиномы различны, говорят о кусочной или локальной интерполяции.

Найдя интерполяционный полином, мы можем вычислить значения функции между узлами, а также определить значение функции даже за пределами заданного интервала (провести экстраполяцию).

Аппроксимация линейной функцией

Пример реализации

Для примера реализации воспользуемся набором значений, полученных в соответствии с уравнением прямой

y = 8 · x — 3

Рассчитаем указанные коэффициенты по методу наименьших квадратов.
Результат сохраняем в форме двумерного массива, состоящего из 2 столбцов.
При следующем запуске программы добавим случайную составляющую к указанному набору значений и снова рассчитаем коэффициенты.

Реализация на Си

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
// Задание начального набора значений
double ** getData(int n) {
  double **f;
  f = new double*[2];
  f[0] = new double[n];
  f[1] = new double[n];
  for (int i = 0; i<n; i++) {
    f[0][i] = (double)i;
    f[1][i] = 8 * (double)i – 3;
    // Добавление случайной составляющей
    f[1][i] = 8*(double)i – 3 + ((rand()%100)-50)*0.05;
  }
  return f;
}
// Вычисление коэффициентов аппроксимирующей прямой
void getApprox(double **x, double *a, double *b, int n) {
  double sumx = 0;
  double sumy = 0;
  double sumx2 = 0;
  double sumxy = 0;
  for (int i = 0; i<n; i++) {
    sumx += x[0][i];
    sumy += x[1][i];
    sumx2 += x[0][i] * x[0][i];
    sumxy += x[0][i] * x[1][i];
  }
  *a = (n*sumxy – (sumx*sumy)) / (n*sumx2 – sumx*sumx);
  *b = (sumy – *a*sumx) / n;
  return;
}
int main() {
  double **x, a, b;
  int n;
  system(“chcp 1251”);
  system(“cls”);
  printf(“Введите количество точек: “);
  scanf(“%d”, &n);
  x = getData(n);
  for (int i = 0; i<n; i++)
    printf(“%5.1lf – %7.3lfn”, x[0][i], x[1][i]);
  getApprox(x, &a, &b, n);
  printf(“a = %lfnb = %lf”, a, b);
  getchar(); getchar();
  return 0;
}

Результат выполнения
Запуск без случайной составляющей
Реализация линейной аппроксимации по МНК
Запуск со случайной составляющей
Реализация линейной аппроксимации по МНК

Построение графика функции

Для наглядности построим график функции, полученный аппроксимацией по методу наименьших квадратов. Подробнее о построении графика функции описано здесь.

 
Реализация на Си

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149

#include <windows.h>
const int NUM = 70; // количество точек
LONG WINAPI WndProc(HWND, UINT, WPARAM, LPARAM);
double **x; // массив данных
      // Определение коэффициентов линейной аппроксимации по МНК
void getApprox(double **m, double *a, double *b, int n) {
  double sumx = 0;
  double sumy = 0;
  double sumx2 = 0;
  double sumxy = 0;
  for (int i = 0; i<n; i++) {
    sumx += m[0][i];
    sumy += m[1][i];
    sumx2 += m[0][i] * m[0][i];
    sumxy += m[0][i] * m[1][i];
  }
  *a = (n*sumxy – (sumx*sumy)) / (n*sumx2 – sumx*sumx);
  *b = (sumy – *a*sumx) / n;
  return;
}
// Задание исходных данных для графика
// (двумерный массив, может содержать несколько рядов данных)
double ** getData(int n) {
  double **f;
  double a, b;
  f = new double*[3];
  f[0] = new double[n];
  f[1] = new double[n];
  f[2] = new double[n];
  for (int i = 0; i<n; i++) {
    double x = (double)i * 0.1;
    f[0][i] = x;
    f[1][i] = 8 * x – 3 + ((rand() % 100) – 50)*0.05;
  }
  getApprox(f, &a, &b, n); // аппроксимация
  for (int i = 0; i<n; i++) {
    double x = (double)i * 0.1;
    f[2][i] = a*x + b;
  }
  return f;
}
// Функция рисования графика
void DrawGraph(HDC hdc, RECT rectClient, double **x, int n, int numrow = 1) {
  double OffsetY, OffsetX;
  double MAX_X = 0;
  double MAX_Y = 0;
  double ScaleX, ScaleY;
  double min, max;
  int height, width;
  int X, Y;    // координаты в окне (в px)
  HPEN hpen;
  height = rectClient.bottom – rectClient.top;
  width = rectClient.right – rectClient.left;
  // Область допустимых значений X
  min = x[0][0];
  max = x[0][0];
  for (int i = 0; i<n; i++) {
    if (x[0][i] < min)
      min = x[0][i];
    if (x[0][i] > max)
      max = x[0][i];
  }
  double temp = max – min;
  MAX_X = max – min;
  OffsetX = min*width / MAX_X;  // смещение X
  ScaleX = (double)width / MAX_X; // масштабный коэффициент X
                  // Область допустимых значений Y
  min = x[1][0];
  max = x[1][0];
  for (int i = 0; i<n; i++) {
    for (int j = 1; j <= numrow; j++) {
      if (x[j][i] < min)
        min = x[j][i];
      if (x[j][i] > max)
        max = x[j][i];
    }
  }
  MAX_Y = max – min;
  OffsetY = max*height / (MAX_Y);  // смещение Y
  ScaleY = (double)height / MAX_Y; // масштабный коэффициент Y
                   // Отрисовка осей координат
  hpen = CreatePen(PS_SOLID, 0, 0); // черное перо 1px
  SelectObject(hdc, hpen);
  MoveToEx(hdc, 0, OffsetY, 0);  // перемещение в точку (0;OffsetY)
  LineTo(hdc, width, OffsetY);   // рисование горизонтальной оси
  MoveToEx(hdc, OffsetX, 0, 0);  // перемещение в точку (OffsetX;0)
  LineTo(hdc, OffsetX, height);  // рисование вертикальной оси
  DeleteObject(hpen);  // удаление черного пера
             // Отрисовка графика функции
  int color = 0xFF; // красное перо для первого ряда данных
  for (int j = 1; j <= numrow; j++) {
    hpen = CreatePen(PS_SOLID, 2, color); // формирование пера 2px
    SelectObject(hdc, hpen);
    X = (int)(OffsetX + x[0][0] * ScaleX);    // координаты начальной точки графика
    Y = (int)(OffsetY – x[j][0] * ScaleY);
    MoveToEx(hdc, X, Y, 0);  // перемещение в начальную точку
    for (int i = 0; i<n; i++) {
      X = OffsetX + x[0][i] * ScaleX;
      Y = OffsetY – x[j][i] * ScaleY;
      LineTo(hdc, X, Y);
    }
    color = color << 8; // изменение цвета пера для следующего ряда
    DeleteObject(hpen); // удаление текущего пера
  }
}
// Главная функция
int  WINAPI  WinMain(HINSTANCE  hInstance,
  HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow) {
  HWND hwnd;
  MSG msg;
  WNDCLASS w;
  x = getData(NUM); // задание исходных данных
  memset(&w, 0, sizeof(WNDCLASS));
  w.style = CS_HREDRAW | CS_VREDRAW;
  w.lpfnWndProc = WndProc;
  w.hInstance = hInstance;
  w.hbrBackground = CreateSolidBrush(0x00FFFFFF);
  w.lpszClassName = “My Class”;
  RegisterClass(&w);
  hwnd = CreateWindow(“My Class”, “График функции”,
    WS_OVERLAPPEDWINDOW, 500, 300, 500, 380, NULL, NULL,
    hInstance, NULL);
  ShowWindow(hwnd, nCmdShow);
  UpdateWindow(hwnd);
  while (GetMessage(&msg, NULL, 0, 0)) {
    TranslateMessage(&msg);
    DispatchMessage(&msg);
  }
  return msg.wParam;
}
// Оконная функция
LONG WINAPI WndProc(HWND hwnd, UINT Message,
  WPARAM wparam, LPARAM lparam) {
  HDC hdc;
  PAINTSTRUCT ps;
  switch (Message) {
  case WM_PAINT:
    hdc = BeginPaint(hwnd, &ps);
    DrawGraph(hdc, ps.rcPaint, x, NUM, 2); // построение графика
    EndPaint(hwnd, &ps);
    break;
  case WM_DESTROY:
    PostQuitMessage(0);
    break;
  default:
    return DefWindowProc(hwnd, Message, wparam, lparam);
  }
  return 0;
}

Результат выполнения
Реализация линейной аппроксимации по МНК (график)

Аппроксимация с фиксированной точкой пересечения с осью y

В случае если в задаче заранее известна точка пересечения искомой прямой с осью y, в решении задачи останется только одна частная производная для вычисления коэффициента a.
Частная производная по a
В этом случае текст программы для поиска коэффициента угла наклона аппроксимирующей прямой будет следующий (имя функции getApprox() заменено на getApproxA() во избежание путаницы).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
// Задание начального набора значений
double ** getData(int n) {
  double **f;
  f = new double*[2];
  f[0] = new double[n];
  f[1] = new double[n];
  for (int i = 0; i<n; i++) {
    f[0][i] = (double)i;
    f[1][i] = 8 * (double)i – 3;
    // Добавление случайной составляющей
    //f[1][i] = 8 * (double)i – 3 + ((rand() % 100) – 50)*0.05;
  }
  return f;
}
// Вычисление коэффициентов аппроксимирующей прямой
void getApproxA(double **x, double *a, double b, int n) {
  double sumx = 0;
  double sumx2 = 0;
  double sumxy = 0;
  for (int i = 0; i<n; i++) {
    sumx += x[0][i];
    sumx2 += x[0][i] * x[0][i];
    sumxy += x[0][i] * x[1][i];
  }
  *a = (sumxy – b*sumx) / sumx2;
  return;
}
int main() {
  double **x, a, b;
  int n;
  system(“chcp 1251”);
  system(“cls”);
  printf(“Введите количество точек: “);
  scanf(“%d”, &n);
  x = getData(n);
  for (int i = 0; i<n; i++)
    printf(“%5.1lf – %7.3lfn”, x[0][i], x[1][i]);
  b = 0;
  getApproxA(x, &a, b, n);
  printf(“a = %lfnb = %lf”, a, b);
  getchar(); getchar();
  return 0;
}

Результат выполнения программы поиска коэффициента угла наклона аппроксимирующей прямой при фиксированном значении b=0:
Аппроксимация при фиксированном b

Назад: Алгоритмизация

Источник

Интерполяция и аппроксимация#

from matplotlib import pyplot as plt


def configure_matplotlib():
    plt.rc('text', usetex=True)
    plt.rcParams["axes.titlesize"] = 28
    plt.rcParams["axes.labelsize"] = 24
    plt.rcParams["legend.fontsize"] = 24
    plt.rcParams["xtick.labelsize"] = plt.rcParams["ytick.labelsize"] = 18
    plt.rcParams["text.latex.preamble"] = r"""
    usepackage[utf8]{inputenc}
    usepackage[english,russian]{babel}
    usepackage{amsmath}
    """

configure_matplotlib()

Интерполяция#

Подмодуль scipy.interpolate содержит в себе методы для интерполяции.

Коротко про интерполяцию можно почитать в википедии. Более подробное изложение можно найти в [2].

Задача интерполирования состоит в том, чтобы по значениям функции (f(x)) в нескольких точках отрезка восстановить ее значения в остальных точках этого отрезка. Разумеется, такая задача допускает сколь угодно много решений. Задача интерполирования возникает, например, в том случае, когда известны результаты измерения (y_h= f(x, k)) некоторой физической величины (f(x)) в точках (x_k, k = 0, 1, …, n), и требуется определить ее значения в других точках. Интерполирование используется также при сгущении таблиц, когда вычисление значений (f(x)) трудоемко. Иногда возникает необходимость приближенной замены или аппроксимации данной функции другими функциями, которые легче вычислить. В частности, рассматривается задача о наилучшем приближении в нормированном пространстве (H), когда заданную функцию (fin H) требуется заменить линейной комбинацией (varphi) заданных элементов из (H) так, чтобы отклонение (||f—varphi||) было минимальным. Результаты и методы теории интерполирования и приближения функций нашли широкое применение в численном анализе, например при выводе формул численного дифференцирования и интегрирования, при построении сеточных аналогов задач математической физики [2].

Для того чтобы рассмотреть интерполяцию, сгенерируем данные. Т.е. сгенерируем массив узлов интерполяционной сетки x_data и значений y_data некоторой функции (f) в узлах этой сетки при разном количестве известных точек.

import numpy as np

L = 0
R = np.pi
n_points = (4, 10, 64, 65)
f = np.sin

xh = np.linspace(L, R, 100) 
yh = f(xh)
    

def generate_data(f, L, R, n):
    x_data = np.linspace(L, R, n-1)
    y_data = f(x_data)
    return x_data, y_data    


def plot_problem(ax, x_data, y_data):
    ax.plot(xh, yh, linewidth=0.5, label="Исходная зависимость")
    ax.scatter(x_data, y_data, marker="x", color="red", label="Известные данные")
    ax.set_xlabel("$x$")
    ax.set_ylabel("$y$")
    

fig, axs = plt.subplots(ncols=2, nrows=2, figsize=(16, 16), layout="tight")
for ax, N in zip(axs.flatten(), n_points):
    x_data, y_data = generate_data(f, L, R, N)
    plot_problem(ax, x_data, y_data)
    ax.set_title(f"Исходные данные ${N=}$")
    ax.legend()

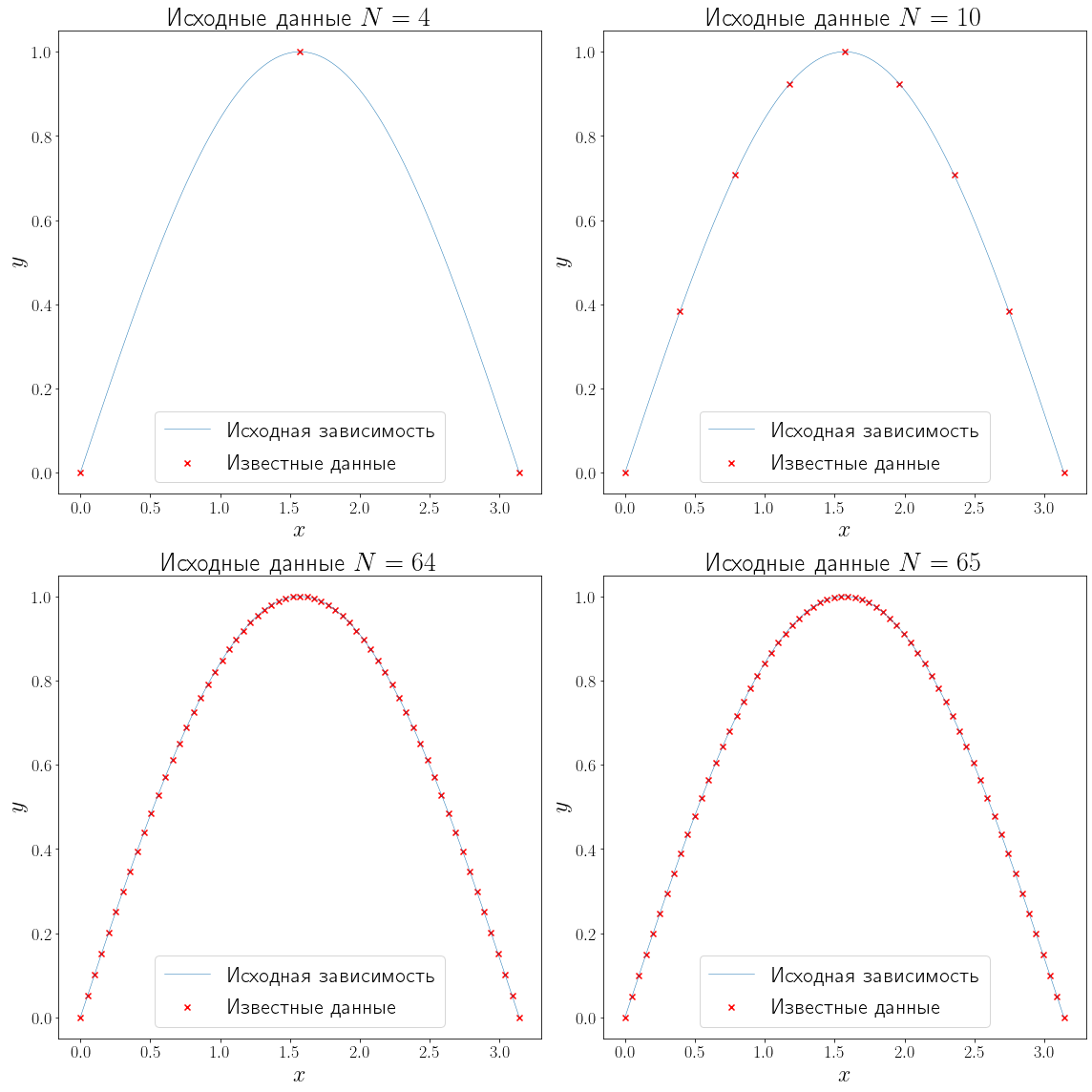
../../_images/interpolation_approx_3_0.png

Теперь когда данные готовы, осталось произвести интерполяцию. Методов интерполяции существует очень много. Рассмотрим полиномиальную интерполяцию и сплайн интерполяцию.

Полиномиальная интерполяция#

Полиномиальная интерполяция основывается на том факте, что существует единственный полином (P_{N}(x) = a_0 + a_1 x + cdots + a_{N} x ^ N ) степени (N), проходящий через точки ({(x_1, y_1), …, (x_{N + 1}, y_{N + 1})}), если (x_i neq x_j quad forall i, j = 1, cdots, N + 1, quad i neq j).

Недостатком полиномиальной интерполяции является её нестабильность. Полиномиальная интерполяция проявляет себя очень плохо при больших (N).

from scipy import interpolate

fig, axs = plt.subplots(ncols=2, nrows=2, figsize=(16, 16), layout="tight")
for ax, N in zip(axs.flatten(), n_points):
    x_data, y_data = generate_data(f, L, R, N)
    plot_problem(ax, x_data, y_data)

    poly = interpolate.KroghInterpolator(x_data, y_data)
    y_poly = poly(xh)
    ax.plot(xh, y_poly, label="Интерполирующий полином")
    
    ax.set_title(f"Результат интерполяции ${N=}$")
    ax.legend()

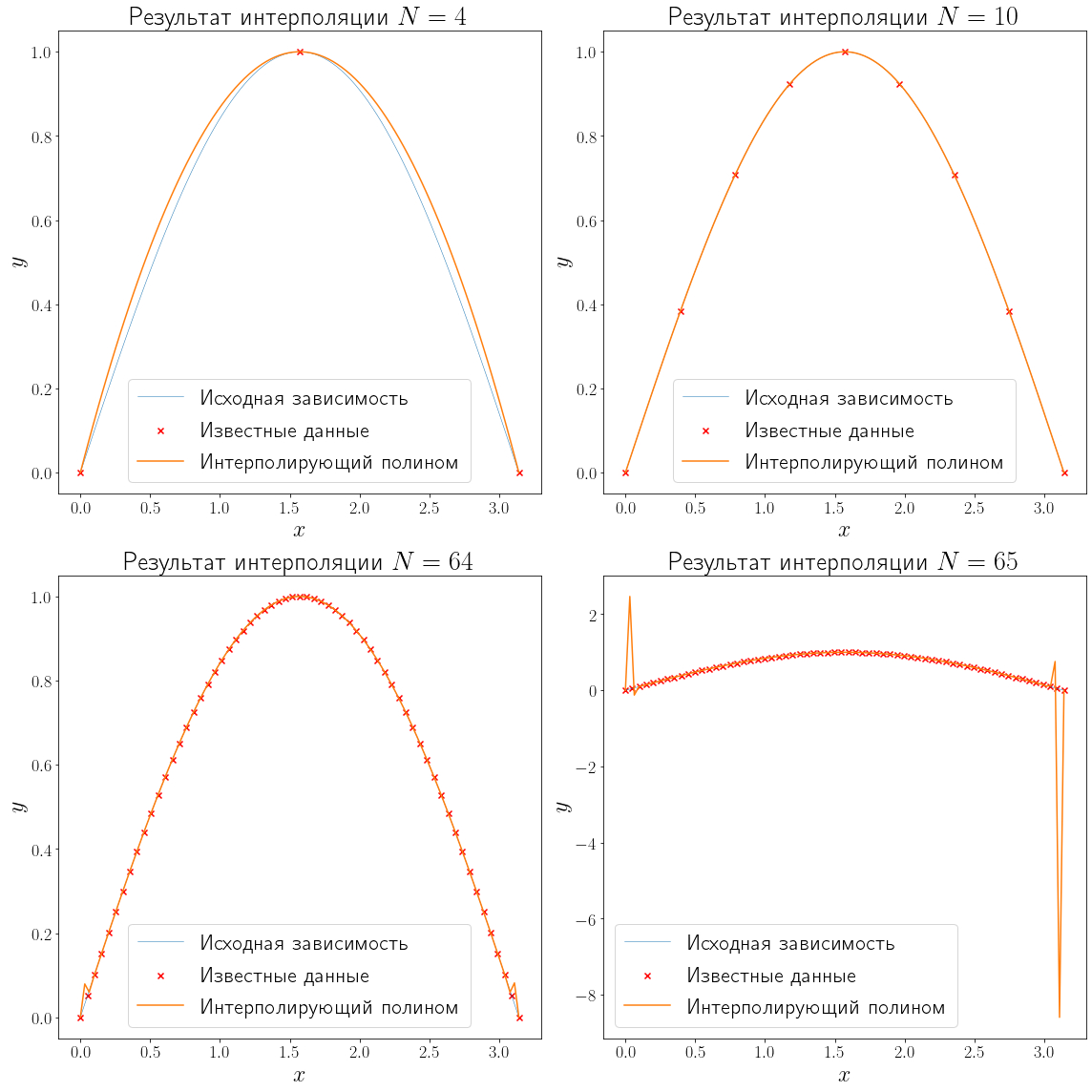
../../_images/interpolation_approx_5_0.png

Сплайн интерполяция#

Интерполирование многочленом … на всем отрезке ([a, b]) с использованием большого числа узлов интерполяции часто приводит к плохому приближению, что объясняется сильным накоплением погрешностей в процессе вычислений. Кроме того, из-за расходимости процесса интерполяции увеличение числа узлов не обязано приводить к повышению точности. Для того чтобы избежать больших погрешностей, весь отрезок ([a, b]) разбивают на частичные отрезки и на каждом из частичных отрезков приближенно заменяют функцию (f(х)) многочленом невысокой степени (так называемая кусочно-полиномиальная интерполяция). Одним из способов интерполирования на всем отрезке является интерполирование с помощью сплайн-функций. Сплайн-функцией или сплайном называют кусочно-полиномиальную функцию, определенную на отрезке ([a, b]) и имеющую на этом отрезке некоторое число непрерывных производных [2].

Например, если взять в качестве сплайн-функции полином первой степени, то на выходе получится кусочно-линейная интерполяция.

x_data, y_data = generate_data(f, L, R, 5)
linear = interpolate.interp1d(x_data, y_data, kind="linear")
y_linear = linear(xh)

fig, ax = plt.subplots(figsize=(10, 8), layout="tight")
ax.plot(xh, y_linear, label="Сплайн первой степени")
plot_problem(ax, x_data, y_data)
ax.legend()
ax.set_title("Кусочно-линейная интерполяция")

Text(0.5, 1.0, 'Кусочно-линейная интерполяция')

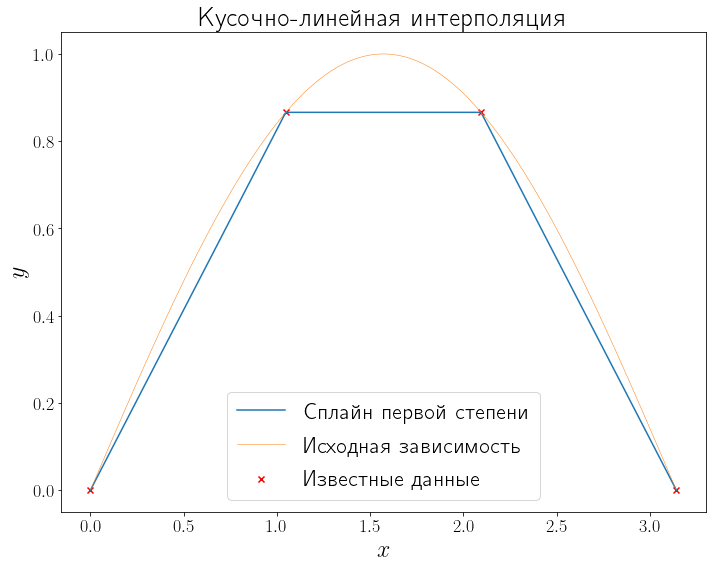
../../_images/interpolation_approx_7_1.png

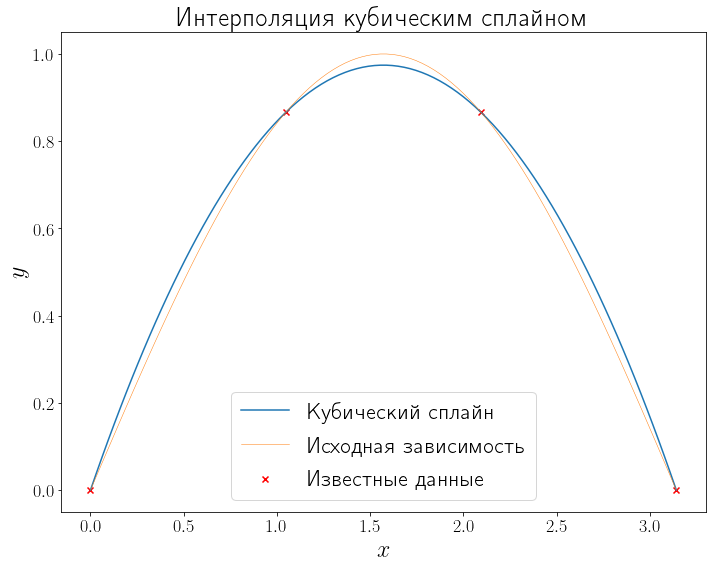
Очень часто выбирают полином третьей степени, которые позволяют строить гладкие интерполирующие полиному и разумно ведут себя между точками во многих случаях.

cubic = interpolate.interp1d(x_data, y_data, kind="cubic")
y_cubic = cubic(xh)

fig, ax = plt.subplots(figsize=(10, 8), layout="tight")
ax.plot(xh, y_cubic, label="Кубический сплайн")
plot_problem(ax, x_data, y_data)
ax.legend()
ax.set_title("Интерполяция кубическим сплайном")

Text(0.5, 1.0, 'Интерполяция кубическим сплайном')

../../_images/interpolation_approx_9_1.png

Аппроксимация функций#

При интерполировании ставится цель восстановить исходную зависимость (y = f(x)) таким образом по набору точек, через которые функция (f) проходит в точности. Но что если значение исходной функции (f) в точках (x_i, , i=0,ldots,N) известно не точно, а в пределах какой-то погрешности или с точностью до какой-то случайной величины, т.е., например, (y_i = f(x_i) + varepsilon_i, , i = 0, ldots, N). В таком случае такое строгое требование на то, чтобы решение (varphi(x)) в точности проходило через все точки ((x_i, y_i), , i=0, …, N) не имеет большого смысла и может быть ослаблено, например, до поиска такой функции (varphi) из определенного класса функций, которая меньше всего отклоняется от значений ((x_i, y_i),, i=0,…, n).

Очень распространенным подходом в таком случае является метод наименьших квадратов, при котором отклонение формализуется в виде суммы квадратов отклонений аппроксимирующей функции (varphi) в точках (x_i, , i=0,ldots,N) от измерений (y_i, , i=0,ldots,N). Пусть решение ищется в классе функций ({varphi_pcolon mathbb{R}tomathbb{R}mid pin P}), тогда задача аппроксимации сводится к задаче минимизации

[
sum_{i=0}^{N}||varphi_p(x_i) – y_i||^2 sim min_{pin P}.
]

Note

Многие методы аппроксимации легко обобщаются на многомерные случаи.

При такой постановке часто выделяют линейную и нелинейную аппроксимации. Аппроксимация является линейной, если (varphi_p(x)) линейно зависит от параметров (p).

Note

Аппроксимация функций реализована во множестве других библиотек, таких как statsmodels, scikit-learn и некоторых других.

Линейная аппроксимация#

Очень распространенным случаем линейной аппроксимации является полиномиальная аппроксимация, при которой решение ищется в виде полинома (P_{N}(x) = a_0 + a_1 x + cdots + a_{n} x^n), т.е. решается задача

[
sum_{i=0}^{N}||a_0 + a_1 x_i + cdots + a_{n} x_i^n – y_i||^2 sim min_{a_0, a_1, ldots, a_n in mathbb{R}^{n+1}}.
]

Если все (x_i, , i=1,ldots,N) все различны, то при (n=N) существует глобальный минимум, который соответствует проходящему через все точки интерполирующему полиному, поэтому обычно решение ищется при (n<N).

Сгенерируем данные для тестирования полиномиальной интерполяции при различных (n). В качестве исходной зависимости выберем функцию

[
f(x)=2e^{-3x} + 4,
]

сгенерируем (N = 11) точек (x_i, , i=0, ldots, 10) равномерно распределенных на отрезке ([0, 1]) и искусственно добавим распределенный по Гауссу шум к значениям функции (f) в этих точках: ({y_i=f(x_i) + varepsilon_i, , varepsilon_i sim mathcal{N}(0, sigma^2), , i=0, ldots, 10}).

L = 0
R = 1

def f(x):
    return 2*np.exp(-3*x) + 4


N = 11
sigma = 0.2
x_data = np.linspace(L, R, N)
y_data = f(x_data) + np.random.normal(loc=0, scale=sigma, size=N)

xh = np.linspace(0, 1, 100) 
yh = f(xh)                   


fig, ax = plt.subplots(figsize=(8, 8), layout="tight")
plot_problem(ax, x_data, y_data)
ax.legend()

<matplotlib.legend.Legend at 0x1c71e0beb50>

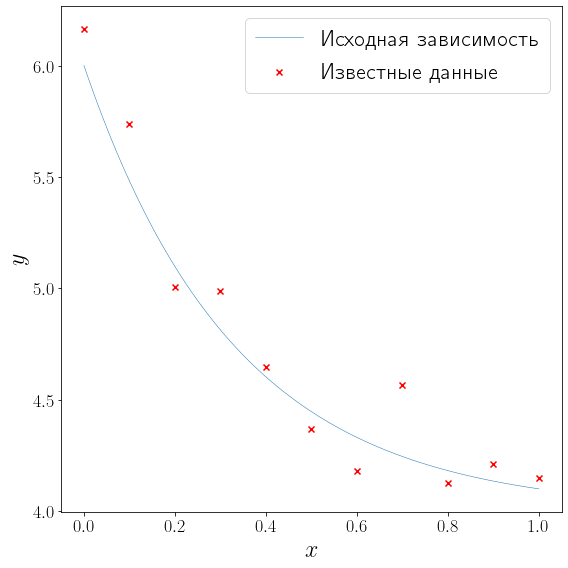
../../_images/interpolation_approx_11_1.png

Решить задачу полиномиальной аппроксимации можно средствами модуля numpy.polynomial. В частности подогнать полином заданной степени методом наименьших квадратов можно с помощью метода numpy.polynomial.Polynomial.fit.

from numpy.polynomial import Polynomial

degrees = (1, 2, 3, 4, 5, 10)


fig, axs = plt.subplots(figsize=(16, 24), nrows=3, ncols=2, layout="tight")
for ax, degree in zip(axs.flatten(), degrees):
    approximation = Polynomial.fit(x_data, y_data, degree)
    plot_problem(ax, x_data, y_data)
    ax.plot(xh, approximation(xh), color="green", label="Аппроксимация")
    ax.set_title(f"$n = {degree}$")
    ax.legend()

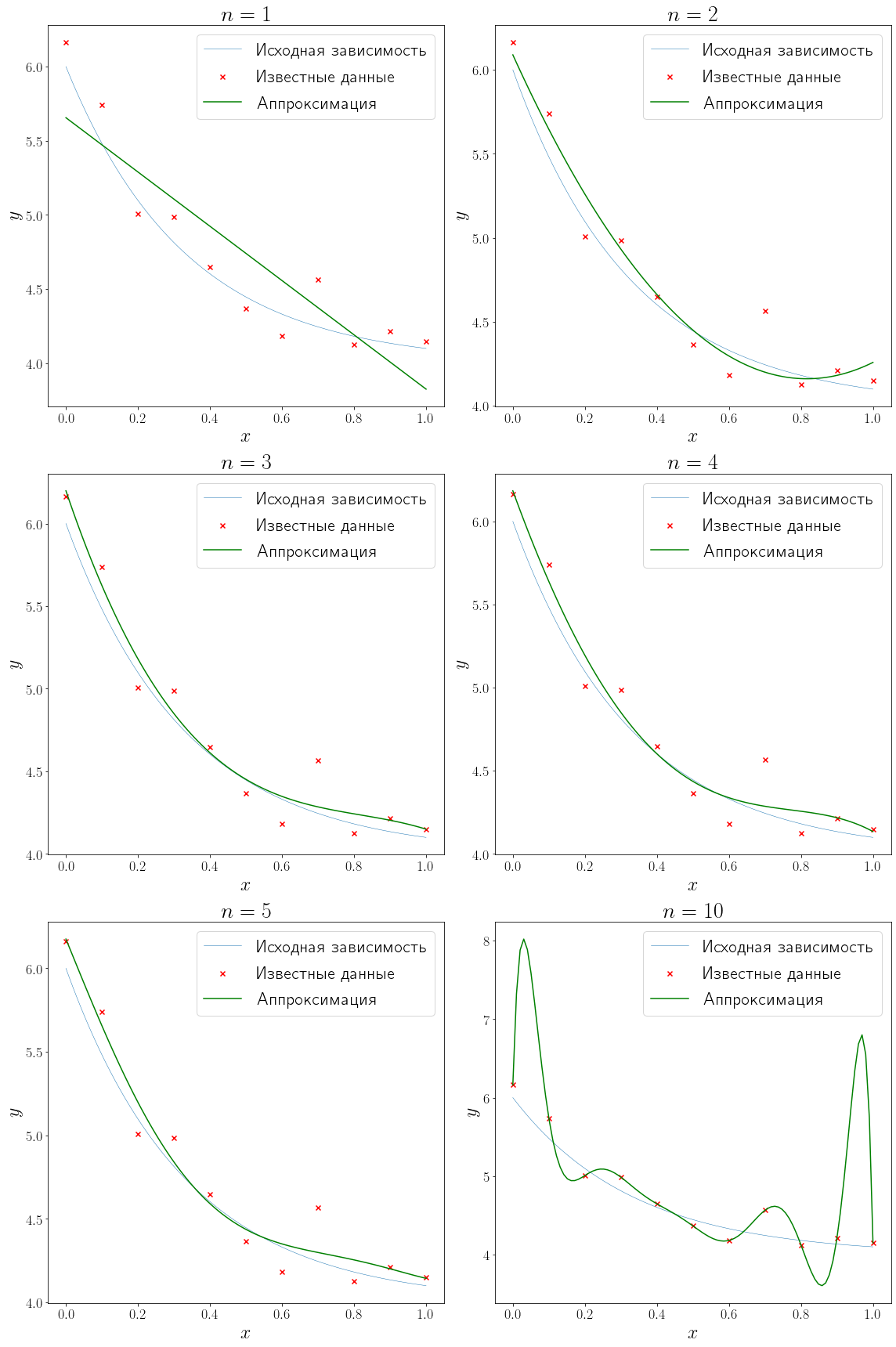
../../_images/interpolation_approx_13_0.png

В более общем случае при линейной аппроксимации решение ищется в виде линейной комбинации любых функций (varphi(x) = c_1varphi_1(x) + cdots + c_nvarphi_n(x)) и задача аппроксимации сводится к подбору коэффициентов (c_i, , i=1,ldots,n) посредством минимизации

[
sum_{i=0}^{N}||c_1 varphi_1(x_1) + cdots + c_n varphi_n(x_i) – y_i||^2 sim min_{c_1, ldots, c_n in mathbb{R}^n}.
]

Полиномиальная интерполяция получается при (varphi_i(x) = x^i). Можно показать, что решение оптимизационной задачи выше эквивалентно минимизации невязки системы линейных алгебраических уравнений

[begin{split}
begin{pmatrix}
varphi_1(x_0) &cdots & varphi_k(n_0) \
vdots & ddots & vdots \
varphi_1(x_N) &cdots & varphi_k(n_N)
end{pmatrix}
begin{pmatrix}
c_1 \ vdots \ c_n
end{pmatrix}=
begin{pmatrix}
y_0 \ vdots \ y_N
end{pmatrix}.
end{split}]

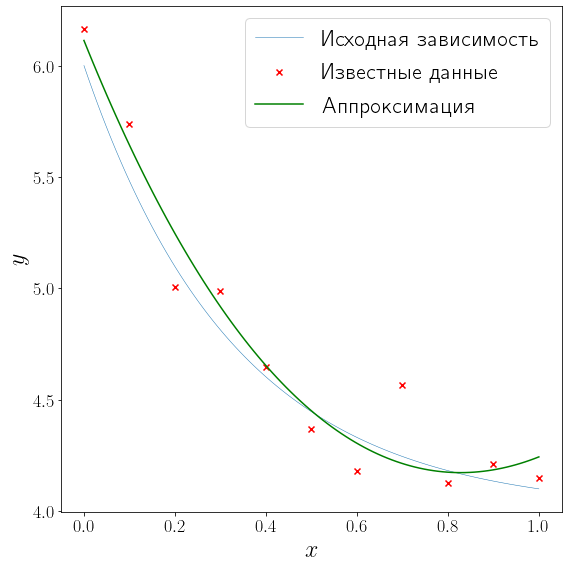
За решение таких задач отвечает метод linalg.lstsq. В качестве примера аппроксимируем тот же набор точек, но решение будем искать в виде

[
varphi_{alpha, beta, gamma}(x) = alpha + beta e^{-x} + gamma x^2.
]

from scipy import linalg

def approximation(x, alpha, beta, gamma):
    return alpha + beta*np.exp(-x) + gamma*np.square(x)


A = np.vstack([
    np.ones_like(x_data), np.exp(-x_data), np.square(x_data)
]).T

b = y_data

(alpha, beta, gamma), *_ = linalg.lstsq(A, b)

fig, ax = plt.subplots(figsize=(8, 8), layout="tight")
plot_problem(ax, x_data, y_data)
ax.plot(xh, approximation(xh, alpha, beta, gamma), color="green", label="Аппроксимация")
ax.legend()

<matplotlib.legend.Legend at 0x1c71e1393d0>

../../_images/interpolation_approx_15_1.png

Нелинейная аппроксимация#

Будем аппроксимировать данные функцией вида

[
varphi_{alpha, beta, gamma}(x) = alpha e^{beta x} + gamma.
]

Исходная функция (f(x)=2e^{-3x} + 4) совпадает с (varphi_{alpha, beta, gamma}(x)) при (alpha=2), (beta=-3) и (gamma=4), т.е. теоретически можно восстановить точное решение.
Аппроксимация не является линейной, т.к. (varphi_{alpha, beta, gamma}) зависит от параметра (beta) экспоненциально. Метод optimize.curve_fit позволяет искать приближенное решение задачи нелинейной аппроксимации.

Чтобы воспользоваться методом optimize.curve_fit, необходимо определить функцию, которая первым своим аргументом принимает (x) (может быть скаляром, а может быть и вектором), а остальными аргументами принимает параметры (p). В примере ниже это функция approximation.

Далее этому методу optimize.curve_fit передаётся эта самая функция, данные, под которые эту функцию необходимо подогнать, и начальное приближение (p_0) используемое в качестве стартовой точки для подбора параметров, при которых достигается минимальное среднее квадратичное отклонение (varvarphi_p) от заданного набора точек.

from scipy import optimize

def approximation(x, alpha, beta, gamma):
    return alpha * np.exp(beta * x) + gamma

(alpha, beta, gamma), _ = optimize.curve_fit(approximation, x_data, y_data, p0=[3, -6, 10])


fig, ax = plt.subplots(figsize=(8, 8), layout="tight")
plot_problem(ax, x_data, y_data)
ax.plot(xh, approximation(xh, alpha, beta, gamma), color="green", label="Аппроксимация")
ax.legend()

print(f"""
Найденные параметры: 
{alpha = :.3f},
{beta = :.3f},
{gamma = :.3f},
""")

Найденные параметры: 
alpha = 2.130,
beta = -3.378,
gamma = 4.081,

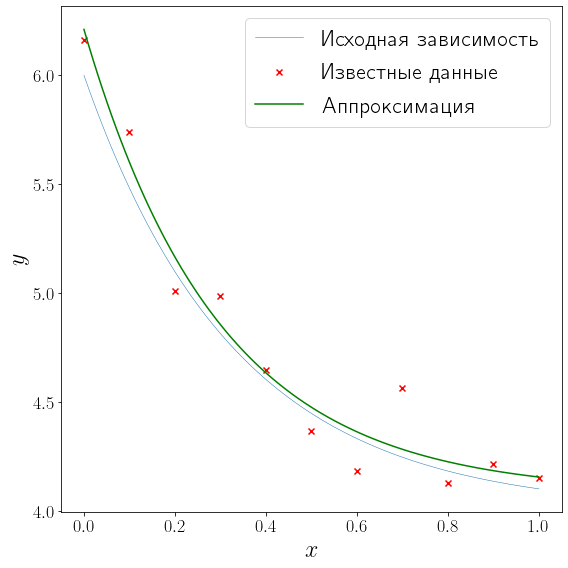
../../_images/interpolation_approx_18_1.png

Видим, что найденные значения коэффициентов (alpha, beta) и (gamma) с неплохой точностью совпали с истинными и аппроксимирующая кривая довольно близко проходит к исходной (f(x)).

Note

В случае нелинейной аппроксимации следует проявлять особую осторожность, т.к. функционал среднеквадратичного отклонения минимизируется численными методами и начальное приближение (p_0) играет большую роль: при не удачном (p_0) алгоритм может сойтись не туда или не сойтись вообще.

Список литературы#

1

Брайан К. Джонс Дэвид Бизли. Python. Книга рецептов. М. ДМК Пресс, 2019. ISBN 978-5-97060-751-0.

2(1,2,3)

Гулин А.В. Самарский А.А. Численные методы. М. Наука, 1989. ISBN 5-02-013996-3.

Источник

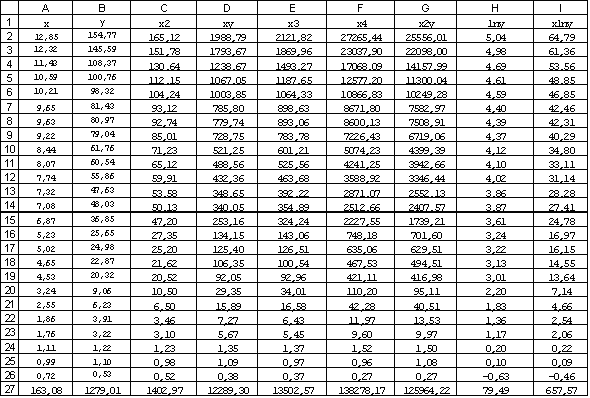
Функция
y=f(x) задана таблицей 1

Таблица
1

Исходные
данные.

12.85

154.77

9.65

81.43

7.74

55.86

5.02

24.98

1.86

3.91

12.32

145.59

9.63

80.97

7.32

47.63

4.65

22.87

1.76

3.22

11.43

108.37

9.22

79.04

7.08

48.03

4.53

20.32

1.11

1.22

10.59

100.76

8.44

61.76

6.87

36.85

3.24

9.06

0.99

1.10

10.21

98.32

8.07

60.54

5.23

25.65

2.55

6.23

0.72

0.53

Требуется
выяснить – какая из функций – линейная,
квадратичная или

экспоненциальная
наилучшим образом аппроксимирует
функцию, заданную таблицей 1.

Решение.

Поскольку
в данном примере каждая пара значений


встречается один раз, то между
и
существует функциональная зависимость.

Для
проведения расчетов данные целесообразно
расположить в виде таблицы 2,

используя
средства табличного процессора Microsoft
Excel.

Таблица
2

Расчет
сумм.

Поясним
как таблица 2 составляется.

Шаг
1. В ячейки A2:A26 заносим значения
.

Шаг
2. В ячейки B2:B26 заносим значения
.

Шаг
3. В ячейку C2 вводим формулу =A2^2.

Шаг
4. В ячейки C3:C26 эта формула копируется.

Шаг
5. В ячейку D2 вводим формулу =A2*B2.

Шаг
6. В ячейки D3:D26 эта формула копируется.

Шаг
7. В ячейку F2 вводим формулу =A2^4.

Шаг
8. В ячейки F3:F26 эта формула копируется.

Шаг
9. В ячейку G2 вводим формулу =A2^2*B2.

Шаг
10. В ячейки G3:G26 эта формула копируется.

Шаг
11. В ячейку H2 вводим формулу =LN(B2).

Шаг
12. В ячейки H3:H26 эта формула копируется.

Шаг
13. В ячейку I2 вводим формулу =A2*LN(B2).

Шаг
14. В ячейки I3:I26 эта формула копируется.

Последующие
шаги делаем с помощью автосуммирования

.

Шаг
15. В ячейку A27 вводим формулу =СУММ(A2:A26).

Шаг
16. В ячейку B27 вводим формулу =СУММ(B2:B26).

Шаг
17. В ячейку C27 вводим формулу =СУММ(C2:C26).

Шаг
18. В ячейку D27 вводим формулу =СУММ(D2:D26).

Шаг
19. В ячейку E27 вводим формулу =СУММ(E2:E26).

Шаг
20. В ячейку F27 вводим формулу =СУММ(F2:F26).

Шаг
21. В ячейку G27 вводим формулу =СУММ(G2:G26).

Шаг
22. В ячейку H27 вводим формулу =СУММ(H2:H26).

Шаг
23. В ячейку I27 вводим формулу =СУММ(I2:I26).

Аппроксимируем
функцию

линейной
функцией
.

Для
определения коэффициентов

и


воспользуемся

системой


Используя
итоговые суммы таблицы 2, расположенные
в ячейках A27, B27, C27 и

D27,
запишем систему в виде


решив
которую, получим

и
.

Таким
образом, линейная аппроксимация имеет
вид
.

Решение
системы проводили, пользуясь средствами
Microsoft Excel. Результаты

представлены
в таблице 3.

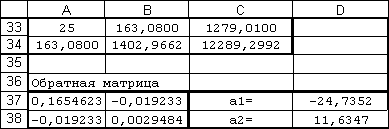
Таблица
3

Результаты
коэффициентов линейной аппроксимации.

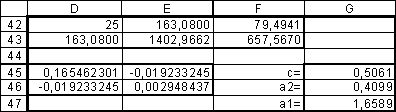
В
таблице 3 в ячейках A37:B38 записана формула
{=МОБР(A33:B34)}.

Функция
{=МОБР(A33:B34) вставляется путём нажатия
Ctrl+Shift+Enter

В
ячейках D37:D38 записана формула
{=МУМНОЖ(A37:B38;C33:C34)}.

Далее
аппроксимируем функцию

квадратичной
функцией

.
Для определения коэффициентов

,


и

воспользуемся
системой


Используя
итоговые суммы таблицы 2,

расположенные
в ячейках A27, B27, C27, D27, E27, F27 и G27 запишем
систему в

виде


решив
которую, получим
,

и

.

Таким
образом, квадратичная аппроксимация
имеет вид



.

Решение
системы проводили, пользуясь средствами
Microsoft Excel. Результаты

представлены
в таблице 4.

Таблица
4

Результаты
коэффициентов квадратичной аппроксимации.

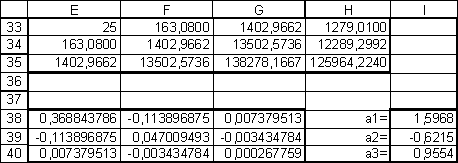
В
таблице 4 в ячейках E38:G40 записана формула
{=МОБР(E33:G35)}.

В
ячейках I38:I40 записана формула
{=МУМНОЖ(E38:G40;H33:H35)}.

Теперь
аппроксимируем функцию

экспоненциальной
функцией

.
Для определения коэффициентов

и


прологарифмируем

значения


и

используя
итоговые суммы таблицы 2, расположенные
в ячейках A27, C27, H27 и I27

получим
систему


где

.

Решив
систему, найдем
,

.

После
потенцирования получим
.

Таким
образом, экспоненциальная аппроксимация
имеет вид



.

Решение
системы проводили, пользуясь средствами
Microsoft Excel. Результаты

представлены
в таблице 5.

Таблица
5

Результаты
коэффициентов экспоненциальной
аппроксимации.

В
таблице 5 в ячейках D45:E46 записана формула
{=МОБР(D42:943)}.

В
ячейках G45:G46 записана формула
{=МУМНОЖ(D45:E46;F42:F43)}.

В
ячейке G47 записана формула =EXP(G45).

Вычислим
среднее арифметическое

и

по формулам:


Результаты
расчета

и

средствами Microsoft Excel представлены в
таблице 6.

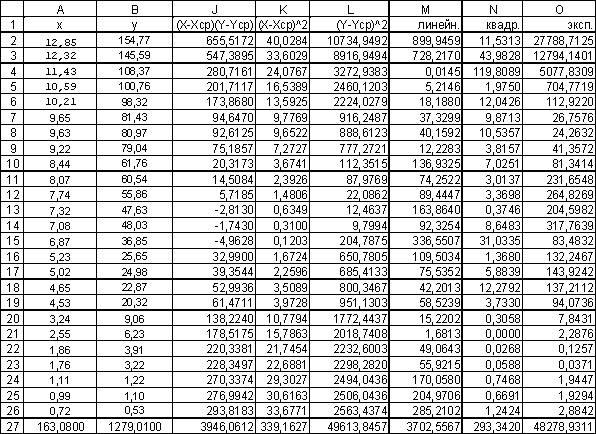
Вычисление
средних значений X и Y.

В
ячейке F49 записана формула =A26/25.В ячейке
F50 записана формула =B26/25.

Для
того, чтобы рассчитать коэффициент
корреляции и коэффициент

детерминированности
данные целесообразно расположить в
виде таблицы 7,

которая
является продолжением таблицы 2.

Таблица
7

Вычисление
остаточных сумм.

Поясним
как таблица 7 составляется.

Ячейки
A2:A27 и B2:B27 уже заполнены (см. табл. 2).

Далее
делаем следующие шаги.

Шаг
1. В ячейку J2 вводим формулу
=(A2-$F$49)*(B2-$F$50).

Шаг
2. В ячейки J3:J26 эта формула копируется.

Шаг
3. В ячейку K2 вводим формулу =(A2-$F$49)^2.

Шаг
4. В ячейки K3:K26 эта формула копируется.

Шаг
5. В ячейку L2 вводим формулу =(B2-$F$50)^2.

Шаг
6. В ячейки L3:L26 эта формула копируется.

Шаг
7. В ячейку M2 вводим формулу
=($D$37+$D$38*A2-B2)^2.

Шаг
8. В ячейки M3:M26 эта формула копируется.

Шаг
9. В ячейку N2 вводим формулу

=($I$38+$I$39*A2+$I$40*A2^2-B2)^2.

Шаг
10. В ячейки N3:N26 эта формула копируется.

Шаг
11. В ячейку O2 вводим формулу

=($G$47*EXP($G$46*A2)-B2)^2.

Шаг
12. В ячейки O3:O26 эта формула копируется.

Последующие
шаги делаем с помощью автосуммирования

.

Шаг
13. В ячейку J27 вводим формулу =СУММ(J2:J26).

Шаг
14. В ячейку K27 вводим формулу =СУММ(K2:K26).

Шаг
15. В ячейку L27 вводим формулу =СУММ(L2:L26).

Шаг
16. В ячейку M27 вводим формулу =СУММ(M2:M26).

Шаг
17. В ячейку N27 вводим формулу =СУММ(N2:N26).

Шаг
18. В ячейку O27 вводим формулу =СУММ(O2:O26).

Теперь
проведем расчеты коэффициента корреляции
по формуле



(только
для линейной аппроксимации)

и
коэффициента детерминированности по
формуле

.
Результаты расчетов средствами Microsoft
Excel представлены в таблице 8.

Таблица
8

Результаты
расчета.

В
таблице 8 в ячейке D53 записана формула
=J27/(K27*L27)^(1/2).

В
ячейке D54 записана формула =1- M27/L27.

В
ячейке D55 записана формула =1- N27/L27.

В
ячейке D56 записана формула =1- O27/L27.

Анализ
результатов расчетов показывает, что
квадратичная аппроксимация

наилучшим
образом описывает экспериментальные
данные.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Данный калькулятор по введенным данным строит несколько моделей регрессии: линейную, квадратичную, кубическую, степенную, логарифмическую, гиперболическую, показательную, экспоненциальную. Результаты можно сравнить между собой по корреляции, средней ошибке аппроксимации и наглядно на графике. Теория и формулы регрессий под калькулятором.

Если не ввести значения x, калькулятор примет, что значение x меняется от 0 с шагом 1.

PLANETCALC, Аппроксимация функции одной переменной

Аппроксимация функции одной переменной

Квадратичная аппроксимация

Аппроксимация степенной функцией

Показательная аппроксимация

Логарифмическая аппроксимация

Гиперболическая аппроксимация

Экспоненциальная аппроксимация

Точность вычисления

Знаков после запятой: 4

Коэффициент линейной парной корреляции

Средняя ошибка аппроксимации, %

Средняя ошибка аппроксимации, %

Средняя ошибка аппроксимации, %

Средняя ошибка аппроксимации, %

Средняя ошибка аппроксимации, %

Логарифмическая регрессия

Средняя ошибка аппроксимации, %

Гиперболическая регрессия

Средняя ошибка аппроксимации, %

Экспоненциальная регрессия

Средняя ошибка аппроксимации, %

Результат

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Линейная регрессия

Уравнение регрессии:
widehat{y}=ax+b

Коэффициент a:
a&=frac{sum x_i sum y_i- nsum x_iy_i}{left(sum x_iright)^2-nsum x_i^2}

Коэффициент b:
b&=frac{sum x_i sum x_iy_i-sum x_i^2sum y_i}{left(sum x_iright)^2-nsum x_i^2}

Коэффициент линейной парной корреляции:
r_{xy}&=frac{nsum x_iy_i-sum x_isum y_i}{sqrt{left(nsum x_i^2-left(sum x_iright)^2right)!!left(nsum y_i^2-left(sum y_iright)^2 right)}}

Коэффициент детерминации:
R^2=r_{xy}^2

Средняя ошибка аппроксимации:
overline{A}=dfrac{1}{n}sumleft|dfrac{y_i-widehat{y}_i}{y_i}right|cdot100%

Квадратичная регрессия

Уравнение регрессии:
widehat{y}=ax^2+bx+c

Система уравнений для нахождения коэффициентов a, b и c:
begin{cases}asum x_i^2+bsum x_i+nc=sum y_i,,\[2pt] asum x_i^3+bsum x_i^2+csum x_i=sum x_iy_i,,\[2pt] asum x_i^4+bsum x_i^3+csum x_i^2=sum x_i^2y_i,;end{cases}

Коэффициент корреляции:
R= sqrt{1-frac{sum(y_i-widehat{y}_i)^2}{sum(y_i-overline{y})^2}},
где
overline{y}= dfrac{1}{n}sum y_i

Коэффициент детерминации:
R^2

Средняя ошибка аппроксимации:
overline{A}=dfrac{1}{n}sumleft|dfrac{y_i-widehat{y}_i}{y_i}right|cdot100%

Кубическая регрессия

Уравнение регрессии:
widehat{y}=ax^3+bx^2+cx+d

Система уравнений для нахождения коэффициентов a, b, c и d:
begin{cases}asum x_i^3+bsum x_i^2+csum x_i+nd=sum y_i,,\[2pt] asum x_i^4+bsum x_i^3+csum x_i^2+dsum x_i=sum x_iy_i,,\[2pt] asum x_i^5+bsum x_i^4+csum x_i^3+dsum x_i^2=sum x_i^2y_i,,\[2pt] asum x_i^6+bsum x_i^5+csum x_i^4+dsum x_i^3=sum x_i^3y_i,;end{cases}

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации – используются те же формулы, что и для квадратичной регрессии.

Степенная регрессия

Уравнение регрессии:
widehat{y}=acdot x^b

Коэффициент b:
b=dfrac{nsum(ln x_icdotln y_i)-sumln x_icdotsumln y_i }{nsumln^2x_i-left(sumln x_iright)^2 }

Коэффициент a:
a=exp!left(dfrac{1}{n}sumln y_i-dfrac{b}{n}sumln x_iright)

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Показательная регрессия

Уравнение регрессии:
widehat{y}=acdot b^x

Коэффициент b:
b=expdfrac{nsum x_iln y_i-sum x_icdotsumln y_i }{nsum x_i^2-left(sum x_iright)^2 }

Коэффициент a:
a=exp!left(dfrac{1}{n}sumln y_i-dfrac{ln b}{n}sum x_iright)

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Гиперболическая регрессия

Уравнение регрессии:
widehat{y}=a + frac{b}{x}

Коэффициент b:
b=dfrac{nsumdfrac{y_i}{x_i}-sumdfrac{1}{x_i}sum y_i }{nsumdfrac{1}{x_i^2}-left(sumdfrac{1}{x_i}right)^2 }

Коэффициент a:
a=dfrac{1}{n}sum y_i-dfrac{b}{n}sumdfrac{1}{x_i}

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации – используются те же формулы, что и для квадратичной регрессии.

Логарифмическая регрессия

Уравнение регрессии:
widehat{y}=a + bln x

Коэффициент b:
b=dfrac{nsum(y_iln x_i)-sumln x_icdot sum y_i }{nsumln^2x_i-left(sumln x_iright)^2 }

Коэффициент a:
a=dfrac{1}{n}sum y_i-dfrac{b}{n}sumln x_i

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации – используются те же формулы, что и для квадратичной регрессии.

Экспоненциальная регрессия

Уравнение регрессии:
widehat{y}=e^{a+bx}

Коэффициент b:
b=dfrac{nsum x_iln y_i-sum x_icdotsumln y_i }{nsum x_i^2-left(sum x_iright)^2 }

Коэффициент a:
a=dfrac{1}{n}sumln y_i-dfrac{b}{n}sum x_i

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации – используются те же формулы, что и для квадратичной регрессии.

Вывод формул

Сначала сформулируем задачу:
Пусть у нас есть неизвестная функция y=f(x), заданная табличными значениями (например, полученными в результате опытных измерений).
Нам необходимо найти функцию заданного вида (линейную, квадратичную и т. п.) y=F(x), которая в соответствующих точках принимает значения, как можно более близкие к табличным.
На практике вид функции чаще всего определяют путем сравнения расположения точек с графиками известных функций.

Полученная формула y=F(x), которую называют эмпирической формулой, или уравнением регрессии y на x, или приближающей (аппроксимирующей) функцией, позволяет находить значения f(x) для нетабличных значений x, сглаживая результаты измерений величины y.

Для того, чтобы получить параметры функции F, используется метод наименьших квадратов. В этом методе в качестве критерия близости приближающей функции к совокупности точек используется суммы квадратов разностей значений табличных значений y и теоретических, рассчитанных по уравнению регрессии.

Таким образом, нам требуется найти функцию F, такую, чтобы сумма квадратов S была наименьшей:
S=sumlimits_i(y_i-F(x_i))^2rightarrow min

Рассмотрим решение этой задачи на примере получения линейной регрессии F=ax+b.
S является функцией двух переменных, a и b. Чтобы найти ее минимум, используем условие экстремума, а именно, равенства нулю частных производных.

Используя формулу производной сложной функции, получим следующую систему уравнений:
begin{cases} sum [y_i - F(x_i, a, b)]cdot F^prime_a(x_i, a, b)=0 \ sum [y_i - F(x_i, a, b)]cdot F^prime_b(x_i, a, b)=0 end{cases}

Для функции вида F(x,a,b)=ax+b частные производные равны:
F^prime_a=x,
F^prime_b=1

Подставив производные, получим:
begin{cases} sum (y_i - ax_i-b)cdot x_i=0 \ sum (y_i - ax_i-b)=0 end{cases}

Далее:
begin{cases} sum y_ix_i - a sum x_i^2-bsum x_i=0 \ sum y_i - asum x_i - nb=0 end{cases}

Откуда, выразив a и b, можно получить формулы для коэффициентов линейной регрессии, приведенные выше.
Аналогичным образом выводятся формулы для остальных видов регрессий.

Источник

Добавить комментарий