“Logit model” redirects here. Not to be confused with Logit function.
Example graph of a logistic regression curve fitted to data. The curve shows the probability of passing an exam (binary dependent variable) versus hours studying (scalar independent variable). See § Example for worked details.
In statistics, the logistic model (or logit model) is a statistical model that models the probability of an event taking place by having the log-odds for the event be a linear combination of one or more independent variables. In regression analysis, logistic regression[1] (or logit regression) is estimating the parameters of a logistic model (the coefficients in the linear combination). Formally, in binary logistic regression there is a single binary dependent variable, coded by an indicator variable, where the two values are labeled “0” and “1”, while the independent variables can each be a binary variable (two classes, coded by an indicator variable) or a continuous variable (any real value). The corresponding probability of the value labeled “1” can vary between 0 (certainly the value “0”) and 1 (certainly the value “1”), hence the labeling;[2] the function that converts log-odds to probability is the logistic function, hence the name. The unit of measurement for the log-odds scale is called a logit, from logistic unit, hence the alternative names. See § Background and § Definition for formal mathematics, and § Example for a worked example.
Binary variables are widely used in statistics to model the probability of a certain class or event taking place, such as the probability of a team winning, of a patient being healthy, etc. (see § Applications), and the logistic model has been the most commonly used model for binary regression since about 1970.[3] Binary variables can be generalized to categorical variables when there are more than two possible values (e.g. whether an image is of a cat, dog, lion, etc.), and the binary logistic regression generalized to multinomial logistic regression. If the multiple categories are ordered, one can use the ordinal logistic regression (for example the proportional odds ordinal logistic model[4]). See § Extensions for further extensions. The logistic regression model itself simply models probability of output in terms of input and does not perform statistical classification (it is not a classifier), though it can be used to make a classifier, for instance by choosing a cutoff value and classifying inputs with probability greater than the cutoff as one class, below the cutoff as the other; this is a common way to make a binary classifier.
Analogous linear models for binary variables with a different sigmoid function instead of the logistic function (to convert the linear combination to a probability) can also be used, most notably the probit model; see § Alternatives. The defining characteristic of the logistic model is that increasing one of the independent variables multiplicatively scales the odds of the given outcome at a constant rate, with each independent variable having its own parameter; for a binary dependent variable this generalizes the odds ratio. More abstractly, the logistic function is the natural parameter for the Bernoulli distribution, and in this sense is the “simplest” way to convert a real number to a probability. In particular, it maximizes entropy (minimizes added information), and in this sense makes the fewest assumptions of the data being modeled; see § Maximum entropy.
The parameters of a logistic regression are most commonly estimated by maximum-likelihood estimation (MLE). This does not have a closed-form expression, unlike linear least squares; see § Model fitting. Logistic regression by MLE plays a similarly basic role for binary or categorical responses as linear regression by ordinary least squares (OLS) plays for scalar responses: it is a simple, well-analyzed baseline model; see § Comparison with linear regression for discussion. The logistic regression as a general statistical model was originally developed and popularized primarily by Joseph Berkson,[5] beginning in Berkson (1944), where he coined “logit”; see § History.
Applications[edit]
Logistic regression is used in various fields, including machine learning, most medical fields, and social sciences. For example, the Trauma and Injury Severity Score (TRISS), which is widely used to predict mortality in injured patients, was originally developed by Boyd et al. using logistic regression.[6] Many other medical scales used to assess severity of a patient have been developed using logistic regression.[7][8][9][10] Logistic regression may be used to predict the risk of developing a given disease (e.g. diabetes; coronary heart disease), based on observed characteristics of the patient (age, sex, body mass index, results of various blood tests, etc.).[11][12] Another example might be to predict whether a Nepalese voter will vote Nepali Congress or Communist Party of Nepal or Any Other Party, based on age, income, sex, race, state of residence, votes in previous elections, etc.[13] The technique can also be used in engineering, especially for predicting the probability of failure of a given process, system or product.[14][15] It is also used in marketing applications such as prediction of a customer’s propensity to purchase a product or halt a subscription, etc.[16] In economics, it can be used to predict the likelihood of a person ending up in the labor force, and a business application would be to predict the likelihood of a homeowner defaulting on a mortgage. Conditional random fields, an extension of logistic regression to sequential data, are used in natural language processing.
Example[edit]
Problem[edit]
As a simple example, we can use a logistic regression with one explanatory variable and two categories to answer the following question:
A group of 20 students spends between 0 and 6 hours studying for an exam. How does the number of hours spent studying affect the probability of the student passing the exam?
The reason for using logistic regression for this problem is that the values of the dependent variable, pass and fail, while represented by “1” and “0”, are not cardinal numbers. If the problem was changed so that pass/fail was replaced with the grade 0–100 (cardinal numbers), then simple regression analysis could be used.
The table shows the number of hours each student spent studying, and whether they passed (1) or failed (0).
| Hours (xk) | 0.50 | 0.75 | 1.00 | 1.25 | 1.50 | 1.75 | 1.75 | 2.00 | 2.25 | 2.50 | 2.75 | 3.00 | 3.25 | 3.50 | 4.00 | 4.25 | 4.50 | 4.75 | 5.00 | 5.50 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pass (yk) | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
We wish to fit a logistic function to the data consisting of the hours studied (xk) and the outcome of the test (yk =1 for pass, 0 for fail). The data points are indexed by the subscript k which runs from 

Model[edit]
Graph of a logistic regression curve fitted to the (xm,ym) data. The curve shows the probability of passing an exam versus hours studying.
The logistic function is of the form:
where μ is a location parameter (the midpoint of the curve, where 
where 




Fit[edit]
The usual measure of goodness of fit for a logistic regression uses logistic loss (or log loss), the negative log-likelihood. For a given xk and yk, write 





The log loss for the k-th point is:
The log loss can be interpreted as the “surprisal” of the actual outcome 











These can be combined into a single expression:
This expression is more formally known as the cross entropy of the predicted distribution 

The sum of these, the total loss, is the overall negative log-likelihood 



Alternatively, instead of minimizing the loss, one can maximize its inverse, the (positive) log-likelihood:
or equivalently maximize the likelihood function itself, which is the probability that the given data set is produced by a particular logistic function:
This method is known as maximum likelihood estimation.
Parameter estimation[edit]
Since ℓ is nonlinear in 



and the maximization procedure can be accomplished by solving the above two equations for 

The values of 

which yields a value for μ and s of:
Predictions[edit]
The 

For example, for a student who studies 2 hours, entering the value 
Similarly, for a student who studies 4 hours, the estimated probability of passing the exam is 0.87:
This table shows the estimated probability of passing the exam for several values of hours studying.
| Hours of study (x) |
Passing exam | ||
|---|---|---|---|
| Log-odds (t) | Odds (et) | Probability (p) | |
| 1 | −2.57 | 0.076 ≈ 1:13.1 | 0.07 |
| 2 | −1.07 | 0.34 ≈ 1:2.91 | 0.26 |
 |
0 | 1 |  = 0.50 = 0.50
|
| 3 | 0.44 | 1.55 | 0.61 |
| 4 | 1.94 | 6.96 | 0.87 |
| 5 | 3.45 | 31.4 | 0.97 |
Model evaluation[edit]
The logistic regression analysis gives the following output.
| Coefficient | Std. Error | z-value | p-value (Wald) | |
|---|---|---|---|---|
| Intercept (β0) | −4.1 | 1.8 | −2.3 | 0.021 |
| Hours (β1) | 1.5 | 0.6 | 2.4 | 0.017 |
By the Wald test, the output indicates that hours studying is significantly associated with the probability of passing the exam (

Generalizations[edit]
This simple model is an example of binary logistic regression, and has one explanatory variable and a binary categorical variable which can assume one of two categorical values. Multinomial logistic regression is the generalization of binary logistic regression to include any number of explanatory variables and any number of categories.
Background[edit]
Figure 1. The standard logistic function 


Definition of the logistic function[edit]
An explanation of logistic regression can begin with an explanation of the standard logistic function. The logistic function is a sigmoid function, which takes any real input 

A graph of the logistic function on the t-interval (−6,6) is shown in Figure 1.
Let us assume that 



And the general logistic function 
In the logistic model, 






Definition of the inverse of the logistic function[edit]
We can now define the logit (log odds) function as the inverse 
and equivalently, after exponentiating both sides we have the odds:
Interpretation of these terms[edit]
In the above equations, the terms are as follows:
Definition of the odds[edit]
The odds of the dependent variable equaling a case (given some linear combination 
So we define odds of the dependent variable equaling a case (given some linear combination 
The odds ratio[edit]
For a continuous independent variable the odds ratio can be defined as:
-
The image represents an outline of what an odds ratio looks like in writing, through a template in addition to the test score example in the “Example” section of the contents. In simple terms, if we hypothetically get an odds ratio of 2 to 1, we can say… “For every one-unit increase in hours studied, the odds of passing (group 1) or failing (group 0) are (expectedly) 2 to 1 (Denis, 2019).
This exponential relationship provides an interpretation for 

For a binary independent variable the odds ratio is defined as 
Multiple explanatory variables[edit]
If there are multiple explanatory variables, the above expression 



Again, the more traditional equations are:
and
where usually 
Definition[edit]
The basic setup of logistic regression is as follows. We are given a dataset containing N points. Each point i consists of a set of m input variables x1,i … xm,i (also called independent variables, explanatory variables, predictor variables, features, or attributes), and a binary outcome variable Yi (also known as a dependent variable, response variable, output variable, or class), i.e. it can assume only the two possible values 0 (often meaning “no” or “failure”) or 1 (often meaning “yes” or “success”). The goal of logistic regression is to use the dataset to create a predictive model of the outcome variable.
As in linear regression, the outcome variables Yi are assumed to depend on the explanatory variables x1,i … xm,i.
- Explanatory variables
The explanatory variables may be of any type: real-valued, binary, categorical, etc. The main distinction is between continuous variables and discrete variables.
(Discrete variables referring to more than two possible choices are typically coded using dummy variables (or indicator variables), that is, separate explanatory variables taking the value 0 or 1 are created for each possible value of the discrete variable, with a 1 meaning “variable does have the given value” and a 0 meaning “variable does not have that value”.)
- Outcome variables
Formally, the outcomes Yi are described as being Bernoulli-distributed data, where each outcome is determined by an unobserved probability pi that is specific to the outcome at hand, but related to the explanatory variables. This can be expressed in any of the following equivalent forms:
The meanings of these four lines are:
- The first line expresses the probability distribution of each Yi : conditioned on the explanatory variables, it follows a Bernoulli distribution with parameters pi, the probability of the outcome of 1 for trial i. As noted above, each separate trial has its own probability of success, just as each trial has its own explanatory variables. The probability of success pi is not observed, only the outcome of an individual Bernoulli trial using that probability.
- The second line expresses the fact that the expected value of each Yi is equal to the probability of success pi, which is a general property of the Bernoulli distribution. In other words, if we run a large number of Bernoulli trials using the same probability of success pi, then take the average of all the 1 and 0 outcomes, then the result would be close to pi. This is because doing an average this way simply computes the proportion of successes seen, which we expect to converge to the underlying probability of success.
- The third line writes out the probability mass function of the Bernoulli distribution, specifying the probability of seeing each of the two possible outcomes.
- The fourth line is another way of writing the probability mass function, which avoids having to write separate cases and is more convenient for certain types of calculations. This relies on the fact that Yi can take only the value 0 or 1. In each case, one of the exponents will be 1, “choosing” the value under it, while the other is 0, “canceling out” the value under it. Hence, the outcome is either pi or 1 − pi, as in the previous line.
- Linear predictor function
The basic idea of logistic regression is to use the mechanism already developed for linear regression by modeling the probability pi using a linear predictor function, i.e. a linear combination of the explanatory variables and a set of regression coefficients that are specific to the model at hand but the same for all trials. The linear predictor function 
where 
The model is usually put into a more compact form as follows:
- The regression coefficients β0, β1, …, βm are grouped into a single vector β of size m + 1.
- For each data point i, an additional explanatory pseudo-variable x0,i is added, with a fixed value of 1, corresponding to the intercept coefficient β0.
- The resulting explanatory variables x0,i, x1,i, …, xm,i are then grouped into a single vector Xi of size m + 1.
This makes it possible to write the linear predictor function as follows:
using the notation for a dot product between two vectors.
This is an example of an SPSS output for a logistic regression model using three explanatory variables (coffee use per week, energy drink use per week, and soda use per week) and two categories (male and female).
Many explanatory variables, two categories[edit]
The above example of binary logistic regression on one explanatory variable can be generalized to binary logistic regression on any number of explanatory variables x1, x2,… and any number of categorical values 
To begin with, we may consider a logistic model with M explanatory variables, x1, x2 … xM and, as in the example above, two categorical values (y = 0 and 1). For the simple binary logistic regression model, we assumed a linear relationship between the predictor variable and the log-odds (also called logit) of the event that 
where t is the log-odds and 

For a more compact notation, we will specify the explanatory variables and the β coefficients as 
with an added explanatory variable x0 =1. The logit may now be written as:
Solving for the probability p that 
,
where 










As in the simple example above, finding the optimum β parameters will require numerical methods. One useful technique is to equate the derivatives of the log likelihood with respect to each of the β parameters to zero yielding a set of equations which will hold at the maximum of the log likelihood:
where xmk is the value of the xm explanatory variable from the k-th measurement.
Consider an example with 




,
where p is the probability of the event that 
Multinomial logistic regression: Many explanatory variables and many categories[edit]
In the above cases of two categories (binomial logistic regression), the categories were indexed by “0” and “1”, and we had two probability distributions: The probability that the outcome was in category 1 was given by 

In general, if we have 


for
Each of the probabilities except 



Note also that for the simple case of 


The log-likelihood that a particular set of K measurements or data points will be generated by the above probabilities can now be calculated. Indexing each measurement by k, let the k-th set of measured explanatory variables be denoted by 

where 
where 


Interpretations[edit]
There are various equivalent specifications and interpretations of logistic regression, which fit into different types of more general models, and allow different generalizations.
As a generalized linear model[edit]
The particular model used by logistic regression, which distinguishes it from standard linear regression and from other types of regression analysis used for binary-valued outcomes, is the way the probability of a particular outcome is linked to the linear predictor function:
Written using the more compact notation described above, this is:
This formulation expresses logistic regression as a type of generalized linear model, which predicts variables with various types of probability distributions by fitting a linear predictor function of the above form to some sort of arbitrary transformation of the expected value of the variable.
The intuition for transforming using the logit function (the natural log of the odds) was explained above[clarification needed]. It also has the practical effect of converting the probability (which is bounded to be between 0 and 1) to a variable that ranges over 
Note that both the probabilities pi and the regression coefficients are unobserved, and the means of determining them is not part of the model itself. They are typically determined by some sort of optimization procedure, e.g. maximum likelihood estimation, that finds values that best fit the observed data (i.e. that give the most accurate predictions for the data already observed), usually subject to regularization conditions that seek to exclude unlikely values, e.g. extremely large values for any of the regression coefficients. The use of a regularization condition is equivalent to doing maximum a posteriori (MAP) estimation, an extension of maximum likelihood. (Regularization is most commonly done using a squared regularizing function, which is equivalent to placing a zero-mean Gaussian prior distribution on the coefficients, but other regularizers are also possible.) Whether or not regularization is used, it is usually not possible to find a closed-form solution; instead, an iterative numerical method must be used, such as iteratively reweighted least squares (IRLS) or, more commonly these days, a quasi-Newton method such as the L-BFGS method.[20]
The interpretation of the βj parameter estimates is as the additive effect on the log of the odds for a unit change in the j the explanatory variable. In the case of a dichotomous explanatory variable, for instance, gender 
An equivalent formula uses the inverse of the logit function, which is the logistic function, i.e.:
The formula can also be written as a probability distribution (specifically, using a probability mass function):
As a latent-variable model[edit]
The logistic model has an equivalent formulation as a latent-variable model. This formulation is common in the theory of discrete choice models and makes it easier to extend to certain more complicated models with multiple, correlated choices, as well as to compare logistic regression to the closely related probit model.
Imagine that, for each trial i, there is a continuous latent variable Yi* (i.e. an unobserved random variable) that is distributed as follows:
where
i.e. the latent variable can be written directly in terms of the linear predictor function and an additive random error variable that is distributed according to a standard logistic distribution.
Then Yi can be viewed as an indicator for whether this latent variable is positive:
The choice of modeling the error variable specifically with a standard logistic distribution, rather than a general logistic distribution with the location and scale set to arbitrary values, seems restrictive, but in fact, it is not. It must be kept in mind that we can choose the regression coefficients ourselves, and very often can use them to offset changes in the parameters of the error variable’s distribution. For example, a logistic error-variable distribution with a non-zero location parameter μ (which sets the mean) is equivalent to a distribution with a zero location parameter, where μ has been added to the intercept coefficient. Both situations produce the same value for Yi* regardless of settings of explanatory variables. Similarly, an arbitrary scale parameter s is equivalent to setting the scale parameter to 1 and then dividing all regression coefficients by s. In the latter case, the resulting value of Yi* will be smaller by a factor of s than in the former case, for all sets of explanatory variables — but critically, it will always remain on the same side of 0, and hence lead to the same Yi choice.
(Note that this predicts that the irrelevancy of the scale parameter may not carry over into more complex models where more than two choices are available.)
It turns out that this formulation is exactly equivalent to the preceding one, phrased in terms of the generalized linear model and without any latent variables. This can be shown as follows, using the fact that the cumulative distribution function (CDF) of the standard logistic distribution is the logistic function, which is the inverse of the logit function, i.e.
Then:
This formulation—which is standard in discrete choice models—makes clear the relationship between logistic regression (the “logit model”) and the probit model, which uses an error variable distributed according to a standard normal distribution instead of a standard logistic distribution. Both the logistic and normal distributions are symmetric with a basic unimodal, “bell curve” shape. The only difference is that the logistic distribution has somewhat heavier tails, which means that it is less sensitive to outlying data (and hence somewhat more robust to model mis-specifications or erroneous data).
Two-way latent-variable model[edit]
Yet another formulation uses two separate latent variables:
where
where EV1(0,1) is a standard type-1 extreme value distribution: i.e.
Then
This model has a separate latent variable and a separate set of regression coefficients for each possible outcome of the dependent variable. The reason for this separation is that it makes it easy to extend logistic regression to multi-outcome categorical variables, as in the multinomial logit model. In such a model, it is natural to model each possible outcome using a different set of regression coefficients. It is also possible to motivate each of the separate latent variables as the theoretical utility associated with making the associated choice, and thus motivate logistic regression in terms of utility theory. (In terms of utility theory, a rational actor always chooses the choice with the greatest associated utility.) This is the approach taken by economists when formulating discrete choice models, because it both provides a theoretically strong foundation and facilitates intuitions about the model, which in turn makes it easy to consider various sorts of extensions. (See the example below.)
The choice of the type-1 extreme value distribution seems fairly arbitrary, but it makes the mathematics work out, and it may be possible to justify its use through rational choice theory.
It turns out that this model is equivalent to the previous model, although this seems non-obvious, since there are now two sets of regression coefficients and error variables, and the error variables have a different distribution. In fact, this model reduces directly to the previous one with the following substitutions:
An intuition for this comes from the fact that, since we choose based on the maximum of two values, only their difference matters, not the exact values — and this effectively removes one degree of freedom. Another critical fact is that the difference of two type-1 extreme-value-distributed variables is a logistic distribution, i.e. 
Example[edit]
As an example, consider a province-level election where the choice is between a right-of-center party, a left-of-center party, and a secessionist party (e.g. the Parti Québécois, which wants Quebec to secede from Canada). We would then use three latent variables, one for each choice. Then, in accordance with utility theory, we can then interpret the latent variables as expressing the utility that results from making each of the choices. We can also interpret the regression coefficients as indicating the strength that the associated factor (i.e. explanatory variable) has in contributing to the utility — or more correctly, the amount by which a unit change in an explanatory variable changes the utility of a given choice. A voter might expect that the right-of-center party would lower taxes, especially on rich people. This would give low-income people no benefit, i.e. no change in utility (since they usually don’t pay taxes); would cause moderate benefit (i.e. somewhat more money, or moderate utility increase) for middle-incoming people; would cause significant benefits for high-income people. On the other hand, the left-of-center party might be expected to raise taxes and offset it with increased welfare and other assistance for the lower and middle classes. This would cause significant positive benefit to low-income people, perhaps a weak benefit to middle-income people, and significant negative benefit to high-income people. Finally, the secessionist party would take no direct actions on the economy, but simply secede. A low-income or middle-income voter might expect basically no clear utility gain or loss from this, but a high-income voter might expect negative utility since he/she is likely to own companies, which will have a harder time doing business in such an environment and probably lose money.
These intuitions can be expressed as follows:
| Center-right | Center-left | Secessionist | |
|---|---|---|---|
| High-income | strong + | strong − | strong − |
| Middle-income | moderate + | weak + | none |
| Low-income | none | strong + | none |
This clearly shows that
- Separate sets of regression coefficients need to exist for each choice. When phrased in terms of utility, this can be seen very easily. Different choices have different effects on net utility; furthermore, the effects vary in complex ways that depend on the characteristics of each individual, so there need to be separate sets of coefficients for each characteristic, not simply a single extra per-choice characteristic.
- Even though income is a continuous variable, its effect on utility is too complex for it to be treated as a single variable. Either it needs to be directly split up into ranges, or higher powers of income need to be added so that polynomial regression on income is effectively done.
As a “log-linear” model[edit]
Yet another formulation combines the two-way latent variable formulation above with the original formulation higher up without latent variables, and in the process provides a link to one of the standard formulations of the multinomial logit.
Here, instead of writing the logit of the probabilities pi as a linear predictor, we separate the linear predictor into two, one for each of the two outcomes:
Two separate sets of regression coefficients have been introduced, just as in the two-way latent variable model, and the two equations appear a form that writes the logarithm of the associated probability as a linear predictor, with an extra term 
In this form it is clear that the purpose of Z is to ensure that the resulting distribution over Yi is in fact a probability distribution, i.e. it sums to 1. This means that Z is simply the sum of all un-normalized probabilities, and by dividing each probability by Z, the probabilities become “normalized”. That is:
and the resulting equations are
Or generally:
This shows clearly how to generalize this formulation to more than two outcomes, as in multinomial logit.
Note that this general formulation is exactly the softmax function as in
In order to prove that this is equivalent to the previous model, note that the above model is overspecified, in that 


As a result, we can simplify matters, and restore identifiability, by picking an arbitrary value for one of the two vectors. We choose to set 
and so
which shows that this formulation is indeed equivalent to the previous formulation. (As in the two-way latent variable formulation, any settings where 
Note that most treatments of the multinomial logit model start out either by extending the “log-linear” formulation presented here or the two-way latent variable formulation presented above, since both clearly show the way that the model could be extended to multi-way outcomes. In general, the presentation with latent variables is more common in econometrics and political science, where discrete choice models and utility theory reign, while the “log-linear” formulation here is more common in computer science, e.g. machine learning and natural language processing.
As a single-layer perceptron[edit]
The model has an equivalent formulation
This functional form is commonly called a single-layer perceptron or single-layer artificial neural network. A single-layer neural network computes a continuous output instead of a step function. The derivative of pi with respect to X = (x1, …, xk) is computed from the general form:
where f(X) is an analytic function in X. With this choice, the single-layer neural network is identical to the logistic regression model. This function has a continuous derivative, which allows it to be used in backpropagation. This function is also preferred because its derivative is easily calculated:
In terms of binomial data[edit]
A closely related model assumes that each i is associated not with a single Bernoulli trial but with ni independent identically distributed trials, where the observation Yi is the number of successes observed (the sum of the individual Bernoulli-distributed random variables), and hence follows a binomial distribution:
An example of this distribution is the fraction of seeds (pi) that germinate after ni are planted.
In terms of expected values, this model is expressed as follows:
so that
Or equivalently:
This model can be fit using the same sorts of methods as the above more basic model.
Model fitting[edit]
|
This section needs expansion. You can help by adding to it. (October 2016) |
Maximum likelihood estimation (MLE)[edit]
The regression coefficients are usually estimated using maximum likelihood estimation.[21][22] Unlike linear regression with normally distributed residuals, it is not possible to find a closed-form expression for the coefficient values that maximize the likelihood function, so that an iterative process must be used instead; for example Newton’s method. This process begins with a tentative solution, revises it slightly to see if it can be improved, and repeats this revision until no more improvement is made, at which point the process is said to have converged.[21]
In some instances, the model may not reach convergence. Non-convergence of a model indicates that the coefficients are not meaningful because the iterative process was unable to find appropriate solutions. A failure to converge may occur for a number of reasons: having a large ratio of predictors to cases, multicollinearity, sparseness, or complete separation.
- Having a large ratio of variables to cases results in an overly conservative Wald statistic (discussed below) and can lead to non-convergence. Regularized logistic regression is specifically intended to be used in this situation.
- Multicollinearity refers to unacceptably high correlations between predictors. As multicollinearity increases, coefficients remain unbiased but standard errors increase and the likelihood of model convergence decreases.[21] To detect multicollinearity amongst the predictors, one can conduct a linear regression analysis with the predictors of interest for the sole purpose of examining the tolerance statistic [21] used to assess whether multicollinearity is unacceptably high.
- Sparseness in the data refers to having a large proportion of empty cells (cells with zero counts). Zero cell counts are particularly problematic with categorical predictors. With continuous predictors, the model can infer values for the zero cell counts, but this is not the case with categorical predictors. The model will not converge with zero cell counts for categorical predictors because the natural logarithm of zero is an undefined value so that the final solution to the model cannot be reached. To remedy this problem, researchers may collapse categories in a theoretically meaningful way or add a constant to all cells.[21]
- Another numerical problem that may lead to a lack of convergence is complete separation, which refers to the instance in which the predictors perfectly predict the criterion – all cases are accurately classified and the likelihood maximized with infinite coefficients. In such instances, one should re-examine the data, as there may be some kind of error.[2][further explanation needed]
- One can also take semi-parametric or non-parametric approaches, e.g., via local-likelihood or nonparametric quasi-likelihood methods, which avoid assumptions of a parametric form for the index function and is robust to the choice of the link function (e.g., probit or logit).[23]
Iteratively reweighted least squares (IRLS)[edit]
Binary logistic regression (

![{displaystyle mathbf {w} ^{T}=[beta _{0},beta _{1},beta _{2},ldots ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/daccbf84c2c936e0559016491efe98eaf0eca430)
![{displaystyle mathbf {x} (i)=[1,x_{1}(i),x_{2}(i),ldots ]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8fc5f11bdd42f672417a3f4e44b3a4e5be28faa)


where 
![{displaystyle {boldsymbol {mu }}=[mu (1),mu (2),ldots ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/800927e9be36f4cac166a68862c04234cffd67b8)
The regressor matrix and ![{displaystyle mathbf {y} (i)=[y(1),y(2),ldots ]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33cbd315328b6ccfc7f216d65e39f92a8ec48694)
Bayesian[edit]
In a Bayesian statistics context, prior distributions are normally placed on the regression coefficients, for example in the form of Gaussian distributions. There is no conjugate prior of the likelihood function in logistic regression. When Bayesian inference was performed analytically, this made the posterior distribution difficult to calculate except in very low dimensions. Now, though, automatic software such as OpenBUGS, JAGS, PyMC3, Stan or Turing.jl allows these posteriors to be computed using simulation, so lack of conjugacy is not a concern. However, when the sample size or the number of parameters is large, full Bayesian simulation can be slow, and people often use approximate methods such as variational Bayesian methods and expectation propagation.
“Rule of ten”[edit]
A widely used rule of thumb, the “one in ten rule”, states that logistic regression models give stable values for the explanatory variables if based on a minimum of about 10 events per explanatory variable (EPV); where event denotes the cases belonging to the less frequent category in the dependent variable. Thus a study designed to use 


Others have found results that are not consistent with the above, using different criteria. A useful criterion is whether the fitted model will be expected to achieve the same predictive discrimination in a new sample as it appeared to achieve in the model development sample. For that criterion, 20 events per candidate variable may be required.[28] Also, one can argue that 96 observations are needed only to estimate the model’s intercept precisely enough that the margin of error in predicted probabilities is ±0.1 with a 0.95 confidence level.[29]
Error and significance of fit[edit]
Deviance and likelihood ratio test ─ a simple case[edit]
In any fitting procedure, the addition of another fitting parameter to a model (e.g. the beta parameters in a logistic regression model) will almost always improve the ability of the model to predict the measured outcomes. This will be true even if the additional term has no predictive value, since the model will simply be “overfitting” to the noise in the data. The question arises as to whether the improvement gained by the addition of another fitting parameter is significant enough to recommend the inclusion of the additional term, or whether the improvement is simply that which may be expected from overfitting.
In short, for logistic regression, a statistic known as the deviance is defined which is a measure of the error between the logistic model fit and the outcome data. In the limit of a large number of data points, the deviance is chi-squared distributed, which allows a chi-squared test to be implemented in order to determine the significance of the explanatory variables.
Linear regression and logistic regression have many similarities. For example, in simple linear regression, a set of K data points (xk, yk) are fitted to a proposed model function of the form 
The minimum value which constitutes the fit will be denoted by 
The idea of a null model may be introduced, in which it is assumed that the x variable is of no use in predicting the yk outcomes: The data points are fitted to a null model function of the form y=b0 with a squared error term:
The fitting process consists of choosing a value of b0 which minimizes 





which is proportional to the square of the (uncorrected) sample standard deviation of the yk data points.
We can imagine a case where the yk data points are randomly assigned to the various xk, and then fitted using the proposed model. Specifically, we can consider the fits of the proposed model to every permutation of the yk outcomes. It can be shown that the optimized error of any of these fits will never be less than the optimum error of the null model, and that the difference between these minimum error will follow a chi-squared distribution, with degrees of freedom equal those of the proposed model minus those of the null model which, in this case, will be 2-1=1. Using the chi-squared test, we may then estimate how many of these permuted sets of yk will yield an minimum error less than or equal to the minimum error using the original yk, and so we can estimate how significant an improvement is given by the inclusion of the x variable in the proposed model.
For logistic regression, the measure of goodness-of-fit is the likelihood function L, or its logarithm, the log-likelihood ℓ. The likelihood function L is analogous to the 

In the case of simple binary logistic regression, the set of K data points are fitted in a probabilistic sense to a function of the form:
where 

and the log-likelihood is:
For the null model, the probability that 
The log-odds for the null model are given by:
and the log-likelihood is:
Since we have 
The optimum 
where 
Also, as an analog to the error of the linear regression case, we may define the deviance of a logistic regression fit as:
which will always be positive or zero. The reason for this choice is that not only is the deviance a good measure of the goodness of fit, it is also approximately chi-squared distributed, with the approximation improving as the number of data points (K) increases, becoming exactly chi-square distributed in the limit of an infinite number of data points. As in the case of linear regression, we may use this fact to estimate the probability that a random set of data points will give a better fit than the fit obtained by the proposed model, and so have an estimate how significantly the model is improved by including the xk data points in the proposed model.
For the simple model of student test scores described above, the maximum value of the log-likelihood of the null model is 


Using the chi-squared test of significance, the integral of the chi-squared distribution with one degree of freedom from 11.6661… to infinity is equal to 0.00063649…
This effectively means that about 6 out of a 10,000 fits to random yk can be expected to have a better fit (smaller deviance) than the given yk and so we can conclude that the inclusion of the x variable and data in the proposed model is a very significant improvement over the null model. In other words, we reject the null hypothesis with 
Goodness of fit summary[edit]
Goodness of fit in linear regression models is generally measured using R2. Since this has no direct analog in logistic regression, various methods[30]: ch.21 including the following can be used instead.
Deviance and likelihood ratio tests[edit]
In linear regression analysis, one is concerned with partitioning variance via the sum of squares calculations – variance in the criterion is essentially divided into variance accounted for by the predictors and residual variance. In logistic regression analysis, deviance is used in lieu of a sum of squares calculations.[31] Deviance is analogous to the sum of squares calculations in linear regression[2] and is a measure of the lack of fit to the data in a logistic regression model.[31] When a “saturated” model is available (a model with a theoretically perfect fit), deviance is calculated by comparing a given model with the saturated model.[2] This computation gives the likelihood-ratio test:[2]
In the above equation, D represents the deviance and ln represents the natural logarithm. The log of this likelihood ratio (the ratio of the fitted model to the saturated model) will produce a negative value, hence the need for a negative sign. D can be shown to follow an approximate chi-squared distribution.[2] Smaller values indicate better fit as the fitted model deviates less from the saturated model. When assessed upon a chi-square distribution, nonsignificant chi-square values indicate very little unexplained variance and thus, good model fit. Conversely, a significant chi-square value indicates that a significant amount of the variance is unexplained.
When the saturated model is not available (a common case), deviance is calculated simply as −2·(log likelihood of the fitted model), and the reference to the saturated model’s log likelihood can be removed from all that follows without harm.
Two measures of deviance are particularly important in logistic regression: null deviance and model deviance. The null deviance represents the difference between a model with only the intercept (which means “no predictors”) and the saturated model. The model deviance represents the difference between a model with at least one predictor and the saturated model.[31] In this respect, the null model provides a baseline upon which to compare predictor models. Given that deviance is a measure of the difference between a given model and the saturated model, smaller values indicate better fit. Thus, to assess the contribution of a predictor or set of predictors, one can subtract the model deviance from the null deviance and assess the difference on a 
Let
Then the difference of both is:
If the model deviance is significantly smaller than the null deviance then one can conclude that the predictor or set of predictors significantly improve the model’s fit. This is analogous to the F-test used in linear regression analysis to assess the significance of prediction.[31]
Pseudo-R-squared[edit]
In linear regression the squared multiple correlation, R2 is used to assess goodness of fit as it represents the proportion of variance in the criterion that is explained by the predictors.[31] In logistic regression analysis, there is no agreed upon analogous measure, but there are several competing measures each with limitations.[31][32]
Four of the most commonly used indices and one less commonly used one are examined on this page:
- Likelihood ratio R2L
- Cox and Snell R2CS
- Nagelkerke R2N
- McFadden R2McF
- Tjur R2T
Hosmer–Lemeshow test[edit]
The Hosmer–Lemeshow test uses a test statistic that asymptotically follows a 
Coefficient significance[edit]
After fitting the model, it is likely that researchers will want to examine the contribution of individual predictors. To do so, they will want to examine the regression coefficients. In linear regression, the regression coefficients represent the change in the criterion for each unit change in the predictor.[31] In logistic regression, however, the regression coefficients represent the change in the logit for each unit change in the predictor. Given that the logit is not intuitive, researchers are likely to focus on a predictor’s effect on the exponential function of the regression coefficient – the odds ratio (see definition). In linear regression, the significance of a regression coefficient is assessed by computing a t test. In logistic regression, there are several different tests designed to assess the significance of an individual predictor, most notably the likelihood ratio test and the Wald statistic.
Likelihood ratio test[edit]
The likelihood-ratio test discussed above to assess model fit is also the recommended procedure to assess the contribution of individual “predictors” to a given model.[2][21][31] In the case of a single predictor model, one simply compares the deviance of the predictor model with that of the null model on a chi-square distribution with a single degree of freedom. If the predictor model has significantly smaller deviance (c.f. chi-square using the difference in degrees of freedom of the two models), then one can conclude that there is a significant association between the “predictor” and the outcome. Although some common statistical packages (e.g. SPSS) do provide likelihood ratio test statistics, without this computationally intensive test it would be more difficult to assess the contribution of individual predictors in the multiple logistic regression case.[citation needed] To assess the contribution of individual predictors one can enter the predictors hierarchically, comparing each new model with the previous to determine the contribution of each predictor.[31] There is some debate among statisticians about the appropriateness of so-called “stepwise” procedures.[weasel words] The fear is that they may not preserve nominal statistical properties and may become misleading.[34]
Wald statistic[edit]
Alternatively, when assessing the contribution of individual predictors in a given model, one may examine the significance of the Wald statistic. The Wald statistic, analogous to the t-test in linear regression, is used to assess the significance of coefficients. The Wald statistic is the ratio of the square of the regression coefficient to the square of the standard error of the coefficient and is asymptotically distributed as a chi-square distribution.[21]
Although several statistical packages (e.g., SPSS, SAS) report the Wald statistic to assess the contribution of individual predictors, the Wald statistic has limitations. When the regression coefficient is large, the standard error of the regression coefficient also tends to be larger increasing the probability of Type-II error. The Wald statistic also tends to be biased when data are sparse.[31]
Case-control sampling[edit]
Suppose cases are rare. Then we might wish to sample them more frequently than their prevalence in the population. For example, suppose there is a disease that affects 1 person in 10,000 and to collect our data we need to do a complete physical. It may be too expensive to do thousands of physicals of healthy people in order to obtain data for only a few diseased individuals. Thus, we may evaluate more diseased individuals, perhaps all of the rare outcomes. This is also retrospective sampling, or equivalently it is called unbalanced data. As a rule of thumb, sampling controls at a rate of five times the number of cases will produce sufficient control data.[35]
Logistic regression is unique in that it may be estimated on unbalanced data, rather than randomly sampled data, and still yield correct coefficient estimates of the effects of each independent variable on the outcome. That is to say, if we form a logistic model from such data, if the model is correct in the general population, the 


where 

Discussion[edit]
Like other forms of regression analysis, logistic regression makes use of one or more predictor variables that may be either continuous or categorical. Unlike ordinary linear regression, however, logistic regression is used for predicting dependent variables that take membership in one of a limited number of categories (treating the dependent variable in the binomial case as the outcome of a Bernoulli trial) rather than a continuous outcome. Given this difference, the assumptions of linear regression are violated. In particular, the residuals cannot be normally distributed. In addition, linear regression may make nonsensical predictions for a binary dependent variable. What is needed is a way to convert a binary variable into a continuous one that can take on any real value (negative or positive). To do that, binomial logistic regression first calculates the odds of the event happening for different levels of each independent variable, and then takes its logarithm to create a continuous criterion as a transformed version of the dependent variable. The logarithm of the odds is the logit of the probability, the logit is defined as follows:
Although the dependent variable in logistic regression is Bernoulli, the logit is on an unrestricted scale.[2] The logit function is the link function in this kind of generalized linear model, i.e.
Y is the Bernoulli-distributed response variable and x is the predictor variable; the β values are the linear parameters.
The logit of the probability of success is then fitted to the predictors. The predicted value of the logit is converted back into predicted odds, via the inverse of the natural logarithm – the exponential function. Thus, although the observed dependent variable in binary logistic regression is a 0-or-1 variable, the logistic regression estimates the odds, as a continuous variable, that the dependent variable is a ‘success’. In some applications, the odds are all that is needed. In others, a specific yes-or-no prediction is needed for whether the dependent variable is or is not a ‘success’; this categorical prediction can be based on the computed odds of success, with predicted odds above some chosen cutoff value being translated into a prediction of success.
Maximum entropy[edit]
Of all the functional forms used for estimating the probabilities of a particular categorical outcome which optimize the fit by maximizing the likelihood function (e.g. probit regression, Poisson regression, etc.), the logistic regression solution is unique in that it is a maximum entropy solution.[36] This is a case of a general property: an exponential family of distributions maximizes entropy, given an expected value. In the case of the logistic model, the logistic function is the natural parameter of the Bernoulli distribution (it is in “canonical form”, and the logistic function is the canonical link function), while other sigmoid functions are non-canonical link functions; this underlies its mathematical elegance and ease of optimization. See Exponential family § Maximum entropy derivation for details.
Proof[edit]
In order to show this, we use the method of Lagrange multipliers. The Lagrangian is equal to the entropy plus the sum of the products of Lagrange multipliers times various constraint expressions. The general multinomial case will be considered, since the proof is not made that much simpler by considering simpler cases. Equating the derivative of the Lagrangian with respect to the various probabilities to zero yields a functional form for those probabilities which corresponds to those used in logistic regression.[36]
As in the above section on multinomial logistic regression, we will consider 








Let pn(x) be the probability, given explanatory variable vector x, that the outcome will be 

The Lagrangian will be expressed as a function of the probabilities pnk and will minimized by equating the derivatives of the Lagrangian with respect to these probabilities to zero. An important point is that the probabilities are treated equally and the fact that they sum to unity is part of the Lagrangian formulation, rather than being assumed from the beginning.
The first contribution to the Lagrangian is the entropy:
The log-likelihood is:
Assuming the multinomial logistic function, the derivative of the log-likelihood with respect the beta coefficients was found to be:
A very important point here is that this expression is (remarkably) not an explicit function of the beta coefficients. It is only a function of the probabilities pnk and the data. Rather than being specific to the assumed multinomial logistic case, it is taken to be a general statement of the condition at which the log-likelihood is maximized and makes no reference to the functional form of pnk. There are then (M+1)(N+1) fitting constraints and the fitting constraint term in the Lagrangian is then:
where the λnm are the appropriate Lagrange multipliers. There are K normalization constraints which may be written:
so that the normalization term in the Lagrangian is:
where the αk are the appropriate Lagrange multipliers. The Lagrangian is then the sum of the above three terms:
Setting the derivative of the Lagrangian with respect to one of the probabilities to zero yields:
Using the more condensed vector notation:
and dropping the primes on the n and k indices, and then solving for 
where:
Imposing the normalization constraint, we can solve for the Zk and write the probabilities as:
The 









Other approaches[edit]
In machine learning applications where logistic regression is used for binary classification, the MLE minimises the Cross entropy loss function.
Logistic regression is an important machine learning algorithm. The goal is to model the probability of a random variable 
Consider a generalized linear model function parameterized by 
Therefore,
and since 


Typically, the log likelihood is maximized,
which is maximized using optimization techniques such as gradient descent.
Assuming the 
where 

Comparison with linear regression[edit]
Logistic regression can be seen as a special case of the generalized linear model and thus analogous to linear regression. The model of logistic regression, however, is based on quite different assumptions (about the relationship between the dependent and independent variables) from those of linear regression. In particular, the key differences between these two models can be seen in the following two features of logistic regression. First, the conditional distribution 
Alternatives[edit]
A common alternative to the logistic model (logit model) is the probit model, as the related names suggest. From the perspective of generalized linear models, these differ in the choice of link function: the logistic model uses the logit function (inverse logistic function), while the probit model uses the probit function (inverse error function). Equivalently, in the latent variable interpretations of these two methods, the first assumes a standard logistic distribution of errors and the second a standard normal distribution of errors.[38] Other sigmoid functions or error distributions can be used instead.
Logistic regression is an alternative to Fisher’s 1936 method, linear discriminant analysis.[39] If the assumptions of linear discriminant analysis hold, the conditioning can be reversed to produce logistic regression. The converse is not true, however, because logistic regression does not require the multivariate normal assumption of discriminant analysis.[40]
The assumption of linear predictor effects can easily be relaxed using techniques such as spline functions.[29]
History[edit]
A detailed history of the logistic regression is given in Cramer (2002). The logistic function was developed as a model of population growth and named “logistic” by Pierre François Verhulst in the 1830s and 1840s, under the guidance of Adolphe Quetelet; see Logistic function § History for details.[41] In his earliest paper (1838), Verhulst did not specify how he fit the curves to the data.[42][43] In his more detailed paper (1845), Verhulst determined the three parameters of the model by making the curve pass through three observed points, which yielded poor predictions.[44][45]
The logistic function was independently developed in chemistry as a model of autocatalysis (Wilhelm Ostwald, 1883).[46] An autocatalytic reaction is one in which one of the products is itself a catalyst for the same reaction, while the supply of one of the reactants is fixed. This naturally gives rise to the logistic equation for the same reason as population growth: the reaction is self-reinforcing but constrained.
The logistic function was independently rediscovered as a model of population growth in 1920 by Raymond Pearl and Lowell Reed, published as Pearl & Reed (1920), which led to its use in modern statistics. They were initially unaware of Verhulst’s work and presumably learned about it from L. Gustave du Pasquier, but they gave him little credit and did not adopt his terminology.[47] Verhulst’s priority was acknowledged and the term “logistic” revived by Udny Yule in 1925 and has been followed since.[48] Pearl and Reed first applied the model to the population of the United States, and also initially fitted the curve by making it pass through three points; as with Verhulst, this again yielded poor results.[49]
In the 1930s, the probit model was developed and systematized by Chester Ittner Bliss, who coined the term “probit” in Bliss (1934), and by John Gaddum in Gaddum (1933), and the model fit by maximum likelihood estimation by Ronald A. Fisher in Fisher (1935), as an addendum to Bliss’s work. The probit model was principally used in bioassay, and had been preceded by earlier work dating to 1860; see Probit model § History. The probit model influenced the subsequent development of the logit model and these models competed with each other.[50]
The logistic model was likely first used as an alternative to the probit model in bioassay by Edwin Bidwell Wilson and his student Jane Worcester in Wilson & Worcester (1943).[51] However, the development of the logistic model as a general alternative to the probit model was principally due to the work of Joseph Berkson over many decades, beginning in Berkson (1944), where he coined “logit”, by analogy with “probit”, and continuing through Berkson (1951) and following years.[52] The logit model was initially dismissed as inferior to the probit model, but “gradually achieved an equal footing with the logit”,[53] particularly between 1960 and 1970. By 1970, the logit model achieved parity with the probit model in use in statistics journals and thereafter surpassed it. This relative popularity was due to the adoption of the logit outside of bioassay, rather than displacing the probit within bioassay, and its informal use in practice; the logit’s popularity is credited to the logit model’s computational simplicity, mathematical properties, and generality, allowing its use in varied fields.[3]
Various refinements occurred during that time, notably by David Cox, as in Cox (1958).[4]
The multinomial logit model was introduced independently in Cox (1966) and Theil (1969), which greatly increased the scope of application and the popularity of the logit model.[54] In 1973 Daniel McFadden linked the multinomial logit to the theory of discrete choice, specifically Luce’s choice axiom, showing that the multinomial logit followed from the assumption of independence of irrelevant alternatives and interpreting odds of alternatives as relative preferences;[55] this gave a theoretical foundation for the logistic regression.[54]
Extensions[edit]
There are large numbers of extensions:
- Multinomial logistic regression (or multinomial logit) handles the case of a multi-way categorical dependent variable (with unordered values, also called “classification”). Note that the general case of having dependent variables with more than two values is termed polytomous regression.
- Ordered logistic regression (or ordered logit) handles ordinal dependent variables (ordered values).
- Mixed logit is an extension of multinomial logit that allows for correlations among the choices of the dependent variable.
- An extension of the logistic model to sets of interdependent variables is the conditional random field.
- Conditional logistic regression handles matched or stratified data when the strata are small. It is mostly used in the analysis of observational studies.
Software[edit]
Most statistical software can do binary logistic regression.
- SPSS
- [1] for basic logistic regression.
- Stata
- SAS
- PROC LOGISTIC for basic logistic regression.
- PROC CATMOD when all the variables are categorical.
- PROC GLIMMIX for multilevel model logistic regression.
- R
glmin the stats package (using family = binomial)[56]lrmin the rms package- GLMNET package for an efficient implementation regularized logistic regression
- lmer for mixed effects logistic regression
- Rfast package command
gm_logisticfor fast and heavy calculations involving large scale data. - arm package for bayesian logistic regression
- Python
Logitin the Statsmodels module.LogisticRegressionin the scikit-learn module.LogisticRegressorin the TensorFlow module.- Full example of logistic regression in the Theano tutorial [2]
- Bayesian Logistic Regression with ARD prior code, tutorial
- Variational Bayes Logistic Regression with ARD prior code , tutorial
- Bayesian Logistic Regression code, tutorial
- NCSS
- Logistic Regression in NCSS
- Matlab
mnrfitin the Statistics and Machine Learning Toolbox (with “incorrect” coded as 2 instead of 0)fminunc/fmincon, fitglm, mnrfit, fitclinear, mlecan all do logistic regression.
- Java (JVM)
- LibLinear
- Apache Flink
- Apache Spark
- SparkML supports Logistic Regression
- FPGA
Logistic Regresesion IP corein HLS for FPGA.
Notably, Microsoft Excel’s statistics extension package does not include it.
See also[edit]
- Logistic function
- Discrete choice
- Jarrow–Turnbull model
- Limited dependent variable
- Multinomial logit model
- Ordered logit
- Hosmer–Lemeshow test
- Brier score
- mlpack – contains a C++ implementation of logistic regression
- Local case-control sampling
- Logistic model tree
References[edit]
- ^ Tolles, Juliana; Meurer, William J (2016). “Logistic Regression Relating Patient Characteristics to Outcomes”. JAMA. 316 (5): 533–4. doi:10.1001/jama.2016.7653. ISSN 0098-7484. OCLC 6823603312. PMID 27483067.
- ^ a b c d e f g h i j k Hosmer, David W.; Lemeshow, Stanley (2000). Applied Logistic Regression (2nd ed.). Wiley. ISBN 978-0-471-35632-5.[page needed]
- ^ a b Cramer 2002, p. 10–11.
- ^ a b Walker, SH; Duncan, DB (1967). “Estimation of the probability of an event as a function of several independent variables”. Biometrika. 54 (1/2): 167–178. doi:10.2307/2333860. JSTOR 2333860.
- ^ Cramer 2002, p. 8.
- ^ Boyd, C. R.; Tolson, M. A.; Copes, W. S. (1987). “Evaluating trauma care: The TRISS method. Trauma Score and the Injury Severity Score”. The Journal of Trauma. 27 (4): 370–378. doi:10.1097/00005373-198704000-00005. PMID 3106646.
- ^ Kologlu, M.; Elker, D.; Altun, H.; Sayek, I. (2001). “Validation of MPI and PIA II in two different groups of patients with secondary peritonitis”. Hepato-Gastroenterology. 48 (37): 147–51. PMID 11268952.
- ^ Biondo, S.; Ramos, E.; Deiros, M.; Ragué, J. M.; De Oca, J.; Moreno, P.; Farran, L.; Jaurrieta, E. (2000). “Prognostic factors for mortality in left colonic peritonitis: A new scoring system”. Journal of the American College of Surgeons. 191 (6): 635–42. doi:10.1016/S1072-7515(00)00758-4. PMID 11129812.
- ^ Marshall, J. C.; Cook, D. J.; Christou, N. V.; Bernard, G. R.; Sprung, C. L.; Sibbald, W. J. (1995). “Multiple organ dysfunction score: A reliable descriptor of a complex clinical outcome”. Critical Care Medicine. 23 (10): 1638–52. doi:10.1097/00003246-199510000-00007. PMID 7587228.
- ^ Le Gall, J. R.; Lemeshow, S.; Saulnier, F. (1993). “A new Simplified Acute Physiology Score (SAPS II) based on a European/North American multicenter study”. JAMA. 270 (24): 2957–63. doi:10.1001/jama.1993.03510240069035. PMID 8254858.
- ^ a b David A. Freedman (2009). Statistical Models: Theory and Practice. Cambridge University Press. p. 128.
- ^ Truett, J; Cornfield, J; Kannel, W (1967). “A multivariate analysis of the risk of coronary heart disease in Framingham”. Journal of Chronic Diseases. 20 (7): 511–24. doi:10.1016/0021-9681(67)90082-3. PMID 6028270.
- ^ Harrell, Frank E. (2001). Regression Modeling Strategies (2nd ed.). Springer-Verlag. ISBN 978-0-387-95232-1.
- ^ M. Strano; B.M. Colosimo (2006). “Logistic regression analysis for experimental determination of forming limit diagrams”. International Journal of Machine Tools and Manufacture. 46 (6): 673–682. doi:10.1016/j.ijmachtools.2005.07.005.
- ^ Palei, S. K.; Das, S. K. (2009). “Logistic regression model for prediction of roof fall risks in bord and pillar workings in coal mines: An approach”. Safety Science. 47: 88–96. doi:10.1016/j.ssci.2008.01.002.
- ^ Berry, Michael J.A (1997). Data Mining Techniques For Marketing, Sales and Customer Support. Wiley. p. 10.
- ^ “How to Interpret Odds Ratio in Logistic Regression?”. Institute for Digital Research and Education.
- ^ Everitt, Brian (1998). The Cambridge Dictionary of Statistics. Cambridge, UK New York: Cambridge University Press. ISBN 978-0521593465.
- ^ For example, the indicator function in this case could be defined as
- ^ Malouf, Robert (2002). “A comparison of algorithms for maximum entropy parameter estimation”. Proceedings of the Sixth Conference on Natural Language Learning (CoNLL-2002). pp. 49–55. doi:10.3115/1118853.1118871.
- ^ a b c d e f g Menard, Scott W. (2002). Applied Logistic Regression (2nd ed.). SAGE. ISBN 978-0-7619-2208-7.[page needed]
- ^ Gourieroux, Christian; Monfort, Alain (1981). “Asymptotic Properties of the Maximum Likelihood Estimator in Dichotomous Logit Models”. Journal of Econometrics. 17 (1): 83–97. doi:10.1016/0304-4076(81)90060-9.
- ^ Park, Byeong U.; Simar, Léopold; Zelenyuk, Valentin (2017). “Nonparametric estimation of dynamic discrete choice models for time series data” (PDF). Computational Statistics & Data Analysis. 108: 97–120. doi:10.1016/j.csda.2016.10.024.
- ^ See e.g.. Murphy, Kevin P. (2012). Machine Learning – A Probabilistic Perspective. The MIT Press. pp. 245pp. ISBN 978-0-262-01802-9.
- ^ Van Smeden, M.; De Groot, J. A.; Moons, K. G.; Collins, G. S.; Altman, D. G.; Eijkemans, M. J.; Reitsma, J. B. (2016). “No rationale for 1 variable per 10 events criterion for binary logistic regression analysis”. BMC Medical Research Methodology. 16 (1): 163. doi:10.1186/s12874-016-0267-3. PMC 5122171. PMID 27881078.
- ^ Peduzzi, P; Concato, J; Kemper, E; Holford, TR; Feinstein, AR (December 1996). “A simulation study of the number of events per variable in logistic regression analysis”. Journal of Clinical Epidemiology. 49 (12): 1373–9. doi:10.1016/s0895-4356(96)00236-3. PMID 8970487.
- ^ Vittinghoff, E.; McCulloch, C. E. (12 January 2007). “Relaxing the Rule of Ten Events per Variable in Logistic and Cox Regression”. American Journal of Epidemiology. 165 (6): 710–718. doi:10.1093/aje/kwk052. PMID 17182981.
- ^ van der Ploeg, Tjeerd; Austin, Peter C.; Steyerberg, Ewout W. (2014). “Modern modelling techniques are data hungry: a simulation study for predicting dichotomous endpoints”. BMC Medical Research Methodology. 14: 137. doi:10.1186/1471-2288-14-137. PMC 4289553. PMID 25532820.
- ^ a b Harrell, Frank E. (2015). Regression Modeling Strategies. Springer Series in Statistics (2nd ed.). New York; Springer. doi:10.1007/978-3-319-19425-7. ISBN 978-3-319-19424-0.
- ^ Greene, William N. (2003). Econometric Analysis (Fifth ed.). Prentice-Hall. ISBN 978-0-13-066189-0.
- ^ a b c d e f g h i j Cohen, Jacob; Cohen, Patricia; West, Steven G.; Aiken, Leona S. (2002). Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences (3rd ed.). Routledge. ISBN 978-0-8058-2223-6.[page needed]
- ^ Allison, Paul D. “Measures of fit for logistic regression” (PDF). Statistical Horizons LLC and the University of Pennsylvania.
- ^ Hosmer, D.W. (1997). “A comparison of goodness-of-fit tests for the logistic regression model”. Stat Med. 16 (9): 965–980. doi:10.1002/(sici)1097-0258(19970515)16:9<965::aid-sim509>3.3.co;2-f. PMID 9160492.
- ^ Harrell, Frank E. (2010). Regression Modeling Strategies: With Applications to Linear Models, Logistic Regression, and Survival Analysis. New York: Springer. ISBN 978-1-4419-2918-1.[page needed]
- ^ a b https://class.stanford.edu/c4x/HumanitiesScience/StatLearning/asset/classification.pdf slide 16
- ^ a b Mount, J. (2011). “The Equivalence of Logistic Regression and Maximum Entropy models” (PDF). Retrieved Feb 23, 2022.
- ^ Ng, Andrew (2000). “CS229 Lecture Notes” (PDF). CS229 Lecture Notes: 16–19.
- ^ Rodríguez, G. (2007). Lecture Notes on Generalized Linear Models. pp. Chapter 3, page 45.
- ^ Gareth James; Daniela Witten; Trevor Hastie; Robert Tibshirani (2013). An Introduction to Statistical Learning. Springer. p. 6.
- ^ Pohar, Maja; Blas, Mateja; Turk, Sandra (2004). “Comparison of Logistic Regression and Linear Discriminant Analysis: A Simulation Study”. Metodološki Zvezki. 1 (1).
- ^ Cramer 2002, pp. 3–5.
- ^ Verhulst, Pierre-François (1838). “Notice sur la loi que la population poursuit dans son accroissement” (PDF). Correspondance Mathématique et Physique. 10: 113–121. Retrieved 3 December 2014.
- ^ Cramer 2002, p. 4, “He did not say how he fitted the curves.”
- ^ Verhulst, Pierre-François (1845). “Recherches mathématiques sur la loi d’accroissement de la population” [Mathematical Researches into the Law of Population Growth Increase]. Nouveaux Mémoires de l’Académie Royale des Sciences et Belles-Lettres de Bruxelles. 18. Retrieved 2013-02-18.
- ^ Cramer 2002, p. 4.
- ^ Cramer 2002, p. 7.
- ^ Cramer 2002, p. 6.
- ^ Cramer 2002, p. 6–7.
- ^ Cramer 2002, p. 5.
- ^ Cramer 2002, p. 7–9.
- ^ Cramer 2002, p. 9.
- ^ Cramer 2002, p. 8, “As far as I can see the introduction of the logistics as an alternative to the normal probability function is the work of a single person, Joseph Berkson (1899–1982), …”
- ^ Cramer 2002, p. 11.
- ^ a b Cramer, p. 13.
- ^ McFadden, Daniel (1973). “Conditional Logit Analysis of Qualitative Choice Behavior” (PDF). In P. Zarembka (ed.). Frontiers in Econometrics. New York: Academic Press. pp. 105–142. Archived from the original (PDF) on 2018-11-27. Retrieved 2019-04-20.
- ^ Gelman, Andrew; Hill, Jennifer (2007). Data Analysis Using Regression and Multilevel/Hierarchical Models. New York: Cambridge University Press. pp. 79–108. ISBN 978-0-521-68689-1.
Further reading[edit]
- Cox, David R. (1958). “The regression analysis of binary sequences (with discussion)”. J R Stat Soc B. 20 (2): 215–242. JSTOR 2983890.
- Cox, David R. (1966). “Some procedures connected with the logistic qualitative response curve”. In F. N. David (1966) (ed.). Research Papers in Probability and Statistics (Festschrift for J. Neyman). London: Wiley. pp. 55–71.
- Cramer, J. S. (2002). The origins of logistic regression (PDF) (Technical report). Vol. 119. Tinbergen Institute. pp. 167–178. doi:10.2139/ssrn.360300.
- Published in: Cramer, J. S. (2004). “The early origins of the logit model”. Studies in History and Philosophy of Science Part C: Studies in History and Philosophy of Biological and Biomedical Sciences. 35 (4): 613–626. doi:10.1016/j.shpsc.2004.09.003.
- Theil, Henri (1969). “A Multinomial Extension of the Linear Logit Model”. International Economic Review. 10 (3): 251–59. doi:10.2307/2525642. JSTOR 2525642.
- Wilson, E.B.; Worcester, J. (1943). “The Determination of L.D.50 and Its Sampling Error in Bio-Assay”. Proceedings of the National Academy of Sciences of the United States of America. 29 (2): 79–85. Bibcode:1943PNAS…29…79W. doi:10.1073/pnas.29.2.79. PMC 1078563. PMID 16588606.
- Agresti, Alan. (2002). Categorical Data Analysis. New York: Wiley-Interscience. ISBN 978-0-471-36093-3.
- Amemiya, Takeshi (1985). “Qualitative Response Models”. Advanced Econometrics. Oxford: Basil Blackwell. pp. 267–359. ISBN 978-0-631-13345-2.
- Balakrishnan, N. (1991). Handbook of the Logistic Distribution. Marcel Dekker, Inc. ISBN 978-0-8247-8587-1.
- Gouriéroux, Christian (2000). “The Simple Dichotomy”. Econometrics of Qualitative Dependent Variables. New York: Cambridge University Press. pp. 6–37. ISBN 978-0-521-58985-7.
- Greene, William H. (2003). Econometric Analysis, fifth edition. Prentice Hall. ISBN 978-0-13-066189-0.
- Hilbe, Joseph M. (2009). Logistic Regression Models. Chapman & Hall/CRC Press. ISBN 978-1-4200-7575-5.
- Hosmer, David (2013). Applied logistic regression. Hoboken, New Jersey: Wiley. ISBN 978-0470582473.
- Howell, David C. (2010). Statistical Methods for Psychology, 7th ed. Belmont, CA; Thomson Wadsworth. ISBN 978-0-495-59786-5.
- Peduzzi, P.; J. Concato; E. Kemper; T.R. Holford; A.R. Feinstein (1996). “A simulation study of the number of events per variable in logistic regression analysis”. Journal of Clinical Epidemiology. 49 (12): 1373–1379. doi:10.1016/s0895-4356(96)00236-3. PMID 8970487.
- Berry, Michael J.A.; Linoff, Gordon (1997). Data Mining Techniques For Marketing, Sales and Customer Support. Wiley.
External links[edit]
Media related to Logistic regression at Wikimedia Commons
- Econometrics Lecture (topic: Logit model) on YouTube by Mark Thoma
- Logistic Regression tutorial
- mlelr: software in C for teaching purposes
Логистическая регрессия является наиболее важным (и, вероятно,
наиболее часто используемым) элементом класса моделей, называемых
обобщенными линейными моделями. В отличие от линейной регрессии,
логистическая регрессия может непосредственно предсказывать значения,
которые ограничены интервалом (0,1), таким как вероятности. Это новый
метод предсказания вероятностей или коэффициентов, и, подобно линейной
регрессии, коэффициенты модели логистической регрессии можно
рассматривать как рекомендации. Это также хороший первый выбор для задач
двоичной классификации.
В этом разделе мы будем использовать пример из медицинской
классификации (прогнозирующий, потребуется ли новорожденному
дополнительное медицинское обслуживание) для проработки всех этапов
создания и использования модели логистической регрессии.
Понимая логистическую регрессию
Логистическая регрессия предсказывает вероятность того, что объект
принадлежит определенной категории, например, вероятность того, что
полет будет задержан. Когда x[i,] представляет собой строку входных
данных (например, место и время полета, время года, погода,
авиаперевозчик), логистическая регрессия находит фиктивную функцию f(x)
такую, что
[P_{y_{[i]} в классе} sim f_{(x_{[i,]})}
= s(a+b_{[1]} x_{[i,1]} + … b_{[n]} x_{[i,n]})]
Здесь s (z) – так называемая сигмоидальная функция, определяемая как
(s(z) = frac{1}{(1 + exp(z))}). Если
(y[i]) – вероятности того, что (x[i,]) принадлежат интересующему классу (в
нашем примере, вероятность того, что полет с определенными
характеристиками будет задержан), тогда задача подгонки состоит в том,
чтобы найти (b[1 ]), …, (b[n]), для которых (f(x[i,])) является наилучшей оценкой (y[i]).R предоставляет простую команду для
поиска этих коэффициентов: glm (). Обратите внимание, что нам не нужно
указывать y[i], которые являются оценками вероятности для запуска glm
(); Метод обучения требует только y[i], которые говорят, находится ли
данный учебный пример в целевом классе.
Сигмоидная функция отображает действительные числа в интервал (0,1)
или вероятности. Обратной к сигмоидной является logit функция, которая
определяется как (log(frac{p}{(1-p)})), где p –
вероятность. Отношение p / (1-p) известно как вероятность(odds), поэтому
в нашем примере про полеты logit представляет собой список вероятностей
(или логарифмических коэффициентов), того что полет будет задерживаться.
Другими словами, вы можете думать о логистической регрессии как линейной
регрессии, которая находит логарифмические коэффициенты вероятност
интересующего вас события.
В частности, логистическая регрессия предполагает, что logit(y)
является линейным к значениям x. Как и линейная регрессия, логистическая
регрессия найдет наилучшие коэффициенты для прогнозирования y, включая
поиск выгодных комбинаций и исключений переменных из модели, когда часть
независимых переменных коррелированы.
В качестве примерного задания, представьте, что вы работаете в
больнице. Цель состоит в том, чтобы разработать план снабжения
неонатального оборудования для оказания неотложной помощи в родильных
отделениях. Новорожденных младенцев оценивают через 1 и 5 минут после
рождения, используя так называемый тест «Апгар», который предназначен
для определения того, нуждается ли ребенок в неотложной или экстренной
медицинской помощи. Ребенку, который получил оценку ниже 7 (по шкале от
0 до 10) по шкале Апгара, требуется дополнительное внимание.
Такого рода дети встречаются довольно редко, поэтому больницам не
хочется тратиться на дополнительное аварийно-спасательное оборудование
для каждой поставки. С другой стороны, детям в группе риска может
понадобиться помощь при этом очень быстро нужно, поэтому превентивная
подготовка может спасти жизнь. Целью данного исследования является
попытка выявление ситуаций с повышенной вероятностью риска загодя, для
того чтобы ресурсы были распределены точно и загодя.
sdata = read.csv("https://www.dropbox.com/s/lx9celfieswn4vq/NatalRisk.csv?dl=1")
head(sdata)## X PWGT UPREVIS CIG_REC GESTREC3 DPLURAL ULD_MECO ULD_PRECIP ULD_BREECH
## 1 2136 155 14 FALSE >= 37 weeks single TRUE FALSE FALSE
## 2 2137 140 13 FALSE >= 37 weeks single FALSE FALSE FALSE
## 3 2138 151 15 FALSE >= 37 weeks single FALSE FALSE FALSE
## 4 2139 118 4 FALSE >= 37 weeks single FALSE FALSE FALSE
## 5 2140 134 11 FALSE >= 37 weeks single FALSE FALSE FALSE
## 6 2141 117 18 FALSE >= 37 weeks single TRUE FALSE FALSE
## URF_DIAB URF_CHYPER URF_PHYPER URF_ECLAM atRisk DBWT ORIGRANDGROUP
## 1 FALSE FALSE FALSE FALSE FALSE 3714 2
## 2 FALSE FALSE FALSE FALSE FALSE 3715 4
## 3 FALSE FALSE FALSE FALSE FALSE 3447 2
## 4 FALSE FALSE FALSE FALSE FALSE 3175 6
## 5 FALSE FALSE FALSE FALSE FALSE 4038 10
## 6 FALSE FALSE FALSE FALSE FALSE 3410 7train <- sdata[sdata$ORIGRANDGROUP<=5,]
test <- sdata[sdata$ORIGRANDGROUP>5,]Командой для построения модели логистической регрессии в R является
модель glm(). В нашем случае зависимой переменной Y является логическая
(булевая) переменная atRisk; все другие переменные в табл. 7.1
представлены независимыми переменными х. Формула для построения модели
для прогнозирования atRisk с помощью этих переменных достаточно длинна
для линейной записи; поэтому создадим формулу командами показаными в
следующем листинге.
complications <- c("ULD_MECO","ULD_PRECIP","ULD_BREECH")
riskfactors <- c("URF_DIAB", "URF_CHYPER", "URF_PHYPER",
"URF_ECLAM")
y <- "atRisk"
x <- c("PWGT",
"UPREVIS",
"CIG_REC",
"GESTREC3",
"DPLURAL",
complications,
riskfactors)
fmla <- paste(y, paste(x, collapse="+"), sep="~")
model <- glm(fmla, data=train, family=binomial(link="logit"))Параметры функции glm(), family определяет предполагаемое
распределение зависимой переменной Y. В нашем случае, мы моделируем Y
как биномиальное распределение, это как если бы мы моделировали
результаты броски монеты, вероятность выпадения решки которых зависит от
x. Параметр “ссылка” – link поясняет функции каким образом привести
модель к линейному виду — преобразует Y через преобразованием указанным
в параметре link, а затем моделируем полученное значение линейной
функции от переменных x. Комбинирование параметров link и family дают
широчайший спектр обобщенных линейных моделей (например, Пуассона, или
пробит). Здесь мы будем обсуждать только логистические модели.
Создание прогнозов с логистической моделью аналогично прогнозированию
с использованием линейной модели – используйте функцию predict ().
train$pred <- predict(model, newdata=train, type="response")
test$pred <- predict(model, newdata=test, type="response")Мы снова сохранили прогнозы для обучающих и тестовых наборов в
качестве столбца pred в соответствующих таблицах Обратите внимание на
дополнительный тип параметра = “response”(«ответ»). Он сообщает функции
predict () возвращать предсказанные вероятности y. Если вы не укажете
type = “response”, то по умолчанию функция predict () вернет вывод link
функции – logit(y).
Одно из преимуществ логистической регрессии заключается в том, что
она сохраняет предельные вероятности данных обучения. Это означает, что
если вы суммируете предсказанные вероятности для всей тренировочной
подвыборки, это количество будет равно количеству положительных
результатов (atRisk == T) в обучающем наборе. Это справедливо также для
подмножеств данных, определяемых переменными, включенными в модель.
Например, в подмножестве данных обучения, train$GESTREC == “<37
weeks” (ребенок был преждевременным), сумма прогнозируемых вероятностей
равна числу положительных примеров обучения.
Если наша цель заключается в использовании модели для классификации
новых образцов в одну из двух категорий (в данном случае – риск-группу
или не подверженную риску), мы хотим, чтобы модель давала высокие оценки
при отнесении в группу и низкие значениям в противном случае. Мы можем
проверить, так ли это, построив распределение баллов для положительных и
отрицательных случаев. Давайте сделаем это на обучающем наборе (мы также
должны построить тестовый набор, чтобы убедиться, что предсказание
аналогичного качества).
library(ggplot2)
ggplot(train, aes(x=pred, color=atRisk, linetype=atRisk)) + geom_density()В идеале мы хотели бы, чтобы распределение баллов было разделено, а
оценки отрицательных экземпляров (ЛОЖЬ) должны быть сосредоточены слева,
а распределение для положительных экземпляров должно быть сосредоточено
справа. В данном случае оба распределения сосредоточены слева, что
означает, что как положительные, так и отрицательные случаи оцениваются
на низком уровне. Это не удивительно, поскольку положительные случаи
(те, в которых ребенок находится в группе риска) редки (около 1,8% от
всех родов в наборе данных). Распределение оценок для отрицательных
случаев уменьшается раньше, чем распределение для положительных
экземпляров. Это означает, что модель выявила субпопуляции в данных, где
процент новорожденных с повышенным риском выше среднего.
Чтобы использовать модель в качестве классификатора, вы должны
выбрать пороговое значение; Баллы выше порога будут классифицироваться
как положительные,а те, что ниже, как отрицательные. Когда вы выбираете
пороговое значение, вы пытаетесь сбалансировать точность классификатора
(какая доля прогнозируемых положительных результатов являются истинно
положительными) и его отзыв (сколько из истинных положительных значений
находит классификатор)
Если распределения баллов положительных и отрицательных примеров
хорошо разделены, как показано на рисунке, мы можем выбрать
соответствующий порог в «долине» между двумя пиками. В данном случае два
распределения не очень хорошо разделены, что указывает на то, что модель
не может построить классификатор, который одновременно обеспечивает
хороший отзыв и хорошую точность.Но мы можем создать классификатор,
который идентифицирует подмножество ситуаций с более высоким уровнем
рождаемости в группе риска, поэтому предварительное выделение ресурсов
для этих ситуаций может быть рекомендовано. Мы будем называть отношение
точности классификатора к средней скорости срабатывания коэффициентом
обогащения. Чем выше мы устанавливаем порог, тем более точным будет
классификатор (мы определим набор ситуаций с гораздо более высоким чем
средний уровнем точности определения родов с повышенным
риском);одновременно мы также будем чаще пропускать(не классифицировать)
ситуации, связанные с риском. При выборе порога мы будем использовать
обучающий набор, так как выбор порога является частью построения
классификатора.
Затем мы можем использовать тестовый набор для оценки
производительности классифицируюшей модели . Чтобы помочь подобрать
порог, мы можем использовать график, см ниже, который показывает
обвременно обогащение и отзыв как функции от пороговго значения. На
рисунке, вы видите, что более высокие пороги приводят к более точной
классификации, за счет упущения(неправильной классификации) большого
количества случаев; Более низкий порог выявит больше критических
ситуаций при родах за счет множества ложных срабатываний. Наилучший
компромисс между точностью и отзывом зависит от объема ресурсов, которым
располагает больница для распределения и сколько их можно оставить в
резерве (или перераспределить) для ситуаций, которые пропустил
классификатор. Хорошим выбором может стать порог в 0,02 (что, кстати, и
составляет общий показатель рождаемости в группах риска). Получающийся
классификатор будет идентифицировать набор потенциальных ситуаций с
повышенным риском, который обнаруживают примерно половину всех реальных
ситуаций, связанных с риском, с истинным положительным уровнем в 2,5
раза выше, чем в среднем(обнаруживаются такие ситуации).
library(ROCR)
library(ggplot2)
library(gplots)##
## Присоединяю пакет: 'gplots'## Следующий объект скрыт от 'package:stats':
##
## lowesslibrary(grid) # Load grid library (you’ll need this for the nplot function below).
predObj <- prediction(train$pred, train$atRisk) # Create ROCR prediction object
precObj <- performance(predObj, measure="prec") # Create ROCR object to calculate precision as a function of threshold
recObj <- performance(predObj, measure="rec")# Create ROCR object to calculate recall as a function of threshold.
precision <- (precObj@y.values)[[1]] # ROCR objects are what R calls S4 objects; the slots (or fields) of an S4 object are stored as lists within the object. You extract the slots from an S4 object using @ notation.
prec.x <- (precObj@x.values)[[1]] # The x values (thresholds) are the same in both predObj and recObj, so you only need to extract them once.
recall <- (recObj@y.values)[[1]]
rocFrame <- data.frame(threshold=prec.x, precision=precision, recall = recall) # Build data frame with thresholds, precision, and recall
nplot <- function(plist) { #Function to plot multiple plots on one page (stacked).
n <- length(plist)
grid.newpage()
pushViewport(viewport(layout=grid.layout(n,1)))
vplayout=function(x,y) {viewport(layout.pos.row=x, layout.pos.col=y)}
for(i in 1:n) {
print(plist[[i]], vp=vplayout(i,1))
}
}
pnull <- mean(as.numeric(train$atRisk)) # Calculate rate of at-risk births in the training set.
p1 <- ggplot(rocFrame, aes(x=threshold)) + # Plot enrichment rate as a function of threshold.
geom_line(aes(y=precision/pnull)) +
coord_cartesian(xlim = c(0,0.05), ylim=c(0,10) )
p2 <- ggplot(rocFrame, aes(x=threshold)) + # Plot recall as a function of threshold
geom_line(aes(y=recall)) +
coord_cartesian(xlim = c(0,0.05) )
nplot(list(p1, p2)) #Show both plots simultaneously.Как только мы подобрали соответствующий порог, мы можем оценить
результирующий классификатор, посмотрев на таблицу показателей точности.
Давайте используем тестовый набор для оценки классификатора с порогом
0,02.
ctab.test <- table(pred=test$pred>0.02, atRisk=test$atRisk)
ctab.test## atRisk
## pred FALSE TRUE
## FALSE 9487 93
## TRUE 2405 116precision <- ctab.test[2,2]/sum(ctab.test[2,])
precision## [1] 0.04601349recall <- ctab.test[2,2]/sum(ctab.test[,2])
recall## [1] 0.5550239enrich <- precision/mean(as.numeric(test$atRisk))
enrich## [1] 2.664159Получающийся классификатор является низкоточным, но идентифицирует
набор потенциальных случаев риска, который содержит 55,5% истинных
положительных случаев в тестовом наборе, что в 2,66 раза превышает общее
среднее. Этот результат хорошо согласуется с результатами тренировочного
набора.
Коэффициенты модели логистической регрессии кодируют отношения между
входными переменными и выводом путем, подобным тому, как это делают
коэффициенты линейной регрессионной модели. Вы можете получить
коэффициенты модели с помощью:
coefficients(model)## (Intercept) PWGT UPREVIS
## -2.86700629 0.00376166 -0.06328943
## CIG_RECTRUE GESTREC3>= 37 weeks DPLURALtriplet or higher
## 0.31316930 -1.54518311 1.39419294
## DPLURALtwin ULD_MECOTRUE ULD_PRECIPTRUE
## 0.31231871 0.81842627 0.19172008
## ULD_BREECHTRUE URF_DIABTRUE URF_CHYPERTRUE
## 0.74923672 -0.34646672 0.56002503
## URF_PHYPERTRUE URF_ECLAMTRUE
## 0.16159872 0.49806435Отрицательные коэффициенты, которые являются статистически значимыми,
соответствуют переменным, которые отрицательно коррелируют с шансами (и,
следовательно, с вероятностью) положительного результата (т.е. того, что
ребенок находится в группе риска). Положительные коэффициенты, которые
являются статистически значимыми, положительно коррелируют с шансами
положительного результата. Как и в случае линейной регрессии, каждая
категориальная переменная расширяется до набора индикаторных переменных.
Если исходная переменная имеет n уровней, будет n-1 индикаторных
переменных; оставшийся 1 уровень включен в свободный член.
Например, переменная DPLURAL имеет три уровня, соответствующих родам
одного ребенка, двойняшкам и тройняшкам или выше. Модель логистической
регрессии имеет два соответствующих коэффициента: DPLURALtwin и
DPLURALtriplet или выше. Контрольный уровень – обычные роды. Оба
коэффициента DPLURAL являются положительными, что указывает на то, что
роды нескольких детей имеют более высокие шансы быть подверженными
риску, чем обычные роды, при прочих равных условиях.
ИНТЕРПРЕТИРУЯ КОЭФФИЦИЕНТЫ
Интерпретация значений коэффициентов является немного более сложным,
в случае с логистической регрессией, чем в случае с линейной регрессией.
Если коэффициент для переменной x[,k] равен b[k], то коэффициенты
положительного результата умножаются на коэффициент exp(b[k]) для
каждого изменения x[,k] на единицу.
Коэффициент для GESTREC3 <37 недель (для недоношенного ребенка)
составляет 1,545183. Так что для недоношенного ребенка вероятность
оказаться в опасности равна exp(1,545183) = 4,68883 раз выше по
сравнению с младенцем, рожденным в течение полного срока, при условии,
что все остальные входные переменные остаются неизменными. В качестве
примера предположим, что для полноценного ребенка с определенными
характеристиками существует вероятность 1% риска (вероятность равна p /
(1-p) или 0,01 / 0,99 = 0,0101); Тогда шансы(odds) для недоношенного
малыша с такими же характеристиками составляют 0,0101 * 4,68883 = 0,047.
Это соответствует вероятности риска = шанс/ (1 + шанс), или 0,047 /
1,047 – около 4,5%.
Аналогичным образом, коэффициент для UPREVIS (число пренатальных
медицинских визитов) составляет около – 0,06. Это означает, что каждый
визит в пренатальный период снижает коэффициент риска для младенца,
подверженного риску, с коэффициентом exp(-0,06) или примерно 0,94.
Предположим, что мать нашего недоношенного ребенка не сделала
предродовых визитов; Ребенок в той же ситуации, чья мать совершила три
дородовых визита на осмотр, будет иметь шансы на риск около
0,047×0,94×0,94×0,94 = 0,039. Это соответствует вероятности оказаться
под угрозой 3,75%.
Таким образом, общим советом в данном случае может быть особый взгляд
на преждевременные роды (и множественные роды), а также поощрять будущих
матерей совершать регулярные пренатальные посещения
###Считывание сводки модели и определение коэффициентов
Как мы уже упоминали ранее, выводам о значениях коэффициентов можно
доверять только , если значения коэффициентов являются статистически
значимыми. Мы также хотим убедиться, что модель действительно что-то
объясняет. Диагностика в summary модели поможет нам определить некоторые
факты о качестве модели.
summary(model)##
## Call:
## glm(formula = fmla, family = binomial(link = "logit"), data = train)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.9732 -0.1818 -0.1511 -0.1358 3.2641
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -2.867006 0.285007 -10.059 < 2e-16 ***
## PWGT 0.003762 0.001487 2.530 0.011417 *
## UPREVIS -0.063289 0.015252 -4.150 3.33e-05 ***
## CIG_RECTRUE 0.313169 0.187230 1.673 0.094398 .
## GESTREC3>= 37 weeks -1.545183 0.140795 -10.975 < 2e-16 ***
## DPLURALtriplet or higher 1.394193 0.498866 2.795 0.005194 **
## DPLURALtwin 0.312319 0.241088 1.295 0.195163
## ULD_MECOTRUE 0.818426 0.235798 3.471 0.000519 ***
## ULD_PRECIPTRUE 0.191720 0.357680 0.536 0.591951
## ULD_BREECHTRUE 0.749237 0.178129 4.206 2.60e-05 ***
## URF_DIABTRUE -0.346467 0.287514 -1.205 0.228187
## URF_CHYPERTRUE 0.560025 0.389678 1.437 0.150676
## URF_PHYPERTRUE 0.161599 0.250003 0.646 0.518029
## URF_ECLAMTRUE 0.498064 0.776948 0.641 0.521489
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 2698.7 on 14211 degrees of freedom
## Residual deviance: 2463.0 on 14198 degrees of freedom
## AIC: 2491
##
## Number of Fisher Scoring iterations: 7В линейной регрессии остатки представляют собой вектор различий между
истинными значениями моделируемой величины и прогнозируемыми выходными
значениями (ошибки). В логистической регрессии остатки отклонений
связаны с логарифмическими вероятностями наблюдения истинного результата
с учетом предсказанной вероятности этого результата. Идея
логарифмического правдоподобия заключается в том, что положительные
экземпляры (y) должны иметь высокую
вероятность возникновения (p) в
модели; Отрицательные экземпляры должны иметь низкую вероятность
возникновения (или, иначе говоря, ((1-p_{y})) должны быть большими). Функция
логарифмического правдоподобия возвращает «совпадение» между результатом
(y) и предсказанной вероятностью
(p_{y}) и наказывает несоответствия
(высокий (p_{y}) для отрицательных
случаев и наоборот).
pred <- predict(model, newdata=train, type="response")
llcomponents <- function(y, py) { y*log(py) + (1-y)*log(1-py)} # Function to return the log likelihoods for each data point. Argument y is the true outcome
# (as a numeric variable, 0/1); argument py is the predicted probability.
edev <- sign(as.numeric(train$atRisk) - pred) * sqrt(-2*llcomponents(as.numeric(train$atRisk), pred)) # Calculate deviance result
summary(edev)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -0.9732 -0.1818 -0.1511 -0.1244 -0.1358 3.2641Модель линейной регрессии строят, минимизируя сумму квадратов
оклонений; модели логистической регрессии можно построить, минимизируя
сумму квадратов отклонений остатков, что эквивалентно максимизации
логарифмической правдоподобия данных с учетом модели.
Логистические модели также могут использоваться для явного вычисления
коэффициентов: для нескольких групп идентичных точек данных (идентичных,
кроме исхода) прогнозируют скорость положительных результатов в каждой
группе. Такие данные называются сгруппированными данными. В случае
сгруппированных данных остатки отклонений могут использоваться в
качестве диагностики для подгонки модели. Вот почему остатки отклонений
включены в итоговый отчет. Мы используем негруппированные данные –
каждая точка данных в обучающем наборе потенциально уникальна. В случае
негруппированных данных диагностика подгонки модели, использующая
остатки отклонений, более недействительна.
Таблица сводных коэффициентов для логистической регрессии имеет тот
же формат, что и таблица коэффициентов для линейной регрессии Столбцы
таблицы представляют * имя коэффициента * его предсказанноее значение *
ошибка этой оценки * Оценка отличия(со знаком) коэффициента от 0
(используя стандартную ошибку как единицу расстояния) * вероятность
увидеть значение коэффициента, по крайней мере такое же большое, как мы
наблюдали, при нулевой гипотезе, что значение коэффициента действительно
0
Это последнее значение, называемое p-значением или значимостью,
указывает нам, следует ли доверять оценочному значению коэффициента.
Стандартное эмпирическое правило состоит в том, что коэффициенты с
p-значениями менее 0,05 являются надежными, хотя некоторые исследователи
предпочитают более строгие пороговые значения. По данным о рождении мы
можем видеть из сводки коэффициентов, что преждевременные роды и
рождение тройни являются сильными предикторами новорожденных,
нуждающихся в дополнительной медицинской помощи: величины коэффициентов
не являются ни пренебрежимо малыми, а значения р указывают на
значимость.
Другими переменными, которые влияют на результат, являются вес матери
(высокий вес указывают на более высокий риск, что несколько неожиданно);
Число медицинских осмотров в пренатальном периоде (чем больше посещений,
тем ниже риск); Окрашивание мекония в амниотической жидкости; И
положение головы ребенка при рождении. Так же может быть положительная
корреляция между курением матери и рождением в группе риска, но данные
не указывают на это окончательно. Ни у одной из других переменных нет
четкой связи с рождением в группе риска
Девиантность(девиация) тут тоже является показателем того, насколько
хорошо модель соответствует данным. Она равна 2-м отрицательным
логарифмическим вероятностям для набора данных, учитывая модель. Если вы
думаете о девиантности как об аналоге дисперсии, то нулевая девиантность
аналогична дисперсии данных с приблизительно средним уровнеи
положительных примеров. Девиантность отклонений аналогично
приблизительной дисперсии данных модели. Мы можем рассчитать
девиантнность как для тренировочных, так и для тестовых наборов.
loglikelihood <- function(y, py) {
sum(y * log(py) + (1-y)*log(1 - py))
}
# Function to calculate the log likelihood of a dataset. Variable y is the outcome in numeric form (1 for positive examples, 0 for negative). Variable py is
# the predicted probability that y==1.
pnull <- mean(as.numeric(train$atRisk))
pnull## [1] 0.01920912null.dev <- -2*loglikelihood(as.numeric(train$atRisk), pnull)
null.dev## [1] 2698.716model$null.deviance## [1] 2698.716pred <- predict(model, newdata=train, type="response") #Predict probabilities for training data.
resid.dev <- 2*loglikelihood(as.numeric(train$atRisk), pred) # Calculate deviance of model for training data
resid.dev## [1] -2462.992model$deviance # For training data, model deviance is stored in the slot model$deviance## [1] 2462.992testy <- as.numeric(test$atRisk) # Calculate null deviance and residual deviance for test data.
testpred <- predict(model, newdata=test,
type="response")
pnull.test <- mean(testy)
null.dev.test <- -2*loglikelihood(testy, pnull.test)
resid.dev.test <- -2*loglikelihood(testy, testpred)
pnull.test## [1] 0.0172713null.dev.test## [1] 2110.91resid.dev.test## [1] 1947.094Первое, что мы можем сделать с нулевыми и остаточными отклонениями, –
это проверить, являются ли предсказания вероятности модели лучше, чем
просто угадывать среднюю скорость срабатываний статистически. Другими
словами, является ли уменьшение отклонения от модели значимым или просто
то, что наблюдалось случайно? Это похоже на вычисление статистики
F-теста, которая сообщается для линейной регрессии. В случае
логистической регрессии тест, который вы запустите, – это тест
хи-квадрат. Чтобы сделать это, вам нужно знать степени свободы для
нулевой модели и фактической модели (о которых сообщается в резюме).
Степени свободы нулевой модели – это количество точек данных минус 1:
df.null = dim (train) [[1]] – 1. Степени свободы модели, которую вы
подгоните, – это количество точек данных минус Число коэффициентов в
модели: df.model = dim (train) [[1]] – length(model$coefficients).
Если количество точек данных в обучающем наборе велико, а df.null –
df.model мало, то вероятность разницы в отклонениях null.dev –
resid.dev, будучи такой большой, как мы наблюдали, приблизительно
распределяется как хи-квадрат со степенями свободы df.null –
df.model.
df.null <- dim(train)[[1]] - 1 # Null model has (number of data points - 1) degrees of freedom.
df.model <- dim(train)[[1]] - length(model$coefficients) # Fitted model has (number of data points - number of coefficients) degrees of freedom.
df.null## [1] 14211df.model## [1] 14198delDev <- null.dev - resid.dev
deldf <- df.null - df.model # Compute difference in deviances and difference in degrees of freedom.
p <- pchisq(delDev, deldf, lower.tail=F) # Estimate probability of seeing the observed difference in deviances under null model (the p-value)
# using chi-squared distribution.
delDev## [1] 5161.708deldf## [1] 13p## [1] 0Полезным критерием пригодности, основанным на отклонениях, является
псевдо-R-квадрат: 1 – (dev.model / dev.null). Псевдо R-квадрат является
аналогом R-квадрата для линейной регрессии. Это показатель того,
насколько отклонение «объясняется» моделью. В идеальном случае вы
хотите, чтобы псевдо-R-квадрат был близок к 1. Рассчитаем
псевдо-R-квадрат как для тестовых, так и для обучающих данных.
pr2 <- 1-(resid.dev/null.dev)
pr2.test <- 1-(resid.dev.test/null.dev.test)
print(pr2.test)## [1] 0.07760427Модель объясняет только 7,7-8,7% отклонения; Это не очень хорошая
прогностическая модель (вам следовало бы заподозрить это уже на пред
рисунке). Это говорит нам о том, что мы еще не определили все факторы,
которые фактически предсказывают рождение детей с повышенным риском.
Метод оценки Фишера представляет собой метод итеративной оптимизации,
аналогичный методу Ньютона, который использует glm() для нахождения
наилучших коэффициентов для модели логистической регрессии. Вы должны
ожидать, что он сходится примерно через шесть-восемь итераций. Если
итераций больше, чем это, тогда алгоритм может не совпадать, и модель
может оказаться недействительной.
Разделение и квази-разделение
Вероятной причиной несведение является разделение или
квази-разделение: одна из переменных модели или некоторая комбинация
переменных модели предсказывает исход отлично, по крайней мере,на
подмножестве обучающих данных. Вы могли бы подумать, что это хорошо, но
по иронии судьбы логистическая регрессия терпит неудачу, когда
переменные слишком хороши в предсказании. В идеале glm() выдаст
предупреждение, когда обнаружит разделение или квази-разделение:
К сожалению, есть ситуации, когда кажется, что никаких предупреждений
не выдается, но есть и другие предупреждающие знаки:
- Необычно большое количество итераций Фишера
- Очень большие коэффициенты, как правило, с чрезвычайно большими
стандартными ошибками - Остаточные отклонения, превышающие нулевые отклонения
Если вы видите какой-либо из этих признаков, модель подозрительна.
Чтобы попытаться решить проблему, удалите все переменные с необычно
большими коэффициентами; Они, вероятно, вызывают разделение.
Что вы должны помнить о логистической регрессии:
- Логистическая регрессия – это метод статистического моделирования
для двоичной классификации. - Сначала попробуйте логистическую регрессию, а затем более сложные
методы, если логистическая регрессия не работает достаточно хорошо. - Логистическая регрессия будет иметь проблемы с проектами с очень
большим числом переменных или категориальными переменными с очень
большим количеством уровней. - Логистическая регрессия хорошо откалибрована: она воспроизводит
предельные вероятности данных. - Логистическая регрессия может хорошо прогнозировать даже при наличии
коррелированных переменных, но коррелированные переменные понижают
качество предсказания. - Чрезмерно большие значения коэффициентов, слишком большие
стандартные ошибки в оценках коэффициента и неправильный знак
коэффициента могут быть показателями коррелированных входных
данных. - Слишком много итераций Фишера или слишком большие коэффициенты с
очень большими стандартными ошибками могут быть признаками того, что
вход или комбинация входов отлично коррелирует с вашей зависимой
переменной. Вам может потребоваться сегментировать данные для решения
этой проблемы. - gl () обеспечивает хороший набор диагностик, но повторная проверка
вашей модели на тестовых данных по-прежнему является наиболее
эффективным способом проверки качества. - Pseudo R-squared – полезная эвристика добротности
Все курсы > Оптимизация > Занятие 5
Как мы уже знаем, несмотря на название, логистическая регрессия решает задачу классификации. Сегодня мы подробно разберем принцип работы и составные части алгоритма логистической регрессии, а также построим модели с одной и несколькими независимыми переменными.
Бинарная логистическая регрессия
Задача бинарной классификации
Вернемся к задаче кредитного скоринга, про которую мы говорили, когда обсуждали принцип машинного обучения. Предположим, что мы собрали данные и выявили зависимость возвращения кредита (ось y) от возраста заемщика (ось x).
Как мы видим, в среднем более молодые заемщики реже возвращают кредит. Возникает вопрос, с помощью какой модели можно описать эту зависимость? Казалось бы, можно построить линейную регрессию таким образом, чтобы она выдавала некоторое значение и, если это значение окажется ниже 0,5 — отнести наблюдение к классу 0, если выше — к классу 1.
- Если $ f_w(x) < 0,5 rightarrow hat{y} = 0 $
- Если $ f_w(x) geq 0,5 rightarrow hat{y} = 1 $
Однако, даже если предположить, что мы удачно провели линию регрессии (а на графике выше мы действительно провели ее вполне удачно), и наша модель может делать качественный прогноз, появление новых данных сместит эту границу, и, как следствие, ничего не добавит, а только ухудшит точность модели.
Теперь часть наблюдений, принадлежащих к классу 1, будет ошибочно отнесено моделью к классу 0.
Кроме этого, линейная регрессия по оси y выдает значения, сильно выходящие за пределы интересующего нас интервала от нуля до единицы.
Откроем ноутбук к этому занятию⧉
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# помимо стандартных библиотек мы также импортируем библиотеку warnings # она позволит скрыть предупреждения об ошибках import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns import warnings # кроме того, импортируем датасеты библиотеки sklearn from sklearn import datasets # а также функции для расчета метрики accuracy и построения матрицы ошибок from sklearn.metrics import accuracy_score, confusion_matrix # построенные нами модели мы будем сравнивать с результатом # класса LogisticRegression библиотеки sklearn from sklearn.linear_model import LogisticRegression # среди прочего, мы построим модели полиномиальной логистической регрессии from sklearn.preprocessing import PolynomialFeatures |
Функция логистической регрессии
Сигмоида
Возможное решение упомянутых выше сложностей — пропустить значение линейной регрессии через сигмоиду (sigmoid function), которая при любом значении X не выйдет из необходимого нам диапазона $0 leq h(x) leq 1 $. Напомню формулу и график сигмоиды.
$$ g(z) = frac{1}{1+e^{-z}} $$

Примечание: обратие внимание, когда z представляет собой большое отрицательное число, знаменатель становится очень большим $ 1 + e^{-(-5)} approx 148, 413 $ и значение сигмоиды стремится к нулю; когда z является большим положительным числом, знаменатель, а вместе с ним и все выражение стремятся к единице $ 1 + e^{-(5)} approx 0,0067 $.
Тогда мы можем построить линейную модель, значение которой будет подаваться в сигмоиду.
$$ z = Xtheta rightarrow h_{theta}(x) = frac{1}{1+e^{-(Xtheta)}} $$
В этом смысле никакой ошибки в названии «логистическая регрессия» нет. Этот алгоритм решает задачу классификации через модель линейной регрессии.
Если вы не помните, почему мы записали множественную линейную функцию как $theta x$, посмотрите предыдущую лекцию.
Приведем код на Питоне.
|
def h(x, thetas): z = np.dot(x, thetas) return 1.0 / (1 + np.exp(–z)) |
Теперь посмотрим, как интерпретировать коэффициенты.
Интерпретация коэффициентов
Для любого значения x через $ h_{theta}(x) $ мы будем получать вероятность от 0 до 1, что объект принадлежит к классу y = 1. Например, если класс 1 означает, что заемщик вернул кредит, то $ h_{theta}(x) = 0,8 $ говорит о том, что согласно нашей модели (с параметрами $theta$), для данного заемщика (x) вероятность возвращения кредита состаляет 80 процентов.
В общем случае мы можем записать вероятность вот так.
$$ h_{theta}(x) = P(y = 1 | x; theta) $$
Это выражение можно прочитать как вероятность принадлежности к классу 1 при условии x с параметрами $theta$ (probability of y = 1 given x, parameterized by $theta$).
Поскольку, как мы помним, сумма вероятностей событий, образующих полную группу, всегда равна единице, вероятность принадлежности к классу 0 будет равна
$$ P(y = 0 | x; theta) = 1-P(y = 1 | x; theta) $$
Решающая граница
Решающая граница (decision boundary) — это порог, который определяет к какому классу отнести то или иное наблюдение. Если выбрать порог на уровне 0,5, то все что выше или равно этому порогу мы отнесем к классу 1, все что ниже — к классу 0.
$$ y = 1, h_{theta}(x) geq 0,5 $$
$$ y = 0, h_{theta}(x) < 0,5 $$
Теперь обратите внимание на сигмоиду. Сигмоида $ g(z) $ принимает значения больше 0,5, если $ z geq 0 $, а так как $ z = Xtheta $, то можно сказать, что
- $h_{theta}(x) geq 0,5$ и $ y = 1$, когда $ Xtheta geq 0 $, и соответственно
- $h_{theta}(x) < 0,5 $ и $ y = 0$, когда $ Xtheta < 0 $.
Уравнение решающей границы
Предположим, что у нас есть два признака $x_1$ и $x_2$. Вместе они образуют так называемое пространство ввода (input space), то есть все имеющиеся у нас наблюдения. Мы можем представить это пространство на координатной плоскости, дополнительно выделив цветом наблюдения, относящиеся к разным классам.
Кроме того, представим, что мы уже построили модель логистической регрессии, и она провела для нас соответствующую границу между двумя классами.

Возникает вопрос. Как, зная коэффициенты $theta_0$, $theta_1$ и $theta_2$ модели, найти уравнение линии решающей границы? Для начала договоримся, что уравнение решающией границы будет иметь вид $x_2 = mx_1 + c$, где m — наклон прямой, а c — сдвиг.
Теперь вспомним, что модель с двумя признаками (до подачи в сигмоиду) имеет вид
$$ z = theta_0 + theta_1 x_1 + theta_2 x_2 $$
Также не забудем, что граница проходит там, где $ h_{theta}(x) = 0,5 $, а значит z = 0. Значит,
$$ 0 = theta_0 + theta_1 x_1 + theta_2 x_2 $$
Чтобы найти с (то есть сдвиг линии решающей границы вдоль оси $x_2$) приравняем $x_1$ к нулю и решим для $x_2$ (именно эта точка и будет сдвигом c).
$$ 0 = theta_0 + 0 + theta_2 x_2 rightarrow x_2 = -frac{theta_0}{theta_2} rightarrow c = -frac{theta_0}{theta_2} $$
Теперь займемся наклоном m. Возьмем некоторую точку на линии решающей границы с координатами $(x_1^a, x_2^a)$, $(x_1^b, x_2^b)$. Тогда наклон m будет равен
$$ m = frac{x_2^b-x_2^a}{x_1^b-x_1^a} $$
Так как эти точки расположены на решающей границе, то справедливо, что
$$ 0 = theta_1x_1^b + theta_2x_2^b + theta_0-(theta_1x_1^a + theta_2x_2^a + theta_0) $$
$$ -theta_2(x_2^b-x_2^a) = theta_1(x_1^b-x_1^a) $$
А значит,
$$ frac{x_2^b-x_2^a}{x_1^b-x_1^a} = -frac{theta_1}{theta_2} rightarrow m = -frac{theta_1}{theta_2} $$
Вычислительная устойчивость сигмоиды
При очень больших отрицательных или положительных значениях z может возникнуть переполнение памяти (overflow).
|
# возьмем большое отрицательное значение z = –999 1 / (1 + np.exp(–z)) |
|
RuntimeWarning: overflow encountered in exp 0.0 |
Преодолеть это ограничение и добиться вычислительной устойчивости (numerical stability) алгоритма можно с помощью следующего тождества.
$$ g(z) = frac{1}{1+e^{-z}} = frac{1}{1+e^{-z}} times frac{e^z}{e^z} = frac{e^z}{e^z(1+e^{-z})} = frac {e^z}{e^z + 1} $$
Что интересно, первая часть тождества устойчива при очень больших положительных значениях z.
|
z = 999 1 / (1 + np.exp(–z)) |
При этом вторая стабильна при очень больших отрицательных значениях.
|
z = –999 np.exp(z) / (np.exp(z) + 1) |
Объединим обе части с помощью условия.
|
def stable_sigmoid(z): if z >= 0: return 1 / (1 + np.exp(–z)) else: return np.exp(z) / (np.exp(z) + 1) |
Примечание. Мы не использовали более лаконичный код, например, функцию np.where(), потому что эта функция прежде чем применить условие рассчитывает оба сценария (в данном случае обе части тождества), а это ровно то, чего мы хотим избежать, чтобы не возникло ошибки. Простое условие с if препятствует выполнению той части кода, которая нам не нужна.
Можно также использовать функцию expit() библиотеки scipy.
|
from scipy.special import expit expit(999), expit(–999) |
Остается написать линейную функцию и подать ее результат в сигмоиду.
|
def h(x, thetas): z = np.dot(x, thetas) return np.array([stable_sigmoid(value) for value in z]) |
Протестируем код. Предположим, что в нашем датасете четыре наблюдения и три коэффициента. Схематично расчеты будут выглядеть следующим образом.
Пропишем это на Питоне.
|
# возьмем массив наблюдений 4 х 3 с числами от 1 до 12 x = np.arange(1, 13).reshape(4, 3) # и трехмерный вектор коэффициентов thetas = np.array([–3, 1, 1]) # подадим их в модель h(x, thetas) |
|
array([0.88079708, 0.26894142, 0.01798621, 0.00091105]) |
Модель работает корректно. Теперь обсудим, как ее обучать, то есть какую функцию потерь использовать для оптимизации параметров $theta$.
Logistic loss или функция кросс-энтропии
В модели логистической регрессии мы не можем использовать MSE. Дело в том, что если мы поместим результат сигмоиды (представляющей собою нелинейную функцию) в MSE, то на выходе получим невыпуклую функцию (non-convex), глобальный минимум которой довольно сложно найти.

Вместо MSE мы будем использовать функцию логистической ошибки, которую еще называют функцией бинарной кросс-энтропии (log loss, binary cross-entropy loss).
График и формула функции логистической ошибки
Вначале посмотрим на нее на графике.

Разберемся, как она работает. Наша модель $h_{theta}(x)$ может выдавать вероятность от 0 до 1, фактические значения $y$ только 0 и 1.
Сценарий 1. Предположим, что для конкретного заемщика в обучающем датасете истинное значение/ целевой класс записан как 1 (то есть заемщик вернул кредит). Тогда «срабатывает» синяя ветвь графика и ошибка измеряется по ней. Соответственно, чем ближе выдаваемая моделью вероятность к единице, тем меньше ошибка.
$$ -log(P(y = 1 | x; theta)) = -log(h_{theta}(x)), y = 1 $$
Сценарий 2. Заемщик не вернул кредит и его целевая переменная записана как 0. Тогда срабатывает оранжевая ветвь. Ошибка модели будет минимальна при значениях, близких к нулю.
$$ -log(1-P(y = 1 | x; theta)) = -log(1-h_{theta}(x)), y = 0 $$
Добавлю, что минус логарифм в данном случае очень удачно отвечает нашему желанию иметь нулевую ошибку при правильном прогнозе и наказать алгоритм высокой ошибкой (асимптотически стремящейся к бесконечности) в случае неправильного прогноза.
В итоге нам нужно будет найти сумму вероятностей принадлежности к классу 1 для сценария 1 и сценария 2.
$$ J(theta) = begin{cases} -log(h_{theta}(x)) | y=1 \ -log(1-h_{theta}(x)) | y=0 end{cases} $$
Однако, для каждого наблюдения нам нужно учитывать только одну из вероятностей (либо $y=1$, либо $y=0$). Как нам переключаться между ними? На самом деле очень просто.
В качестве переключателя можно использовать целевую переменную. В частности, умножим левую часть функции на $y$, а правую на $1-y$. Тогда, если речь идет о классе 1, первая часть умножится на единицу, вторая на ноль и исчезнет. Если речь идет о классе 0, произойдет обратное, исчезнет левая часть, а правая останется. Получается
$$ J(theta) = -frac{1}{n} sum y cdot log(h_{theta}(x)) + (1-y) cdot log(1-h_{theta}(x)) $$
Рассмотрим ее работу на учебном примере.
Расчет логистической ошибки
Предположим, мы построили модель и для каждого наблюдения получили некоторый прогноз (вероятность).
|
# выведем результат работы модели (вероятности) y_pred и целевую переменную y output = pd.DataFrame({ ‘y’ :[1, 1, 1, 0, 0, 1, 1, 0], ‘y_pred’ :[0.93, 0.81, 0.78, 0.43, 0.54, 0.49, 0.22, 0.1] }) output |
Найдем вероятность принадлежности к классу 1.
|
# оставим вероятность, если y = 1, и вычтем вероятность из единицы, если y = 0 output[‘y=1 prob’] = np.where(output[‘y’] == 0, 1 – output[‘y_pred’], output[‘y_pred’]) output |
Возьмем отрицательный логарифм из каждой вероятности.
|
output[‘-log’] = –np.log(output[‘y=1 prob’]) output |
Выведем каждое из получившихся значений на графике.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
plt.figure(figsize = (10, 8)) # создадим точки по оси x в промежутке от 0 до 1 x_vals = np.linspace(0, 1) # выведем кривую функции логистической ошибки plt.plot(x_vals, –np.log(x_vals), label = ‘-log(h(x)) | y = 1’) # выведем каждое из значений отрицательного логарифма plt.scatter(output[‘y=1 prob’], output[‘-log’], color = ‘r’) # зададим заголовок, подписи к осям, легенду и сетку plt.xlabel(‘h(x)’, fontsize = 16) plt.ylabel(‘loss’, fontsize = 16) plt.title(‘Функция логистической ошибки’, fontsize = 18) plt.legend(loc = ‘upper right’, prop = {‘size’: 15}) plt.grid() plt.show() |
Как мы видим, так как мы всегда выражаем вероятность принадлежности к классу 1, графически нам будет достаточно одной ветви. Остается сложить результаты и разделить на количество наблюдений.
Окончательный вариант
Напишем функцию логистической ошибки, которую будем использовать в нашем алгоритме.
|
def objective(y, y_pred): # рассчитаем функцию потерь для y = 1, добавив 1e-9, чтобы избежать ошибки при log(0) y_one_loss = y * np.log(y_pred + 1e–9) # также рассчитаем функцию потерь для y = 0 y_zero_loss = (1 – y) * np.log(1 – y_pred + 1e–9) # сложим и разделим на количество наблюдений return –np.mean(y_zero_loss + y_one_loss) |
Проверим ее работу на учебных данных.
|
objective(output[‘y’], output[‘y_pred’]) |
Теперь займемся поиском производной.
Производная функции логистической ошибки
Предположим, что $G(theta)$ — одна из частных производных описанной выше функции логистической ошибки $J(theta)$,
$$ G = y cdot log(h) + (1-y) cdot log(1-h) $$
где h — это сигмоида $1/1+e^{-z}$, а $z(theta)$ — линейная функция $xtheta$. Тогда по chain rule нам нужно найти производные следующих функций
$$ frac{partial G}{partial theta} = frac{partial G}{partial h} cdot frac{partial h}{partial z} cdot frac{partial z}{partial theta} $$
Производная логарифмической функции
Начнем с производной логарифмической функции.
$$ frac{partial}{partial x} ln f(x) = frac{1}{f(x)} $$
Теперь, помня, что x и y — это константы, найдем первую производную.
$$ frac{partial G}{partial h} left[ y cdot log(h) + (1-y) cdot log(1-h) right] $$
$$ = y cdot frac{partial G}{partial h} [log(h)] + (1-y) cdot frac{partial G}{partial h} [log(1-h)] $$
$$ = frac{1}{h}y + frac{1}{1-h} cdot frac{partial G}{partial h} [1-h] cdot (1-y) $$
Упростим выражение (не забыв про производную разности).
$$ = frac{h}{y} + frac{frac{partial G}{partial h} (1-h) (1-y)}{1-h} = frac{h}{y}+frac{(0-1)(1-y)}{1-h} $$
$$ = frac{y}{h}-frac{1-y}{1-h} = frac{y-h}{h(1-h)} $$
Теперь займемся производной сигмоиды.
Производная сигмоиды
Вначале упростим выражение.
$$ frac{partial h}{partial z} left[ frac{1}{1+e^{-z}} right] = frac{partial h}{partial z} left[ (1+e^{-z})^{-1}) right] $$
Теперь перейдем к нахождению производной
$$ = -(1+e^{-z})^{-2}) cdot (-e^{-z}) = frac{e^{-z}}{(1+e^{-z})^2} $$
$$ = frac{1}{1+e^{-z}} cdot frac{e^{-z}}{1+e^{-z}} = frac{1}{1+e^{-z}} cdot frac{(1+e^{-z})-1}{1+e^{-z}} $$
$$ = frac{1}{1+e^{-z}} cdot left( frac{1+e^{-z}}{1+e^{-z}}-frac{1}{1+e^{-z}} right) $$
$$ = frac{1}{1+e^{-z}} cdot left( 1-frac{1}{1+e^{-z}} right) $$
В терминах предложенной выше нотации получается
$$ h(1-h) $$
Производная линейной функции
Наконец найдем производную линейной функции.
$$ frac{partial z}{partial theta} = x $$
Перемножим производные и найдем градиент по каждому из признаков j для n наблюдений.
$$ frac{partial J}{partial theta} = frac{y-h}{h(1-h)} cdot h(1-h) cdot x_j cdot frac{1}{n} = x_j cdot (y-h) cdot frac{1}{n} $$
Замечу, что хотя производная похожа на градиент функции линейной регрессии, на самом деле это разные функции, $h$ в данном случае сигмоида.
Для нахождения градиента (всех частных производных одновременно) перепишем формулу в векторной нотации.
$$ nabla_{theta} J = X^T(h(Xtheta)-y) times frac{1}{n} $$
Схематично для четырех наблюдений и трех коэффициентов нахождение градиента будет выглядеть следующим образом.
Объявим соответствующую функцию.
|
def gradient(x, y, y_pred, n): return np.dot(x.T, (y_pred – y)) / n |
На всякий случай напомню, что прогнозные значения (y_pred) мы получаем с помощью объявленной ранее функции $h(x, thetas)$.
Подготовка данных
В качестве примера возьмем встроенный в sklearn датасет, в котором нам предлагается определить класс вина по его характеристикам.
|
# импортируем датасет о вине из модуля datasets data = datasets.load_wine() # превратим его в датафрейм df = pd.DataFrame(data.data, columns = data.feature_names) # добавим целевую переменную df[‘target’] = data.target # посмотрим на первые три строки df.head(3) |
Целевая переменная
Посмотрим на количество наблюдений и признаков (размерность матрицы), а также уникальные значения (классы) в целевой переменной.
|
df.shape, np.unique(df.target) |
|
((178, 14), array([0, 1, 2])) |
Как мы видим, у нас три класса, а должно быть два, потому что пока что мы создаем алгоритм бинарной классификации. Отфильтруем значения так, чтобы осталось только два класса.
|
# применим маску датафрейма и удалим класс 2 df = df[df.target != 2] # посмотрим на результат df.shape, df.target.unique() |
|
((130, 14), array([0, 1])) |
Отбор признаков
Наша целевая переменная выражена бинарной категорией или, как еще говорят, находится на дихотомической шкале (dichotomous variable). В этом случае применять коэффициент корреляции Пирсона не стоит и можно использовать точечно-бисериальную корреляцию (point-biserial correlation). Рассчитаем корреляцию признаков и целевой переменной нашего датасета.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# импортируем модуль stats из библиотеки scipy from scipy import stats # создадим два списка, один для названий признаков, второй для корреляций columns, correlations = [], [] # пройдемся по всем столбцам датафрейма кроме целевой переменной for col in df.drop(‘target’, axis = 1).columns: # поместим название признака в список columns columns.append(col) # рассчитаем корреляцию этого признака с целевой переменной # и поместим результат в список корреляций correlations.append(stats.pointbiserialr(df[col], df[‘target’])[0]) # создадим датафрейм на основе заполненных списков # и применим градиентную цветовую схему pd.DataFrame({‘column’: columns, ‘correlation’: correlations}).style.background_gradient() |
Наиболее коррелирующим с целевой переменной признаком является пролин (proline). Визуально оценим насколько сильно отличается этот показатель для классов вина 0 и 1.
|
# зададим размер графика plt.figure(figsize = (10, 8)) # на точечной диаграмме выведем пролин по оси x, а класс вина по оси y sns.scatterplot(x = df.proline, y = df.target, s = 80); |
Теперь посмотрим на зависимость двух признаков (спирт и пролин) от целевой переменной.
|
# зададим размер графика plt.figure(figsize = (10, 8)) # на точечной диаграмме по осям x и y выведем признаки, # с помощью параметра hue разделим соответствующие классы целевой переменной sns.scatterplot(x = df.alcohol, y = df.proline, hue = df.target, s = 80) # добавим легенду, зададим ее расположение и размер plt.legend(loc = ‘upper left’, prop = {‘size’: 15}) # выведем результат plt.show() |
В целом можно сказать, что классы линейно разделимы (другими словами, мы можем провести прямую между ними). Поместим признаки в переменную X, а целевую переменную — в y.
|
X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] |
Масштабирование признаков
Как и в случае с линейной регрессией, для алгоритма логистической регрессии важно, чтобы признаки были приведены к одному масштабу. Для этого используем стандартизацию.
|
# т.е. приведем данные к нулевому среднему и единичному СКО X = (X – X.mean()) / X.std() X.head() |
Проверим результат.
|
X.alcohol.mean(), X.alcohol.std(), X.proline.mean(), X.proline.std() |
|
(6.8321416900009635e-15, 1.0, -5.465713352000771e-17, 1.0) |
Теперь мы готовы к созданию и обучению модели.
Обучение модели
Вначале объявим уже знакомую нам функцию, которая добавит в датафрейм столбец под названием x0, заполненный единицами.
|
def add_ones(x): # важно! метод .insert() изменяет исходный датафрейм return x.insert(0,‘x0’, np.ones(x.shape[0])) |
Применим ее к нашему датафрейму с признаками.
|
# добавим столбец с единицами add_ones(X) # и посмотрим на результат X.head() |
Создадим вектор начальных весов (он будет состоять из нулей), а также переменную n, в которой будет храниться количество наблюдений.
|
thetas, n = np.zeros(X.shape[1]), X.shape[0] thetas, n |
|
(array([0., 0., 0.]), 130) |
Кроме того, создадим список, в который будем записывать размер ошибки функции потерь.
Теперь выполним основную работу по минимизации функции потерь и поиску оптимальных весов (выполнение кода ниже у меня заняло около 30 секунд).
|
# в цикле из 20000 итераций for i in range(20000): # рассчитаем прогнозное значение с текущими весами y_pred = h(X, thetas) # посчитаем уровень ошибки при текущем прогнозе loss_history.append(objective(y, y_pred)) # рассчитаем градиент grad = gradient(X, y, y_pred, n) # используем градиент для улучшения весов модели # коэффициент скорости обучения будет равен 0,001 thetas = thetas – 0.001 * grad |
Посмотрим на получившиеся веса и финальный уровень ошибки.
|
# чтобы посмотреть финальный уровень ошибки, # достаточно взять последний элемент списка loss_history thetas, loss_history[–1] |
|
(array([ 0.23234188, -1.73394252, -1.89350543]), 0.12282503517421262) |
Модель обучена. Теперь мы можем сделать прогноз и оценить результат.
Прогноз и оценка качества
Прогноз модели
Объявим функцию predict(), которая будет предсказывать к какому классу относится то или иное наблюдение. От функции $h(x, thetas)$ эта функция будет отличаться тем, что выдаст не только вероятность принадлежности к тому или иному классу, но и непосредственно сам предполагаемый класс (0 или 1).
|
def predict(x, thetas): # найдем значение линейной функции z = np.dot(x, thetas) # проведем его через устойчивую сигмоиду probs = np.array([stable_sigmoid(value) for value in z]) # если вероятность больше или равна 0,5 – отнесем наблюдение к классу 1, # в противном случае к классу 0 # дополнительно выведем значение вероятности return np.where(probs >= 0.5, 1, 0), probs |
Вызовем функцию predict() и запишем прогноз класса и вероятность принадлежности к этому классу в переменные y_pred и probs соответственно.
|
# запишем прогноз класса и вероятность этого прогноза в переменные y_pred и probs y_pred, probs = predict(X, thetas) # посмотрим на прогноз и вероятность для первого наблюдения y_pred[0], probs[0] |
|
(0, 0.022908352078195617) |
Здесь важно напомнить, что вероятность, близкая к нулю, говорит о пренадлжености к классу 0. В качестве упражнения выведите класс последнего наблюдения и соответствующую вероятность.
Метрика accuracy и матрица ошибок
Оценим результат с помощью метрики accuracy и матрицы ошибок.
|
# функцию accuracy_score() мы импортировали в начале ноутбука accuracy_score(y, y_pred) |
|
# функцию confusion_matrix() мы импортировали в начале ноутбука # столбцами будут прогнозные значения (Forecast), # строками – фактические (Actual) pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’], index = [‘Actual 0’, ‘Actual 1’]) |
Как мы видим, алгоритм ошибся пять раз. Дважды он посчитал, что наблюдение относится к классу 1, хотя на самом деле это был класс 0, и трижды, наоборот, неверно отнес класс 1 к классу 0.
Решающая граница
Выше мы уже вывели уравнение решающей границы. Воспользуемся им, чтобы визуально оценить насколько удачно классификатор справился с поставленной задачей.
|
# рассчитаем сдвиг (c) и наклон (m) линии границы c, m = –thetas[0]/thetas[2], –thetas[1]/thetas[2] c, m |
|
(0.1227046263531282, -0.915731474695505) |
|
# найдем минимальное и максимальное значения для спирта (ось x) xmin, xmax = min(X[‘alcohol’]), max(X[‘alcohol’]) # найдем минимальное и максимальное значения для пролина (ось y) ymin, ymax = min(X[‘proline’]), max(X[‘proline’]) # запишем значения оси x в переменную xd xd = np.array([xmin, xmax]) xd |
|
array([-2.15362589, 2.12194856]) |
|
# подставим эти значения, а также значения сдвига и наклона в уравнение линии yd = m * xd + c # в результате мы получим координаты двух точек, через которые проходит линия границы (xd[0], yd[0]), (xd[1], yd[1]) |
|
((-2.1536258890738247, 2.0948476376971197), (2.1219485561396647, -1.8204304541886445)) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# зададим размер графика plt.figure(figsize = (11, 9)) # построим пунктирную линию по двум точкам, найденным выше plt.plot(xd, yd, ‘k’, lw = 1, ls = ‘–‘) # дополнительно отобразим наши данные, sns.scatterplot(x = X[‘alcohol’], y = X[‘proline’], hue = y, s = 70) # которые снова снабдим легендой plt.legend(loc = ‘upper left’, prop = {‘size’: 15}) # минимальные и максимальные значения по обеим осям будут границами графика plt.xlim(xmin, xmax) plt.ylim(ymin, ymax) # по желанию, разделенные границей половинки можно закрасить # tab: означает, что цвета берутся из палитры Tableau # plt.fill_between(xd, yd, ymin, color=’tab:blue’, alpha = 0.2) # plt.fill_between(xd, yd, ymax, color=’tab:orange’, alpha = 0.2) # а также добавить обозначения переменных в качестве подписей к осям # plt.xlabel(‘x_1’) # plt.ylabel(‘x_2’) plt.show() |
На графике хорошо видны те пять значений, в которых ошибся наш классификатор.
Написание класса
Остается написать класс бинарной логистической регрессии.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
class LogReg(): # в методе .__init__() объявим переменные для весов и уровня ошибки def __init__(self): self.thetas = None self.loss_history = [] # метод .fit() необходим для обучения модели # этому методу мы передадим признаки и целевую переменную # кроме того, мы зададим значения по умолчанию # для количества итераций и скорости обучения def fit(self, x, y, iter = 20000, learning_rate = 0.001): # метод создаст “правильные” копии датафрейма x, y = x.copy(), y.copy() # добавит столбец из единиц self.add_ones(x) # инициализирует веса и запишет в переменную n количество наблюдений thetas, n = np.zeros(x.shape[1]), x.shape[0] # создадим список для записи уровня ошибки loss_history = [] # в цикле равном количеству итераций for i in range(iter): # метод сделает прогноз с текущими весами y_pred = self.h(x, thetas) # найдет и запишет уровень ошибки loss_history.append(self.objective(y, y_pred)) # рассчитает градиент grad = self.gradient(x, y, y_pred, n) # и обновит веса thetas -= learning_rate * grad # метод выдаст веса и список с историей ошибок self.thetas = thetas self.loss_history = loss_history # метод .predict() делает прогноз с помощью обученной модели def predict(self, x): # метод создаст “правильную” копию модели x = x.copy() # добавит столбец из единиц self.add_ones(x) # рассчитает значения линейной функции z = np.dot(x, self.thetas) # передаст эти значения в сигмоиду probs = np.array([self.stable_sigmoid(value) for value in z]) # выдаст принадлежность к определенному классу и соответствующую вероятность return np.where(probs >= 0.5, 1, 0), probs # ниже приводятся служебные методы, смысл которых был разобран ранее def add_ones(self, x): return x.insert(0,‘x0’, np.ones(x.shape[0])) def h(self, x, thetas): z = np.dot(x, thetas) return np.array([self.stable_sigmoid(value) for value in z]) def objective(self, y, y_pred): y_one_loss = y * np.log(y_pred + 1e–9) y_zero_loss = (1 – y) * np.log(1 – y_pred + 1e–9) return –np.mean(y_zero_loss + y_one_loss) def gradient(self, x, y, y_pred, n): return np.dot(x.T, (y_pred – y)) / n def stable_sigmoid(self, z): if z >= 0: return 1 / (1 + np.exp(–z)) else: return np.exp(z) / (np.exp(z) + 1) |
Проверим работу написанного нами класса. Вначале подготовим данные и обучим модель.
|
# проверим работу написанного нами класса # поместим признаки и целевую переменную в X и y X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] # приведем признаки к одному масштабу X = (X – X.mean())/X.std() # создадим объект класса LogReg model = LogReg() # и обучим модель model.fit(X, y) # посмотрим на атрибуты весов и финального уровня ошибки model.thetas, model.loss_history[–1] |
|
(array([ 0.23234188, –1.73394252, –1.89350543]), 0.12282503517421262) |
Затем сделаем прогноз и оценим качество модели.
|
# сделаем прогноз y_pred, probs = model.predict(X) # и посмотрим на класс первого наблюдения и вероятность y_pred[0], probs[0] |
|
(0, 0.022908352078195617) |
|
# рассчитаем accuracy accuracy_score(y, y_pred) |
|
# создадим матрицу ошибок pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’], index = [‘Actual 0’, ‘Actual 1’]) |
Модель показала точно такой же результат. Методы класса LogReg работают. Теперь давайте сравним работу нашего класса с классом LogisticRegression библиотеки sklearn.
Сравнение с sklearn
Обучение модели
Вначале обучим модель.
|
# подготовим данные X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] X = (X – X.mean())/X.std() # создадим объект класса LogisticRegression и запишем его в переменную model model = LogisticRegression() # обучим модель model.fit(X, y) # посмотрим на получившиеся веса модели model.intercept_, model.coef_ |
|
(array([0.30838852]), array([[-2.09622008, -2.45991159]])) |
Прогноз
Теперь необходимо сделать прогноз и найти соответствующие вероятности. В классе LogisticRegression библиотеки sklearn метод .predict() отвечает за предсказание принадлежности к определенному классу, а метод .predict_proba() отвечает за вероятность такого прогноза.
|
# выполним предсказание класса y_pred = model.predict(X) # и найдем вероятности probs = model.predict_proba(X) # посмотрим на класс и вероятность первого наблюдения y_pred[0], probs[0] |
|
(0, array([0.9904622, 0.0095378])) |
Модель предсказала для первого наблюдения класс 0. При этом, обратите внимание, что метод .predict_proba() для каждого наблюдения выдает две вероятности, первая — это вероятность принадлежности к классу 0, вторая — к классу 1.
Оценка качества
Рассчитаем метрику accuracy.
|
accuracy_score(y, y_pred) |
И построим матрицу ошибок.
|
pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’], index = [‘Actual 0’, ‘Actual 1’]) |
Как мы видим, хотя веса модели и предсказанные вероятности немного отличаются, ее точность осталась неизменной.
Решающая граница
Построим решающую границу.
|
# найдем сдвиг и наклон для уравнения решающей границы c, m = –model.intercept_ / model.coef_[0][1], –model.coef_[0][0] / model.coef_[0][1] c, m |
|
(array([0.12536569]), -0.8521526076691505) |
|
# посмотрим на линию решающей границы plt.figure(figsize = (11, 9)) xmin, xmax = min(X[‘alcohol’]), max(X[‘alcohol’]) ymin, ymax = min(X[‘proline’]), max(X[‘proline’]) xd = np.array([xmin, xmax]) yd = m*xd + c plt.plot(xd, yd, ‘k’, lw=1, ls=‘–‘) sns.scatterplot(x = X[‘alcohol’], y = X[‘proline’], hue = y, s = 70) plt.legend(loc = ‘upper left’, prop = {‘size’: 15}) plt.xlim(xmin, xmax) plt.ylim(ymin, ymax) plt.show() |
Бинарная полиномиальная регрессия
Идея бинарной полиномиальной логистической регрессии (binary polynomial logistic regression) заключается в том, чтобы использовать полином внутри сигмоиды и соответственно создать нелинейную границу между двумя классами.
Полиномиальные признаки
Уравнение полинома на основе двух признаков будет выглядеть следующим образом.
$$ y = theta_{0}x_0 + theta_{1}x_1 + theta_{2}x_2 + theta_{3} x_1^2 + theta_{4} x_1x_2 + theta_{5} x_2^2 $$
Реализуем этот алгоритм на практике и посмотрим, улучшатся ли результаты. Вначале, подготовим и масштабируем данные.
|
X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] X = (X – X.mean())/X.std() |
Теперь преобразуем наши данные так, как если бы мы использовали полином второй степени.
Смысл создания полиномиальных признаков мы детально разобрали на занятии по множественной линейной регрессии.
|
# создадим объект класса PolynomialFeatures # укажем, что мы хотим создать полином второй степени polynomial_features = PolynomialFeatures(degree = 2) # преобразуем данные с помощью метода .fit_transform() X_poly = polynomial_features.fit_transform(X) |
Сравним исходные признаки с полиномиальными.
|
# посмотрим на первое наблюдение X.head(1) |
|
# должно получиться шесть признаков X_poly[:1] |
|
array([[1. , 1.44685785, 0.77985116, 2.09339765, 1.12833378, 0.60816783]]) |
Моделирование и оценка качества
Обучим модель, сделаем прогноз и оценим результат.
|
# создадим объект класса LogisticRegression poly_model = LogisticRegression() # обучим модель на полиномиальных признаках poly_model = poly_model.fit(X_poly, y) # сделаем прогноз y_pred = poly_model.predict(X_poly) # рассчитаем accuracy accuracy_score(y_pred, y) |
Построим матрицу ошибок.
|
pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’], index = [‘Actual 0’, ‘Actual 1’]) |
Для того чтобы визуально оценить качество модели, построим два графика: фактических классов и прогнозных. Вначале создадим датасет, в котором будут исходные признаки (alcohol, proline) и прогнозные значения (y_pred).
|
# сделаем копию исходного датафрейма с нужными признаками predictions = df[[‘alcohol’, ‘proline’]].copy() # и добавим новый столбец с прогнозными значениями predictions[‘y_pred’] = y_pred # посмотрим на результат predictions.head(3) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# создадим два подграфика с помощью функции plt.subplots() # расположим подграфики на одной строке fig, (ax1, ax2) = plt.subplots(1, 2, # пропишем размер, figsize = (14, 6), # а также расстояние между подграфиками по горизонтали gridspec_kw = {‘wspace’ : 0.2}) # на левом подграфике выведем фактические классы sns.scatterplot(data = df, x = ‘alcohol’, y = ‘proline’, hue = ‘target’, palette = ‘bright’, s = 50, ax = ax1) ax1.set_title(‘Фактические классы’, fontsize = 14) # на правом – прогнозные sns.scatterplot(data = predictions, x = ‘alcohol’, y = ‘proline’, hue = ‘y_pred’, palette = ‘bright’, s = 50, ax = ax2) ax2.set_title(‘Прогноз’, fontsize = 14) # зададим общий заголовок fig.suptitle(‘Бинарная полиномиальная регрессия’, fontsize = 16) plt.show() |
Как вы видите, нам не удалось добиться улучшения по сравнению с обычной полиномиальной регрессией.
Напомню, что создание подграфиков мы подробно разобрали на занятии по исследовательскому анализу данных.
В качестве упражнения предлагаю вам выяснить, какая степень полинома позволит улучшить результат прогноза на этих данных и насколько, таким образом, улучшится качество предсказаний.
Перейдем ко второй части нашего занятия.
Мультиклассовая логистическая регрессия
Как поступить, если нужно предсказать не два класса, а больше? Сегодня мы рассмотрим два подхода: one-vs-rest и кросс-энтропию. Начнем с того, что подготовим данные.
Подготовка данных
Вернем исходный датасет с тремя классами.
|
# вновь импортируем датасет о вине data = datasets.load_wine() # превратим его в датафрейм df = pd.DataFrame(data.data, columns = data.feature_names) # приведем признаки к одному масштабу df = (df – df.mean())/df.std() # добавим целевую переменную df[‘target’] = data.target # убедимся, что у нас присутствуют все три класса df.target.value_counts() |
|
1 71 0 59 2 48 Name: target, dtype: int64 |
В целевой переменной большое двух классов, а значит точечно-бисериальный коэффициент корреляции мы использовать не можем. Воспользуемся корреляционным отношением (correlation ratio).
|
# код ниже был подробно разобран на предыдущем занятии def correlation_ratio(numerical, categorical): values = np.array(numerical) ss_total = np.sum((values.mean() – values) ** 2) cats = np.unique(categorical, return_inverse = True)[1] ss_betweengroups = 0 for c in np.unique(cats): group = values[np.argwhere(cats == c).flatten()] ss_betweengroups += len(group) * (group.mean() – values.mean()) ** 2 return np.sqrt(ss_betweengroups/ss_total) |
|
# создадим два списка, один для названий признаков, второй для значений корреляционного отношения columns, correlations = [], [] # пройдемся по всем столбцам датафрейма кроме целевой переменной for col in df.drop(‘target’, axis = 1).columns: # поместим название признака в список columns columns.append(col) # рассчитаем взаимосвязь этого признака с целевой переменной # и поместим результат в список значений корреляционного отношения correlations.append(correlation_ratio(df[col], df[‘target’])) # создадим датафрейм на основе заполненных списков # и применим градиентную цветовую схему pd.DataFrame({‘column’: columns, ‘correlation’: correlations}).style.background_gradient() |
Теперь наибольшую корреляцию с целевой переменной показывают флавоноиды (flavanoids) и пролин (proline). Их и оставим.
|
df = df[[‘flavanoids’, ‘proline’, ‘target’]].copy() df.head(3) |
Посмотрим, насколько легко можно разделить эти классы.
|
# зададим размер графика plt.figure(figsize = (10, 8)) # построим точечную диаграмму с двумя признаками, разделяющей категориальной переменной будет класс вина sns.scatterplot(x = df.flavanoids, y = df.proline, hue = df.target, palette = ‘bright’, s = 100) # добавим легенду plt.legend(loc = ‘upper left’, prop = {‘size’: 15}) plt.show() |
Перейдем непосредственно к алгоритмам мультиклассовой логистической регрессии. Начнем с подхода one-vs-rest.
Подход one-vs-rest
Подход one-vs-rest или one-vs-all предполагает, что мы отделяем один класс, а остальные наоборот объединяем. Так мы поступаем с каждым классом и строим по одной модели логистической регрессии относительно каждого из класса. Например, если у нас три класса, то у нас будет три модели логистической регрессии. Далее мы смотрим на получившиеся вероятности и выбираем наибольшую.
$$ h_theta^{(i)}(x) = P(y = i | x; theta), i in {0, 1, 2} $$
При таком подходе сам по себе алгоритм логистической регрессии претерпевает лишь несущественные изменения, главное правильно подготовить данные для обучения модели.
Подготовка датасетов
|
# поместим признаки и данные в соответствующие переменные x1, x2 = df.columns[0], df.columns[1] target = df.target.unique() target |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# сделаем копии датафреймов ovr_0, ovr_1, ovr_2 = df.copy(), df.copy(), df.copy() # в каждом из них сделаем целевым классом 0-й, 1-й или 2-й классы # например, в ovr_0 первым классом будет класс 0, а классы 1 и 2 – нулевым ovr_0[‘target’] = np.where(df[‘target’] == target[0], 1, 0) ovr_1[‘target’] = np.where(df[‘target’] == target[1], 1, 0) ovr_2[‘target’] = np.where(df[‘target’] == target[2], 1, 0) # выведем разделение на классы на графике fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize = (16, 4), gridspec_kw = {‘wspace’: 0.2, ‘hspace’: 0.08}) sns.scatterplot(data = ovr_0, x = x1, y = x2, hue = ‘target’, s = 50, ax = ax1) ax1.set_title(‘Прогнозирование класса 0’, fontsize = 14) sns.scatterplot(data = ovr_1, x = x1, y = x2, hue = ‘target’, s = 50, ax = ax2) ax2.set_title(‘Прогнозирование класса 1’, fontsize = 14) sns.scatterplot(data = ovr_2, x = x1, y = x2, hue = ‘target’, s = 50, ax = ax3) ax3.set_title(‘Прогнозирование класса 2’, fontsize = 14) plt.show() |
Обучение моделей
|
models = [] # поочередно обучим каждую из моделей for ova_n in [ovr_0, ovr_1, ovr_2]: X = ova_n[[‘flavanoids’, ‘proline’]] y = ova_n[‘target’] model = LogReg() model.fit(X, y) # каждую обученную модель поместим в список models.append(model) |
|
# убедимся, что все работает # например, выведем коэффициенты модели 1 models[0].thetas |
|
array([-0.99971466, 1.280398 , 2.04834457]) |
Прогноз и оценка качества
|
# вновь перенесем данные из исходного датафрейма X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] # в список probs будем записывать результат каждой модели # для каждого наблюдения probs = [] for model in models: _, prob = model.predict(X) probs.append(prob) |
|
# очевидно, для каждого наблюдения у нас будет три вероятности # принадлежности к целевому классу probs[0][0], probs[1][0], probs[2][0] |
|
(0.9161148288779738, 0.1540913395345091, 0.026621132600103174) |
|
# склеим и изменим размерность массива таким образом, чтобы # строки были наблюдениями, а столбцы вероятностями all_probs = np.concatenate(probs, axis = 0).reshape(len(probs), –1).T all_probs.shape |
|
# каждая из 178 строк – это вероятность одного наблюдения # принадлежать к классу 0, 1, 2 all_probs[0] |
|
array([0.91611483, 0.15409134, 0.02662113]) |
Обратите внимание, при использовании подхода one-vs-rest вероятности в сумме не дают единицу.
|
# например, первое наблюдение вероятнее всего принадлежит к классу 0 np.argmax(all_probs[0]) |
|
# найдем максимальную вероятность в каждой строке, # индекс вероятности [0, 1, 2] и будет прогнозом y_pred = np.argmax(all_probs, axis = 1) # рассчитаем accuracy accuracy_score(y, y_pred) |
|
# выведем матрицу ошибок pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’, ‘Forecast 2’], index = [‘Actual 0’, ‘Actual 1’, ‘Actual 2’]) |
Сравним фактическое и прогнозное распределение классов на точечной диаграмме.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
predictions = df[[‘flavanoids’, ‘proline’]].copy() predictions[‘y_pred’] = y_pred fig, (ax1, ax2) = plt.subplots(1, 2, figsize = (14, 6), gridspec_kw = {‘wspace’: 0.2, ‘hspace’: 0.08}) sns.scatterplot(data = df, x = ‘flavanoids’, y = ‘proline’, hue = ‘target’, palette = ‘bright’, s = 50, ax = ax1) ax1.set_title(‘Фактические классы’, fontsize = 14) sns.scatterplot(data = predictions, x = ‘flavanoids’, y = ‘proline’, hue = ‘y_pred’, palette = ‘bright’, s = 50, ax = ax2) ax2.set_title(‘Прогноз one-vs-rest’, fontsize = 14) plt.show() |
Написание класса
Поместим достигнутый выше результат в класс.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 |
class OVR_LogReg(): def __init__(self): self.models_thetas = [] self.models_loss = [] def fit(self, x, y, iter = 20000, learning_rate = 0.001): dfs = self.preprocess(x, y) models_thetas, models_loss = [], [] for ovr_df in dfs: x = ovr_df.drop(‘target’, axis = 1).copy() y = ovr_df.target.copy() self.add_ones(x) loss_history = [] thetas, n = np.zeros(x.shape[1]), x.shape[0] for i in range(iter): y_pred = self.h(x, thetas) loss_history.append(self.objective(y, y_pred)) grad = self.gradient(x, y, y_pred, n) thetas -= learning_rate * grad models_thetas.append(thetas) models_loss.append(loss_history) self.models_thetas = models_thetas self.models_loss = models_loss def predict(self, x): x = x.copy() probs = [] self.add_ones(x) for t in self.models_thetas: z = np.dot(x, t) prob = np.array([self.stable_sigmoid(value) for value in z]) probs.append(prob) all_probs = np.concatenate(probs, axis = 0).reshape(len(probs), –1).T y_pred = np.argmax(all_probs, axis = 1) return y_pred, all_probs def preprocess(self, x, y): x, y = x.copy(), y.copy() x[‘target’] = y classes = x.target.unique() dfs = [] ovr_df = None for c in classes: ovr_df = x.drop(‘target’, axis = 1).copy() ovr_df[‘target’] = np.where(x[‘target’] == classes[c], 1, 0) dfs.append(ovr_df) return dfs def add_ones(self, x): return x.insert(0,‘x0’, np.ones(x.shape[0])) def h(self, x, thetas): z = np.dot(x, thetas) return np.array([self.stable_sigmoid(value) for value in z]) def objective(self, y, y_pred): y_one_loss = y * np.log(y_pred + 1e–9) y_zero_loss = (1 – y) * np.log(1 – y_pred + 1e–9) return –np.mean(y_zero_loss + y_one_loss) def gradient(self, x, y, y_pred, n): return np.dot(x.T, (y_pred – y)) / n def stable_sigmoid(self, z): if z >= 0: return 1 / (1 + np.exp(–z)) else: return np.exp(z) / (np.exp(z) + 1) |
Проверим класс в работе.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] model = OVR_LogReg() model.fit(X, y) y_pred, probs = model.predict(X) accuracy_score(y_pred, y) |
Сравнение с sklearn
Для того чтобы применить подход one-vs-rest в классе LogisticRegression, необходимо использовать значение параметра multi_class = ‘ovr’.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] ovr_model = LogisticRegression(multi_class = ‘ovr’) ovr_model = ovr_model.fit(X, y) y_pred = ovr_model.predict(X) accuracy_score(y_pred, y) |
Мультиклассовая полиномиальная регрессия
Как мы увидели в предыдущем разделе, линейная решающая граница допустила некоторое количество ошибок. Попробуем улучшить результат, применив мультиклассовую полиномиальную логистическую регрессию.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] polynomial_features = PolynomialFeatures(degree = 7) X_poly = polynomial_features.fit_transform(X) poly_ovr_model = LogisticRegression(multi_class = ‘ovr’) poly_ovr_model = poly_ovr_model.fit(X_poly, y) y_pred = poly_ovr_model.predict(X_poly) accuracy_score(y_pred, y) |
Результат, по сравнению с моделью sklearn без полиномиальных признаков, стал чуть лучше. Однако это было достигнуто за счет полинома достаточно высокой степени (degree = 7), что неэффективно с точки зрения временной сложности алгоритма.
Посмотрим, какие нелинейные решающие границы удалось построить алгоритму.
|
predictions = df[[‘flavanoids’, ‘proline’]].copy() predictions[‘y_pred’] = y_pred fig, (ax1, ax2) = plt.subplots(1, 2, figsize = (14, 6), gridspec_kw = {‘wspace’: 0.2, ‘hspace’: 0.08}) sns.scatterplot(data = df, x = ‘flavanoids’, y = ‘proline’, hue = ‘target’, palette = ‘bright’, s = 50, ax = ax1) ax1.set_title(‘Фактические классы’, fontsize = 14) sns.scatterplot(data = predictions, x = ‘flavanoids’, y = ‘proline’, hue = ‘y_pred’, palette = ‘bright’, s = 50, ax = ax2) ax2.set_title(‘Полиномиальная регрессия’, fontsize = 14) plt.show() |
Softmax Regression
Еще один подход при создании мультиклассовой логистической регрессии заключается в том, чтобы не разбивать многоклассовые данные на несколько датасетов и использовать бинарный классификатор, а сразу применять функции, которые подходят для работы с множеством классов.
Такую регрессию часто называют Softmax Regression из-за того, что в ней используется уже знакомая нам по занятию об основах нейросетей функция softmax. Вначале подготовим данные.
Подготовка признаков
Возьмем признаки flavanoids и proline и добавим столбец из единиц.
|
def add_ones(x): # важно! метод .insert() изменяет исходный датафрейм return x.insert(0,‘x0’, np.ones(x.shape[0])) |
|
X = df[[‘flavanoids’, ‘proline’]] add_ones(X) X.head(3) |
Кодирование целевой переменной
Напишем собственную функцию для one-hot encoding.
|
def ohe(y): # количество примеров и количество классов examples, features = y.shape[0], len(np.unique(y)) # нулевая матрица: количество наблюдений x количество признаков zeros_matrix = np.zeros((examples, features)) # построчно проходимся по нулевой матрице и с помощью индекса заполняем соответствующее значение единицей for i, (row, digit) in enumerate(zip(zeros_matrix, y)): zeros_matrix[i][digit] = 1 return zeros_matrix |
|
y = df[‘target’] y_enc = ohe(df[‘target’]) y_enc[:3] |
|
array([[1., 0., 0.], [1., 0., 0.], [1., 0., 0.]]) |
Такой же результат можно получить с помощью класса LabelBinarizer.
|
lb = LabelBinarizer() lb.fit(y) lb.classes_ |
|
y_lb = lb.transform(y) y_lb[:5] |
|
array([[1, 0, 0], [1, 0, 0], [1, 0, 0], [1, 0, 0], [1, 0, 0]]) |
Инициализация весов
Создадим нулевую матрицу весов. Она будет иметь размерность: количество признаков (строки) х количество классов (столбцы). Приведем схематичный пример для четырех наблюдений, трех признаков (включая сдвиг $theta_0$) и трех классов.
Инициализируем веса.
|
thetas = np.zeros((3, 3)) thetas |
|
array([[0., 0., 0.], [0., 0., 0.], [0., 0., 0.]]) |
Функция softmax
Подробнее изучим функцию softmax. Приведем формулу.
$$ text{softmax}(z)_{i} = frac{e^{z_i}}{sum_{k=1}^N e^{z_k}} $$
Рассмотрим ее реализацию на Питоне.
Напомню, что $ z = (-Xtheta) $. Соответственно в нашем случае мы будем умножать матрицу 178 x 3 на 3 x 3.
В результате получим матрицу 178 x 3, где каждая строка — это прогнозные значения принадлежности одного наблюдения к каждому из трех классов.
|
z = np.dot(–X, thetas) z.shape |
Так как мы умножаем на ноль, при первой итерации эти значения будут равны нулю.
|
array([[0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.]]) |
Для того чтобы обеспечить вычислительную устойчивость softmax мы можем вычесть из z максимальное значение в каждой из 178 строк (пока что, опять же на первой итерации, оно равно нулю).
$$ text{softmax}(z)_{i} = frac{e^{z_i-max(z)}}{sum_{k=1}^N e^{z_k-max(z)}} $$
|
# axis = -1 – это последняя ось # keepdims = True сохраняет размерность (в данном случае двумерный массив) np.max(z, axis = –1, keepdims = True)[:5] |
|
array([[0.], [0.], [0.], [0.], [0.]]) |
|
z = z – np.max(z, axis = –1, keepdims = True) z[:5] |
|
array([[0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.]]) |
Смысл такого преобразования⧉ в том, что оно делает значения z нулевыми или отрицательными.
|
arr = np.array([–2, 3, 0, –7, 6]) arr – max(arr) |
|
array([ -8, -3, -6, -13, 0]) |
Далее, число возводимое в увеличивающуюся отрицательную степень стремится к нулю, а не к бесконечности и, таким образом, не вызывает переполнения памяти. Найдем числитель и знаменатель из формулы softmax.
|
numerator = np.exp(z) numerator[:5] |
|
array([[1., 1., 1.], [1., 1., 1.], [1., 1., 1.], [1., 1., 1.], [1., 1., 1.]]) |
|
denominator = np.sum(numerator, axis = –1, keepdims = True) denominator[:5] |
|
array([[3.], [3.], [3.], [3.], [3.]]) |
Разделим числитель и знаменатель и, таким образом, вычислим вероятность принадлежности каждого из наблюдений (строки результата) к одному из трех классов (столбцы).
|
softmax = numerator / denominator softmax[:5] |
|
array([[0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333]]) |
На первой итерации при одинаковых $theta$ мы получаем, что логично, одинаковые вероятности принадлежности к каждому из классов. Напишем функцию.
|
def stable_softmax(x, thetas): z = np.dot(–x, thetas) z = z – np.max(z, axis = –1, keepdims = True) numerator = np.exp(z) denominator = np.sum(numerator, axis = –1, keepdims = True) softmax = numerator / denominator return softmax |
|
probs = stable_softmax(X, thetas) probs[:3] |
|
array([[0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333]]) |
Примечание. Обратите внимание, что сигмоида — это частный случай функции softmax для двух классов $[z_1, 0]$. Вероятность класса $z_1$ будет равна
$$ softmax(z_1) = frac{e^{z_1}}{e^{z_1}+e^0} = frac{e^{z_1}}{e^{z_1}+1} $$
Если разделить и числитель, и знаменатель на $e^{z_1}$, то получим
$$ sigmoid(z_1) = frac{e^{z_1}}{1 + e^{-z_1}} $$
Вычислять вероятность принадлежности ко второму классу нет необходимости, достаточно вычесть результат сигмоиды из единицы.
Теперь нужно понять, насколько сильно при таких весах ошибается наш алгоритм.
Функция потерь
Вспомним функцию бинарной кросс-энтропии. То есть функции ошибки для двух классов.
$$ L(y, theta) = -frac{1}{n} sum y cdot log(h_{theta}(x)) + (1-y) cdot log(1-h_{theta}(x)) $$
Напомню, что y выступает в роли своего рода переключателя, сохраняющего одну из частей выражения, и обнуляющего другую. Теперь посмотрите на функцию категориальной (многоклассовой) кросс-энтропии (categorical cross-entropy).
$$ L(y_{ohe}, softmax) = -sum y_{ohe} log(softmax) $$
Разберемся, что здесь происходит. $y_{ohe}$ содержит закодированную целевую переменную, например, для наблюдения класса 0 [1, 0, 0], softmax содержит вектор вероятностей принадлежности наблюдения к каждому из классов, например, [0,3 0,4 0,3] (мы видим, что алгоритм ошибается).
В данном случае закодированная целевая переменная также выступает в виде переключателя. Здесь при умножении «срабатывает» только первая вероятность $1 times 0,3 + 0 times 0,4 + 0 times 0,4 $. Если подставить в формулу, то получаем (np.sum() добавлена для сохранения единообразия с формулой выше, в данном случае у нас одно наблюдение и сумма не нужна).
|
y_ohe = np.array([1, 0, 0]) softmax = np.array([0.3, 0.4, 0.4]) –np.sum(y_ohe * np.log(softmax)) |
Если бы модель в своих вероятностях ошибалась меньше, то и общая ошибка была бы меньше.
|
y_ohe = np.array([1, 0, 0]) softmax = np.array([0.4, 0.3, 0.4]) –np.sum(y_ohe * np.log(softmax)) |
Функция $-log$ позволяет снижать ошибку при увеличении вероятности верного (сохраненного переключателем) класса.
|
x_arr = np.linspace(0.001,1, 100) sns.lineplot(x=x_arr,y=–np.log(x_arr)) plt.title(‘Plot of -log(x)’) plt.xlabel(‘x’) plt.ylabel(‘-log(x)’); |
Напишем функцию.
|
# добавим константу в логарифм для вычислительной устойчивости def cross_entropy(probs, y_enc, epsilon = 1e–9): n = probs.shape[0] ce = –np.sum(y_enc * np.log(probs + epsilon)) / n return ce |
Рассчитаем ошибку для нулевых весов.
|
ce = cross_entropy(probs, y_enc) ce |
Для снижения ошибки нужно найти градиент.
Градиент
Приведем формулу градиента без дифференцирования.
$$ nabla_{theta}J = frac{1}{n} times X^T cdot (y_{ohe}-softmax) $$
По сути, мы умножаем транспонированную матрицу признаков (3 x 178) на разницу между закодированной целевой переменной и вероятностями функции softmax (178 x 3).
|
def gradient_softmax(X, probs, y_enc): # если не добавить функцию np.array(), будет выводиться датафрейм return np.array(1 / probs.shape[0] * np.dot(X.T, (y_enc – probs))) |
|
gradient_softmax(X, probs, y_enc) |
|
array([[-0.00187266, 0.06554307, -0.06367041], [ 0.31627721, 0.02059572, -0.33687293], [ 0.38820566, -0.28801792, -0.10018774]]) |
Обучение модели, прогноз и оценка качества
Выполним обучение модели.
|
loss_history = [] # в цикле for i in range(30000): # рассчитаем прогнозное значение с текущими весами probs = stable_softmax(X, thetas) # посчитаем уровень ошибки при текущем прогнозе loss_history.append(cross_entropy(probs, y_enc, epsilon = 1e–9)) # рассчитаем градиент grad = gradient_softmax(X, probs, y_enc) # используем градиент для улучшения весов модели thetas = thetas – 0.002 * grad |
Посмотрим на получившиеся коэффициенты (напомню, что первая строка матрицы это сдвиг (intercept, $theta_0$)) и достигнутый уровень ошибки.
|
array([[ 0.11290134, -0.90399727, 0.79109593], [-1.7550965 , -0.7857371 , 2.5408336 ], [-1.93839311, 1.77140542, 0.16698769]]) |
|
loss_history[0], loss_history[–1] |
|
(1.0986122856681098, 0.2569641080523888) |
Сделаем прогноз и оценим качество.
|
y_pred = np.argmax(stable_softmax(X, thetas), axis = 1) |
|
accuracy_score(y, y_pred) |
|
pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’, ‘Forecast 2’], index = [‘Actual 0’, ‘Actual 1’, ‘Actual 2’]) |
Написание класса
Объединим созданные выше компоненты в класс.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
class SoftmaxLogReg(): def __init__(self): self.loss_ = None self.thetas_ = None def fit(self, x, y, iter = 30000, learning_rate = 0.002): loss_history = [] self.add_ones(x) y_enc = self.ohe(y) thetas = np.zeros((x.shape[1], y_enc.shape[1])) for i in range(iter): probs = self.stable_softmax(x, thetas) loss_history.append(self.cross_entropy(probs, y_enc, epsilon = 1e–9)) grad = self.gradient_softmax(x, probs, y_enc) thetas = thetas – 0.002 * grad self.thetas_ = thetas self.loss_ = loss_history def predict(self, x, y): return np.argmax(self.stable_softmax(x, thetas), axis = 1) def stable_softmax(self, x, thetas): z = np.dot(–x, thetas) z = z – np.max(z, axis = –1, keepdims = True) numerator = np.exp(z) denominator = np.sum(numerator, axis = –1, keepdims = True) softmax = numerator / denominator return softmax def cross_entropy(self, probs, y_enc, epsilon = 1e–9): n = probs.shape[0] ce = –np.sum(y_enc * np.log(probs + epsilon)) / n return ce def gradient_softmax(self, x, probs, y_enc): return np.array(1 / probs.shape[0] * np.dot(x.T, (y_enc – probs))) def add_ones(self, x): return x.insert(0,‘x0’, np.ones(x.shape[0])) def ohe(self, y): examples, features = y.shape[0], len(np.unique(y)) zeros_matrix = np.zeros((examples, features)) for i, (row, digit) in enumerate(zip(zeros_matrix, y)): zeros_matrix[i][digit] = 1 return zeros_matrix |
Обучим модель, сделаем прогноз и оценим качество.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] model = SoftmaxLogReg() model.fit(X, y) model.thetas_, model.loss_[–1] |
|
(array([[ 0.11290134, -0.90399727, 0.79109593], [-1.7550965 , -0.7857371 , 2.5408336 ], [-1.93839311, 1.77140542, 0.16698769]]), 0.2569641080523888) |
|
y_pred = model.predict(X, y) accuracy_score(y, y_pred) |
Сравнение с sklearn
Для того чтобы использовать softmax логистическую регрессию в sklearn, соответствующему классу нужно передать параметр multi_class = ‘multinomial’.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] # создадим объект класса LogisticRegression и запишем его в переменную model model = LogisticRegression(multi_class = ‘multinomial’) # обучим нашу модель model.fit(X, y) # посмотрим на получившиеся веса модели model.intercept_, model.coef_ |
|
(array([ 0.09046097, 1.12593099, -1.21639196]), array([[ 1.86357908, 1.89698292], [ 0.86696131, -1.43973164], [-2.73054039, -0.45725129]])) |
|
y_pred = model.predict(X) accuracy_score(y, y_pred) |
Подведем итог
Сегодня мы разобрали множество разновидностей и подходов к использованию логистической регрессии. Давайте систематизируем изученный материал с помощью следующей схемы.
Рассмотрим обучение нейронных сетей.
Математический аппарат и назначение бинарной логистической регрессии — популярного инструмента для решения задач регрессии и классификации. ROC-анализ тесно связан с бинарной логистической регрессией и применяется для оценки качества моделей: позволяет выбрать аналитику модель с наилучшей прогностической силой, проанализировать чувствительность и специфичность моделей, подобрать порог отсечения.
- Введение
- Логистическая регрессия
- ROC-анализ
- Канонический алгоритм построения ROC-кривой
Введение
Логистическая регрессия — полезный классический инструмент для решения задачи регрессии и классификации. ROC-анализ — аппарат для анализа качества моделей. Оба алгоритма активно используются для построения моделей в медицине и проведения клинических исследований.
Логистическая регрессия получила распространение в скоринге для расчета рейтинга заемщиков и управления кредитными рисками. Поэтому, несмотря на свое «происхождение» из статистики, логистическую регрессию и ROC-анализ почти всегда можно увидеть в наборе Data Mining алгоритмов.
Логистическая регрессия
Логистическая регрессия — это разновидность множественной регрессии, общее назначение которой состоит в анализе связи между несколькими независимыми переменными (называемыми также регрессорами или предикторами) и зависимой переменной. Бинарная логистическая регрессия применяется в случае, когда зависимая переменная является бинарной (т.е. может принимать только два значения). С помощью логистической регрессии можно оценивать вероятность того, что событие наступит для конкретного испытуемого (больной/здоровый, возврат кредита/дефолт и т.д.).
Все регрессионные модели могут быть записаны в виде формулы:
y = F (x_1,, x_2, ,dots, , x_n)
В множественной линейной регрессии предполагается, что зависимая переменная является линейной функцией независимых переменных, т.е.:
y = a,+,b_1,x_1,+,b_2,x_2,+,dots,+,b_n,x_n
Можно ли ее использовать для задачи оценки вероятности исхода события? Да, можно, вычислив стандартные коэффициенты регрессии. Например, если рассматривается исход по займу, задается переменная y со значениями 1 и 0, где 1 означает, что соответствующий заемщик расплатился по кредиту, а 0, что имел место дефолт.
Однако здесь возникает проблема: множественная регрессия не «знает», что переменная отклика бинарна по своей природе. Это неизбежно приведет к модели с предсказываемыми значениями большими 1 и меньшими 0. Но такие значения вообще не допустимы для первоначальной задачи. Таким образом, множественная регрессия просто игнорирует ограничения на диапазон значений для y.
Для решения проблемы задача регрессии может быть сформулирована иначе: вместо предсказания бинарной переменной, мы предсказываем непрерывную переменную со значениями на отрезке [0,1] при любых значениях независимых переменных. Это достигается применением следующего регрессионного уравнения (логит-преобразование):
P = frac{1}{1+,e^{-y}}
где P — вероятность того, что произойдет интересующее событие e — основание натуральных логарифмов 2,71…; y — стандартное уравнение регрессии.
Зависимость, связывающая вероятность события и величину y, показана на следующем графике (рис. 1):
Рис. 1 — Логистическая кривая
Поясним необходимость преобразования. Предположим, что мы рассуждаем о нашей зависимой переменной в терминах основной вероятности P, лежащей между 0 и 1. Тогда преобразуем эту вероятность P:
P’ = log_e Bigl(frac{P}{1-P}Bigr)
Это преобразование обычно называют логистическим или логит-преобразованием. Теоретически P’ может принимать любое значение. Поскольку логистическое преобразование решает проблему об ограничении на 0-1 границы для первоначальной зависимой переменной (вероятности), то эти преобразованные значения можно использовать в обычном линейном регрессионном уравнении. А именно, если произвести логистическое преобразование обеих частей описанного выше уравнения, мы получим стандартную модель линейной регрессии.
Существует несколько способов нахождения коэффициентов логистической регрессии. На практике часто используют метод максимального правдоподобия. Он применяется в статистике для получения оценок параметров генеральной совокупности по данным выборки. Основу метода составляет функция правдоподобия (likehood function), выражающая плотность вероятности (вероятность) совместного появления результатов выборки
L,(Y_1,,Y_2,,dots,,Y_k;,theta) = p,(Y_1;, theta)cdotdotscdotp,p,(Y_k;,theta)
Согласно методу максимального правдоподобия в качестве оценки неизвестного параметра принимается такое значение theta=theta(Y_1,…,Y_k), которое максимизирует функцию L.
Нахождение оценки упрощается, если максимизировать не саму функцию L, а натуральный логарифм ln(L), поскольку максимум обеих функций достигается при одном и том же значении theta:
L^*(Y;,theta) = ln,(L,(Y;,theta),) rightarrow max
В случае бинарной независимой переменной, которую мы имеем в логистической регрессии, выкладки можно продолжить следующим образом. Обозначим через P_i вероятность появления единицы: P_i=Prob(Y_i=1). Эта вероятность будет зависеть от X_iW, где X_i — строка матрицы регрессоров, W — вектор коэффициентов регрессии:
P_i = F,(X_i W),, F(z) = frac{1}{1+,e^{-z}}
Логарифмическая функция правдоподобия равна:
L^* = sum_{i epsilon I_1}ln{P_i(W)} + sum_{i epsilon I_0}ln{(1-P_i(W))} = sum_{i=1}^{k} [Y_i ln {P_i (W)}+(1-Y_i)ln {(1 – P_i(W))}]
где I_0, I_1— множества наблюдений, для которых Y_i=0 и Y_i=1 соответственно.
Можно показать, что градиент g и гессиан H функции правдоподобия равны:
g = sum_i (Y_i,-,P_i),X_i
H=-sum_i P_i,(1,-,P_i),X_i^T,X_i,leq 0
Гессиан всюду отрицательно определенный, поэтому логарифмическая функция правдоподобия всюду вогнута. Для поиска максимума можно использовать метод Ньютона, который здесь будет всегда сходиться (выполнено условие сходимости метода):
W_{t+1},=,W_t,-,(H,(W_t))^{-1},g_t(W_t),=,W_t,-,Delta W_t
Логистическую регрессию можно представить в виде однослойной нейронной сети с сигмоидальной функцией активации, веса которой есть коэффициенты логистической регрессии, а вес поляризации — константа регрессионного уравнения (рис. 2).
Рис. 2 — Представление логистической регрессии в виде нейронной сети
Однослойная нейронная сеть может успешно решить лишь задачу линейной сепарации. Поэтому возможности по моделированию нелинейных зависимостей у логистической регрессии отсутствуют. Однако для оценки качества модели логистической регрессии существует эффективный инструмент ROC-анализа, что является несомненным ее преимуществом.
Для расчета коэффициентов логистической регрессии можно применять любые градиентные методы: метод сопряженных градиентов, методы переменной метрики и другие.
ROC-анализ
ROC-кривая (Receiver Operator Characteristic) — кривая, которая наиболее часто используется для представления результатов бинарной классификации в машинном обучении. Название пришло из систем обработки сигналов. Поскольку классов два, один из них называется классом с положительными исходами, второй — с отрицательными исходами. ROC-кривая показывает зависимость количества верно классифицированных положительных примеров от количества неверно классифицированных отрицательных примеров.
В терминологии ROC-анализа первые называются истинно положительным, вторые — ложно отрицательным множеством. При этом предполагается, что у классификатора имеется некоторый параметр, варьируя который, мы будем получать то или иное разбиение на два класса. Этот параметр часто называют порогом, или точкой отсечения (cut-off value). В зависимости от него будут получаться различные величины ошибок I и II рода.
В логистической регрессии порог отсечения изменяется от 0 до 1 — это и есть расчетное значение уравнения регрессии. Будем называть его рейтингом.
Для понимания сути ошибок I и II рода рассмотрим четырехпольную таблицу сопряженности (confusion matrix), которая строится на основе результатов классификации моделью и фактической (объективной) принадлежностью примеров к классам.
- TP (True Positives) — верно классифицированные положительные примеры (так называемые истинно положительные случаи).
- TN (True Negatives) — верно классифицированные отрицательные примеры (истинно отрицательные случаи).
- FN (False Negatives) — положительные примеры, классифицированные как отрицательные (ошибка I рода). Это так называемый «ложный пропуск» — когда интересующее нас событие ошибочно не обнаруживается (ложно отрицательные примеры).
- FP (False Positives) — отрицательные примеры, классифицированные как положительные (ошибка II рода). Это ложное обнаружение, т.к. при отсутствии события ошибочно выносится решение о его присутствии (ложно положительные случаи).
Что является положительным событием, а что — отрицательным, зависит от конкретной задачи. Например, если мы прогнозируем вероятность наличия заболевания, то положительным исходом будет класс «Больной пациент», отрицательным — «Здоровый пациент». И наоборот, если мы хотим определить вероятность того, что человек здоров, то положительным исходом будет класс «Здоровый пациент», и так далее.
При анализе чаще оперируют не абсолютными показателями, а относительными — долями (rates), выраженными в процентах:
- Доля истинно положительных примеров (True Positives Rate): TPR = frac{TP}{TP,+,FN},cdot,100 ,%
- Доля ложно положительных примеров (False Positives Rate): FPR = frac{FP}{TN,+,FP},cdot,100 ,%
Введем еще два определения: чувствительность и специфичность модели. Ими определяется объективная ценность любого бинарного классификатора.
Чувствительность (Sensitivity) — это и есть доля истинно положительных случаев:
S_e = TPR = frac{TP}{TP,+,FN},cdot,100 ,%
Специфичность (Specificity) — доля истинно отрицательных случаев, которые были правильно идентифицированы моделью:
S_p = frac{TN}{TN,+,FP},cdot,100 ,%
Заметим, что FPR=100-Sp
Попытаемся разобраться в этих определениях.
Модель с высокой чувствительностью часто дает истинный результат при наличии положительного исхода (обнаруживает положительные примеры). Наоборот, модель с высокой специфичностью чаще дает истинный результат при наличии отрицательного исхода (обнаруживает отрицательные примеры). Если рассуждать в терминах медицины — задачи диагностики заболевания, где модель классификации пациентов на больных и здоровых называется диагностическим тестом, то получится следующее:
- Чувствительный диагностический тест проявляется в гипердиагностике — максимальном предотвращении пропуска больных.
- Специфичный диагностический тест диагностирует только доподлинно больных. Это важно в случае, когда, например, лечение больного связано с серьезными побочными эффектами и гипердиагностика пациентов не желательна.
ROC-кривая получается следующим образом:
-
Для каждого значения порога отсечения, которое меняется от 0 до 1 с шагом d_x (например, 0,01) рассчитываются значения чувствительности Se и специфичности Sp. В качестве альтернативы порогом может являться каждое последующее значение примера в выборке.
-
Строится график зависимости: по оси Y откладывается чувствительность Se, по оси X — FPR=100-Sp — доля ложно положительных случаев.
Канонический алгоритм построения ROC-кривой
Входы: L — множество примеров f[i] — рейтинг, полученный моделью, или вероятность того, что i-й пример имеет положительный исход; min и max — минимальное и максимальное значения, возвращаемые f; d_x — шаг; P и N — количество положительных и отрицательных примеров соответственно.
- t=min
- повторять
- FP=TP=0
- для всех примеров i принадлежит L {
- если f[i]>=t тогда // этот пример находится за порогом
- если i положительный пример тогда
- { TP=TP+1 }
- иначе // это отрицательный пример
- { FP=FP+1 }
- }
- Se=TP/P*100
- point=FP/N // расчет (100 минус Sp)
- Добавить точку (point, Se) в ROC-кривую
- t=t+d_x
- пока (t>max)
В результате вырисовывается некоторая кривая (рис. 3).
Рис. 3 — ROC-кривая
График часто дополняют прямой y=x.
Заметим, что имеется более экономичный способ расчета точек ROC-кривой, чем тот, который приводился выше, т.к. его вычислительная сложность нелинейная и равна O(n^2): для каждого порога необходимо «пробегать» по записям и каждый раз рассчитывать TP и FP. Если же двигаться вниз по набору данных, отсортированному по убыванию выходного поля классификатора (рейтингу), то можно за один проход вычислить значения всех точек ROC-кривой, последовательно обновляя значения TP и FP.
Для идеального классификатора график ROC-кривой проходит через верхний левый угол, где доля истинно положительных случаев составляет 100% или 1,0 (идеальная чувствительность), а доля ложно положительных примеров равна нулю. Поэтому чем ближе кривая к верхнему левому углу, тем выше предсказательная способность модели. Наоборот, чем меньше изгиб кривой и чем ближе она расположена к диагональной прямой, тем менее эффективна модель. Диагональная линия соответствует «бесполезному» классификатору, т.е. полной неразличимости двух классов.
При визуальной оценке ROC-кривых расположение их относительно друг друга указывает на их сравнительную эффективность. Кривая, расположенная выше и левее, свидетельствует о большей предсказательной способности модели. Так, на рис. 4 две ROC-кривые совмещены на одном графике. Видно, что модель «A» лучше.
Рис. 4 — Сравнение ROC-кривых
Визуальное сравнение кривых ROC не всегда позволяет выявить наиболее эффективную модель. Своеобразным методом сравнения ROC-кривых является оценка площади под кривыми. Теоретически она изменяется от 0 до 1,0, но, поскольку модель всегда характеризуются кривой, расположенной выше положительной диагонали, то обычно говорят об изменениях от 0,5 («бесполезный» классификатор) до 1,0 («идеальная» модель).
Эта оценка может быть получена непосредственно вычислением площади под многогранником, ограниченным справа и снизу осями координат и слева вверху — экспериментально полученными точками (рис. 5). Численный показатель площади под кривой называется AUC (Area Under Curve). Вычислить его можно, например, с помощью численного метода трапеций:
AUC = int f(x),dx = sum_i Bigl[ frac{X_{i+1},+,X_i}{2}Bigr],cdot ,(Y_{i+1},-, Y_i)
Рис. 5 — Площадь под ROC-кривой
С большими допущениями можно считать, что чем больше показатель AUC, тем лучшей прогностической силой обладает модель. Однако следует знать, что:
- показатель AUC предназначен скорее для сравнительного анализа нескольких моделей;
- AUC не содержит никакой информации о чувствительности и специфичности модели.
В литературе иногда приводится следующая экспертная шкала для значений AUC, по которой можно судить о качестве модели:
Идеальная модель обладает 100% чувствительностью и специфичностью. Однако на практике добиться этого невозможно, более того, невозможно одновременно повысить и чувствительность, и специфичность модели. Компромисс находится с помощью порога отсечения, т.к. пороговое значение влияет на соотношение Se и Sp. Можно говорить о задаче нахождения оптимального порога отсечения (optimal cut-off value).
Порог отсечения нужен для того, чтобы применять модель на практике: относить новые примеры к одному из двух классов. Для определения оптимального порога нужно задать критерий его определения, т.к. в разных задачах присутствует своя оптимальная стратегия. Критериями выбора порога отсечения могут выступать:
- Требование минимальной величины чувствительности (специфичности) модели. Например, нужно обеспечить чувствительность теста не менее 80%. В этом случае оптимальным порогом будет максимальная специфичность (чувствительность), которая достигается при 80% (или значение, близкое к нему «справа» из-за дискретности ряда) чувствительности (специфичности).
- Требование максимальной суммарной чувствительности и специфичности модели, т.е. Cuttunderline{,,,}off_o = max_k (Se_k,+,Sp_k)
- Требование баланса между чувствительностью и специфичностью, т.е. когда Se approx Sp: Cuttunderline{,,,}off_o = min_k ,bigl |Se_k,-,Sp_k bigr |
Второе значение порога обычно предлагается пользователю по умолчанию. В третьем случае порог есть точка пересечения двух кривых, когда по оси X откладывается порог отсечения, а по оси Y — чувствительность или специфичность модели (рис. 6).
Рис. 6 — «Точка баланса» между чувствительностью и специфичностью
Существуют и другие подходы, когда ошибкам I и II рода назначается вес, который интерпретируется как цена ошибок. Но здесь встает проблема определения этих весов, что само по себе является сложной, а часто не разрешимой задачей.
Литература
- Цыплаков А. А. Некоторые эконометрические методы. Метод максимального правдоподобия в эконометрии. Учебное пособие.
- Fawcett T. ROC Graphs: Notes and Practical Considerations for Researchers // 2004 Kluwer Academic Publishers.
- Zweig M.H., Campbell G. ROC Plots: A Fundamental Evaluation Tool in Clinical Medicine // Clinical Chemistry, Vol. 39, No. 4, 1993.
- Davis J., Goadrich M. The Relationship Between Precision-Recall and ROC Curves // Proc. Of 23 International Conference on Machine Learning, Pittsburgh, PA, 2006.
Другие материалы по теме:
Применение логистической регрессии в медицине и скоринге
Machine learning в Loginom на примере задачи c Kaggle
Статистическая модель для двоичной зависимой переменной
В статистика, логистика модель (или модель логита ) используется для моделирования вероятности существования определенного класса или события, например, пройден / не пройден, выиграл / проиграл, жив / мертв или здоров / болен. Это может быть расширено для моделирования нескольких классов событий, таких как определение наличия на изображении кошки, собаки, льва и т. Д. Каждому обнаруживаемому на изображении объекту будет присвоена вероятность от 0 до 1 с суммой, равной единице.
Логистическая регрессия – это статистическая модель, которая в своей базовой форме использует логистическую функцию для моделирования двоичной зависимой переменной, хотя существует множество более сложных расширений. В регрессионном анализе, логистическая регрессия (или логит-регрессия ) – это оценка параметров логистической модели (форма двоичная регрессия ). Математически бинарная логистическая модель имеет зависимую переменную с двумя возможными значениями, например годен / не годен, которая представлена индикаторной переменной , где два значения помечены как «0» и «1». В логистической модели логарифм-шансы (логарифм от шансов ) для значения с меткой «1» представляет собой линейную комбинацию одной или нескольких независимых переменных («предикторов»); каждая независимая переменная может быть двоичной переменной (два класса, кодируемых индикаторной переменной) или непрерывной переменной (любое действительное значение). Соответствующая вероятность значения, помеченного «1», может варьироваться от 0 (обязательно значение «0») до 1 (безусловно, значение «1»), отсюда и маркировка; функция, которая преобразует логарифмические шансы в вероятность, является логистической функцией, отсюда и название. единица измерения для логарифмической шкалы шансов называется логит, от log istic un it, отсюда и альтернативные названия. Можно также использовать аналогичные модели с другой сигмовидной функцией вместо логистической функции, например, пробит-модель ; определяющей характеристикой логистической модели является то, что увеличение одной из независимых переменных мультипликативно увеличивает шансы данного результата с постоянной скоростью, при этом каждая независимая переменная имеет свой собственный параметр; для двоичной зависимой переменной это обобщает отношение шансов.
. В модели двоичной логистической регрессии зависимая переменная имеет два уровня (категориальный ). Выходы с более чем двумя значениями моделируются с помощью полиномиальной логистической регрессии и, если несколько категорий упорядочены, с помощью порядковой логистической регрессии (например, порядковый номер пропорционального шанса логистическая модель). Сама модель логистической регрессии просто моделирует вероятность выхода с точки зрения входных данных и не выполняет статистическую классификацию (это не классификатор), хотя ее можно использовать для создания классификатора, например, путем выбора порогового значения. значение и классификация входных данных с вероятностью выше порогового значения как один класс, ниже порогового значения как другой; это обычный способ создания бинарного классификатора . Коэффициенты обычно не вычисляются с помощью выражения в замкнутой форме, в отличие от линейного метода наименьших квадратов ; см. § Примерка модели. Логистическая регрессия как общая статистическая модель была первоначально разработана и популяризирована в первую очередь Джозефом Берксоном, начиная с Берксона (1944) harvtxt error: no target: CITEREFBerkson1944 (help ), где он придумал “логит”; см. § История.
Содержание
- 1 Приложения
- 2 Примеры
- 2.1 Логистическая модель
- 2.2 Вероятность сдачи экзамена по сравнению с часами обучения
- 3 Обсуждение
- 4 Логистическая регрессия по сравнению с другими подходами
- 5 Интерпретация скрытой переменной
- 6 Логистическая функция, шансы, отношение шансов и логит
- 6.1 Определение логистической функции
- 6.2 Определение обратной логистической функции
- 6.3 Интерпретация этих терминов
- 6.4 Определение шансов
- 6.5 Отношение шансов
- 6.6 Множественные объясняющие переменные
- 7 Подгонка модели
- 7.1 «Правило десяти»
- 7.2 Оценка максимального правдоподобия (MLE)
- 7.2.1 Функция кросс-энтропии потерь
- 7.3 Итеративно пересчитываемые наименьшие квадраты (IRLS)
- 7.4 Оценка согласия
- 7.4.1 Тесты на отклонение и отношение правдоподобия
- R-квадрат
- 7.4.3 Тест Хосмера – Лемешоу
- 8 Коэффициенты
- 8.1 Тест отношения правдоподобия
- 8.2 Статистика Вальда
- 8.3 Выборка случай-контроль
- 9 Формальные математические характеристики на
- 9.1 Настройка
- 9.2 Как обобщенная линейная модель
- 9.3 Как модель со скрытыми переменными
- 9.4 Двусторонняя модель со скрытыми переменными
- 9.4.1 Пример
- 9.5 Как ” лог-линейная модель
- 9.6 В качестве однослойного персептрона
- 9.7 В терминах биномиальных данных
- 10 Байесовская
- 11 История
- 12 Расширения
- 13 Программное обеспечение
- 14 См. также
- 15 Ссылки
- 16 Дополнительная литература
- 17 Внешние ссылки
Приложения
Логистическая регрессия используется в различных областях, включая машинное обучение, большинство областей медицины и социальных наук. Например, шкала оценки травм и тяжести травм (TRISS ), которая широко используется для прогнозирования смертности травмированных пациентов, была первоначально разработана Бойдом и др. с использованием логистической регрессии. Многие другие медицинские шкалы, используемые для оценки степени тяжести состояния пациента, были разработаны с использованием логистической регрессии. Логистическая регрессия может использоваться для прогнозирования риска развития данного заболевания (например, диабет ; ишемическая болезнь сердца ) на основе наблюдаемых характеристик пациента (возраст, пол, индекс массы тела, результаты различных анализов крови и т. д.). Другой пример может заключаться в том, чтобы предсказать, проголосует ли непальский избиратель за Конгресс Непала, Коммунистическую партию Непала или любую другую партию, на основании возраста, дохода, пола, расы, государства проживания, голосов на предыдущих выборах и т. Д. используется в инженерии, особенно для прогнозирования вероятности отказа данного процесса, системы или продукта. Он также используется в приложениях маркетинга, таких как прогнозирование склонности клиента к покупке продукта или прекращению подписки и т. Д. В экономике его можно использовать для прогнозирования вероятности того, что человек выбрав работу, и бизнес-приложение должно было бы прогнозировать вероятность того, что домовладелец не сможет выполнить свои обязательства по ипотеке . Условные случайные поля, расширение логистической регрессии для последовательных данных, используются в обработке естественного языка.
Примеры
Логистическая модель
Давайте попробуем понять логистическую регрессию, рассмотрев логистическую модель с заданными параметрами, а затем увидев, как можно оценить коэффициенты на основе данных. Рассмотрим модель с двумя предикторами, x 1 { displaystyle x_ {1}}






- ℓ = log b p 1 – p = β 0 + β 1 x 1 + β 2 x 2 { displaystyle ell = log _ {b} { frac {p} {1-p}} = beta _ {0} + beta _ {1} x_ {1} + beta _ {2} x_ {2}}
Мы можем восстановить шансы, возведя в степень логарифмические шансы:
- p 1 – p = b β 0 + β 1 x 1 + β 2 x 2 { displaystyle { frac {p } {1-p}} = b ^ { beta _ {0} + beta _ {1} x_ {1} + beta _ {2} x_ {2}}}
.
С помощью простых алгебраических манипуляций вероятность того, что Y = 1 { displaystyle Y = 1}
- p = b β 0 + β 1 x 1 + β 2 x 2 b β 0 + β 1 x 1 + β 2 Икс 2 + 1 знак равно 1 1 + б – (β 0 + β 1 Икс 1 + β 2 Икс 2) { Displaystyle p = { frac {b ^ { beta _ {0} + beta _ {1} x_ {1} + beta _ {2} x_ {2}}} {b ^ { beta _ {0} + beta _ {1} x_ {1} + beta _ {2} x_ {2}} +1}} = { frac {1} {1 + b ^ {- ( beta _ {0} + beta _ {1} x_ {1} + beta _ {2} x_ {2})}} }}
.
Приведенная выше формула показывает, что как только β i { displaystyle beta _ {i}}






Мы рассмотрим пример с b = 10 { displaystyle b = 10}



- log 10 p 1 – p = ℓ = – 3 + x 1 + 2 x 2 { displaystyle log _ {10} { frac {p} {1-p}} = ell = -3 + x_ {1} + 2x_ {2}}
где p { displaystyle p}

Это можно интерпретировать следующим образом:
- β 0 = – 3 { displaystyle beta _ {0} = – 3}
– y- перехватить. Это логарифм события, что Y = 1 { displaystyle Y = 1}
, когда предикторы x 1 = x 2 = 0 { displaystyle x_ {1} = x_ {2} = 0}
. Возведя в степень, мы можем увидеть, что когда x 1 = x 2 = 0 { displaystyle x_ {1} = x_ {2} = 0}
вероятность того, что Y = 1 { displaystyle Y = 1}
от 1 до 1000 или 10–3 { displaystyle 10 ^ {- 3}}
. Точно так же вероятность события, что Y = 1 { displaystyle Y = 1}
, когда x 1 = x 2 = 0 { displaystyle x_ {1} = x_ {2} = 0}
можно вычислить как 1 / (1000 + 1) = 1/1001 { displaystyle 1 / (1000 + 1) = 1/1001}
.
- β 1 = 1 { displaystyle beta _ {1} = 1}
означает, что увеличение x 1 { displaystyle x_ {1}}
на 1 увеличивает логарифмические шансы на 1 { displaystyle 1}
. Таким образом, если x 1 { displaystyle x_ {1}}
увеличивается на 1, шансы того, что Y = 1 { displaystyle Y = 1}
увеличиваются на коэффициент 10 1 { displaystyle 10 ^ {1}}
. Обратите внимание, что вероятность из Y = 1 { displaystyle Y = 1}
также увеличилась, но не настолько, насколько увеличились шансы.
- β 2 = 2 { displaystyle beta _ {2} = 2}
означает, что увеличение x 2 { displaystyle x_ {2}}
на 1 увеличивает журнал -odds по 2 { displaystyle 2}
. Таким образом, если x 2 { displaystyle x_ {2}}
увеличивается на 1, шансы того, что Y = 1 { displaystyle Y = 1}
увеличиваются на коэффициент 10 2. { displaystyle 10 ^ {2}.}
Обратите внимание, как влияние x 2 { displaystyle x_ {2}}
на логарифмические шансы вдвое больше, чем эффект x 1 { displaystyle x_ {1}}
, но влияние на шансы в 10 раз больше. Но влияние на вероятность из Y = 1 { displaystyle Y = 1}
не в 10 раз больше, это только влияние на шансы В 10 раз больше.
Чтобы оценить параметры β i { displaystyle beta _ {i}}
Вероятность сдачи экзамена в зависимости от часов обучения
Чтобы ответить на следующий вопрос:
Группа из 20 студентов тратит от 0 до 6 часов на подготовку к экзамену. Как количество часов, потраченных на обучение, влияет на вероятность сдачи студентом экзамена?
Причина использования логистической регрессии для этой проблемы заключается в том, что значения зависимой переменной, пройден и не пройден, хотя и представлены «1» и «0», не являются количественными числами. Если проблема была изменена таким образом, что результат «прошел / не прошел» был заменен оценкой 0–100 (количественные числа), то можно было использовать простой регрессионный анализ .
В таблице показано количество часов, потраченных каждым студентом на обучение, а также его прохождение (1) или неудача (0).
| Часы | 0,50 | 0,75 | 1,00 | 1,25 | 1,50 | 1,75 | 1,75 | 2,00 | 2,25 | 2,50 | 2,75 | 3,00 | 3,25 | 3,50 | 4,00 | 4,25 | 4,50 | 4,75 | 5,00 | 5,50 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Пройдено | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
График показывает вероятность сдачи экзамена в зависимости от количества часов обучения, с кривой логистической регрессии, подобранной к данным.
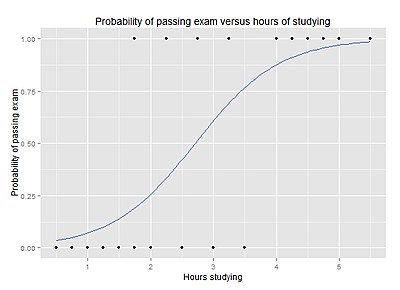
Анализ логистической регрессии дает следующий результат.
| Коэффициент | Стандартная ошибка | z- значение | P-значение (Wald) | |
|---|---|---|---|---|
| Intercept | -4.0777 | 1,7610 | −2,316 | 0,0206 |
| Часы | 1,5046 | 0,6287 | 2,393 | 0,0167 |
Вывод показывает, что количество часов обучения в значительной степени связано с вероятностью сдачи экзамена (p = 0,0167 { displaystyle p = 0,0167}


- Лог-шансы сдачи экзамена = 1,5046 ⋅ Часы – 4,0777 = 1,5046 ⋅ (Часы – 2,71) Шансы сдачи экзамена = exp (1,5046 ⋅ часов – 4,0777) = exp (1,5046 ⋅ (часов – 2,71)) Вероятность сдачи экзамена = 1 1 + exp (- (1,5046 ⋅ часов – 4,0777)) { displaystyle { begin {align} { text {Лог-шансы сдачи экзамена}} = 1,5046 cdot { text {Часы}} – 4,0777 = 1,5046 cdot ({ text {Часы}} – 2,71) \ { text {Шансы на сдачу экзамена }} = exp left (1.5046 cdot { text {Hours}} – 4.0777 right) = exp left (1.5046 cdot ({ text {Hours}} – 2,71) right) \ { text {Вероятность сдачи экзамена}} = { frac {1} {1+ exp left (- left (1.5046 cdot { text {Hours}} – 4.0777 right) right)}} end {align}}}
Один дополнительный час обучения, по оценкам, увеличит логарифмические шансы успешного прохождения экзамена на 1,5046, поэтому умножение шансов на прохождение экзамена на exp (1,5046) ≈ 4,5. { displaystyle exp (1.5046) приблизительно 4.5.}
Например, для студента, который учится 2 часа, ввод значения Часы = 2 { displaystyle { text {Hours}} = 2}
- Вероятность сдачи экзамена = 1 1 + exp (- (1,5046 ⋅ 2 – 4,0777)) = 0,26 { displaystyle { text {Вероятность сдачи экзамена}} = { frac {1} {1+ exp left (- left (1.5046 cdot 2-4.0777 right) right)}} = 0,26}
Аналогично, для студента, который учится 4 часа, оценочная вероятность сдача экзамена составляет 0,87:
- Вероятность сдачи экзамена = 1 1 + exp (- (1,5046 ⋅ 4 – 4,0777)) = 0,87 { displaystyle { text {Вероятность сдачи экзамена}} = { frac {1 } {1+ exp left (- left (1.5046 cdot 4-4.0777 right) right)}} = 0,87}
В этой таблице показана вероятность сдачи экзамена для нескольких значений часов обучения.
| Часы. учебы | Сдача экзамена | ||
|---|---|---|---|
| Журналы | Запросы | Вероятность | |
| 1 | −2,57 | 0,076 ≈ 1: 13,1 | 0,07 |
| 2 | −1,07 | 0,34 ≈ 1: 2,91 | 0,26 |
| 3 | 0,44 | 1,55 | 0,61 |
| 4 | 1,94 | 6,96 | 0,87 |
| 5 | 3,45 | 31,4 | 0,97 |
Результат анализа логистической регрессии дает p -значение p = 0,0167 { displaystyle p = 0,0167}

Обсуждение
Логистическая регрессия может быть биномиальной, порядковой или полиномиальной. Биномиальная или двоичная логистическая регрессия имеет дело с ситуациями, в которых наблюдаемый результат для зависимой переменной может иметь только два возможных типа: «0» и «1» (которые могут представлять, например, «мертвый» vs. «жив» или «победа» против «проигрыша»). Полиномиальная логистическая регрессия имеет дело с ситуациями, в которых результат может иметь три или более возможных типа (например, «болезнь A» против «болезни B» против «болезни C»), которые не упорядочены. Порядковая логистическая регрессия имеет дело с упорядоченными зависимыми переменными.
В бинарной логистической регрессии результат обычно кодируется как «0» или «1», поскольку это приводит к наиболее простой интерпретации. Если конкретный наблюдаемый результат для зависимой переменной является заслуживающим внимания возможным результатом (называемым «успехом», «экземпляром» или «случаем»), он обычно кодируется как «1», а противоположный результат (называемый «сбой» или «неэкземпляр» или «не случай») как «0». Двоичная логистическая регрессия используется для прогнозирования шансов наличия случая на основе значений независимых переменных (предикторов). Шансы определяются как вероятность того, что конкретный исход является случаем, деленный на вероятность того, что это не случай.
Как и другие формы регрессионного анализа, логистическая регрессия использует одну или несколько переменных-предикторов, которые могут быть непрерывными или категориальными. Однако, в отличие от обычной линейной регрессии, логистическая регрессия используется для прогнозирования зависимых переменных, которые принимают принадлежность к одной из ограниченного числа категорий (рассматривая зависимую переменную в биномиальном случае как результат Бернулли. испытание ), а не непрерывный результат. Учитывая эту разницу, предположения линейной регрессии нарушаются. В частности, остатки не могут быть нормально распределены. Кроме того, линейная регрессия может делать бессмысленные прогнозы для двоичной зависимой переменной. Что необходимо, так это способ преобразования двоичной переменной в непрерывную, которая может принимать любое реальное значение (отрицательное или положительное). Для этого биномиальная логистическая регрессия сначала вычисляет шансы события, происходящего для разных уровней каждой независимой переменной, а затем берет свой логарифм, чтобы создать непрерывный критерий как преобразованную версию зависимая переменная. Логарифм шансов – это логит вероятности, логит определяется следующим образом:
-
- логит p = ln p 1 – p для 0 < p < 1. {displaystyle operatorname {logit} p=ln {frac {p}{1-p}}quad {text{for }}0
- логит p = ln p 1 – p для 0 < p < 1. {displaystyle operatorname {logit} p=ln {frac {p}{1-p}}quad {text{for }}0
Хотя зависимая переменная в логистической регрессии Бернулли, логит неограниченного масштаба. Логит-функция – это функция связи в таком виде обобщенной линейной модели, то есть
-
- logit E (Y) = β 0 + β 1 x { displaystyle operatorname {logit} operatorname { mathcal {E}} (Y) = beta _ {0} + beta _ {1} x}
- logit E (Y) = β 0 + β 1 x { displaystyle operatorname {logit} operatorname { mathcal {E}} (Y) = beta _ {0} + beta _ {1} x}
Y – это распределенная Бернулли переменная ответа, а x – переменная-предиктор; значения β – линейные параметры.
Затем логит вероятности успеха подбирается для предикторов. Прогнозируемое значение логита преобразуется обратно в прогнозируемые шансы с помощью обратного натурального логарифма – экспоненциальной функции . Таким образом, хотя наблюдаемая зависимая переменная в бинарной логистической регрессии представляет собой переменную 0 или 1, логистическая регрессия оценивает шансы, как непрерывную переменную, того, что зависимая переменная является «успехом». В некоторых приложениях все, что нужно, – это ставки. В других случаях требуется конкретный прогноз типа «да» или «нет» для определения того, является ли зависимая переменная «успехом»; это категориальное предсказание может быть основано на вычисленных шансах на успех, при этом предсказанные шансы выше некоторого выбранного значения отсечения переводятся в предсказание успеха.
Предположение о линейных эффектах предиктора можно легко ослабить с помощью таких методов, как сплайн-функции.
Логистическая регрессия по сравнению с другими подходами
Логистическая регрессия измеряет взаимосвязь между категориальной зависимой переменной и одну или несколько независимых переменных путем оценки вероятностей с использованием логистической функции , которая является кумулятивной функцией распределения логистического распределения. Таким образом, он обрабатывает тот же набор проблем, что и пробит-регрессия, используя аналогичные методы, причем последний использует вместо этого кумулятивную кривую нормального распределения. Эквивалентно, в интерпретации скрытых переменных этих двух методов, первый предполагает стандартное логистическое распределение ошибок, а второй – стандартное нормальное распределение ошибок.
Логистический регрессию можно рассматривать как частный случай обобщенной линейной модели и, таким образом, аналог линейной регрессии. Однако модель логистической регрессии основана на совершенно иных предположениях (о взаимосвязи между зависимыми и независимыми переменными) от предположений линейной регрессии. В частности, ключевые различия между этими двумя моделями можно увидеть в следующих двух особенностях логистической регрессии. Во-первых, условное распределение y ∣ x { displaystyle y mid x}
Логистическая регрессия является альтернативой методу Фишера 1936 года, линейному дискриминантному анализу. Если допущения линейного дискриминантного анализа верны, обусловленность может быть отменена для получения логистической регрессии. Однако обратное неверно, поскольку логистическая регрессия не требует многомерного нормального допущения дискриминантного анализа.
Интерпретация скрытых переменных
Логистическая регрессия может пониматься просто как нахождение β { displaystyle beta}
- y = {1 β 0 + β 1 x + ε>0 0 else { displaystyle y = { begin {cases} 1 beta _ {0} + beta _ {1} x + varepsilon>0 \ 0 { text {else}} end {cases}}}
где ε { displaystyle varepsilon}
Соответствующая скрытая переменная: y ′ = β 0 + β 1 x + ε { displaystyle y ‘= beta _ {0} + beta _ { 1} х + varepsilon}









Логистическая функция, шансы, отношение шансов и логит

σ (t) { displaystyle sigma (t)}

σ (t) ∈ (0, 1) { displaystyle sigma (t) in (0,1)}

t { displaystyle t}

Определение логистической функции
Объяснение логистической регрессии можно начать с объяснения стандартной логистической функции . Логистическая функция – это сигмовидная функция, которая принимает любой реальный ввод t { displaystyle t}


- σ (t) = etet + 1 = 1 1 + e – t { displaystyle sigma (t) = { frac {e ^ {t}} {e ^ {t} +1}} = { frac {1} {1 + e ^ {- t}}}}
График логистической функции на t-интервале (−6,6) показан на рисунке 1.
Предположим, что t { displaystyle t}



- t = β 0 + β 1 x { displaystyle t = beta _ {0} + beta _ {1 } x}
И общая логистическая функция p: R → (0, 1) { displaystyle p: mathbb {R} rightarrow (0,1)}
- p (x) = σ (t) = 1 1 + e – (β 0 + β 1 x) { displaystyle p (x) = sigma (t) = { frac {1} { 1 + e ^ {- ( beta _ {0} + beta _ {1} x)}}}}
В логистической модели p (x) { displaystyle p (x)}






Определение обратной логистической функции
Теперь мы можем определить функцию logit (логарифм шансов) как обратную g = σ – 1 { displaystyle g = sigma ^ {- 1}}
- g (p (x)) = σ – 1 (p (x)) = logit p (x) = ln (p (x) 1 – p (x)) знак равно β 0 + β 1 Икс, { Displaystyle g (p (x)) = sigma ^ {- 1} (p (x)) = operatorname {logit} p (x) = ln left ({ frac {p (x)} {1-p (x)}} right) = beta _ {0} + beta _ {1} x,}
и, что то же самое, после возведения в степень обе стороны мы имеем шансы:
- p (x) 1 – p (x) = e β 0 + β 1 x. { displaystyle { frac {p (x)} {1-p (x)}} = e ^ { beta _ {0} + beta _ {1} x}.}
Толкование этих терминов
В приведенных выше уравнениях используются следующие члены:
- g { displaystyle g}
– логит-функция. Уравнение для g (p (x)) { displaystyle g (p (x))}
показывает, что logit (т. Е. Логарифм шансов или натуральный логарифм шансы) эквивалентно выражению линейной регрессии.
- ln { displaystyle ln}
обозначает натуральный логарифм.
- p (x) { displaystyle p (x)}
– вероятность того, что зависимая переменная соответствует случаю, при некоторой линейной комбинации предикторов. Формула для p (x) { displaystyle p (x)}
показывает, что вероятность того, что зависимая переменная равна случаю, равна значению логистической функции выражения линейной регрессии. Это важно, поскольку показывает, что значение выражения линейной регрессии может изменяться от отрицательной до положительной бесконечности, и все же после преобразования результирующее выражение для вероятности p (x) { displaystyle p (x)}
находится в диапазоне от 0 до 1.
- β 0 { displaystyle beta _ {0}}
– отрезок из уравнения линейной регрессии (значение критерий, когда предиктор равен нулю).
- β 1 x { displaystyle beta _ {1} x}
– коэффициент регрессии, умноженный на некоторое значение предиктора.
- base e { displaystyle e}
обозначает экспоненциальную функцию.
Определение шансов
Шансы зависимой переменной, равной случаю (при некоторой линейной комбинации x { displaystyle x}
Итак, мы определяем шансы зависимой переменной, равные случаю (при некоторой линейной комбинации x { displaystyle x}
- шансы = e β 0 + β 1 x. { displaystyle { text {odds}} = e ^ { beta _ {0} + beta _ {1} x}.}
Отношение шансов
Для непрерывной независимой переменной шансы соотношение может быть определено как:
- ИЛИ = шансы (x + 1) шансы (x) = (F (x + 1) 1 – F (x + 1)) (F (x) 1 – F (x)) знак равно е β 0 + β 1 (Икс + 1) е β 0 + β 1 Икс = е β 1 { Displaystyle mathrm {ИЛИ} = { гидроразрыва { OperatorName {odds} (х + 1)} { operatorname {odds} (x)}} = { frac { left ({ frac {F (x + 1)} {1-F (x + 1)}} right)} { left ({ frac {F (x)} {1-F (x)}} right)}} = { frac {e ^ { beta _ {0} + beta _ {1} (x + 1)}} { e ^ { beta _ {0} + beta _ {1} x}}} = e ^ { beta _ {1}}}
Эта экспоненциальная зависимость дает интерпретацию для β 1 { displaystyle beta _ {1}}

Для двоичной независимой переменной отношение шансов определяется как adbc { displaystyle { frac {ad} {bc}}}
Множественное объяснение Или переменные
Если есть несколько независимых переменных, приведенное выше выражение β 0 + β 1 x { displaystyle beta _ {0} + beta _ {1} x}


Опять же, более традиционные уравнения:
- log p 1 – p = β 0 + β 1 x 1 + β 2 x 2 + ⋯ + β mxm { displaystyle log { frac { p} {1-p}} = beta _ {0} + beta _ {1} x_ {1} + beta _ {2} x_ {2} + cdots + beta _ {m} x_ {m }}
и
- p = 1 1 + b – (β 0 + β 1 x 1 + β 2 x 2 + ⋯ + β mxm) { displaystyle p = { frac {1} {1 + b ^ {- ( beta _ {0} + beta _ {1} x_ {1} + beta _ {2} x_ {2} + cdots + beta _ {m} x_ {m})}}} }
где обычно b = e { displaystyle b = e}
Подгонка модели
Логистическая регрессия – важный алгоритм машинного обучения. Цель состоит в том, чтобы смоделировать вероятность того, что случайная величина Y { displaystyle Y}
Рассмотрим обобщенную линейную модель функция, параметризованная с помощью θ { displaystyle theta}
- h θ (X) = 1 1 + e – θ TX = Pr (Y = 1 ∣ X; θ) { displaystyle h _ { theta} ( X) = { frac {1} {1 + e ^ {- theta ^ {T} X}}} = Pr (Y = 1 mid X; theta)}
Следовательно,
- Pr (Y = 0 ∣ X; θ) = 1 – час θ (X) { displaystyle Pr (Y = 0 mid X; theta) = 1-h _ { theta} (X)}
и поскольку Y ∈ {0, 1} { displaystyle Y in {0,1 }}


- L (θ ∣ y; x) = Pr (Y ∣ X; θ) Знак равно ∏ я Pr (yi ∣ xi; θ) знак равно ∏ ih θ (xi) yi (1 – час θ (xi)) (1 – yi) { displaystyle { begin {выровнено} L ( theta mid y; x) = Pr (Y mid X; theta) \ = prod _ {i} Pr (y_ {i} mid x_ {i}; theta) \ = prod _ { i} h _ { theta} (x_ {i}) ^ {y_ {i}} (1-h _ { theta} (x_ {i})) ^ {(1-y_ {i})} end {выровнено }}}
Как правило, логарифм правдоподобия максимизируется,
- N – 1 log L (θ ∣ y; x) = N – 1 ∑ i = 1 N log Pr (yi ∣ xi; θ) { Displaystyle N ^ {- 1} log L ( theta mid y; x) = N ^ {- 1} sum _ {i = 1} ^ {N} log Pr (y_ {i} mid x_{i};theta)}
which is maximized using optimization techniques such as gradient descent.
Assuming the ( x, y) {displaystyle (x,y)}
- lim N → + ∞ N − 1 ∑ i = 1 N log Pr ( y i ∣ x i ; θ) = ∑ x ∈ X ∑ y ∈ Y Pr ( X = x, Y = y) log Pr ( Y = y ∣ X = x ; θ) = ∑ x ∈ X ∑ y ∈ Y Pr ( X = x, Y = y) ( − log Pr ( Y = y ∣ X = x) Pr ( Y = y ∣ X = x ; θ) + log Pr ( Y = y ∣ X = x)) = − D KL ( Y ∥ Y θ) − H ( Y ∣ X) {displaystyle {begin{aligned}lim limits _{Nrightarrow +infty }N^{-1}sum _{i=1}^{N}log Pr(y_{i}mid x_{i};theta)=sum _{xin {mathcal {X}}}sum _{yin {mathcal {Y}}}Pr(X=x,Y=y)log Pr(Y=ymid X=x;theta)\[6pt]={}sum _{xin {mathcal {X}}}sum _{yin {mathcal {Y}}}Pr(X=x,Y=y)left(-log {frac {Pr(Y=ymid X=x)}{Pr(Y=ymid X=x;theta)}}+log Pr(Y=ymid X=x)right)\[6pt]={}-D_{text{KL}}(Yparallel Y_{theta })-H(Ymid X)end{aligned}}}
where H ( X ∣ Y) {displaystyle H(Xmid Y)}

“Rule of ten”
A widely used rule of thumb, the “one in ten rule “, states that logistic regression models give stable values for the explanatory variables if based on a minimum of about 10 events per explanatory variable (EPV); где событие обозначает случаи, относящиеся к менее частой категории в зависимой переменной. Thus a study designed to use k { displaystyle k}


Другие получили результаты, которые не согласуются с вышеизложенным, с использованием других критериев. Полезным критерием является то, будет ли подобранная модель, как ожидается, достичь той же прогностической дискриминации в новой выборке, которую она достигла в образце для разработки модели. Для этого критерия может потребоваться 20 событий для каждой переменной-кандидата. Кроме того, можно утверждать, что 96 наблюдений необходимы только для оценки точки пересечения модели с достаточной точностью, чтобы предел ошибки в прогнозируемых вероятностях составлял ± 0,1 при уровне достоверности 0,95.
Оценка максимального правдоподобия (MLE)
Коэффициенты регрессии обычно оцениваются с использованием оценки максимального правдоподобия. В отличие от линейной регрессии с нормально распределенными остатками, невозможно найти выражение в замкнутой форме для значений коэффициентов, которые максимизируют функцию правдоподобия, поэтому вместо этого следует использовать итерационный процесс; например метод Ньютона. Этот процесс начинается с предварительного решения, его немного изменяют, чтобы посмотреть, можно ли его улучшить, и повторяют это изменение до тех пор, пока улучшения не прекратятся, после чего процесс считается сходимым.
В некоторых случаях, модель может не достичь сходимости. Несходимость модели указывает на то, что коэффициенты не имеют смысла, поскольку итерационный процесс не смог найти подходящие решения. Неспособность сойтись может произойти по ряду причин: наличие большого отношения предикторов к случаям, мультиколлинеарность, разреженность или полное разделение.
- Наличие большого отношения от переменных к наблюдениям приводит к чрезмерно консервативной статистике Вальда (обсуждается ниже) и может привести к несходимости. Регуляризованная логистическая регрессия специально предназначена для использования в этой ситуации.
- Мультиколлинеарность относится к недопустимо высоким корреляциям между предикторами. По мере увеличения мультиколлинеарности коэффициенты остаются несмещенными, но увеличиваются стандартные ошибки и уменьшается вероятность сходимости модели. Чтобы обнаружить мультиколлинеарность среди предикторов, можно провести линейный регрессионный анализ с интересующими предикторами с единственной целью изучения статистики толерантности, используемой для оценки того, является ли мультиколлинеарность неприемлемо высокой.
- Разрезанность данных означает наличие большая доля пустых ячеек (ячеек с нулевым счетчиком). Нулевое количество ячеек особенно проблематично для категориальных предикторов. С непрерывными предикторами модель может вывести значения для нулевого количества ячеек, но это не относится к категориальным предикторам. Модель не будет сходиться при нулевом количестве ячеек для категориальных предикторов, потому что натуральный логарифм нуля является неопределенным значением, поэтому окончательное решение модели не может быть достигнуто. Чтобы решить эту проблему, исследователи могут свернуть категории теоретически значимым образом или добавить константу ко всем ячейкам.
- Другой числовой проблемой, которая может привести к отсутствию сходимости, является полное разделение, которое относится к случаю, когда предикторы отлично предсказывают критерий – все случаи точно классифицируются. В таких случаях следует повторно изучить данные, поскольку существует вероятность ошибки.
- Можно также использовать полупараметрические или непараметрические подходы, например, с помощью методов локальной вероятности или непараметрической квазиправдоподобия., что позволяет избежать предположений о параметрической форме для функции индекса и устойчиво к выбору функции связи (например, пробит или логит).
Функция потери кросс-энтропии
В приложениях машинного обучения, где логистические регрессия используется для двоичной классификации, MLE минимизирует функцию потерь перекрестной энтропии .
Метод наименьших квадратов с итеративным перевесом (IRLS)
Двоичная логистическая регрессия (y = 0 { displaystyle y = 0}

![{displaystyle mathbf {w} ^{T}=[beta _{0},beta _{1},beta _{2},ldots ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/daccbf84c2c936e0559016491efe98eaf0eca430)
![{displaystyle mathbf {x} (i)=[1,x_{1}(i),x_{2}(i),ldots ]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8fc5f11bdd42f672417a3f4e44b3a4e5be28faa)


- wk + 1 = (XTS k X) – 1 XT (S k X wk + y – μ k) { displaystyle mathbf {w} _ {k + 1} = left ( mathbf {X} ^ {T} mathbf {S} _ {k} mathbf {X} right) ^ {- 1} mathbf {X} ^ {T} left ( mathbf {S} _ {k } mathbf {X} mathbf {w} _ {k} + mathbf {y} – mathbf { boldsymbol { mu}} _ {k} right)}
где S = diag (μ (я) (1 – μ (я))) { Displaystyle mathbf {S} = operatornam e {diag} ( mu (i) (1- mu (i)))}
![{displaystyle {boldsymbol {mu }}=[mu (1),mu (2),ldots ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/800927e9be36f4cac166a68862c04234cffd67b8)
- X = [1 x 1 (1) x 2 (1)… 1 x 1 (2) x 2 (2)… ⋮ ⋮ ⋮] { displaystyle mathbf {X} = { begin {bmatrix} 1 x_ {1} (1) x_ { 2} (1) ldots \ 1 x_ {1} (2) x_ {2} (2) ldots \ vdots vdots vdots end {bmatrix}}}
Матрица регрессора и y (i) = [y (1), y (2),…] T { displaystyle mathbf {y} (i) = [y (1), y (2), ldots] ^ {T}}![{displaystyle mathbf {y} (i)=[y(1),y(2),ldots ]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33cbd315328b6ccfc7f216d65e39f92a8ec48694)
Оценка качества соответствия
Качество соответствия в моделях линейной регрессии обычно измеряется с использованием R. Поскольку у этого нет прямого аналога в логистической регрессии, вместо него можно использовать различные методы, включая следующие.
Тесты на отклонение и отношение правдоподобия
В линейном регрессионном анализе рассматривается разделение дисперсии с помощью вычислений суммы квадратов – дисперсия критерия по существу делится на дисперсию учитывается предикторами и остаточной дисперсией. В анализе логистической регрессии отклонение используется вместо вычисления суммы квадратов. Отклонение аналогично вычислению суммы квадратов в линейной регрессии и является мерой отсутствия соответствия данным в модели логистической регрессии. Когда доступна «насыщенная» модель (модель с теоретически идеальным соответствием), отклонение рассчитывается путем сравнения данной модели с насыщенной моделью. Это вычисление дает критерий отношения правдоподобия :
- D = – 2 ln вероятность подобранной модели вероятность насыщенной модели. { displaystyle D = -2 ln { frac { text {вероятность подобранной модели}} { text {вероятность насыщенной модели}}}.}
В приведенном выше уравнении D представляет отклонение и ln представляет собой натуральный логарифм. Логарифм этого отношения правдоподобия (отношение подобранной модели к насыщенной модели) даст отрицательное значение, следовательно, потребуется отрицательный знак. Можно показать, что D соответствует приблизительному распределению хи-квадрат. Меньшие значения указывают на лучшее соответствие, поскольку подобранная модель меньше отклоняется от насыщенной модели. При оценке по распределению хи-квадрат незначительные значения хи-квадрат указывают на очень небольшую необъяснимую дисперсию и, следовательно, хорошее соответствие модели. И наоборот, значительное значение хи-квадрат указывает на то, что значительная величина дисперсии необъяснима.
Когда насыщенная модель недоступна (общий случай), отклонение вычисляется просто как −2 · (логарифмическая вероятность подобранной модели), и ссылка на логарифмическую вероятность насыщенной модели может быть удалена из всех это следует без вреда.
Два показателя отклонения особенно важны в логистической регрессии: нулевое отклонение и отклонение модели. Нулевое отклонение представляет собой разницу между моделью только с точкой пересечения (что означает «без предикторов») и насыщенной моделью. Отклонение модели представляет собой разницу между моделью с хотя бы одним предиктором и насыщенной моделью. В этом отношении нулевая модель обеспечивает основу для сравнения моделей предикторов. Учитывая, что отклонение является мерой разницы между данной моделью и насыщенной моделью, меньшие значения указывают на лучшее соответствие. Таким образом, чтобы оценить вклад предиктора или набора предикторов, можно вычесть отклонение модели из нулевого отклонения и оценить разницу по a χ s – p 2, { displaystyle chi _ {sp} ^ { 2},}
Пусть
- D null = – 2 ln вероятность нулевой модели правдоподобия насыщенной модели D подобранная = – 2 ln вероятность подобранной модели вероятность насыщенной модели. { displaystyle { begin {align} D _ { text {null}} = – 2 ln { frac { text {вероятность нулевой модели}} { text {вероятность насыщенной модели}}} \ [6pt] D _ { text {fit}} = – 2 ln { frac { text {вероятность подобранной модели}} { text {вероятность насыщенной модели}}}. End {align}}}
Тогда разница обоих составляет:
- D нуль – D подобран = – 2 (ln вероятность нулевой модели, вероятность насыщенной модели – ln вероятность подобранной модели, вероятность насыщенной модели) = – 2 ln (вероятность нулевой модели вероятность насыщенной модели) (вероятность подобранной модели вероятность насыщенной модели) = – 2 ln вероятность нулевой модели вероятность подобранной модели. { displaystyle { begin {align} D _ { text {null}} – D _ { text {fit}} = – 2 left ( ln { frac { text {вероятность нулевой модели}} { text {вероятность насыщенной модели}}} – ln { frac { text {вероятность соответствия модели}} { text {вероятность насыщенной модели}}} right) \ [6pt] = – 2 ln { frac { left ({ dfrac { text {вероятность нулевой модели}} { text {вероятность насыщенной модели}}} right)} { left ({ dfrac { text {вероятность подобранной модели}} { text {вероятность насыщенной модели}}} right)}} \ [6pt] = – 2 ln { frac { text {вероятность нулевой модели}} { text {вероятность подобранной модели}}}. end {align}}}
Если отклонение модели значительно меньше нулевого отклонения, то можно сделать вывод, что предиктор или набор предикторов значительно улучшили соответствие модели. Это аналогично F-критерию, используемому в анализе линейной регрессии для оценки значимости прогноза.
Псевдо-R-квадрат
В линейной регрессии для оценки используется множественная корреляция в квадрате. степень согласия, поскольку она представляет собой долю дисперсии критерия, которая объясняется предикторами. В логистическом регрессионном анализе нет согласованной аналогичной меры, но есть несколько конкурирующих мер, каждая из которых имеет ограничения.
На этой странице рассматриваются четыре наиболее часто используемых индекса и один менее часто используемый:
- Отношение правдоподобия R² L
- R² Кокса и Снелла CS
- Nagelkerke R² N
- McFadden R2 McF
- Tjur R² T
R²Lопределяется Коэном:
-
- RL 2 = D null – D соответствует D значение NULL. { displaystyle R _ { text {L}} ^ {2} = { frac {D _ { text {null}} – D _ { text {fit}}} {D _ { text {null}}}}. }
- RL 2 = D null – D соответствует D значение NULL. { displaystyle R _ { text {L}} ^ {2} = { frac {D _ { text {null}} – D _ { text {fit}}} {D _ { text {null}}}}. }
Это наиболее аналогичный показатель квадрату множественных корреляций в линейной регрессии. Он представляет собой пропорциональное уменьшение отклонения, при котором отклонение рассматривается как мера отклонения, аналогичная, но не идентичная дисперсии в анализе линейной регрессии. Одним из ограничений отношения правдоподобия R² является то, что оно не связано монотонно с отношением шансов, а это означает, что оно не обязательно увеличивается по мере увеличения отношения шансов и не обязательно уменьшается по мере уменьшения отношения шансов.
R²CS- альтернативный индекс качества соответствия, связанный со значением R² из линейной регрессии. Он задается следующим образом:
-
- R CS 2 = 1 – (L 0 LM) 2 / n = 1 – e 2 (ln (L 0) – ln (LM)) / n { displaystyle { begin { выровнено} R _ { text {CS}} ^ {2} = 1- left ({ frac {L_ {0}} {L_ {M}}} right) ^ {2 / n} \ [5pt ] = 1-e ^ {2 ( ln (L_ {0}) – ln (L_ {M})) / n} end {align}}}
- R CS 2 = 1 – (L 0 LM) 2 / n = 1 – e 2 (ln (L 0) – ln (LM)) / n { displaystyle { begin { выровнено} R _ { text {CS}} ^ {2} = 1- left ({ frac {L_ {0}} {L_ {M}}} right) ^ {2 / n} \ [5pt ] = 1-e ^ {2 ( ln (L_ {0}) – ln (L_ {M})) / n} end {align}}}
где L M и {{mvar | L 0 } – вероятности для подгоняемой модели и нулевой модели соответственно. Индекс Кокса и Снелла проблематичен, поскольку его максимальное значение составляет 1 – L 0 2 / n { displaystyle 1-L_ {0} ^ {2 / n}}
R²Nобеспечивает корректировку R² Кокса и Снеллиуса, так что максимальное значение равно 1. Тем не менее, коэффициенты Кокса и Снелла и отношение правдоподобия R²s показывают большее соответствие друг с другом, чем любой из них с коэффициентом Нагелькерке R2. Конечно, это может быть не так для значений, превышающих 0,75, поскольку индекс Кокса и Снелла ограничен этим значением. Отношение правдоподобия R² часто предпочтительнее альтернатив, поскольку оно наиболее аналогично R² в линейной регрессии, не зависит от базовой ставки (R² Кокса и Снелла и Нагелькерке увеличиваются по мере увеличения доли случаев от 0 до 0,5) и варьируется от 0 до 1.
R²McF определяется как
-
- R McF 2 = 1 – ln (LM) ln (L 0), { displaystyle R _ { text {McF }} ^ {2} = 1 – { frac { ln (L_ {M})} { ln (L_ {0})}},}
- R McF 2 = 1 – ln (LM) ln (L 0), { displaystyle R _ { text {McF }} ^ {2} = 1 – { frac { ln (L_ {M})} { ln (L_ {0})}},}
и предпочтительнее R² CS пользователя Allison. Тогда два выражения R² McF и R² CS связаны соответственно соотношением
-
- R CS 2 = 1 – (1 L 0) 2 (R McF 2) n R McF 2 Знак равно – N 2 ⋅ пер (1 – R CS 2) пер L 0 { displaystyle { begin {matrix} R _ { text {CS}} ^ {2} = 1- left ({ dfrac {1 } {L_ {0}}} right) ^ { frac {2 (R _ { text {McF}} ^ {2})} {n}} \ [1.5em] R _ { text {McF}} ^ {2} = – { dfrac {n} {2}} cdot { dfrac { ln (1-R _ { text {CS}} ^ {2})} { ln L_ {0}}} end {matrix}}}
- R CS 2 = 1 – (1 L 0) 2 (R McF 2) n R McF 2 Знак равно – N 2 ⋅ пер (1 – R CS 2) пер L 0 { displaystyle { begin {matrix} R _ { text {CS}} ^ {2} = 1- left ({ dfrac {1 } {L_ {0}}} right) ^ { frac {2 (R _ { text {McF}} ^ {2})} {n}} \ [1.5em] R _ { text {McF}} ^ {2} = – { dfrac {n} {2}} cdot { dfrac { ln (1-R _ { text {CS}} ^ {2})} { ln L_ {0}}} end {matrix}}}
Однако сейчас Эллисон предпочитает R² T, который является относительно новым показателем, разработанным Tjur. Его можно рассчитать в два этапа:
- Для каждого уровня зависимой переменной найдите среднее значение предсказанных вероятностей события.
- Возьмите абсолютное значение разницы между этими средними значениями
A слово предостережения при интерпретации статистики псевдо-R². Причина, по которой эти индексы соответствия называются псевдо-R², заключается в том, что они не представляют пропорционального уменьшения ошибки, как это делает R² в линейной регрессии. Линейная регрессия предполагает гомоскедастичность, что дисперсия ошибки одинакова для всех значений критерия. Логистическая регрессия всегда будет гетероскедастической – дисперсии ошибок различаются для каждого значения прогнозируемой оценки. Для каждого значения прогнозируемой оценки будет свое значение пропорционального уменьшения ошибки. Следовательно, неуместно думать о R² как о пропорциональном сокращении ошибки в универсальном смысле логистической регрессии.
Тест Хосмера – Лемешоу
Тест Хосмера – Лемешоу использует статистику теста, которая асимптотически следует χ 2 { displaystyle chi ^ {2}}
Коэффициенты
После подбора модели исследователи, вероятно, захотят изучить вклад отдельных предикторов. Для этого они захотят изучить коэффициенты регрессии. В линейной регрессии коэффициенты регрессии представляют изменение критерия для каждого изменения единицы в предикторе. Однако в логистической регрессии коэффициенты регрессии представляют изменение логита для каждого изменения единицы в предикторе. Учитывая, что логит не является интуитивно понятным, исследователи, вероятно, сосредоточатся на влиянии предсказателя на экспоненциальную функцию коэффициента регрессии – отношения шансов (см. определение ). В линейной регрессии значимость коэффициента регрессии оценивается путем вычисления t-критерия. В логистической регрессии существует несколько различных тестов, предназначенных для оценки значимости отдельного предиктора, в первую очередь тест отношения правдоподобия и статистика Вальда.
Тест отношения правдоподобия
Рассмотренный выше тест отношения правдоподобия для оценки соответствия модели также является рекомендуемой процедурой для оценки вклада отдельных «предикторов» в данную модель.. В случае модели с одним предиктором, просто сравнивают отклонение модели предиктора с отклонением от нулевой модели на распределении хи-квадрат с одной степенью свободы. Если модель предиктора имеет значительно меньшее отклонение (c.f хи-квадрат с использованием разницы в степенях свободы двух моделей), то можно сделать вывод, что существует значимая связь между “предиктором” и результатом. Хотя некоторые общие статистические пакеты (например, SPSS) действительно предоставляют статистику теста отношения правдоподобия, без этого требовательного к вычислениям теста было бы труднее оценить вклад отдельных предикторов в случае множественной логистической регрессии. Чтобы оценить вклад отдельных предикторов, можно ввести предикторы иерархически, сравнивая каждую новую модель с предыдущей, чтобы определить вклад каждого предиктора. Статистики спорят о целесообразности так называемых «пошаговых» процедур. Есть опасения, что они могут не сохранить номинальные статистические свойства и могут ввести в заблуждение.
Статистика Вальда
В качестве альтернативы, при оценке вклада отдельных предикторов в данную модель, можно исследовать значимость статистика Вальда. Статистика Вальда, аналогичная t-критерию линейной регрессии, используется для оценки значимости коэффициентов. Статистика Вальда представляет собой отношение квадрата коэффициента регрессии к квадрату стандартной ошибки коэффициента и асимптотически распределяется как распределение хи-квадрат.
- W j = β j 2 SE β j 2 { displaystyle W_ {j} = { frac { beta _ {j} ^ {2}} {SE _ { beta _ {j}} ^ {2}}}}
Хотя несколько статистических пакетов (например, SPSS, SAS) сообщают статистику Вальда для оценки вклада отдельных предикторов, статистика Вальда имеет ограничения. Когда коэффициент регрессии велик, стандартная ошибка коэффициента регрессии также имеет тенденцию быть больше, увеличивая вероятность ошибки типа II. Статистика Вальда также имеет тенденцию к смещению, когда данные скудны.
Выборка случай-контроль
Предположим, случаи редки. Тогда мы могли бы пожелать отбирать их чаще, чем их распространенность в популяции. Например, предположим, что есть заболевание, которым страдает 1 человек из 10 000, и для сбора данных нам необходимо пройти полное обследование. Проведение тысяч медицинских осмотров здоровых людей для получения данных только по нескольким больным может оказаться слишком дорогостоящим. Таким образом, мы можем оценить большее количество больных, возможно, все редкие исходы. Это также ретроспективная выборка, или, что то же самое, ее называют несбалансированными данными. Как показывает практический опыт, выборка контролей с частотой, в пять раз превышающей количество наблюдений, даст достаточные контрольные данные.
Логистическая регрессия уникальна тем, что ее можно оценивать на несбалансированных данных, а не на случайно выбранных данных, и по-прежнему дают правильные оценки коэффициентов влияния каждой независимой переменной на результат. То есть, если мы сформируем логистическую модель из таких данных, если модель верна для генеральной совокупности, все параметры β j { displaystyle beta _ {j}}


- β ^ 0 ∗ = β ^ 0 + log π 1 – π – журнал π ~ 1 – π ~ { displaystyle { widehat { beta}} _ {0} ^ {*} = { widehat { beta}} _ {0} + log { frac { pi} {1- pi}} – log {{ tilde { pi}} over {1 – { tilde { pi}}}}}
где π { displaystyle pi }

Формальная математическая спецификация
Существуют различные эквивалентные спецификации логистической регрессии, которые вписываются в разные типы более общих моделей. Эти разные спецификации позволяют делать разные полезные обобщения.
Настройка
Базовая настройка логистической регрессии выглядит следующим образом. Нам дан набор данных, содержащий N точек. Каждая точка i состоит из набора из m входных переменных x 1, i… x m, i (также называемых независимых переменных, переменных-предикторов, функций, или атрибуты) и двоичной выходной переменной Y i (также известной как зависимая переменная, переменная ответа, выходная переменная или класс), т.е. может принимать только два возможных значения: 0 (часто означает «нет» или «неудача») или 1 (часто означает «да» или «успех»). Целью логистической регрессии является использование набора данных для создания модели прогнозирования переменной результата.
Некоторые примеры:
- Наблюдаемые результаты – это наличие или отсутствие определенного заболевания (например, диабета) у группы пациентов, а объясняющие переменные могут быть характеристиками пациентов, которые считаются соответствующими (пол, раса, возраст, артериальное давление, индекс массы тела и т. д.).
- Наблюдаемые результаты – это голоса (например, Демократический или республиканец ) группы людей, участвующих в выборах, а независимые переменные – это демографические характеристики каждого человека (например, пол, раса, возраст, доход и т. д.). В таком случае один из двух результатов произвольно кодируется как 1, а другой – как 0.
Как и в линейной регрессии, предполагается, что переменные результата Y i зависят от независимых переменных x 1, i… x m, i.
- Объясняющие переменные
Как показано выше в приведенных выше примерах, поясняющие переменные могут быть любого типа : вещественные, двоичные, категориальные и т. Д. Основное различие между непрерывными переменными (такими как доход, возраст и кровяное давление ) и дискретные переменные (например, пол или раса). Дискретные переменные, относящиеся к более чем двум возможным вариантам выбора, обычно кодируются с использованием фиктивных переменных (или индикаторных переменных ), то есть отдельные независимые переменные, принимающие значение 0 или 1, создаются для каждого возможного значение дискретной переменной, где 1 означает «переменная имеет данное значение», а 0 означает «переменная не имеет этого значения».
Например, четырехсторонняя дискретная переменная группы крови с возможными значениями «A, B, AB, O» может быть преобразована в четыре отдельные двусторонние фиктивные переменные, » is-A, is-B, is-AB, is-O “, где только один из них имеет значение 1, а все остальные имеют значение 0. Это позволяет сопоставить отдельные коэффициенты регрессии для каждого возможного значения дискретная переменная. (В таком случае только три из четырех фиктивных переменных независимы друг от друга в том смысле, что, как только значения трех переменных известны, четвертая определяется автоматически. Таким образом, необходимо кодировать только три из четырех возможностей в качестве фиктивных переменных. Это также означает, что когда все четыре возможности закодированы, общая модель не может быть идентифицируемой при отсутствии дополнительных ограничений, таких как ограничение регуляризации. Теоретически это может вызвать проблемы, но в действительности почти все модели логистической регрессии снабжены ограничениями регуляризации.)
- Переменные результата
Формально результаты Y i описываются как данные с распределением Бернулли, где каждый результат определяется ненаблюдаемой вероятностью p i, которая специфична для данного результата, но связана с независимыми переменными. Это может быть выражено в любой из следующих эквивалентных форм:
-
- Y i ∣ x 1, i,…, xm, i ∼ Bernoulli (pi) E [Y i ∣ x 1, i,…, xm, i ] = pi Pr (Y i = y ∣ x 1, i,…, xm, i) = {pi, если y = 1 1 – pi, если y = 0 Pr (Y i = y ∣ x 1, i,…, xm, я) = piy (1 – pi) (1 – y) { displaystyle { begin {выровнено} Y_ {i} mid x_ {1, i}, ldots, x_ {m, i} sim operatorname {Bernoulli} (p_ {i}) \ operatorname { mathcal {E}} [Y_ {i} mid x_ {1, i}, ldots, x_ {m, i}] = p_ { i} \ Pr (Y_ {i} = y mid x_ {1, i}, ldots, x_ {m, i}) = { begin {cases} p_ {i} { text {если }} y = 1 \ 1-p_ {i} { text {if}} y = 0 end {cases}} \ Pr (Y_ {i} = y mid x_ {1, i}, ldots, x_ {m, i}) = p_ {i} ^ {y} (1-p_ {i}) ^ {(1-y)} end {align}}}
- Y i ∣ x 1, i,…, xm, i ∼ Bernoulli (pi) E [Y i ∣ x 1, i,…, xm, i ] = pi Pr (Y i = y ∣ x 1, i,…, xm, i) = {pi, если y = 1 1 – pi, если y = 0 Pr (Y i = y ∣ x 1, i,…, xm, я) = piy (1 – pi) (1 – y) { displaystyle { begin {выровнено} Y_ {i} mid x_ {1, i}, ldots, x_ {m, i} sim operatorname {Bernoulli} (p_ {i}) \ operatorname { mathcal {E}} [Y_ {i} mid x_ {1, i}, ldots, x_ {m, i}] = p_ { i} \ Pr (Y_ {i} = y mid x_ {1, i}, ldots, x_ {m, i}) = { begin {cases} p_ {i} { text {если }} y = 1 \ 1-p_ {i} { text {if}} y = 0 end {cases}} \ Pr (Y_ {i} = y mid x_ {1, i}, ldots, x_ {m, i}) = p_ {i} ^ {y} (1-p_ {i}) ^ {(1-y)} end {align}}}
Значения этих четыре строки:
- Первая строка выражает распределение вероятностей для каждого Y i : с учетом независимых переменных, оно следует распределению Бернулли с параметрами p i, вероятность результата 1 для испытания i. Как отмечалось выше, каждое отдельное испытание имеет собственную вероятность успеха, так же как каждое испытание имеет свои собственные объясняющие переменные. Вероятность успеха p i не наблюдается, только результат отдельного испытания Бернулли с использованием этой вероятности.
- Вторая строка выражает тот факт, что ожидаемое значение каждого Y i равна вероятности успеха p i, которая является общим свойством распределения Бернулли. Другими словами, если мы запустим большое количество испытаний Бернулли с одинаковой вероятностью успеха p i, а затем возьмем среднее значение для всех результатов 1 и 0, то результат будет близок к p <335.>я. Это связано с тем, что при таком усреднении просто вычисляется доля наблюдаемых успехов, которые, как мы ожидаем, сойдутся с основной вероятностью успеха.
- Третья строка записывает функцию вероятности-массы распределение Бернулли, определяющее вероятность увидеть каждый из двух возможных результатов.
- Четвертая строка – это еще один способ записи функции вероятности массы, который позволяет избежать написания отдельных случаев и более удобен для определенных типов расчеты. Это основано на том факте, что Y i может принимать только значение 0 или 1. В каждом случае один из показателей будет равен 1, «выбирая» значение под ним, а другой – 0 », аннулирование “значения под ним. Следовательно, результатом будет либо p i, либо 1 – p i, как в предыдущей строке.
- Функция линейного предиктора
Основная идея логистической регрессии заключается в использовании механизм, уже разработанный для линейной регрессии путем моделирования вероятности p i с использованием функции линейного предиктора, то есть линейной комбинации пояснительной переменные и набор коэффициентов регрессии, которые относятся к рассматриваемой модели, но одинаковы для всех испытаний. Функция линейного предиктора f (i) { displaystyle f (i)}
-
- f (i) = β 0 + β 1 x 1, я + ⋯ + β mxm, я, { displaystyle f (i) = beta _ {0} + beta _ {1} x_ {1, i} + cdots + beta _ {m} x_ {m, i},}
- f (i) = β 0 + β 1 x 1, я + ⋯ + β mxm, я, { displaystyle f (i) = beta _ {0} + beta _ {1} x_ {1, i} + cdots + beta _ {m} x_ {m, i},}
где β 0,…, β m { displaystyle beta _ {0}, ldots, beta _ {m}}
Модель обычно принимают в более компактном виде:
- Коэффициенты регрессии β 0, β 1,…, β m сгруппированы в один вектор β размером m + 1.
- Для каждой точки данных i, дополнительная пояснительная псевдопеременная x 0, i добавляется с фиксированным значением 1, соответствующим коэффициенту точки пересечения β 0.
- . Полученные независимые переменные x 0, i, x 1, i,…, x m, i затем группируются в один вектор Xiразмера m + 1.
Это позволяет записать функцию линейного предиктора следующим образом:
-
- f (i) = β ⋅ X i, { displaystyle f (i) = { boldsymbol { beta}} cdot mathbf {X} _ {i},}
- f (i) = β ⋅ X i, { displaystyle f (i) = { boldsymbol { beta}} cdot mathbf {X} _ {i},}
используя обозначение для скалярное произведение между двумя векторами.
Как обобщенная линейная модель
Конкретная модель, используемая логистической регрессией, которая отличает ее от стандартной линейной регрессии и от других типов регрессионного анализа, используемый для результатов с двоичным значением, – это способ связи вероятности конкретного результата с функцией линейного предиктора:
- logit (E [Y i ∣ x 1, i,…, хм, я]) знак равно логит (пи) знак равно пер (пи 1 – пи) = β 0 + β 1 Икс 1, я + ⋯ + β mxm, я { displaystyle operatorname {logit} ( Operatorname { mathcal {E}} [Y_ {i} mid x_ {1, i}, ldots, x_ {m, i}]) = operatorname {logit} (p_ {i}) = ln left ({ гидроразрыв {p_ {i}} {1-p_ {i}}} right) = beta _ {0} + beta _ {1} x_ {1, i} + cdots + beta _ {m} x_ {m, i}}
Написано с использованием более компактной записи, описанной выше, это:
- logit (E [Y i ∣ X i]) = logit (pi) = ln (pi 1 – пи) знак равно β ⋅ Икс я { Displaystyle OperatorName {logit} ( operatorname { mathcal {E}} [Y_ {i} mid mathbf {X} _ {i}]) = OperatorName {logit} ( число Пи}) = ln left ({ frac {p_ {i}} {1-p_ {i}}} right) = { boldsymbol { beta}} cdot mathbf {X} _ {i}}
Эта формулировка выражает логистическую регрессию как тип обобщенной линейной модели, которая прогнозирует переменные с различными типами распределений вероятностей путем подгонки линейной функции-предиктора вышеуказанной формы к некоторому виду произвольное преобразование ожидаемого значения переменной.
Интуиция для преобразования с использованием функции логита (натуральный логарифм шансов) была объяснена выше. Он также имеет практический эффект преобразования вероятности (которая ограничена от 0 до 1) в переменную, которая находится в диапазоне (- ∞, + ∞) { displaystyle (- infty, + infty)}
Обратите внимание, что и вероятности p i, и коэффициенты регрессии не наблюдаются, и средства их определения не являются частью самой модели. Обычно они определяются какой-либо процедурой оптимизации, например оценка максимального правдоподобия, которая находит значения, которые наилучшим образом соответствуют наблюдаемым данным (т. Е. Дают наиболее точные прогнозы для уже наблюдаемых данных), обычно при условии регуляризации условий, которые стремятся исключить маловероятные значения, например чрезвычайно большие значения для любого из коэффициентов регрессии. Использование условия регуляризации эквивалентно выполнению максимальной апостериорной (MAP) оценки, расширению максимальной вероятности. (Регуляризация чаще всего выполняется с использованием регуляризующей функции в квадрате, что эквивалентно помещению гауссовского априорного распределения с нулевым средним для коэффициентов, но другие регуляризаторы также возможно.) Независимо от того, используется ли регуляризация, обычно невозможно найти решение в закрытой форме; вместо этого должен использоваться итеративный численный метод, такой как итеративно перевывешенный метод наименьших квадратов (IRLS) или, что чаще в наши дни, квазиньютоновский метод, такой как L -BFGS метод.
Интерпретация оценок параметра β j заключается в аддитивном влиянии на логарифм шансов для изменения единицы в независимой переменной j. В случае дихотомической объясняющей переменной, например, пол e β { displaystyle e ^ { beta}}
Эквивалентная формула использует обратную логит-функцию, которая является логистической функцией, то есть:
- E [Y i ∣ X i] = pi = logit – 1 (β ⋅ Икс я) знак равно 1 1 + е – β ⋅ Икс я { displaystyle operatorname { mathcal {E}} [Y_ {i} mid mathbf {X} _ {i}] = p_ {i} = operatorname {logit} ^ {- 1} ({ boldsymbol { beta}} cdot mathbf {X} _ {i}) = { frac {1} {1 + e ^ {- { boldsymbol { beta}} cdot mathbf {X} _ {i}}}}}
Формулу также можно записать как распределение вероятностей (в частности, используя функцию массы вероятности ):
- Pr (Y i = y ∣ X i) = piy (1 – pi) 1 – y = (e β ⋅ X i 1 + e β ⋅ X i) y (1 – e β ⋅ X я 1 + е β ⋅ Икс я) 1 – Y знак равно е β ⋅ Икс я ⋅ Y 1 + е β ⋅ Икс я { displaystyle Pr (Y_ {i} = y mid mathbf {X} _ {i}) = {p_ {i}} ^ {y} (1-p_ {i}) ^ {1-y} = left ({ frac {e ^ {{ boldsymbol { beta}} cdot mathbf { X} _ {i}}} {1 + e ^ {{ boldsymbol { beta}} cdot mathbf {X} _ {i}}}} right) ^ {y} left (1 – { frac {e ^ {{ boldsymbol { beta}} cdot mathbf {X} _ {i}}} {1 + e ^ {{ boldsymbol { beta}} cdot mathbf {X} _ {i}}}} right) ^ {1-y} = { frac {e ^ {{ boldsymbol { beta}} cdot mathbf {X} _ {i} cdot y}} {1 + e ^ {{ boldsymbol { beta}} cdot mathbf {X} _ {i}}}}}
В качестве модели скрытых переменных
Вышеуказанное модель имеет эквивалентную формулировку как модель со скрытыми переменными. Эта формулировка является общей в теории моделей дискретного выбора и упрощает распространение на некоторые более сложные модели с множественными коррелированными вариантами выбора, а также сравнение логистической регрессии с тесно связанной пробит-моделью ..
Представьте себе, что для каждого испытания i существует непрерывная скрытая переменная Yi(т.е. ненаблюдаемая случайная величина ), которая распределяется следующим образом:
- Y i ∗ = β ⋅ Икс я + ε { displaystyle Y_ {i} ^ { ast} = { boldsymbol { beta}} cdot mathbf {X} _ {i} + varepsilon ,}
где
- ε ∼ Логистика (0, 1) { Displaystyle varepsilon sim operatorname {Logistic} (0,1) ,}
т.е. скрытая переменная может быть записана непосредственно в терминах функции линейного предсказания и аддитивной случайной переменной ошибки, которая распределяется в соответствии со стандартным логистическим распределением.
Тогда Y i можно рассматривать как индикатор того, является ли эта скрытая переменная положительной:
- Y i = {1, если Y i ∗>0, т.е. – ε < β ⋅ X i, 0 otherwise. {displaystyle Y_{i}={begin{cases}1{text{if }}Y_{i}^{ast }>0 { text {ie}} – varepsilon <{boldsymbol {beta }}cdot mathbf {X} _{i},\0{text{otherwise.}}end{cases}}}
Выбор моделирования конкретной переменной ошибки y со стандартным логистическим распределением, а не с общим логистическим распределением с произвольными значениями местоположения и масштаба, кажется ограничивающим, но на самом деле это не так. Следует иметь в виду, что мы можем сами выбирать коэффициенты регрессии и очень часто можем использовать их для компенсации изменений параметров распределения переменной ошибки. Например, распределение переменных логистической ошибки с ненулевым параметром местоположения μ (который устанавливает среднее значение) эквивалентно распределению с нулевым параметром местоположения, где μ добавлен к коэффициенту пересечения. Обе ситуации дают одно и то же значение для Y i независимо от настроек независимых переменных. Точно так же произвольный параметр масштабирования s эквивалентен установке параметра масштабирования на 1 и последующему делению всех коэффициентов регрессии на s. В последнем случае результирующее значение Y i будет в s раз меньше, чем в первом случае, для всех наборов независимых переменных, но, что важно, оно всегда будет оставаться на той же стороне 0, и, следовательно, приводят к тому же выбору Y i.
(Обратите внимание, что это предсказывает, что несоответствие параметра масштаба не может быть перенесено в более сложные модели, где доступно более двух вариантов.)
Оказывается, эта формулировка в точности эквивалентна к предыдущей, сформулированной в терминах обобщенной линейной модели и без каких-либо скрытых переменных. Это можно показать следующим образом, используя тот факт, что кумулятивная функция распределения (CDF) стандартного логистического распределения является логистической функцией , которая является обратной логит-функции , т.е.
- Pr (ε < x) = logit − 1 ( x) {displaystyle Pr(varepsilon
Тогда:
- Pr (Y i = 1 ∣ X i) = Pr (Y i ∗>0 ∣ X i) = Pr (β ⋅ X i + ε>0) = Pr (ε>- β ⋅ X i) = Pr (ε < β ⋅ X i) (because the logistic distribution is symmetric) = logit − 1 ( β ⋅ X i) = p i (see above) {displaystyle {begin{aligned}Pr(Y_{i}=1mid mathbf {X} _{i})=Pr(Y_{i}^{ast }>0 mid mathbf {X} _ {i}) \ [5pt] = Pr ({ boldsymbol { beta}} cdot mathbf {X} _ {i} + varepsilon>0) \ [5pt] = Pr ( varepsilon>- { boldsymbol { beta}} cdot mathbf {X} _ {i}) \ [5pt] = Pr ( varepsilon <{boldsymbol {beta }}cdot mathbf {X} _{i}){text{(because the logistic distribution is symmetric)}}\[5pt]=operatorname {logit} ^{-1}({boldsymbol {beta }}cdot mathbf {X} _{i})\[5pt]=p_{i}{text{(see above)}}end{aligned}}}
Эта формулировка – стандартная для моделей дискретного выбора – проясняет взаимосвязь между логистической регрессией («логит модель “) и пробит-модель, в которой используется переменная ошибки, распределенная в соответствии с переход к стандартному нормальному распределению вместо стандартного логистического распределения. Как логистическое, так и нормальное распределения симметричны базовой унимодальной форме «колоколообразной кривой». Единственное отличие состоит в том, что логистическое распределение имеет несколько более тяжелые хвосты, что означает, что оно менее чувствительно к внешним данным (и, следовательно, несколько более надежно для моделирования неверных спецификаций или ошибочных данных)..
Модель двусторонних латентных переменных
Еще одна формулировка использует две отдельные скрытые переменные:
- Y i 0 ∗ = β 0 ⋅ X i + ε 0 Y i 1 ∗ = β 1 ⋅ Икс я + ε 1 { Displaystyle { begin {align} Y_ {i} ^ {0 ast} = { boldsymbol { beta}} _ {0} cdot mathbf {X} _ {я } + varepsilon _ {0} , \ Y_ {i} ^ {1 ast} = { boldsymbol { beta}} _ {1} cdot mathbf {X} _ {i} + varepsilon _ {1} , end {align}}}
где
- ε 0 ∼ EV 1 (0, 1) ε 1 ∼ EV 1 (0, 1) { displaystyle { begin {выравнивается } varepsilon _ {0} sim operatorname {EV} _ {1} (0,1) \ varepsilon _ {1} sim operatorname {EV} _ {1} (0,1) конец {выровнено}}}
где EV 1 (0,1) – стандартный тип 1 распределение экстремальных значений : т.е.
- Pr (ε 0 = x) Знак равно Pr (ε 1 знак равно Икс) знак равно е – хе – е – х { Displaystyle Pr ( varepsilon _ {0} = х) = Pr ( varepsilon _ {1} = х) = е ^ {- х } e ^ {- e ^ {- x}}}
Тогда
- Y i = {1, если Y i 1 ∗>Y i 0 ∗, 0 в противном случае. { displaystyle Y_ {i} = { begin {cases} 1 { text {if}} Y_ {i} ^ {1 ast}>Y_ {i} ^ {0 ast}, \ 0 { text {в противном случае.}} end {case}}}
Эта модель имеет отдельную скрытую переменную и отдельную набор коэффициентов регрессии для каждого возможного результата зависимой переменной. Причина этого разделения заключается в том, что оно позволяет легко расширить логистическую регрессию на многозначные категориальные переменные, как в модели полиномиального логита. модели, естественно моделировать каждый возможный результат, используя другой набор коэффициентов регрессии. Также возможно мотивировать каждую из отдельных скрытых переменных как теоретическую полезность, связанную с выполнением соответствующего выбора, и, таким образом, мотивировать логистическую регрессию с точки зрения теории полезности (с точки зрения полезности t Согласно теории, рациональный субъект всегда выбирает выбор с наибольшей связанной полезностью.) Это подход, используемый экономистами при формулировании моделей дискретного выбора, поскольку он обеспечивает теоретически прочную основу и облегчает интуитивное понимание модели, что, в свою очередь, упрощает рассмотрение различных видов расширений. (См. Пример ниже.)
Выбор распределения экстремальных значений типа 1 кажется довольно произвольным, но он заставляет математику работать, и может быть возможно оправдать его использование через теория рационального выбора.
Оказывается, что эта модель эквивалентна предыдущей модели, хотя это кажется неочевидным, поскольку теперь существует два набора коэффициентов регрессии и переменных ошибок, а переменные ошибок имеют разные распространение. Фактически, эта модель сводится непосредственно к предыдущей со следующими заменами:
- β = β 1 – β 0 { displaystyle { boldsymbol { beta}} = { boldsymbol { beta}} _ {1} – { boldsymbol { beta}} _ {0}}
- ε = ε 1 – ε 0 { displaystyle varepsilon = varepsilon _ {1} – varepsilon _ {0}}
Интуиция для это происходит из-за того, что, поскольку мы выбираем на основе максимального из двух значений, имеет значение только их разница, а не точные значения – и это эффективно удаляет одну степень свободы. Другой важный факт заключается в том, что разница двух переменных типа 1 с распределением экстремальных значений является логистическим распределением, то есть ε = ε 1 – ε 0 ∼ Logistic (0, 1). { displaystyle varepsilon = varepsilon _ {1} – varepsilon _ {0} sim operatorname {Logistic} (0,1).}
- Pr (Y i = 1 ∣ X i) = Pr (Y i 1 ∗>Y i 0 ∗ ∣ X i) = Pr (Y i 1 ∗ – Y i 0 ∗>0 ∣ X i) = Pr (β 1 ⋅ X i + ε 1 – (β 0 ⋅ X i + ε 0)>0) = Pr ((β 1 ⋅ X i – β 0 ⋅ X i) + (ε 1 – ε 0)>0) = Pr (( β 1 – β 0) ⋅ X i + (ε 1 – ε 0)>0) = Pr ((β 1 – β 0) ⋅ X i + ε>0) (замените ε, как указано выше) = Pr (β ⋅ X i + ε>0) (замените β, как указано выше) = Pr (ε>- β ⋅ X i) (теперь такая же, как в модели выше) = Pr (ε < β ⋅ X i) = logit − 1 ( β ⋅ X i) = p i {displaystyle {begin{aligned}Pr(Y_{i}=1mid mathbf {X} _{i})={}Pr left(Y_{i}^{1ast }>Y_ {i} ^ {0 ast} mid mathbf {X} _ {i} right) \ [5pt] = {} Pr left (Y_ {i} ^ {1 ast} -Y_ {i} ^ {0 ast}>0 mid mathbf {X} _ {i} right) \ [5pt] = {} Pr left ({ boldsymbol { beta}} _ {1} cdot mathbf {X} _ { i} + varepsilon _ {1} – left ({ boldsymbol { beta}} _ {0} cdot mathbf {X} _ {i} + varepsilon _ {0} right)>0 right) \ [5pt] = {} Pr left (({ boldsymbol { beta}} _ {1} cdot mathbf {X} _ {i} – { boldsymbol { beta}} _ {0} cdot mathbf {X} _ {i}) + ( vareps ilon _ {1} – varepsilon _ {0})>0 right) \ [5pt] = {} Pr (({ boldsymbol { beta}} _ {1} – { boldsymbol { бета}} _ {0}) cdot mathbf {X} _ {i} + ( varepsilon _ {1} – varepsilon _ {0})>0) \ [5pt] = {} Pr (({ boldsymbol { beta}} _ {1} – { boldsymbol { beta}} _ {0}) cdot mathbf {X} _ {i} + varepsilon>0) { text { (замените}} varepsilon { text {как указано выше)}} \ [5pt] = {} Pr ({ boldsymbol { beta}} cdot mathbf {X} _ {i} + varepsilon>0) { text {(replace}} { boldsymbol { beta}} { text {как указано выше)}} \ [5pt] = {} Pr ( varepsilon>- { boldsymbol { beta }} cdot mathbf {X} _ {i}) { text {(теперь такая же, как в модели выше)}} \ [5pt] = {} Pr ( varepsilon <{boldsymbol {beta }}cdot mathbf {X} _{i})\[5pt]={}operatorname {logit} ^{-1}({boldsymbol {beta }}cdot mathbf {X} _{i})\[5pt]={}p_{i}end{aligned}}}
Пример
В качестве примера рассмотрим выборы на уровне провинции, где выбор делается между правоцентристской партией и левой центристская партия и сепаратистская партия (например, Parti Québécois, которая хочет, чтобы Квебек отделился от Канады ). Затем мы использовали бы три скрытые переменные, по одной для каждого выбора. Затем, в соответствии с теорией полезности, мы можем интерпретировать скрытые переменные как выражающие полезность, которая возникает в результате принятия каждого из вариантов выбора. Мы также можем интерпретировать коэффициенты регрессии как показывающие силу, которую связанный фактор (т. Е. Объясняющая переменная) имеет в содействии полезности, или, точнее, количество, на которое изменение единицы в объясняющей переменной изменяет полезность данного выбора. Избиратель может ожидать, что правоцентристская партия снизит налоги, особенно для богатых. Это не дало бы людям с низким доходом никакой выгоды, то есть никаких изменений в полезности (поскольку они обычно не платят налоги); принесет умеренную выгоду (то есть несколько больше денег или умеренное повышение полезности) для людей среднего уровня; принесет значительные выгоды людям с высокими доходами. С другой стороны, можно ожидать, что левоцентристская партия повысит налоги и компенсирует их повышением благосостояния и другой помощью для нижних и средних классов. Это принесет значительную положительную пользу людям с низким доходом, возможно, слабую пользу людям со средним доходом и значительную отрицательную пользу людям с высокими доходами. Наконец, сепаратистская партия не будет предпринимать никаких прямых действий в отношении экономики, а просто отделится. Избиратель с низким или средним доходом может в основном не ожидать от этого явной выгоды или убытка от полезности, но избиратель с высоким доходом может ожидать отрицательной полезности, поскольку он / она, вероятно, будет владеть компаниями, которым будет труднее вести бизнес. такая среда и, вероятно, потеряете деньги.
Эти интуиции можно выразить следующим образом:
| Центр-справа | В центре-слева | Сецессионист | |
|---|---|---|---|
| Высокий доход | сильный + | сильный – | сильный – |
| средний доход | умеренный + | слабый + | нет |
| малообеспеченный | нет | сильный + | нет |
Это ясно показывает что
- Для каждого выбора должны существовать отдельные наборы коэффициентов регрессии. Если сформулировать это с точки зрения полезности, это очень легко увидеть. Разные варианты по-разному влияют на чистую полезность; кроме того, эффекты различаются сложным образом, что зависит от характеристик каждого человека, поэтому должны быть отдельные наборы коэффициентов для каждой характеристики, а не просто одна дополнительная характеристика для каждого выбора.
- Даже если доход есть непрерывная переменная, ее влияние на полезность слишком сложно, чтобы рассматривать ее как единственную переменную. Либо ее необходимо напрямую разделить на диапазоны, либо необходимо добавить более высокие степени дохода, чтобы эффективно выполнить полиномиальную регрессию по доходу.
В качестве «лог-линейной» модели
Еще одна формулировка объединяет описанную выше формулировку двусторонних латентных переменных с исходной формулировкой выше без латентных переменных и в процессе обеспечивает ссылку на одну из стандартных формулировок полиномиального логита.
Здесь, вместо записи logit вероятностей p i в качестве линейного предиктора мы разделяем линейный предиктор на два, по одному для каждого из двух результатов:
- ln Pr ( Y я знак равно 0) знак равно β 0 ⋅ Икс я – пер Z пер Pr (Y я = 1) = β 1 ⋅ Икс я – пер Z { displaystyle { begin {align} ln Pr (Y_ { i} = 0) = { boldsymbol { beta}} _ {0} cdot mathbf {X} _ {i} – ln Z \ ln Pr (Y_ {i} = 1) = { boldsymbol { beta}} _ {1} cdot mathbf {X} _ {i} – ln Z end {align}}}
Обратите внимание, что были введены два отдельных набора коэффициентов регрессии, просто как в модели с двусторонней скрытой переменной, и два уравнения представляют собой форму, которая записывает логарифм связанной вероятности в качестве линейного предиктора с дополнительным членом – ln Z { displaystyle – ln Z}
- Pr (Y i = 0) = 1 Z e β 0 ⋅ X i Pr (Y i = 1) = 1 Z e β 1 ⋅ X i { displaystyle { begin {выровнено} Pr (Y_ {i} = 0) = { frac {1} {Z}} e ^ {{ boldsymbol { beta}} _ {0} cdot mathbf {X} _ {i }} \ [5pt] Pr (Y_ {i} = 1) = { frac {1} {Z}} e ^ {{ boldsymbol { beta}} _ {1} cdot mathbf {X } _ {i}} end {align}}}
В этой форме ясно, что цель Z – гарантировать, что результирующее распределение по Y i действительно будет распределение вероятностей, т. е. сумма равна 1. Это означает, что Z – это просто сумма всех ненормированных вероятностей, и при делении каждой вероятности на Z вероятности становятся «нормализованными ». То есть:
- Z = е β 0 ⋅ Икс я + е β 1 ⋅ Икс я { displaystyle Z = e ^ {{ boldsymbol { beta}} _ {0} cdot mathbf {X} _ { i}} + e ^ {{ boldsymbol { beta}} _ {1} cdot mathbf {X} _ {i}}}
, и в результате получаются уравнения
- Pr (Y i = 0) = е β 0 ⋅ X, т.е. β 0 ⋅ X i + e β 1 ⋅ X i Pr (Y i = 1) = e β 1 X, то есть β 0 X i + e β 1 ⋅ X i. { displaystyle { begin {align} Pr (Y_ {i} = 0) = { frac {e ^ {{ boldsymbol { beta}} _ {0} cdot mathbf {X} _ {i }}} {e ^ {{ boldsymbol { beta}} _ {0} cdot mathbf {X} _ {i}} + e ^ {{ boldsymbol { beta}} _ {1} cdot mathbf {X} _ {i}}}} \ [5pt] Pr (Y_ {i} = 1) = { frac {e ^ {{ boldsymbol { beta}} _ {1} cdot mathbf {X} _ {i}}} {e ^ {{ boldsymbol { beta}} _ {0} cdot mathbf {X} _ {i}} + e ^ {{ boldsymbol { beta}} _ {1} cdot mathbf {X} _ {i}}}}. End {align}}}
Или обычно:
- Pr (Y i = c) = e β c ⋅ X i ∑ он β час ⋅ Икс я { Displaystyle Pr (Y_ {я} = с) = { гидроразрыва {е ^ {{ boldsymbol { beta}} _ {с} cdot mathbf {X} _ {я} }} { sum _ {h} e ^ {{ boldsymbol { beta}} _ {h} cdot mathbf {X} _ {i}}}}}
Это ясно показывает, как обобщить эту формулировку к более чем двум исходам, как в полиномиальный логит. Обратите внимание, что эта общая формулировка является в точности функцией softmax, как в
- Pr (Y i = c) = softmax (c, β 0 ⋅ X i, β 1 ⋅ X i,…). { displaystyle Pr (Y_ {i} = c) = operatorname {softmax} (c, { boldsymbol { beta}} _ {0} cdot mathbf {X} _ {i}, { boldsymbol { beta}} _ {1} cdot mathbf {X} _ {i}, dots).}
Чтобы доказать, что это эквивалентно предыдущей модели, обратите внимание, что указанная выше модель является завышенной, в что Pr (Y i = 0) { displaystyle Pr (Y_ {i} = 0)}


- Pr (Y i = 1) = e (β 1 + C) ⋅ X ie (β 0 + C) ⋅ X i + e (β 1 + C) ⋅ X i = e β 1 ⋅ X, т.е. C ⋅ X, т.е. β 0 ⋅ X, т.е. C ⋅ X i + e β 1 ⋅ X, т.е. C ⋅ X i = e C ⋅ X, т.е. β 1 ⋅ X, то есть C ⋅ X i (e β 0 X i + e β 1 ⋅ X i) = e β 1 X, то есть β 0 ⋅ X i + e β 1 ⋅ X i. { Displaystyle { begin {align} Pr (Y_ {i} = 1) = { frac {e ^ {({ boldsymbol { beta}} _ {1} + mathbf {C}) cdot mathbf {X} _ {i}}} {e ^ {({ boldsymbol { beta}} _ {0} + mathbf {C}) cdot mathbf {X} _ {i}} + e ^ {({ boldsymbol { beta}} _ {1} + mathbf {C}) cdot mathbf {X} _ {i}}}} \ [5pt] = { frac {e ^ {{ boldsymbol { beta}} _ {1} cdot mathbf {X} _ {i}} e ^ { mathbf {C} cdot mathbf {X} _ {i}}} {e ^ {{ boldsymbol { beta}} _ {0} cdot mathbf {X} _ {i}} e ^ { mathbf {C} cdot mathbf {X} _ {i}} + e ^ {{ boldsymbol { beta}} _ {1} cdot mathbf {X} _ {i}} e ^ { mathbf {C} cdot mathbf {X} _ {i}}}} \ [5pt] = { frac {e ^ { mathbf {C} cdot mathbf {X} _ {i}} e ^ {{ boldsymbol { beta}} _ {1} cdot mathbf {X} _ {i}} } {e ^ { mathbf {C} cdot mathbf {X} _ {i}} (e ^ {{ boldsymbol { beta}} _ {0} cdot mathbf {X} _ {i}} + e ^ {{ boldsymbol { beta}} _ {1} cdot mathbf {X} _ {i}})}} \ [5pt] = { frac {e ^ {{ boldsymbol { beta}} _ {1} cdot mathbf {X} _ {i}}} {e ^ {{ boldsymbol { beta}} _ {0} cdot mathbf {X} _ {i}} + e ^ {{ boldsymbol { beta}} _ {1} cdot mathbf {X} _ {i}}}}. end {выравнивается}} }
В результате мы можем упростить дело и восстановить идентифицируемость, выбрав произвольное значение для одного из двух векторов. Мы решили установить β 0 = 0. { displaystyle { boldsymbol { beta}} _ {0} = mathbf {0}.}
- e β 0 ⋅ X i = e 0 ⋅ X i = 1 { displaystyle e ^ {{ boldsymbol { beta}} _ {0} cdot mathbf {X} _ {i}} = e ^ { mathbf {0} cdot mathbf {X} _ {i}} = 1}
и поэтому
- Pr (Y i = 1) = e β 1 ⋅ X i 1 + e β 1 ⋅ X i = 1 1 + e – β 1 ⋅ X i = pi { displaystyle Pr (Y_ {i} = 1) = { frac {e ^ {{ boldsymbol { beta}} _ {1} cdot mathbf {X} _ {i}}} {1 + e ^ {{ boldsymbol { beta}} _ {1} cdot mathbf {X} _ {i}}}} = { frac {1} {1 + e ^ {- { boldsymbol { beta}} _ {1} cdot mathbf {X} _ {i}}}} = p_ {i}}
, что показывает, что эта формулировка действительно эквивалентна предыдущей формулировке. (Как и в формулировке двусторонней скрытой переменной, любые настройки, где β = β 1 – β 0 { displaystyle { boldsymbol { beta}} = { boldsymbol { beta}} _ {1} – { boldsymbol { beta}} _ {0}}
Обратите внимание, что большинство методов лечения модели полиномиального логита начинается либо с расширения «лог-линейная» формулировка, представленная здесь, или формулировка двусторонней скрытой переменной, представленная выше, поскольку обе ясно показывают способ, которым модель может быть расширена для многосторонних результатов. В целом представление со скрытыми переменными более распространено в эконометрике и политологии, где господствуют модели дискретного выбора и теория полезности, в то время как “лог-линейная” формулировка здесь более распространена в информатике, например машинное обучение и обработка естественного языка.
Как однослойный перцептрон
Модель имеет эквивалентную формулировку
- pi = 1 1 + e – (β 0 + β 1 x 1, i + ⋯ + β kxk, i). { displaystyle p_ {i} = { frac {1} {1 + e ^ {- ( beta _ {0} + beta _ {1} x_ {1, i} + cdots + beta _ {k } x_ {k, i})}}}. ,}
Эту функциональную форму обычно называют однослойной перцептроном или однослойной искусственной нейронной сетью. Однослойная нейронная сеть вычисляет непрерывный результат вместо пошаговой функции . Производная p i по X = (x 1,…, x k) вычисляется из общей формы:
- y = 1 1 + e – f (X) { displaystyle y = { frac {1} {1 + e ^ {- f (X)}}}}
где f (X) – аналитический функция в X. При таком выборе однослойная нейронная сеть идентична модели логистической регрессии. Эта функция имеет непрерывную производную, что позволяет использовать ее в обратном распространении. Эта функция также является предпочтительной, потому что ее производная легко вычисляется:
- d y d X = y (1 – y) d f d X. { displaystyle { frac { mathrm {d} y} { mathrm {d} X}} = y (1-y) { frac { mathrm {d} f} { mathrm {d} X}}. ,}
В терминах биномиальных данных
Тесно связанная модель предполагает, что каждое i связано не с одним испытанием Бернулли, а с n iнезависимыми одинаково распределенными испытаниями, где наблюдение Y i – это количество наблюдаемых успехов (сумма отдельных случайных величин, распределенных по Бернулли), и, следовательно, следует биномиальному распределению :
- Y i ∼ Bin (ni, pi), для я = 1,…, n { displaystyle Y_ {i} , sim operatorname {Bin} (n_ {i}, p_ {i}), { text {for}} i = 1, dots, n}
Примером этого распределения является доля семян (p i), которые прорастают после посадки n i.
В терминах ожидаемых значений эта модель выражается следующим образом:
- p i = E [Y i n i | Икс i], { displaystyle p_ {i} = operatorname { mathcal {E}} left [ left. { Frac {Y_ {i}} {n_ {i}}} , right | , mathbf {X} _ {i} right] ,,}
, так что
- logit (E [Y ini | X i]) = logit (pi) = ln (pi 1 – пи) знак равно β ⋅ Икс я, { displaystyle operatorname {logit} left ( operatorname { mathcal {E}} left [ left. { frac {Y_ {i}} {n_ {i}}}} , right | , mathbf {X} _ {i} right] right) = operatorname {logit} (p_ {i}) = ln left ({ frac {p_ {i}} { 1-p_ {i}}} right) = { boldsymbol { beta}} cdot mathbf {X} _ {i} ,,}
Или, что эквивалентно:
- Pr (Y i = y ∣ X i) знак равно (niy) piy (1 – pi) ni – y = (niy) (1 1 + e – β ⋅ X i) y (1 – 1 1 + e – β ⋅ X i) ni – y. { displaystyle Pr (Y_ {i} = y mid mathbf {X} _ {i}) = {n_ {i} select y} p_ {i} ^ {y} (1-p_ {i}) ^ {n_ {i} -y} = {n_ {i} select y} left ({ frac {1} {1 + e ^ {- { boldsymbol { beta}} cdot mathbf {X}) _ {i}}}} right) ^ {y} left (1 – { frac {1} {1 + e ^ {- { boldsymbol { beta}} cdot mathbf {X} _ {i }}}} right) ^ {n_ {i} -y} ,.}
Эта модель может быть адаптирована с использованием тех же методов, что и описанная выше более базовая модель.
Байесовский

σ (x) { displaystyle sigma (x)}

Φ (π 8 x) { displaystyle Phi ({ sqrt { frac { pi} {8}}} x)}

В контексте байесовской статистики предшествующие распределения обычно помещаются в коэффициенты регрессии, обычно в форма гауссовых распределений. В логистической регрессии не существует сопряженного предшествующего функции правдоподобия . Когда байесовский вывод был выполнен аналитически, это затрудняло вычисление апостериорного распределения, за исключением очень малых измерений. Однако теперь автоматическое программное обеспечение, такое как OpenBUGS, JAGS, PyMC3 или Stan, позволяет вычислять эти апостериорные компоненты с помощью моделирования, поэтому о супружестве не вызывает беспокойства. Однако, когда размер выборки или количество параметров велико, полное байесовское моделирование может быть медленным, и люди часто используют приближенные методы, такие как вариационные байесовские методы и распространение математических ожиданий.
История
Подробная история логистической регрессии приведена в Cramer (2002). Логистическая функция была разработана как модель роста населения и названа «логистической» Пьером Франсуа Ферхюльстом в 1830-х и 1840-х годах под руководством Адольфа Кетле ; подробнее см. Логистическая функция § История. В своей самой ранней статье (1838 г.) Ферхюльст не уточнил, как он подгоняет кривые к данным. В своей более подробной статье (1845) Ферхюльст определил три параметра модели, заставив кривую проходить через три наблюдаемые точки, что дало плохие прогнозы.
Логистическая функция была независимо разработана в химии как модель автокатализ (Вильгельм Оствальд, 1883). Автокаталитическая реакция – это реакция, в которой один из продуктов сам по себе является катализатором той же реакции, в то время как подача одного из реагентов является фиксированной. Это естественным образом приводит к логистическому уравнению по той же причине, что и рост населения: реакция является самоусиливающейся, но ограниченной.
Логистическая функция была независимо заново открыта как модель роста населения в 1920 году Раймондом Перлом и Лоуэллом Ридом, опубликованным как Pearl Reed (1920). ошибка harvtxt: нет цели: CITEREFPearlReed1920 (help ), что привело к его использованию в современной статистике. Первоначально они не знали о работе Ферхюльста и предположительно узнали о ней от Л. Гюстав дю Паскье, но они не поверили ему и не приняли его терминологию. Удный Юле в 1925 году признал приоритет Verhulst, и термин «логистика» был возрожден и с тех пор используется. Перл и Рид сначала применили модель к населению Соединенных Штатов, а также сначала подогнали кривую, проведя ее через три точки; как и в случае с Verhulst, это снова дало плохие результаты.
В 1930-х годах пробит-модель была разработана и систематизирована Честером Иттнером Блиссом, который ввел термин «пробит». “в Bliss (1934) harvtxt error: нет цели: CITEREFBliss1934 (help ), и John Gaddum в Gaddum (1933) Ошибка harvtxt: нет цели: CITEREFGaddum1933 (help ), и модель соответствует оценке максимального правдоподобия по Рональду А. Фишеру в Fisher (1935) ошибка harvtxt: нет цели: CITEREFFisher1935 (help ), как дополнение к работе Блисс. Пробит-модель в основном использовалась в биопроб, и ей предшествовали более ранние работы, датированные 1860 годом; см. Пробит-модель § История. Пробит-модель повлияла на последующее развитие логит-модели, и эти модели конкурировали друг с другом.
Логистическая модель, вероятно, впервые была использована в качестве альтернативы пробит-модели в биотесте Эдвином Бидвеллом Уилсоном и его ученица Джейн Вустер в Wilson Worcester (1943). Однако разработка логистической модели в качестве общей альтернативы пробит-модели была в основном связана с работой Джозефа Берксона на протяжении многих десятилетий, начиная с Berkson (1944) harvtxt error: нет цели: CITEREFBerkson1944 (help ), где он придумал “logit” по аналогии с “probit” и продолжил до Berkson (1951) harvtxt error: no target: CITEREFBerkson1951 (помощь ) и последующие годы. Логит-модель изначально отвергалась как уступающая пробит-модели, но «постепенно достигла равенства с логит-моделью», особенно в период с 1960 по 1970 г. К 1970 году логит-модель достигла паритета с пробит-моделью, которая использовалась в статистических журналах, а затем превзошел его. Эта относительная популярность была обусловлена принятием логита за пределами биотеста, а не вытеснением пробита в рамках биотеста, и его неформальным использованием на практике; Популярность логита объясняется вычислительной простотой, математическими свойствами и универсальностью логит-модели, что позволяет использовать ее в различных областях.
За это время были внесены различные усовершенствования, в частности, Дэвидом Коксом, поскольку in Cox (1958).
Модель полиномиального логита была представлена независимо в Cox (1966) и Thiel (1969), что значительно расширило область применения и популярность модели логита. В 1973 году Дэниел Макфадден связал полиномиальный логит с теорией дискретного выбора, в частности, аксиомой выбора Люса, показывая, что полиномиальный логит следует из предположения независимость от нерелевантных альтернатив и интерпретация вероятностей альтернатив как относительных предпочтений; это дало теоретическую основу для логистической регрессии.
Расширения
Существует большое количество расширений:
- Полиномиальная логистическая регрессия (или полиномиальный логит ) обрабатывает случай многосторонней категориальной зависимой переменной (с неупорядоченными значениями, также называемой «классификацией»). Обратите внимание, что общий случай наличия зависимых переменных с более чем двумя значениями называется политомической регрессией.
- Упорядоченная логистическая регрессия (или упорядоченный логит ) обрабатывает порядковые зависимые переменные ( упорядоченные значения).
- Смешанный логит – это расширение полиномиального логита, которое позволяет корреляции между вариантами выбора зависимой переменной.
- Расширением логистической модели на наборы взаимозависимых переменных является условное случайное поле.
- Условная логистическая регрессия обрабатывает сопоставленные или стратифицированные данные, когда страты небольшие. Он в основном используется при анализе наблюдательных исследований.
Программное обеспечение
Большинство статистических программ может выполнять бинарную логистическую регрессию.
- SPSS
- [1] для базовой логистической регрессии.
- Stata
- SAS
- PROC LOGISTIC для базовой логистической регрессии.
- PROC CATMOD когда все переменные являются категориальными.
- PROC GLIMMIX для многоуровневой модели логистическая регрессия.
- R
glmв пакете статистики (с использованием family = binomial)lrmв rms пакете- GLMNET для эффективной реализации регуляризованной логистической регрессии
- lmer для смешанной логистической регрессии
- команда пакета Rfast
gm_logisticдля быстрой и тяжелые вычисления с использованием крупномасштабных данных. - пакет arm для байесовской логистической регрессии
- Python
Logitв модуле Statsmodels.LogisticRegressionв модуле Scikit-learn.LogisticRegressorв модуле TensorFlow.- Полный пример логистической регрессии в учебном пособии Theano [2]
- Байесовская логистическая регрессия с предшествующим кодом ARD, учебник
- Вариационная байесовская логистическая регрессия с предшествующим кодом ARD, учебник
- код Байесовской логистической регрессии , учебник
- NCSS
- Matlab
mnrfitв (с «неправильным» кодом 2 вместо 0)fminunc / fmincon, fitglm, mnrfit, fitclinear, mleмогут выполнять логистическую регрессию.
- Java (JVM )
- LibLinear
- Apache Flink
- Apache Spark
- SparkML поддерживает логистическую регрессию
- FPGA
Примечательно, что пакет расширения статистики Microsoft Excel не включает его.
См. Также
Портал математики
Ссылки
Дополнительная литература
Внешние ссылки
СМИ, связанные с логистической регрессией на Wikimedia Commons
- Лекция по эконометрике (тема: модель логита) на YouTube от Марка Тома
- Учебник по логистической регрессии
- mlelr : программное обеспечение на C для обучения цели
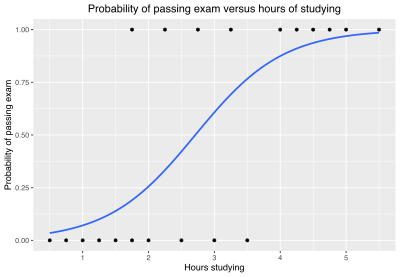






















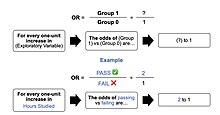



![{displaystyle {begin{aligned}Y_{i}mid x_{1,i},ldots ,x_{m,i} &sim operatorname {Bernoulli} (p_{i})\operatorname {mathbb {E} } [Y_{i}mid x_{1,i},ldots ,x_{m,i}]&=p_{i}\Pr(Y_{i}=ymid x_{1,i},ldots ,x_{m,i})&={begin{cases}p_{i}&{text{if }}y=1\1-p_{i}&{text{if }}y=0end{cases}}\Pr(Y_{i}=ymid x_{1,i},ldots ,x_{m,i})&=p_{i}^{y}(1-p_{i})^{(1-y)}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49627157ac00e729a38538029505c210f99955d7)


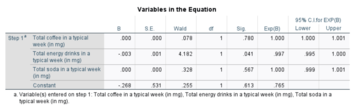















![{displaystyle operatorname {logit} (operatorname {mathbb {E} } [Y_{i}mid x_{1,i},ldots ,x_{m,i}])=operatorname {logit} (p_{i})=ln left({frac {p_{i}}{1-p_{i}}}right)=beta _{0}+beta _{1}x_{1,i}+cdots +beta _{m}x_{m,i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be13d1b675b8fb6e9db4835cd151b5fc9076e282)
![{displaystyle operatorname {logit} (operatorname {mathbb {E} } [Y_{i}mid mathbf {X} _{i}])=operatorname {logit} (p_{i})=ln left({frac {p_{i}}{1-p_{i}}}right)={boldsymbol {beta }}cdot mathbf {X} _{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55adb25231d3cea8f63c4fe56a8677f6eb59415f)
![{displaystyle operatorname {mathbb {E} } [Y_{i}mid mathbf {X} _{i}]=p_{i}=operatorname {logit} ^{-1}({boldsymbol {beta }}cdot mathbf {X} _{i})={frac {1}{1+e^{-{boldsymbol {beta }}cdot mathbf {X} _{i}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/337230f2ea410541cdcf94442ce37b92515dd364)





![{displaystyle {begin{aligned}Pr(Y_{i}=1mid mathbf {X} _{i})&=Pr(Y_{i}^{ast }>0mid mathbf {X} _{i})\[5pt]&=Pr({boldsymbol {beta }}cdot mathbf {X} _{i}+varepsilon _{i}>0)\[5pt]&=Pr(varepsilon _{i}>-{boldsymbol {beta }}cdot mathbf {X} _{i})\[5pt]&=Pr(varepsilon _{i}<{boldsymbol {beta }}cdot mathbf {X} _{i})&&{text{(because the logistic distribution is symmetric)}}\[5pt]&=operatorname {logit} ^{-1}({boldsymbol {beta }}cdot mathbf {X} _{i})&\[5pt]&=p_{i}&&{text{(see above)}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67ce399af3b2241cc7121b48c60ceaf626e430c5)





![{displaystyle {begin{aligned}Pr(Y_{i}=1mid mathbf {X} _{i})={}&Pr left(Y_{i}^{1ast }>Y_{i}^{0ast }mid mathbf {X} _{i}right)&\[5pt]={}&Pr left(Y_{i}^{1ast }-Y_{i}^{0ast }>0mid mathbf {X} _{i}right)&\[5pt]={}&Pr left({boldsymbol {beta }}_{1}cdot mathbf {X} _{i}+varepsilon _{1}-left({boldsymbol {beta }}_{0}cdot mathbf {X} _{i}+varepsilon _{0}right)>0right)&\[5pt]={}&Pr left(({boldsymbol {beta }}_{1}cdot mathbf {X} _{i}-{boldsymbol {beta }}_{0}cdot mathbf {X} _{i})+(varepsilon _{1}-varepsilon _{0})>0right)&\[5pt]={}&Pr(({boldsymbol {beta }}_{1}-{boldsymbol {beta }}_{0})cdot mathbf {X} _{i}+(varepsilon _{1}-varepsilon _{0})>0)&\[5pt]={}&Pr(({boldsymbol {beta }}_{1}-{boldsymbol {beta }}_{0})cdot mathbf {X} _{i}+varepsilon >0)&&{text{(substitute }}varepsilon {text{ as above)}}\[5pt]={}&Pr({boldsymbol {beta }}cdot mathbf {X} _{i}+varepsilon >0)&&{text{(substitute }}{boldsymbol {beta }}{text{ as above)}}\[5pt]={}&Pr(varepsilon >-{boldsymbol {beta }}cdot mathbf {X} _{i})&&{text{(now, same as above model)}}\[5pt]={}&Pr(varepsilon <{boldsymbol {beta }}cdot mathbf {X} _{i})&\[5pt]={}&operatorname {logit} ^{-1}({boldsymbol {beta }}cdot mathbf {X} _{i})\[5pt]={}&p_{i}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be3b57ca6773ef745cdfd82367611e9394215f9e)

![{displaystyle {begin{aligned}Pr(Y_{i}=0)&={frac {1}{Z}}e^{{boldsymbol {beta }}_{0}cdot mathbf {X} _{i}}\[5pt]Pr(Y_{i}=1)&={frac {1}{Z}}e^{{boldsymbol {beta }}_{1}cdot mathbf {X} _{i}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e1e2a04fd15f2e5617c0606a7644fe719823960)

![{displaystyle {begin{aligned}Pr(Y_{i}=0)&={frac {e^{{boldsymbol {beta }}_{0}cdot mathbf {X} _{i}}}{e^{{boldsymbol {beta }}_{0}cdot mathbf {X} _{i}}+e^{{boldsymbol {beta }}_{1}cdot mathbf {X} _{i}}}}\[5pt]Pr(Y_{i}=1)&={frac {e^{{boldsymbol {beta }}_{1}cdot mathbf {X} _{i}}}{e^{{boldsymbol {beta }}_{0}cdot mathbf {X} _{i}}+e^{{boldsymbol {beta }}_{1}cdot mathbf {X} _{i}}}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fa489d73be139142872ddccccecd567635525d5)


![{displaystyle {begin{aligned}Pr(Y_{i}=1)&={frac {e^{({boldsymbol {beta }}_{1}+mathbf {C} )cdot mathbf {X} _{i}}}{e^{({boldsymbol {beta }}_{0}+mathbf {C} )cdot mathbf {X} _{i}}+e^{({boldsymbol {beta }}_{1}+mathbf {C} )cdot mathbf {X} _{i}}}}\[5pt]&={frac {e^{{boldsymbol {beta }}_{1}cdot mathbf {X} _{i}}e^{mathbf {C} cdot mathbf {X} _{i}}}{e^{{boldsymbol {beta }}_{0}cdot mathbf {X} _{i}}e^{mathbf {C} cdot mathbf {X} _{i}}+e^{{boldsymbol {beta }}_{1}cdot mathbf {X} _{i}}e^{mathbf {C} cdot mathbf {X} _{i}}}}\[5pt]&={frac {e^{mathbf {C} cdot mathbf {X} _{i}}e^{{boldsymbol {beta }}_{1}cdot mathbf {X} _{i}}}{e^{mathbf {C} cdot mathbf {X} _{i}}(e^{{boldsymbol {beta }}_{0}cdot mathbf {X} _{i}}+e^{{boldsymbol {beta }}_{1}cdot mathbf {X} _{i}})}}\[5pt]&={frac {e^{{boldsymbol {beta }}_{1}cdot mathbf {X} _{i}}}{e^{{boldsymbol {beta }}_{0}cdot mathbf {X} _{i}}+e^{{boldsymbol {beta }}_{1}cdot mathbf {X} _{i}}}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f545a36890435f35e006242acda552c8f62dcd0)






![{displaystyle p_{i}=operatorname {mathbb {E} } left[left.{frac {Y_{i}}{n_{i}}},right|,mathbf {X} _{i}right],,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2b159f2ac064c09122cc087d3d9e8d3bbb415f9)
![{displaystyle operatorname {logit} left(operatorname {mathbb {E} } left[left.{frac {Y_{i}}{n_{i}}},right|,mathbf {X} _{i}right]right)=operatorname {logit} (p_{i})=ln left({frac {p_{i}}{1-p_{i}}}right)={boldsymbol {beta }}cdot mathbf {X} _{i},,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4629c0d5675907b48d10f5173bbc338f262e540a)
















![{displaystyle {begin{aligned}D_{text{null}}&=-2ln {frac {text{likelihood of null model}}{text{likelihood of the saturated model}}}\[6pt]D_{text{fitted}}&=-2ln {frac {text{likelihood of fitted model}}{text{likelihood of the saturated model}}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d85ab8f60a3e7685815b132b3a80d03d26d9745a)
![{displaystyle {begin{aligned}D_{text{null}}-D_{text{fitted}}&=-2left(ln {frac {text{likelihood of null model}}{text{likelihood of the saturated model}}}-ln {frac {text{likelihood of fitted model}}{text{likelihood of the saturated model}}}right)\[6pt]&=-2ln {frac {left({dfrac {text{likelihood of null model}}{text{likelihood of the saturated model}}}right)}{left({dfrac {text{likelihood of fitted model}}{text{likelihood of the saturated model}}}right)}}\[6pt]&=-2ln {frac {text{likelihood of the null model}}{text{likelihood of fitted model}}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd851b7e234a5483dbb21da9fff7d9d2419e3e3e)




















![{displaystyle {begin{aligned}&lim limits _{Nrightarrow +infty }N^{-1}sum _{i=1}^{N}log Pr(y_{i}mid x_{i};theta )=sum _{xin {mathcal {X}}}sum _{yin {mathcal {Y}}}Pr(X=x,Y=y)log Pr(Y=ymid X=x;theta )\[6pt]={}&sum _{xin {mathcal {X}}}sum _{yin {mathcal {Y}}}Pr(X=x,Y=y)left(-log {frac {Pr(Y=ymid X=x)}{Pr(Y=ymid X=x;theta )}}+log Pr(Y=ymid X=x)right)\[6pt]={}&-D_{text{KL}}(Yparallel Y_{theta })-H(Ymid X)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b300972d40831096c1ab7bdf34338a71eca96d9)

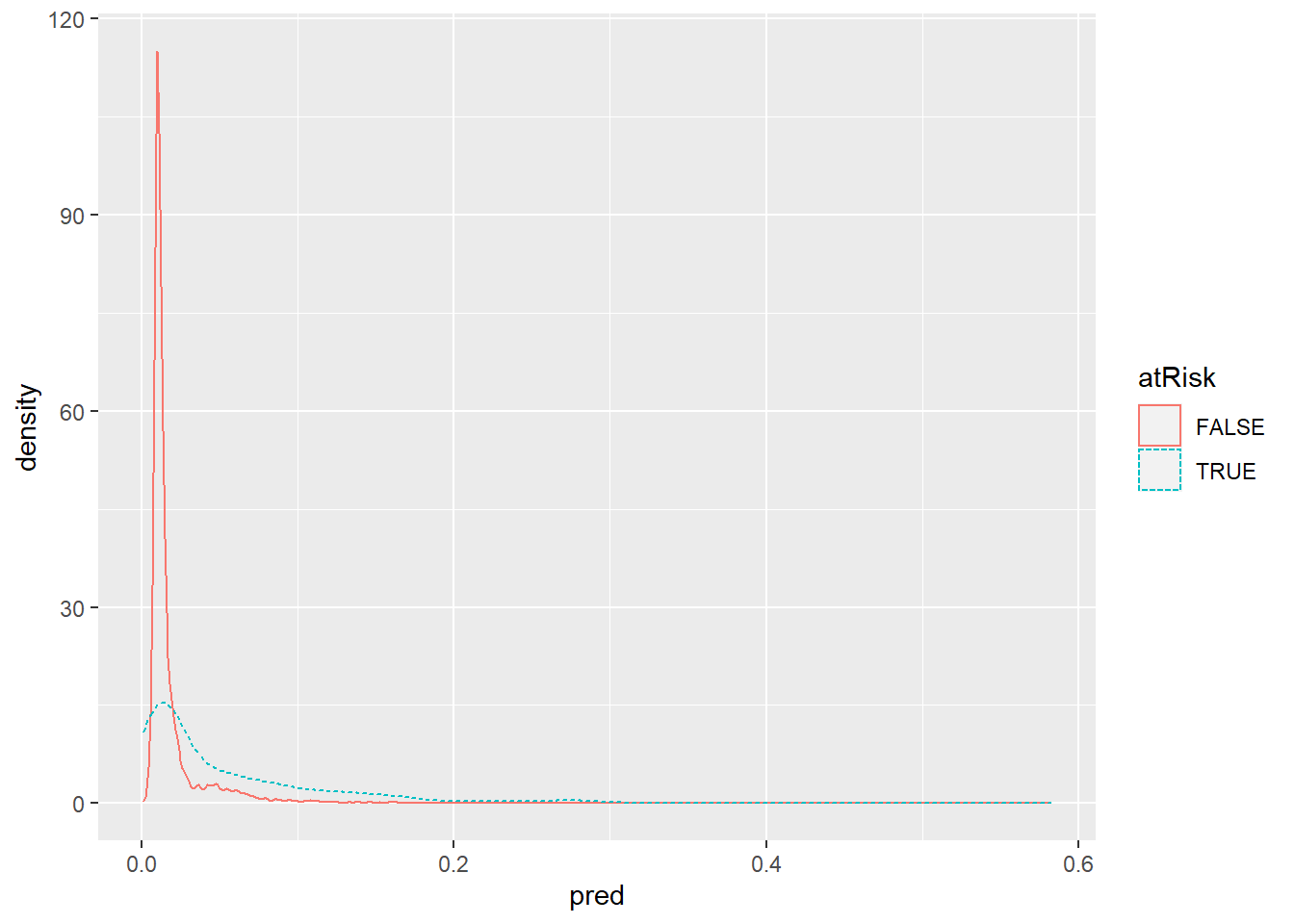
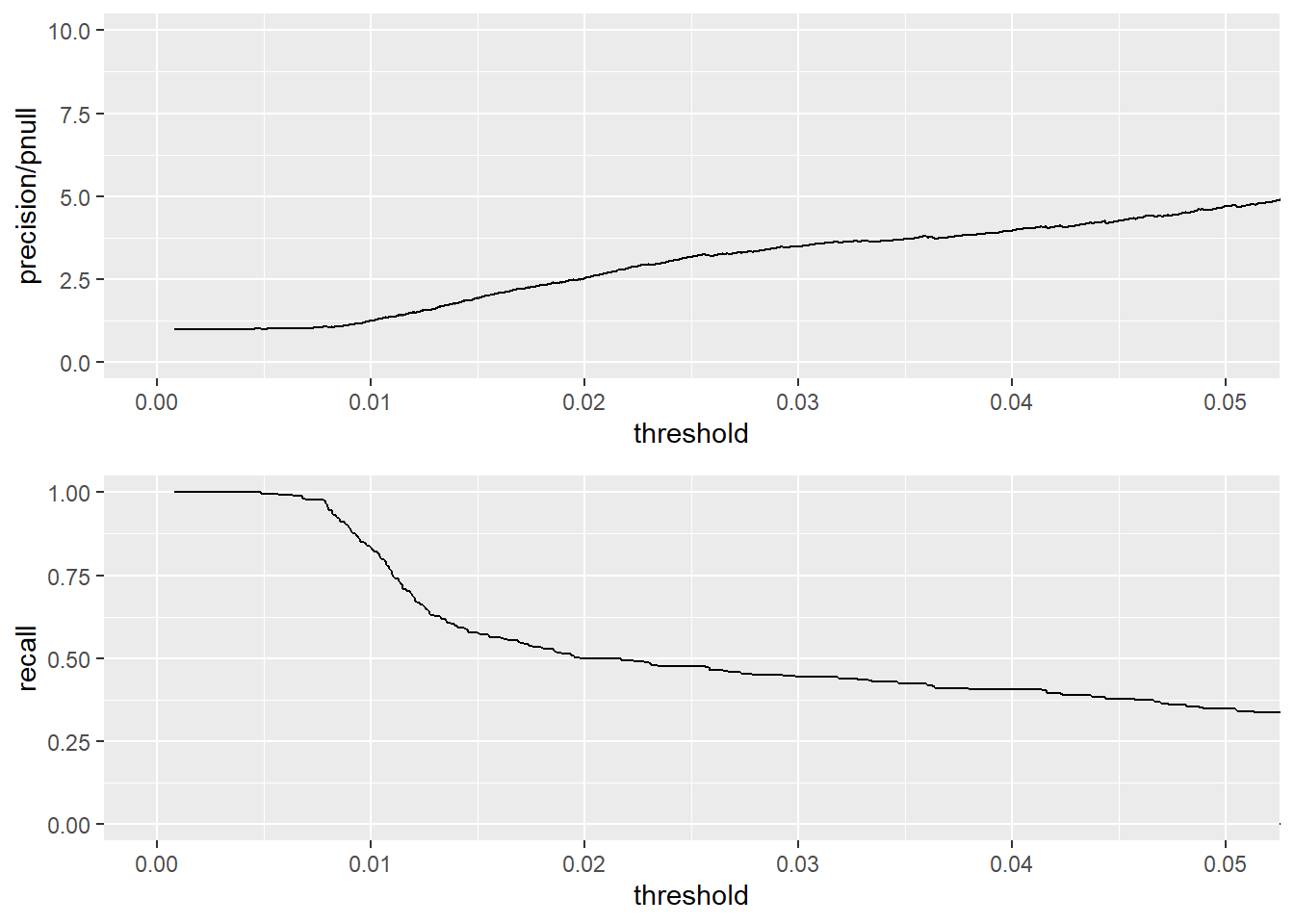
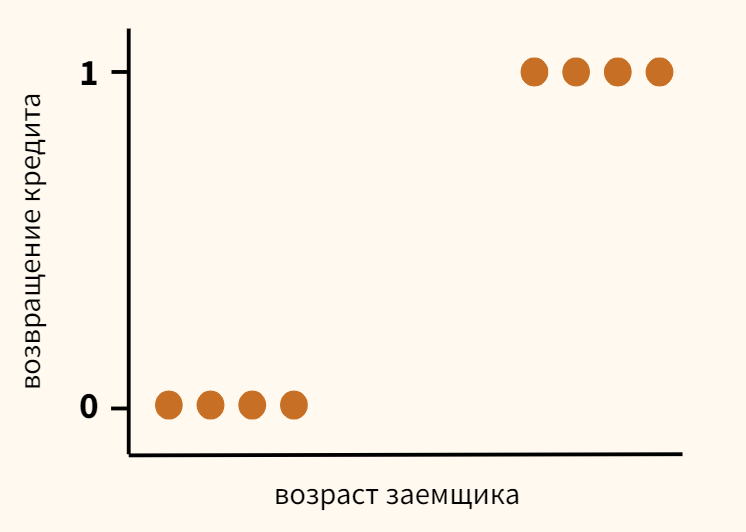

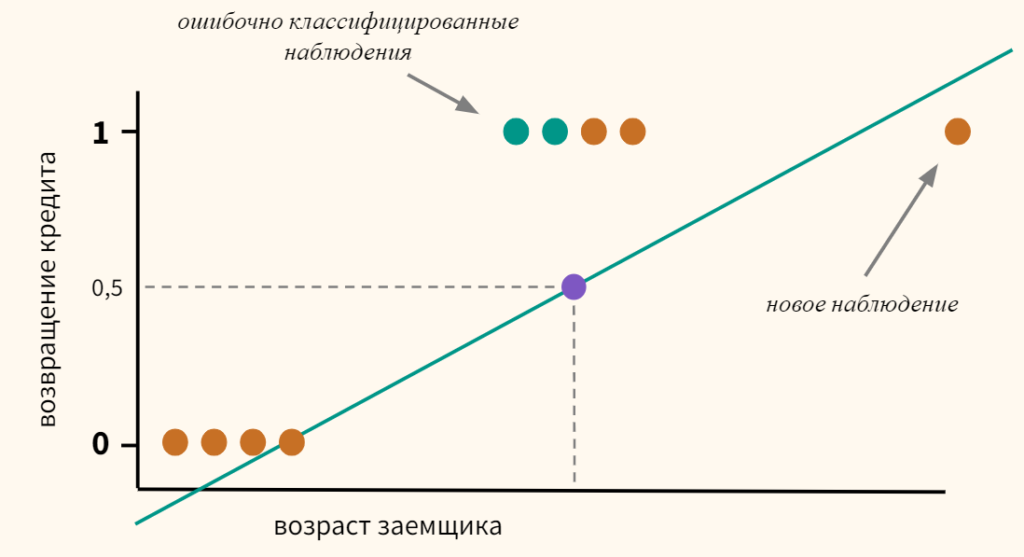
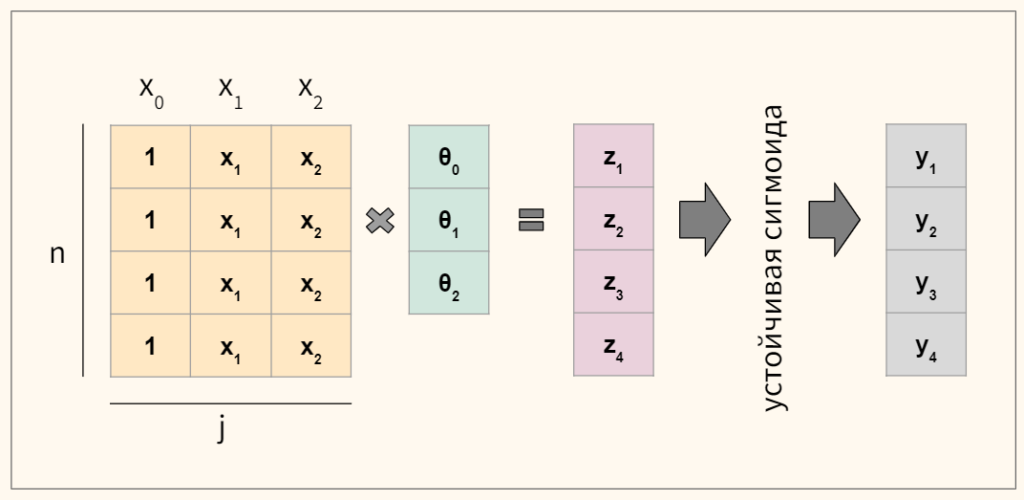



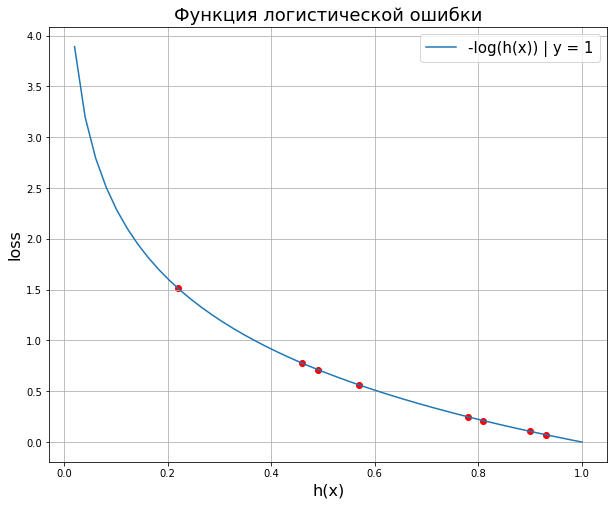




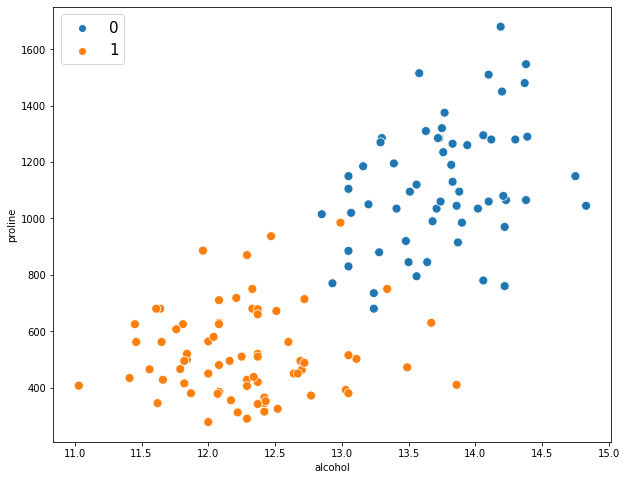









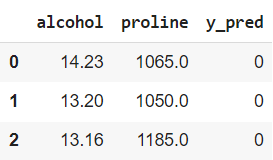
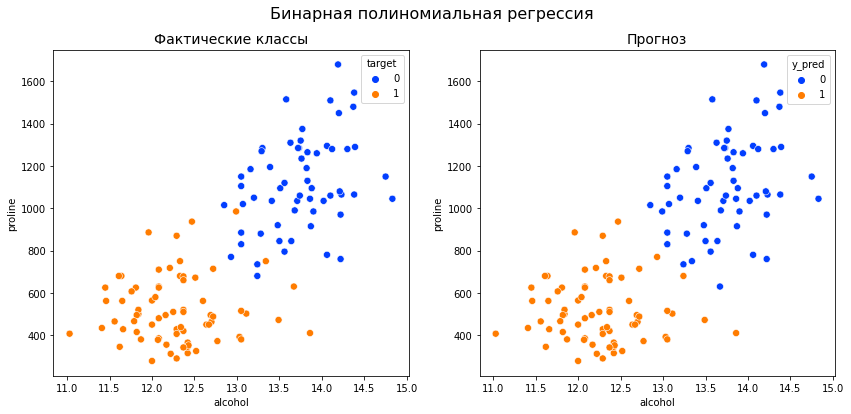

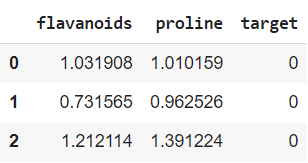

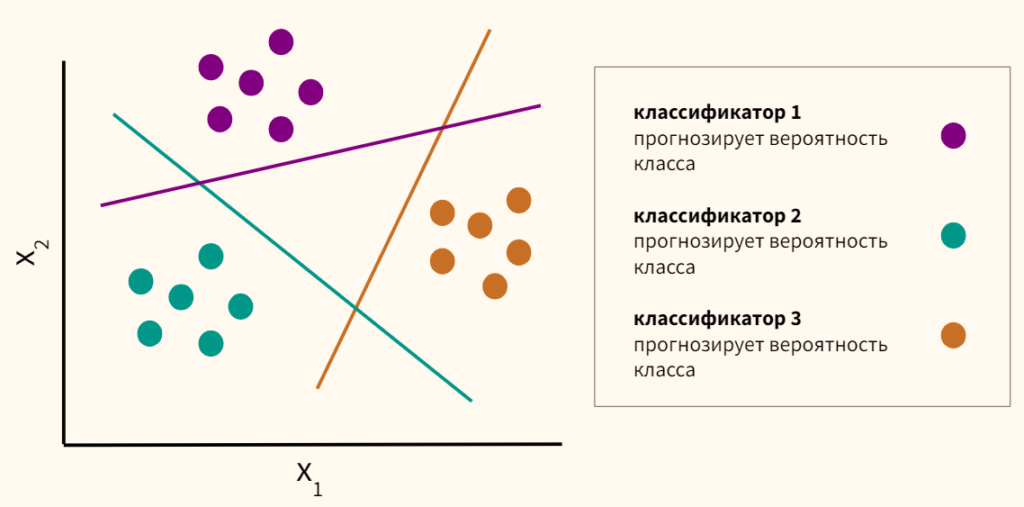


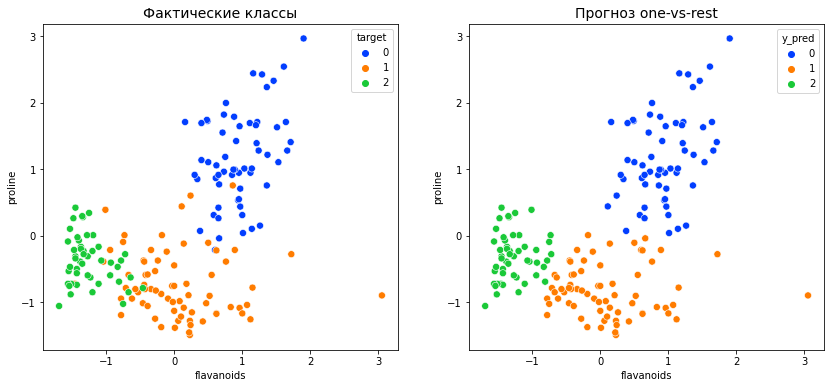







 .
. .
.
 . Возведя в степень, мы можем увидеть, что когда x 1 = x 2 = 0 { displaystyle x_ {1} = x_ {2} = 0}
. Возведя в степень, мы можем увидеть, что когда x 1 = x 2 = 0 { displaystyle x_ {1} = x_ {2} = 0} . Точно так же вероятность события, что Y = 1 { displaystyle Y = 1}
. Точно так же вероятность события, что Y = 1 { displaystyle Y = 1} .
. . Таким образом, если x 1 { displaystyle x_ {1}}
. Таким образом, если x 1 { displaystyle x_ {1}} . Обратите внимание, что вероятность из Y = 1 { displaystyle Y = 1}
. Обратите внимание, что вероятность из Y = 1 { displaystyle Y = 1} . Таким образом, если x 2 { displaystyle x_ {2}}
. Таким образом, если x 2 { displaystyle x_ {2}} Обратите внимание, как влияние x 2 { displaystyle x_ {2}}
Обратите внимание, как влияние x 2 { displaystyle x_ {2}}



 – логит-функция. Уравнение для g (p (x)) { displaystyle g (p (x))}
– логит-функция. Уравнение для g (p (x)) { displaystyle g (p (x))} показывает, что logit (т. Е. Логарифм шансов или натуральный логарифм шансы) эквивалентно выражению линейной регрессии.
показывает, что logit (т. Е. Логарифм шансов или натуральный логарифм шансы) эквивалентно выражению линейной регрессии. обозначает натуральный логарифм.
обозначает натуральный логарифм. – коэффициент регрессии, умноженный на некоторое значение предиктора.
– коэффициент регрессии, умноженный на некоторое значение предиктора. обозначает экспоненциальную функцию.
обозначает экспоненциальную функцию.

![{displaystyle {begin{aligned}R_{text{CS}}^{2}=1-left({frac {L_{0}}{L_{M}}}right)^{2/n}\[5pt]=1-e^{2(ln(L_{0})-ln(L_{M}))/n}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d7fd894a2491abc493151c9aecafec2bb3cd9b8)

![{displaystyle {begin{matrix}R_{text{CS}}^{2}=1-left({dfrac {1}{L_{0}}}right)^{frac {2(R_{text{McF}}^{2})}{n}}\[1.5em]R_{text{McF}}^{2}=-{dfrac {n}{2}}cdot {dfrac {ln(1-R_{text{CS}}^{2})}{ln L_{0}}}end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f5537e92777913de25ddaa5b8909c8e7f008ccf)
![{ displaystyle { begin {align} Y_ {i} mid x_ {1, i}, ldots, x_ {m, i} sim operatorname {Bernoulli} (p_ {i}) \ operatorname { mathcal {E}} [Y_ {i} mid x_ {1, i}, ldots, x_ {m, i}] = p_ {i} \ Pr (Y_ {i} = y mid x_ {1, i}, ldots, x_ {m, i}) = { begin {cases} p_ {i} { text {if}} y = 1 \ 1-p_ {i} { text {if}} y = 0 end {case}} \ Pr (Y_ {i} = y mid x_ {1, i}, ldots, x_ {m, i}) = p_ {i} ^ {y} (1-p_ {i}) ^ {(1-y)} end {выровнено }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60a58e896d8e9edcbf146709ae5be055e2a1a838)
![{displaystyle operatorname {logit} (operatorname {mathcal {E}} [Y_{i}mid x_{1,i},ldots,x_{m,i}])=operatorname {logit} (p_{i})=ln left({frac {p_{i}}{1-p_{i}}}right)=beta _{0}+beta _{1}x_{1,i}+cdots +beta _{m}x_{m,i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2389d119a0c95c1f52b98396ac9762de04067bdd)
![{displaystyle operatorname {logit} (operatorname {mathcal {E}} [Y_{i}mid mathbf {X} _{i}])=operatorname {logit} (p_{i})=ln left({frac {p_{i}}{1-p_{i}}}right)={boldsymbol {beta }}cdot mathbf {X} _{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66290b1bc5ddfd2fc7fc2971372a79ba65e28f89)
![{displaystyle operatorname {mathcal {E}} [Y_{i}mid mathbf {X} _{i}]=p_{i}=operatorname {logit} ^{-1}({boldsymbol {beta }}cdot mathbf {X} _{i})={frac {1}{1+e^{-{boldsymbol {beta }}cdot mathbf {X} _{i}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74c2849bc48454b0a177375d2c69c557ffd2836d)




![{displaystyle {begin{aligned}Pr(Y_{i}=1mid mathbf {X} _{i})=Pr(Y_{i}^{ast }>0 mid mathbf {X} _ {i}) \ [5pt] = Pr ({ boldsymbol { beta}} cdot mathbf {X} _ {i} + varepsilon>0) \ [5pt] = Pr ( varepsilon>- { boldsymbol { beta}} cdot mathbf { X} _ {i}) \ [5pt] = Pr ( varepsilon <{boldsymbol {beta }}cdot mathbf {X} _{i}){text{(because the logistic distribution is symmetric)}}\[5pt]=operatorname {logit} ^{-1}({boldsymbol {beta }}cdot mathbf {X} _{i})\[5pt]=p_{i}{text{(see above)}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d9f767289fb1baf367d01371bafd39857ac05c3)
![{displaystyle p_{i}=operatorname {mathcal {E}} left[left.{frac {Y_{i}}{n_{i}}},right|,mathbf {X} _{i}right],,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0123cbc81b998479d4519f00a89ba3d5ba1bfcc5)
![{displaystyle operatorname {logit} left(operatorname {mathcal {E}} left[left.{frac {Y_{i}}{n_{i}}},right|,mathbf {X} _{i}right]right)=operatorname {logit} (p_{i})=ln left({frac {p_{i}}{1-p_{i}}}right)={boldsymbol {beta }}cdot mathbf {X} _{i},,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdb8db87748853ad7609116b81d41ab7ecaad708)
