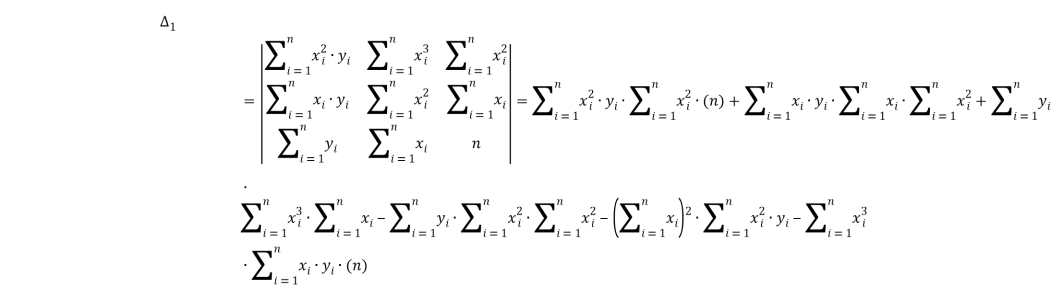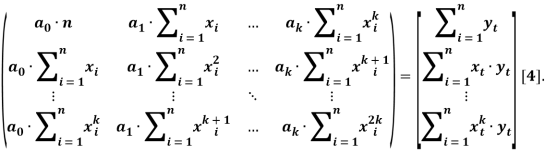Библиографическое описание:
Селютин, А. Д. Аппроксимация полиномов n степени методом наименьших квадратов / А. Д. Селютин. — Текст : непосредственный // Молодой ученый. — 2018. — № 16 (202). — С. 91-96. — URL: https://moluch.ru/archive/202/49571/ (дата обращения: 21.05.2023).
Вданной статье рассмотрено решение проблемы уменьшения суммы квадратов отклонений определённых функций от искомых переменных для полиномиальных уравнений n степени. Приведено подробное решение для уравнений 2 степени, рассматриваемой проблемы. Представлена рабочая программа.
Ключевые слова: метод наименьших квадратов, полиномы, полиномиальная регрессия, оконное приложение.
Метод наименьших квадратов — один из методов статистики, имеющий различное практическое применение, в основе которого лежит минимизация суммы квадратов отклонений функций от подлежащих нахождению переменных [4].
История создания.
Одной из основных задач, для решения которой применяется метод наименьших квадратов, является решение систем линейных уравнений, в которых число неизвестных переменных меньше, чем число уравнений. Впервые, метод был применён в 1796 году Фридрихом Гауссом, а в 1805 году Адриен Лежандр опубликовал метод под насущным названием. Метод в дальнейшем был доработан и улучшен [4].
Суть метода.
Допустим, что x — группа nнеизвестных переменных: –набор функций от группы переменных. Целью является подбор таких x, чтобы значения функций были близки к yi [3]. Следовательно, суть метода наименьших квадратов может быть выражена следующей формулой:
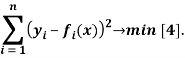
Полиномиальная регрессия.
Допустим, что имеется nзначений переменной yи соответствующих переменных x. Необходимо аппроксимировать корреляцию между yи xопределённой функцией f(x,a), где a–известные параметры.
В случае, когда имеется некоторая полиномиальная регрессионная зависимость, например: 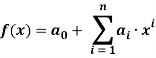
а также
Тогда, матричные уравнения будут иметь следующий вид:
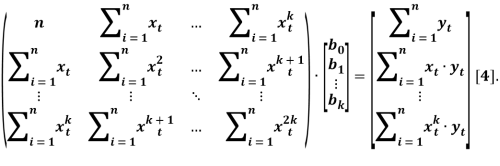
Цель работы.
Целью проводимой работы является вывод рабочих формул, минимизирующих сумму квадратов отклонений полиномиальной функции 2 степени, а также создание практической программы, позволяющей находить коэффициенты квадратичной функции и полинома nстепени. Приложение будет являться оконным (будет предусмотрена возможность построения графика по заданным точкам).
Математическое решение проблемы для полиномов 2 степени.
Пусть дан полином второй степени вида:
Пусть задана функция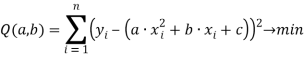
Тогда: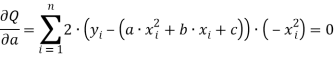
В итоге имеем:
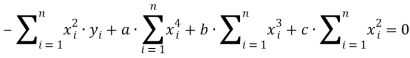
Тогда: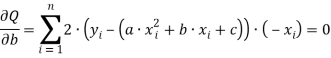
В итоге имеем: 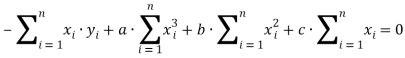
Тогда: 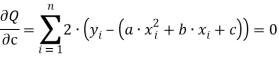
В итоге имеем: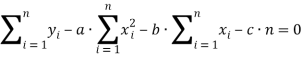
Составим систему линейных уравнений:
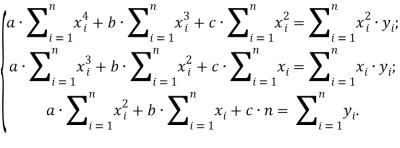
Решим систему. Найдём определитель системы:
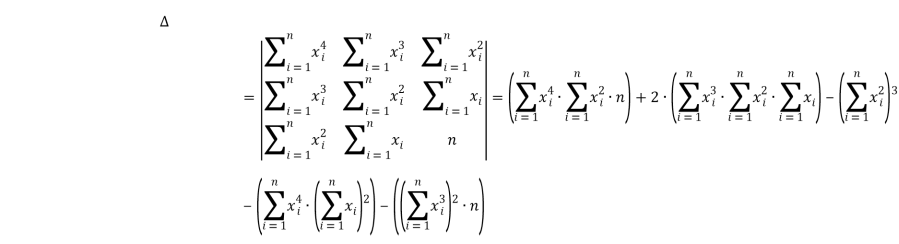
Найдём первый частный определитель системы:
Найдём второй частный определитель системы:
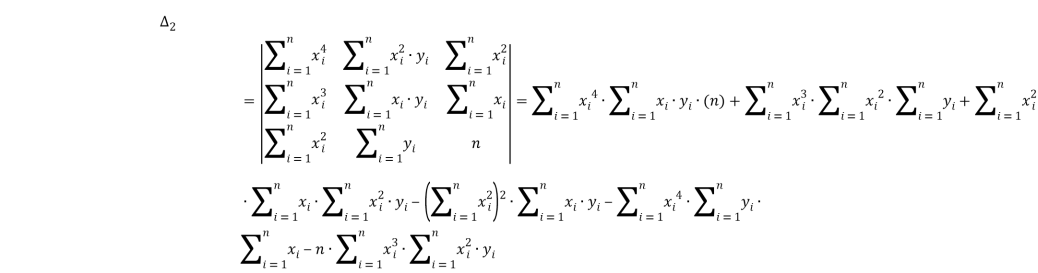
Найдём третий частный определитель системы:
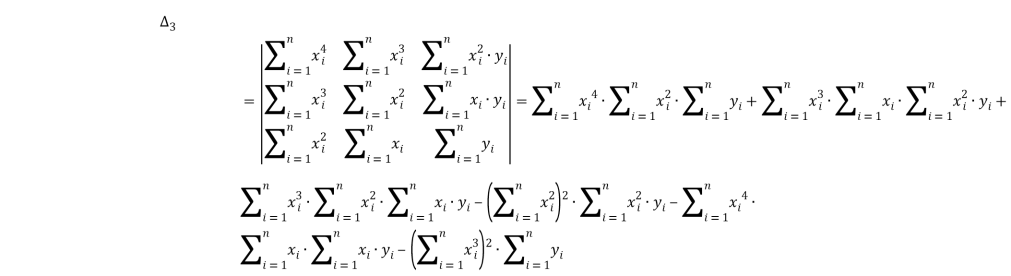
, b=
, c=
.
Решение проблемы для полиномов n степени.
Пусть дан полином вида: , где
, а
длина отрезка известных нам значений [2].
Необходимо найти такие параметры , чтобы сумма квадратов отклонений
от
в точках
была минимальной, то есть
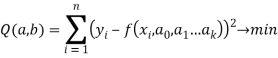
Задача сводится к решению системы уравнений:
Для решения будем использовать метод Гаусса. Результат решения системы можно наблюдать в работе оконного приложения на языке программирования C#.
Программа
Оконное приложение на языке программирования C# для определения коэффициентов аппроксимации полиномов nстепени.
Основная работа программы приходится на обработчик нажатия кнопки вычислить. Считывается степень полинома. Вычисляется кол-во точек. Далее по заданным точкам заполняется матрица сумм. Далее матрица сумм приводится к такому виду, чтобы на главной диагонали не было нулей. Высчитываются коэффициенты аппроксимации.
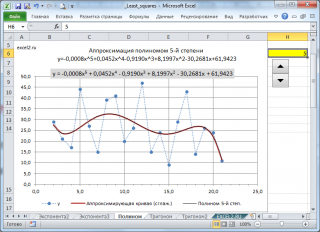
Программа позволяет импортировать данные из текстового файла, строить график получившейся функции и сохранять его в формате.png, экспортировать в текстовый файл получившиеся коэффициенты.
Оконные формы приложения:
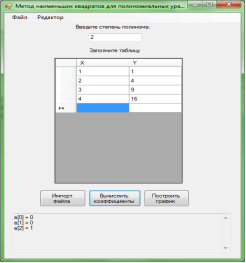
Рис. 1. Оконное приложение, реализующее метод наименьших квадратов для полиномиальных уравнений n степени.
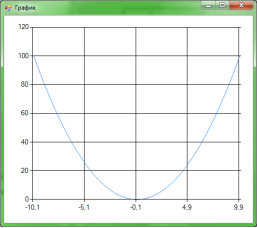
Рис. 2. Полученный график, аппроксимированной функции.
Программа доступна к использованию по ссылке: https://yadi.sk/d/G9WiaoGe3UYqsJ
Вывод
В ходе работы были выведены рабочие формулы, минимизирующие сумму квадратов отклонений полиномиальной функции второй и n-ой степени, а также была создана практическая программа, позволяющая находить коэффициенты аппроксимируемой функции.
Разработанная программа может применяться при расчётах в эконометрике для наглядного определения зависимостей одних зависимостей от других, также в оценке параметров однофакторной эконометрической модели и других областях науки.
Литература:
- Письменный Т.Д — Конспект лекций по высшей математике
- NetBeansURL: https://netbeans.org/ (Дата обращения: 5.4.18).
- Аппроксимация функций полиномом методом наименьших квадратов.URL: http://www.alexeypetrov.narod.ru/C/sqr_less_about.html (Дата обращения: 6.4.18)
- Материал из Википедии — свободной энциклопедии. Метод наименьших квадратов. URL: https://ru.wikipedia.org/wiki/Метод_наименьших_квадратов (Дата обращения: 6.4.18).
Основные термины (генерируются автоматически): оконное приложение, сумма квадратов отклонений, частный определитель системы, вид, квадрат, матрица сумм, полиномиальная регрессия, полиномиальная функция, практическая программа, язык программирования.
Приближение многочленом с условием прохождения через точки
Время на прочтение
6 мин
Количество просмотров 7.4K
При моделировании данных методом наименьших квадратов, кривая обычно не проходит через точки измерений (рис. 1).
Что, если нужно, чтобы эта кривая точно проходила через одну или несколько особо выделенных точек (рис. 2 – показаны зелёными кружочками)?
Тогда читаем дальше.
1. Мотивация
Рассмотрим обычную задачу приближения многочленом и посмотрим, чего нам в ней не хватает.
Дано N точек на плоскости (xi,yi) – значения неизвестной функции f(x). Требуется найти многочлен p(x) степени M (M<N), наилучшим образом приближающий эту функцию.
Часто полагают, что “наилучшим” является многочлен, сумма квадратов отклонений которого от заданных точек минимальна:
В таком виде задача решается широко известным методом наименьших квадратов (МНК).
При M<N-1 многочлен p(x), вообще говоря, не проходит через все заданные точки (xi, yi) (рис. 1). Более того, часто оказывается, что он не проходит ни через одну из них.
Само по себе это не плохо. Обычно данные, по которым строится приближение, содержат погрешности измерений. Даже лучше, что многочлен не проходит через все точки, так как при этом ошибки измерений сглаживаются.
Однако бывает, что о моделируемой зависимости имеются дополнительные сведения. Например, моделируется отклик датчика на некую величину. И из физических соображений ясно, что этот отклик строго равен нулю при равенстве нулю величины. При моделировании характеристики такого датчика может оказаться, что аппроксимирующий многочлен не пройдет через нуль. В результате модель даст большую погрешность в районе нуля.
В такой ситуации хотелось бы найти многочлен со следующими свойствами:
-
Точно проходит через нуль
-
Имеет наименьшую сумму квадратов отклонений от остальных измеренных значений
В статье описывается метод, позволяющий найти такой многочлен. Более того, можно потребовать точного прохождения многочлена не через одну, а несколько выделенных точек.
2. Решение
2.1. Взвешенный метод наименьших квадратов
Как ингредиент нам потребуется взвешенный метод наименьших квадратов, который минимизирует сумму квадратов отклонений с весовыми коэффициентами в каждой точке:
Где wi – весовые коэффициенты. Обычно взвешенный МНК используется для учета погрешностей измерений в каждой точке, поэтому в литературе часто используют не понятие веса, а обратную дисперсию σ2 погрешностей:
Взвешенный МНК хорошо описан в книге [1], гл. 15.1, 15.4.
2.2. Точное прохождение через нуль
Начнём с простого случая: потребуем точного прохождения многочлена p(x) через нуль.
Для этого найдём многочлен q(x) степени M-1 по модифицированным точкам (xi, yi/xi) с помощью взвешеннго МНК, выбрав в качестве весов wi=xi2; и умножим его на x. Тогда:
Он будет иметь степень M и точно проходить через нуль.
Рассмотрим сумму квадратов его отклонений от остальных точек (xi, yi):
Но именно эта величина и минимизируется взвешенным МНК по модифицированным точкам. Поэтому многочлен p(x) будет соответствовать и второму условию задачи – иметь наименьшую сумму квадратов отклонений от (xi, yi).
2.3. Точное прохождение через одну произвольную точку
Усложним задачу и потребуем точного прохождения многочлена p(x) через одну произвольно заданную точку (ξ,η).
Путём замены переменных u=x-ξ, v=y-η, задача сводится к рассмотренной выше. Находим коэффициенты многочлена p0(u), проходящего через нуль и имеющего наименьшую сумму квадратов отклонений p0(ui)-vi. Далее переходим к исходным переменным:
Для нахождения коэффициентов p(x) можно провести алгебраические манипуляции с коэффициентами p0(x-ξ), но есть и более простой на практике способ. Поскольку у нас в программе уже имеется реализация обычного МНК, то можно просто вычислить значения p(x) по формуле (1) в каких-нибудь M+1 или более точках, и применить к этим значениям обычный МНК, задав степень многочлена M. Тем самым и будут найдены коэффициенты p(x).
2.4. Точное прохождение через несколько точек
И, наконец, самый общий случай – потребуем точного прохождения многочлена p(x) через K заданных точек (ξi, ηi). Следует выбирать K ≤ M, в противном случае задача вырождается в интерполяцию.
Переходя к решению, введем многочлен z(x) степени K:
Он имеет нули в точках ξ1, ξ2, … ξK.
Также введем интерполяционный многочлен Лагранжа L(x) степени K-1, проходящий через точки (ξi, ηi) [1], гл. 3.1.
Используем взвешенный МНК для нахождения многочлена q(x) степени M-K по модифицированным точкам: (xi, (yi-L(xi))/z(xi)) с весовыми коэффициентами wi=z(xi)2. Получим коэффициенты {aj} для q(x), которые минимизируют сумму:
Теперь составим многочлен p(x) как:
Докажем, что p(x) является решением задачи.
-
Прохождение через точки (ξi, ηi) обеспечивается тем, что z(ξi)=0, обращая в нуль первое слагаемое. Второе слагаемое в этих же точках, L(x), проходит через (ξi, ηi) по построению.
-
Степень p(x) равна M, так как степень произведения многочленов q(x) и z(x) равна сумме степеней множителей. В данном случае M-K+K=M. Сумма же многочленов имеет степень старшего из слагаемых. Степень L(x) равна K-1, что по условию меньше M.
-
Запишем сумму квадратов отклонений в точках (xi, yi):
Но это совпадает с величиной (2), которая минимизировалась при нахождении коэффициентов q(x). Следовательно, p(xi) имеет наименьшую сумму квадратов отклонений от yi. Что и требовалось доказать.
Для нахождения коэффициентов p(x) можно провести алгебраические манипуляции с q(x), z(x) и L(x), но это еще сложнее, чем в разделе 2.3. выше. Так что здесь тоже рекомендуется вычислить значения p(x) в M+1 или более точках по формуле (3) и применить к ним обычный МНК.
3. Цена вопроса и рекомендации к применению
За всё в этой жизни приходится платить. Наложение условия точного прохождения через точки (ξi, ηi) на многочлен p(x) приводит к тому, что сумма квадратов его отклонений от остальных точек (xi, yi) оказывается, вообще говоря, выше, чем без наложения условий.
Фактически, мы решили задачу условной оптимизации суммы квадратов отклонений p(xi)-yi. Как и в других задачах условной оптимизации, достигаемое значение целевой функции получается хуже, чем при оптимизации безусловной. В противном случае и безусловная оптимизация дала бы тот же результат.
Когда же следует применять описанный метод? Тогда, когда о моделируемой зависимости имеются “железобетонные” сведения, что она должна проходить через точки (ξi, ηi) независимо от экспериментальных данных (xi, yi).
В моей практике был один такой случай. Моделировалась нелинейная характеристика датчика. Истинный вид функциональной зависимости был неизвестен. Оставалось только использовать многочлены в попытке хоть как-то компенсировать нелинейность. Но многочлены плохо описывали характеристику около нуля. Полученные обычным МНК, они стремились не проходить через нуль. Тем не менее, из физических соображений было ясно, что характеристика датчика должна проходить через нуль. Вот тогда наложение условия и пригодилось. Его применение позволило улучшить компенсацию нелинейности в окрестностях нуля и уменьшить относительную погрешность прибора в целом.
4. Пример с конкретными числами
Этот пример был использован для построения графиков, приведенных на рис. 1 и рис. 2.
В качестве “истинной зависимости” был взят следующий многочлен:
Где T3(x) – многочлен Чебышева третьего порядка. Модификации применены к нему для того, чтобы отобразить интересный участок графика в диапазон x,y ∈ [0; 1]. p1(x) проходит через точки (0,0) и (1,1). Разложение его по степеням x выглядит так:
В качестве данных для метода наименьших квадратов (обычного и условного) взяты значения p1(x) в 11 равноотстоящих точках между 0 и 1 с шагом в 0,1. К значениям многочлена была добавлена нормально распределенная “ошибка измерений” δi с дисперсией σ2=0,04. В точках x1=0 и x11=1 ошибка не добавлялась. По случайным числам карты легли следующим образом:
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
xi |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
|
δi |
0 |
-0,1617 |
0,0162 |
0,0294 |
-0,0458 |
0,3358 |
0,2476 |
-0,1325 |
-0,3986 |
-0,4477 |
0 |
Приближение обычным МНК по заданным точкам при M=3 дало следующие коэффициенты:
График p2(x) изображен на рис. 1. Достигнутая сумма квадратов отклонений p2(x)-yi составила 0,4019.
Для испытания описываемого в разд. 2.4. метода было поставлено условие точного прохождения многочлена через точки (0,0) и (1,1), а в остальных точках – минимизация суммы квадратов отклонений. В результате был получен следующий многочлен:
Его график изображен на рис. 2. Достигнутая сумма квадратов отклонений p3(x)-yi составила 0,5046.
Из приведенного примера можно сделать вывод, что теоретические выкладки подтвердились. Был найден многочлен p3(x), приближающий “экспериментальные данные” и проходящий через точки (0,0) и (1,1). Как предсказывалось в разд. 3, сумма квадратов его отклонений от точек (xi, yi) оказалась больше, чем у многочлена p2(x), найденного обычным МНК. Тем не менее, эта жертва может быть оправданной, если прохождение p3(x) через точки (0,0) и (1,1) важнее.
Что касается совпадения коэффициентов многочленов p2(x) и p3(x) с коэффициентами “истинного” многочлена p1(x) – то на паре-тройке наборов тестовых данных особой закономерности не выявилось. Наверное, есть смысл провести тест Монте-Карло и сравнить распределения коэффициентов p2(x) и p3(x) на большой выборке.
Заключение
В статье был получено обобщение метода наименьших квадратов, позволяющее налагать на многочлен условие прохождения через заданные точки.
Задачу удалось свести к применению взвешенного метода наименьших квадратов и интерполяции многочленом Лагранжа. Поскольку обе операции сводятся к решению системы линейных уравнений, то и описанный в статье метод сохраняет эту (невысокую) вычислительную сложность. Точное решение можно получить за конечное число действий и (при должной усидчивости или использовании систем компьютерной алгебры) выразить аналитически.
Возможны обобщения метода для задач приближения не только многочленами, а и другими функциями. Но эта тема обширна и может быть рассмотрена только в отдельных публикациях.
Литература
[1] William H. Press и др. “Numerical Recipes in C++: The Art of Scientific Computing”, Second Edition. Cambridge University Press, ISBN 0-521-75033-4
Рассмотрим
решение задачи 2 в Matlab
Задача
2. Известна табличная зависимость y
от x:
|
x |
10.1 |
10.2 |
10.3 |
10.8 |
10.9 |
11 |
11.1 |
11.4 |
12.2 |
13.3 |
13.8 |
14 |
14.4 |
14.5 |
15 |
15.6 |
15.8 |
17 |
18.1 |
19 |
|
y |
24 |
36 |
26 |
45 |
34 |
37 |
55 |
51 |
75 |
84 |
74 |
91 |
85 |
87 |
94 |
92 |
96 |
97 |
98 |
99 |
Для
подбора коэффициентов полинома k-й
степени методом наименьших квадратов в Matlab есть функция polyfit ( x – массив абсцисс экспериментальных
точек, y
– массив ординат экспериментальных точек, k – степень полинома). Функция
возвращает массив коэффициентов полинома. Затем можно вычислить значение
полинома в любой точке с помощью функции polyval (k, t). В массиве k хранятся коэффициенты полинома, t – точка, в которой необходимо
вычислить значение полинома. Функция polyval (k,
t)
вычисляет значение полинома в точке t
по формуле k1-t^n +k2*t^(n-1)+…+ kn*t + k(n+1) С помощью функций polyfit, polyval можно подобрать
зависимости y=a0+a1*x+a2*x^2 и y=b0+b1*x+b2*x^2+b3*x^3, что показано в следующей
программе.
>>
x=[10.1,
10.2, 10.3, 10.8, 10.9, 11, 11.1, 11.4, 12.2, 13.3, 13.8, 14, 14.4, 14.5, 15,
15.6, 15.8, 17, 18.1, 19];
>>
y=[24,
36, 26, 45, 34, 37, 55, 51, 75, 84, 74, 91, 85, 87, 94, 92, 96, 97, 98, 99];
%
подбор коэффициентов полинома 2-ц степени с помощью МНК
>> a=polyfit(x, y,2);
%
подбор коэффициентов полинома 3-й степени с помощью МНК
>> b=polyfit (x, y,3);
%
определение массива для построения графика функции
>> t=x(1):0.1:x(lenght(x));
%
вычисление значений подобранных полиномов в точках t (i)
>> p2t=polyval (a, t);
>> p3t=polyval(b,t);
% построение графика функции
>>plot (x, y, ‘ko’, t, p2t, ‘r-‘, t, p3t,
‘b-.’);
Title (“Подбор зависимости методом
наименьших квадратов”);
Legend (“Экспериментальные значения ”,
“полином 2-й степени”, “полином 3-й степени”);
Grid on;
Несколько
сложнее в Matlab
подобрать параметры зависимости y=c0+c1*x^2+c2+x^3 методом наименьших квадратов.
Эта задача эквивалентна поиску минимума функции S( c0,c1,c2) = ∑(i=0:n) (y1-c0-c1*xi^2-c2*xi^3)^2, которую можно решить
двумя способами:
·
С помощью функции fminsearch найти минимум функции S;
·
Можно найти частные производные S(c0,c1,c2) =∑(i=0:n)(y1-c0-c1*xi^2-c2*xi^3)^2 по с0,с1,с2, приравнять их к нулю,
решить полученную систему линейных алгебраических уравнений.
Рассмотрим оба
способа последовательно.
Первый
способ решения. Для поиска
минимума функции многих переменных в Matlab можно использовать функцию fminsearch (fun, x0). Fun – функция, минимум которой
необходимо найти, x0
– вектор начального приближения точки минимума. Функция fminsearch возвращает массив, в
котором хранятся координаты точки минимума и само значение минимума.
В нашей задаче
необходимо создать М-функцию, вычисляющую значение S(c0,c1,c2) по формуле ∑(i=0:n)(y1-c0-c1*xi^2-c2*xi^3)^2. Текст этой функции
приведен ниже:
function
s=f_mnk(c)
global x;
global y;
s=0;
for i=1:lenght(x)
s=s+(y(i)-c(1)-c(2)*x(i)^2-c(3)*x(i)^3)^2;
end
end
Затем
необходимо обратиться к функции fminsearch(fun, x0) для поиска минимума S(c0,c1,c2), после чего можно будет изобразить график
подобранной функции.
Программа:
>>
global x;
>>
global y;
>> c=[2,
1, 0];
>>
x=[10.1, 10.2, 10.3, 10.8, 10.9, 11, 11.1, 11.4, 12.2, 13.3, 13.8, 14, 14.4,
14.5, 15, 15.6, 15.8, 17, 18.1, 19];
>>
y=[24, 36, 26, 45, 34, 37, 55, 51, 75, 84, 74, 91, 85, 87, 94, 92, 96, 97, 98,
99];
>> [c,
err]=fminsearch(‘f_mnk’,c)
>> t=x(1):0.1:x(lenght(x));
>> p2t=c(3)*t.^3+c(2)*t.^2+c(1);
>>plot (x,y, ‘ko’, t, p2t, ‘r-’);
>>legend(‘Экспериментальные значения’, ‘Подобранная
кривая’);
>>grid on;
Второй способ решения начинается с формирования системы линейных
алгебраических уравнений. Для этого продифференцируем функцию S(c0,c1,c2) = ∑(i=0:n)(y1-c0-c1*xi^2-c2*xi^3)^2 по c0,c1,c2 и приравняем все частные производные к нулю.
Далее
приведена функция my_mnk (x, y),
реализующая подбор зависимости вторым способом.
function c=m_mnk(x, y)
n=length(x);
sx=0; sx2=0; sx3=0; sx4=0; sx5=0; sx6=0; sy=0; syx=0;
syx3=0;
for i=1:length(x)
sx=sx+x(i); sx2=sx2+x(i)^2; sx3=sx3+x(i)^3;
sx4=sx4+x(i)^4; sx5=sx5+x(i)^5; sx6=sx6+x(i)^6;
sy=sy+y(i); syx2= syx2+y(i)*x(i)^2; syx3=
syx3+y(i)*x(i)^3;
end;
%
формирование матрицы коэффициентов системы *
A(1,1)=n; A(1,2)=sx2; A(1,3)=sx3;
A(2,1)=sx2; A(2,2)=sx4; A(2,3)=sx5;
A(3,1)=sx3; A(3,2)=sx5; A(3,3)=sx6;
%
формирование вектора правой части системы *
B(1)=sy; B(2)=syx2; B(3)=syx3;
%
решение системы *
% нахождение
параметров подбираемой зависимости
C=A^(-1)*B’
End
Параметры
зависимости y=c0+c1*x^2+c2*x^3, найденные первым и
вторым способом, полностью совпадают.
Параметры любой другой зависимости в Matlab можно также реализовать аналогично:
решив задачу оптимизации функции S(a0,a1…ak) или сформировав систему уравнений и решив ее в
Matlab. Желательно приводить
подбираемую функцию к такому виду, чтобы система была системой линейных
алгебраических уравнений.
Содержание
§
Вспомогательная страница к разделу
☞
ИНТЕРПОЛЯЦИЯ.
Все числа в настоящем разделе предполагаются вещественными.
Метод наименьших квадратов
Пусть из физических соображений можно считать (предполагать), что
величины $ x_{} $ и $ y_{} $ связаны линейной зависимостью вида $ y=kx+b $,
а неизвестные коэффициенты $ k_{} $ и $ b_{} $ должны быть оценены экспериментально.
Экспериментальные данные представляют собой $ m>1 $ точек на координатной
плоскости $ (x_1,y_1), dots, (x_m,y_m) $. Если бы эти опыты производились
без погрешностей, то подстановка данных в уравнение приводила бы нас к
системе из $ m_{} $ линейных уравнений для двух неизвестных $ k_{} $ и $ b_{} $:
$$
y_1=k,x_1+b, dots, y_m=k,x_m+b .
$$
Из любой пары уравнений этой системы можно было бы однозначно определить
коэффициенты $ k_{} $ и $ b_{} $.
Однако, в реальной жизни опытов без погрешностей
не бывает
Письмо в редакцию:
Дорогая редакция! Формулировку закона Ома следует уточнить следующим образом:«Если использовать тщательно отобранные и безупречно подготовленные исходные материалы, то при наличии некоторого навыка из них можно сконструировать электрическую цепь, для которой измерения отношения тока к напряжению, даже если они проводятся в течение ограниченного времени, дают значения, которые после введения соответствующих поправок оказываются равными постоянной величине».
Источник: А.М.Б.Розен. Физики шутят. М.Мир.1993.
Будем предполагать, что величины $ x_{1},dots,x_m $
известны точно, а им соответствующие $ y_1,dots,y_m $ — приближенно.
Если $ m>2 $, то при любых различных $ x_{i} $ и $ x_j $ пара точек
$ (x_{i},y_i) $ и $ (x_{j},y_j) $ определяет прямую. Но другая пара точек определяет
другую прямую, и у нас нет оснований выбрать какую-нибудь одну из всех прямых.
Часто в задаче удаленность точки от прямой измеряют не расстоянием, а разностью ординат $ k,x_i+b-y_i $, и выбирают прямую так, чтобы
сумма квадратов всех таких разностей была минимальна. Коэффициенты $ k_0 $ и $ b_{0} $ уравнения этой прямой дают некоторое решение стоящей
перед нами задачи, которое отнюдь не является решением системы линейных
уравнений
$$ k,x_1+b=y_1,dots, k,x_{m}+b=y_m $$
(вообще говоря, несовместной).
Рассмотрим теперь обобщение предложенной задачи. Пусть искомая зависимость
между величинами $ y_{} $ и $ x_{} $ полиномиальная:
$$
y_1=f(x_1),dots , y_m=f(x_m), quad npu quad f(x)=a_0+a_1x+dots+a_{n-1}x^{n-1}
$$
Величина $ varepsilon_i=f(x_i)-y_i $ называется $ i_{} $-й невязкой1). Уравнения
$$
left{begin{array}{ccl}
a_0+a_1x_1+dots+a_{n-1}x_1^{n-1}&=&y_1, \
a_0+a_1x_2+dots+a_{n-1}x_2^{n-1}&=&y_2, \
dots & & dots \
a_0+a_1x_m+dots+a_{n-1}x_m^{n-1}&=&y_m
end{array}
right.
$$
называются условными. Матрица этой системы — матрица Вандермонда (она не обязательно квадратная).
Предположим что данные интерполяционной таблицы
$$
begin{array}{c|ccccc}
x & x_1 & x_2 & dots & x_m \ hline
y & y_1 & y_2 &dots & y_m
end{array}
$$
не являются достоверными: величины $ x_{} $ нам известны практически без искажений (т.е. на входе процесса мы имеем абсолютно достоверные данные), а вот измерения величины $ y_{} $ подвержены случайным (несистематическим) погрешностям.
Задача. Построить полином $ f_{}(x) $ такой, чтобы величина
$$
sum_{j=1}^m [f(x_j)-y_j]^2
$$
стала минимальной. Решение задачи в такой постановке известно как метод наименьшик квадратов2).
В случае $ deg f_{} =m-1 $ мы возвращаемся к задаче интерполяции в ее классической постановке. Практический интерес, однако, представляет случай $ deg f_{} < m-1 $, т.е. случай когда экспериментальных данных больше (обычно — много больше) чем значений параметров (коэффициентов полинома $ f_{} $), которые требуется определить.
Так, в случае $ deg f_{}=1 $ речь идет о построении прямой $ y=ax+b $ на плоскости $ (x,y) $, обеспечивающей
$$ min (varepsilon_1^2+varepsilon_2^2+dots + varepsilon_m^2) , . $$
Здесь $ varepsilon_j = a,x_j+b-y_j $.

Т
Теорема. Если $ mge n_{} $ и узлы интерполяции $ x_{1},dots,x_m $ все различны, то
существует единственный набор коэффициентов $ a_{0},dots,a_{n-1} $, обеспечивающий
минимальное значение для
$$
sum_{j=1}^m (a_0+a_1x_j+dots+a_{n-1}x_j^{n-1} -y_j)^2 .
$$
Этот набор определяется как решение системы нормальных уравнений
$$
underbrace{
left(begin{array}{llllll}
s_0 &s_1&s_2&ldots&s_{n-2}& s_{n-1}\
s_1 &s_2&s_3&ldots&s_{n-1}& s_{n}\
s_2 &s_3&s_4&ldots&s_{n}& s_{n+1}\
vdots& & & && vdots\
s_{n-1} &s_n&s_{n+1}&ldots &s_{2n-3}&s_{2n-2}
end{array}right)}_{displaystyle S_{ntimes n}}
left(begin{array}{l}
a_0 \ a_1 \ a_2 \ vdots \ a_{n-1} end{array} right)=
left(begin{array}{l}
t_0 \ t_1 \ t_2 \ vdots \ t_{n-1} end{array} right)
$$
при $ s_{k} = x_1^k+dots+x_m^k, t_{k} = x_1^ky_1+dots+x_m^k y_m $.
Если одно из значений $ x_{j} $ равно $ 0_{} $ , то полагаем $ 0^{0} = 1 $, так что $ s_{0}=m $
при любых $ {x_{1},dots, x_m} subset mathbb R $.
Доказательство. Рассмотрим сумму как полином от неопределенных
коэффициентов $ {a_{j}}_{j=0}^{n-1} $:
$$F(a_0,dots,a_{n-1})=
sum_{i=1}^m [f(x_i)-y_i]^2=
$$
$$
=sum_{i=1}^m [(a_0+a_1x_i+dots+a_{n-1}x_i^{n-1})-y_i]^2 .
$$
На основании теоремы из пункта ЭКСТРЕМУМЫ ПОЛИНОМА такая функция может принимать экстремальные значения только на вещественных решениях системы уравнений
$$
partial F / partial a_0=0, dots, partial F / partial a_{n-1}=0 .
$$
Распишем выражение для $ partial F / partial a_j $:
$$partial F / partial a_j =sum_{i=1}^m 2,[f(x_i)-y_i]
frac{partial (a_0+a_1x_i+dots+a_{n-1}x_i^{n-1})}{partial a_j}
$$
$$
=2, sum_{i=1}^m [f(x_i)-y_i] x_i^{j}=$$
$$=2, sum_{i=1}^m left[left(a_0x_i^{j}+a_1x_i^{j+1}+dots+a_{n-1}x_i^{j+n-1}
right)-y_ix_i^{j} right]=
$$
$$= 2left[a_0, sum_{i=1}^m x_i^{j}+a_1, sum_{i=1}^m x_i^{j+1}+
dots+a_{n-1}, sum_{i=1}^m x_i^{j+n-1}- sum_{i=1}^m y_ix_i^{j} right]=$$
$$=2 [a_0, s_j+a_1, s_{j+1}+dots+a_{n-1},s_{j+n-1}-t_j ] $$
Таким образом, условия $ left{partial F / partial a_j=0 right}_{j=0}^n $ можно переписать в виде
системы нормальных уравнений.
Покажем теперь, что матрица этой системы имеет ненулевой определитель.
Действительно, матрица $ S_{} $ — ганкелева. При $ m=n_{} $
$$S = left(begin{array}{ccccc}
1 &1&1&ldots&1\
x_1 &x_2&x_3&ldots&x_{n}\
vdots&& & &vdots\
x_1^{n-1} &x_2^{n-1}&x_3^{n-1}&ldots&x_n^{n-1}
end{array}right) cdot
left(begin{array}{ccccc}
1 &x_1&x_1^2&ldots&x_1^{n-1}\
1 &x_2&x_2^2&ldots&x_2^{n-1}\
ldots&& & &ldots\
1 &x_n&x_n^2&ldots&x_n^{n-1}
end{array}right) , .
$$
По теореме Бине-Коши вычисление определителя сводится к вычислению определителя Вандермонда:
$$
det S =prod_{1le j<kle n} (x_k-x_j)^2 .$$
Воспользуемся той же теоремой и для случая $ m>n $:
$$S=left(begin{array}{ccccc}
1 &1&1&ldots&1\
x_1 &x_2&x_3&ldots&x_{m}\
vdots&& & &vdots\
x_1^{n-1} &x_2^{n-1}&x_3^{n-1}&ldots&x_m^{n-1}
end{array}right) cdot
left(begin{array}{ccccc}
1 &x_1&x_1^2&ldots&x_1^{n-1}\
1 &x_2&x_2^2&ldots&x_2^{n-1}\
ldots&& & &ldots\
1 &x_m&x_m^2&ldots&x_m^{n-1}
end{array}right)$$
$$det S = sum_{1le j_1< j_2 <dots < j_n le m} left|begin{array}{cccc}
1 &1&ldots&1\
x_{j_1} &x_{j_2}&ldots&x_{j_n}\
vdots&& &vdots\
x_{j_1}^{n-1} &x_{j_2}^{n-1}&ldots&x_{j_n}^{n-1}
end{array}right| cdot
left|begin{array}{cccc}
1 &x_{j_1}&ldots&x_{j_1}^{n-1}\
1 &x_{j_2}&ldots&x_{j_2}^{n-1}\
ldots&& &ldots\
1 &x_{j_n}&ldots&x_{j_n}^{n-1}
end{array}right|=$$
$$=sum_{1le j_1< j_2 <dots < j_n le m} prod_{1le L < K le n} (x_{j_K}-x_{j_L})^2
.$$
Каждое слагаемое неотрицательно и отлично от нуля поскольку,
по предположению, все $ {x_j}_{j=1}^m $ различны. Поэтому $ det S >0 $.
По теореме Крамера система нормальных уравнений имеет единственное решение.
Осталось недоказанным утверждение, что полученное решение доставляет именно минимум сумме квадратов невязок. Этот факт следует из доказательства более общего утверждения — о псевдорешении системы
линейных уравнений. Этот результат приводится
☟
НИЖЕ.
♦
Собственно минимальное значение величины cуммы квадратов невязок, а точнее усреднение по количеству узлов
$$
sigma=frac{1}{m}sum_{j=1}^m (f(x_j) -y_j)^2
$$
называется среднеквадратичным отклонением.

?
Показать, что линейный полином $ y=a_{0}+a_1x $, построенный по методу наименьших квадратов, определяет на плоскости $ (x_{},y) $ прямую, проходящую через центроид
$$
(overline{x},overline{y}) = left(frac{x_1+x_2+ dots+x_m}{m},
frac{y_1+y_2+ dots+y_m}{m} right) .
$$
системы точек $ (x_{1},y_1),dots,(x_m,y_m) $.
П
Пример. По методу наименьших квадратов построить уравнение прямой, аппроксимирующей множество точек плоскости, заданных координатами из таблицы
$$
begin{array}{c|cccccc}
x & 0.5 & 1 & 1.5 & 2 & 2.5 & 3 \ hline
y & 0.35 & 0.80 & 1.70 & 1.85 & 3.51 & 1.02
end{array}
$$
Решение. Имеем
$$
s_0=6, s_1=0.5 + 1 + 1.5 + 2 + 2.5 + 3=10.5, $$
$$ s_2=0.5^2 + 1^2 + 1.5^2 + 2^2 + 2.5^2 + 3^2=22.75,
$$
$$t_0=0.35 + 0.80 + 1.70 + 1.85 + 3.51 + 1.02=9.23,
$$
$$
t_1
=0.5cdot 0.35 + 1 cdot 0.80 + 1.5 cdot 1.70 + 2 cdot 1.85 +
$$
$$
+2.5 cdot 3.51 + 3 cdot 1.02=19.06 .
$$
Решаем систему нормальных уравнений
$$
left(
begin{array}{cc}
6 & 10.5 \
10.5 & 22.75
end{array}
right)
left(
begin{array}{c}
a_0 \ a_1
end{array}
right)=
left(
begin{array}{c}
9.23 \ 19.06
end{array}
right),
$$
получаем уравнение прямой в виде
$$ y= 0.375 + 0.665, x .$$
Вычислим и полиномы более высоких степеней.
$$ f_2(x)=-1.568+3.579, x-0.833,x^2 , $$
$$ f_3(x)=2.217-5.942,x+5.475,x^2-1.201, x^3 , $$
$$ f_4(x)= -4.473+17.101,x-19.320,x^2+9.205, x^3-1.487,x^4 , $$
$$ f_5(x)= 16.390-71.235,x+111.233,x^2-77.620,x^3+25.067,x^4-3.0347, x^5 . $$
Среднеквадратичные отклонения:
$$
begin{array}{c|ccccc}
deg & 1 & 2 & 3 & 4 & 5 \ hline
sigma & 0.717 & 0.448 & 0.204 &0.086 & 0
end{array}
$$
♦
Возникает естественный вопрос: полином какой степени следует разыскивать в МНК? При увеличении степени точность приближения, очевидно, увеличивается. Вместе с тем, увеличивается сложность решения системы нормальных уравнений и даже при небольших степенях $ n $ (меньших $ 10 $) мы столкнемся с проблемой чувствительности решения к точности представления входных данных.
Влияние систематических ошибок
П
Пример. Уравнение прямой, аппроксимирующей множество точек плоскости, заданных координатами из таблицы
$$
begin{array}{c|cccccc}
x & 0.5 & 1 & 1.5 & 2 & 2.5 & 3 \ hline
y & 0.35 & 0.80 & 1.70 & 1.85 & 2.51 & 2.02
end{array}
$$
имеет вид (охра)
$$ y=0.175+0.779, x , . $$
Теперь заменим значение $ y_5 $ на $ 0.2 $. Уравнение прямой принимает вид:
$$ y=0.483+0.383, x , . $$
График (зеленый) существенно изменился. Почему это произошло? — Дело в том, что эффективность метода наименьших квадратов зависит от нескольких предположений относительно входных данных: в нашем случае — значений $ y $. Предполагается, что эти величины являлись результатами экспериментов, измерений, и, если они подвержены погрешностям, то эти погрешности носят характер несистематических флуктуаций вокруг истинных значений. Иными словами, изначально предполагается, что в действительности точки плоскости должны лежать на некоторой прямой. И только несовершенство наших методов измерений (наблюдений) демонстрирует смещение их с этой прямой. Ответ для исходной таблицы визуально подтвержает это предположение: экспериментальные точки концентрируются вокруг полученной прямой и величины невязок (отклонений по $ y $-координате) имеют «паритет» по знакам: примерно половина точек лежит выше прямой, а половина — ниже.
После замены значения $ y_5 $ на новое, значительно отличающееся от исходного, существенно меняется величина $ 5 $-й невязки $ varepsilon_5= ax_5+b-y_5 $. А поскольку в минимизируемую функцию эта невязка входи еще и в квадрате, то понятно, что изначальная прямая просто не в состоянии правильно приблизить новую точку.
Эта проблема становится актуальной в тех случаях, когда в «истинно случайный» процесс привносятся намеренные коррективы.
Данные начинают подвергаться существенным искажениям, возможно, даже имеющим «злой» умысел3).
Как бороться с ошибками такого типа? Понятно, что решение возможно в предположении, что число таких — систематических — ошибок должно быть существенно меньшим общего количества экспериментальных данных. Понятно, что каким-то образом эти «выбросы» надо будет исключить из рассмотрения, т.е. очистить «сырые» данные от «мусора» — прежде чем подсовывать их в метод наименьших квадратов (см.
☞
цитату). Как это сделать? — Ответ на этот вопрос постепенно излагается
☞
ЗДЕСЬ.
Псевдорешение системы линейных уравнений
Рассмотрим теперь обобщение задачи предыдущего пункта.
В практических задачах часто бывает нужно найти решение, удовлетворяющее
большому числу возможно противоречивых требований. Если такая задача
сводится к системе линейных уравнений
$$
left{begin{array}{ccc}
a_{11}x_1 +a_{12}x_2+ldots+a_{1n}x_n &=&b_1\
a_{21}x_1 +a_{22}x_2+ldots+a_{2n}x_n &=&b_2\
ldots& & ldots \
a_{m1}x_1 +a_{m2}x_2+ldots+a_{mn}x_n &=&b_m
end{array}right.
iff
AX={mathcal B}
$$
при числе уравнений $ m_{} $ большем числа неизвестных $ n_{} $, то такая
переопределенная система, как правило, несовместна. В этом случае задача может быть решена только путем выбора некоторого
компромисса — все требования могут быть удовлетворены не полностью, а лишь до некоторой степени.
Псевдорешением системы $ AX={mathcal B} $ называется столбец $ Xin mathbb R^n $, обеспечивающий минимум величины
$$
sum_{i=1}^m [a_{i1}x_1 +a_{i2}x_2+ldots+a_{in}x_n-b_i]^2 .
$$
Такому определению можно также соотнести
вероятностную интерпретацию. Пусть для определения неизвестных величин
$ x_{1},dots,x_n $ проводятся $ m_{} $ экспериментов, описываемых линейными
уравнениями:
$$
a_{i1}x_1 +a_{i2}x_2+ldots+a_{in}x_n =b_i quad npu quad iin {1,dots,m}
.
$$
При этом величины $ { a_{ij} }, i in {1,dots, m}, jin {1,dots, n} $ — известные постоянные, не подверженные
сопутствующим экспериментам (наблюдениям) погрешностям, а вот величины $ {b_{i}}_{i=1}^m $ этим
погрешностям подвержены. Формально каждое из равенств следует рассматривать как приближенное.
Понятно, что при таких обстоятельствах не имеет смысла гоняться за точным решением системы $ AX={mathcal B} $ (его может и не
существовать вовсе!). Искать следует приближенное решение, оптимальное
в некотором смысле. Оказывается, что именно выбор критерия в виде минимума квадратов разностей левых и правых частей уравнения
обеспечивает то, что псевдорешение дает максимально правдоподобные значения неизвестных величин $ x_1,dots,x_{n} $.
T
Теорема. Существует псевдорешение системы
$$
AX={mathcal B}
$$
и оно является решением системы
$$
left[A^{top}A right]X=A^{top} {mathcal B} .
$$
Это решение будет единственным тогда и только тогда, когда $ operatorname{rank} A =n $.
Система $ left[A^{top}A right]X=A^{top} {mathcal B} $ называется нормальной системой по отношению к системе $ AX={mathcal B} $. Формально она получается
домножением системы $ AX={mathcal B} $ слева на матрицу $ A^{top} $. Заметим также, что если $ m=n_{} $ и $ det A ne 0 $, то
псевдорешение системы совпадает с решением в традиционном смысле.
Доказательство
☞
ЗДЕСЬ.
Метод наименьших квадратов, рассмотренный в предыдущем пункте, является частным случаем задачи о псевдорешении системы линейных уравнений; в нём матрица $ A $ совпадает с матрицей Вандермонда.
Если нормальная система имеет бесконечное количество решений, то обычно в
качестве псевдорешения берут какое-то одно из них — как правило то, у которого минимальна сумма квадратов компонент («длина»).
П
Пример. Найти псевдорешение системы
$$x_1+x_2 = 2, x_1-x_2 = 0, 2, x_1+x_2 = 2 .$$
Решение. Имеем:
$$A=left( begin{array}{rr}
1 & 1 \
1 & -1 \
2 & 1
end{array}
right),
operatorname{rank} A =2,
{mathcal B} =
left( begin{array}{r}
2 \ 0 \ 2
end{array}
right),
A^{top}A= left( begin{array}{rr}
6 & 2 \
2 & 3
end{array}
right),
A^{top} {mathcal B} =
left( begin{array}{r}
6 \ 4
end{array}
right).
$$
Ответ. $ x_1=5/7, x_2 = 6/7 $.
?
Показать, что матрица $ A^{top}A $ всегда симметрична.
?
На дубовой колоде лежит мелкая монетка. К колоде

по очереди подходят четыре рыцаря и каждый наносит удар мечом, стараясь
попасть по монетке. Все промахиваются. Расстроенные,
рыцари уходят в харчевню пропивать злосчастную монетку. Укажите
максимально правдоподобное ее расположение, имея перед глазами зарубки:
$$
begin{array}{rrcr}
3, x &- 2, y&=& 6,\
x &-3,y&=&-3,\
11,x& + 14,y&=& 154, \
4,x&+y&=&48.
end{array}
$$
Геометрическая интерпретация
Псевдообратная матрица
Эта матрица определяется не только для квадратной матрицы.
Пусть сначала матрица $ A_{} $ порядка $ mtimes n_{} $ — вещественная и $ m ge n_{} $ (число строк не меньше числа столбцов).
Если $ operatorname{rank} (A) = n $ (столбцы матрицы линейно независимы), то псевдообратная к матрице $ A_{} $ определяется как матрица
$$ A^{+}=(A^{top}A)^{-1} A^{top} . $$
Эта матрица имеет порядок $ n times m_{} $. Матрица $ (A^{top}A)^{-1} $ существует ввиду того факта, что при условии $ operatorname{rank} (A) = n $ будет выполнено $ det (A^{top} A) > 0 $ (см. упражнение в пункте
☞
ТЕОРЕМА БИНЕ-КОШИ или же пункт
☞
СВОЙСТВА ОПРЕДЕЛИТЕЛЯ ГРАМА ). Очевидно, что $ A^{+} cdot A = E_{n} $, т.е. псевдообратная матрица является левой обратной для матрицы $ A_{} $. В случае $ m=n_{} $ псевдообратная матрица совпадает с обратной матрицей: $ A^{+}=A^{-1} $.
П
Пример. Найти псевдообратную матрицу к матрице
$$ A= left( begin{array}{cc}
1 & 0 \
0 & 1 \
1 & 1
end{array}
right) .
$$
Решение.
$$
A^{top}= left( begin{array}{ccc}
1 & 0 & 1 \
0 & 1 & 1
end{array}
right) Rightarrow A^{top} cdot A =
left( begin{array}{cc}
2 & 1 \
1 & 2
end{array}
right) Rightarrow
$$
$$
Rightarrow
(A^{top} cdot A)^{-1} =
left( begin{array}{cc}
2/3 & -1/3 \
-1/3 & 2/3
end{array}
right)
Rightarrow
$$
$$
Rightarrow
quad A^{+} = (A^{top} cdot A)^{-1} A^{top} =
left( begin{array}{rrr}
2/3 & -1/3 & 1/3 \
-1/3 & 2/3 & 1/3
end{array}
right) .
$$
При этом
$$
A^{+} cdot A =
left( begin{array}{cc}
1 & 0 \
0 & 1
end{array}
right),quad A cdot A^{+} =
left( begin{array}{rrr}
2/3 & -1/3 & 1/3 \
-1/3 & 2/3 & 1/3 \
1/3 & 1/3 & 2/3
end{array}
right) ,
$$
т.е. матрица $ A^{+} $ не будет правой обратной для матрицы $ A_{} $.
♦
?
Вычислить псевдообратную матрицу для
$$ mathbf{a)} left( begin{array}{cc}
1 & 0 \
1 & 1 \
1 & 1
end{array}
right) quad ; quad
mathbf{b)}
left( begin{array}{c}
x_1 \
x_2 \
x_3
end{array}
right)
.
$$
Концепция псевдообратной матрицы естественным образом возникает из понятия псевдорешения системы линейных уравнений. Если $ A^{+} $ существует, то псевдорешение (как правило, переопределенной и несовместной!) системы уравнений $ AX=mathcal B_{} $ находится по формуле $ X= A^{+} mathcal B $ при любом столбце $ mathcal B_{} $.
Верно и обратное: если
$ E_{[1]}, E_{[2]},dots, E_{[m]} $ – столбцы единичной матрицы $ E_m $:
$$
E_{[1]}=left(
begin{array}{c}
1 \ 0 \ 0 \ vdots \ 0
end{array}
right),
E_{[2]}=left(
begin{array}{c}
0 \ 1 \ 0 \ vdots \ 0
end{array}
right),dots,
E_{[m]}=left(
begin{array}{c}
0 \ 0 \ 0 \ vdots \ 1
end{array}
right),
$$
а псевдорешение системы уравнений $ AX=E_{[j]} $ обозначить $ X_{j} $ (оно существует и единственно при условии $ operatorname{rank} (A) = n $), то
$$ A^{+}=left[X_1,X_2,dots,X_m right] . $$
Т
Теорема. Пусть $ A_{} $ вещественная матрица порядка $ mtimes n_{} $, $ m ge n_{} $ и $ operatorname{rank} (A) = n $. Тогда псевдообратная матрица $ A^{+} $ является решением задачи минимизации
$$ min_{Xin mathbb R^{ntimes m}} |AX-E_m|^2 $$
где минимум разыскивается по всем вещественным матрицам $ X_{} $ порядка $ ntimes m_{} $, а $ || cdot || $ означает евклидову норму матрицы (норму Фробениуса) :
$$ |[h_{jk}]_{j,k}|^2=sum_{j,k} h_{jk}^2 . $$
При сделанных предположениях решение задачи единственно.
Образно говоря, если уж невозможно найти обратную матрицу для матрицы $ A_{mtimes n}^{} $, давайте найдем хотя бы такую матрицу $ X_{ntimes m} $, чтобы отклонение произведения $ Acdot X $ от единичной матрицы $ E_m $, вычисленное как квадрат евклидова расстояния между матрицами $ Acdot X $ и $ E_m $, было бы минимальным.
С учетом этого результата понятно как распространить понятие псевдообратной матрицы на случай вещественной матрицы $ A_{mtimes n}^{} $, у которой число строк меньше числа столбцов: $ m < n_{} $.
Будем искать эту матрицу как решение задачи минимизации
$$ min_{Yin mathbb R^{ntimes m}} |YA-E_n|^2 $$
где минимум разыскивается по всем вещественным матрицам $ Y_{} $ порядка $ ntimes m_{} $. Пусть $ operatorname{rank} (A) = m $, т.е. строки матрицы линейно независимы. Тогда псевдообратная к матрице $ A_{} $ определяется как матрица
$$ A^{+}= A^{top} (Acdot A^{top})^{-1} . $$
Очевидно, что в этом случае $ Acdot A^{+}=E_m $.
Задачи
Источники
[1]. Беклемишев Д.В. Дополнительные главы линейной алгебры. М.Наука.1983, с.187-234
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью полинома (до 6-й степени включительно).
В
основной статье про МНК
было рассмотрено приближение линейной функцией. В этой статье рассмотрим приближение полиномиальной функцией (с 3-й до 6-й степени) следующего вида: y=b
0
+b
1
x+b
2
x
2
+b
3
x
3
+…+b
6
x
6
Примечание
: В инструменте MS EXCEL
Линия тренда
, который доступен для диаграмм типа
Точечная и График
, можно построить
линию тренда
на основе полинома с максимальной степенью 6. В
файле примера
продемонстрировано полное совпадение
линии тренда
диаграммы и линии, вычисленной с помощью формул.
Покажем, как вычислить коэффициенты
b
линии тренда, заданной полиномом.
Как известно,
квадратичная зависимость y=b
0
+b
1
x+b
2
x
2
,
подробно рассмотренная в статье
МНК: Квадратичная зависимость в MS EXCEL
, является частным случаем полиномиальной y=b
0
+b
1
x+b
2
x
2
+b
3
x
3
+… зависимости (в этом случае степень полинома равна 2). Соответственно, используя тот же подход (приравнивание к 0 частных производных), можно вычислить коэффициенты любого полинома.
Примечание
: Существует еще один метод вычисления коэффициентов – замена переменных, который рассмотрен в конце статьи.
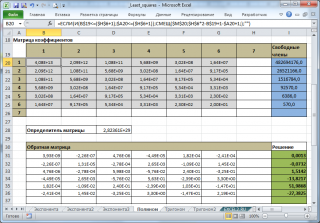
Для нахождения m+1 коэффициента полинома m-й степени составим систему из m+1 уравнения и решим ее
методом обратной матрицы
. Для квадратного уравнения (m=2) нам потребовалось вычислить сумму значений
х
с 1-й до 4-й степени, а для полинома m-й степени необходимо вычислить значения
х
с 1-й до 2*m степени.
Примечание
: Для удобства суммы степеней значений
х
можно вычислить в отдельном диапазоне (
файл примера
столбцы К:М).
В
файле примера
создана универсальная форма для вычисления коэффициентов полиномов.
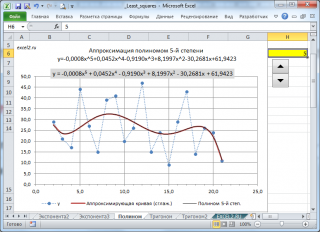
Выбрав с помощью
элемента управления Счетчик
нужную степень полинома, автоматически получим аппроксимацию наших данных выбранным полиномом (будет построен соответствующий график).
Примечание:
При использовании полиномов высокой степени необходимо следить за тем, чтобы количество пар значений (х
i
; y
i
) превышало степень полинома хотя бы на несколько значений (для обеспечения точности аппроксимации). Кроме того, график функции полинома степени m имеет m-1 точку перегиба. Понятно, что точек данных должно быть гораздо больше, чем точек перегиба, чтобы такой изменчивый тренд стал очевидным (если утрировать, то бессмысленно строить по двум точкам параболу, логичнее построить прямую).
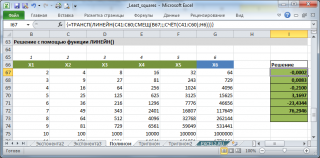
Как видно из расчетов, в MS EXCEL этот путь является достаточно трудоемким. Гораздо проще в MS EXCEL реализовать другой подход для вычисления коэффициентов полинома – с помощью замены переменных.
С помощью замены переменных x
i
=x
i
полиномиальную зависимость y=b
0
+b
1
x+b
2
x
2
+b
3
x
3
+… можно свести к линейной. Теперь переменная
y
зависит не от одной переменной
х
в
m
разных степенях, а от m независимых переменных x
i
. Поэтому для нахождения коэффициентов полинома мы можем использовать функцию
ЛИНЕЙН()
. Этот подход также продемонстрирован в
файле примера
.