Как найти коэффициенты производящей функции

Метод
рекуррентных соотношений позволяет
решать многие комбинаторные задачи. Но
в ряде случаев рекуррентные соотношения
трудно составить, а иногда ещё трудней
решить. Часто эти трудности удается
обойти, используя производящие функции.
Понятие производящей функции тесно
связано с понятием бесконечного
степенного ряда.

Здесь
необходимо знать: понятие ряда, сумма
ряда, степенной ряд, сходимость степенных
рядов, свойства сходящихся рядов,
операции над ними. Эти понятия изложены
в любом учебнике по математическому
анализу, и мы их опускаем.

Определение
1: Пусть
дана числовая последовательность:
.
Образуем степенной ряд с этими
коэффициентами:.
Если этот ряд сходится в некоторой
области к функции,
то эту функцию называютпроизводящей
для последовательности чисел
.

Примеры: 1)
Для степенного ряда
,
члены которого можно рассматривать как
геометрическую прогрессию, знаменатель.
Значит, степенной ряд при условиисходится к своей сумме.
Таким образом, получаем:

,
если.

Значит,
функция
является производящей для последовательности
чисел(коэффициенты степенного ряда).

2) Аналогично
можно получить:

.

Значит,
функция
является производящей для последовательности
чисел.

3)
Из формулы бинома Ньютона следует:

,

т.е.
функция
является производящей для чисел вида,
где.

С
помощью последней производящей функции
можно доказать некоторые свойства чисел
,
т. е. для биномиальных коэффициентов.
Например:

;

;

(здесь
обе суммы конечны и обрываются, когда
значения
истанут больше).

Кроме того:

,

,

.

В
последнем равенстве, если
,
то считают, что.
Поэтомуменяется отдо наименьшего из чисел,
.

Последнее
равенство можно доказать следующим
образом:

,

.

Отсюда
следует: .

Применяя
в левой части формулу биному Ньютона и
раскрывая скобки в правой части,
приравниваем коэффициенты при одинаковых
степенях
,
получаем требуемую формулу.

В
частном случае, когда
,
получаем равенство:

,.

Проиллюстрируем
на примерах применение производящих
функций к решению некоторых комбинаторных
задач.

1)
Рассмотрим разбиение числа
на слагаемые, каждое из которых равно
одному из чисел.
При этом слагаемые не повторяются и их
порядок не играет роли.

Для
решения задачи рассмотрим выражение
.
Раскрывая скобки, получим слагаемые
вида,
где– некоторые из чисел.
Поэтому
встретится
в сумме столько раз, сколькими способами
можно разбить
на слагаемые требуемым образом.

Например,
если надо узнать, сколькими способами
можно заплатить 78 копеек, беря не более
одной монеты каждого достоинства, то
надо составить выражение:

,

раскрыть
скобки и найти коэффициент при слагаемом

.

2)
Если требуется разложить число
на слагаемые,
каждое из которых может встречаться в
разложении один или несколько раз, тогда
количество слагаемых в скобках
увеличивается.

Например: 1)
Сколькими способами можно заплатить
29 коп., используя монеты по 2 и 5 коп?

Т.е.
надо найти число способов разбить число
29 на слагаемые, равные 2 и 5, причем порядок
слагаемых роли не играет, и каждое
слагаемое может повторяться несколько
раз. Для этого составим выражение:

.

Ясно,
что при раскрытии скобок выражение
войдет в разложение с коэффициентом,
равным числу решений уравнения
.
В частности, коэффициент при
дает ответ на вопрос задачи.

Вместо
раскрытия скобок можно поступить иначе:
составить производящую функцию. Эта
функция представляет собой произведение
двух дробей:

.

Разделив
«уголком» числитель на знаменатель,
находим коэффициент при выражении
.

2)
Поступающий в ВУЗ должен сдать 4 экзамена,
причем для поступления достаточно
набрать 17 балов. Сколькими способами
абитуриент может сдать экзамены, чтобы
поступить в ВУЗ?

Требуется
узнать, сколькими способами можно
представить число 17 в виде суммы 4-х
слагаемых, принимающих значения 3, 4, 5,
причем здесь порядок слагаемых имеет
значение.

Для
решения этой задачи можно взять
производящую функцию
.
При раскрытии скобок каждое слагаемоевстретится столько раз, сколькими
способами можноразбить на сумму 4-х слагаемых, принимающих
значения 3, 4 и 5. При этом встречаются
члены, получаемые друг из друга
перестановкой слагаемых.

В
выражении
можно раскрыть скобки по полиномиальной
теореме, а можно следующим образом:

.

Поэтому
.

.

Перемножая
почленно эти выражения, найдем, что
коэффициент при
равен 16. Значит, разложение можно сделать
16 способами.

Между
производящими функциями и рекуррентными
соотношениями существует тесная связь.

Пусть
– производящая функция для последовательности
чисел.
Это означает, чтоявляется суммой степенного ряда:.

Пусть
– многочлены, причеми
,
значит, дробь
– правильная (в противном случае можно
выделить целую часть). Раскладывая дробь
в ряд, получим:

.

Раскрывая
скобки справа и приравнивая коэффициенты
при одинаковых степенях
,
получаем:

При

считаем, что
.
А дальше все соотношения имеют вид:,
где,
т.к.не
имеет членов степени
,
,
…

Таким
образом, коэффициенты ряда
,
,…
удовлетворяют рассмотренному рекуррентному
соотношению. Коэффициенты этого
соотношения зависят только от знаменателя
дроби. Числитель нужен только для
нахождения первых членоврекуррентной
последовательности.

Обратно,
если задано рекуррентное соотношение
и заданы члены
,
то, вычисляя значения,
получим производящую функциюдля последовательности чисел.

Полученную
алгебраическую дробь можно разлагать
на элементарные дроби и производить
алгебраические преобразования.

Соседние файлы в папке 26-03-2013_00-36-55

• #
• #
• #
• #

Производящие функции — туда и обратно

«Производящая функция является устройством, отчасти напоминающим мешок. Вместо того чтобы нести отдельно много предметов, что могло бы оказаться затруднительным, мы собираем их вместе, и тогда нам нужно нести лишь один предмет — мешок».
                                                                                                                                                               Д. Пойа

Введение

Математика делится на два мира — дискретный и непрерывный. В реальном мире есть место и для того и для другого, и часто к изучению одного явления можно подойти с разных сторон. В этой статье мы рассмотрим метод решения задач с помощью производящих функций — мостика ведущего из дискретного мира в непрерывный, и наоборот.

Идея производящих функций достаточно проста: сопоставим некоторой последовательности <g₀, g₁, g₂, …, g_n> — дискретному объекту, степенной ряд g₀ + g₁z + g₂z² +… + g_nzⁿ +… — объект непрерывный, тем самым мы подключаем к решению задачи целый арсенал средств математического анализа. Обычно говорят, последовательность генерируется, порождается производящей функцией. Важно понимать, что это символьная конструкция, то есть вместо символа z может быть любой объект, для которого определены операции сложения и умножения.

История возникновения производящих функций

Известно, что начало методу производящих функций положил английский математик Абрахам де Муавр, а дальнейшему развитию и продолжению данного метода мы обязаны великому математику, имя которого Леонард Эйлер.

В 50-х годах XVIII века Эйлер решал следующую задачу: какие грузы можно взвесить с помощью гирь в 2⁰, 2¹, 2²,…, 2ⁿ грамм и сколькими способами? При решении этой задачи он использовал никому неизвестный на то время метод производящих функций, которому и посвящена данная статья. К этой задаче мы вернёмся немного позже, после того как разберёмся более подробно с устройством производящих функций.

Метод производящих функций

Изучение этого мощного механизма позволяющего решать многие задачи, мы начнём с простенькой задачи: сколькими способами можно расположить в линию чёрные и белые шары, общее количество которых равно n?

Обозначим белый шар символом ○, чёрный — ●, T_n — искомое количество расположений шаров. Символом Ø — обозначим нулевое количество шаров. Как и любое решение комбинаторной задачи начнём с тривиальных случаев:

Если n=1, то очевидно имеется 2 способа — взять либо белый шар ○, либо взять чёрный шар ●, таким образом, T₂ = 2.

Если n=2, то имеется 4 способа расположений: ○○, ○●, ●○, ●●.

Рассмотрим случай для n=3. Мы можем начать белым шаром и продолжить 4-мя комбинациями, описанными выше ○○○, ○○●, ○●○, ○●●, или же мы можем начать чёрным шаром и аналогично продолжить 4-мя шарами ●○○, ●○●, ●●○, ●●●.

В итоге количество шаров удвоилось, то есть T₃ = 2T₂. Аналогично T₄ = 2T₃, то есть, обобщая для всех n, получаем рекуррентное уравнение T_n = 2T_n-1 которое и является решением для данной задачи. Решение такого уравнения можно легко угадать — T_n = 2ⁿ (так как 2⋅2^n-1 = 2ⁿ).

А что если у нас плохо с угадыванием? И что делать, если уравнение будет сложнее? А вообще причём здесь производящие функции?

«Просуммируем» все возможные комбинации расположений шаров:

G = Ø + ○ + ● + ○○ + ○● + ●○ + ●● + ○○○ + ○○● + ○●○ + ○●● + ●○○ + ●○● + ●●○ + ●●● +…

Вопрос о допустимости такой нелепой на первый взгляд суммы опустим. Будем складывать и умножать последовательности шаров. Со сложением всё понятно, но что значит умножить одну последовательность шаров на другую? Перемножив ○● на ●○ мы получим не что иное как ○●●○. Заметим, однако, что произведение шаров в отличие от произведения чисел не является коммутативным, так как ○●⋅●○ ≠ ●○⋅○●. Символ Ø — в произведении играет роль мультипликативной единицы, то есть Ø ⋅ ○○● = ○○● ⋅ Ø = ○○● и коммутирует с любой последовательностью шаров.

Производя с рядом G последовательность манипуляций, а именно вынося за скобки левый белый и чёрный шары

G = Ø + ○ (Ø + ○ + ● + ○○ + ○● + ●○ + ●● + …) + ● (Ø + ○ + ● + ○○ + ○● + ●○ + ●● + …) = Ø + ○G +●G

получим уравнение G = Ø + ○G +●G.

Несмотря на то, что умножение некоммутативно, и мы фактически не различаем левое и правое деление, попробуем всё же «решить» это уравнение, на свой страх и риск. Получим,

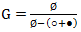
Учитывая формулу суммы геометрической прогрессии 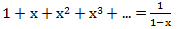, имеем

.

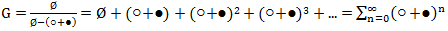В этой сумме так же учтены все возможные варианты разбиения в точности по одному разу. Далее воспользуемся формулой бинома Ньютона: , где — число сочетаний из n по k. Тогда с учетом этого имеем:

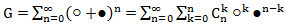
Коэффициент при ○^k ●^n-k равный числу сочетаний из n по k, показывает общее количество последовательностей из n шаров содержащих ○ шары в количеств k штук и ● шары в количестве n-k штук. Таким образом, общее количество расположений n шаров есть сумма по всем возможным значениям k. Как известно .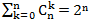

Эту формулу можно было получить непосредственно из 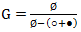заменив Ø на 1, а ○ и ● на z (в виду их равнозначности). Получим 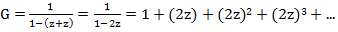то есть коэффициент при zⁿ равен 2ⁿ.

Обсуждение метода

Так что же позволяет данному методу быть работоспособным при решении различных задач?

Алгоритм решения задачи можно описать примерно следующим образом: рассматривается некоторая бесконечная сумма, которая в конечном итоге представляет собой формальный степенной ряд G(z) = g₀ + g₁z + g₂z² +… + g_nzⁿ +… причем коэффициенты g_k (не заданные в явном виде) — являются ключом к решению исходной задачи. То, что ряд является формальным, говорит о том, что z — является просто символом, то есть вместо него может быть любой объект: число, шар, кость домино и т.д. В отличие от степенных рядов в анализе формальным степенным рядам не придается числовых значений и, соответственно, нет смысла говорить о сходимости таких рядов для числовых аргументов.

G(z) = g₀ + g₁z + g₂z² +… + g_nzⁿ +… — называется производящей функцией для последовательности <g₀, g₁, g₂, …, g_n>. Заметим, однако, что хотя G(z) — функция, это всё таки формальная запись, то есть мы не можем подставить вместо z любое значение z = z₀, за исключением z = 0, так как G(0) = g₀.

Затем производя различные преобразования с бесконечной суммой G(z) мы преобразуем её к замкнутому (компактному) виду. То есть у производящей функции есть 2 представления: бесконечное и замкнутое и, как правило, для решения задачи необходимо бесконечный вид преобразовать к замкнутому, а затем замкнутый вид разложить в степенной ряд, и тем самым получить значения для коэффициентов g_k.

Отвечая на поставленный вначале вопрос можно сказать так: успех данного метода связан с возможностью записать производящую функцию в замкнутом виде. Так, например, производящая функция для последовательности <1, 1, 1, …, 1> в бесконечном виде представляется как 1 + x + x² + x³ + …, а в замкнутом .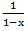

А теперь вооружившись знаниями, вернемся к задаче, которую решал Эйлер.

Итак, задача звучит следующим образом: какие грузы можно взвесить с помощью гирь в 2⁰, 2¹, 2²,…, 2ⁿ грамм и сколькими способам?

Я не знаю, как долго Эйлер придумывал решение для этой задачи, но оно поражает своей неожиданностью. Посудите сами. Эйлер рассматривает произведение G(z) = (1+z)(1+z²)(1+z⁴)… которое после раскрытия скобок представляется в виде бесконечного ряда G(z) = 1 + g₁z + g₂z² + g₃z³ +….

Что же из себя представляют коэффициенты g_k? Каждый g_k — это коэффициент при z^k, а z^k — получается как произведение каких-то одночленов z^2m, то есть g^k — это в точности число разных представлений числа k в виде суммы некоторых из чисел 1, 2, 2², 2³,…, 2^m,…. Другими словами g_k — это число способов взвешивания груза в k грамм заданными гирями. Как раз то, что мы искали!

Следующий шаг Эйлера поражает не менее предыдущего. Он умножает обе части равенства на (1-z).

(1-z)G(z) = (1-z)(1+z)(1+z²)(1+z⁴)(1+z⁸)…
(1-z)G(z) = (1-z2)(1+z²)(1+z⁴)(1+z⁸)…
(1-z)G(z) = (1-z⁴)(1+z⁴)(1+z⁸)…
(1-z)G(z) = 1

С одной стороны G(z) = 1 + g₁z + g₂z² + g₃z³ +… с другой стороны мы только что получили . Последнее равенство есть не что иное, как сумма геометрической прогрессии, которая равна . Сопоставляя эти два равенства, получаем g₁ = g₂ = g₃ =… = 1, то есть любой груз в k грамм можно взвесить гирями в 1, 2, 4, 8,… грамм притом единственным способом.

Решение рекуррентных соотношений

Производящие функции подходят для решения не только комбинаторных задач. Оказывается, с их помощью можно решать рекуррентные соотношения.

Начнем со всеми знакомой последовательностью чисел Фибоначчи. Каждый из нас знает её рекуррентный вид: F₀ = 0, F₁ = 1, F_n = F_n-1 + F_n-2, n ≥ 2. Однако не каждый знает вид этой формулы в замкнутом виде и это не удивительно, ведь она содержит иррациональное число(«золотое сечение») в своём составе.

Итак, имеем

F₀ = 0,
F₁ = 1,
F_n = F_n-1 + F_n-2, n ≥ 2

Умножим каждую строчку на z⁰, z¹, …, zⁿ соответственно:

z⁰ ⋅ F₀ = 0,
z¹ ⋅ F₁ = z,
zⁿ ⋅ F_n = zⁿ ⋅ F_n-1 + zⁿ ⋅ F_n-2, n ≥ 2

Просуммируем эти равенства:

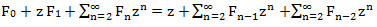
Обозначим левую часть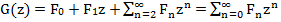

Рассмотрим каждое из слагаемых в правой части:

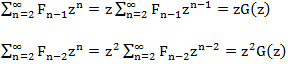
Имеем следующее уравнение G(z) = z + z G(z) + z² G(z) решая которое относительно G(z) находим

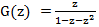— производящая функция для последовательности чисел Фибоначчи.

Разложим её на сумму простейших дробей, для этого найдем корни уравнения 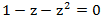. Решая это простое квадратное уравнение, получаем: 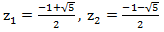. Тогда нашу производящую функцию можно разложить следующим образом:

Следующим шагом является нахождение коэффициентов a и b. Для этого умножим дроби на общий знаменатель:

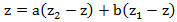
Подставляя в это уравнение значение z = z₁ и z = z₂, находим

Напоследок немного преобразуем выражение для производящей функции

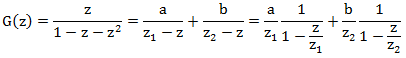
Теперь каждая из дробей представляет собой сумму геометрической прогрессии.

По формуле находим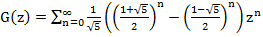

Но ведь мы искали G(z) в виде . Отсюда делаем вывод, что

Эту формулу можно переписать в другом виде не используя «золотое сечение»:

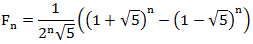
что достаточно трудно было ожидать, учитывая красивое рекуррентное уравнение.

Давайте запишем общий алгоритм решения рекуррентных уравнений, используя производящие функции. Он записывается в 4 шага:

1. Запишите одно уравнение, выражающее gn через другие элементы последовательности. Это уравнение должно оставаться справедливым для всех целых n с учетом того, что g_-1=g_-2=….=0.
2. Умножьте обе части уравнения на zⁿ и просуммируйте по всем n. В левой части получится сумма , которая равна производящей функции G(z). Правую часть следует преобразовать так, чтобы она превратилась в какое-то другое выражение, включающее G(z).
3. Решите полученное уравнение, получив для G(z) выражение в замкнутом виде.
4. Разложите G(z) в степенной ряд и прочитайте коэффициент при zⁿ, это и будет замкнутый вид для g_n.

Причина, по которой данный метод работает, заключается в том, что единая функция G(z) представляет всю последовательность g_n и это представление допускает многие преобразования.

Прежде чем переходить к следующему примеру, рассмотрим 2 операции, совершаемые над производящими функциями, которые часто оказываются полезными.

Дифференцирование и интегрирование производящих функций

Для производящих функций обычное определение производной можно записать следующим образом.

Пусть G = G(z) – производящая функция. Производной этой функции называется функция 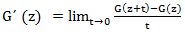. Дифференцирование, очевидно, линейная операция, поэтому для того, чтобы понять, как оно действует на производящих функциях, достаточно посмотреть на его действие, на степенях переменной. Имеем

Тем самым, действие дифференцирования на произвольной производящей функции
G (z) = g₀ + g₁z + g₂z² + g₃z³ +… дает G΄(z) = g₁ + 2g₂z + 3g₃z² + 4g₄z³ +….

Интегралом называется функция

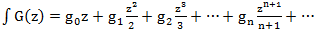
Операция дифференцирования обратна операции интегрирования:

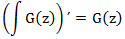
Операция же интегрирования производной приводит к функции с нулевым свободным членом, и поэтому результат, отличается от исходной функции,

Нетрудно заметить, что для функций, представимых в виде степенных рядов, формула для производной соответствует обычной. Формула для интеграла соответствует значению интеграла с переменным верхним пределом

Используя только что полученные знания о дифференцировании и интегрировании производящих функций, попробуем решить следующее рекуррентное уравнение:

g₀ = 1,
g₁ = 1,
g_n = g_n-1 + 2g_n-2 + (-1)ⁿ

Будем следовать вышеописанному алгоритму. Первое условие алгоритма выполнено. Умножим обе части всех равенств на z в соответствующей степени и просуммируем:

z⁰⋅ g₀ = 1,
z¹ ⋅ g₁ = z,
zⁿ ⋅ g_n = zⁿ ⋅ g_n-1 + 2zⁿ ⋅ g_n-2 + (-1)ⁿ ⋅ zⁿ

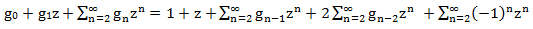
Левая часть 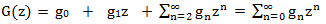представляет собой производящую функцию в бесконечном виде.

Попытаемся выразить правую часть через G(z). Рассмотрим каждое слагаемое:

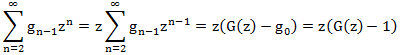
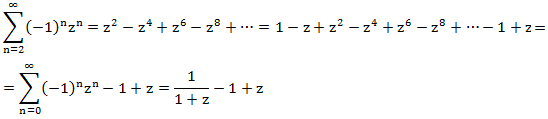
Составляем уравнение:

Это и есть производящая функция для заданного рекуррентного уравнения. Раскладывая её на простейшие дроби (например, методом неопределенных коэффициентов или методом подстановки различных значений z), получаем:

Второе и третье слагаемые легко раскладываются в степенной ряд, а вот с первым придется чуть повозиться. Используя правило дифференцирования производящих функций имеем:

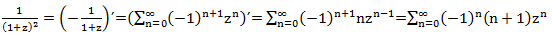
Собственно всё. Раскладываем каждое слагаемое в степенной ряд и получаем ответ:

С одной стороны мы искали G(z) в виде 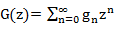, с другой стороны .

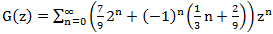Значит, .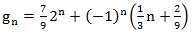

Вместо заключения

Производящие функции нашли большое применение в математике, поскольку являются мощным оружием при решении многих практических задач, связанных, например, с перечислением, распределением и разбиением множеств объектов различной природы. Кроме того применение производящих функций позволяет доказать некоторые комбинаторные формулы, которые иначе получить очень трудно. Например, разложение функции 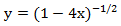в степенной ряд имеет вид 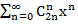, то есть справедливо равенство:

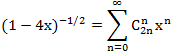
Возводя в квадрат обе части этого равенства получим

Приравнивая коэффициенты при xⁿ в левой и правой частях, получаем

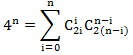
Эта формула имеет прозрачный комбинаторный смысл, но доказать её непросто. Еще в 80-е годы XX века появились публикации, посвященный этому вопросу.

Определение:

Производящая функция (англ. generating function) — это формальный степенной ряд вида , порождающий (производящий) последовательность .

Метод производящих функций был разработан Эйлером в 1750-х годах.

Применение

Производящая функция используется для:

• Компактной записи информации о последовательности.
• Нахождения зависимости для последовательности , заданной рекуррентным соотношением. Например, для чисел Фибоначчи.
• Нахождения рекуррентного соотношения для последовательности — вид производящей функции может помочь найти формулу.
• Исследования асимптотического поведения последовательности.
• Доказательства тождеств с последовательностями.
• Решения задачи подсчета объектов в комбинаторике. Например, в доказательстве пентагональной теоремы или в задаче нахождения количества расстановок ладей на доске .
• Вычисления бесконечных сумм.

Примеры производящих функций

Рассмотрим производящие функции для различных комбинаторных последовательностей:

• — производящая функция для разности количества разбиений числа в четное и нечетное число различных слагаемых. Например, коэффициент при равен , потому что существует два разбиения на четное число различных слагаемых и одно на нечетное (). Правильность этого легко осознать, если понять, что каждая скобка представляет какое-то слагаемое и мы можем его взять (второе слагаемое — ) или не взять (первое — ). Эта производящая функция используется в комбинаторном доказательстве пентагональной теоремы.

• — производящая функция для последовательности , где — число разбиений числа на слагаемые.

• — производящая функция для последовательности , где — число разбиений на различные слагаемые.

• — производящая функция для последовательности , где — число разбиений на нечётные слагаемые. С помощью метода производящих функций можно доказать, что производящие функции последовательностей равны, соответственно :

Примеры решений задач методом производящих функций

Решение рекуррентных соотношений

Существует целый класс последовательностей, задаваемых рекуррентным соотношением, например, — числа Фибоначчи или —
числа Каталана. Метод производящих функций позволяет получить выражение для через номер элемента в последовательности в замкнутом виде, то есть в таком виде, что выражение можно вычислить, предполагая, что достаточно мало.

Пусть последовательность удовлетворяет некоторому рекуррентному соотношению. Мы хотим получить выражение для (при ) в замкнутом виде. Алгоритм получения замкнутого выражения для чисел , удовлетворяющих рекуррентному соотношению, с помощью производящих функций состоит из 4 шагов:

1. Записать рекуррентное соотношение и начальные данные для него в следующем виде (если порядок соотношения равен , то есть количество предшествующих элементов, требуемых для вычисления элемента с номером , равно ):

2. Домножить каждую строчку на в соответствующей степени и просуммировать строчки для всех .
3. В полученном уравнении привести все суммы к замкнутому виду. Получить уравнение для производящей функции.
4. Выразить в явном виде (решить уравнение, полученное на предыдущем шаге) и разложить производящую функцию в ряд по степеням .

Для демонстрации универсальности метода рассмотрим довольно произвольное рекуррентное соотношение:

Запишем производящую функцию для этой последовательности и преобразуем правую часть:

Для того, чтобы замкнуть последнюю сумму воспользуемся очень важным приемом, который используется при преобразовании производящих функций. Фактически мы имеем дело с последовательностью (в нашем случае последовательность ). Такая последовательность получается путём дифференцирования функции , производящей для , с последующим умножением результата на :

Тогда замкнем последнее слагаемое следующим образом:

Таким образом, наше последнее слагаемое примет вид:

Это уравнение для производящей функции. Из него выражаем :

Разложим знаменатель на множители и разобьём дробь на сумму простых дробей ^[1]:

Разложим первое слагаемое в ряд, используя расширенные биномиальные коэффициенты ^[2]:

Расчет дисперсии геометрического распределения

Метод производящих функций также используется для нахождения математического ожидания и дисперсии различных распределений в теории вероятностей. Например, в геометрическом распределении ^[3] для нахождения дисперсии нужно найти два мат. ожидания:

которые фактически являются производящими функциями последовательностей и :

.

Тогда:

Пример задачи на нахождение производящей функции

Задача:

Рассмотрим множество путей на прямой, состоящих из шагов длины вправо и влево. Найдите производящую функцию для числа таких путей из шагов, начинающихся в и оканчивающихся в .

Заметим, что для того, чтобы закончить путь в , необходимо совершить равное число шагов вправо и влево. Тогда задача сводится к тому, чтобы выбрать позиций для, например, шагов вправо из всего шагов. Тогда ответом будет сумма от нуля до бесконечности по всех . То есть:

Рассмотрим , где — число Каталана. Тогда, заметим что . Так как , то справедливо равенство:

Мы знаем, что производящая функция для чисел Каталана равна . Найдем .

Соответственно, ответом будет производящая функция вида:

Задача:

Рассмотрим множество путей на прямой, состоящих из шагов длины вправо и влево. Найдите производящую функцию для числа таких путей из шагов, начинающихся и оканчивающихся в и не заходящих в отрицательную полупрямую.

Заметим, что задача аналогична Правильной скобочной последовательности. Тогда производящей функцией для нашей задачи будет производящая функция для правильной скобочной последовательности, а именно:

Приложения

Примеры простых производящих функций

На последнем шаге приведения производящей функции к замкнутому виду требуется разложить полученные слагаемые в ряд. Для этого можно воспользоваться таблицей основных производящих функций ^[4].

Все суммы выполняются по переменной от до . Элементы последовательности нумеруются от .

Последовательность	Производящая функция в виде ряда	Производящая функция в замкнутом виде
( нулей в начале)
(повторяется через )

См. также

• Производящая функция Дирихле

Примечания

Источники информации

• Вайнштейн Ф., Разбиение чисел. Журнал “Квант” № 11, 1988 год
• Производящие функции
• Wikipedia — Generating function
• Нахождение количества разбиений числа на слагаемые. Пентагональная теорема Эйлера
• Graham, Knuth, and Patashnik: Concrete Mathematics

Обычная производящая функция — это функция вида

. Разберем на примере, как ее использовать.

Представим, что нам нужно найти, сколькими способами можно составить сумму

. При этом можно использовать по одному элементу из каждого из следующих двух наборов:

и

.

Рассмотрим два многочлена:

— это количество способов составить сумму

с помощью одного элемента из каждого набора.

Например, коэффициент

во втором многочлене равен

. Значит, существует один способ составить сумму из четырех, используя только один элемент из набора.

Теперь рассмотрим произведение многочленов:

В полиномиальном произведении

— количество способов составить сумму из

, когда берется по одному числу из каждого набора.

Разложим произведение:

Коэффициент

равен нулю при

, так как мы не можем получить сумму больше

. Если взять самые большие числа из каждого набора, то получится число

.

То же самое относится и к

. Берем самые маленькие числа из наборов и получаем

.

Когда

, коэффициент равен трем. Это означает, что есть три способа получить число

. Если c помощью формулы дистрибутивности мы развернем произведение полностью, то увидим, что три члена

получаются из произведений:

Производящая функция придает смысл коэффициенту

, но не придает смысла

. Она кодирует числа объектов с помощью формальных степенных рядов — многочленов с бесконечно большим количеством членов.

В разобранном примере можно было просто подсчитать количество способов получения числа 10 путем проверки. Но производящие функции полезны, когда многочлены выражены в более компактной форме — например, с помощью суммы геометрического ряда.

Привет, сегодня поговорим про генератриса, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
генератриса, производящая функция , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

В комбинаторике
генератриса –
производящая функция последовательности или образующая функция ( англ. Generating function ) последовательности – это формальный степенной ряд

.

В математике можно выделить два больших направления: одно изучает непрерывные объекты, другое – дискретные. В реальном мире есть место и для того и для другого подхода и часто к изучению одного и того же явления можно подойти с разных точек зрения. Разумеется, между этими направлениями существует множество связей. Статья посвящена одной из них. Идея производящей функции очень простая. Сопоставим последовательности a0, a1, …, an, … (дискретному объекту) степенной ряд a0 + a1x + … + anxn + … (непре- рывный объект). Поступив так, мы подключаем к изучению дискретных объектов мощный арсенал средств математического анализа. Заметим, что в рассмотренных ниже примерах степенные ряды сходятся на некоторой окрестности нуля, хотя существует теория формальных степенных рядов, которая рассматривает и степенные ряды, сходящиеся только в точке 0. Справедлива теорема единственности: если при некотором положительном “с” функция f(x) представима в виде степенного ряда a0 + + a1x + … + anxn + … на интервале (−с, с), то коэффициенты ai ряда определяются однозначно. Есть и иные конструкции производящих функций – одна из них затронута в конце статьи. Мы будем использовать известные из базового курса математического анализа свойства степенных рядов без дополнительных указаний. Некоторые свойства и применения степенных рядов приведены в . Метод производящих функций очень продуктивен, в частности при решении комбинаторных задач. При- ведем некоторые начальные примеры. 1. Самым известным примером производящей функции является, конечно, бином Ньютона

Экспоненциальная производящая функция последовательности (образующая функция) – это формальный степенной ряд

.

Довольно часто производящая функция последовательности (образующая функция) последовательности является одновременно рядом Тейлора известной аналитической функции , и это можно использовать при исследовании свойств самой последовательности. Тем не менее, производящая функция последовательности необязательно соответствует аналитическая функция.

Например, два ряда

и

имеют радиус сходимости ноль, то есть разбегаются во всех точках, кроме нуля, а в нуле оба дают 1, то есть как функции они совпадают; тем не менее, как производящая функция последовательности (то есть формальные ряды) они разные.

Производящая функция последовательности (образующие функции) предоставляют возможность просто описывать сложные последовательности в комбинаторике, а иногда помогают найти для них явные формулы. Метод производящая функция последовательности был разработан Эйлером в 50-х годах XVIII века .

Свойства производящей функции

Примеры производящей функции

пусть равно количеству вариантов представления числа в виде , где – неотъемлемые целые числа и фиксировано, тогда

теперь число можно найти как коэффициент при в расписании по степеняx . Для этого можно воспользоваться определением биномиальных коэффициентов или же непосредственно взять n раз производную в нуле:

Определения

Производящая функция – это устройство, чем-то похожее на сумку. Вместо того, чтобы нести множество мелких предметов отдельно, что может быть неудобно, мы кладем их все в сумку, и тогда у нас остается только один предмет – сумка.

– Джордж Полиа , Математика и правдоподобные рассуждения (1954).

Производящая функция – это бельевая веревка, на которую мы вешаем последовательность чисел для отображения.

– Герберт Уилф , Генерирующая функциональность (1994).

Обычная производящая функция (OGF

Обыкновенная производящая функция последовательности _п является

Когда термин ” производящая функция” используется без уточнения, он обычно означает обычную производящую функцию.

Если _п является функцией вероятности массовой из дискретной случайной величины , то ее обычная производящая функция называется функцией вероятности генерации .

Обычную производящую функцию можно обобщить на массивы с несколькими индексами. Например, обычная производящая функция двумерного массива a _{m, n} (где n и m – натуральные числа) имеет вид

Экспоненциальная производящая функция (EGF)

Экспоненциальная производящая функция последовательности _п является

Экспоненциальные производящие функции обычно более удобны, чем обычные производящие функции для задач комбинаторного перечисления, которые включают помеченные объекты.

Производящая функция Пуассона

Производящая функция Пуассона последовательности _п является

Серия Ламберта

Серии Ламберта последовательности _п является

Коэффициенты ряда Ламберта в разложениях в степенной ряд для целых чисел связаны суммой делителей . Основная статья содержит еще несколько классических или, по крайней мере, хорошо известных примеров, связанных со специальными арифметическими функциями в теории чисел . В серии Ламберта индекс n начинается с 1, а не с 0, поскольку в противном случае первый член не был бы определен.

Серия Bell

Серии Белл из последовательности _п является выражением с точки зрения как неопределенном х и простого р и задается

Производящие функции ряда Дирихле (ДГФ)

Формальные ряды Дирихле часто классифицируются как производящие функции, хотя они не являются строго формальными степенными рядами. Производящий ряд функций Дирихле последовательности _п является

Функция генерирования ряд Дирихля особенно полезна , когда _п является мультипликативной функцией , в этом случае он имеет Эйлера продукт выражение в терминах рядов Bell функции в

Если _п является характером Дирихля , то его функция производящего ряда Дирихля называется L-рядом Дирихля . У нас также есть связь между парой коэффициентов в разложениях в ряд Ламберта выше и их DGF. А именно, мы можем доказать, что если и только если где – дзета-функция Римана .

Функции генерации полиномиальной последовательности

Идея создания функций может быть распространена на последовательности других объектов. Так, например, полиномиальные последовательности биномиального типа порождаются

где p _n ( x ) – последовательность многочленов, а f ( t ) – функция определенного вида. Последовательности Шеффера генерируются аналогичным образом. См. Основную статью об обобщенных полиномах Аппеля для получения дополнительной информации.

Обычные производящие функции

Примеры генерирующих функций для простых последовательностей

Полиномы – это частный случай обычных производящих функций, соответствующих конечным последовательностям, или, что эквивалентно, последовательностям, которые обращаются в нуль после определенной точки. Они важны тем, что многие конечные последовательности можно с пользой интерпретировать как производящие функции, такие как полином Пуанкаре и другие.

Фундаментальной производящей функцией является постоянная последовательность 1, 1, 1, 1, 1, 1, 1, 1, 1, …, обычная производящая функция которой является геометрическим рядом

Левая часть – это разложение правой части в ряд Маклорена . В качестве альтернативы, равенство может быть подтверждено умножением степенного ряда слева на 1 – x и проверкой того, что результатом является постоянный степенной ряд 1 (другими словами, что все коэффициенты, кроме одного из x ⁰ , равны 0) . Более того, других степенных рядов с этим свойством быть не может. Следовательно, левая часть обозначает мультипликативную обратную единицу – x в кольце степенных рядов.

Выражения для обычной производящей функции других последовательностей легко выводятся из этого. Например, замена x → ax дает производящую функцию для геометрической последовательности 1, a , a ² , a ³ , … для любой константы a :

(Равенство также следует непосредственно из того факта, что левая часть является разложением правой части в ряд Маклорена.) В частности,

Можно также ввести регулярные “пробелы” в последовательности, заменив x некоторой степенью x , так, например, для последовательности 1, 0, 1, 0, 1, 0, 1, 0, …. получается порождающий функция

Возводя в квадрат исходную производящую функцию или находя производную обеих частей по x и делая замену переменной n → n + 1, можно увидеть, что коэффициенты образуют последовательность 1, 2, 3, 4, 5, …, так что

а третья степень имеет в качестве коэффициентов треугольные числа 1, 3, 6, 10, 15, 21, …, член которых n является биномиальным коэффициентом , чтобы

В более общем смысле, для любого неотрицательного целого числа k и ненулевого действительного значения a верно, что

С

можно найти обычную производящую функцию для последовательности 0, 1, 4, 9, 16, … квадратных чисел путем линейной комбинации производящих последовательностей биномиальных коэффициентов:

Мы также можем поочередно расширять, чтобы сгенерировать ту же последовательность квадратов как сумму производных геометрического ряда в следующей форме:

По индукции аналогично можно показать для натуральных чисел что

где обозначают числа Стирлинга второго рода и где производящая функция, так что аналогичные производящие функции можно составить по интегралу -я степень обобщает результат в приведенном выше квадратном случае. В частности, поскольку мы можем написать, мы можем применить хорошо известное тождество с конечной суммой, включающее числа Стирлинга, чтобы получить это ^[10]

Рациональные функции Линейная рекурсивная последовательность

Обычная производящая функция последовательности может быть выражена как рациональная функция (отношение двух многочленов конечной степени) тогда и только тогда, когда последовательность является линейной рекурсивной последовательностью с постоянными коэффициентами; это обобщает приведенные выше примеры. И наоборот, каждая последовательность, порожденная частью многочленов, удовлетворяет линейной рекуррентности с постоянными коэффициентами; эти коэффициенты идентичны коэффициентам полинома знаменателя дроби (поэтому они могут быть непосредственно считаны). Это наблюдение показывает, что легко решить производящие функции последовательностей, определяемых линейным конечно-разностным уравнениемс постоянными коэффициентами, а значит, и для явных замкнутых формул для коэффициентов этих производящих функций. Прототипный пример здесь – вывести формулу Бине для чисел Фибоначчи с помощью методов производящих функций.

Отметим также, что класс рациональных производящих функций в точности соответствует производящим функциям, перечисляющим квазиполиномиальные последовательности вида ^[11]

где взаимные корни, , являются фиксированными скалярами и где является многочленом от для всех .

В общем, произведения Адамара рациональных функций порождают рациональные производящие функции. Аналогично, если– двумерная рациональная производящая функция, то соответствующая ей диагональная производящая функция ,, является алгебраическим . Например, если мы положим ^[12]

то производящая функция диагонального коэффициента этой производящей функции задается известной формулой OGF

Этот результат вычисляется многими способами, включая интегральную формулу Коши или контурное интегрирование , взятие комплексных вычетов или прямое манипулирование формальными степенными рядами от двух переменных.

Операции над производящими функциями

Умножение дает свертку

Умножение обычных производящих функций дает дискретную свертку (произведение Коши ) последовательностей. Например, последовательность кумулятивных сумм (сравните с несколько более общей формулой Эйлера – Маклорена )

последовательности с обычной производящей функцией G ( a _n ; x ) имеет производящую функцию

поскольку 1 / (1 – x ) – обычная производящая функция для последовательности (1, 1, …). См. Также раздел о свертках в разделе приложений этой статьи ниже, где приведены дополнительные примеры решения проблем с помощью сверток производящих функций и интерпретаций.

Сдвиг индексов последовательностей

Для целых чисел , мы имеем следующие два аналогичных тождества для модифицированных производящих функций, перечисляющих варианты сдвинутой последовательности а также , соответственно:

Дифференциация и интеграция производящих функций

У нас есть следующие разложения в степенной ряд для первой производной производящей функции и ее интеграла:

Операцию дифференцирования-умножения второго тождества можно повторить. раз умножить последовательность на , но для этого нужно чередовать дифференцирование и умножение. Если вместо этого дифференцирования последовательно, эффект умножается на ^й падающий факториал :

Используя числа Стирлинга второго рода , это можно превратить в другую формулу для умножения наследующим образом (см. основную статью о преобразованиях производящих функций ):

Обращение отрицательного порядка этой формулы степеней последовательности, соответствующей операции повторного интегрирования, определяется преобразованием дзета-ряда и его обобщениями, определяемыми как основанное на производной преобразовании производящих функций , или, альтернативно, почленно путем выполнения интегрального преобразования в последовательности производящая функция. Связанные операции выполнения дробной интеграции на порождающей функции последовательности обсуждаются здесь .

Перечисление арифметических последовательностей

В этом разделе мы приводим формулы для производящих функций, перечисляющих последовательность учитывая обычную производящую функцию где , , а также (см. основную статью о преобразованиях ). Для, это просто знакомое разложение функции на четные и нечетные части (т.е. четные и нечетные степени):

В более общем плане предположим, что и это обозначает ^й примитивный корень из единицы . Тогда как приложение дискретного преобразования Фурье имеем формулу ^[13]

Для целых чисел , еще одна полезная формула, обеспечивающая несколько перевернутые арифметические прогрессии – эффективное повторение каждого коэффициентараз – порождаются тождеством ^[14]

P-рекурсивные последовательности и голономные производящие функции

Определения

Формальный степенной ряд (или функция) называется голономным, если он удовлетворяет линейному дифференциальному уравнению вида ^[15]

где коэффициенты находятся в области рациональных функций, . Эквивалентно, голономно, если векторное пространство над натянутое на множество всех его производных конечномерно.

Поскольку мы можем очистить знаменатели, если это необходимо в предыдущем уравнении, мы можем предположить, что функции, являются многочленами от . Таким образом, мы можем видеть эквивалентное условие голономности производящей функции, если ее коэффициенты удовлетворяют P-рекуррентности вида

для всех достаточно больших и где – фиксированные многочлены конечной степени от . Другими словами, свойства того, что последовательность P-рекурсивна и имеет голономную производящую функцию, эквивалентны. Голономные функции закрываются операцией произведения Адамара. по производящим функциям.

Примеры

Функции , , , , , функция дилогарифма, обобщенные гипергеометрические функции а функции, определяемые степенным рядом и несходящиеся все голономны. Примеры P-рекурсивных последовательностей с голономными производящими функциями включают: а также , где такие последовательности, как а также не являются P-рекурсивными из-за характера особенностей в соответствующих им производящих функциях. Точно так же функции с бесконечным числом особенностей, такие как, , а также не являются голономными функциями.

Программа для работы с P-рекурсивными последовательностями и голономными производящими функциями [ править ]

Инструменты для обработки и работы с P-рекурсивными последовательностями в системе Mathematica включают пакеты программного обеспечения, предоставленные для некоммерческого использования на сайте программного обеспечения алгоритмической комбинаторики RISC Combinatorics Group . Несмотря на то, что это в основном закрытый исходный код, особенно мощные инструменты в этом программном пакете предоставляются пакетом Guess для угадывания P-повторений для произвольных входных последовательностей (полезно для экспериментальной математики и исследований) и пакетом Sigma , который может находить P-повторения для много сумм и решение для замкнутых решений P-рекуррент, включающих обобщенные гармонические числа . ^[16]Другие пакеты, перечисленные на этом конкретном сайте RISC, специально предназначены для работы с функциями генерации голономии . ( В зависимости от того, насколько подробно эта статья посвящена теме, существует множество других примеров полезных программных инструментов, которые можно перечислить здесь или на этой странице в другом разделе. )

Связь с преобразованием Фурье с дискретным временем Дискретное преобразование Фурье

Когда ряд абсолютно сходится ,

– дискретное преобразование Фурье последовательности a ₀ , a ₁ , ….

Асимптотический рост последовательности

В расчетах часто скорость роста коэффициентов степенного ряда может использоваться для определения радиуса сходимости степенного ряда. Обратное тоже может иметь место; часто радиус сходимости производящей функции может использоваться для вывода асимптотического роста базовой последовательности.

Например, если обычная производящая функция G ( a _n ; x ), имеющая конечный радиус сходимости r, может быть записана как

где каждая из A ( x ) и B ( x ) является функцией, аналитической для радиуса сходимости больше r (или целой ), и где B ( r ) ≠ 0, то

с использованием гамма-функции , биномиального коэффициента или коэффициента мультимножества .

Часто такой подход может повторяться для создания нескольких терминов в асимптотический ряд для в _п . Об этом говорит сайт https://intellect.icu . В частности,

Затем можно искать асимптотический рост коэффициентов этой производящей функции, находя A , B , α, β и r для описания производящей функции, как указано выше.

Аналогичный асимптотический анализ возможен для экспоненциальных производящих функций. С экспоненциальной производящей функцией, то _п / п ! который растет согласно этим асимптотическим формулам.

Асимптотический рост последовательности квадратов

Как показано выше, обычная производящая функция для последовательности квадратов имеет вид

При r = 1, α = −1, β = 3, A ( x ) = 0 и B ( x ) = x +1 мы можем проверить, что квадраты растут, как и ожидалось, как и квадраты:

Асимптотический рост каталонских чисел

Обычная производящая функция для каталонских чисел:

При r = 1/4, α = 1, β = −1/2, A ( x ) = 1/2 и B ( x ) = −1/2 мы можем заключить, что для каталонских чисел

Двумерные и многомерные производящие функции

Для массивов с несколькими индексами можно определить производящие функции от нескольких переменных. Их называют многомерными производящими функциями или, иногда, суперпроизводящими функциями . Для двух переменных их часто называют двумерными производящими функциями .

Например, поскольку является обычной производящей функцией для биномиальных коэффициентов для фиксированного n , можно запросить двумерную производящую функцию, которая генерирует биномиальные коэффициентыдля всех k и n . Для этого рассмотримкак сама последовательность в n , и найти производящую функцию в y, которая имеет эти значения последовательности в качестве коэффициентов. Поскольку производящая функция для является

производящая функция для биномиальных коэффициентов:

Представление цепными дробями (J-дроби типа Якоби

Определения

Разложения (формальных) цепных дробей типа Якоби и Стилтьеса (соответственно J-дробей и S-дробей ), рациональные конвергенты представляют степенные ряды с точным порядком – еще один способ выразить обычно расходящиеся обычные производящие функции для многих специальных одно- и двумерных последовательностей. Конкретная форма цепных дробей типа Якоби (J-дроби) раскрывается, как в следующем уравнении, и имеет следующие соответствующие разложения в степенной ряд по отношению к для некоторых конкретных, зависящих от приложения последовательностей компонентов, а также , где обозначает формальную переменную во втором разложении степенного ряда, приведенном ниже: ^[17]

Коэффициенты , сокращенно обозначаемый , в предыдущих уравнениях соответствуют матричным решениям уравнений

где , для , если , и где для всех целых чисел , мы имеем соотношение формулы сложения, задаваемое формулой

Свойства h- ^й сходящейся функции

Для (хотя на практике, когда ), можно определить рациональную сходится к бесконечной J-дроби, , расширенный на

покомпонентно по последовательностям, а также , рекурсивно определяемый

Более того, рациональность сходящейся функции для всех влечет дополнительные конечно-разностные уравнения и свойства сравнения, которым удовлетворяет последовательность , а для если тогда у нас есть сравнение

для несимвольного, детерминированного выбора последовательностей параметров, а также , когда , т. е. когда эти последовательности неявно не зависят от вспомогательного параметра, такого как , , или же как в примерах, приведенных в таблице ниже.

Примеры

В следующей таблице приведены примеры формул закрытых формул для последовательностей компонентов, найденных вычислительным методом (и впоследствии доказавших свою правильность в цитируемых ссылках ^[18] ) в нескольких частных случаях предписанных последовательностей., порожденные общими разложениями J-дробей, определенных в первом пункте. Здесь мы определяем и параметры , а также чтобы быть неизвестными в отношении этих разложений, где предписанные последовательности , перечисленных путем разложения этих J-фракции определены в терминах Q-Похгаммере символа , символ Похгаммера , и биномиальных коэффициенты .

Радиусы сходимости этих рядов, соответствующих приведенному выше определению J-дробей типа Якоби, в общем случае отличаются от радиусов сходимости соответствующих разложений в степенные ряды, определяющих обычные производящие функции этих последовательностей.

Примеры Примеры производящих функций

Производящими функциями для последовательности квадратных чисел a _n = n ² являются:

Обычная производящая функция

Экспоненциальная производящая функция

Серия Ламберта

В качестве примера тождества ряда Ламберта, не приведенного в основной статье , мы можем показать, что дляу нас есть это ^[19]

где у нас есть тождество частного случая для производящей функции функции делителя ,, данный

Серия Bell [ править ]

Производящая функция ряда Дирихле

используя дзета-функцию Римана .

Последовательность a _k, порожденная производящей функцией ряда Дирихле (DGF), соответствующей:

где – дзета-функция Римана , имеет обычную производящую функцию:

Многомерные производящие функции

Многовариантные производящие функции возникают на практике при вычислении количества таблиц непредвиденных обстоятельств неотрицательных целых чисел с заданными суммами по строкам и столбцам. Предположим, что в таблице есть r строк и c столбцов; суммы строк и суммы столбцов . Тогда, согласно IJ Good , ^[20] количество таких таблиц является коэффициентом

в

В двумерном случае неполиномиальные примеры двойной суммы так называемых ” двойных ” или ” супер ” производящих функций видавключают следующие производящие функции с двумя переменными для биномиальных коэффициентов , чисел Стирлинга и чисел Эйлера : ^[21]

Применение

Различные методы: оценка сумм и решение других проблем с помощью генерирующих функций

Пример 1. Формула суммы гармонических чисел

Производящие функции дают нам несколько методов для управления суммами и установления тождеств между суммами.

Самый простой случай возникает, когда . Тогда мы знаем, что для соответствующих обычных производящих функций.

Например, мы можем манипулировать , где – гармонические числа . Позволять– обычная производящая функция номеров гармоник. потом

и поэтому

С использованием , Свертка с выходами числителя

который также можно записать как

Пример 2: Модифицированные суммы биномиальных коэффициентов и биномиальное преобразование [ править ]

В качестве еще одного примера использования производящих функций для связывания последовательностей и управления суммами для произвольной последовательности определим две последовательности сумм

для всех , и постараемся выразить вторую сумму через первую. Мы предлагаем подход, основанный на производящих функциях.

Сначала мы используем биномиальное преобразование, чтобы записать производящую функцию для первой суммы как

Поскольку производящая функция для последовательности дан кем-то , мы можем записать производящую функцию для второй суммы, определенной выше, в виде

В частности, мы можем записать эту модифицированную функцию генерации суммы в виде

для , , , а также где .

Наконец, отсюда следует, что мы можем выразить вторую сумму через первые суммы в следующей форме:

Пример 3: Генерация функций для взаимно рекурсивных последовательностей

В этом примере мы переформулируем пример производящей функции, приведенный в разделе 7.3 « Конкретной математики» (см. Также раздел 7.1 того же справочника, где приведены красивые изображения производящих рядов функций). В частности, предположим, что мы ищем общее количество путей (обозначенных) выложить прямоугольник с немаркированным домино. Пусть вспомогательная последовательность,, можно определить как количество способов преодоления rectangle-minus-corner секция полного прямоугольника. Мы стремимся использовать эти определения, чтобы дать формулу в замкнутой форме дляне разрушая это определение, чтобы рассмотреть случаи вертикального и горизонтального домино. Обратите внимание, что обычные производящие функции для наших двух последовательностей соответствуют ряду

Если мы рассмотрим возможные конфигурации, которые можно дать, начиная с левого края прямоугольник, мы можем выразить следующие взаимозависимые или взаимно рекурсивные рекуррентные отношения для наших двух последовательностей, когда определено, как указано выше, где , , , а также :

Поскольку у нас есть это для всех целых чисел , производящие функции со сдвигом индекса удовлетворяют (кстати, у нас есть и соответствующая формула, когда дано ), мы можем использовать указанные выше начальные условия и предыдущие два рекуррентных соотношения, чтобы увидеть, что у нас есть следующие два уравнения, связывающие производящие функции для этих последовательностей, задаваемые формулой

что затем подразумевает, решая систему уравнений (и это особый трюк нашего метода здесь), что

Таким образом, выполняя алгебраические упрощения последовательности, полученной в результате разложения производящей функции на вторые частичные дроби в предыдущем уравнении, мы находим, что и это

для всех целых чисел . Мы также отмечаем, что тот же метод смещенных производящих функций, применяемый к рекуррентным функциям второго порядка для чисел Фибоначчи, является типичным примером использования производящих функций для решения рекуррентных соотношений в одной переменной, уже рассмотренной или, по крайней мере, намекаемой в подразделе, посвященном рациональным функции, указанные выше.

Свертка (продукты Коши)

Дискретная свертка членов двух формальных степенных рядов превращает произведение производящих функций в производящую функцию, перечисляющую свернутую сумму исходных членов последовательности (см. Произведение Коши ).

1. Рассмотрим A ( z ) и B ( z ) обычные производящие функции.

2. Рассмотрим A ( z ) и B ( z ) экспоненциальные производящие функции.

3.Рассмотрим тройную свернутую последовательность, полученную из произведения трех обычных производящих функций.

4. рассмотрите -кратная свертка последовательности с самой собой для некоторого положительного целого числа (см. пример приложения ниже)

Умножение производящих функций или свертка лежащих в их основе последовательностей может соответствовать понятию независимых событий в определенных сценариях подсчета и вероятности. Например, если мы примем условное обозначение, что функция, генерирующая вероятность , или pgf , случайной величины обозначается , то можно показать, что для любых двух случайных величин ^[22]

если а также независимы. Точно так же количество способов оплаты центов номиналом в монетах достоинств в наборе (т. е. в копейках, никелях, десятицентовиках, четвертях и полдолларах соответственно) генерируется продуктом

и более того, если мы позволим центы , чтобы быть выплачен в монетах любого натурального номинала, мы приходим к генерации для числа таких комбинаций изменений, вырабатываемого статсумма порождающей функции расширенной бесконечной д-Похгаммер символа продуктом.

Пример: производящая функция для каталонских чисел

Пример, в котором полезны свертки производящих функций, позволяет нам найти конкретную функцию замкнутой формы, представляющую обычную производящую функцию для каталонских чисел ,. В частности, эта последовательность имеет комбинаторную интерпретацию как количество способов вставить круглые скобки в произведение.так что порядок умножения полностью указан. Например, что соответствует двум выражениям а также . Отсюда следует, что последовательность удовлетворяет рекуррентному соотношению, заданному формулой

и, следовательно, имеет соответствующую свернутую производящую функцию, , удовлетворяющий

С , тогда мы приходим к формуле для этой производящей функции, заданной как

Обратите внимание, что первое уравнение, неявно определяющее выше означает, что

что затем приводит к другому “простому” (как по форме) разложению этой производящей функции в цепную дробь.

Пример: связующие деревья вееров и свертки сверток

Вентилятор порядка определяется как граф на вершинах с участием ребра соединяются по следующим правилам: Вершина соединяется одним ребром друг с другом вершины и вершины соединяется одним ребром со следующей вершиной для всех . ^[23] Есть один веер первого порядка, три вентилятора второго порядка, восемь вентиляторов третьего порядка и так далее. Остов подграф графа , который содержит все исходные вершины и который содержит достаточно края , чтобы сделать этот подграф подключен, но не так много ребер , что существует цикл в подграфа. Спрашиваем, сколько остовных деревьев любителя порядка возможны для каждого .

В качестве наблюдения мы можем подойти к вопросу, посчитав количество способов соединения смежных наборов вершин. Например, когдау нас есть это , который представляет собой сумму по -кратные свертки последовательности для . В более общем смысле, мы можем записать формулу для этой последовательности как

из которого мы видим, что обычная производящая функция для этой последовательности задается следующей суммой сверток как

из которого мы можем извлечь точную формулу для последовательности, взяв частичное разложение последней производящей функции.

Неявные производящие функции и формула обращения Лагранжа

Представляем бесплатный параметр (метод змеиного масла)

Иногда сумма сложно, и его не всегда легко оценить. Другой метод (названный Х. Уилфом «змеиное масло») – это метод «свободного параметра» для оценки этих сумм.

Оба обсуждаемых до сих пор метода как предел при суммировании. Когда n не появляется явно в суммировании, мы можем рассматривать как «бесплатный» параметр и рассматривать как коэффициент изменим порядок суммирования на а также , и попробуйте вычислить внутреннюю сумму.

Например, если мы хотим вычислить

мы можем лечить как “свободный” параметр и установите

Суммирование местами («змеиный жир») дает

Теперь внутренняя сумма . Таким образом

Тогда получаем

Производящие функции доказывают совпадения

Мы говорим, что две производящие функции (степенные ряды) конгруэнтны по модулю , написано если их коэффициенты сравнимы по модулю для всех , т. е. для всех соответствующих случаев целых чисел (обратите внимание, что нам не нужно предполагать, что здесь целое число – оно вполне может быть полиномиально значным в некоторых неопределенных , Например). Если ” более простая ” правая производящая функция,, является рациональной функцией , то вид этих последовательностей предполагает, что последовательность в конечном итоге является периодической по модулю фиксированных частных случаев целочисленных. Например, мы можем доказать, что числа Эйлера ,, удовлетворяют следующему сравнению по модулю : ^[24]

Один из наиболее полезных, если не откровенно мощных, методов получения сравнений для последовательностей, перечисляемых специальными производящими функциями по модулю любых целых чисел (т. Е. Не только степеней простых чисел ) дан в разделе, посвященном представлению непрерывными дробями (даже несходящихся) обычных производящих функций J-дробями выше. Мы процитируем один конкретный результат, относящийся к генерации рядов, расширенных посредством представления цепной дробью, из лекций Ландо о производящих функциях следующим образом:

Теорема: (Сравнения для рядов , порожденных разложениями непрерывных дробей). Предположим, что производящая функцияпредставлена ​​бесконечной цепной дробью вида

и это обозначает сходящаяся к этому разложению цепной дроби, определенная таким образом, что для всех . Тогда 1) функция рационально для всех где мы предполагаем, что один из критериев делимости выполняется, т. е. для некоторых ; и 2) если целое число делит продукт , то имеем .

Производящие функции также могут использоваться в других целях при доказательстве сравнений для их коэффициентов. Мы приводим следующие два конкретных примера, выводящих частные сравнения чисел Стирлинга первого рода и статистической суммы (математика). которые демонстрируют универсальность производящих функций при решении задач, связанных с целочисленными последовательностями .

Числа Стирлинга по модулю малых целых чисел

Основная статья о числах Стирлинга , порожденная конечных продуктами

предоставляет обзор сравнений для этих чисел, полученных строго из свойств их производящей функции, как в разделе 4.6 справочника Уилфа по акции Generatingfunctionology . Мы повторяем основной аргумент и замечаем, что при уменьшении по модулю, каждая из этих производящих функций конечного произведения удовлетворяет

что означает, что четность этих чисел Стирлинга совпадает с четностью биномиального коэффициента

и, следовательно, показывает, что даже когда .

Точно так же мы можем уменьшить правые произведения, определяющие производящие функции числа Стирлинга по модулю для получения несколько более сложных выражений при условии, что

Сравнения для функции распределения

В этом примере мы задействуем часть механизма бесконечных произведений, разложения в степенной ряд которых порождают разложения многих специальных функций и перечисляют функции разбиения. В частности, напомним , что статсумма генерируется обратным бесконечным произведением символа q-Поххаммера (или произведением z-Поххаммера, в зависимости от случая), задаваемым формулой

Эта статистическая сумма удовлетворяет многим известным свойствам сравнения , которые, в частности, включают следующие результаты, хотя все еще остается много открытых вопросов о формах связанных целочисленных сравнений для функции: ^[25]

Мы покажем, как использовать производящие функции и манипуляции с конгруэнциями для формальных степенных рядов, чтобы дать очень элементарное доказательство первого из этих сравнений, перечисленных выше.

Во-первых, заметим, что производящая функция биномиального коэффициента, , удовлетворяет тому, что каждый из его коэффициентов делится на за исключением тех, которые соответствуют полномочиям , все из которых в противном случае имеют остаток по модулю . Таким образом, мы можем написать

что, в частности, показывает нам, что

Отсюда легко видеть, что делит каждый коэффициент в бесконечном произведении разложения

Наконец, поскольку мы можем записать производящую функцию для статистической суммы как

мы можем приравнять коэффициенты при в предыдущих уравнениях, чтобы доказать желаемый результат сравнения, а именно: для всех .

Преобразования производящих функций

Есть ряд преобразований производящих функций, которые предоставляют другие приложения (см. Основную статью ). Преобразование обычной производящей функции (OGF) последовательности обеспечивает метод преобразования производящей функции для одной последовательности в производящую функцию, перечисляющую другую. Эти преобразования обычно включают интегральные формулы, включающие последовательность OGF (см. Интегральные преобразования ) или взвешенные суммы по производным высшего порядка этих функций (см. Преобразования производных ).

Преобразования производящей функции могут вступить в игру, когда мы стремимся выразить производящую функцию для сумм

в виде с участием функции создания исходной последовательности. Например, если суммы, то производящая функция для модифицированных сумм выражений имеет вид ^[26] (см. Также биномиальное преобразование и преобразование Стирлинга ).

Существуют также интегральные формулы для преобразования между OGF последовательности, , и его экспоненциальная производящая функция, или EGF, , и наоборот

при условии, что эти интегралы сходятся при подходящих значениях .

Другие приложения

Генерирующие функции используются для:

• Найдите замкнутую формулу для последовательности, заданной в рекуррентном соотношении. Например, рассмотрим числа Фибоначчи .
• Найдите рекуррентные соотношения для последовательностей – вид производящей функции может предлагать формулу рекуррентности.
• Найдите взаимосвязи между последовательностями – если производящие функции двух последовательностей имеют похожую форму, то сами последовательности могут быть связаны.
• Изучите асимптотическое поведение последовательностей.
• Докажите идентичность с помощью последовательностей.
• Решать задачи перечисления в комбинаторике и кодировать их решения. Многочлены Ладьи являются примером применения в комбинаторике.
• Оценивайте бесконечные суммы.

Другие производящие функции

Примеры

Примеры полиномиальных последовательностей, генерируемых более сложными производящими функциями, включают:

• Многочлены Аппеля
• Полиномы Чебышева
• Многочлены разности
• Обобщенные полиномы Аппеля
• Q-разностные полиномы

Другие последовательности, генерируемые более сложными производящими функциями:

• Двойные экспоненциальные производящие функции. Например: Массив Эйткена: треугольник чисел.
• Произведения Адамара производящих функций / диагональных производящих функций и соответствующие им интегральные преобразования

Полиномы свертки

В статье Кнута под названием « Полиномы свертки » ^[27] обобщенный класс последовательностей полиномов свертки определяется их специальными производящими функциями вида

для некоторой аналитической функции с расширением степенного ряда таким, что . Мы говорим, что семейство многочленов,, образует сверточное семейство, если и если выполняется следующее условие свертки для всех и для всех :

Мы видим, что для семейств сверток, не являющихся тождественно нулевыми, это определение эквивалентно требованию, чтобы последовательность имела обычную производящую функцию первой формы, указанной выше.

Последовательность полиномов свертки, определенная в обозначениях выше, имеет следующие свойства:

Для фиксированного ненулевого параметра , мы модифицировали производящие функции для этих последовательностей полиномов свертки, заданных формулой

где неявно определяется функциональным уравнением вида. Более того, мы можем использовать матричные методы (как в справочнике), чтобы доказать, что с учетом двух последовательностей полиномов свертки, а также , с соответствующими производящими функциями, а также , то для произвольных у нас есть личность

Примеры полиномиальных последовательностей свертки включают биномиальный степенной ряд ,, так называемые древесные многочлены , числа Белла ,, То многочлены Лагерра , и Стирлинга свертка многочлены .

Таблицы специальных производящих функций

Первоначальный список специальных математических рядов находится здесь . Ряд полезных и специальных функций, генерирующих последовательность, можно найти в разделах 5.4 и 7.4 « Конкретной математики» и в разделе 2.5 « Генераторная функциональность» Уилфа . Другие особые функции генерации, которые следует отметить, включают записи в следующей таблице, которая никоим образом не является полной. ^[28]

Формальный степенной ряд Формула производящей функции Заметки – номер гармоники первого порядка число Бернулли число Фибоначчи и обозначает возрастающий факториал или символ Поххаммера и некоторое целое число – функция полилогарифма иявляется обобщенным гармоническим числом для является числом Стирлинга второго рода и где отдельные члены в разложении удовлетворяют Случай с двумя переменными задается формулой

История

Джордж Полиа пишет по математике и правдоподобным рассуждениям :

Название «производящая функция» принадлежит Лапласу . Однако, не называя его, Эйлер использовал устройство производящих функций задолго до Лапласа [..]. Он применил этот математический инструмент к нескольким задачам комбинаторного анализа и теории чисел .

Метод производящих функций был разработан Эйлером в 1750-х годах; классическим примером служит пентагональная теорема Эйлера.

Переводна русский язык « производящая функция последовательности » термина « generating function » с английского не достаточно удачным. Лучше использовать вместо более употребляемый термин в украинском математической литературе – « образующая функция », которому соответствует русское « производящая функция »

Cм. также

• таблица производящих функций ,
• понятие – производящая функция ,
• производящая функция моментов , пфм ,
• производящая функция последовательности , генератриса ,
• производящая функция канонического преобразования ,
• Производящая функция последовательности целочисленной случайной величины
• рекуррентное соотношение
• Момент-генерирующая функция
• Вероятностно-производящая функция
• Преобразование производящей функции
• Теорема взаимности Стэнли
• Приложения к разбиению (теория чисел)
• Комбинаторные принципы
• Циклическое просеивание
• Z-преобразование

Я хотел бы услышать твое мнение про генератриса Надеюсь, что теперь ты понял что такое генератриса, производящая функция
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Теория вероятностей. Математическая статистика и Стохастический анализ