Продолжаем начатую тему, посвященную работе ПИД-регулятора, и сегодня речь пойдет непосредственно и исключительно о настройке ПИД-регулятора. Начнем, как полагается, с теоретических моментов, затем же плавно перейдем к практическому примеру на базе регулятора температуры на STM32, созданному нами в той, первой, статье.
Настройка ПИД-регулятора. Теория.
И, собственно, данная настройка заключается в том, чтобы вычислить или подобрать оптимальные значения коэффициентов:
- K_p – коэффициент усиления пропорциональной составляющей
- K_i – коэффициент усиления интегрирующей составляющей
- K_d – коэффициент усиления дифференцирующей составляющей
По большому счету, при использовании ПИД-регулятора необходимо построить модель всей системы в целом и математически вычислить необходимые значения коэффициентов. В таком случае значения можно рассчитать очень точно. Но на практике математический расчет коэффициентов – задача далеко не тривиальная и требует глубоких знаний теории автоматического управления, поэтому в большинстве случаев используются другие, упрощенные, методы настройки.
Существует целый ряд различных способов, которые определяют вполне конкретные шаги, которые необходимо предпринимать. Мы же разберем один из них, а именно – метод Циглера-Никольса, ввиду того, что он получил наибольшее распространение и популярность.
Метод Циглера-Никольса.
Заключается он в последовательном выполнении следующих операций:
- Обнуляем все коэффициенты регулятора.
- Задаем некоторое целевое значение регулируемого параметра (например, температуры).
- Постепенно начинаем увеличивать пропорциональный коэффициент и следим за реакцией системы.
- При определенном значении K_p возникнут незатухающие колебания регулируемой величины.
- Фиксируем это значение, а также период колебаний системы.
На этом практическая часть метода заканчивается. Из полученных значений рассчитываем коэффициенты:
K_p = 0.6cdot K \ K_i = (2cdot K_p)medspace/medspace T \ K_d = (K_pcdot T)medspace/medspace 8
Здесь K – тот самый коэффициент пропорциональной составляющей, при котором возникли колебания, а T – период этих колебаний. Рассмотрим псевдо-пример для получения более полного представления о данном процессе. Пусть при K_p равном 10, возникают колебания следующего рода:
Период составляет 0.1 с. Производим расчеты по вполне конкретным формулам и получаем:
K_p = 0.6cdot 10 = 6 \ K_i = (2cdot 6)medspace/medspace 0.1 = 120 \ K_d = (6cdot 0.1)medspace/medspace 8 = 0.075
Все, на этом процедура окончена.
Метод довольно прост, но применить его можно далеко не всегда. И получаемые результаты также будут оптимальными далеко не всегда. На практике я метод Циглера-Никольса применял считанное число раз, больше доверяясь экспериментально-аналитическому способу, которому и буде посвящена последующая часть статьи.
Суть метода можно описать максимально кратко:
- Берем систему.
- Меняем один из коэффициентов.
- Смотрим за реакцией системы.
- Анализируем произошедшее и принимаем решение о дальнейших действиях.
Данный метод также вполне можно назвать «методом проб и ошибок», тем не менее это работает. Главное иметь представление о том, как система функционирует и как она реагирует на изменения, чтобы производимые манипуляции не носили хаотичный, близкий к случайному характер. Кроме того, не следует менять несколько значений сразу, тогда отслеживание результата становится практически неосуществимым. Поменяли-посмотрели-поменяли-посмотрели…
Сами значения коэффициентов могут принимать абсолютно разные значение, от 0 до десятков-сотен тысяч. Это все зависит, в первую очередь, от конкретной системы, и следует даже просто из того, что регулируемые и регулирующие параметры могут быть абсолютно разными.
Пусть, к примеру, у нас температура может меняться от 20°C до 40°C, при этом мощность нагревателя – от 100 Вт до 1000 Вт. Это частный случай. Берем абсолютно другую систему, там ПИД-регулятор контролирует угол наклона гиростабилизированной платформы. Объект регулирования – угол наклона, выходное воздействие – сигнал для управления двигателем, вращающим платформу. При этом рабочий диапазон углов: [-0.1°; 0.1°]. То есть изначально мы имеем абсолютно другие порядки участвующих в работе системы параметров, соответственно, и коэффициенты ПИД-регулятора могут иметь значения, разнящиеся на несколько порядков.
Перечислим еще некоторые свойства, которые призваны помочь в анализе работы системы и настройке ПИД-регулятора:
- Увеличение коэффициента усиления пропорциональной составляющей приводит к увеличению быстродействия, но снижению устойчивости системы.
- Интегральная составляющая служит для уменьшения статической ошибки, о чем мы говорили в предыдущей статье. При увеличении K_i компенсация ошибки будет происходить быстрее.
- Увеличение K_d позволяет повысить стабильность системы, но слишком большое значение может также стать причиной возникновения колебаний, поэтому, как и для остальных коэффициентов, нужно все манипуляции производить аккуратно и в меру.
Не для всех систем целесообразно использовать все три составляющие, иногда достаточно и нескольких из них. Собственно, на этой ноте переходим к практическому примеру настройки ПИД-регулятора. Произведем базовую, максимально наглядную, настройку, дабы получить в первом приближении нормально функционирующую систему. Система крайне инертная и медленная по своей сути, так что можно столкнуться с проблемами, напоминаю структурную схему творения:
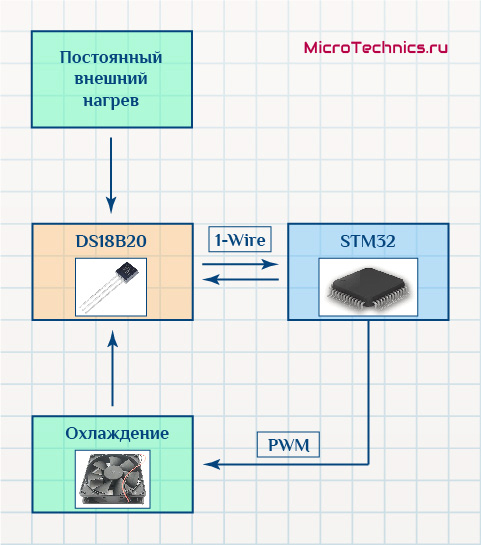
Пример настройки ПИД-регулятора на микроконтроллере STM32.
Итак, проект мы создали в первой части, сейчас же целенаправленно займемся настройкой значений:
float Kp = 0; float Ki = 0; float Kd = 0;
На данный момент все коэффициенты в нуле, то есть регулятор не функционирует. Начинаем последовательно производить настройку описанным экспериментально-аналитическим способом. Прикинем возможные диапазоны значений. Итак, пусть невязка (разница между текущим значением температуры и целевым) равна 1°C. Выходной сигнал может изменяться от 0 до 1000 (длительность импульсы ШИМ-сигнала для управления охлаждением). Если поставим K_p равным 100, то на это значение невязки получим длительность импульса выходного ШИМ-сигнала равной 100, вполне адекватное значение.
Для анализа поведения системы будем производить следующее:
- Задаем целевое значение 30°C, ждем пока система стабилизируется.
- Задаем целевое значение 40°C, аналогично ожидаем эффекта.
- Строим график зависимости температуры датчика от времени и анализируем полученное.
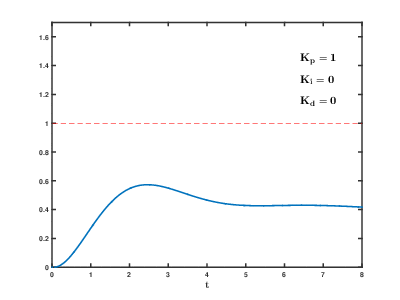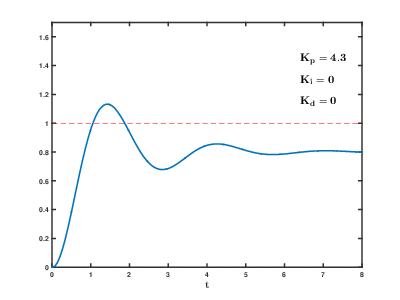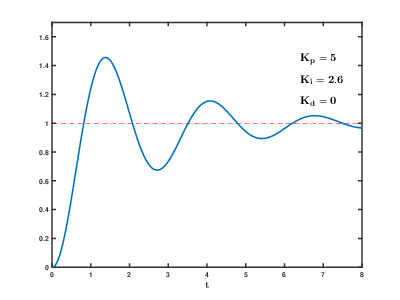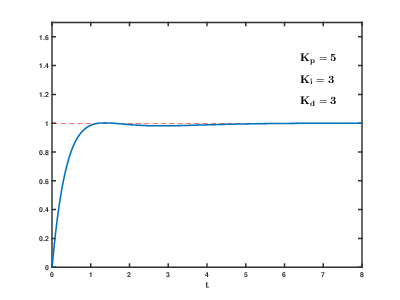
Приступаем, тест №1:
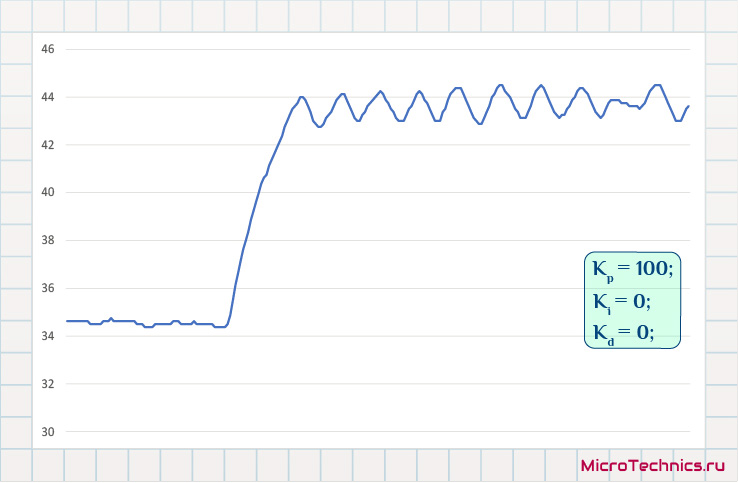
Видим, что все точно в соответствии с теорией – при использовании только пропорциональной составляющей система не может выйти на требуемые значения из-за статической ошибки. Отлично, добавим интегрирующую составляющую, задав некоторое значение K_i:
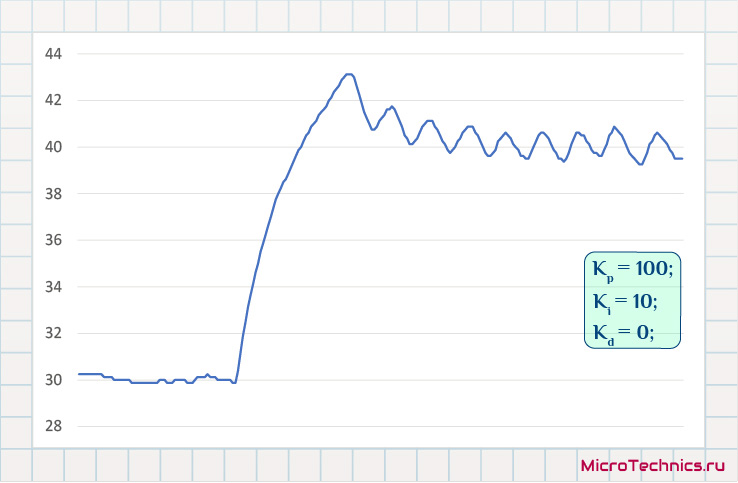
На этот раз уже все иначе – целевое значение более-менее установить удается, но имеем неслабый выброс при подходе к значению. Логичным шагом будет увеличение коэффициента усиления дифференцирующей составляющей:
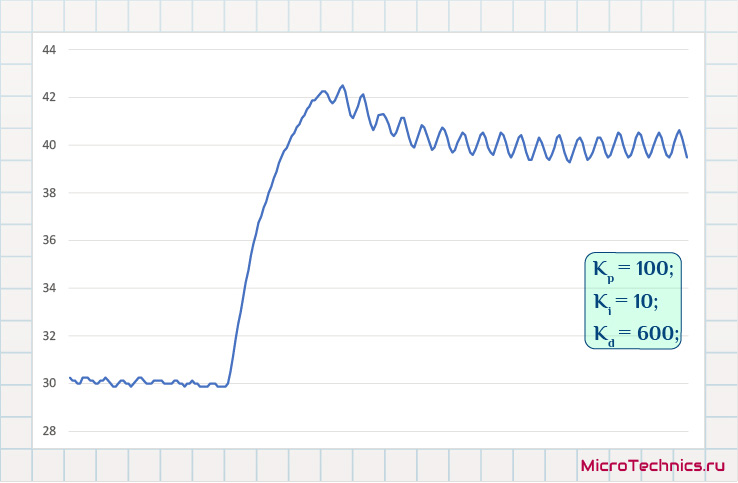
Так, стало получше (амплитуда выброса уменьшилась), увеличиваем K_d еще:
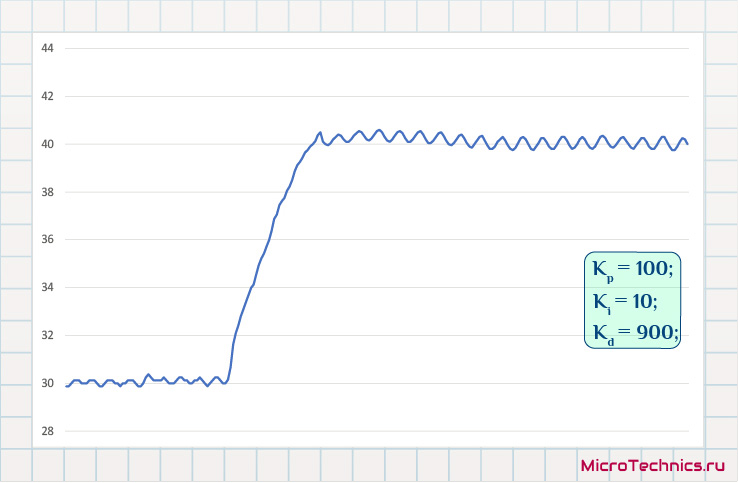
Отлично, выброс практически погасили, но выходить на нужное значение хотелось бы побыстрее. Вывод очевиден – увеличиваем коэффициент усиления пропорциональной составляющей (K_p):
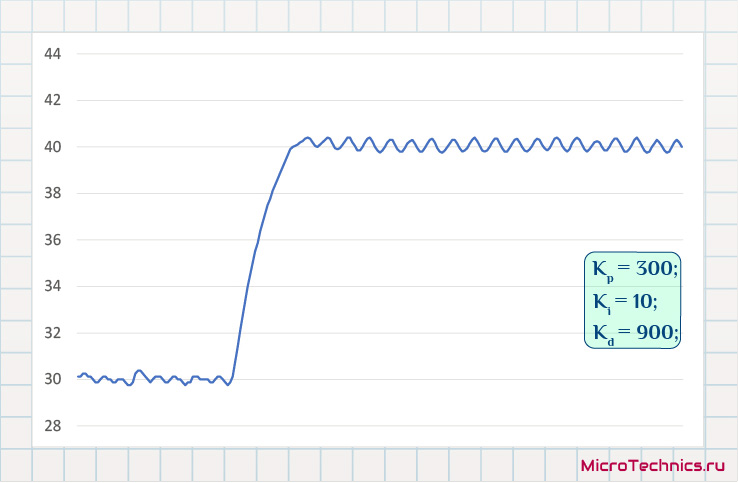
Вот, намного приятнее, посмотрим на последние два варианта друг относительно друга:
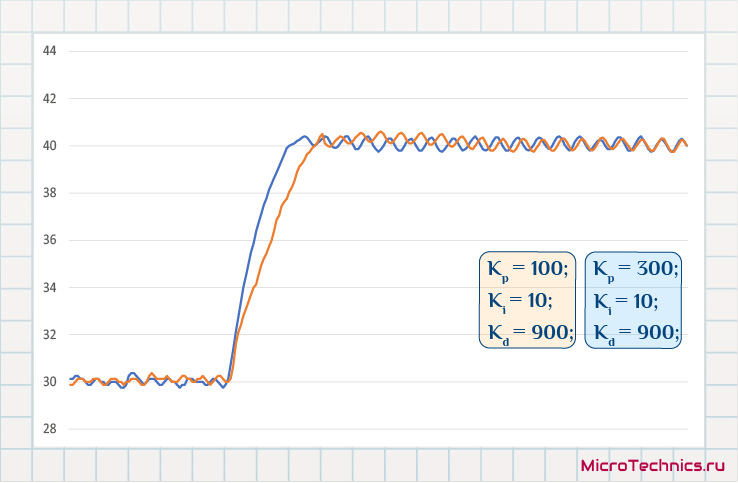
Вполне себе ничего результат в итоге. Опять же система очень инертная изначально, датчик производит измерения не слишком быстро, да и шаг дискретизации приличный – 0.125 °C. Так что результат вполне годный. Наблюдаемые промежуточные графики очень хорошо демонстрируют суть протекающих процессов, а это и было нашей целью – получение наглядного примера, дополняющего рассмотренные теоретические аспекты. Так что на этом заканчиваем на сегодня, следите за обновлениями и спасибо за внимание 🤝
Ссылка на проект – MT_PID_Project.
5.5.1. Качество регулирования
5.5.2. Выбор параметров регулятора
5.5.3. Ручная настройка, основанная на правилах
5.5.4. Методы оптимизации
Перед тем, как рассчитывать параметры регулятора, необходимо сформулировать цель и критерии качества регулирования, а также ограничения на величины и скорости изменения переменных в системе. Традиционно основные качественные показатели формулируются исходя из требований к форме реакции замкнутой системы на ступенчатое изменение уставки. Однако такой критерий очень ограничен. В частности, он ничего не говорит о величине ослабления шумов измерений или влияния внешних возмущений, может дать ошибочное представление о робастности системы.
Поэтому для полного описания или тестирования системы с ПИД-регулятором нужен ряд дополнительных показателей качества, о которых речь пойдет ниже.
В общем случае выбор показателей качества не может быть формализован полностью и должен осуществляться исходя из смысла решаемой задачи.
5.5.1. Качество регулирования
Выбор критерия качества регулирования зависит от цели, для которой используется регулятор. Такой целью может быть:
- поддержание постоянного значения параметра (например, температуры);
- слежение за изменением уставки или программное управление;
- управление демпфером в резервуаре с жидкостью и т.д.
Для той или иной задачи наиболее важными могут быть следующие факторы:
- форма отклика на внешнее возмущение (время установления, перерегулирование, коэффициент затухания и др.);
- форма отклика на шумы измерений;
- форма отклика на сигнал уставки;
- робастность по отношению к разбросу параметров объекта управления;
- требования к экономии энергии в управляемой системе;
- минимум шумов измерений и др.
Для классического ПИД-регулятора параметры, которые являются наилучшими для слежения за уставкой, в общем случае отличаются от параметров, наилучших для ослабления влияния внешних возмущений. Для того, чтобы оба параметра одновременно были оптимальными, необходимо использовать ПИД-регуляторы с двумя степенями свободы (см. раздел “Принцип разомкнутого управления”).
Например, точное слежение за изменением уставки необходимо в системах управления движением, в робототехнике. В системах управления технологическими процессами, где уставка обычно остается длительное время без изменений, требуется максимальное ослабление влияния нагрузки (внешних возмущений). В системах управления резервуарами с жидкостью требуется обеспечение ламинарности потока (минимизация дисперсии выходной переменной регулятора).
Ослабление влияния внешних возмущений
Как было показано в разделе “Запас устойчивости и робастность”, обратная связь ослабляет влияние внешних возмущений в ![]() раз за исключением тех частот, на которых
раз за исключением тех частот, на которых ![]() . Внешние возмущения могут быть приложены к объекту в самых разных его частях, однако, когда конкретное место неизвестно, считают, что возмущение воздействует на вход объекта. В этом случае отклик системы на внешние возмущения определяется передаточной функцией (см. (5.42))
. Внешние возмущения могут быть приложены к объекту в самых разных его частях, однако, когда конкретное место неизвестно, считают, что возмущение воздействует на вход объекта. В этом случае отклик системы на внешние возмущения определяется передаточной функцией (см. (5.42))
|
(5.109) |
Поскольку внешние возмущения обычно лежат в низкочастотной части спектра, где ![]() , и, следовательно,
, и, следовательно, ![]() , то предыдущее выражение можно упростить:
, то предыдущее выражение можно упростить:
|
(5.110) |
Таким образом, для ослабления влияния внешних возмущений (в частности, влияния нагрузки) можно уменьшить постоянную интегрирований ![]() .
.
Во временной области реакцию на внешние возмущения оценивают по отклику на единичный скачок ![]() (см. рис. 5.56).
(см. рис. 5.56).
Ослабление влияния шумов измерений
Передаточная функция от точки приложения шума (рис. 5.35) на выход системы имеет вид (см. (5.42)):
|
(5.111) |
Благодаря спаду АЧХ объекта на высоких частотах функция чувствительности стремится к 1 (см. рис. 5.81). Поэтому ослабить влияние шумов измерений с помощью обратной связи невозможно. Однако эти шумы легко устраняются применением фильтров нижних частот, а также правильным экранированием и заземлением [Денисенко, Денисенко].
Робастность к вариации параметров объекта
Замкнутая система остается устойчивой при изменении параметров объекта на величину ![]() , если выполняется условие (5.100).
, если выполняется условие (5.100).
Критерии качества во временной области
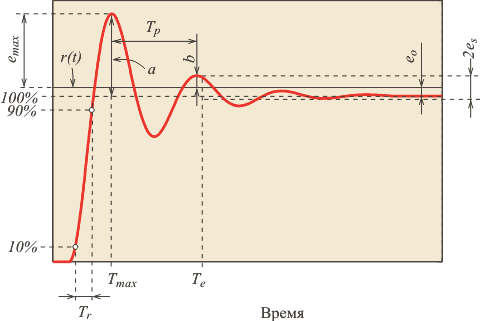
Для оценки качества регулирования в замкнутой системе с ПИД-регулятором обычно используют ступенчатое входное воздействие и ряд критериев для описания формы переходного процесса (рис. 5.84):
|
|
(5.112) |
|
|
(5.113) |
|
|
(5.114) |
|
|
(5.115) |
Отметим, что в литературе встречаются и другие определения декремента затухания, в частности, как ![]() или как коэффициент в показателе степени экспоненты, описывающей огибающую затухающих колебаний;
или как коэффициент в показателе степени экспоненты, описывающей огибающую затухающих колебаний;
|
|
|
|
Рис. 5.84. Критерии качества регулирования во временной области |
Рис. 5.85. Критерии качества регулирования в частотной области |
Для систем управления движением в качестве тестового сигнала чаще используют не функцию скачка, а линейно нарастающий сигнал, поскольку электромеханические системы обычно имеют ограниченную скорость нарастания выходной величины.
Приведенные выше критерии используются как для оценки качества реакции на изменение уставки, так и на воздействие внешних возмущений и шумов измерений.
Частотные критерии качества
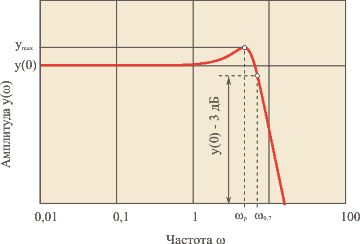
В частотной области обычно используются следующие критерии, получаемые из графика амплитудно-частотной характеристики замкнутой системы ![]() (см. рис. 5.85):
(см. рис. 5.85):
|
|
(5.114) |
Частотные критерии у реальных регуляторов не могут быть однозначно связаны с временными критериями из-за нелинейностей (обычно это нелинейности типа ограничений) и алгоритмов устранения эффекта интегрального насыщения. Однако приближенно можно установить следующие зависимости между критериями в частотной и временной области:
- частота максимума передаточной характеристики замкнутой системы приблизительно соответствует периоду затухающих колебаний отклика на ступенчатое входное воздействие:
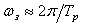 ;
; - чем медленнее затухают колебания, там больше показатель колебательности
 .
.
5.5.2. Выбор параметров регулятора
В общей теории автоматического управления структура регулятора выбирается исходя из модели объекта управления. При этом более сложным объектам управления соответствуют более сложные регуляторы. В нашем же случае структура регулятора уже задана – мы рассматриваем ПИД-регулятор, причем эта структура очень простая. Поэтому ПИД-регулятор не всегда может дать хорошее качество регулирования, хотя в подавляющем большинстве приложений в промышленности применяются именно ПИД-регуляторы.
Впервые методику расчета параметров ПИД-регуляторы предложили Зиглер и Никольс в 1942 году [Ziegler]. Эта методика очень проста и дает не очень хорошие результаты. Тем не менее, она до сих пор часто используется на практике, хотя с тех пор появилось множество более точных методов.
После расчета параметров регулятора обычно требуется его ручная подстройка для улучшения качества регулирования. Для этого используется ряд правил, хорошо обоснованных теоретически.
Для настройки ПИД-регуляторов можно использовать и общие методы теории автоматического управления, такие, как метод назначения полюсов и алгебраические методы. В литературе опубликовано и множество других методов, которые имеют преимущества в конкретных применениях. Мы приводим ниже только самые распространенные из них.
Все аналитические (формульные) методы настройки регуляторов основаны на аппроксимации динамики объекта моделью первого или второго порядка с задержкой. Причиной этого является невозможность аналитического решения систем уравнений, которое необходимо при использовании моделей более высокого порядка. Поэтому в последние годы, в связи с появлением мощных контроллеров и персональных компьютеров, получили развитие и распространение численные методы оптимизации. Они являются гибким инструментом для оптимальной настройки параметров регулятора для моделей любой сложности и легко учитывают нелинейности объекта управления и требования к робастности.
Настройка параметров регулятора по методу Зиглера и Никольса
Зиглер и Никольс предложили два метода настройки ПИД-регуляторов [Ziegler]. Один из них основан на параметрах отклика объекта на единичный скачок; второй метод основан на частотных характеристиках объекта управления.
|
Табл. 27. Формулы для расчета коэффициентов регулятора по методу Зиглера-Никольса |
||||||
|
Расчет по отклику на скачок |
Расчет по частотным параметрам |
|||||
|
Регулятор |
|
|
|
|
|
|
|
П |
|
– |
– |
|
– |
– |
|
ПИ |
|
|
– |
|
|
– |
|
ПИД |
|
|
|
|
|
|
Примечание. Система обозначений параметров регулятора и формулы соответствует уравнению (5.36).
Для расчета параметров ПИД-регулятора по первому методу Зиглера-Никольса используются всего два параметра: ![]() и
и ![]() (см. рис. 5.29 и пояснения к нему в тексте). Формулы для расчета коэффициентов ПИД-регулятора сведены в табл. 27.
(см. рис. 5.29 и пояснения к нему в тексте). Формулы для расчета коэффициентов ПИД-регулятора сведены в табл. 27.
|
|
|
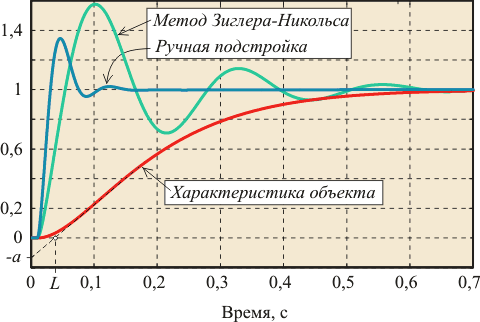
Рис. 5.86. Результат настройки ПИД-регулятора по методу Зиглера-Никольса для объекта второго порядка с задержкой: |
В качестве примера на рис. 5.86 приведен отклик на единичный скачок системы с объектом второго порядка и ПИД-регулятором, настроенным по табл. 27 и переходная характеристика самого объекта управления. Из характеристики объекта получены значения ![]() и
и ![]() . По табл.1 для этих значений
. По табл.1 для этих значений ![]() и
и ![]() можно найти коэффициенты ПИД регулятора:
можно найти коэффициенты ПИД регулятора: ![]() ,
, ![]() ,
, ![]() . На рис. 5.86 приведен также отклик на единичный скачок той же системы при параметрах
. На рис. 5.86 приведен также отклик на единичный скачок той же системы при параметрах ![]() ,
, ![]() ,
, ![]() , полученных путем ручной подстройки. Как видим, метод Зиглера-Никольса дает параметры, далекие от оптимальных. Это объясняется не только упрощенностью самого метода (он использует только 2 параметра для описания объекта), но и тем, что параметры регулятора в этом методе определялись Зиглером и Никольсом исходя из требования к декременту затухания, равному 4, что и дает медленное затухание процесса колебаний.
, полученных путем ручной подстройки. Как видим, метод Зиглера-Никольса дает параметры, далекие от оптимальных. Это объясняется не только упрощенностью самого метода (он использует только 2 параметра для описания объекта), но и тем, что параметры регулятора в этом методе определялись Зиглером и Никольсом исходя из требования к декременту затухания, равному 4, что и дает медленное затухание процесса колебаний.
Метод Зиглера-Никольса никак не учитывает требования к запасу устойчивости системы, что является вторым его недостатком. Судя по медленному затуханию переходного процесса в системе, этот метод дает слишком малый запас устойчивости.
Второй метод Зиглера-Никольса (частотный метод) в качестве исходных данных для расчета использует частоту ![]() , на которой сдвиг фаз в разомкнутом контуре достигает 180˚, и модуль коэффициента передачи объекта на этой частоте
, на которой сдвиг фаз в разомкнутом контуре достигает 180˚, и модуль коэффициента передачи объекта на этой частоте ![]() . О методике определении этих параметров см. раздел “Частотная идентификация в режиме релейного регулирования”. Зная параметр
. О методике определении этих параметров см. раздел “Частотная идентификация в режиме релейного регулирования”. Зная параметр ![]() , сначала находят период собственных колебаний системы
, сначала находят период собственных колебаний системы ![]() , затем по табл.1 определяют параметры регулятора. Точность настройки регулятора и недостатки обоих методов Зиглера-Никольса одинаковы.
, затем по табл.1 определяют параметры регулятора. Точность настройки регулятора и недостатки обоих методов Зиглера-Никольса одинаковы.
Метод CHR
В отличие от Зиглера и Никольса, которые использовали в качестве критерия качества настройки декремент затухания, равный 4, Chien, Hrones и Reswick (CHR) [Chien] использовали критерий максимальной скорости нарастания при отсутствии перерегулирования или при наличии не более чем 20%-ного перерегулирования. Такой критерий позволяет получить больший запас устойчивости, чем в методе Зиглера-Никольса.
CHR метод дает две разные системы параметров регулятора. Одна из них получена при наблюдении отклика на изменение уставки (табл. 28), вторая – при наблюдении отклика на внешние возмущения (табл. 29). Какую систему параметров выбирать – зависит от того, что важнее для конкретного регулятора: качество регулирования при изменении уставки, или ослабление внешних воздействий. Если же важно и то, и другое, то необходимо использовать регуляторы с двумя степенями свободы (см. раздел “Принцип разомкнутого управления”).
Метод CHR использует аппроксимацию объекта моделью первого порядка с задержкой (5.5).
|
Табл. 28. Формулы для расчета коэффициентов регулятора по методу CHR, по отклику на изменение уставки |
||||||
|
Без перерегулирования |
С 20%-ным перерегулированием |
|||||
|
Регулятор |
|
|
|
|
|
|
|
П |
|
– |
– |
|
– |
– |
|
ПИ |
|
|
– |
|
|
– |
|
ПИД |
|
|
|
|
|
|
Примечание. Система обозначений параметров регулятора и формулы соответствует уравнению (5.36).
|
Табл. 29. Формулы для расчета коэффициентов регулятора по методу CHR, по отклику на внешние возмущения |
||||||
|
Без перерегулирования |
С 20%-ным перерегулированием |
|||||
|
Регулятор |
|
|
|
|
|
|
|
П |
|
– |
– |
|
– |
– |
|
ПИ |
|
|
– |
|
|
– |
|
ПИД |
|
|
|
|
|
|
Примечание. Система обозначений параметров регулятора и формулы соответствует уравнению (5.36).
В методе CHR используются те же исходные параметры ![]() и
и ![]() , что и в методе Зиглера-Никольса.
, что и в методе Зиглера-Никольса.
Обратим внимание, что пропорциональный коэффициент в методе CHR меньше, чем в методе Зиглера-Никольса.
5.5.3. Ручная настройка, основанная на правилах
Расчет параметров по формулам не может дать оптимальной настройки регулятора, поскольку аналитически полученные результаты основываются на сильно упрощенных моделях объекта. В частности, в них не учитывается всегда присутствующая нелинейность типа “ограничение” для управляющего воздействия (см. раздел “Интегральное насыщение”). Кроме того, модели используют параметры, идентифицированные с некоторой погрешностью. Поэтому после расчета параметров регулятора желательно сделать его подстройку. Подстройку можно выполнить на основе правил, которые используются для ручной настройки. Эти правила получены из опыта, теоретического анализа и численных экспериментов. Они сводятся к следующему [Astrom]:
- увеличение пропорционального коэффициента увеличивает быстродействие и снижает запас устойчивости;
- с уменьшением интегральной составляющей ошибка регулирования с течением времени уменьшается быстрее;
- уменьшение постоянной интегрирования уменьшает запас устойчивости;
- увеличение дифференциальной составляющей увеличивает запас устойчивости и быстродействие.
Перечисленные правила применяются также для регуляторов, использующих методы экспертных систем и нечеткой логики.
Ручную настройку с помощью правил удобно выполнять с применением интерактивного программного обеспечения на компьютере, временно включенном в контур управления. Для оценки реакции системы на изменение уставки, внешние воздействия или шумы измерений подают искусственные воздействия и наблюдают реакцию на них. После выполнения настройки значения коэффициентов регулятора записывают в память ПИД-контроллера, а компьютер удаляют.
Отметим, что применение правил возможно только после предварительной настройки регулятора по формулам. Попытки настроить регулятор без начального приближенного расчета коэффициентов могут быть безуспешными. Сформулированные выше правила справедливы только в окрестности оптимальной настройки регулятора. Вдали от нее эффекты могут быть иными, см. раздел “Классический ПИД-регулятор”
При регулировке тепловых процессов настройка по правилам может занять недопустимо много времени.
5.5.4. Методы оптимизации
Методы оптимизации для нахождения параметров регулятора концептуально очень просты и аналогичны численным методам идентификации параметров объекта (см. раздел “Методы минимизации критериальной функции”). Выбирается критерий минимизации, в качестве которого может быть один из показателей качества или комплексный критерий, составленный из нескольких показателей с разными весовыми коэффициентами. К критерию добавляются ограничения, накладываемые требованиями робастности. Таким путем получается критериальная функция, зависящая от параметров ПИД-регулятора. Далее используются численные методы минимизации критериальной функции с заданными ограничениями, которые и позволяют найти искомые параметры ПИД-регулятора.
Методы, основанные на оптимизации, имеют следующие достоинства:
- позволяют получить оптимальные значения параметров, не требующие дальнейшей подстройки;
- не требуют упрощения модели объекта, модель может быть как угодно сложной;
- позволяют быстро достичь конечного результата (избежать процедуры длительной подстройки параметров).
Однако реализация данного подхода связана с большими проблемами, которые не один десяток лет являются предметов научных исследований. К этим проблемам относится:
- низкая надежность метода (во многих случаях вычислительный процесс может расходиться и искомые коэффициенты не будут найдены);
- низкая скорость поиска минимума для овражных функций и функций с несколькими минимумами.
Тем не менее, методы оптимизации являются мощным средством настройки ПИД-регуляторов с помощью специально разработанных для этого компьютерных программ (см. раздел “Программные средства настройки”).
Данная статья посвящена исследованию методов настройки непрерывных ПИД-регуляторов на примере объектов первого и второго порядка и второго порядка с запаздыванием, а также выбору оптимальной настройки регулятора путем сравнения полученных результатов.
Сразу оговорюсь, что это не статья, а скорее реферат, то есть информация, собранная из разных источников с некой оценкой полезности и эффективности/применимости каждого метода.
Начнем с того, что с настройкой ПИД регулятора можно столкнуться где угодно, например, на преобразователе частоты, и хорошо, если это будет регулятор давления, они настраиваются достаточно просто, если не считать особенностей настройки ПИД, чтобы ПЧ гарантировано “уходил в сон”, то есть если отсутствует расход воды, частоник может снизить обороты до указанных минимальных, а дальше просто остановить двигатель и ждать, когда ошибка регулирования не превысит какую-то тоже настроенную величину. В термоконтроллерах чаще всего есть автонастройка, но не всегда она дает приемлемые показатели работы. На сервоприводах контур положения часто тоже имеет ПИ регулятор, он хоть и представляет из себя только часть от ПИД-регулятора, но общие принципы настройки тоже присутствуют, тк имеются основные канал пропорциональный и интегральный.
А что если регулятор не имеет автонастройки и регулируемый объект достаточно сложен, например, чтобы вывести в автонастройку агрегат мощностью 100кВт требуется ее прогрев и работа, а это может составить десятки минут (а иногда и часы, а время- деньги, особенно если это время работы энергоемкого прибора) не говоря уже о себестоимости материала. Тут стоит для начала разобраться в особенностях самого ПИД, чтобы подобрать во-первых подходящий метод, а во-вторых, понять где и как стоит добиваться устойчивости в первую очередь, а где и как можно и потом делать тонкую настройку.
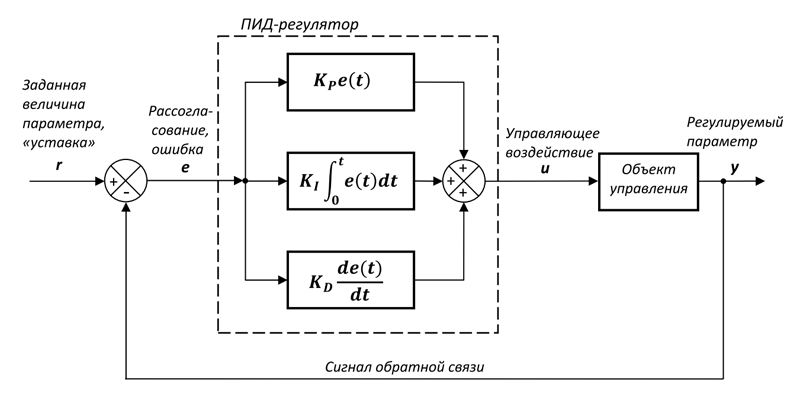
Структура регулятора по классике приведена на картинке, хотя существуют варианты, когда коэффициенты объединяются, это конечно усложняет работу, но общий принцип остается один, главное вовремя заметить, что изменение коэффициента пропорционального влияет например на интегральный канал.
- Пропорциональный канал выдает величину выходного сигнала, который рассчитывается как ошибка (разница, рассогласование) e(t) сигнала обратной связи (ОС) и сигнала задания r, умноженная на коэффициент Kp, который опять же может быть выражен и как 1/Tp – постоянная времени пропорционального канала регулятора. Если убрать (обнулив коэффициенты) остальные составляющий ПИД-регулятора, то результат такого регулятора будет иметь статическую ошибку, тк пропорциональный канал может только компенсировать часть рассогласования. Дальнейшее увеличение значение коэффициента в попытках увеличить эффективность, приведет к перерегулированию (превышению величины над уставкой, иногда многократному и повторяющемуся, в худшем случае в виде автоколебаний) при появлении большого рассогласования (например пуск или резкое изменение параметра). Данный канал отвечает за быстродействие регулятора в целом и наибольшую часть работы (компенсация большей части рассогласования).
- Интегральный канал в общем тоже берет за основу ошибку регулирования, но при этом выход интегрирует эту ошибку, умноженную на коэффициент Ki (1/Ti). Это дает возможность компенсации статической ошибки, если система не испытывает внешних возмущений (со временем конечно, если процесс не устойчивый, это событие может и не наступить), но не избавляет от динамической. Попытки уменьшить динамическую ошибку или как-то уменьшить время, за которое регулятор компенсирует ошибку, приведут к тому, что тоже появится перерегулирование и почти гарантировано автоколебания (ну как минимум несколько затухающих даже на фоне отсутствия перерегулирования в целом, если пропорциональный канал имеет слабое значение).
- Дифференциальный канал подает на выход скорость изменения ошибки de/dt, умноженную на коэффициент Kd (1/Td), что дает возможность как бы предугадать описанное выше резкое изменение рассогласования (пуск или резкое изменение параметра) и тем самым помочь своим более медленным братьям компенсировать величину ошибки. В дальнейшем, когда вступят в дело каналы пропорциональный и интегральный, роль дифференциального канала должна затухать. Конечно отыграют и электрические составляющие, и задержка расчета, и механика с инерцией, которая часто является самой долгой в перечне задержек, но что-то все же можно получить и от этого канала. Дифференциальный канал чувствителен к ВЧ-помехам. Поэтому, при построении системы регулирования, необходимо принять меры для защиты от помех. Кстати в теории дифференциальный канал может уменьшить значение перерегулирования, полученного при настройки пропорционального и интегрального канала за счет более быстрого уменьшения ошибки регулирования до вмешательства других каналов.
Итак теперь перейдем непосредственно к методам настройки
Ручная настройка или метод настройки “по графикам”.
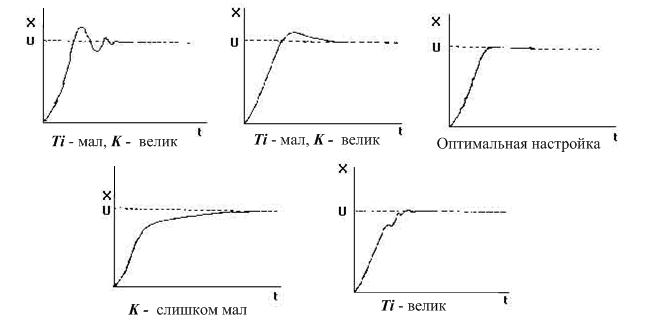
Часто можно услышать о простейшем подходе к настройке (сейчас говорим о ручной), когда вручную настраивают сперва Kp, предварительно обнулив остальные каналы, потом Ki, а последним Kd, оценивая результат работы чисто по графикам процессе (так называемый эмпирический и эвристический методы), либо пользуясь ТАУ (нахождение частоты устойчивости и отступ от нее на 2-4 лога), такая инструкция встречается практически для всех ПЧ и даже сервоприводов, возможно это оправдано тем, что процесс быстрый и графики можно получить без особых затрат просто перебирая коэффициенты по логарифмической шкале, но для температуры так будет настраивать неудобно. Да-да если коэффициент равный двум слишком мал, а введение в коэффициент цифры 4 не дало необходимого изменения, нет смысла вводить K=6, нужно вводить 8, а потом 16, смысл в том, что мы тем самым ищем нужную нам частоту среза, а она как многие помнят из ТАУ у нас на логарифмической шкале выложена, и если она далеко, то перебор по обычной шкале сильно удлинит время поиска.
Важное замечание: даже для одного и того же объекта процедуру настройки ПИД регулятора следует повторять, если изменились параметры объекта (например, загрузка печи) или значительно изменилась рабочая температура (остывание и соответственно отток мощности зависит от градиента температур).
Второй вариант больше подходит для долгих процессов (температура) – предварительно нужно вывести систему на границу устойчивости. Для этого нужно вывести регуляторы И и Д (записать нули), оставив только П (пропорциональный), устойчивость необходимо проверять на той температуре, которая близка к рабочей, то есть эксперименты с большим Кр нужно проводить уже после выхода на установившийся процесс, до этого лучше постараться выбрать коэффициент поменьше, либо уменьшить его уже когда перескочили уставку. На установившемся процессе добиваемся увеличением Кп коэффициента появления заметных колебаний, либо если колебания уже есть, то уменьшаем Кр до их исчезновения, полученный коэффициент Кркр запомним. Что делать с полученной частотой среза (частота, на которой настройка теряет устойчивость)? Переведем ее в период колебаний τ (хотя можно сразу измерить именно период колебаний τ). Далее для термоконтроллеров Термодат предлагает следующую таблицу.
| Тип регулирования | Пропорциональный коэффициент Kp |
Интегральный коэффициент Ki |
Дифференциальный коэффициент Kd |
| Только P | 2*Кркр | Выключено | Выключено |
| P+I | 2.2*Кркр | 0.8* τ | Выключено |
| P+I+D | 1.7*Кркр | 0.5*τ | 0.12*τ |
Для других применений думаю лучше пользоваться методом “по графикам” для ручной настройки.
Тангенциальный метод настройки ПИД-регулятора (первый метод Зиглера-Никольса).
Следующий метод, который предлагается опять же для настройки ПИД регулировки температуры, это Тангенциальный метод.
В тангенциальном методе для нахождения ПИД коэффициентов используется переходная характеристика объекта, в случае терморегулирования кривая разогрева объекта.
Для начала опишу метод, который предлагается производителем приборов Термодат (коэффициенты соответственно могут отличаться у разных производителей).
В режиме ручного управления контроллера задается некоторое значение мощности на нагрузке. Значение мощности должно быть таким, чтобы установившаяся температура не превысила допустимого значения. Нужно дождаться установления температуры Т1, в этом режиме и в некоторый момент времени скачком изменить значение мощности (например: на 5%). Записать процесс изменения температуры (на компьютере, на самописце или по точкам, вручную) до установления нового устоявшегося значения температуры Т2.
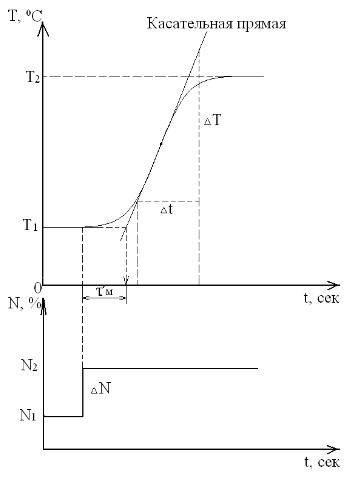
Провести касательную к полученной кривой в точке, где наклон касательной будет максимален.
Определить «мёртвое» время процесса как промежуток времени, прошедший с момента изменения мощности до момента времени, определяемого точкой пересечения касательной и средней линии температуры первого устойчивого состояния Т1 (до изменения мощности нагрева).
Определить величину относительного наклона касательной по формуле:
К = (∆T/∆t)/∆N.
∆T – изменение температуры в °С,
∆t – соответствующее изменение времени в секундах,
∆N – изменение мощности в %.
Установите значения коэффициентов Kp, Ki, Kd в соответствии с таблицей.
| Тип регулирования | Пропорциональный коэффициент Kp |
Интегральный коэффициент Ki |
Дифференциальный коэффициент Kd |
| Только P | 100*τм*К | Выключено | Выключено |
| P+I | 111*τм*К | 3.3*τм | Выключено |
| P+I+D | 83*τм*К | 2*τм | 0.25*τм |
К сожалению данный метод имеет еще пару трактовок, посему приведу обе, а решать какая лучше подойдет вам. Оба используют только два параметра для описания объекта, проводится линия по участку, соответствующему максимальному наклону графика переходной характеристики.
Первый вариант основан на поиске мертвого времени и длительности переходного процесса.
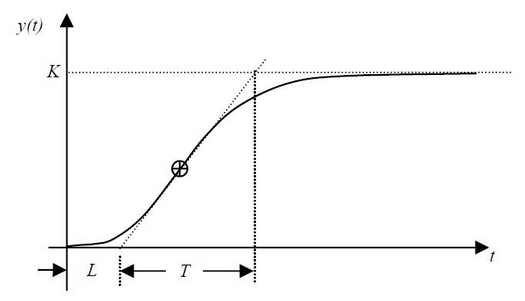
В первом случае ищется пересечение с осью времени и с мнимой линией максимального задания, значения параметров L и T, используются в расчете, формулы приведены в таблице:
| Тип регулирования | Пропорциональный коэффициент Kp |
Интегральный коэффициент Ti=Kp/Ki |
Дифференциальный коэффициент Td=Kd/Kp |
| Только P | T/L | Выключено | Выключено |
| P+I | 0.9*T/L | L/0.3 | Выключено |
| P+I+D | 1.2*T/L | 2*L | 0.5*L |
Второй вариант использует: a и L, которые определяются по графику переходной характеристике объекта управления так:
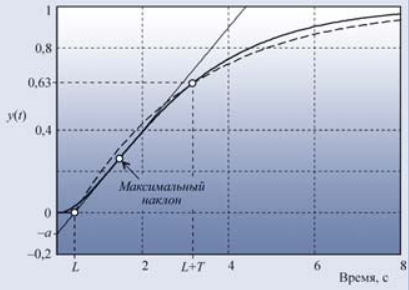
Формулы для расчета коэффициентов сведены в следующую таблицу:
| Тип регулирования | Пропорциональный коэффициент Kp |
Интегральный коэффициент Ti |
Дифференциальный коэффициент Td |
| Только P | 1/a | Выключено | Выключено |
| P+I | 0,9/a | 3*L/Kp | Выключено |
| P+I+D | 1,2/a | 0,9*L/Kp | 0.5*L/Kp |
Замечание: метод Зиглера-Никольса даёт параметры, далёкие от оптимальных. Это объясняется не только упрощённостью самого метода (он использует только 2 параметра для описания объекта), но и тем, что параметры регулятора в этом методе определялись Зиглером и Никольсом, исходя из требования к декременту затухания, равному 4, что и даёт медленное затухание процесса колебаний.
Метод Зиглера-Никольса никак не учитывает требования к запасу устойчивости системы, что является вторым его недостатком. Судя по медленному затуханию переходного процесса в системе, этот метод даёт слишком малый запас устойчивости. Но все же для начальной настройки вполне пойдет.
Метод колебаний (или второй частотный метод Зиглера-Никольса)
Данный метод основан на поиске частоты устойчивости, на которой сдвиг по фазе в разомкнутом контуре равен 180°.
Назначить уставку Тус, равной температуре регулирования (или 0.7Тус, если перегрев во время настройки нежелателен, а он может быть значительным).
Тоже существует два варианта, первый упрощенный от Термодата:
Включить позиционный (пороговый) режим регулирования.
В установившемся режиме колебаний температуры измерить период τ колебаний температуры (время между соседними максимальными или минимальными значениями температуры). Измерить также полный размах колебаний температуры ΔТ=Тmax-Тmin (разность максимального и минимального значений температуры).
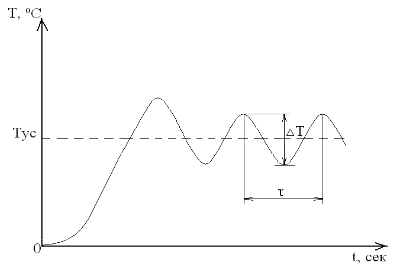
Установите значения коэффициентов Kp, Ki, Kd в соответствии с таблицей. Параметр «Ограничение ПИД» или «Зона» (если он есть в приборе) сделать равным Kp.
| Тип регулирования | Пропорциональный коэффициент Kp |
Интегральный коэффициент Ki |
Дифференциальный коэффициент Kd |
| Только P | 1.4*∆Т | Выключено | Выключено |
| P+I | 1.6*∆Т | 2.4*τ | Выключено |
| P+I+D | 1.2*∆Т | 1.5*τ | 0.2*τ |
Второй вариант такой:
Настройка пропорциональной компоненты (Kp)
1.Перед настройкой зоны пропорциональности интегральная и дифференциальная компоненты отключаются (Kи =0, Kд = 0) и задаем некоторое целевое значение регулируемого параметра (например, температуры):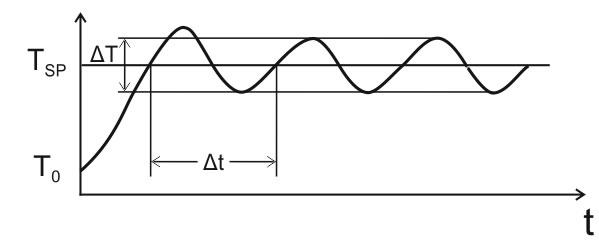
Тο — начальная температура в системе;
Тsp — заданная температура (уставка);
∆T — размах колебаний температуры (в расчетах не участвует);
∆t — период колебаний температуры.
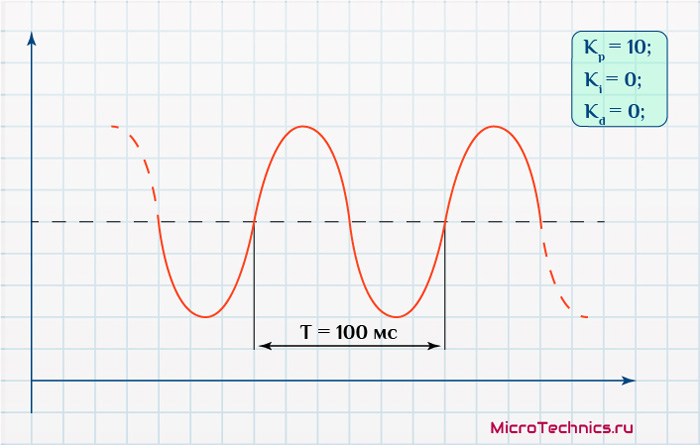
2.Меняем значение пропорциональной составляющей Kp от минимума (можно от 0) до момента, пока не появятся устойчивые колебания системы с периодом ∆t. Фиксируем это значение как Kуст, а также период колебаний системы ∆t. Система должна находится в постоянном колебательном процессе, притом колебательный процесс незатухающий, колебания должны быть одинаковы относительно Тsp.
После получения данной кривой на нашем объекте, засекаем время периода колебаний ∆t – полный период. Данное время есть характеристика системы, оборудования.
3.На этом практическая часть метода заканчивается. Из полученных значений рассчитываем коэффициенты ПИД:
Kp=0.6⋅Kуст
Ki=(2⋅Kp)/∆t
Kd=(Kp⋅∆t)/8
Здесь Kуст – тот самый коэффициент пропорциональной составляющей, при котором возникли колебания, а ∆t – период этих колебаний.
Второй вариант, когда надо найти постоянные времени Ti и Td
Используя полученные параметры рассчитываем Ти и Тд по таблице.
| Пропорциональный коэффициент Kp |
Интегральный коэффициент Ti |
Дифференциальный коэффициент Td |
|
| П-регулятор | 0.5*Kуст | ||
| ПИ-регулятор | 0.4*Kуст | 0.8*∆t/Kp | |
| ПИД-регулятор | 0.6*Kуст | 0.5*∆t/Kp | 0.125*∆t/Kp |
Хочется сказать, что данный метод не несет за собой никаких улучшений, просто он построен на другом способе поиска, недостатки те же, что и у метода Зиглера-Никольса первого.
Метод CHR (Chien, Hrones и Reswick) или Чина-Хронеса-Ресвика, если по-русски
Этот метод предполагает предварительное определение времени задержки L и времени выравнивания T по переходной характеристике объекта. Ну это мы делали и для Зиглера-Никольса, но в отличие от Зиглера и Никольса, которые использовали в качестве критерия качества настройки декремент затухания, равный 4, Chien, Hrones и Reswick (CHR) использовали критерий максимальной скорости нарастания при отсутствии перерегулирования или при наличии не более чем 20 процентного перерегулирования. Такой критерий позволяет получить больший запас устойчивости, чем в методе Зиглера-Никольса. Метод CHR даёт две разные системы параметров регулятора. Одна из них получена при наблюдении отклика на изменение уставки (таблица), вторая – при наблюдении отклика на внешние возмущения (не представлена). Какую систему параметров выбирать, зависит от того, что важнее для конкретного регулятора: качество регулирования при изменении уставки или ослабление внешних воздействий (в жизни изменение уставки вызывает намного более существенные процессы в регулятора, потому лучше настраивать по этой таблице, будет настройка не “в малом”, а “в большом”). Если же важно и то и другое, то необходимо использовать регуляторы с двумя степенями свободы. Метод CHR использует аппроксимацию объекта моделью первого порядка с задержкой. В CHR используются те же исходные параметры a и L, что и в методе Зиглера-Никольса. Обратим внимание, что пропорциональный коэффициент в методе CHR меньше, чем в методе Зиглера-Никольса.
Формулы для определения коэффициентов приведены в таблице:
| Без перерегулирования | С 20% перерегулированием | |||||
| Пропорциональный коэффициент Kp |
Интегральный коэффициент Ti |
Дифференциальный коэффициент Td |
Пропорциональный коэффициент Kp |
Интегральный коэффициент Ti |
Дифференциальный коэффициент Td |
|
| П-регулятор | 0.3/a | 0.7/a | ||||
| ПИ-регулятор | 0.35/a | 1.2*L/Kp | 0.6/a | L/Kp | ||
| ПИД-регулятор | 0.6/a | L/Kp | 0.5*L/Kp | 0.95/a | 1.4*L/Kp | 0.47*L/Kp |
Остальные методы, а именно Спектральный метод, метод Куна, метод Стогестада, метод Шеделя требуют уже больших знаний ТАУ и самое главное требуют либо реальной переходной характеристики, которую придется искать методом интерполяции и аппроксимации, либо вовсе моделирования объекта управления. Если вкратце, то суть методов можно описать парой предложений.
Спектральный метод
Спектральный метод предполагает компенсацию нулями регулятора нежелательных полюсов объекта.
На основе полюсов объекта {p1, p2} определяются компенсирующие значения постоянных времени интегрального и дифференцирующего каналов:
Tи = |1/p1|, Tд = |1/p2|.
и коэффициенты регулятора Kp и Kd в виде:
Kp = Ki(Tи + Tд), Kd = Ki*Tи*Tд/(Tи + Tд).
Метод Куна
Параметром, характеризующим быстродействие любых рассматриваемых объектов, является суммарная постоянная времени. Метод настройки Куна (или метод «Т-правило») основан на аппроксимации объекта звеном третьего порядка. Параметры ПИД-регулятора Ti и Td выбирают, таким образом, чтобы компенсировать два полюса. Расчетные значения для регулятора даны в таблице, но я здесь ее приводить не стану.
Метод Стогестада
По идентифицированным параметрам модели ОУ находят необходимые параметры настройки регулятора. Принцип синтеза ПИД-регулятора с использованием метода Стогестада заключается в следующем: задание желаемого вида переходной характеристики замкнутой САУ (желаемый вид описывается инерционным звеном первого порядка) путем выбора постоянной времени.
Для апериодического звена второго порядка с транспортным запаздыванием параметры ПИД-регулятора могут быть найдены по следующим формулам:
kp = T1/k*(Tc+τ), Ti=min[T1;c(Tc+τ)],Td=T2.
где T1, T2, k и τ–параметры объекта; с–параметр, который рекомендуют принимать равным 4, для обеспечения апериодического вида переходного процесса на выходе системы управления (например пароперегревателем котла).
Метод Шеделя
Метод Шеделя основан на принципе каскадного коэффициента демпфирования. В методе обобщается понятие коэффициента демпфирования на случай системы 3-го порядка. Параметры ПИД-регулятора должны быть выбраны таким образом, чтобы коэффициенты демпфирования системы принимали определенные значения. Их если будет интересно лучше поискать в справочниках.
Часть 1. От практики к теории.
Часть 2. Реализация регулятора – от простого к настоящему.
Часть 3. Реализация регулятора – вот теперь регулятор.
Часть 4. Мир развивается, а «велосипед» остается.
Инженерные единицы переменных и масштабирование.
В полноценных ПЛК, поддерживающих значения с плавающей точкой, переменные технологического процесса отображаются в «инженерных» единицах – Па, метры в секунду, миллиметры и т.д., при этом ошибка на входе ПИД-функции имеет размерность переменной процесса. Например, в нашем примере, ошибка может быть в миллиметрах уровня (0-1000мм), а выход ПИД-функции будет в процентах открытия клапана (0-100%). Поскольку коэффициенты ПИД-функции связывают ошибку с выходным значение, то значение коэффициентов будет зависеть от размерности переменных. Например, при шкале уровня 0-1000мм коэффициент П-функции будет 0,1 (на 10мм ошибки уровня клапан переместиться на 1%). Но если размерность уровня принять в 0-1 метр, то коэффициент П-функции должен быть 100 (в тысячу раз больше, т.к. размерность изменилась на 1000).
Чтобы коэффициенты ПИД-функции не были привязаны к размерности, при реализации ПИД-регулятора перед ПИД-функцией всегда используется масштабирование «инженерных» единиц в условные. Условные единицы будут зависеть от ПЛК, для целочисленных знаковых вычислений это максимальное значение переменной 0-32767 (положительный диапазон), для плавающей точки 0-100 (или 0-1 или..).
Следовательно, в практической реализации регулятора добавляются функциональные блоки, выполняющие масштабирование входных и выходных переменных в условные единицы, а ПИД-функция оперирует уже с переменными в условных единицах. PV – переводится в переменную RPV, SP в RSP, ROP в OP.

Можно заметить, что значение ошибки Е может принимать как положительные, так и отрицательные значения, соответственно выход ПИД-функции ROP также может принимать любое положительное или отрицательное значение. Поэтому кроме масштабирования ROP в OP необходимо анализировать выход OP за допустимый диапазон. В практических реализация ПИД-регулятора для выходной переменной может задаваться как масштабирование, так и допустимые границы диапазона (например, для выхода на клапан инженерные единицы будут 0-100%, а допустимые границы -5…105%)
Чтобы не путаться в дальнейшем рассмотрении нашего примера, для всех переменных значения в «инженерных» единицах примем 0-100, тогда диапазоны инженерных единиц будут совпадать с диапазоном в условных единицах.
Ручное управление выходом регулятора. Безударный переход из ручного в автоматический режим, смещение выхода.
Для возможности практического использования, кроме просто ПИД-функции, регулятор как минимум должен иметь возможность ручного управления процессом.
В нашем примере, управление расходом на отходящем трубопроводе посредством регулирующего клапана, в реальной системе может выполняться как в автоматическом режиме с использованием ПИД-функции, так и в ручном режиме, когда оператор непосредственно задает значение выхода регулятора (положение клапана). Для этого в реализации регулятора необходимо предусмотреть еще несколько параметров:
– режим руч/авт – режим работы регулятора, в ручном режиме оператор непосредственно задает значение выхода регулятора OP, в автоматическом оператор задает уставку регулятору SP, а регулятор формирует выходное значение OP;
– значение выхода ManOP – значение выхода регулятора для ручного режима, в ручном режиме значение ManOP записывается в OP;
Соответственно в реализации регулятора для выходного значения OP необходимо выполнить селектор: в ручном режиме OP=ManOP, в автоматическом OP=ROP (после масштабирования и ограничения диапазона). Но на самом деле все не так просто.
Когда регулятор находится в ручном режиме, ПИД-функция продолжает рассчитывать выходное значение ROP, и это значение ROP будет отличаться от текущего заданного в ручную выхода регулятора OP=ManOp. Не соответствие значений ManOP и ROP в ручном режиме приводит к «удару» при переводе регулятора из ручного в автоматический режим.
Например, вы перевели регулятор в ручной режим, «успокоили» процесс в ручном режиме подобрав необходимое положение клапана ManOP=23. При этом уставка SP=30, а переменная процесса PV остановилась на значении 25, т.е. на входе П-функции есть ошибка Е=5, и при П-коэффициенте kP=2 выход П-функции будет ROP=kP*E=2*5=10. Теперь переводим регулятор в автоматический режим, селектор переключает выход с ManOP на ROP и значение OP «ударно» меняется с 23 на 10, движение клапана вносит возмущение, и уже стабилизированный в ручном режиме процесс снова приходит в движение.
– PV tracking – чтобы избавится от ошибки при переключении из ручного в автоматический режим, можно реализовать функцию «отслеживание входной переменной». Когда регулятор находится в ручном режиме, значение переменной процесса PV копируется в значение уставки SP, и при переключении в автоматический режим, уставка и текущее значение переменной равны (PV=SP), следовательно ошибка на входе П-функции равна 0, т.е. в предыдущем примере при переключении в автоматический режим SP=PV=25. Ошибки нет, но … выход клапана все равно ударно изменится.
Если вы включили функцию PV tracking или постарались, и в ручном режиме вывели переменную процесса на значение уставки, т.е. SP=PV и получили при этом значение выхода, например, ManOP=55 (клапан открыт на 55%), тогда ошибка в момент переключения в автоматический режим будет E=RPV-RSP=0, и все вроде хорошо, но выходное значение П-функции будет равно НУЛЮ (ROP=E*kP=0*2=0) и при перевод регулятора в автоматический режим клапан закроется. Если этот клапан регулировал подачу топливного газа в печь, печь отключится со всеми вытекающими последствиями.
Это и называется «удар при переключении режима», и значит нужно реализовать алгоритм безударного переключения и ввести еще одну переменную:
– смещение выхода offset – дополнительная переменная, которая содержит расхождение между значением выхода регулятора в ручном режиме ManOP и значением, рассчитанным П-функцией ROP (с учетом масштабирования и ограничения диапазона).
В ручном режиме offset=ManOP-ROP, в автоматическом режиме OP=ROP+offset. Если вернуться к примеру с потухшей печью, в ручном режиме регулятора смещение выхода будет offset=ManOP-ROP=55-0=55. Тогда при переключении в автоматический режим выход регулятора будет равен OP=ROP+offset=55, и теперь выход регулятора будет рассчитываться с учетом смещения. Значение смещения будет сохраняться до следующего переключения в ручной режим.
Сразу хочу заметить, что в реализации ПИ-регулятора функцию смещения выполняет И-составляющая, и отдельная переменная «смещение» не используется, в этом случае для обеспечения безударного перехода НЕЛЬЗЯ полностью отключать И-составляющую. Если требуется режим П-регулятора, то для И-составляющей надо установить минимальный, но не нулевой И-коэффициент (или максимальное время интегрирования).
Только при реализации двух функций: «отслеживание входной переменной» (PV tracking) и «смещение выхода» (offset) мы обеспечиваем безударное переключение регулятора из ручного в автоматический режим.
Аналогично, при переходе из автоматического режима в ручной будет «скачком» меняться значение выхода с ROP на ManOP, но с этом бороться проще. Надо в автоматическом режиме записывать текущее значение OP в ManOP, тогда при переводе из автоматического режима в ручной ManOP будет равно текущему значению OP, «скачка» не будет.
Часть 4. И наконец про И и Д.
Как объяснялось в предыдущих частях статьи, регулятор с одной П-функцией всегда имеет статическую ошибку в установившемся режиме, что во многих случаях просто неприемлемо. В эру паровых машин, когда и появились П-регуляторы, обороты машины зависели от нагрузки, что не нравилось инженерам. В поисках решения был придуман «изодром», дополнительное устройство в регуляторе, позволяющее исключить статическую ошибку. Есть обоснованное подозрение, что устройство изначально было изобретено инженерами, а потом уже математики дали ему описание и обозвали интегральным звеном. В начале первой часть дана ссылка на теоретический курс, там про изодром все доступно описано с картинками.
Итак, переходим к описанию практической реализации И-составляющей, она же изодромное звено (хоть это не совсем корректно), или более «инженерно-программистское» название «интегральная сумма». Название «интегральная сумма» выражает суть этой функции, поэтому дальше и будем часто его использовать.
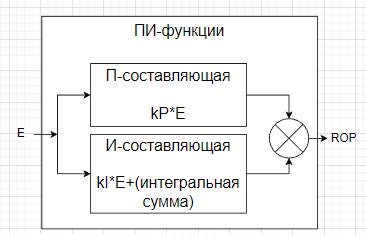
И-составляющая – это еще одна функция регулятора, на входе которой ошибка (рассогласование), а выходное значение суммируется с выходом П-функции и формирует значение ROP.
В каждом цикле выполнения И-функции значение ошибки E умножается на коэффициент kI и прибавляется к значению интегральной суммы Isum=Isum+kI*E.
Во многих реализациях ПИ-регулятора вместо коэффициент kI используется переменная “время интегрирования” tI, тогда формула И-составляющей будет выглядеть так Isum=tc/tI*E+Isum. Если период контура tc – константа, то время интегрирования tI будет обратной величиной к kI. Ну и надо помнить, что время интегрирования не может иметь нулевое значение (деление на ноль). Использование в ПЛК времени интегрирования для И-функции осталось в наследие от пневматических и механических И-регуляторов.
Работа П+И-функций.
После того, как на входе ПИ-функций сформировалась ошибка, и П-функция сдвинула клапан в соответствующее положение, ошибка на входе все равно сохраняется. Поэтому в каждом цикле выполнения ПИ-функций к интегральной сумме прибавляется некоторое значение (kI*E), и интегральная сумма меняет выход регулятор, сдвигая положение клапана. При этом ошибка E уменьшается, соответственно уменьшается значение П-составляющей. Поскольку ошибке E может быть как положительной, так и отрицательной, то интегральная сумма может увеличиваться или уменьшаться.

На следующем цикле интегральная сумма опять увеличивается, выход снова сдвигается, ошибка и значение П-составляющей еще уменьшаются. И так до тех пор, пока ошибка не будет равна нулю, соответственно и П-составляющая будет равна нулю, а выход ROP будет определяться только значением интегральной суммы.

Понятно, что если коэффициент kI будет большой, интегральная сумма будет меняться очень быстро и регулятор потеряет устойчивость. И надо учитывать влияние изменения интегральной суммы на изменение значения П-функции. При низком значении kI от И-составляющей практически нет пользы, при высоком регулятор потеряет устойчивость, причем потеря устойчивости может проявится при возмущающем воздействии на объект.
Вроде все просто, но на практике есть тонкости.
Возвращаемся к исходному примеру, с уровнем в емкости и клапаном. По какой-то причине клапан не справлялся и уровень в емкости оставался «перелитым» несколько часов, при этом на входе ПИ-функции сохранялась ошибка и соответственно выполнялся расчет интегральной суммы. За это время интегральная сумма достигнет астрономических значений, соответственно выход ROP будет находится в «зашкаленном» состоянии долгое время даже после снижения уровня и изменении знака ошибки, т.е. ПИ-регулятор будет неработоспособным. Если функция смещения выхода offset реализована с использованием интегральной суммы, тогда чтобы вернуть интегральную сумму к «разумному» значению, необходимо перевести регулятор в ручной режим, установить выход OP в нужное значение и перевести регулятор снова в автоматический режим (или каким-то другим способом сбросить накопленное значение интегральной суммы). Но для полноценной работы нужно в регуляторе реализовать простой алгоритм, который поможет избежать «зашкаливания» интегральной суммы. Нужно отслеживать значение ОР и при выходе за допустимый диапазон (например 5-95%) останавливать расчет интегральной суммы и значение «замораживается». Но даже при этом иногда приходится «передергивать» регулятор автомат-руки-автомат чтобы он начал корректно работать.
И еще одна полезная функция в ПИ-регуляторе – задание зоны нечувствительности. Нулевого значения ошибки достичь физически невозможно, к нему можно только стремиться, поэтому на входе ПИ-функции всегда есть значение ошибки, пусть даже ничтожное и часто с переменным знаком. И значение переменной процесса в силу бесконечного количества причин может колебаться в пределах 1-2%. Это приводит к постоянному расчету ПИ-функций, небольшому изменению выхода и ненужному подергиванию клапана (исполнительного устройства). Чтобы избежать этого, в регуляторе задается параметр «зона нечувствительности» и задается значение, например 1%, когда ошибка меньше этого значения, ПИ-функция не выполняется и выход не изменяется.
И еще пару слов про Д-составляющую.
Часто можно услышать мнение, что И-составляющая делает регулятор неустойчивым, поэтому нужна Д-составляющая, чтобы компенсировать «недостатки» И-составляющей. Это заблуждение.
Д-составляющая или дифференциальное звено, формирует реакцию регулятора на быстрое изменение ошибки (или входной переменной). Д-функция вычисляет разницу ошибки на текущем и предыдущем шаге, умножает на коэффициент kD и прибавляет к выходу ROP.

Классический пример использования Д-функции – стабилизация положения самолет. Воздух не является статичным, при движении летательного аппарата на планер постоянно действуют кратковременные возмущающие воздействия. Чтобы компенсировать влияние возмущений и используется Д-функция, которая также кратковременно отклоняет элероны, интерцепторы, рули высоты или направления. Когда смотришь на крыло летящего самолета видно, что элероны и интерцепторы постоянно «подергиваются». Сейчас конечно ПИД-регуляторы в стабилизации летательных аппаратов не используются, но изначально эту роль выполняла Д-функция.
С Д-функцией тоже есть момент, когда вы меняете уставку регулятору, например на 10%, у вас мгновенно меняется ошибка, что приведет к «скачку» значения Д-функции, поэтому в реализации обычно можно выбрать, что будет подаваться на вход Д-функции: ошибка Е или переменная процесса PV. Значение E и PV меняются синхронно, но чтобы избежать скачка при корректировки уставки, логично привязать Д-функцию к PV.
На первых порах инженерной деятельности я пытался «приспособить» Д-функцию для работы в регуляторах на технологическом процессе, но пришел к выводу, что в большинстве случаев она не имеет смысла. В большинстве своем процессы медленные, кратковременных возмущений, которые требуют реакции регулятора просто нет. Исполнительные механизмы тоже медленные и не могут (и не должны) реагировать на кратковременное изменение выхода регулятора. Да и отклик технологического процесса на управляющее воздействие в целом тоже медленный. Д-функция просто «реагирует на шумы» в контуре регулирования, мешая работе ПИ-функции и бессмысленно дергая выход регулятора. Понятно, задачи бывают разные, я говорю про то, с чем сталкивался, но я всегда выключал Д-функцию и не помню случая, когда приходилось ее использовать.
На этом описание ПИД-регулятора в минимальном объеме, необходимом для практического использования, можно считать выполненным. Каждый производитель ПЛК может реализовывать дополнительный функционал для решения определенных задач.
В некоторых реализациях ПИД-регуляторов есть возможность выбора «зависимых» и «независимых» коэффициентов. Независимые я описывал выше, это когда в каждой функции П И Д используются свои коэффициенты kP, kI, kD. При зависимых коэффициентах функции заключаются в скобки и коэффициент kP выносится за скобку и называется коэффициент усиления регулятора, выглядит это так ROP=kP*(E+kI*E+kD*(En-E(n-1)). Наверно есть применения, когда такой подход востребован.
Часто на практике используют каскадное построение регуляторов, когда выход первого регулятора является заданием для второго. Пример, регулирование температуры верха колонны подачей орошения, на трубопроводе орошения установлен расходомер и клапан, на колонне датчик температуры. Для регулирования температуры надо управлять расходом жидкости через клапан. Первый контур регулирования связывает температуру в колонне с расходом, второй контур – расход и клапан. У каскадного регулятора есть три режима работы:
1. Ручное управление клапаном – оператор непосредственно задает положение клапана;
2. Автоматическое поддержание заданного расхода – оператор задает уставку по расходу во втором контуре, регулятор управляет клапаном для поддержания заданного расхода;
3. Каскадное регулирование – оператор задает уставку по температуре в колонне (уставка первого контура), первый контур регулирования формирует требуемый расход орошения и передает его в качестве уставки второму контуру (выход ОР первого контура является уставкой для второго контура), второй контур управляет клапаном, чтобы обеспечить требуемый расход.
Каскадные регуляторы используют из-за большей гибкости настройки (для медленного контура температуры можно настроить медленный регулятор, для более быстрого контура расхода и регулятор будет более быстрый), возмущения в контуре расхода, изменение производительности насоса или гидравлики в трубопроводе компенсируются вторым быстрым контуром без внесения возмущения в первый контур, что увеличивает качество регулирования. И у оператора есть возможность задать поддержание как температуры, так и отдельно расхода орошения, что бывает очень полезным.
Глава 8. Типовые законы регулирования. Одноконтурные САР
8.1. Основные типы автоматических регуляторов
Регулятор на основе усилительного звена называется П-регулятором (пропорциональный). Его положительной характеристикой является высокое быстродействие: при отклонении регулируемой величины от заданного значения регулятор выдает регулирующее воздействие, пропорциональное величине отклонения x, что обеспечивает быструю компенсацию возмущения. Существенным недостатком П-регулятора является наличие статической ошибки в переходном процессе АСР с П-регулятором (рис. 37). Статическая ошибка возникает потому, что у П-регулятора между регулируемой величиной x и регулирующим воздействием xр существует зависимость, однозначно определяемая коэффициентом K. Поэтому генерировать регулирующее воздействие xр для компенсации возмущения xв П-регулятор может только путем изменения регулируемой величины x, что и создает статическую ошибку.
Регулятор на основе интегрирующего звена (48) называется И‑регулятором:
Если xвых усилительного звена (П-регулятор) однозначно определяется величиной правой части уравнения, что является причиной возникновения статической погрешности в АСР с П-регулятором, то правая часть уравнения (48) интегрирующего звена (И-регулятор) определяет не величину, а скорость изменения xвых. Величина xвых будет изменяться до тех пор, пока правая часть уравнения (48) не станет равна нулю, т. е. пока регулируемая величина x при наличии возмущения xв не вернется к заданному значению. Следовательно, в АСР с И-регулятором не возникает статическая погрешность.
Однако у И-регулятора имеется свой недостаток сравнительно с П-регулятором: в случае возникновения возмущения регулирующее воздействие П-регулятора меняется быстрее, чем у И-регулятора с его конечной скоростью, что замедляет процесс компенсации возмущения и ухудшает критерии качества регулирования (рис. 40).

Рис. 40. Переходные процессы в АСР с П- и И-регуляторами
Таким образом, П-регулятор обеспечивает высокое быстродействие (что уменьшает динамическую ошибку), но не может обеспечить при наличии возмущения заданное значение регулируемой величины (статическая ошибка). И-регулятор, наоборот, не создает статическую ошибку, но вследствие относительно медленного изменения xр имеет большую динамическую ошибку.
Сравнивая характеристики П- и И-регуляторов можно сделать вывод: если включить усилительное и интегрирующие звенья параллельно, то автоматический регулятор будет лишен указанных недостатков. Такой регулятор называется ПИ-регулятором (рис. 41).

Рис. 41. Принципиальная схема АСР с ПИ-регулятором
Действительно, быстродействие ПИ-регулятора обеспечивает усилительное звено, а статическую ошибку снимает интегрирующее звено. Для управления производственными процессами чаще всего используются ПИ-регуляторы.
Кривая разгона идеального ПИ-регулятора показана на рис. 42 .
Уравнение ПИ-регулятора при нулевых начальных условиях имеет вид:

Отношение коэффициентов Kp1/Kp определяет степень влияния интегрирующей части, и его обратная величина называется временем изодрома Tи.

Время изодрома – это время, в течение которого интегрирующее звено изменяет регулирующее воздействие xр ПИ-регулятора на величину Dxр, равную предварительному изменению Dxр усилительного звена (рис. 42). Поэтому иногда время изодрома называют временем удвоения.

Рис. 42. График кривой разгона идеального ПИ-регулятора:
а – скачкообразное изменение входного воздействия x;
б – реакция (кривая разгона) ПИ-регулятора xр
Уравнение ПИ-регулятора можно записать как

откуда передаточная функция

Амплитудно-фазовая характеристика:

В том случае, если рассмотренные регуляторы не обеспечивают требуемое качество регулирования, необходимо увеличить интенсивность процесса компенсации возмущения. Этого можно достигнуть увеличением регулирующего воздействия, которое в свою очередь определяется коэффициентом усиления автоматического регулятора Kp
. Однако ниже будет показано, что увеличение коэффициента усиления регулятора в АСР приводит к тому, что в системе начинают генерироваться незатухающие колебания.
В связи с этим представляет интерес рассмотреть алгоритм, который реализует дифференцирующее звено.
Входной величиной любого регулятора является кривая разгона регулируемой величины (рис. 27), которая определяется величиной возмущения и передаточной функцией объекта регулирования (9). В свою очередь, регулирующее воздействие xp (рис. 27) определяется кривой разгона x и передаточной функцией регулятора.
На рис. 43 показана реакция дифференцирующего звена (Д‑регулятора) на входное воздействие в виде кривой разгона в соответствии с уравнением (51).

Рис. 43. Реакция дифференцирующего звена на кривую разгона
а –изменение входного воздействия x в виде кривой разгона;
б – реакция xр дифференцирующего звена
Из рис. 43,а следует, что дифференцирующее звено обеспечивает большее регулирующее воздействие в начале переходного процесса. Это означает, что дифференцирующий регулятор активно компенсирует возмущение и исключает возникновение незатухающих колебаний.
Если включить дифференцирующее звено параллельно ПИ‑регулятору (рис. 44), то получим ПИД-регулятор, обеспечивающий интенсивную компенсацию возмущений. При этом недостаток дифференцирующего звена (при Хвх = const, Хвых = 0 ) компенсируется усилительным и интегрирующим звеньями.

Рис. 44. Принципиальная схема АСР с ПИД-регулятором
На рис. 45 показана кривая разгона ПИД-регулятора.

Рис. 45. Кривая разгона ПИД-регулятора
На рис. 46 показаны переходные процессы на с различными регуляторами. ПИД-регулятор уменьшает динамическую ошибку сравнительно с ПИ-регулятором на 25–30%. Также можно объединить дифференцирующее звено с усилительным звеном и улучшить показатели П-регулятора, получив ПД-регулятор.

Все пять типов рассмотренных автоматических регуляторов имеют общую особенность своего функционирования – обеспечивают стабилизацию регулируемой величины после окончания переходного процесса.
8.2. Критерии качества регулирования
Качество процесса регулирования в АСР характеризуют следующие показатели (критерии) (рис. 16):

Рис. 16. Показатели качества регулирования:
1 – переходной процесс без статической ошибки;
2 – переходной процесс со статической ошибкой
1. Максимальное отклонение в процессе регулирования от заданного значения (динамическая ошибка) ΔХдин.
2. Статическая ошибка ΔХст – возможные отклонения от заданного значения по окончании переходного процесса при использовании некоторых типов регуляторов (подробнее такие АСР рассмотрены ниже).
3. Длительность переходного процесса Тр – период времени с момента начала отклонения регулируемого параметра от задания до возвращения его к заданному значению с определенной степенью точности регулирования ±Δ.
Например, если ±Δ=±25%, это означает, что для заданного значения температуры в 100 °С процесс регулирования будет завершен при достижении диапазона (100 ± 2,5) °С.
4. Степень затухания показывает характер затухания переходного процесса регулирования:


Для того, чтобы переходный процесс затухал за 2 ¸ 3 периода колебаний, степень затухания должна быть равна

5. Степень колебательности процесса m определяет характер колебательности процесса и равна отношению действительной части корня характеристического уравнения к коэффициенту при его мнимой части. Степень колебательности связана со степенью затухания следующим соотношением:

6. Интегральный квадратичный критерий – критерий, определяющий площадь под кривой переходного процесса, возведенной в квадрат (рис. 17):

Уменьшение интегрального критерия соответствует ускорению процесса регулирования.

Рис. 17. Интегральный квадратичный критерий качества регулирования
Однако все приведенные шесть критериев качества не определяют величину потерь производства при отклонениях регулируемой величины от оптимального значения в переходных процессах регулирования. Для определения таких потерь можно использовать экономический критерий.
7. Экономический критерий рассмотрим на примере, регулирования температуры химического реактора θ, когда степень превращения Q в реакторе определяется температурой (рис. 18а).
Разделим переходной процесс на равные интервалы времени Δt и запишем значения θ
в этих точках по графику (18, б). На графике (18, а) для этих температур определим уменьшение степени превращения вследствие отклонения от оптимального режима, а затем сделаем расчет потерь исходных продуктов для каждого интервала Δθ, суммируем эти потери для всего переходного процесса и представим потери в денежном выражении.

Рис. 18. Экономический критерий качества регулирования:
а – зависимость степени превращения Q от температуры θ;
б – переходный процесс регулирования температуры
Совместно со специалистом по технологии или по его заданию необходимо определить, какой из указанных критериев для рассматриваемой АСР является превалирующим, и задать максимально допустимую величину этого критерия, т. е. определить, какое качество регулирования должна обеспечить проектируемая АСР.
8.3. Выбор закона регулирования
При выборе регулятора следует определиться с группой регулирующих устройств – непрерывного, релейного или импульсного действия. Такой выбор ориентировочно может быть сделан по величине отношения запаздывания к постоянной времени объекта τ/Tоб:
· при отношении τ/Tоб меньше 0.2 целесообразно использовать регулятор релейного действия;
· если отношение τ/Tоб от 0.2 до 1.0, то нужно использовать регулятор непрерывного действия;
· при отношении τ/Tоб больше единицы можно использовать регулятор импульсного действия, или специальные регуляторы, например, регулятор («предиктор») Смита.
Затем необходимо определиться с типом регулятора, т.е. выбрать определенный закон регулирования: П-, И-, ПИ-, ПД- или ПИД-закон
8.4. Методы расчета одноконтурных САР
Как указывалось выше, качество автоматического регулирования определяется свойствами системы в целом, т. е. суммарными свойствами объекта и регулятора. Поскольку объект обычно является неизменяемой частью системы, то обеспечить определенные свойства системы, а следовательно и заданное качество регулирования, можно соответствующим подбором свойств автоматического регулятора, что зависит от параметров его настройки. В свою очередь, параметры настройки являются коэффициентами передачи в уравнении автоматического регулятора.
Таким образом, параметры настройки автоматического регулятора определяются свойствами объекта регулирования, т. е. величинами τоб, Тоб, Коб.
8.4.1. Расчет по “приближенным” формулам
Приближенные формулы для расчета параметров настройки автоматических регуляторов (Kр – коэффициент усиления; Tи – время изодрома; Тд – время дифференцирования) сведены в следующую таблицу:
Таблица 8.1. Формулы для приближенного расчета
параметров настройки регуляторов

Формулы сгруппированы в столбцы в зависимости от характера переходного процесса, который желательно получить, используя рассчитанный таким образом регулятор: апериодический или с перерегулированием в 20 %. В формулы входят следующие свойства объекта регулирования: Коб – коэффициент усиления; Тоб – постоянная времени; τоб – время запаздывания (полного).

Рис. 53. Кривые разгона:
1 – фактическая кривая разгона промышленного объекта;
2 – аппроксимированная (приближенная) кривая разгона
Необходимо отметить, что для пневматических регуляторов требуется определять не Kp, а диапазон дросселирования:

Рассмотрим методику более точного определения параметров настройки на примере расчета наиболее «популярного» регулятора – ПИ-регулятора.
8.4.2. Метод незатухающих колебаний
(метод Циглера-Никольса)
При использовании метода незатухающих колебаний [6], который иногда также называется по именам авторов методом Циглера-Никольса, поиск оптимальных параметров настройки осуществляется по величине критического коэффициента усиления П-регулятора и величине периода автоколебательного процесса.

Рис. 54. К поиску параметров настройки методом Циглера-Никольса
Расчет параметров настройки регуляторов проводится в два этапа.
1. На исследуемом объекте устанавливается П-регулятор и, последовательно увеличивая коэффициент усиления (уменьшая диапазон дросселирования), АСР выводится в режим незатухающих колебаний (автоколебаний на границе устойчивости). При этом фиксируется величина коэффициента усиления П-регулятора Ккрр и период незатухающих автоколебаний Т (рис. 54).
2. На втором этапе по величинам Кркр и Т определяются параметры настройки П-, ПИ- и ПИД-регуляторов:



Метод незатухающих колебаний не требует сложных вычислений, но имеет свои характерные недостатки:
· получить Кркр и Т можно только на действующем объекте, оснащенном АСР с П-регулятором;
· не все объекты химической технологии допускают режим автоколебаний;
· практически трудно уловить момент начала автоколебаний.
Данные недостатки имеют место лишь при настройке регулятора методом Циглера-Никольса непосредственно на действующем объекте. Если заменить реальный объект его математической моделью, данный метод лишается указанных недостатков, кроме того, моделирование позволяет на порядок ускорить процесс поиска параметров настройки. Но для выполнения моделирования требуется достаточно точное математическое описание объекта регулирования, а получить его удается не всегда.
8.4.3. Метод расширенных частотных характеристик
Уравнение ПИ-регулятора (65) или (66):

Передаточная функция ПИ-регулятора:


Знак «минус» указывает, что действие регулятора направлено против возмущения.
Из передаточной функции получаем амплитудно-фазовую характеристику ПИ-регулятора путем замены p на iw:

Так как по формуле Эйлера



с затуханием за три периода

Заменив iw на комплексную переменную (-mw+iw), получаем расширенную амплитудно-фазовую характеристику (РАФХ)Ю

Расширенными такие характеристики называются потому, что они как бы «расширены» по отношению к обычной АФХ (рис. 56).
Предположим, что объект регулирования имеет передаточную функцию второго порядка следующего вида:

Для дальнейшего математического моделирования АСР передаточную функцию необходимо преобразовать:


Рис. 56. АФХ объекта регулирования с самовыравниванием:
1 – обычная; 2 – расширенная
Расширенная амплитудно-фазовая характеристика объекта регулирования при замене p на (-mw+iw) будет иметь вид:




Где Rоб(m,w) -расширенная амплитудно-частотная характеристика объекта; Fоб(m,w) -расширенная фазочастотная харктеристика объекта. Величина 40w в выражении для Fоб (m,w) опеделяет угол в радианах и для пересчета в градусы неоходимо 40w умножить на 57,3
Условием нахождения замкнутой АСР на границе устойчивости является уравнение:

Аналогично, исходным уравнением для получения заданной степени колебательности m, а следовательно, определенной степени затухания y, является соотношение:

Это соотношение двух комплексных чисел возможно в том случае, если произведение модулей РАФХ равно единице, а аргументы (фазы) равны между собой, т. е.


Решая эти уравнения относительно S0 и Kp, получаем:



Обычно принимают степень колебательности m = 0,221, что соответствует степени затухания ψ=0,75 и обеспечивает затухание процесса регулирования примерно за три периода. Тогда

Уравнения для определения параметров настройки ПИ-регулятора можно преобразовать:


Подставляя в приведенные уравнения численные значения частоты w от 0 до значения, когда S0 становится отрицательной величиной, строим на плоскости параметров настройки кривую равной степени колебательности


Пример кривых равной степени колебательности в плоскости параметров настройки ПИ-регулятора показан на рис. 57. Графики процессов регулирования с различными параметрами настройки ПИ-регулятора при m = 0,221 показаны на рис. 58. Все процессы регулирования, показанные на рис. 58, реализованы ПИ-регулятором с параметрами настройки, полученными по кривой равной степени колебательности в точках 1, 2, 3, 4 (рис. 57), и все имеют m = 0,221, т. е. затухают примерно за три периода, но обладают существенно различным характером.
В связи с этим возникает задача определения оптимальных параметров настройки на кривой равной степени колебательности.

Рис. 57. Кривые равной степени колебательности
В качестве критерия оптимальности выбираем продолжительность переходного процесса – время регулирования (т. е. быстродействие АСР) и отсутствие постоянной или врéменной статической ошибки. Это исключает из рассмотрения параметры настройки в точке 4 (параметры настройки П-регулятора) и в точке 3 (врéменная статическая ошибка) (рис. 58).

Рис. 58. Графики процессов регулирования для ПИ-регулятора
с различными параметрами настройки в точках 1, 2, 3 и 4
при степени колебательности m =0,221
Быстродействие автоматического регулятора прежде всего зависит от величины регулирующего воздействия, которое для ПИ-регулятора, как следует из уравнения (65), прямо пропорционально величине коэффициента усиления Kp и обратно пропорционально времени изодрома Tи. Расчеты показывают, что если двигаться по кривой равной степени колебательности вправо, то величина регулирующего воздействия при прочих равных условиях сначала возрастает и достигает максимального значения на кривой равной степени колебательности вблизи ее вершины, когда

а затем начинает уменьшаться в связи с резким увеличением Tи (рис. 57).

Рис. 59. Выбор оптимальных параметров настройки
Таким образом, оптимальные параметры настройки ПИ-регулятора находятся в точке 2 на кривой равной степени колебательности (рис. 59).
Источник
Плютто В. П., Дубровский И. И. Элементы теории управления химико-технологическими процессами и системами. Конспект лекций: Учеб. пособие – М.: РХТУ им. Д. И. Менделеева, 2003. – 127 с.