
Необходимость определения коэффициента наклона прямой на графике возникает во многих научных задачах, связанных с анализом зависимостей между величинами. Скорость изменения одной величины относительно другой может быть определена через этот коэффициент. В данной статье мы обсудим подробно процесс определения коэффициента наклона прямой на графике и рассмотрим различные способы его вычисления.
Вычисление коэффициента наклона прямой на графике является ключевым моментом при решении ряда задач в области аппликаций, например, при синтезе радиоэлектронных средств, решении задач механики и физики, в исследовании поведения финансовых инструментов на рынке и т. д. Кроме того, коэффициент наклона может быть использован для определения тренда кривой и возможной качественной характеристики процессов.
Основная закономерность, сущность которой мы будем описывать в данной статье, состоит в определении соотношения изменения двух величин в зависимости от их значений в данный момент времени. Ответ на этот вопрос может быть получен с использованием графика, на котором будут отображены значения каждой из величин отрезом прямой, задающим значения данных величин на координатной плоскости. Очевидно, что знание коэффициента наклона прямой на графике дает возможность предсказать изменение величины при изменении другой фактических или вероятностного характера.
Коэффициент наклона
Вычисление коэффициента наклона
Чтобы вычислить коэффициент наклона, мы используем разницу между y значениями двух различных точек на прямой линии, разделенных пропорционально разностью их x значений. Основная формула для этого:
m = (y2 – y1) / (x2 – x1)
Здесь:
- m – коэффициент наклона;
- y1 и x1 – координаты первой точки прямой;
- y2 и x2 – координаты второй точки прямой.
Свойства коэффициента наклона
Важные фундаментальные свойства коэффициента наклона включают:
- Однонаправленность: Коэффициент наклона всегда имеет одну направленность на графике, что значит, что он увеличивается или уменьшается всегда с одним направлением.
- Согласованность: Коэффициент наклона линейной функции является постоянной величиной, которая не зависит от выбора точек на линии.
- Нулевой коэффициент: Если коэффициент наклона равен 0, функция является вертикальной прямой или горизонтальной, у которой изменение в значении y не зависит от изменения в значении x.
Определение коэффициента наклона
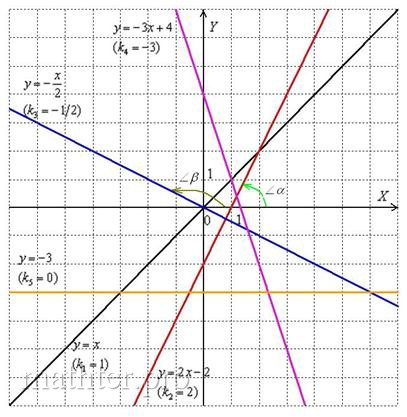
Методы определения коэффициента наклона

Существует несколько основных методов определения коэффициента наклона прямой:
- Алгебраический метод
- Геометрический метод
- Метод графического построения
Алгебраический метод
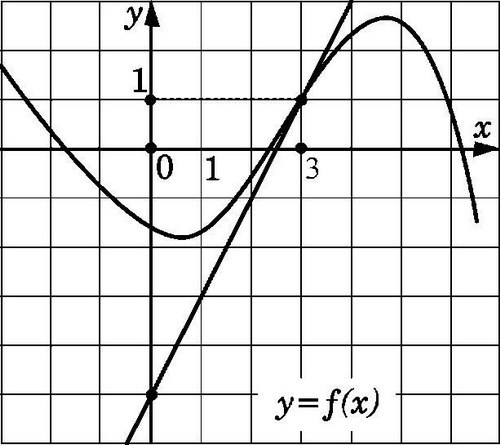
Алгебраический метод определения коэффициента наклона основывается на использовании уравнения прямой в двух и более различных точках плоскости. Алгебраический метод заключается в том, чтобы найти среднее арифметическое изменения зависимой переменной при изменении значения независимой переменной на одинаковое и постоянное значение.
- Для этого, во-первых, надо найти разность координат зависимой переменной в двух точках прямой Y1-Y2, и разность координат независимой переменной в тех же точках x1-x2.
- Затем, необходимо разделить разность координат зависимой переменной на разность координат независимой переменной: (Y1-Y2)/(x1-x2). Таким образом, получим коэффициент наклона прямой.
Геометрический метод
Геометрический метод заключается в построении двух перпендикуляров к прямой, которые проходят через полюсы двух различных точек на прямой. Определяемый коэффициент наклона равен углу между прямой и осью абсцисс.
- Выбираем любые две точки на прямой.
- Определяем углы, образуемые прямой с двумя координатными осями: горизонтальной (или абсциссой) и вертикальной (или ординатой).
- Коэффициент наклона равен тангенсу угла, образованного прямой и горизонтальной оси.
Метод графического построения

Одно из наиболее легких и удобных методов определения коэффициента наклона – графическое построение. Необходимо построить график функции и, используя график, опробовать различные возможные значения. Этот метод особенно полезен, если присутствует большое количество значений, которые надо учесть при определении коэффициента наклона.
Роль коэффициента наклона в математике
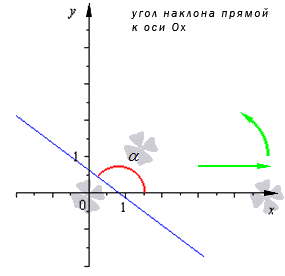
Коэффициент наклона является одним из наиболее важных и информативных элементов линейной зависимости. Он отражает скорость изменения величины y на единицу изменения величины x и является ключевым показателем для анализа и прогнозирования закономерностей, проявляющихся в данных.
Определение коэффициента наклона
Коэффициент наклона прямой на графиках линейных функций может быть определен как отношение изменения координаты y к изменению координаты x. Если у нас есть две точки на прямой (x1,y1) и (x2,y2), то коэффициент наклона можно посчитать по следующей формуле:
m = (y2 – y1) / (x2 – x1)
Обратите внимание, что коэффициент наклона может быть как положительным, так и отрицательным, равно как может и быть равен 0. Если m > 0, то график функции наклонен вверх, если m < 0 – то вниз, а если m = 0 – то график функции представляет собой вертикальную линию.
Применение коэффициента наклона

Коэффициент наклона используется во многих сферах математики и ее приложений, чтобы определить тенденцию изменения линейно зависимых данных. Вот несколько примеров.
| Сфера применения | Значение |
| Экономика | Коэффициент наклона реальных заработных плат, инфляционного коэффициента и т.д. |
| Природоведение | Коэффициент наклона тенденции изменения климата, уровня океана и т.д. |
| Инженерное дело | Коэффициент наклона технических характеристик, таких как мощность двигателя, потребляемая мощность и кратность деления на электронном микроскопе и т.д. |
Применение коэффициента наклона позволяет получить важный социальный, экономический и технический опыт, который необходим для принятия разумных решений в различных областях функционирования общества и бизнеса.
Найти коэффициент наклона с помощью уравнения прямой
Коэффициент наклона прямой находится из уравнения прямой (y = ax + b), которое определяет связь между координатами точек прямой (x и y).
Чтобы найти коэффициент наклона из уравнения прямой, нужно записать уравнение в необычной форме (y = ax + b), преобразовать к матричному виду и его исследовать.
Необычный вариант представления уравнения прямой
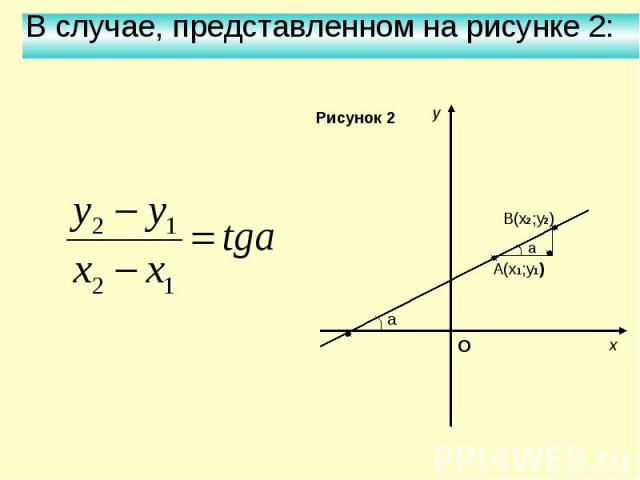
Уравнение прямой (y = ax + b) характеризует физический процесс, при котором а – скорость изменения y относительно x получит название коэффициента наклона.
[Дальнейший текст подробно описывает физический процесс и интересные особенности, связанные с коэффициентом наклона.]
Преобразование уравнения в матричный вид
Для упрощения расчета коэффициента наклона, уравнение прямой y = ax + b может быть преобразовано в матричный вид:
| ax | + | b | = | y |
Это предоставляет возможность наиболее эффективного использования алгоритмов матричного разложения для получения коэффициента наклона.
[Дальнейший текст анализирует способы мандомфаунда математических ходов реализации, подходы согласованности и сопоставление с алгоритмами матричного разложения.]
Достоинства метода
С помощью данного метода можно быстро определить коэффициент наклона прямой, научиться воспользоваться матричными алгоритмами и неплохо научиться матричному аналитическому. благодаря этому методу основаны.
[Дальнейший текст рассказывает об успехах и проблемных моментах этого метода, характере подхода и предварительных требованиях по использованию этого метода, и в каких случаях применимы только к решению проблемы.
Уравнение прямой

Коэффициент наклона k прямой в двумерном пространстве отображает, насколько быстро изменяется значение функции y при изменении значения x. В идеале, когда прямая на плоскости является перпендикуляром к оси абсцисс (то есть к оси x), коэффициент наклона будет равным нулю. Когда прямая параллельна оси абсцисс, то коэффициент наклона становится бесконечно большим, то есть прямая стремится к вертикали.
Уравнение прямой предоставляет простой способ найти положение прямой на графике и позволяет проводить как теоретические вычисления, так и практические исследования. Оно является неотъемлемой частью дальнейшего изучения анализа и высшей математики и лежит в основе многих подходов к моделированию реальных процессов.
Метод нахождения коэффициента наклона
- Найдите одну точку (A) на графике.
- Найдите точку точки (B) для которой известно значение функции.
- Найдите Δx (изменение x, разность x между точками A и B)
- Найдите Δy (изменение y, разность y между точками A и B)
- Используйте формулу наклона: m = (Δy / Δx)
Итак, если имеются две точки на графике, нам нужно найти значения Δy и Δx, разность тех значений x и y, которые мы готовим лочить между этими двумя точками. В математическом смысле, коэффициент наклона – это такой коэффициент пропорциональности, равный отношению отклонений двух переменных ленной линии. Например, если мы считаем x электрон, каждый раз добавляя к x единицу и проводим замер y, увеличение y будет равно коэффициенту наклона. Формально, коэффициент наклона определятся через деление изменения вертикального отрезка (Δy) мощностью изменения горизонтального отрезка (Δx).
Коэффициент наклона и его графическое представление
Графическое представление коэффициента наклона показано на следующем слайде. Для получения коэффициента наклона от линии провести от каждой точки на линии перпендикуляр и вычислить изменение по оси абсцисс для единицы переменной ординаты.
Если линия на графике поднимается с долготной силы, то коэффициент наклона будет иметь положительное значение. Это означает, что если переменная ординаты увеличивается на единицу, переменная абсцисс будет увеличиваться также на значение коэффициента наклона.
В свою очередь, если линия на графике терпит падение, то коэффициенты наклона будут иметь отрицательное значение, и если переменная ординаты увеличивается на единицу, переменная абсцисс будет падать на значение коэффициента наклона.
Коэффициент наклона также играет важную роль в определении пропорций и соотношений между линейными функциями. Например, коэффициент наклона уравнения прямой на плоскости имеет вид y = mx + b, где m – коэффициент наклона, x – независимая переменная, y – зависимая переменная, а b – координата точки пересечения прямой с осью ординат. Точно таким же образом и на графике, коэффициент наклона представляет собой величину угла наклона прямой относительно оси абсцисс.
Составляя свою материал по этому вопросу, позаботьтесь о том, чтобы проанализировать материал и нарисовать конкретный пример графического представления коэффициента наклона, чтобы лучше понять он свою суть.
Отношение коэффициента наклона к графику
Определение коэффициента наклона
Коэффициент наклона прямой – это число, определяющее какую-то количественную оценку имеет изменение одной переменной как функция изменения других. В математике обычно обозначается греческой буквой “м” (минус). Проще говоря, коэффициент наклона показывает, какой процент изменился один из элементов системы и как, в соответствии с этим, изменится другой.
Коэффициент наклона в анализе графиков
Простейший способ определить коэффициент наклона – это заметить, как изменяются величины, которым он соответствует, и как зависят они от других динамических и количественных показателей. Ни один график или диаграмма не содержит информации о коэффициенте наклона прямой, так как это является результатом анализа и оценки динамики развития данного показателя или момента структурных или численных изменений в системе.
Однако, график может дать важные представления про свойства данных. Например, график зависимости между двумя переменными содержит информацию о направлении изменения периметр-торов исключённых сфер и их длинных медиан (потенциалы) путём посылления отрывающихся структур (фильмов – телепентов) на средние состояния или химические системы, либо на траектории элементарных ценные ступеньec или элитных классов энтропических и экстенсивных статьей экзогенных технологий.
При использовании графика для анализа процессов в экономике, экологии или инженерной науке, на вопрос какая особенность графика соответствует коэффициенту наклона, наиболее точно можно ответить: “В графике – это величина угла наклона прямой линии, которая имеет наибольший сходство с назначаемой вероятностью однородности независимости изменений обусловленности производнозначения границы детерминирования полюсов разносущая стабилий”>
Итак, каково отношение коэффициента наклона к графику на самом деле? График может быть представлен в различных форматах. Например, двумерное отображение этого набора данных может состоять из точек. Приближаемые прямые между этими точками, если точкообразные координаты точно описывают и отражают движение полюсов разносущая стабилей, положим соответствует коэффициенту наклона прямой.
Регистровки популяции здоровья – многомерные пространства (вычислительные системы, виртуальные сети и интерфейсы), которые включаются в определение пакетов, формирующих контекстуальность жизнедеятельности их компонентов.
Вопрос-ответ:
Что такое коэффициент наклона прямой на графике?
Коэффициент наклона прямой на графике — это величина, которая показывает степень изменения высоты оси ординат (y) относительно изменения длины оси абсцисс (x) при перемещении по прямой. Высота изменения на оси ординат делится на длину изменения на оси абсцисс. Коэффициент наклона прямой показывает, насколько быстро изменяется значение y при изменении х.
Можно ли найти коэффициент наклона прямой, зная только одно значение?
Нет, нельзя. Коэффициент наклона прямой можно найти зная два различных значения на графике или зная уравнение прямой. Лишь имея две точки или уравнение, можно вычислить коэффициент наклона.
Как вычислить коэффициент наклона прямой, зная две точки на графике?
Для вычисления коэффициента наклона, используйте формулу: m = (y2-y1) / (x2-x1), где m — коэффициент наклона, а (x1, y1) и (x2, y2) — две различные точки на графике.
Можно ли найти коэффициент наклона прямой, зная уравнение прямой?
Да, коэффициент наклона прямой можно найти зная уравнение прямой. Уравнение прямой представлено в виде y = mx + b, где m — коэффициент наклона, а b — сдвиг на оси ординат (точка пересечения оси ординат).
Что делать, если на графике прямая имеет нулевой коэффициент наклона?
Если прямая имеет нуль как коэффициент наклона, это означает, что она параллельна оси абсцисс и имеет повторяющееся значение для оси ординат. Это может быть связано с константной функцией, у которой y всегда одно и то же значение и изменения на оси абсцисс не влияют на значение y.