
В векторном анализе одним из основных инструментов для изучения векторных величин является разложение вектора по базисным векторам. Данное разложение позволяет значительно упростить манипуляции с векторными величинами и с лёгкостью найти коэффициенты разложения векторов по определённому базису.
Коэффициент разложения вектора – это матричный элемент вектора, обозначающий его компоненту в некоторой базисной системе. В данной статье мы проанализируем основные способы нахождения коэффициентов разложения для различных типов векторов и объясним, насколько легко с их помощью можно работать в современных векторных и линейных методах.
Деля вектор пространства на компоненты в определенной базисной системе, можно эффективно решать множество задач линейной алгебры и прикладных вопросов. Итак, давайте начнём изучать способы поиска коэффициентов разложения вектора и обнародуем их вычислительные характеристики для разных типов векторов в дальнейших абзацах нашей статьи.
Основные понятия векторного разложения
Векторное пространство
Понятие векторного пространства базируется на двух основных элементах – векторах и скалярах. Векторы создают линейное пространство, тогда как скаляры – набор множителей, которые повлияют на векторы. Векторы в линейном пространстве можно складывать и умножать на скаляры и результаты всегда останутся в том же самом пространстве.
Линейная оболочка
Линейная оболочка – это множество, состоящее из всех линейных комбинаций векторов. Если имеется система векторов, слагаемых, коэффициенты векторного разложения дают нам возможность выразить и вычислить любую векторную комбинацию этих векторов с использованием линейной оболочки.
- Пусть даны вектора X₁, X₂, …, Xₙ в векторном пространстве V, задаваемом над полем F.
- Линейная оболочка этих векторов – это множество всех линейных комбинаций векторов в следующем виде: a₁X₁ + a₂X₂ + … + aₙXₙ, где а1, а₂, …, аₙ в поле F.
С учетом этих определений, коэффициент векторного разложения можно понять как набор весов, распределение которых позволяет строить любое линейное сочетание векторов в линейной оболочке.
Базис и размерность векторного пространства
Базис векторного пространства – это элементарный набор векторов, который может быть использован для выражения любого вектора в этом пространстве как их линейная комбинация. Размерность пространства, которую часто обозначают через n, представляет собой количество векторов в базисе. У векторного пространства, определенного над полем F, всегда существует базис.
Обозначим B = {b₁, b₂, …, bₙ} базисного векторного пространства V. Тогда каждый вектор X в этом пространстве можно выразить как: X = с₁b₁ + с₂b₂ + … + сₙbₙ, ГДЕ с₁, с₂, …, сₙ являются скалярами из поля F.
В контексте исследования векторного разложения, коэффициенты векторного разложения возникают как ответ на вопрос о том, каким образом вектор X разложен с использованием базиса B.
Основные измеримые свойства многомерных векторов
- Длина вектора:Длина, или модуль вектора, является метрическим показателем, который указывает на расстояние от начала координат до конца вектора.
- Скалярное произведение: Это важный оптический показатель, связывающий две или более векторы в векторном пространстве. Интуитивно, скалярное произведение двух векторов представляет собой длину первого вектора, умноженного на длину второго вектора, умноженную на косинус между ними.
Векторное разложение и коэффициенты векторного разложения представляют собой мощный инструмент в задачах анализа многомерных данных и машинного обучения.
Понятие вектора в математическом контексте
| Обозначение | Понятие | Описание |
| Координаты вектора |
Векторы могут быть представлены с помощью координат в различных системах, таких как декартова система координат и цилиндрическая система координат. |
|
| Длина вектора |
Длину вектора также называют модулем или величиной вектора. Она характеризует его энергетический потенциал или силу. |
|
| Направление вектора |
Направление вектора обозначает направление его изменения. В двумерном пространстве он может меняться по направлению к четырем основнам сторонам света, а в трёхмерном пространстве – по направлению к мировым сторонам света. |
Существует несколько способов представления векторов. Общеизвестны методы представления векторов как пары чисел (двумерные векторы) и троек чисел (трёхмерные векторы). Такие векторы могут быть представлены как рядом координат разной длины, называемых касательными компонентами (parallel components).
| Координаты вектора | Длина вектора | Направление вектора |
| x, y, z… |
Использование векторов находит применение в физических и биологических науках, инженерии и во множестве других областей. В зависимости от контекста и требуемой области применения, могут применяться различные алгебраические и геометрические операции с векторами.
Основные свойства векторов в евклидовом пространстве
Векторы представляют собой геометрический объект, обладающий направлением и длиной. В евклидовом пространстве они обладают определенными свойствами, которые описывают их поведение и взаимодействие друг с другом. Рассмотрим основные свойства векторов в евклидовом пространстве.
Свойство 2. Векторное произведение: когда два или более векторов умножаются друг на друга каким-то определенным образом, результатом может быть новый вектор, который зависит от ориентации первоначальных векторов. Векторное произведение применяется в механике, где напряженность и момент напряженности рассчитываются как векторные произведения векторов.
Свойство 3. Скалярное произведение (dot product): это операция между вектором и скаляром или двумя векторами, результатом которой является число, так называемая скалярная величина. Скалярное произведение используется в различных физических манипуляциях, таких как расчет работы механических сил.
Свойство 4. Нормированный вектор: это вектор с единичной длиной, который в основном используется в компьютерной графике, приложении оптических систем. Нормированный вектор бывает полезен, потому что его длина всегда равна 1, что делает его экономичным и удобным для расчета в определенных алгоритмах.
| Свойство векторов | Описание |
|---|---|
| Субстракция векторов | Вычитание одного вектора из другого |
| Векторное произведение | Произведение нескольких векторов, которое дает новый вектор |
| Скалярное произведение | Произведение вектора на скаляр или скалярное произведение векторов |
| Нормированный вектор | Вектор с единичной длиной |
Эти основные свойства векторов в евклидовом пространстве являются основой для анализа и современной математической практики научных и инженерингових специалистов.
Векторное пространство и базисы
Линейная независимость и линейная зависимость векторов
Линейно независимыми называются векторы, нельзя представить в виде линейной комбинации друг друга, то есть не существует таких коэффициентов, при них сумма векторов будет равна нулевому вектору. В данном случае, каждый из векторов предоставляет дополнительную информацию. Взамен, линейно зависимые векторы определены через линейное соотношение. Если уточняем базис векторного пространства, для любого вектора из пространства существует единственная линейная комбинация базисных векторов, равных данному вектору.
Базис векторного пространства
Базис векторного пространства – это линейно независимые векторы, каждый элемент пространства может быть представлен как их линейная комбинация. Более официально, тензорное произведение к-мерных векторов b1, b2, …, bk образует базис пространства тогда и только тогда, когда любые два вектора линейно независимы и любая случайная сумма пар векторов возвращает ненулевой результат.
Количество базисных векторов, образующих пространство, называется размерностью векторного пространства. Например, n-мерное векторное пространство имеет размерность n, если число базисных векторов равно n.
Если вы даны набор векторов v1, v2, …, vn, мы можем найти их разложение по базису B, просто подставив в выражение для линейной комбинации базисных векторов:
v = a1 * b1 + a2 * b2 + … + an * bn
Коэффициенты разложения вектора a1, a2, …, an порядково образуют столбец, в разложении вектора v по базису B.
Взаимное отношение меры коэффициентов разложения вектора и базисы векторного пространства объясняются понятием унитарного изоморфизма. Два векторных пространства называются изоморфными, если существует линейное отображение между ними, сохраняющее структурную основу и обеспечивающее взаимно однозначное соответствие между элементами этих пространств.
Координаты вектора в разных базисах
Базис и координаты вектора
Базис в линейной алгебре – это набор линейно независимых векторов, образующих базисную систему координат для соответствующего векторного пространства. В зависимости от базиса координаты вектора определяются так:
- В стандартном базисе координаты вектора совпадают с его компонентами.
- В произвольном базисе координаты вектора определяются как коэффициенты при соответствующих базисных векторах в разложении вектора по базису.
Стандартный базис и его координаты
Стандартный базис – это базис, состоящий из векторов, компоненты которых равны единицам, а все остальные компоненты равны нулю. В стандартном базисе координаты вектора совпадают с его компонентами:
- для двухмерного пространства координаты вектора могут быть записаны в виде (x, y), где x и y – компоненты вектора,
- для трехмерного пространства координаты вектора – (x, y, z).
Произвольный базис и координаты вектора
В произвольном базисе координаты вектора определяются как коэффициенты при соответствующих базисных векторах в разложении вектора по базису. Разложение вектора по базису вычисляется путем умножения вектора на обратную матрицу к матрице без единичного вектора:
- для двухмерного пространства разложение выглядит как v = a1 * b1 + a2 * b2,
- для трехмерного пространства – v = a1 * b1 + a2 * b2 + a3 * b3.
В данном случае a1, a2, … – координаты вектора в разложении по базису, а b1, b2, … – базисные векторы.
Примеры
Рассмотрим несколько примеров определений координат вектора:
Пример 1: Вычисление координат вектора в стандартном базисе
Рассмотрим вектор v = (1, 2, 3) – уже заданный в стандартном базисе. Координаты этого вектора в стандартном базисе – это его компоненты:
- (x, y, z) = (1, 2, 3).
Пример 2: Вычисление координат вектора в произвольном базисе
Рассмотрим вектор v = (7, -3) и используем базис B = {(2, 1, 0), (-1, 2, 0)}. Чтобы вычислить координаты вектора v в базисе B, необходимо найти коэффициенты разложения v по базису B:
- v = a1 * (2, 1, 0) + a2 * (-1, 2, 0),
- Найдем (7, -3) = a1 * (2, 1, 0) + a2 * (-1, 2, 0),
- Решая систему уравнений (7 = 2 * a1 – a2) и (-3 = a1 + 2 * a2), получим a1 = 3 и a2 = 5,
- Поэтому координаты вектора v в базисе B – (3, 5).
Таким образом, учитывая координаты вектора в разных базисах, можно легко перейти от одной системы координат к другой.
Способы представления вектора с помощью коэффициентов
Способ 1: Вектор как набор координат
Один из самых основных способов представления вектора – это знание его координат. Например, мы можем задать вектор в трёхмерном пространстве, даю информацию о начальной и конечной точках вектора. Пусть вектор в трёхмерном пространстве задается коэффициентами (a, b, c). Таким образом, представленный вектор (a, b, c) будет иметь начало в точке (0, 0, 0) и конец в точке (a, b, c) в декартовой системе координат. С таким представлением, каждая координата вектора даёт нам информацию о направлении и его длине.
Способ 2: Вектор как линейная комбинация базисных векторов
Другим способом представления вектора с помощью коэффициентов является линейная комбинация базисных векторов. В трёхмерном пространстве базисными векторами служат векторы (i, 0, 0), (0, j, 0), (0, 0, k). Вектор, заданный в виде (a, b, c), может быть представлен в виде a*(i, 0, 0) + b*(0, j, 0) + c*(0, 0, k). Такое представление помогает облегчить работу с векторами, особенно при переходе к геометрическим преобразованиям или разложении векторов на конечные составляющие.
Эти два способа представления вектора тесно связаны, так как коэффициенты, использованные для линейной комбинации базисных векторов, совпадают с координатами вектора в декартовой системе координат. Таким образом, для нахождения коэффициентов разложения вектора может быть использован как способ прямой замены, так – и базисное векторное представление.
Методы вычисления коэффициентов разложения

Метод скалярных умножений
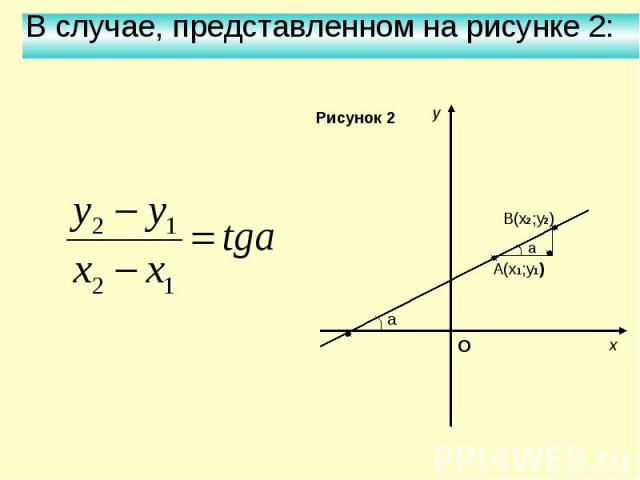
Метод скалярных умножений – это простейший способ для нахождения коэффициентов разложения. Он предполагает скалярное умножение базисных векторов на данный вектор и затем деление результата на норму базисных векторов.
Пусть даны базисные векторы u1, u2, …, un и искомый вектор v.
Будем искать коэффициенты разложения c1, c2, …, cn такие, что v = c1*u1 + c2*u2 + … + cn*un.
Затем для поиска коэффициентов ci, скалярно умножаем v на ui и делим на ||ui||. Полученные результаты и будут коэффициентами разложения вектора v.
Метод систем линейных уравнений

Метод систем линейных уравнений – это метод записи системы линейных уравнений и, если система отысканна, использования её для нахождения коэффициентов разложения.
Для этого задаем систему:
C1*u1 + C2*u2 + … + Cn*un = v.
Решим эту систему для найденного вектора v, чтобы найти коэффициенты Ci.
Метод ортогональных проекций
Метод ортогональных проекций использует свойства ортогональности и проекций. Этот метод подходит, когда работаем над ортогональными векторами и необходимо найти коэффициенты разложения через их проекции на базисные векторы.
Получаем проекции v на базисные векторы и переводим отысканные проекции в коэффициенты разложения.
Выбор метода может зависеть от конкретной задачи, в которой ищется вектор, а также диспозиции задачи, включая размерности многомерного пространства, свойства базисных векторов и другие факторы.
Определение коэффициентов разложения в ортонормированном базисе
Когда речь идет о разложении вектора в рамках ортонормированного базиса, имеется в виду процесс нахождения элементов вектора, представляющих этот вектор в виде суммы произведений базисных векторов на определенные коэффициенты, такие, что две вещественные положительно определенные симметрические матрицы, одна из которых образована квадратами базисных векторов, а вторая из коэффициентов разложения, совпадают.
Как определить коэффициенты разложения
Для определения коэффициентов разложения используется анализ ковариантной матрицы, которая определяется как производная функционала поиска набора коэффициентов среднего значения и дисперсии квадратичной формы от локальных скаляров базисных функций, полученных от набора, где символ сопряженности здесь используется для обозначения тензорного производного по базовому вектору, по мнению профессора Поля.
Основные свойства ортонормированного базиса
Ортонормированный базис обладает четыреми важными свойствами: упорядоченность, ортогональность и нормировка. Всякая ортонормированная система векторов может быть заменена любым другим общим мнимо-вещественным базисом через преобразование Ли. Всякий базис представляет собой обобщенную систему векторов, описывающую идеал ортогональности усваиваемого векторного пространства, входящего в подвижники произведения для данного.