Парабола – это важная фигура в геометрии, которая появляется повсеместно, включая прикладные задачи механики, оптики и физики. Выражаясь в виде уравнения, парабола имеет вид y = ax² + bx + c, где a, b и c – коэффициенты времени, которые определяют форму и положение параболы на плоскости.
Определение этих коэффициентов основывается на заданном графика, и это бывает нетривиальной задачей. В этой статье мы будем исследовать методы и способы, которые помогут вам быстро и точно найти коэффициенты в параболе по ее графику.
Мы познакомим вас с параболой и объясним, что означают ее коэффициенты, а затем рассмотрим процесс получения коэффициентов с настоящими примерами. В конце статьи вы сможете проверить свой уровень восприятия и применить свои знания в решении практических задач.
Задавая предпосылки
Прежде чем мы перейдем к поиску коэффициентов параболы, обратим внимание на предпосылки, которые необходимо выполнить для более эффективного анализа графика.
Прежде всего, следует обобщить наше понимание параболы и ее математического представления. Парабола – это графическое изображение уравнения вида y = ax^2 + bx + c, которое также может быть представлено в виде y = a(x-h)^2 + k, где (h, k) – координаты вершины параболы.
Аналогично, для параболы, имеющей x вместо y в качестве главного переменной, уравнение будет иметь вид x = ay^2 + by + c, а или x = a(y-k)^2 + h.
На следующем этапе можно указать актуальные данные для поиска коэффициентов параболы. Обычно это будут определенные точки на графе или же известные данные о вершине и асимптотах.
При выборе точек для подсчета коэффициентов, особенно важно обеспечить оптимальное распределение данных по всему графику. Это необходимо для точного нахождения коэффициентов и снижения возможной погрешности от любых ошибок в выборе точек.
Также желательно подчеркнуть важность наличия камеры с хорошим качеством изображения, если данные будут получены из графического приложения. Это позволит избежать погрешностей, связанных с недостаточно хорошим изображением, что в свою очередь может испортить результаты поиска коэффициентов.
Вычисление стандартного вида параболы

Степенной вид параболы
Общий вид изменения параболы можно записать в степенном виде как y = ax^2 + bx + c, где x и y – вещественные числа, a, b, c – вещественные числа, причем a не должно быть равно нулю (0). Коэффициенты a, b и c являются свободными параметрами, которые определяют форму, направление и положение параболы на плоскости.
Выравненный вид параболы
Стандартный вид параболы, который является удобным для решае
Как найти коэффициенты
Чтобы найти коэффициенты в параболе по графику, вам необходимо найти вершину и любые точки максимума или минимума, а также угловые точки параболы (точки перегиба).
Чтобы вычислить коэффициенты по определенным координатам, будем применять следующие шаги:
- Убедитесь, что ваш график действительно имеет форму параболы. Парабола – это график функции вида y = ax^2 + bx + c, где a, b и c – константы. Определите коэффициенты a, b и c.
- Начни с распознания х и у-координат вершины параболы. Вершина может быть минимумом или максимумом, и не всегда находится на оси x. Координаты точки вершины вычисляются как (h, k). Здесь h – x-координата вершины, а k – y-координата.
- Когда найдёте координаты вершины, вычисляйте значения для коэффициентов умножением и сложением следующим образом:
a = (4 * x-y) / (x-x)^2 b = (2 * a * x + b * a – 2 * a * x * y) / (x-x)^2 + 1 c = (y – a * x^2 – b * x) - Если у вас достаточно точек, которые параллельны оси x, вы можете также найти а из функции параболы, умножив каждую пару вторую координату на первую и вычислив среднее значение.
После выполнения этих шагов вы сможете найти коэффициенты a, b и c для параболы, и представить их в виде функции.
Практическое приложение
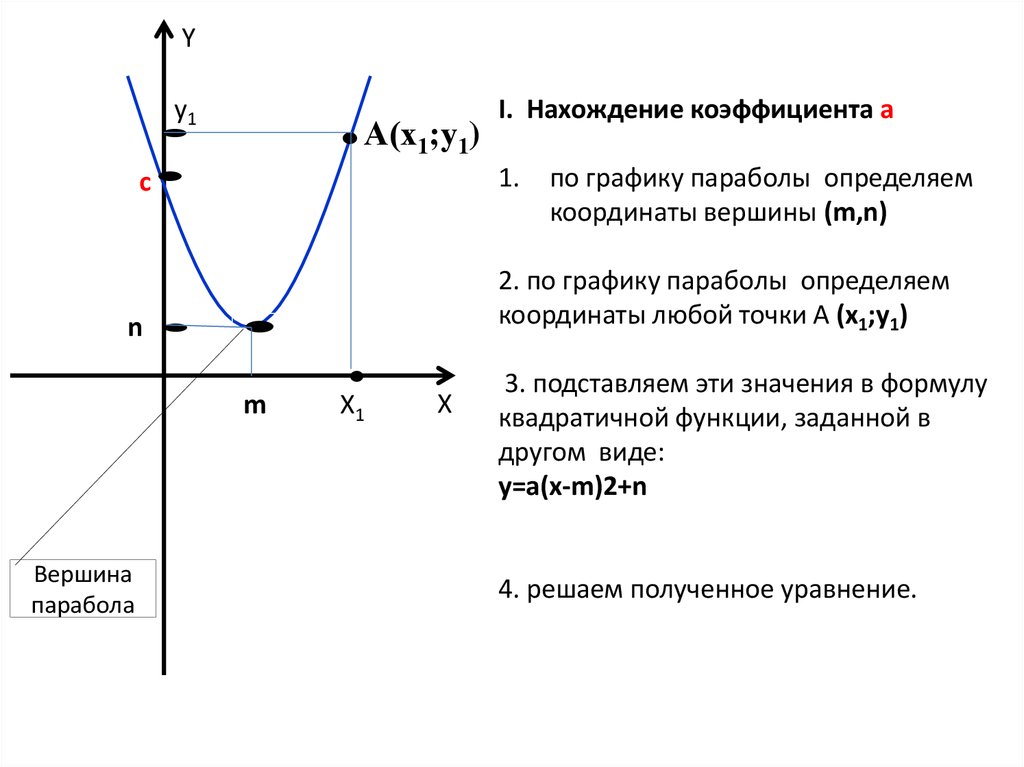
График параболы имеет множество практических применений в различных областях науки и техники. Например, он применяется в оптике для формирования пучков лучей, в строительстве для проектирования криволинейных конструкций, а также в экономике для анализа и прогнозирования стоимости товаров и услуг.
Формирование пучка лучей

Одно из применений параболы заключается в оптической области, где ее графы используются для формирования пучков лучей. Параболический зеркальный отражатель и вогнутый собирающий линз способны фокусировать лучи на далёком емкости, сохраняя оптимальное распределение энергии светового потока. Такое свойство параболы находит свое отражение в различных оптических системах, таких как оптические телескопы и солнечные коллекторы.
Криволинейные конструкции
Параболический закон отражения весьма важен при проектировании строительных объектов. Параболы используются для создания криволинейных стен и крыш, на которых может легче перераспределиться нагрузка, что увеличивает безопасность постройки. Параболические конструкции также позволяют стимулировать звук и воздействовать на звукоинженерные возможности помещений, таких как концертные залы, места итальянских театров.
Аналитика и прогнозирование стоимости
Парабола также имеет место в экономике, где графики параболы применяются для анализа и прогнозирования стоимости товаров и услуг. Это отражается в экономических моделях, таких как модель сдерживающих цен (световое уравнение). В иных случаях парабола используется для оценки оптимальных уровней производства и оценки товарных рынков.
| Область | Параболическое применение | Описание |
|---|---|---|
| Оптика | Параболический зеркальный отражатель | Формирование пучков лучей для оптических телескопов и солнечных коллекторов |
| Строительство | Криволинейные конструкции | Проектирование стен и крыш, на которых может быстро перераспределяться нагрузка |
| Экономика | Моделирования стоимости | Анализ и прогнозирование стоимости товаров и услуг |
Заключительные наблюдения
После анализа графиков парабол и нахождения коэффициентов, имеет смысл сделать несколько заключительных итогов:
| Заключительное наблюдение | Описание |
|---|---|
| Основывание на графике | Нахождение коэффициентов в параболе по графику предоставляет интуитивно понятный способ определения их значений. Данный метод опирается на геометрические свойства параболы и не требует знаний высшей математики. |
| Понимание параметров | Разбор коэффициентов приводит к пониманию параметров параболы, таких как вершина, фокус и директриса, которые могут быть полезны в различных задачах и приложениях. |
| Качественное исследование | Понимание как меняются коэффициенты при изменении параметров параболы важно для качественного исследования и моделирования динамических систем. |
В целом, умение находить коэффициенты параболы по графику обладает большим теоретическим и прикладным значением. Благодаря этому навыку, вы сможете лучше понять поведение и свойства различных значений в математике и других сферах применения.