Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.

На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Остановимся подробнее на свойствах функций.
Нули функции
Определение
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

На рисунке он пересекает ось х при х=-1; х=4; х=6. Эти точки пересечения выделены красным цветом.
Внимание!
Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.
График функции у=k/x выглядит следующим образом:
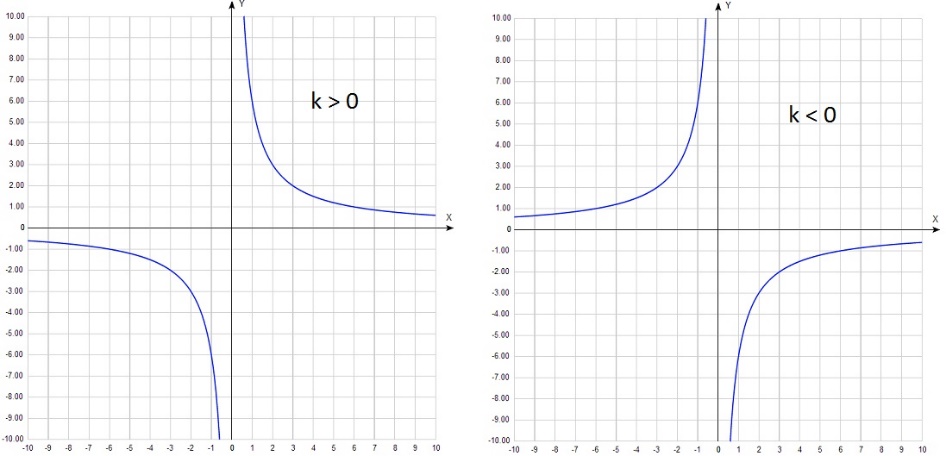
По данному рисунку видно, что нулей функции не существует.
Как найти нули функции?
- Для того чтобы найти нули функции, которая задана формулой, надо подставить вместо у число нуль и решить полученное уравнение.
- Если график функции дан на рисунке, то ищем точки пересечения графика с осью х.
Рассмотрим примеры нахождения нулей функции.
Пример №1. Найти нули функции (если они существуют):
а) у= –11х +22
б) у= (х + 76)(х – 95)
в) у= – 46/х
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
Находим х, разделив 22 на 11: х=22:11
Получим х=2.
Таким образом, мы нашли нуль функции: х=2
б) Аналогично во втором случае. Подставляем вместо у число 0 и решаем уравнение вида 0=(х + 76)(х – 95). Вспомним, что произведение двух множителей равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0. Таким образом, так как у нас два множителя, составляем два уравнения: х + 76 = 0 и х – 95 = 0. Решаем каждое, перенося числа 76 и -95 в правую часть, меняя знаки на противоположные. Получаем х = – 76 и х = 95. Значит, нули функции это числа (-76) и 95.
в) в третьем случае: если вместо у подставить 0, то получится 0 = – 46/х, где для нахождения значения х нужно будет -46 разделить на нуль, что сделать невозможно. Значит, нулей функции в этом случае нет.
Пример №2. Найти нули функции у=f(x) по заданному графику.

Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Определение
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.

Рассмотрим по нашему рисунку, на какие промежутки разбивается область определения данной функции [-3; 7] ее нулями. По графику видно, что это 4 промежутка: [-3; -1), (-1;4), (4; 6) и (6; 7]. Помним, что значения из области определения смотрим по оси х.
На рисунке синим цветом выделены части графика в промежутках [-3; -1) и (4; 6), которые расположены ниже оси х. Зеленым цветом выделены части графика в промежутках (-1;4) и (6; 7], которые расположены выше оси х.
Значит, что в промежутках [-3; -1) и (4; 6) функция принимает отрицательные значения, а в промежутках (-1;4) и (6; 7] она принимает положительные значения. Это и есть промежутки знакопостоянства.
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).

Функция принимает положительные значения в промежутках [-2; -1) и (3; 8). Обратите внимание, что эти части на рисунке выделены зеленым цветом.
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.

На графике видно, что с увеличением значения х от -3 до 2 значения у тоже увеличиваются. Также с увеличением значения х от 5 до 7 значения у опять увеличиваются. Проще говоря, слева направо график идет вверх (синие линии). То есть в промежутках [-3; 2] и [5; 7] функция у=f(x) является возрастающей.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Определение
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Даниил Романович | Просмотров: 15.9k
Что значит положительное и отрицательное значение функции? Объясните пожалуйста
Ученик
(39),
закрыт
8 лет назад
Naumenko
Высший разум
(856085)
8 лет назад
в таблице приведены изображения графиков нескольких функций.
значения у зависят от значений х и в зависимости от формулы. вычислений могут принимать значения
больше нуля- расположены НАД осью х – положительные. и ПОД осью х- отрицательные.
одни не хуже и не лучше других – положительные + и отрицательные – это ориентиры на координатной плоскости всего-навсего.
В предыдущем уроке мы подробно разобрали,
как построить параболу.
В этом уроке мы разберем, как решать типовые задачи на квадратичную функцию.
Как найти нули квадратичной функции
Запомните!
![]()
Чтобы найти координаты точек нулей функции, нужно
в исходную функцию подставить вместо «y» число
ноль.
Рассмотрим задачу.
Найти нули квадратичной
функции «y = x2 − 3».
Подставим в исходную функцию вместо «y» ноль и решим полученное
квадратное уравнение.
0 = x2 − 3
x2 − 3 = 0
x1;2 =
| 0 ± √02 − 4 · 1 · (−3) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
x1;2 = ±√3
Ответ: нули функции «y = x2 − 3» :
x1 = √3;
x2 = −√3 .
Как найти при каких значениях
«x» квадратичная функция принимает заданное
числовое значение
Запомните!
![]()
Чтобы найти при каких значениях «x» квадратичная функция принимает заданное числовое значение,
нужно:
- вместо «y» подставить в функцию заданное числовое значение;
- решить полученное квадратное уравнение относительно «x».
Рассмотрим задачу.
При каких значениях «x» функция
«y = x2 − x − 3» принимает значение
«−3».
Подставим в исходную функцию
«y = x2 − x − 3» вместо «y = −3» и
найдем «x».
y = x2 − x − 3
−3 = x2 − x − 3
x2 − x − 3 = −3
x2 − x − 3 + 3 = 0
x2 − x = 0
x1;2 =
| 1 ± √12 − 4 · 1 · 0 |
| 2 · 1 |
x1;2 =
x1;2 =
| x1 = | x2 = |
| x1 = | x2 = |
| x1 = 1 | x2 = 0 |
Ответ: при «x = 0» и
«x = 1» функция «y = x2 − x − 3»
принимает значение «y = −3».
Как найти координаты точек пересечения параболы и прямой
Запомните!
![]()
Чтобы найти точки пересечения параболы с прямой нужно:
- приравнять правые части функций (те части функций, в которых содержатся «x»);
- решить полученное уравнение относительно «x»;
- подставить полученные числовые значения «x»
в любую из функций и найти координаты точек по оси «Оy».
Рассмотрим задачу.
Найти координаты точек пересечения параболы «y = x2»
и прямой «y = 3 − 2x».
Приравняем правые части функций и решим
полученное уравнение относительно «x».
x2 = 3 − 2x
x2 − 3 + 2x = 0
x2 + 2x − 3 = 0
x1;2 =
| −2 ± √22 − 4 · 1 · (−3) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
| x1 = | x2 = |
| x1 = | x2 = |
| x1 = 1 | x2 = −3 |
Теперь подставим в любую из заданных функций (например, в
«y = 3 − 2x») полученные
числовые значения «x», чтобы найти координаты
«y» точек пересечения.
1) x = −3
y = 3 − 2x
y(−3) = 3 − 2 · (−3) = 3 − (−6) = 3 + 6 = 9
(·) A (−3; 9) — первая точка пересечения.
2) x = 1
y = 3 − 2x
y(1) = 3 − 2 · 1 = 3 − 2 = 1
(·) B (1; 1) — вторая точка пересечения.
Запишем полученные точки пересечения с их координатами в ответ.
Ответ: точки пересечения параболы
«y = x2»
и прямой «y = 3 − 2x»:
(·) A (−3; 9) и
(·) B (1; 1).
Как определить, принадлежит ли точка графику функции параболы
Запомните!
![]()
Чтобы проверить принадлежность точки параболе нет необходимости строить график функции.
Достаточно подставить координаты точки в формулу функции (координату по оси
«Ox» вместо
«x», а координату по оси
«Oy» вместо «y») и выполнить арифметические расчеты.
- Если получится верное равенство, значит, точка принадлежит графику функции.
- Если получится неверное равенство, значит, точка
не принадлежит графику функции.
Рассмотрим задачу:
Не строя графика функции «y = x2», определить, какие точки принадлежат ему:
(·) А(2; 6),
(·) B(−1; 1).
Подставим в функцию
«y = x2»
координаты точки (·) А(2; 6).
y = x2
6 = 22
6 = 4
(неверно)
Значит, точка (·) А(2; 6)
не принадлежит графику функции
«y = x2».
Подставим в функцию
«y = x2»
координаты точки (·) B(−1; 1).
y = x2
1 = (−)12
1 = 1
(верно)
Значит, точка (·) B(−1; 1)
принадлежит графику функции
«y = x2».
Как найти точки пересечения параболы с осями координат
Рассмотрим задачу
Найти координаты точек пересечения параболы
«y = x2 −3x + 2» с осями координат.
Сначала определим точки пересечения функции с осью «Ox».
На графике функции эти точки выглядят так:
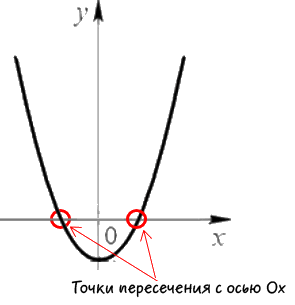
Как видно на рисунке выше, координата «y» точек пересечения с осью «Ox»
равна нулю, поэтому подставим «y = 0» в
исходную функцию «y = x2 −3x + 2»
и найдем их координаты по оси «Ox».
0 = x2 −3x + 2
x2 −3x + 2 = 0
x1;2 =
| 3 ± √32 − 4 · 1 · 2 |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
| x1 = | x2 = |
| x1 = | x2 = |
| x1 = 2 | x2 = 1 |
Запишем координаты точек пересечения графика с осью «Ox»:
(·) A (2; 0) и
(·) B (1; 0).
Теперь найдем координаты точки пересечения с осью «Oy».
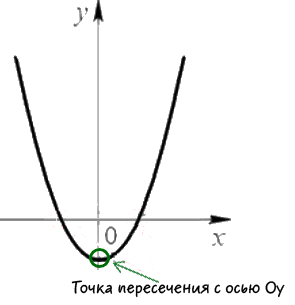
Как видно на рисунке выше, координата «x»
точки пересечения с осью «Oy» равна нулю.
Подставим «x = 0»
в исходную функцию
«y = x2 −3x + 2»
и найдем координату точки по оси
«Oy».
y(0) = 02 − 3 · 0 + 2 = 2
Выпишем координаты полученной точки: (·) C (0; 2)
Запишем в ответ все координаты точек пересечения параболы с осями.
Ответ: точки пересечения с осью «Ox»:
(·) A (2; 0) и
(·) B (1; 0).
С осью «Oy»: (·)C (0; 2).
Как определить при каких значениях x функция принимает
положительные или
отрицательные значения
Напоминаем, что когда в задании говорится «функция принимает
значения» — речь идет о
значениях«y».
Другими словами, необходимо ответить на вопрос: при каких значениях
«x», координата
«y» положительна или отрицательна.
Запомните!
![]()
Чтобы по графику функции определить, где функция принимает положительные или отрицательные значения нужно:
- провести прямые через точки в местах, где график пересекает ось «Ox»;
- определить положительные или отрицательные значения принимает функция на промежутках между проведенными прямыми;
- записать ответ для каждого промежутка относительно «x».
Рассмотрим задачу.
С помощью графика квадратичной функции, изображенного на рисунке, ответить:
При каких значениях «x» функция принимает 1) положительные значения; 2) отрицательные значения.
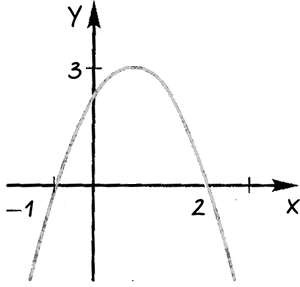
Проведем через точки, где график функции пересекает ось «Ox» прямые.
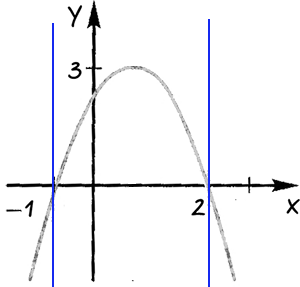
Определим области, где функция принимает отрицательные или положительные значения.
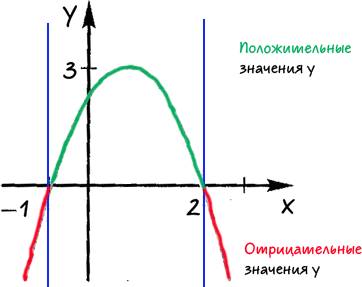
Подпишем над каждой полученной областью, какие значения принимает
«x» в каждой из выделенных областей.
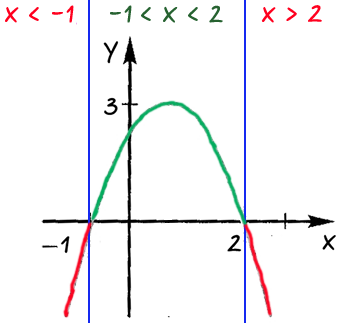
Ответ: при «x < −1» и
«x > 2» функция принимает отрицательные значения;
при «−1 < x < 2» функция принимает
положительные значения.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
На
прошлом уроке мы с вами изучили понятие функция. Изучили её график и научились
находить область определения и область значений функции.
Свойства
функций:
·
нули
функции;
·
промежутки
знакопостоянства функции;
·
промежутки
монотонности функции.
Нули
функции
Определение:
Нулями
функции называют такие значения аргумента, при которых
функция равна нулю.
В
данном случае функция задана графически и мы
определили нули функции по графику. Так же нули функции можно находить по
формуле, с помощью которой задана функция.
Решив
уравнение, мы найдём те значения х, при которых функция равна нулю.
Стоит
обратить внимание на то, что не каждая функция имеет нули.
График
не пересекает ось икс ни в одной точке.
Промежутки
знакопостоянства функции
Определение:
Промежутки
знакопостоянства функции
– это такие промежутки из области определения, на которых данная функция
принимает значения только одного знака, либо положительные, либо отрицательные.
Функция
принимает положительные значения:
И
отрицательные значения:
Запишите
промежутки знакопостоянства функции:
Положительные
и отрицательные значения функции:
Промежутки
монотонности функции
Определение:
Функция
называется возрастающей в некотором промежутке, если большему значению
аргумента из этого промежутка соответствует большее значение функции.
Определение:
Функция
называется убывающей в некотором промежутке, если большему значению
аргумента из этого промежутка соответствует меньшее значение функции.
Определение:
Промежутками
монотонности называют такие промежутки из области
определения, на которых функция либо возрастает, либо убывает.
Опишем
свойства функции:
Графиком
является прямая, поэтому для построения достаточно
двух точек:
Найдём
значения функции:
Областью
определения и областью значений будет множество всех действительных чисел. Ведь
х и у могут быть любыми числами.
Найдём
нули функции:
Запишем
промежутки знакопостоянства:
Запишем
промежутки монотонности:
На этой странице вы узнаете
- Где проходит граница между теплом и холодом?
- Почему успех фильма не всегда зависит от наличия экшн-сцен?
- Чем кофе похож на функцию, ее первообразную и производную?
Многие из нас чем-то похожи на родителей. Не являясь их точной копией, мы перенимаем определенные черты. То же самое происходит и с графиками. О том, какие особенности “наследуют” друг у друга графики функции, производной и первообразной, поговорим в статье.
Связь графика функции и производной
Подготовим карандаши и линейки, мы начинаем погружение в мир графиков. Почему графики — это круто? Они дают нам наглядное представление о функции. Мы можем проанализировать ее, не прибегая к сложным формулам и трудоемким вычислениям.
Воспринимать визуальную информацию всегда легче. А графики — это как раз визуальное описание функции.
Возьмем график произвольной функции.
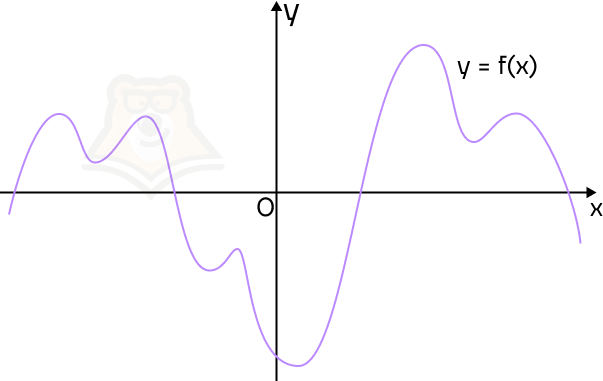
Прежде чем приступать к дальнейшему изучению материала, рекомендуем ознакомиться с «Определением и графиком функции», а также «Производной».
Мы точно видим, на каких промежутках график будет возрастать, а на каких убывать. Если представить, что мы пойдем по направлению оси х, то график будет возрастать на подъемах в горку и убывать на спусках с нее. Отметим промежутки возрастания зеленым фоном, а промежутки убывания красным.
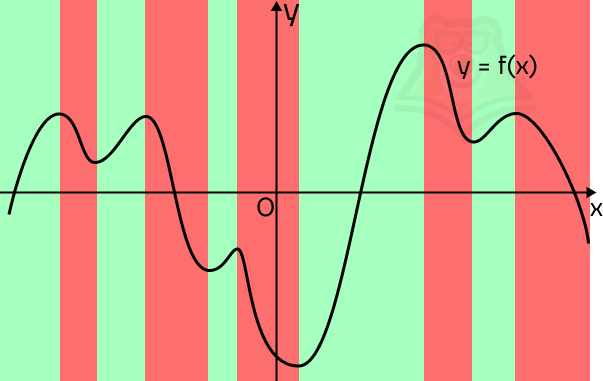
В зеленых промежутках производная будет положительна, а в красных отрицательна. Пока что просто запомним этот факт.
Обратим внимание на границы между зелеными и красными зонами. В этих точках функция будет менять свой знак с положительного на отрицательный или обратно. Такие точки называются точками экстремума.
Экстремум — это точка, в которой достигается максимальное или минимальное значение функции на заданном отрезке.
Точки экстремума — точки, в которых достигается экстремум.
В точках экстремума производная равна 0.
Теперь попробуем построить примерный график производной. Для начала опустим точки экстремума. Где они будут лежать на графике производной? На оси х.
Вспомним, что в точках экстремума производная функции будет равна 0. Пусть график будет задан
y = f'(x), тогда в точках экстремума получаем y = 0. Это и есть ось х.
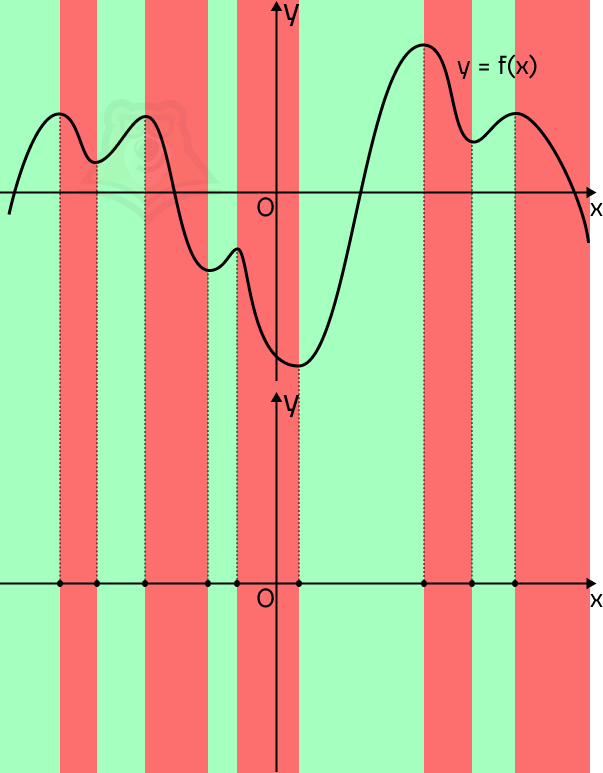
Так мы получили целых 9 точек, через которые пройдет производная. Осталось провести через них примерный график.
Вспомним, что:
- производная положительна на промежутках возрастания функции;
- производная отрицательна на промежутках убывания функции.
Как понять, что все точки на графике производной будут положительны или отрицательны? Достаточно посмотреть на то, с какой стороны от оси х они располагаются.
Положительные значения всегда будут лежать выше оси х. Это связано со значением y: значения функции будут положительны при положительных значениях у, и отрицательны при отрицательных значениях у.
Можно представить, что ось х — это полюс, который разделяет тропики и льды. Над осью х всегда будет светить солнце, а температура будет положительной. А вот под осью х всегда будут льды и снега, и температура — отрицательной.
Следовательно, знак производной на ее графике будет совпадать со знаком температуры в тропиках или льдах.
Итак, как нам нарисовать график производной? На зеленых участках ее график будет лежать над осью х, а на красных участках — под ней.
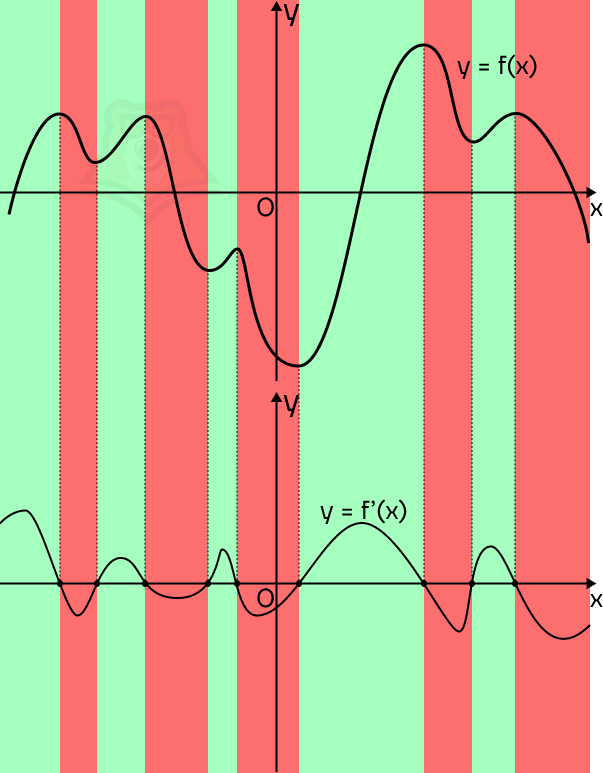
Подведем итоги:
- В точках экстремума функции график производной будет проходить через ось х.
- На промежутках возрастания функции график производной будет лежать выше оси х.
- На промежутках убывания функции график производной будет лежать ниже оси х.
Эти зависимости можно отследить на любых графиках функции и ее производной.
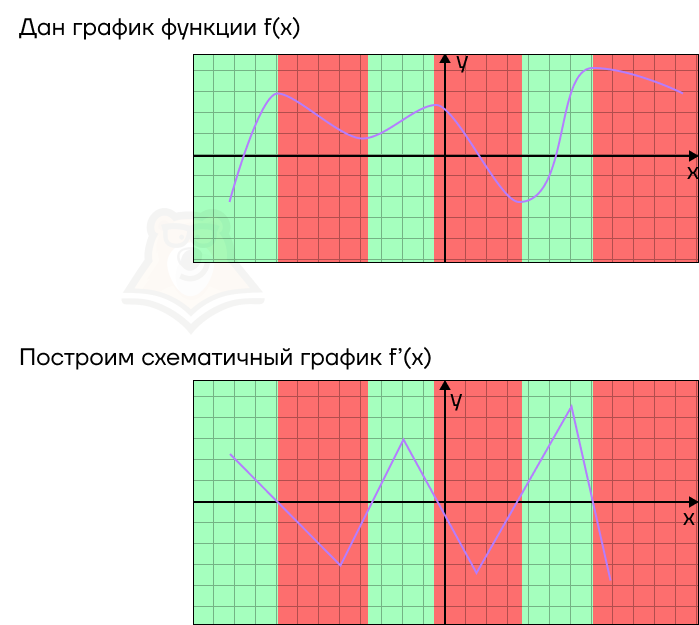
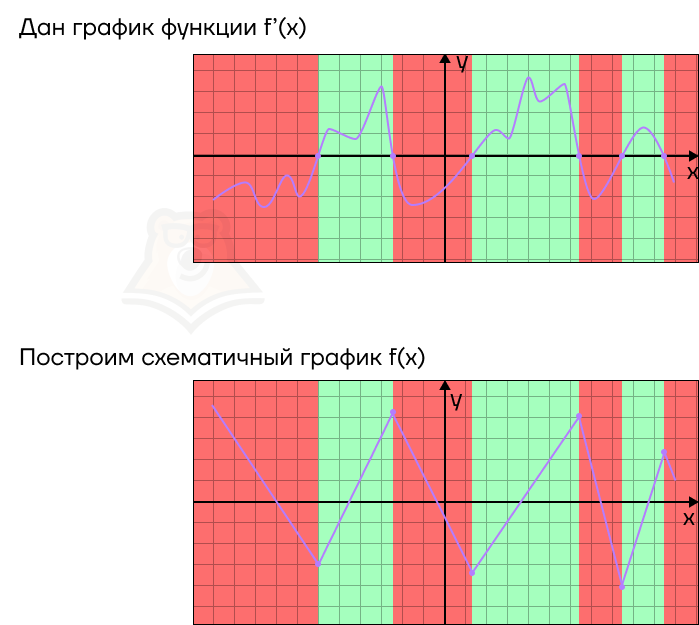
Если провести обратные рассуждения, то по графику производной можно восстановить примерный график функции. В этом случае:
- В точках, где график производной пересекает ось х, будут лежать точки экстремума. При этом если в точке производная меняет значение с положительного на отрицательное, то это точка максимума, а если с отрицательного на положительное, то это точка минимума.
- На промежутках, где график производной будет лежать выше оси х, функция будет возрастать.
- На промежутках, где график производной будет лежать ниже оси х, функция будет убывать.
Разберем несколько примеров, где можно применить эти знания.
Пример 1. На рисунке изображен график функции f(x) и отмечены пять точек на оси абсцисс: x1, x2, x3, x4, x5. В скольких из этих точек производная функции отрицательна?
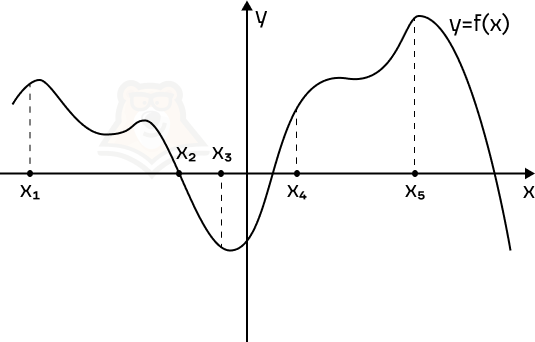
Решение. Производная отрицательна на промежутках убывания функции. Отметим такие промежутки.
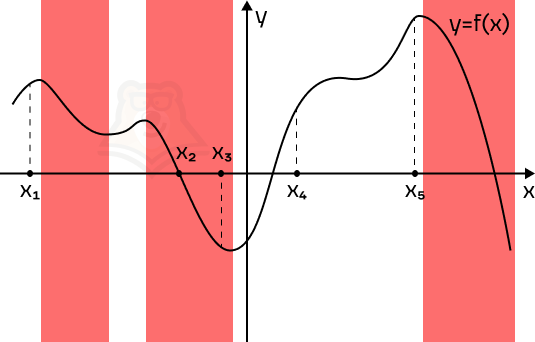
В точках, которые попали в эти промежутки, производная отрицательная. Всего таких точек 2.
Ответ: 2
Пример 2. На рисунке изображен график функции y = f'(x) — производной функции f(x), определенной на интервале (-5; 3). Найдите точку максимума функции f(x).
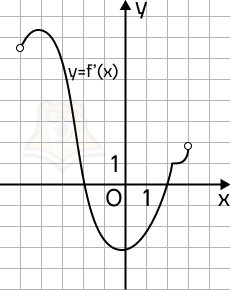
Решение. Точки экстремума на графике производной лежат на оси х. На данном графике таких точки две: x = -2, x = 2.
Точка максимума — это точка, в которой производная меняет знак с положительного на отрицательный. По графику определяем, что это точка x = -2.
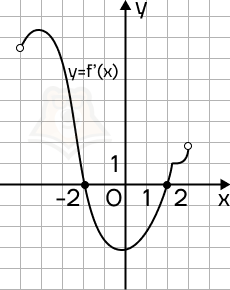
Ответ: -2
Представим, что мы составили графики “Заинтересованность зрителей фильмом” и “Наличие в фильме экшн-сцен”. Совпадут ли эти графики? Скорее всего, нет.
Экшн-сцены могут вызывать интерес у зрителей, равно как и романтические сцены или смешные повороты сюжета. Получается, что наличие экшн-сцен и заинтересованность фильмом — это разные величины в кинематографе, хотя и связаны между собой.
Также и графики производной и функции: они зависят друг от друга, но иллюстрируют совсем разные свойства функции, поэтому сильно отличаются.
Связь графика функции и первообразной
Мы разобрались, как связаны графики функции и ее производной. Есть ли связь между графиком функции и «Первообразной»?
Вспомним один важный факт: если взять производную от первообразной, то получим функцию.
F'(x) = f(x)
Похоже на функцию и ее производную, верно? На самом деле, ситуации ничем не отличаются.
В этом случае изначальной функцией будет первообразная, а ее производной — функция. Для наглядности составим таблицу.
| Было | Взяли производную | Стало | |
| Функция и производная | f(x) | f'(x) | f'(x) |
| Функция и первообразная | F(x) | F'(x) | f(x) |
Получается, для функции и первообразной будут действовать почти те же правила, что и для функции и ее производной.
При решении заданий с графиками первообразной достаточно проанализировать уравнение F'(x) = f(x). Рассмотрим несколько примеров.
Пример 3. На рисунке изображен график функции y = F(x) — одной из первообразных функции f(x) и отмечены шесть точек на оси абсцисс x1, x2, x3, x4, x5, x6. В скольких из этих точек функция f(x) отрицательна?
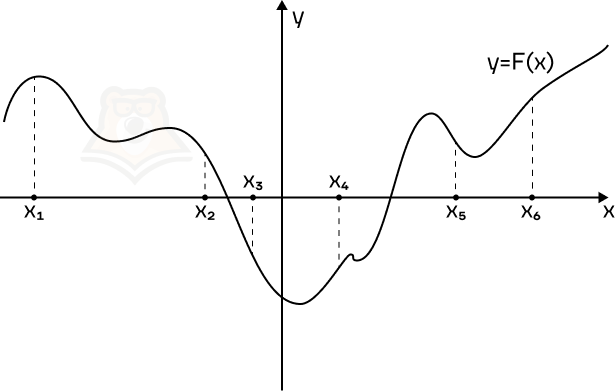
Решение. Поскольку F'(x) = f(x), то функция f(x) будет отрицательна в тех же точках, в которых будет отрицательна F'(x).
Поскольку на графике изображена функция y = F(x), то ее производная будет отрицательна на промежутках убывания функции. Отметим их красным.
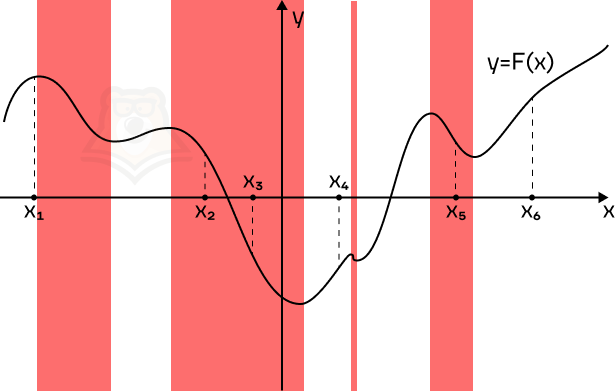
В эти промежутки попадают 3 из 6 точек.
Ответ: 3.
Пример 4. На рисунке изображен график функции y = F(x) — одной из первообразных функции f(x), определенной на интервале (-6; 7). Пользуясь рисунком, определите количество решений уравнения f(x) = 0 на отрезке [-5; 4].
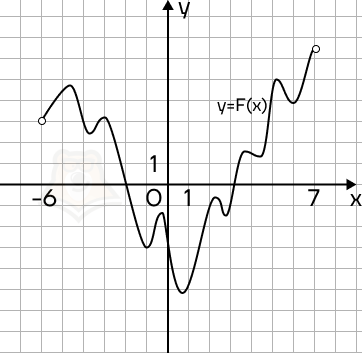
Решение. Вспомним, что F'(x) = f(x). Тогда если f(x) = 0, то и F'(x) = 0. Следовательно, на заданном промежутке нужно найти точки экстремума.
Отметим заданный промежуток красными линиями. На промежутке всего 9 точек экстремума, значит, в 9 точках f(x) будет равна 0.
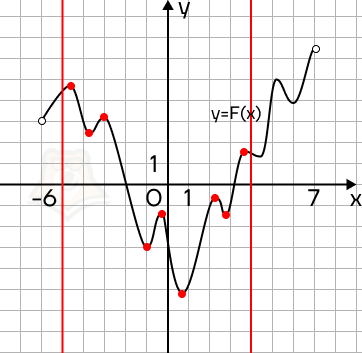
Ответ: 9
Представим, что в качестве функции у нас выступают кофейные зерна. Тогда производная — то, что мы получаем в результате их переработки — это вкусный напиток.
Из чего получаются сами кофейные зерна? Их собирают с кофейного дерева. То есть зерна будут производной от кофейного дерева, а кофейное дерево — это первообразная.
Так мы можем отследить следующую цепочку: кофейное дерево → кофейные зерна → кофе. И эта цепочка наглядно иллюстрирует связь первообразной, функции и ее производной.
Фактчек
- Графики функции, производной и первообразной связаны между собой.
- В точках экстремума функции график производной будет проходить через ось х.
- На промежутках возрастания функции график производной будет лежать выше оси х.
- На промежутках убывания функции график производной будет лежать ниже оси х.
- Для решения задач с первообразной необходимо вспомнить, что F'(x) = f(x). Любой график можно проанализировать с помощью этого уравнения также, как анализируются графики функции и ее производной.
Проверь себя
Задание 1.
На каких промежутках будет производная функции будет положительна?
- На промежутках убывания функции.
- На промежутках возрастания функции.
- В точках экстремума.
- Невозможно определить по графику.
Задание 2.
На каких промежутках производная функции будет отрицательна?
- На промежутках возрастания функции.
- На промежутках убывания функции.
- В точках экстремума.
- Невозможно определить по графику.
Задание 3.
На рисунке изображен график производной функции f(x), на котором отмечена точка. Чем будет являться эта точка для функции f(x)?
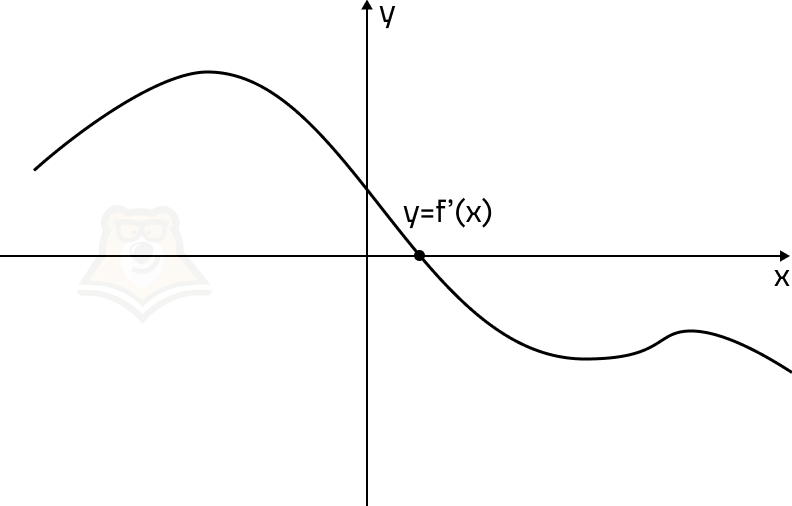
- Точка максимума функции.
- Точка минимума функции.
- Любая произвольная точка на функции.
- Невозможно определить по графику.
Задание 4.
Выберите верный вариант:
- F(x) = f'(x)
- F(x) = f(x)
- F'(x) = f'(x)
- F'(x) = f(x)
Ответы: 1. — 2 2. — 2 3. — 1 4. — 4
