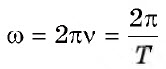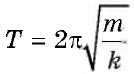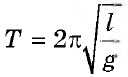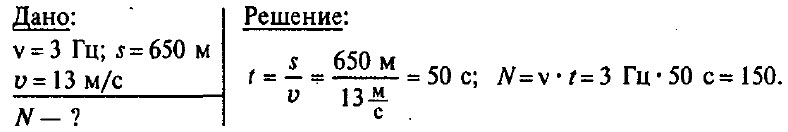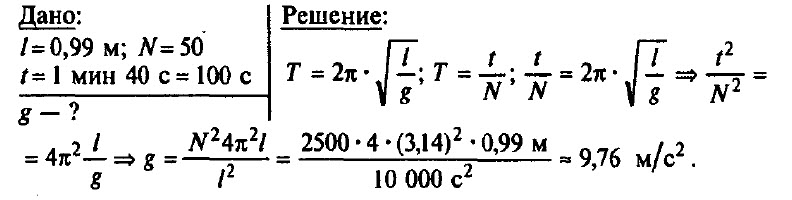Задачи на Механические колебания с решениями
Формулы, используемые на уроках «Задачи на Механические колебания».
Название величины |
Обозначение |
Единица измерения |
Формула |
Амплитуда колебаний |
A |
м |
|
Период колебаний |
T |
с |
T = 1 / v ;T = t / N |
Частота колебаний |
v |
Гц |
v = 1 / T ;v = N / t |
Число колебаний за какое-то время |
N |
N = t /T ;N = vt |
|
Время |
t |
с |
t = NT ;t = N / v |
Циклическая частота колебаний |
ω |
Гц |
|
Период колебаний пружинного маятника |
T |
c |
|
Период колебаний математического маятника |
T |
c |
|
Уравнение гармонических колебаний |
x(t) = Asin(ωt+φ0) |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Шарик на нити совершил 60 колебаний за 2 мин. Определите период и частоту колебаний шарика.
Задача № 2.
На рисунке изображен график зависимости координаты от времени колеблющегося тела.
По графику определите: 1) амплитуду колебаний; 2) период колебаний; 3) частоту колебаний; 4) запишите уравнение координаты.
Задача № 3.
Амплитуда незатухающих колебаний точки струны 2 мм, частота колебаний 1 кГц. Какой путь пройдет точка струны за 0,4 с? Какое перемещение совершит эта точка за один период колебаний?
Задача № 4.
Пользуясь графиком изменения координаты колеблющегося тела от времени, определить амплитуду, период и частоту колебаний. Записать уравнение зависимости x(t) и найти координату тела через 0,1 и 0,2 с после начала отсчета времени.
Задача № 5.
Какова длина математического маятника, совершающего гармонические колебания с частотой 0,5 Гц на поверхности Луны? Ускорение свободного падения на поверхности Луны 1,6 м/с2.
Задача № 6.
Груз массой 400 г совершает колебания на пружине с жесткостью 250 Н/м. Амплитуда колебаний 15 см. Найти полную механическую энергию колебаний и наибольшую скорость движения груза.
Задача № 7.
Частота колебаний крыльев вороны в полете равна в среднем 3 Гц. Сколько взмахов крыльями сделает ворона, пролетев путь 650 м со скоростью 13 м/с?
Задача № 8.
Гармоническое колебание описывается уравнением
Чему равны циклическая частота колебаний, линейная частота колебаний, начальная фаза колебаний?
Задача № 9.
Математический маятник длиной 0,99 м совершает 50 полных колебаний за 1 мин 40 с. Чему равно ускорение свободного падения в данном месте на поверхности Земли? (Можно принять π2 = 9,87.)
Задача № 10.
ОГЭ
Как и во сколько раз изменится период колебаний пружинного маятника, если шарик на пружине заменить другим шариком, радиус которого вдвое меньше, а плотность — в два раза больше?
Задача № 11.
ЕГЭ
Два математических маятника за одно и то же время совершают — первый N1 = 30, а второй — N2 = 40 колебаний. Какова длина каждого из них, если разность их длин Δl = 7 см?
Краткая теория для решения Задачи на Механические колебания.
Это конспект по теме «ЗАДАЧИ на Механические колебания». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на
- Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
как найти число колебаний, зная частоту и время? формулу напишите)
Лина Соколова
Ученик
(209),
на голосовании
12 лет назад
Голосование за лучший ответ
Ильгиз Тухватуллин
Мастер
(1346)
12 лет назад
n=T/1 вроде бы ну частота по идее это величина показывающая кол-во колебаний в единицу времени
МерелинМурло
Мудрец
(10958)
12 лет назад
N=ню * t
Похожие вопросы
Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):
- амплитуда,
- период,
- частота,
- циклическая частота,
- фаза,
- начальная фаза.
Рис. 1. Основные характеристики колебаний – это амплитуда, период и начальная фаза
Такие величины, как амплитуду и период, можно определить по графику колебаний.
Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.
Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.
А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.
Что такое амплитуда
Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.
Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.
В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.
Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.
К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».
С помощью графика амплитуду можно определить так (рис. 2):
Рис. 2. Амплитуда – это максимальное отклонение от горизонтальной оси либо вверх, либо вниз. Горизонтальная ось проходит через уровень нуля на оси, на которой отмечены амплитуды
Что такое период
Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.
Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.
( large T left( c right) ) – период колебаний.
Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.
Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.
Рис. 3. Период колебаний – это горизонтальное расстояние между двумя похожими точками на графике
Период – это время одного полного колебания.
На графике период найти удобнее одним из таких способов (рис. 4):
Рис. 4. Удобно определять период, как расстояние между двумя соседними вершинами, либо между двумя впадинами
Что такое частота
Обозначают ее с помощью греческой буквы «ню» ( large nu ).
Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».
Поэтому, размерность частоты — это единицы колебаний в секунду:
( large nu left( frac{1}{c} right) ).
Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large displaystyle frac{1}{c} = c^{-1} ).
Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.
Одно колебание в секунду соответствует частоте в 1 Герц.
[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]
Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:
[ large boxed{ nu = frac{1}{T} }]
Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).
Рис. 5. На графике частота – это количество периодов, уместившихся в одну секунду
Что такое циклическая частота
Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.
Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:
( large displaystyle omega left( frac{text{рад}}{c} right) )
Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).
Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».
Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:
[ large boxed{ omega = 2pi cdot nu }]
Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.
Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.
Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).
И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.
Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.
Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).
Рис. 6. На графике циклическая (круговая) частота – это количество периодов, уместившихся в 2 пи секунд
Что такое начальная фаза и как определить ее по графику колебаний
Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.
Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).
(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).
Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.
Рис. 7. Угол отклонения качелей перед началом колебаний
Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.
Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.
Рис. 8. Вертикальное положение стартовой точки в момент времени t = 0 и сдвиг графика по горизонтали определяется начальной фазой
Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.
Определим угол (large varphi_{0} ) с помощью графика колебаний.
Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина (large varphi_{0} ) — в радианах. Значит, нужно связать формулой кусочек времени (large Delta t) и соответствующий ему начальный угол (large varphi_{0} ).
Как вычислить начальный угол по интервалу смещения
Алгоритм нахождения начального угла состоит из нескольких несложных шагов.
- Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
- Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.
[large T = 5 – 1 = 4 left( text{сек} right)]
Из графика следует, что период T = 4 сек.
- Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):
[large frac{Delta t }{T} = frac{1}{4} ]
Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.
- Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.
Для этого используем формулу:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )
Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.
- В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.
Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:
[large varphi_{0} = — frac{pi }{2} ]
Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».
Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).
Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».
А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».
Примечания:
- Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
- На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.
Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.
Что такое фаза колебаний
Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.
Рис. 9. Угол отклонения от равновесия – фаза, изменяется в процессе колебаний
В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).
Различия между фазой и начальной фазой
Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.
Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.
Рис. 10. Перед началом колебаний задаем начальную фазу — начальный угол отклонения от равновесия. А угол, который изменяется во время колебаний, называют фазой
Как на графике колебаний отметить фазу
На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.
На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.
Рис. 11. На графике колебаний фаза – это точка, скользящая по кривой. В различные моменты времени она находится в разных положениях на графике
А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.
Как определить фазу с помощью формулы
Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.
Время колебаний t будет величиной переменной.
Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.
Что такое разность фаз
Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.
Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.
Обозначим их:
( large varphi_{01}) – для первого процесса и,
( large varphi_{02}) – для второго процесса.
Рис. 12. Для двух колебаний можно ввести понятие разности фаз
Определим разность фаз между первым и вторым колебательными процессами:
[large boxed{ Delta varphi = varphi_{01} — varphi_{02} }]
Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.
Как связаны характеристики колебаний — формулы
Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.
Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.
- Связь между периодом, количеством колебаний и общим временем колебательного процесса:
[large boxed{ T cdot N = t }]
( large T left( c right) ) – время одного полного колебания (период колебаний);
( large N left( text{шт} right) ) – количество полных колебаний;
( large t left( c right) ) – общее время для нескольких колебаний;
- Период и частота колебаний связаны так:
[large boxed{ T = frac{1}{nu} }]
(large nu left( text{Гц} right) ) – частота колебаний.
- Количество и частота колебаний связаны формулой:
[large boxed{ N = nu cdot t}]
- Связь между частотой и циклической частотой колебаний:
[large boxed{ nu cdot 2pi = omega }]
(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.
- Фаза и циклическая частота колебаний связаны так:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
(large varphi_{0} left( text{рад} right) ) — начальная фаза;
(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;
- Между фазой и количеством колебаний связь описана так:
[large boxed{ varphi = N cdot 2pi }]
- Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.
Период колебаний, формула
Повторяющиеся движения или процессы, которые воспроизводят все состояния предыдущего цикла являются периодическими.
Одной из характеристик периодических процессов или колебаний является период.
Период колебаний — Это время за которое периодический процесс проходит полностью один цикл.
Период колебаний, формула
Для того чтобы найти период колебаний, необходимо взять определенный временной интервал и подсчитать количество циклов, после чего воспользоваться формулой:
Если
| ∆t | определенный временной интервал, | секунд |
|---|---|---|
| N | количество циклов, | шт. |
| f | частота колебаний (число циклов в одну секунду), | Герц |
то
[ T = frac{∆t}{N} = frac{1}{f} ]
Пример определения периода колебаний
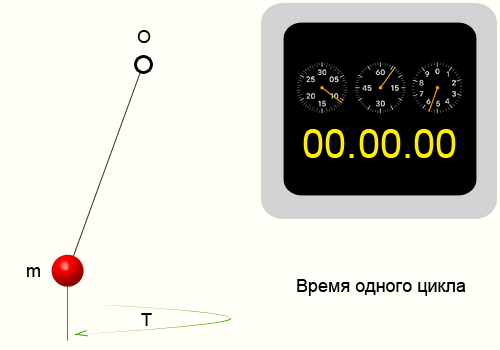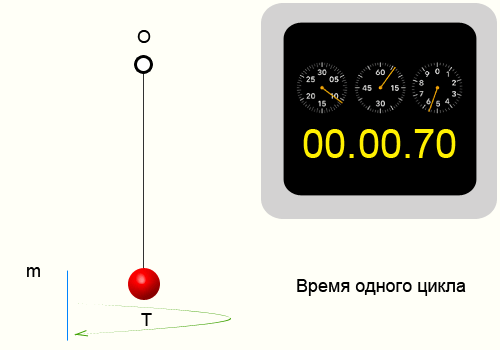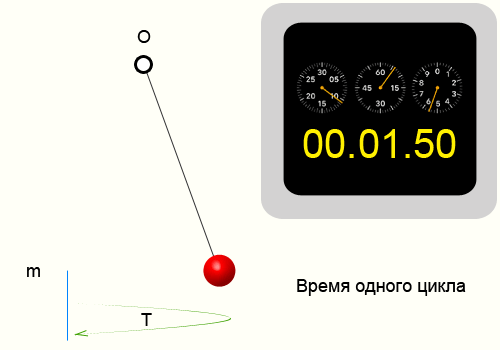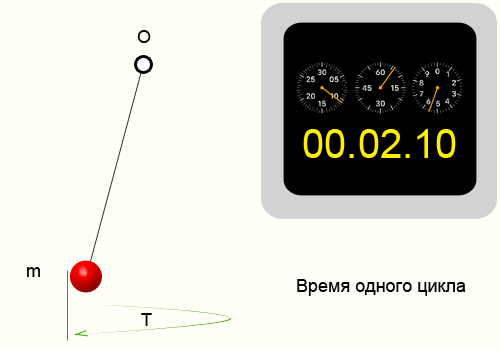
Например возьмем кусочек пластилина и подвесим его на нитке.
Отведем нитку от положения равновесия и отпустим. На сотовом телефоне в момент отпускания запустим секундомер.
Отсчитаем 10 циклов, т.е. нить 10 раз вернется в ту же точку из которой мы ее отпустили.
Секундомер показал 14.35 секунд, соответственно приблизительный период колебаний нити 1.435 секунд.
Вычислить, найти период колебаний по формуле 1
Как найти период колебаний зная частоту
Период колебаний, формула |
стр. 533 |
|---|
§
6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ Основные
формулы
• Уравнение
гармонических колебаний
где х
— смещение
колеблющейся точки от положения
равновесия;
t
— время; А,
ω,
φ—
соответственно амплитуда, угловая
частота,
начальная фаза колебаний;
—
фаза колебаний в момент t.
• Угловая частота
колебаний
, или
,
где ν
и
Т — частота и период колебаний.
• Скорость точки,
совершающей гармонические колебания,
• Ускорение при
гармоническом колебании
• Амплитуда
А
результирующего
колебания, полученного при сложении
двух колебаний с одинаковыми частотами,
происходящих по одной прямой, определяется
по формуле
где
a1
и
А2—
амплитуды
составляющих колебаний; φ1
и
φ2—
их
начальные фазы.
•
Начальная фаза φ
результирующего колебания может быть
найдена
из формулы
•
Частота биений,
возникающих при сложении двух колебаний,
происходящих
по одной прямой с различными, но близкими
по значению
частотами ν1
и
ν2,
•
Уравнение траектории
точки, участвующей в двух взаимно
перпендикулярных
колебаниях с амплитудами A1
и A2
и начальными
фазами φ1
и φ2,
Если
начальные фазы φ1
и
φ2
составляющих колебаний одинаковы,
то уравнение траектории принимает вид
т. е. точка движется
по прямой.
В том
случае, если разность фаз
,
уравнение
принимает вид
т. е. точка движется
по эллипсу.
• Дифференциальное
уравнение гармонических колебаний
материальной точки
, или
,
где
m
—
масса точки; k
—
коэффициент
квазиупругой силы (k=тω2).
•
Полная энергия
материальной точки, совершающей
гармонические
колебания,
• Период
колебаний тела, подвешенного на пружине
(пружинный
маятник),
где
m
—
масса тела; k
—
жесткость
пружины.
Формула справедлива для упругих
колебаний в пределах, в которых
выполняется закон Гука (при малой массе
пружины в сравнении
с массой тела).
Период колебаний
математического маятника
где
l
— длина маятника; g
—
ускорение
свободного падения. Период
колебаний физического маятника
где J
— момент инерции колеблющегося тела
относительно оси
колебаний;
а
— расстояние центра масс маятника от
оси колебаний;
— приведенная
длина физического маятника.
Приведенные
формулы являются точными для случая
бесконечно малых амплитуд. При
конечных амплитудах эти формулы дают
лишь приближенные результаты. При
амплитудах не более
ошибка в значении периода не превышает
1 %.
Период
крутильных колебаний тела, подвешенного
на упругой нити,
где J
—
момент
инерции тела относительно оси, совпадающей
с упругой нитью; k
—
жесткость
упругой нити, равная отношению упругого
момента, возникающего при закручивании
нити, к углу, на который нить закручивается.
• Дифференциальное
уравнение затухающих колебаний
, или
,
где r
— коэффициент сопротивления; δ
— коэффициент
затухания:
; ω0—
собственная угловая частота колебаний
*
• Уравнение
затухающих колебаний
где A
(t) —
амплитуда
затухающих колебаний в момент t;
ω
— их угловая частота.
• Угловая частота
затухающих колебаний
О Зависимость
амплитуды затухающих колебаний от
времени
I
где
А0
— амплитуда
колебаний в момент t=0.
• Логарифмический
декремент колебаний
где
A
(t) и
A
(t+T) —
амплитуды
двух последовательных колебаний,
отстоящих по времени друг от друга на
период.
• Дифференциальное
уравнение вынужденных колебаний
, или
,
где
—
внешняя периодическая сила, действующая
на
колеблющуюся
материальную точку и вызывающая
вынужденные
колебания;
F0
—
ее
амплитудное значение;
•
Амплитуда вынужденных
колебаний
•
Резонансная частота
и резонансная амплитуда
и
Примеры решения
задач
Пример
1. Точка
совершает колебания по закону
x(t)= ,
где
А=2
см.
Определить начальную фазу φ,
если
x(0)= см
и х,(0)<0.
Построить векторную диаграмму для
мо-
мента t=0.
Решение.
Воспользуемся уравнением движения и
выразим смещение в момент t=0
через начальную фазу:
О
найдем начальную фазу:
*
В приведенных ранее формулах
гармонических колебаний та же
величина
обозначалась просто ω
(без индекса 0).
Подставим
в это выражение заданные значения x(0)
и А:
φ=
= .
Значению аргумента
удовлетворяют
два
значения угла:
Для
того чтобы решить, какое из этих значений
угла φ
удовлет-
воряет
еще и условию
,
найдем сначала
:
Подставив
в это выражение значение t=0
и поочередно значения
начальных
фаз
и
,
найдем
Т
как всегда A>0
и ω>0,
то условию удовлетворяет
толь
ко
первое значение начальной фазы.
Таким
образом, искомая начальная
фаза
По
найденному значению φ
постро-
им
векторную диаграмму (рис. 6.1).
Пример
2. Материальная
точка
массой т=5
г совершает гармоничес-
кие колебания
с частотой ν
=0,5 Гц.
Амплитуда
колебаний A=3
см. Оп-
ределить: 1) скорость υ
точки
в мо-
мент времени, когда смещение
х=
=
1,5 см; 2) максимальную силу
Fmax,
действующую
на точку; 3)
Рис.
6.1 полную
энергию Е
колеблющейся
точ
ки.
Решение.
1. Уравнение гармонического колебания
имеет вид
(1)
а
формулу скорости получим, взяв первую
производную по времени от смещения:
(2)
Чтобы
выразить скорость через смещение, надо
исключить из формул (1) и (2) время. Для
этого возведем оба уравнения в квадрат,
разделим первое на А2,
второе
на A2
ω
2
и сложим:
, или
Решив
последнее уравнение относительно υ,
найдем
Выполнив вычисления
по этой формуле, получим
см/с.
Знак
плюс соответствует случаю, когда
направление скорости совпадает
с положительным направлением оси х,
знак
минус — когда
направление скорости совпадает с
отрицательным направлением оси
х.
Смещение при
гармоническом колебании кроме уравнения
(1) может быть определено также уравнением
Повторив
с этим уравнением такое же решение,
получим тот же ответ.
2.
Силу действующую на точку, найдем по
второму закону Ньютона:
(3)
где а
— ускорение
точки, которое получим, взяв производную
по времени
от скорости:
, или
Подставив выражение
ускорения в формулу (3), получим
Отсюда максимальное
значение силы
Подставив
в это уравнение значения величин π,
ν,
т
и
A,
найдем
3.
Полная энергия колеблющейся точки есть
сумма кинетической и
потенциальной энергий, вычисленных для
любого момента времени.
Проще
всего вычислить полную энергию в момент,
когда кинетическая
энергия достигает максимального
значения. В этот момент потенциальная
энергия равна нулю. Поэтому полная
энергия E
колеблющейся точки равна максимальной
кинетической энергии
Tmax:
(4)
Максимальную
скорость определим из формулы (2),
положив
:
.
Подставив выражение скорости в фор-
мулу
(4), найдем
Подставив
значения величин в эту формулу и произведя
вычисления, получим
или
мкДж.
Пример
3.
На концах тонкого стержня длиной l
=
1 м и массой m3=400
г
укреплены шарики малых размеров массами
m1=200
г
и
m2=300г.
Стержень
колеблется около горизонтальной оси,
перпен-
дикулярной
стержню и проходящей через его середину
(точка О на рис. 6.2). Определить период Т
колебаний,
совершаемых стержнем.
Решение.
Период колебаний физического маятника,
каким является стержень с шариками,
определяется соотношением
(1)
г
J
—
момент
инерции маятника относительно оси
колебаний; т
— его
масса; lС
— расстояние
от центра масс маятника
до оси.
Момент
инерции данного маятника равен сумме
моментов
инерции шариков J1
и
J2
и
стержня J3:
(2)
Принимая
шарики за материальные точки, выразим
моменты их инерции:
Так
как ось проходит через середину стержня,
то
его
момент инерции относительно этой оси
J3=
= .
Подставив
полученные выражения
J1
,
J2
и
J3
в формулу (2), найдем общий момент инерции
фи-
зического маятника:
Произведя
вычисления по этой формуле, найдем
Рис.
6.2 Масса маятника состоит из масс шариков
и массы
стержня:
Расстояние
lС
центра
масс маятника от оси колебаний найдем,
исходя
из следующих соображений. Если ось х
направить
вдоль стержня
и начало координат совместить с точкой
О,
то
искомое расстояние
l
равно координате центра масс маятника,
т. е.
, или
Подставив
значения величин m1,
m2,
m,
l
и произведя вычисления,
найдем
см.
Произведя
расчеты по формуле (1), получим период
колебаний физического
маятника:
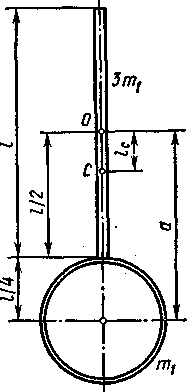
Пример
4. Физический
маятник представляет собой стержень
длиной
l=
1 м и массой 3т1
с прикрепленным
к одному из его концов
обручем
диаметром
и
массой т1.
Горизонтальная
ось Oz
маятника
проходит через середину стержня
перпендикулярно ему (рис. 6.3). Определить
период Т
колебаний
такого маятника.
Решение.
Период
колебаний физического маятника
определяется
по формуле
(1)
где
J
—
момент
инерции маятника относительно оси
колебаний; т
— его
масса; lC
— расстояние
от центра масс
маятника до оси колебаний.
Момент
инерции маятника равен сумме моментов
инерции стержня J1
и
обруча J2:
(2).
Момент
инерции стержня относительно
оси,
перпендикулярной
стержню и проходящей
через
его центр масс, определяется по форму-
ле
.
В данном случае т=3т1
и
Момент
инерции обруча найдем, восполь-
зовавшись
теоремой Штейнера
,
где
J
—
момент
инерции относительно про-
извольной
оси;
J0
—
момент
инерции отно-
сительно
оси, проходящей через центр масс
параллельно
заданной оси; а
— расстояние
между
указанными осями. Применив эту фор-
мулу
к обручу, получим
Рис. 6.3
Подставив
выражения J1
и
J2
в формулу
(2), найдем момент инерции маятника
относительно оси вращения:
Расстояние
lС
от
оси маятника до его центра масс равно
Подставив
в формулу (1) выражения J,
lс
и массы маятника
, найдем период его колебаний:
После
вычисления по этой формуле получим
T=2,17
с.
Пример
5. Складываются
два колебания одинакового направле-
ния,
выражаемых уравнениями
;
х2=
=,
где А1=1
см,
A2=2
см,
с,
с, ω
=
=.
1. Определить начальные фазы φ1
и φ
2
составляющих коле-
баний.
2. Найти амплитуду А
и
начальную фазу φ
результирующего колебания.
Написать уравнение результирующего
колебания.
Решение.
1. Уравнение гармонического колебания
имеет вид
(1)
Преобразуем
уравнения, заданные в условии задачи,
к такому же
виду:
(2)
Из
сравнения выражений (2) с равенством (1)
находим начальные фазы
первого и второго колебаний:
рад и
рад.
2.
Для определения амплитуды А
результирующего
колебания удобно воспользоваться
векторной диаграммой,
представленной на рис.
6.4.
Согласно теореме косинусов, получим
(3)
где
— разность фаз составляющих колебаний.
Так
как
,
то, подставляя найденные
значения
φ2
и φ1
получим
рад.
Рис. 6.4
Подставим
значения А1
,
А2
и
в формулу (3)
и
произведем вычисления:
A=2,65
см.
Тангенс
начальной фазы φ
результирующего колебания опреде-
лим
непосредственно из рис. 6.4:
, отку-
да
начальная фаза
Подставим
значения А1,
А2,
φ
1,
φ
2
и произведем вычисления:
= рад.
Так
как угловые частоты складываемых
колебаний одинаковы,
то
результирующее колебание будет иметь
ту же частоту ω.
Это
позволяет
написать уравнение результирующего
колебания в виде
, где A=2,65
см,
,
рад.
Пример
6. Материальная
точка участвует одновременно в двух
взаимно перпендикулярных гармонических
колебаниях, уравнения
которых
(1).
(2)
где
a1=1
см,
A2=2
см,
.
Найти уравнение траектории точ-
ки.
Построить траекторию с соблюдением
масштаба и указать
направление
движения точки.
Решение.
Чтобы
найти уравнение траектории точки,
исключим
время t
из
заданных уравнений (1) и (2). Для этого
восполь-
зуемся
формулой
.
В данном случае
, поэтому
Так
как согласно формуле (1)
,
то уравнение траекто-
рии
(3)
Полученное
выражение представляет собой уравнение
параболы, ось которой совпадает с осью
Ох.
Из
уравнений (1) и (2) следует, что смещение
точки по осям координат ограничено и
заключено в пределах от —1 до +1 см по
оси Ох
и
от —2 до +2 см по оси Оу.
Для
построения траектории найдем по уравнению
(3) значения у,
соответствующие
ряду значений х,
удовлетворяющих
условию
см, и составим таблицу:
|
X |
-1 |
—0,75 |
—0,5 |
0 |
+0,5 |
+ 1 |
|
у, |
0 |
±0,707 |
±1 |
±1,41 |
±1,73 |
±2 |
Начертив
координатные оси и выбрав масштаб,
нанесем на плоскость
хОу
найденные
точки. Соединив их плавной кривой,
получим траекторию точки, совершающей
колебания
в соответствии с уравнениями движения
(1) и (2) (рис. 6.5).
Рис. 6.5
Для
того чтобы указать направление движения
точки, проследим за тем, как изменяется
ее положение с течением времени. В
начальный момент t=0
координаты точки
равны x(0)=1
см и y(0)=2
см. В последующий
момент времени, например при t1=l
с,
координаты точек изменятся и станут
равными х
(1)=
—1
см, y(t)=0.
Зная
положения
точек в начальный и последующий
(близкий) моменты времени, можно указать
направление движения точки по траектории.
На рис. 6.5 это направление движения
указано стрелкой (от точки А
к
началу
координат). После того как в момент
t2
= 2 с колеблющаяся точка достигнет
точки D,
она
будет двигаться в обратном направлении.
Задачи
Кинематика
гармонических колебаний
6.1.
Уравнение колебаний точки имеет вид
,
где
ω=π
с-1,
τ=0,2
с. Определить период Т
и
начальную фазу φ
колебаний.
6.2.
Определить
период Т,
частоту
v
и
начальную фазу φ
колебаний,
заданных уравнением
,
где ω=2,5π
с-1,
τ=0,4
с.
6.3.
Точка
совершает колебания по закону
,
где
A=4
см. Определить начальную фазу φ,
если: 1) х(0)=2
см
и
;
2)
х(0)
=см
и
;
3) х(0)=2см
и
;
4)
х(0)=
и
.
Построить векторную диаграмму
для
момента
t=0.
6.4.
Точка
совершает колебания .по закону
,
где
A=4
см. Определить начальную фазу φ,
если: 1) х(0)=2
см
и
; 2) x(0)=
см и
;
3) х(0)=
см и
;
4)
x(0)=см
и
.
Построить векторную диаграмму для
момента
t=0.