Как найти количество автоморфизмов

Национальный
исследовательский институт

Московский
Энергетический Институт (Технический
Университет)

Институт
автоматики и вычислительной техники

Кафедра
Прикладной математики

Лабораторная
работа №4

по
дисциплине:

Параллельные
системы

тема:
«Задачи на графах»

вариант
№5 – «Поиск автоморфизмов графа»

Выполнил:

Бочаров
Иван Андреевич

Проверил:

Панков
Николай Александрович

Москва

2012
г.

Введение

Дадим
определение основному понятию,
используемому в данной работе – понятию
автоморфизма графа. Сперва рассмотрим
неориентированный граф без петель.

Автоморфизм
графа – произвольная подстановка

на множестве вершин графа, сохраняющая
отношение смежности, т.е.

такова, что образы

и

вершин

и

смежны тогда и только тогда, когда смежны
сами вершины u и v.
Следует заметить, что очевидным образом
это определение можно распространить
на случай взвешенного ориентированного
графа без петель – перестановка помимо
отношения смежности должна сохранять
веса рёбер между смежными вершинами.

Известно,
что множество автоморфизмов графа
образует группу с операцией композиции
в качестве операции умножения.

Очевидно,
что каждый граф имеет хотя бы один
автоморфизм – тривиальную подстановку
.
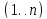
По этой причине для нас интерес
представляют только нетривиальные
автоморфизмы. Граф, для которого
единственный возможный автоморфизм –
это тождественное отображение, называется
асимметрическим.

Метод решения

На
данный момент не существует эффективного
алгоритма поиска автоморфизмов графа.
Все имеющиеся на сегодняшний день
алгоритмы являются модификациями
полного перебора (метод ветвей и границ
и т.п.).

В
данной работе используется полный
перебор. Граф представляется матрицей
смежности (–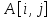
вес ребра из вершины

в вершину).
Для каждой нити параметром служит
структура, несущая в себе информацию о
числе подстановок, которое необходимо
проверить, и об индексе перестановки,
с которой нить должна начинать проверку
на принадлежность к группе автоморфизмов
графа. Также в поля этой структуры
записывается результат – количество
автоморфизмов, принадлежащих подмножеству
множества подстановок, проверенных
нитью, и их индексы.

При
запуске нити по индексу определяется
начальная перестановка, а затем в цикле
проверяются все перестановки. Следует
заметить, что перестановки упорядочены
в лексикографическом порядке.

Результаты

Основные
результаты были получены при тестировании
разработанной программы на так называемых
полных графах. Очевидно, что в полных
графах группа автоморфизмов графа
совпадает с множеством всех подстановок
графа и имеет мощность
,
где

– количество вершин графа. В связи с
так называемым комбинаторным взрывом
решение задачи поиска автоморфизмов
графа может занимать значительное
время.

Для каждого
графа и количества нитей время было
измерено 5 раз и в качестве конечного
значения была выбрана медиана полученного
множества.

Испытания
проводились на стенде со следующей
конфигурацией:

CPU: Intel Core
i5 2500 МГц Ivy
Bridge (3210M)

Количество ядер: 2 физических, 4
виртуальных

Кэш: 3 Mb L2
(L3) Cache

RAM: 4096
Мб DDR3-1600МГц

ОС: MS
Windows 7 Home Basic x64

Таблица результатов (время
в секундах):

Число нитей/Размер графа	7	8	9	10	11	12	ТГ,n=11
1	0,016	0,234	2,496	31,278	458,781	6889,355	3,898
2	0,015	0,124	1,357	17,862	288,803	4175,366	2,19
3	0,015	0,124	1,185	14,415	236,15	3414,605	1,946
4	0,015	0,093	1,061	12,916	220,647	3191,22	1,804
5	0,016	0,11	1,123	13,915	228,653		1,877
6	0,015	0,094	1,06	12,854	224,826		1,925
Число автоморфизмов	5040	40320	362880	3628800	39916800	479001600	1152

Ускорение

Число нитей/Размер графа	7	8	9	10	11	12	ТГ,n=11
2	1,067	1,887	1,839	1,751	1,589	1,650	1,780
3	1,067	1,887	2,106	2,170	1,943	2,018	2,003
4	1,067	2,516	2,352	2,422	2,079	2,159	2,161
5	1,000	2,127	2,223	2,248	2,006		2,077
6	1,067	2,489	2,355	2,433	2,041		2,025

Изоморфизм, гомоморфизм и автоморфизм графов

Для ориентированного графа множество дуг можно рассматривать как график бинарного отношения непосредственной достижимости, заданного на множестве вершин.

В неориентированном графе множество ребер является множеством неупорядоченных пар. Для каждой неупорядоченной пары можно считать, что вершины и связаны симметричным бинарным отношением , то есть и .

Таким образом, с каждым неориентированным и ориентированным графом связано бинарное отношение . Это отношение будем называть отношением смежности.

С алгебраической точки зрения как ориентированный, так и неориентированный граф можно рассматривать как модель, сигнатура которой состоит из одного бинарного отношения: . В классической теории графов изучаются преимущественно конечные модели такого рода.

При указанном подходе различия между ориентированным и неориентированным графами проявляется только в свойствах отношения смежности . Если это отношение симметрично, то граф называют неориентированным, и с этой точки зрения неориентированный граф можно считать частным случаем ориентированного.

Примечание. При таком подходе в неориентированном графе могут быть петли, если отношение содержит некоторые элементы диагонали, в частности является рефлексивным.

Применяя к данному частному случаю моделей общие понятия гомоморфизма и изоморфизма, мы можем сформулировать следующие определения.

Определение 5.14. Отображение множества вершин графа в множество вершин графа называют гомоморфизмом графов (графа в граф ), если для любых двух вершин, смежных в первом графе, их образы при отображении смежны во втором графе, т.е. если

Биективный гомоморфизм , такой, что любые две вершины смежны в первом графе тогда и только тогда, когда их образы смежны во втором графе, т.е.

называют изоморфизмом графов и (графа на граф ), а графы и — изоморфными, что записывают в виде .

Гомоморфизм графов, который является эпиморфизмом, называется также гомоморфизмом одного графа на другой.

Возвращаясь к нашему определению графа посредством двух множеств: множества вершин и множества ребер (дуг) , получим следующие варианты определений гомоморфизма и изоморфизма.

Гомоморфизм неориентированного графа в неориентированный граф есть такое отображение , что для любых двух вершин первого графа, соединенных ребром, их образы при отображении h также соединены ребром, т.е.

Гомоморфизм ориентированного графа в ориентированный граф есть такое отображение , что для любых двух вершин первого графа, таких, что есть дуга, ведущая из в , из вершины тоже ведет дуга в , т.е.

Изоморфизм неориентированного графа на неориентированный граф есть такая биекция , при которой две вершины и графа соединены ребром тогда и только тогда, когда соединены ребром их образы и , т.е.

Аналогично изоморфизм ориентированного графа на ориентированный граф есть такая биекция , при которой в ориентированном графе из вершины ведет дуга в вершину тогда и только тогда, когда в ориентированном графе из образа вершины ведет дуга в образ вершины , т.е.

---

Пример 5.12. а. На рис. 5.29 отображение , где есть гомоморфизм ориентированного графа в ориентированный граф .

Обратим внимание на петлю : эта петля является образом дуги , так как и . В противоположность этому петля не имеет прообраза в .

На этом же рисунке более толстыми стрелками выделен подграф графа , порожденный подмножеством вершин , Этот подграф будет гомоморфным образом графа . Удаляя петлю в вершине , получим (для того же подмножества вершин) порожденный подграф, являющийся строгим гомоморфным образом графа . Отметим, что каждая дуга в строгом гомоморфном образе ориентированного графа имеет прообраз в .

б. На рис. 5.30 неориентированный граф есть строгий гомоморфный образ графа (если рассматривать неориентированные графы без петель).

в. На рис. 5.31 отображение h не является гомоморфизмом на , поскольку , но (петли нет); , хотя и т.д. Легко сообразить, что любой двухвершинный гомоморфный образ графа на рис. 5.31 должен иметь петлю, и, следовательно, не является гомоморфным образом ни при каком отображении.

г. На рис. 5.32 изображен один граф из множества двухвершинных гомоморфных образов .

д. Графы, изображенные на рис. 5.33, изоморфны, и изоморфизмом является, например, отображение , такое, что

---

Дополнения графов

Зачастую для того, чтобы распознать изоморфизм графов, удобно перейти от исходных графов к их дополнениям.

Определение 5.15. Неориентированный (ориентированный) граф называют дополнением неориентированного [ориентированного) графа , где — дополнение множества до множества всех неупорядоченных [упорядоченных пар) на .

Можно доказать, что графы изоморфны тогда и только тогда, когда изоморфны их дополнения. Например, перейдем к дополнениям графов, изображенных на рис. 5.33. Анализ указанных дополнений (рис. 5.34) позволяет сразу обнаружить их изоморфизм, а следовательно, и изоморфизм исходных графов.

Более сложные случаи распознавания изоморфизма (главным образом, для неориентированных графов) будут рассмотрены в последующей лекции.

---

Автоморфизм графов

Определение 5.16. Автоморфизм графа — это любая подстановка множества его вершин, являющаяся изоморфизмом на себя.

Можно показать, что композиция двух любых автоморфизмов графа снова есть автоморфизм этого графа, а подстановка, обратная к автоморфизму, опять-таки есть автоморфизм. Таким образом, множество всех автоморфизмов данного графа образует группу по операции композиции, которая является подгруппой симметрической группы множества вершин графа. Ее называют группой автоморфизмов данного графа.

Рассмотрим некоторые примеры групп автоморфизмов.

Для графа, изображенного на рис. 5.35,а, группа автоморфизмов порождается транспозициями (1 4) и (2 3), что легко усматривается из анализа дополнения этого графа (рис. 5.35,б). Очевидно, что группа автоморфизмов графа есть подгруппа группы перестановок множества его вершин. Поэтому, согласно теореме 2.13 Лагранжа, порядок группы автоморфизмов графа есть делитель факториала числа его вершин. В частности, для графа на рис. 5.35, а группа автоморфизмов имеет порядок 4 и состоит из тождественной подстановки и подстановок . Очевидно, что 4! делится на 4.

Можно доказать, что автоморфизмы неориентированного графа сохраняют степени, а ориентированного графа — полустепени исхода и захода всех его вершин. Это свойство позволяет упростить описание автоморфизмов графа.

---

Пример 5.13. Найдем нетривиальные (т.е. отличные от тождественной подстановки) автоморфизмы неориентированного графа, изображенного на рис. 5.36. Так как среди вершин графа лишь одна вершина имеет степень 1 и лишь одна вершина имеет степень 2, то при любом изоморфизме эти вершины перейдут в себя. Значит, при изоморфизме возможны лишь перестановки вершин и .

Итак, для любого автоморфизма этого графа . Поскольку , то , и, следовательно, поскольку — единственная вершина, смежная с , всегда , т.е. вершина переходит в себя. Таким образом, единственным нетривиальным автоморфизмом данного графа будет транспозиция — “отражение” квадрата относительно диагонали .

---

Иногда группу автоморфизмов графа легко найти именно из чисто геометрических соображений при удачном изображении графа. Автоморфизм есть не что иное, как преобразование графа (геометрической фигуры), при котором граф совмещается с самим собой. Поэтому группу автоморфизмов графа можно изучать, анализируя его как геометрическую фигуру.

Пример 5.14. Для графа, изображенного на рис. 5.37, из геометрических соображений вытекает, что автоморфизм сводится к повороту графа на 60° по часовой стрелке вокруг центра тяжести треугольника .

Следовательно, группа автоморфизмов порождается подстановкой , являющейся композицией трех циклов:

Заметим, что ни один цикл, входящий в , сам по себе не будет автоморфизмом данного графа. Так, если мы рассмотрим цикл

, то и , но .

---

В заключение сформулируем без доказательства теорему, доказанную Фрухтом в 1938 г. и характеризующую все конечные группы в терминах групп автоморфизмов конечных неориентированных графов.

Теорема 5.5 (теорема Фрухта). Каждая конечная группа изоморфна группе автоморфизмов конечного неориентированного графа.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Чтобы быть в этом уверенным, необходимо доказать, что других автоморфизмов нет. Для этого полезно заметить, что граф имеет по 3 вершины степеней 2, 3, 5. Значит любой автоморфизм должен сохранять группы вершин {1,2,3}; {4,5,6}; {7,8,9}.

Если, например, автоморфизм оставляет неподвижной каждую из вершин 1,2,3, то нетрудно показать, что он оставляет неподвижными 4,5,6 и 7,8,9.
Если на первых трех вершинах он действует по правилу 1->2->3->1 (вращение), то другие три тройки он перемещает по тому же правилу: 4->5->6->4; 7->8->9->7.
И т.д, еще 4-ре таких выкладки.

Окончательно, между перестановками на символах 1,2,3 и автоморфизмами графа имеется биективное соответствие.

В математической области теории графов , автоморфизм графа является формой симметрии , в которой график отображается на себя, сохраняя при этом возможность соединения края вершины.

Формально автоморфизм графа G  = ( V , E ) – это перестановка σ множества вершин V такая, что пара вершин ( u , v ) образует ребро тогда и только тогда, когда пара (σ ( u ), σ ( v )) также образуют ребро. То есть, это изоморфизм графов из G к себе. Таким образом можно определить автоморфизмы как для ориентированных, так и для неориентированных графов . Композиция двух автоморфизмов еще один автоморфизм, а множество автоморфизмов данного графа, при операции композиции, образует группу , в группу автоморфизмов графа. В противоположном направлении, по теореме Фрухта , все группы могут быть представлены как группа автоморфизмов связного графа – точнее, кубического графа .

Вычислительная сложность

Построение группы автоморфизмов по крайней мере так же сложно (с точки зрения ее вычислительной сложности ), как решение проблемы изоморфизма графов , определение того, соответствуют ли два заданных графа вершина за вершиной и ребро за ребром. Действительно, G и H изоморфны тогда и только тогда, когда несвязный граф, образованный несвязным объединением графов G и H, имеет автоморфизм, который меняет местами две компоненты. Фактически, простой подсчет автоморфизмов полиномиально эквивалентен изоморфизму графов.

Проблема автоморфизма графа – это проблема проверки наличия у графа нетривиального автоморфизма. Он принадлежит к классу вычислительной сложности NP . Подобно проблеме изоморфизма графов, неизвестно, имеет ли она алгоритм с полиномиальным временем или он является NP-полным . Существует алгоритм с полиномиальным временем для решения проблемы автоморфизма графов для графов, в которых степени вершин ограничены константой. Проблема автоморфизма графов за полиномиальное время сводится к проблеме изоморфизма графов, но обратная редукция неизвестна. Напротив, твердость известна, когда автоморфизмы ограничены определенным образом; например, определение существования автоморфизма без неподвижной точки (автоморфизма, не фиксирующего вершину) является NP-полным, а проблема подсчета таких автоморфизмов является ♯P-полной .

Алгоритмы, программное обеспечение и приложения

Хотя для общей проблемы автоморфизма графов не известны алгоритмы наихудшего случая с полиномиальным временем, найти группу автоморфизмов (и распечатать неизбыточный набор генераторов) для многих больших графов, возникающих в приложениях, довольно просто. Для этой задачи доступно несколько программных инструментов с открытым исходным кодом, включая NAUTY , BLISS и SAUCY . SAUCY и BLISS особенно эффективны для разреженных графов, например, SAUCY обрабатывает некоторые графы с миллионами вершин за считанные секунды. Однако BLISS и NAUTY также могут создавать канонические метки, тогда как SAUCY в настоящее время оптимизирован для решения автоморфизма графов. Важное наблюдение состоит в том, что для графа с n вершинами группа автоморфизмов может быть определена не более чем с n-1 генераторами, и вышеуказанные программные пакеты гарантированно удовлетворяют этой границе как побочному эффекту их алгоритмов (минимальные наборы генераторы труднее найти и не особенно полезны на практике). Также кажется, что общая поддержка (т. Е. Количество перемещаемых вершин) всех генераторов ограничена линейной функцией n , что важно при анализе этих алгоритмов во время выполнения. Однако по состоянию на март 2012 года этот факт не установлен.

Практические приложения автоморфизма графов включают рисование графов и другие задачи визуализации, решение структурированных примеров логической удовлетворенности, возникающих в контексте формальной проверки и логистики . Молекулярная симметрия может предсказывать или объяснять химические свойства.

Отображение симметрии

Несколько графиков рисования ученые исследовали алгоритмы для рисования графиков таким образом , что автоморфизмы графа становятся видимыми как симметрии рисунка. Это можно сделать либо с помощью метода, который не ориентирован на симметрии, но который автоматически генерирует симметричные рисунки, когда это возможно, либо путем явного определения симметрий и их использования для направления размещения вершин на рисунке. Не всегда возможно отобразить все симметрии графика одновременно, поэтому может потребоваться выбрать, какие симметрии отображать, а какие оставить невидимыми.

Семейства графов, определяемые их автоморфизмами

Несколько семейств графов определяются наличием определенных типов автоморфизмов:

• Асимметричный граф неориентированный граф с только тривиальным автоморфизмом.
• Вершина-симметрический граф неориентированный граф , в котором каждая вершина может быть отображена на автоморфизм в любую другую вершину.
• Края симметрический граф неориентированный граф , в котором каждое ребро может быть отображен на автоморфизм в любой другой край.
• Симметрический граф представляет собой график , таким образом, что каждая пара смежных вершин может быть отображена на автоморфизм в любую другую пару смежных вершин.
• Расстояние-симметрический граф представляет собой график таким образом, что каждая пара вершин может быть отображен на автоморфизм в любой другой паре вершин , которые находятся на одинаковом расстоянии друг от друга.
• Пол-симметрический граф представляет собой график , который является краевым транзитивен , но не вершиной-транзитивны.
• Половинной симметрический граф представляет собой график , который является вершиной-симметрический и ребра транзитивны , но не симметричным.
• Кососимметрична граф представляет собой ориентированный граф вместе с перестановкой а на вершинах, отображающие края к краям , но изменяет направление каждого ребра. Кроме того, требуется, чтобы σ была инволюцией .

Отношения включения между этими семьями показаны в следующей таблице:

дистанционно-транзитивный		дистанционно-регулярный		строго регулярный
симметричный (дугово-транзитивный)		t -транзитивный, t ≥ 2
(если подключен)
вершинно- и реберно-транзитивные		реберно-транзитивные и регулярные		реберно-транзитивный
вершинно-транзитивный		обычный
Граф Кэли

Смотрите также

• Алгебраическая теория графов
• Отличительная окраска

использованная литература

внешние ссылки

• Вайсштейн, Эрик В. “Автоморфизм графа” . MathWorld .