Как найти количество булевых функций

Критерий Поста — одна из центральных теорем в теории булевых функций, устанавливающая необходимое и достаточное условие для того, чтобы некоторый набор булевых функций обладал достаточной выразительностью, чтобы представить любую булеву функцию. Впервые сформулирован американским математиком Эмилем Постом.

В середине 60-х годов почти одновременно в СССР и во Франции появились работы, где с иных позиций и в более доступной форме излагались результаты Поста. В 80-е годы сразу целому ряду исследователей с использованием различных подходов и различной техники удалось получить достаточно компактные доказательства результатов Поста.
Алгебраический подход в изучении замкнутых классов булевых функций (подалгебр итеративной алгебры Поста над множеством ) принадлежит А. И. Мальцеву.

Алгебра Поста и замкнутые классы[править | править код]

Булева функция — это функция типа , где , а — арность. Количество различных функций арности равно , общее же количество различных булевых функций бесконечно. Вместе с тем, очевидно, что многие функции могут быть выражены через другие с использованием оператора суперпозиции. Например, давно известно, что из дизъюнкции и отрицания можно, используя законы де Моргана, получить конъюнкцию. Кроме того, любая булева функция может быть представлена в виде ДНФ, то есть, в терминах конъюнкции, дизъюнкции и отрицания. Возникает естественный вопрос: как определить, будет ли данный набор функций достаточным, чтобы представить любую булеву функцию? Такие наборы называются функционально полными. Теорема Поста даёт ответ на этот вопрос. Поскольку условие теоремы является необходимыми и достаточным, её называют также критерием.

Идея теоремы состоит в том, чтобы рассматривать множество всех булевых функций как алгебру относительно операции суперпозиции. Сейчас она носит имя алгебра Поста. Эта алгебра содержит в качестве своих подалгебр множества функций, замкнутых относительно суперпозиции. Их называют ещё замкнутыми классами. Пусть — некоторое подмножество . Замыканием множества называется минимальная подалгебра , содержащая . Иными словами, замыкание состоит из всех функций, которые являются суперпозициями . Очевидно, что будет функционально полно тогда и только тогда, когда . Таким образом, вопрос, будет ли данный класс функционально полон, сводится к проверке того, совпадает ли его замыкание с .

Оператор является оператором замыкания. Иными словами, он обладает (среди прочих) свойствами:

Говорят, что множество функций порождает замкнутый класс (или класс порождается множеством функций ), если . Множество функций называется базисом замкнутого класса , если и для любого подмножества множества , отличного от .

Если к подалгебре , не совпадающей с прибавить один элемент, ей не принадлежащий, и образовать замыкание, результатом будет новая подалгебра, содержащая данную. При этом, она совпадёт с , в том и только в том случае, если между исходной подалгеброй, и нет никаких других подалгебр, то есть, если исходная подалгебра была максимальной. Таким образом, для того, чтобы проверить, что данное множество функций функционально полно, достаточно убедиться, что оно не входит целиком ни в одну из максимальных подалгебр . Оказывается, что таких подалгебр всего пять, и вопрос принадлежности к ним может быть решён просто и эффективно.

Двойственность, монотонность, линейность. Критерий полноты[править | править код]

Ниже приведены некоторые следствия, вытекающие из теорем о двойственных функциях.

Перейдем теперь к выяснению полноты конкретных наборов функций.

Основные классы функций: [править | править код]

Теорема о замкнутости основных классов функций[править | править код]

Отметим, что ни один из замкнутых классов целиком не содержится в объединении остальных четырёх. Это вытекает из следующих соотношений:

1. 
2. 
3. 
4. 
5. 

Формулировка критерия[править | править код]

То есть когда в ней можно реализовать пять функций: несамодвойственную, немонотонную, нелинейную, не сохраняющую 0 и не сохраняющую 1.

Доказательство[править | править код]

Доказательство критерия Поста основано на том, что система функций (И, ИЛИ и НЕ) является полной. Таким образом, любая система, в которой реализуемы эти три функции, также является полной. Докажем, что в системе, удовлетворяющей критерию Поста, всегда можно реализовать конъюнкцию, дизъюнкцию и отрицание.

Имея функцию, не сохраняющую 0, получим инвертор или константу 1[править | править код]

Рассмотрим функцию, не принадлежащую классу Т₀. Для неё

Эта функция может принадлежать, а может не принадлежать классу Т₁.

Имея функцию, не сохраняющую 1, получим инвертор или константу 0[править | править код]

Рассмотрим функцию, не принадлежащую классу Т₁. Для неё

Эта функция может принадлежать, а может не принадлежать классу Т₀.

Имея инвертор и несамодвойственную функцию, получим одну из констант[править | править код]

Рассмотрим функцию, не принадлежащую классу S самодвойственных функций. Для неё найдётся такой набор входных переменных X, что

Пусть, например, тогда и мы имеем константу 1.

Аналогично, если, например, тогда и мы имеем константу 0.

В любом случае, имея инвертор и несамодвойственную функцию мы можем получить одну из констант.

Имея инвертор и одну из констант, получим другую константу[править | править код]

Если в одном из вышеперечисленных случаев мы получили инвертор и одну из констант, вторую константу получим с помощью инвертора: или

Имея немонотонную функцию и обе константы, получим инвертор[править | править код]

Для немонотонной функции обязательно найдётся такой набор входных переменных, что

и

Пусть, например, и . Тогда .

В любом случае, имея немонотонную функцию и обе константы, мы можем получить инвертор.

Имеем инвертор и обе константы[править | править код]

В предыдущих подразделах мы перебрали все возможные варианты (см. рисунок) и пришли к выводу, что имея функции, не принадлежащие классам Т₀, Т₁, S и M, мы всегда можем различными способами получить инвертор и обе константы.

Имея нелинейную функцию, инвертор и константу 1, получим конъюнкцию[править | править код]

Нелинейная функция по определению имеет в полиноме Жегалкина хотя бы один член, содержащий конъюнкцию нескольких переменных. Пусть, например, имеется некоторая нелинейная функция

Зададимся целью построить на её основе конъюнкцию

Присвоим переменным значения 1, получим:

Очевидно, что в общем случае после такого преобразования получится функция вида

где квадратные скобки означают, что выделенный ими член может присутствовать в окончательном выражении, а может и нет.

В простейшем случае при отсутствии других членов сразу получаем конъюнкцию: :

Рассмотрим другие варианты.

• 
• 
• 
• .
• 
• 
• 

Любое из этих выражений, используя инвертор, можно привести к конъюнкции.

Таким образом, имея нелинейную функцию, инвертор и константу 1 всегда можно получить конъюнкцию.

Имея конъюнкцию и инвертор, получим дизъюнкцию[править | править код]

Имея инвертор и конъюнкцию, всегда можно получить дизъюнкцию:

• Теорема доказана.

Следствие[править | править код]

Функция в одиночку является полной системой тогда и только тогда, когда:

1. 
2. 
3. не является самодвойственной

Примерами функций, в одиночку являющихся полной системой, будут штрих Шеффера и стрелка Пирса .

Теорема о максимальном числе функций в базисе[править | править код]

Доказательство[править | править код]

1) Докажем, что из любой полной системы функций можно выделить полную подсистему, состоящую не более чем из четырёх функций.

Согласно критерию Поста, в полной системе должны присутствовать пять функций:

Рассмотрим функцию . Возможны два случая:

2) Покажем, что существует базис из четырёх функций. Рассмотрим систему функций . Эта система полна:

Однако ни одна его подсистема не полна:

• 
• 
• 
• 

Теорема доказана.

Примечания[править | править код]

Литература[править | править код]

• Марченков С. С. Замкнутые классы булевых функций. — М.: Физматлит, 2000.
• Фудзисава Т., Касами Т. Математика для радиоинженеров: теория дискретных структур. — М.: Радио и связь, 1984. — 240 с.
• Алексеев В. Б. Дискретная математика (II семестр). — М., МГУ, 2002. — 44 с.
• Белоусов А. И., Ткачев С. Б. Дискретная математика. — М.: МГТУ, 2006. — 744 с. — ISBN 5-7038-2886-4.
• Гиндикин С. Г. Алгебра логики в задачах. — М.: Наука, 1972. — 288 с.

Ссылки[править | править код]

• Учебник по дискретной математике. Суперпозиция функций. Замыкание набора функции.Замкнутые классы функций. Полные наборы. Базисы, mini-soft.ru

См. также[править | править код]

• Булева функция
• Законы де Моргана
• Алгебра логики
• Стрелка Пирса
• Дискретная математика

Определение:

Бу́лева фу́нкция (или логи́ческая функция, или функция а́лгебры ло́гики, англ. Boolean function) от переменных — отображение , где — булево множество.

Элементы булева множества и обычно интерпретируют как логические значения «истинно» и «ложно», хотя в общем случае они рассматриваются как формальные символы, не несущие определенного смысла. Элементы декартова произведения называют булевыми векторами. Множество всех булевых функций от любого числа переменных часто обозначается , а от n переменных — . Булевы функции названы так по фамилии математика Джорджа Буля.

Основные сведения

Определение:

А́рность (англ. arity) функции — количество ее аргументов.

Каждая булева функция арности полностью определяется заданием своих значений на своей области определения, то есть на всех булевых векторах длины . Число таких векторов равно . Поскольку на каждом векторе булева функция может принимать значение либо , либо , то количество всех n-арных булевых функций равно . То, что каждая булева функция задаётся конечным массивом данных, позволяет представлять их в виде таблиц. Такие таблицы носят название таблиц истинности и в общем случае имеют вид:

Таблица истинности

Практически все булевы функции малых арностей ( и ) сложились исторически и имеют конкретные имена. Если значение функции не зависит от одной из переменных (то есть строго говоря для любых двух булевых векторов, отличающихся лишь в значении этой переменной, значение функции на них совпадает), то эта переменная называется фиктивной (англ. dummy variable).

Нульарные функции

При количество булевых функций равно , первая из них тождественно равна , а вторая . Их называют булевыми константами — тождественный нуль и тождественная единица.

Унарные функции

При число булевых функций равно .

Таблица значений булевых функций от одной переменной:

Функции от одной переменной
0
1
Сохраняет 0	✓	✓
Сохраняет 1		✓		✓
Самодвойственная		✓	✓
Монотонная	✓	✓		✓
Линейная	✓	✓	✓	✓

Названия булевых функций от одной переменной:

Обозначение	Название
	тождественный ноль, тождественная ложь, тождественное “НЕТ”
	тождественная функция, логическое “ДА”, “YES”(англ.)
	отрицание, логическое “НЕТ”, “НЕ”, “НИ”, “NOT”(англ.), “NO”(англ.)
	тождественная единица, тождественная истина, тождественное “ДА”, тавтология

Бинарные функции

При число булевых функций равно .

Таблица значений булевых функций от двух переменных:

Функции от двух переменных:
x	y
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
Сохраняет 0	✓	✓	✓	✓	✓	✓	✓	✓
Сохраняет 1		✓		✓		✓		✓		✓		✓		✓		✓
Самодвойственная				✓		✓					✓		✓
Монотонная	✓	✓		✓		✓		✓								✓
Линейная	✓			✓		✓	✓			✓	✓		✓			✓

Названия булевых функций от двух переменных:

Обозначение	Другие обозначения	Название
		тождественный ноль, тождественная ложь, тождественное “НЕТ”
	И И	2И, конъюнкция
		больше, инверсия прямой импликации
	ДА1	первый операнд
		меньше, инверсия обратной импликации
	ДА2	второй операнд
		сложение по модулю 2, не равно, ксор, исключающее «или»
	ИЛИ ИЛИ	2ИЛИ, дизъюнкция
	ИЛИ-НЕ ИЛИ-НЕ	НЕ-2ИЛИ, 2ИЛИ-НЕ, антидизъюнкция, функция Да́ггера, функция Ве́бба, стрелка Пи́рса
		равенство, эквивалентность
	НЕ2	отрицание (негация, инверсия) второго операнда
		больше или равно, обратная импликация (от второго аргумента к первому)
	НЕ1	отрицание (негация, инверсия) первого операнда
		меньше или равно, прямая (материальная) импликация (от первого аргумента ко второму)
	И-НЕ И-НЕ	НЕ-2И, 2И-НЕ, антиконъюнкция, Штрих Шеффера
		тождественная единица, тождественная истина, тождественное “ДА”, тавтология

Тернарные функции

При число булевых функций равно . Некоторые из них определены в следующей таблице:

Таблица истинности некоторых тернарных функций
0	0	0	1	1	0	1	0	1	0	0	0	0	0
0	0	1	0	1	1	1	0	0	1	0	0	0	1
0	1	0	0	1	1	1	0	0	1	0	0	0	1
0	1	1	0	0	1	1	0	0	0	1	1	1	1
1	0	0	0	1	1	1	0	0	1	0	1	0	1
1	0	1	0	0	1	1	0	0	0	1	0	1	1
1	1	0	0	0	1	1	0	0	0	1	1	1	1
1	1	1	0	0	0	0	1	1	1	1	1	1	1

Названия булевых функций трех переменных:

Обозначения	Другие обозначения	Названия
		3-ИЛИ-НЕ, функция Вебба, функция Даггера, стрелка Пирса
		Переключатель по большинству с инверсией, 3-ППБ-НЕ, мажоритарный клапан с инверсией
		Неравенство
		3-И-НЕ, штрих Шеффера
	И И И	3-И, минимум
		Равенство
		Тернарное сложение по модулю 2
	И ИЛИ И ИЛИ И	переключатель по большинству, 3-ППБ, мажоритарный клапан
		Разряд займа при тернарном вычитании
		Разряд переноса при тернарном сложении
	ИЛИ ИЛИ ИЛИ	3-ИЛИ, максимум

Представление функции формулой

Определение:

Если выбрать некоторый набор булевых функций , то с использованием выбранных функций можно записать некоторые другие булевы функции. Такая запись булевой функции называется формулой (англ. formula).

Например, если , то функция представляется в виде

Тождественность и двойственность

Определение:

Две булевы функции тождественны (англ. identical) друг другу, если на любых одинаковых наборах аргументов они принимают равные значения.

Тождественность функций f и g можно записать, например, так:

Просмотрев таблицы истинности булевых функций, легко получить такие тождества:

А проверка таблиц, построенных для некоторых суперпозиций, даст следующие результаты:

(дистрибутивность конъюнкции и дизъюнкции)

Определение:

Функция называется двойственной (англ. duality) функции , если .

Легко показать, что в этом равенстве и можно поменять местами, то есть функции и двойственны друг другу. Из простейших функций двойственны друг другу константы и , а из законов де Моргана следует двойственность конъюнкции и дизъюнкции. Тождественная функция, как и функция отрицания, двойственна сама себе.

Если в булевом тождестве заменить каждую функцию на двойственную ей, снова получится верное тождество. В приведённых выше формулах легко найти двойственные друг другу пары.

Суперпозиции

Определение:

Суперпозиция функций, композиция функций (англ. function composition) — функция, полученная из некоторого множества функций путем подстановки одной функции в другую или отождествления переменных.

Множество всех возможных не эквивалентных друг другу суперпозиций данного множества функций образует замыкание данного множества функций.

Пусть нам дан некоторый набор булевых функций . Получить новую функцию, являющеюся композицией функций из , мы можем следующими способами:

• Подстановкой одной функции в качестве некоторого аргумента для другой;
• Отождествлением аргументов функций.

Полнота системы, критерий Поста

Определение:

Замыкание множества функций (англ. сlosure) — подмножество всех булевых функций, что любую из этих функций можно выразить через функции исходного множества.

Определение:

Множество булевых функций называется полной системой (англ. complete set), если замыкание этого множества совпадает с множеством всех функций.

Американский математик Эмиль Пост ^[1] сформулировал необходимое и достаточное условие полноты системы булевых функций. Для этого он ввел в рассмотрение следующие замкнутые классы булевых функций:

• функции, сохраняющие константу и ,
• самодвойственныые функции ,
• монотонные функции ,
• линейные функции .

Набор булевых функций является полным тогда и только тогда, когда он не содержится полностью ни в одном из классов , иными словами, когда в нем имеется хотя бы одна функция, не сохраняющая ноль, хотя бы одна функция, не сохраняющая один, хотя бы одна несамодвойственная функция, хотя бы одна немонотонная функция и хотя бы одна нелинейная функция.

Представление булевых функций

Теорема Поста открывает путь к представлению булевых функций синтаксическим способом, который в ряде случаев оказывается намного удобнее чем таблицы истинности. Отправной точкой здесь служит нахождение некоторой полной системы функций . Тогда каждая булева функция сможет быть представлена некоторым термом в сигнатуре , который в данном случае называют также формулой. Относительно выбраной системы функций полезно знать ответы на следующие вопросы:

• Как построить по данной функции представляющую её формулу?
• Как проверить, что две разные формулы эквивалентны, то есть задают одну и ту же функцию?
  • В частности: существует ли способ приведения произвольной формулы к эквивалентной её канонической форме, такой что, две формулы эквивалентны тогда и только тогда, когда их канонические формы совпадают?
• Как по данной функции построить представляющую её формулу с теми или иными заданными свойствами (например, наименьшего размера), и возможно ли это?

Положительные ответы на эти и другие вопросы существенно увеличивают прикладное значение выбранной системы функций.

Дизъюнктивная нормальная форма (ДНФ)

Основная статья: ДНФ

Определение:

Дизъюнктивная нормальная форма (ДНФ) (англ. disjunctive normal form, DNF) — нормальная форма, в которой булева функция задана как дизъюнкция некоторого числа простых конъюнктов.

Любая булева формула благодаря использованию закона двойного отрицания, закона де Моргана и закона дистрибутивности может быть записана в ДНФ.

Примеры ДНФ:

.

.

Конъюнктивная нормальная форма (КНФ)

Основная статья: КНФ

Определение:

Конъюнктивная нормальная форма, КНФ (англ. conjunctive normal form, CNF) — нормальная форма, в которой булева функция имеет вид конъюнкции нескольких простых дизъюнктов.

Любая булева формула с помощью использования закона двойного отрицания, закона де Моргана и закона дистрибутивности может быть записана в КНФ.

Пример КНФ:

Полином Жегалкина

Определение:

Полином Жегалкина (англ. Zhegalkin polynomial) — полином с коэффициентами вида и , где в качестве произведения берётся конъюнкция, а в качестве сложения исключающее или.

Полином Жегалкина имеет следующий вид:

С помощью полинома Жегалкина можно выразить любую булеву функцию, так как он строится из следующего набора функций: , который, в свою очередь, по теореме Поста является полным.

Примеры:

Тождественные функции. Выражение функций друг через друга

Определение:

Тождественные функции — функции, которые при любых одинаковых аргументах принимают равные значения.

Приведение тождественной функции есть выражение булевой функции через другие.

Запись булевой функции в ДНФ, КНФ, а также выражение с помощью полинома Жегалкина — способы выражения одних булевых функций через другие.

Пример:

Выразим следующие функции через систему функций .

Подстановка одной функции в другую

Определение:

Подстановкой (англ. substitution) функции в функцию называется замена -того аргумента функции значением функции :

Допускается также не только подстановка одной функции в другую, но и подстановка функции в саму себя.

При подстановке функции вместо -того аргумента функции , результирующая функция будет принимать аргументы, которые можно разделить на следующие блоки:

1.	— аргументы функции до подставленного значения функции
2.	— используются как аргументы для вычисления значения функции
3.	— аргументы функции после подставленного значения функции

Пример:

Исходные функции: — подстановка функции вместо второго аргумента функции . В данном примере при помощи подстановки мы получили функцию .

Отождествление переменных

Определение:

Отождествлением переменных (англ. identification of variables) называется подстановка -того аргумента функции вместо -того аргумента:

Таким образом, при отождествлении переменных мы получаем функцию с количеством аргументов .

Пример:

— исходная функция — функция с отождествленными первым и вторым аргументами Очевидно, в данном примере мы получили функцию — проектор единственного аргумента.

Схемы из функциональных элементов

Определение:

Схема из функциональных элементов, логическая схема (англ. logic diagram) — размеченный ориентированный граф без циклов, в некотором базисе , в котором: 1. вершины, в которые не входят ребра, называются входами схемы, и каждая из них помечена некоторой переменной (разным вершинам соответствуют разные переменные); 2. в каждую из остальных вершин входит одно или более ребер (зависит от выбранного базиса ). Такие вершины называются функциональными элементами и реализуют какую-либо булеву функцию из базиса .

Отождествление переменных осуществляется при помощи ветвления проводников.

Чтобы осуществить подстановку одной функции в другую нужно выход логического элемента, который реализует первую функцию, направить на вход логического элемента, который реализует вторую функцию.

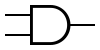
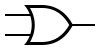
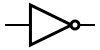
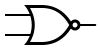
Некоторые логические элементы:

И	ИЛИ	НЕ	Штрих Шеффера	Стрелка Пирса

Стандартный базис

Определение:

Стандартный базис — система булевых функций:

Если рассматривать множество бинарных булевых функций , то для выражения любой булевой функции данного множества (кроме стрелки Пирса и штриха Шеффера) через стандартный базис достаточно выразить тождественные функции для эквиваленции, импликации и константы с использованием функций, принадлежащих стандартному базису, т. к. все остальные операции можно выразить через данные 3 функции с помощью отрицания:

Функции являются отрицаниями функций соответственно.

Тождественность функций можно доказать с помощью таблицы истинности.

Пример:

Выразим через стандартный базис обратную импликацию .

Полнота стандартного базиса

Утверждение:

Данное утверждение – следствие теоремы об СДНФ. Если рассмотреть функцию, не равную тождественному нулю, то она представима в виде СДНФ, в которой используются функции стандартного базиса. Способ выражения тождественного нуля через функции стандартного базиса уже был описан выше.

Замечание:

По закону де Моргана:

Следовательно, стандартный базис является избыточным, в то время как безызбыточными являются подмножества системы:

(конъюнктивный базис Буля)

(дизъюнктивный базис Буля)

Теоремы о числе функций в базисе

Теорема:

Максимально возможное число булевых функций в безызбыточном базисе — четыре.

Доказательство:

Рассмотрим произвольный безызбыточный базис . Тогда по теореме Поста содержит следующие функции (не обязательно различные): , где — классы Поста. Значит, так как — безызбыточный базис, а система — полная, то Рассмотрим . Возможны два случая: 1. , тогда также не сохраняет единицу и немонотонная, т.е. . Значит, . 2. , тогда несамодвойственная, т.е. . Значит, .

Теорема:

Для любого числа найдётся базис , что .

Доказательство:

Приведём примеры базисов для каждого : ; ; ; ; Докажем, что последняя система является базисом: ; ; ; (доказывается с помощью таблицы истинности).

См. также

• Специальные формы КНФ
• Сокращенная и минимальная ДНФ
• Пороговая функция
• Cумматор
• Полные системы функций. Теорема Поста о полной системе функций

Примечания

Источники информации

• Гаврилов Г. П., Сапоженко А. А. Сборник задач по дискретной математике. — М.: Наука, 1969.
• Кузнецов О. П., Адельсон-Вельский Г. М. Дискретная математика для инженера. — М.: «Энергия», 1980. — 344 с.
• Марченков С. С. Замкнутые классы булевых функций. — М.: Физматлит, 2000.
• Яблонский С. В. Введение в дискретную математику. — М.: Наука, 1986.
• Алексеев В. Б. Дискретная математика (курс лекций, II семестр). Сост. А. Д. Поспелов
• Быкова С. В., Буркатовская Ю. Б., Булевы функции, учебно-методический комплекс, Томск, 2006
• Учебные пособия кафедры математической кибернетики ВМиК МГУ
• Булева функция — Википедия
• http://psi-logic.narod.ru/bool/bool.htm

В математике булевой функцией называют функцию типа , где — булево множество, а — неотрицательное целое число, которое называют арностью. Элементы 1 (единица) и 0 (ноль) стандартно интерпретируют как истину и ложь, хотя в общем случае их смысл может быть любым. Элементы называют булевыми векторами. В случае булева функция превращается в булеву константу.

Основные сведения

Каждая булева функция арности полностью определяется заданием своих значений на своей области определения, то есть на всех булевых векторах длины . Число таких векторов равно . Поскольку на каждом векторе функция может принимать значение либо 0, либо 1, количество всех n-арных булевых функций равно . То, что каждая булева функция задаётся конечным массивом данных, позволяет представлять их в виде таблиц. Такие таблицы носят название таблиц истинности и в общем случае имеют вид:

0	0		0
1	0		0
0	1		0
1	1		0
0	1		1
1	1		1

Практически все булевы функции малых арностей (0, 1 и 2) сложились исторически и имеют конкретные имена.

Нульарные функции

При количество булевых функций сводится к двум, первая из них тождественно равна 0, а вторая 1. Их называют булевыми константами.

Унарные функции

При число булевых функций равно . Им соответствуют следующие таблицы истинности.

x	g1 ()	g2 (=)	g3 (1)	g4 (0)
0	1	0	1	0
1	0	1	1	0

Здесь:

• g₁(x) — отрицание (обозначения: ),
• g₂(x) — тождественная функция,
• g₃(x) и g₄(x) — соответственно, тождественная истина и тождественная ложь.

Бинарные функции

При число булевых функций равно . Им соответствуют следующие таблицы истинности.

x	y		f1 ()	f2 ()	f3 ()	f4 ()	f5 ()	f6 ()	f7 ()	f8 (  )
0	0		0	0	1	0	1	1	1	1
0	1		0	1	0	1	0	1	0	1
1	0		0	1	0	1	1	0	0	1
1	1		1	1	1	0	1	1	0	0
x	y		f9	f10	f11	f12	f13	f14	f15	f16
0	0		0	0	1	1	0	0	1	0
0	1		0	1	1	0	0	1	1	0
1	0		1	0	0	1	1	0	1	0
1	1		0	0	0	0	1	1	1	0

Здесь:

• f₁(x, y) — конъюнкция (обозначения: x&y, ),
• f₂(x, y) — дизъюнкция (обозначение: ),
• f₃(x, y) — эквивалентность (обозначения: ),
• f₄(x, y) — исключающее «или» (сложение по модулю 2; обозначения: ),
• f₅(x, y) — импликация от y к x (обозначения: ),
• f₆(x, y) — импликация от x к y (обозначения: ),
• f₇(x, y) — стрелка Пи́рса(функция Да́ггера, функция Ве́бба, антидизъюнкция; обозначение: ),
• f₈(x, y) — штрих Ше́ффера (антиконъюнкция; обозначение: ),
• f₉(x, y) — отрицание импликации f₆(x, y),
• f₁₀(x, y) — отрицание импликации f₅(x, y),
• f₁₁(x, y) = g₁(x),
• f₁₂(x, y) = g₁(y),
• f₁₃(x, y) = g₂(x),
• f₁₄(x, y) = g₁(y),
• f₁₅(x, y), f₁₆(x, y) — тождественная истина и тождественная ложь.

Полные системы булевых функций

Суперпозиция и замкнутые классы функций

Результат вычисления булевой функции может быть использован в качестве одного из агрументов другой функции. Результат такой операции суперпозиции можно рассматривать как новую булеву функцию со своей таблицей истинности. Например, функции (суперпозиция конъюнкции, дизъюнкции и двух отрицаний) будет соответствовать следующая таблица:

0	0	0		1
0	0	1		1
0	1	0		1
0	1	1		1
1	0	0		0
1	0	1		0
1	1	0		1
1	1	1		0

Говорят, что множество функций замкнуто относительно операции суперпозиции, если любая суперпозиция функций из данного множества тоже входит в это же множество. Замкнутые множества функций называют также замкнутыми классами.

В качестве простейших примеров замкнутых классов булевых функций можно назвать множество , состоящее из одной тождественной функции, или множество , все функции из которого тождественно равны нулю вне зависимости от своих аргументов. Замкнуты также множество функций и множество всех унарных функций. А вот объединение замкнутых классов может таковым уже не являться. Например, объединив классы и , мы с помощью суперпозиции сможем получить константу 1, которая в исходных классах отсутствовала.

Разумеется, множество всех возможных булевых функций тоже является замкнутым.

Тождественность и двойственность

Две булевы функции тождественны друг другу, если на любых одинаковых наборах аргументов они принимают равные значения. Тождественность функций f и g можно записать, например, так:
)

Просмотрев таблицы истинности булевых функций, легко получить такие тождества:

А проверка таблиц, построенных для некоторых суперпозиций, даст следующие результаты:

(дистрибутивность конъюнкции и дизъюнкции)

Функция называется двойственной функции , если . Легко показать, что в этом равенстве f и g можно поменять местами, то есть функции f и g двойственны друг другу. Из простейших функций двойственны друг другу константы 0 и 1, а из законов де Моргана следует двойственность конъюнкции и дизъюнкции. Тождественная функция, как и функция отрицания, двойственна сама себе.

Если в булевом тождестве заменить каждую функцию на двойственную ей, снова получится верное тождество. В приведённых выше формулах легко найти двойственные друг другу пары.

Полнота системы, критерий Поста

Система булевых функций называется полной, если можно построить их суперпозицию, тождественную любой другой заранее заданной функции. Говорят ещё, что замыкание данной системы совпадает с множеством .

Американский математик Эмиль Пост ввёл в рассмотрение следующие замкнутые классы булевых функций:

Им было доказано, что любой замкнутый класс булевых функций, не совпадающий с , целиком содержится в одном из этих пяти так называемых предполных классов, но при этом ни один из пяти не содержится целиком в объединении четырёх других. Таким образом критерий Поста для полноты системы сводится к выяснению, не содержится ли вся эта система целиком в одном из предполных классов. Если для каждого класса в системе найдётся функция, не входящая в него, то такая система будет полной, и с помощью входящих в неё функций можно будет получить любую другую булеву функцию.

Заметим, что существуют функции, не входящие ни в один из классов Поста. Любая такая функция сама по себе образует полную систему. В качестве примеров можно назвать функцию Шеффера или стрелку Пирса.

Представление булевых функций

Теорема Поста открывает путь к представлению булевых функций, синтаксическим способом, который в ряде случаев оказывается намного удобнее чем таблицами истинности. Отправной точкой здесь служит нахождение некоторой полной системы функций . Тогда каждая булева функция сможет быть представлена некоторым термом в сигнатуре , который в данном случае называют также формулой. Относительно выбраной системы функций полезно знать ответы на следующие вопросы:

• Как построить по данной функции представляющую её формулу?
• Как проверить, что две разные формулы эквивалентны, то есть задают одну и ту же функцию?
  • В частности: существует ли способ приведения произвольной формулы к эквивалентной её канонической форме, такой что, две формулы эквивалентны тогда и только тогда, когда их канонические формы совпадают?
• Как по данной функции построить представляющую её формулу с теми или иными заданными свойствами (например наименьшего размера), и возможно ли это?

Положительные ответы на эти и другие вопросы существенно увеличивают прикладное значение выбранной системы функций.

Дизъюнктивная нормальная форма (ДНФ)

Простой конъюнкцией, или конъюнктом, называется конъюнкция некоторого конечного набора переменных, или их отрицаний, причём каждая переменная встречается не более одного раза. Дизъюнктивной нормальной формой или ДНФ называется дизъюнкция простых конъюнкций. Например   — является ДНФ.

Совершенной дизъюнктивной нормальной формой, или СДНФ относительно некоторого заданного конечного набора переменных называется такая ДНФ, у которой в каждую конъюнкцию входят все переменные данного набора, причём в одном и том же порядке. Например: .

Легко убедится, что каждой булевой функции соответствует некоторая ДНФ, и даже СДНФ. Для этого достаточно взять таблицу истинности этой функции и найти все булевы векторы, на которых её значение равно 1. Для каждого такого вектора строится конъюнкция , где . Если взять дизъюнкцию этих конъюнкций, то результатом очевидно будет СДНФ. Поскольку на всех булевых векторах её значения совпадают со значениями исходной функции, она будет СДНФ этой функции. Например, для импликации , результатом будет , что можно упростить до .

Шаблон:Section-stub

Конъюнктивная нормальная форма (КНФ)

Конъюнктивная нормальная форма (КНФ) определяется двойственно к ДНФ. Простой дизъюнкцией или дизъюнктом называется дизъюнкция одной или нескольких переменных или их отрицаний, причём каждая переменная входит в неё не более одного раза. КНФ — это конъюнкция простых дизъюнкций.

Совершенной конъюнктивной нормальной формой (СКНФ), относительно некоторого заданного конечного набора переменных, называется такая КНФ, у которой в каждую дизъюнкцию входят все переменные данного набора, причём в одном и том же порядке. Поскольку (С)КНФ и (С)ДНФ взаимодвойственны, свойства (С)КНФ повторяют все свойства (С)ДНФ, грубо говоря, «с точностью до наоборот».

КНФ может быть преобразована к эквивалентной ей ДНФ, путём раскрытия скобок по правилу:

которое выражает дистрибутивность конъюнкции относительно дизъюнкции. После этого, необходимо в каждой конъюнкции удалить повторяющиеся переменные или их отрицания, а также выбросить из дизъюнкции все конъюнкции, в которых встречается переменная вместе со своим отрицанием. При этом, результатом не обязательно будет СДНФ, даже если исходная КНФ была СКНФ. Точно также, можно всегда перейти от ДНФ к КНФ. Для этого следует использовать правило

выражающее дистрибутивность дизъюнкции относительно конъюнкции. Результат нужно преобразовать способом, описанным выше, заменив слово «конъюнкция» на «дизъюнкция» и наоборот.

Шаблон:Section-stub

Полиномы Жегалкина

Шаблон:Planned

BDD

Шаблон:Planned

См. также

• Булева алгебра
• Исчисление высказываний
• Битовые операции

Литература

• Яблонский С.В. Введение в дискретную математику. — М.: Наука. — 1986
• Гаврилов Г.П., Сапоженко А.А. Сборник задач по дискретной математике. — М.: Наука. — 1969
• Алексеев В.Б. Дискретная математика (курс лекций, II семестр). Сост. А.Д. Поспелов

Ссылки

• Быкова С.В., Буркатовская Ю.Б., Булевы функции, учебно-методический комплекс, Томск, 2006
• http://olddesign.isu.ru/~slava/do/disc/fr_bools.htm
• http://psi-logic.narod.ru/bool/bool.htm
• Учебные пособия кафедры математической кибернетики ВМиК МГУ

Шаблон:Computer-sci-stub

There are two independent questions here:

1. Show that the number of boolean functions on n variables obeys the recurrence relation.
2. Solve the recurrence relation.

Let’s address each in turn.

Deriving the Recurrence

Let’s start with boolean functions of a single variable. These functions will assign either 0 or 1 to the input 0 and either 0 or 1 to the input 1. This means that there are four possible functions based on those possible outputs. In fact, you can list them all here:

f(0) = 0    g(0) = 0   h(0) = 1   i(0) = 1
f(1) = 0    g(1) = 1   h(1) = 0   i(1) = 1

Therefore, T(1) = 4.

Now, let’s think about how many (n + 1)-variable boolean functions there are. You can think of an (n + 1)-variable boolean function f(b₁, b₂, …, b_n, b_n+1) as being defined in terms of two other n-variable boolean functions g and h:

g(b₁, b₂, …, b_n) = f(b₁, b₂, …, b_n, 0)

h(b₁, b₂, …, b_n) = f(b₁, b₂, …, b_n, 1)

In other words, for any pair of n-variable boolean functions g and h, you can derive a unique (n + 1)-variable boolean function. There are T(n)² pairs of n-variable boolean functions, so the total number of (n + 1)-variable boolean functions is T(n)². Thus T(n + 1) = T(n)².

Solving the Recurrence

Now, we have to figure out how to solve the recurrence

T(1) = 4

T(n + 1) = T(n)²

This is a great place to try unrolling the first few terms:

• T(1) = 4
• T(2) = 16
• T(3) = 256
• T(4) = 65536

These are all powers of two, so it might be a good idea to rewrite them as 2^k for various choices of k. Doing that yields

• T(1) = 2²
• T(2) = 2⁴
• T(3) = 2⁸
• T(4) = 2¹⁶

From this, it seems like the pattern is that T(n) = 2²ⁿ. We can formalize this by induction:

• T(1) = 4 = 2²¹
• T(n + 1) = T(n)² = (2²ⁿ)² = 2^{2 · 2n} = 2^{2n + 1}

So everything checks out.

There’s another way to think about this. Any string of n boolean variables can be thought of as a binary number ranging from 0 to 2ⁿ – 1. That is, there are 2ⁿ choices of n boolean variables. For each of those choices, there are two possible outputs from a function, either 0 or 1. Therefore, you can think about the number of n-variable boolean functions as the number of functions from a set of 2ⁿ elements to a set of two elements. The choice of the output of the function on one input is totally independent of the choice of output of the function on another input, so we’re making 2ⁿ independent decisions of whether to assign 0 or 1. There are 2²ⁿ ways to do this, matching the bound from before.

Hope this helps!

В предыдущей лекции мы уже говорили о булевых функциях от одного и от двух аргументов. Введем понятие булевой функции от произвольного конечного числа аргументов.

Определение 10.1. Булевой функцией от n аргументов называется функция , заданная на множестве и принимающая значения в двухэлементном множестве . Другими словами, булева функция от аргументов сопоставляет каждому упорядоченному набору длины , составленному из элементов 0 и 1, либо 0, либо 1.

Булева функция от аргументов обозначается так: .

Две булевы функции от аргументов и называются равными, если любым одинаковым наборам значений аргументов обе эти функции сопоставляют одинаковые элементы из множества , т.е. для любых элементов .

Ранее уже встречались булевы функции от трех аргументов, например

В частности, было показано, что и . Перечисленные функции построены с помощью суперпозиций (или последовательного применения) более простых функций.

---

Суперпозиция булевых функций

Определение 10.2. Суперпозицией булевых функций в булеву функцию называется новая булева функция, получающаяся из функции подстановкой вместо (всех или некоторых) аргументов функций соответственно . Полученная функция зависит от аргументов.

Например, если и , то

Или если и , то имеем

Опишем еще одну процедуру, которую можно проделывать с булевыми функциями. Зафиксировав один из аргументов булевой функции от аргументов, т.е. придав этому аргументу какое-нибудь конкретное постоянное значение (из двухэлементного множества ), получим функцию от аргументов. Так, фиксируя в функции k-й аргумент , можем получить две новые булевы функции от аргументов:

и .

Например, из функции от трех аргументов фиксированием первого аргумента получаем следующие функции от двух аргументов:

Предлагаем посмотреть самостоятельно, какие получатся функции из функции при последовательном фиксировании остальных ее аргументов .

---

Число булевых функций

Перечислив ранее все булевы функции от одного аргумента и от двух аргументов, мы видели, что первых имеется всего четыре, а вторых — шестнадцать. Возникает вопрос, сколько будет разных булевых функций от трех аргументов, от четырех аргументов и т.д. Нельзя ли указать формулу, по которой вычислялось бы число булевых функций от аргументов? Ответ на поставленный вопрос дает следующая теорема.

Теорема 10.3 (о числе булевых функций от аргументов). Число различных булевых функций от аргументов равно .

Доказательство. Чтобы задать булеву функцию от аргументов, нужно перечислить все наборы из нулей и единиц значений, которые могут принимать ее аргументы , и для каждого такого набора указать значение функции , которое она принимает на этом наборе.

Выясним сначала, сколько существует различных наборов , составленных из нулей и единиц, значений для аргументов . Покажем, что это число равно . Доказательство будем вести методом математической индукции по числу . В самом деле, для имеется всего два набора значений переменного . Это 0 и 1. Так что для число наборов равно . Предположим, что для аргументов имеется точно различных наборов , составленных из 0 и 1, значений для к аргументов. Тогда среди всевозможных различных наборов значений для аргумента имеется, согласно предположению индукции, точно наборов вида и точно наборов вида . Следовательно, всего будет различных наборов. Тем самым доказано с помощью индукции утверждение о числе различных наборов.

Таким образом, для задания функции от аргументов нужно указать ее значение для каждого из различных наборов значений ее аргументов. Если каждое значение функции равно нулю, то такая функция постоянна. Она называется константа 0. Если каждое значение функции равно единице, то это вторая постоянная функция, называемая константа 1. Мы указали лишь две различные функции от аргументов. Сколько же их существует всего? Ровно столько, сколько имеется разных наборов длины , составленных из нулей и единиц (см. таблицу).

Разных наборов длины , составленных из нулей и единиц, как показано в начале доказательства теоремы, имеется , где — длина набора. Таким образом, число разных булевых функций от аргументов равно точно . Теорема доказана.

---

Выражение булевых функций через конъюнкцию, дизъюнкцию и отрицание

У нас уже возникали вопросы относительно выражения одних булевых функций через другие, и на некоторые из них мы уже дали ответ. Как будет показано ниже, существуют такие булевы функции (уже хорошо известные нам), через которые выражаются все (вообще все, от любого числа аргументов!) булевы функции. Этим замечательным свойством обладают взятые вместе конъюнкция, дизъюнкция и отрицание. Прежде чем сформулировать и доказать основную теорему этого пункта, обратимся к следующей важной лемме.

Лемма 10.4 (о разложении функции по переменной). Для произвольной булевой функции справедливы следующие формулы, называемые формулами разложения этой функции по переменной

Доказательство. Докажем справедливость первой формулы. Нужно проверить, что функции, стоящие в обеих частях равенства, при одинаковых значениях их аргументов принимают равные значения. Рассмотрим сначала всевозможные наборы значений аргументов следующего вида , т.е. будем придавать аргументам значения: . При этом безразлично, каковы именно значения . Вычислив, какое значение принимает на наборах такого вида функция, стоящая в правой части доказываемого равенства, убедимся, что оно совпадает со значением, принимаемым функцией, стоящей в левой части этого равенства, на том же наборе значений аргументов. В самом деле,

Теперь рассмотрим всевозможные наборы значений аргументов вида , т.е. будем придавать аргументам значения: . Аналогично вычисляем значение, принимаемое функцией, стоящей в правой части доказываемого равенства, на наборах такого вида:

Итак, функции из обеих частей равенства принимают одинаковые значения при одинаковых значениях их аргументов. Следовательно, эти функции равны и доказываемая формула справедлива.

Совершенно аналогично доказывается вторая формула.

Заметим, что подобным образом могут быть записаны формулы разложения булевой функции по любой ее переменной. Запишите, например, такие разложения по последней переменной.

---

Представление булевых функций через конъюнкцию, дизъюнкцию и отрицание

Теорема 10.5 (о представлении булевых функций через конъюнкцию, дизъюнкцию и отрицание). Всякая булева функция может быть представлена в виде суперпозиции конъюнкции, дизъюнкции и отрицания; причем знак отрицания стоит только непосредственно около переменной и не стоит ни перед одной из внутренних скобок.

Доказательство будем вести методом математической индукции по числу аргументов функции .

В предыдущем параграфе перечислены все булевы функции от одного аргумента. Их всего четыре. Напомним их (используя равенства теоремы 9.3, пункт и):

Отсюда видно, что все функции от одного аргумента выражаются через конъюнкцию, дизъюнкцию и отрицание; причем знак отрицания стоит только непосредственно около переменных. Это означает, что утверждение теоремы справедливо при .

Предположим, что теорема верна для всех функций от аргументов. Докажем ее для функций от аргумента. Пусть — произвольная булева функция от аргумента. На основании предыдущей леммы запишем разложение данной функции по последней переменной:

Как отмечалось в начале настоящего параграфа, фиксирование в булевой функции одного аргумента приводит к булевой функции с числом аргументов на единицу меньшим, нежели число аргументов исходной функции. Так что каждая из функций и есть булева функция от аргументов. Но согласно предположению индукции, все такие функции выражаются через конъюнкцию, дизъюнкцию и отрицание, причем знак отрицания стоит только непосредственно около переменных и не стоит ни перед одной из внутренних скобок. Принимая это во внимание, видим, что правая часть последнего равенства представляет собой суперпозицию лишь трех функций — конъюнкции, дизъюнкции и отрицания. Причем отрицание стоит около переменной . Это и доказывает окончательно теорему.

---

Булевы функции и формулы алгебры высказываний

Установим сначала соответствие между формулами алгебры высказываний и булевыми функциями. Это делается следующим образом. Во-первых, определяется взаимно-однозначное соответствие между пропозициональными переменными и булевыми переменными, при котором прописная буква, обозначающая пропозициональную переменную, соответствует той же самой строчной букве, обозначающей булеву переменную:

Во-вторых, устанавливается соответствие между знаками логических связок и одноименных булевых функций:

Наконец скобкам ставятся в соответствие те же скобки. Тогда каждой формуле алгебры высказываний соответствует единственная булева функция, а каждой булевой функции соответствует формула алгебры высказываний. Чтобы найти для данной формулы алгебры высказываний соответствующую ей булеву функцию, достаточно каждую прописную букву формулы заменить на такую же строчную букву, а каждый символ логической операции — на символ одноименной булевой функции.

Например, формуле соответствует булева функция .

Если булева функция задана с помощью формулы, то для того чтобы найти соответствующую этой функции формулу алгебры высказываний, нужно в выражении для булевой функции заменить строчные буквы такими же прописными буквами, а каждый символ булевой функции заменить соответственно символом одноименной логической операции . Здесь возникает неоднозначность такого обратного соответствия, поскольку булева функция может иметь множество различных формульных выражений. Например, функция, рассмотренная в предыдущем абзаце, имеет также следующие формульные выражения:

Этим выражениям сопоставляются соответственно следующие формулы алгебры высказываний:

Следовательно, все перечисленные формулы соответствуют одной и той же булевой функции.

Возникает вопрос, всякой ли булевой функции соответствует некоторая формула алгебры высказываний. Другими словами, всякая ли булева функция может быть выражена (представлена) некоторой формулой алгебры высказываний. Если булева функция задана с помощью формулы, то соответствующая этой функции формула алгебры высказываний отыскивается так, как описано в предыдущем абзаце. Если же булева функция задана не в виде формулы, то, в силу теоремы 10.5, формульное выражение для нее тем не менее существует, и, следовательно, представляющая ее формула алгебры высказываний может быть найдена по правилу, описанному выше.

Итак, отметим еще раз, что каждой формуле алгебры высказываний соответствует единственная определяемая этой формулой булева функция, что будет для нас важным в дальнейшем.

---

Нормальные формы булевых функций

На основе теоремы 10.5 всякая булева функция может быть представлена некоторой формулой алгебры высказываний. Нетрудно понять, что всякая формула алгебры высказываний, равносильная формуле, представляющей некоторую булеву функцию ; будет представлять функцию, равную . В частности, одной из таких представляющих формул будет совершенная дизъюнктивная нормальная форма (если данная булева функция не равна тождественно 0, т.е. представляющая формула не тождественно ложна) или совершенная конъюнктивная нормальная форма (если данная булева функция не равна тождественно 1, т.е. представляющая формула не является тавтологией). Отыскав совершенную нормальную форму для формулы алгебры высказываний, представляющей данную булеву функцию (применяя правила, полученные в теоремах 5.2 и 5.4), можно перейти от этой формы к формульному выражению для данной булевой функции. Его будем называть совершенной (дизъюнктивной или конъюнктивной) нормальной формой булевой функции, сокращенно СДН-формой или соответственно СКН-формой. Каждая из них для данной булевой функции, если она существует, единственна.

Приобретя опыт работы с булевыми функциями, можно отыскивать их нормальные формы, не переходя к символике алгебры высказываний. При этом, если функция задана каким-то формульным выражением, то для его тождественного преобразования следует пользоваться свойствами булевых функций, установленными в теоремах 9.3–9.5, а если функция задана своими значениями на всех наборах значений аргументов (т.е. если она задана таблично), то следует применять правила, полученные в теоремах 5.2 и 5.4, переведя их предварительно на язык булевых функций.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.