Производная положительна только тогда, когда функция возрастает. То есть, нам необходимо найти точки, в которых функция растет. Смотрим на график нашей функции: функция растет на промежутках: от (x=-7) до (x=0) и от (x = 6) до (x=12).
Так как по условию нам нужны только ЦЕЛЫЕ точки, в которых производная положительна, то это будут: (x=—6); (x=-5), (x=-4), (x=-3), (x=-2), (x=-1), (x=7), (x=8), (x=9), (x=10), (x=11). Всего точек получилось (11). Я отметил их зеленым цветом.
Обратите внимание, что точки (x=-7), (x=0), (x=6), (x=12) мы не считаем, так как в этих точках у нас будут минимумы и максимумы функции, а в них производная равна нулю, то есть не положительна.
Ответ: (11.)
Пример 2
На рисунке 6 изображен график функции, определенной на промежутке ((-10;12)). Найдите количество точек, в которых производная функции равна нулю.
Задания
Версия для печати и копирования в MS Word
Тип 7 № 7089 
i
На рисунке изображен график функции y = f(x), определенной на интервале (−1; 13). Определите количество целых точек, в которых производная функции положительна.
Спрятать решение
Решение.
Производная функции положительна на тех интервалах, на которых функция возрастает, т. е. на интервалах (−1; 0), (1; 2) и (6,6; 10). В них содержатся целые точки 7, 8 и 9. Всего 3 точки.
Ответ: 3.
Аналоги к заданию № 27487: 6867 7089 559401 … Все
Кодификатор ФИПИ/Решу ЕГЭ:
3.2.1 Монотонность функции. Промежутки возрастания и убывания;
4.1.1 Понятие о производной функции, геометрический смысл производной;
4.2.1 Применение производной к исследованию функций и построению графиков.
Спрятать решение
·
Прототип задания
·
Видеокурс
·
Помощь
Рассмотрим задания из №6 ЕГЭ, в которых по графику функции требуется определить точки, в которых производная положительна либо отрицательна.
№1
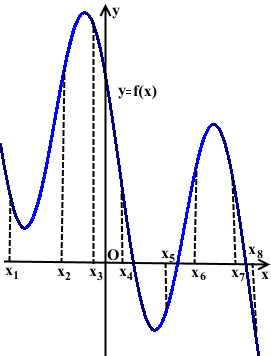
На рисунке изображён график дифференцируемой функции y=f(x). На оси абсцисс отмечены восемь точек: x1, x2 ,x3, x4, … , x8. Среди этих точек найдите все точки, в которых производная функции f(x) положительна. В ответе укажите количество найденных точек.
Решение:
Производная функции f'(x) положительна там, где функция y=f(x) возрастает:
f'(x)>0, если f(x) возрастает.
Выделяем промежутки возрастания функции y=f(x) и определяем количество точек, принадлежащих этим промежуткам.
Промежуткам возрастания функции y=f(x) принадлежат три точки: x2, x5 и x6.
Значит, производная функции в этих трёх точках положительна:
f'(x2)>0,
f'(x5)>0,
f'(x6)>0.
Ответ: 3.
№2
На рисунке изображён график функции y=f(x) и отмечены девять точек на оси абсцисс: x1, x2 ,x3, x4 …x8, x9. В скольких из этих точек производная функции f(x) отрицательна?
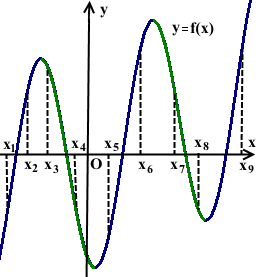
Решение:
Производная функции f'(x) отрицательна там, где функция y=f(x) убывает:
f'(x)<0, если f(x) убывает.
Выделяем промежутки убывания функции y=f(x) и определяем количество точек, принадлежащих этим промежуткам.
Промежуткам убывания функции y=f(x) принадлежат четыре точки: x3, x4, x7 и x8. Значит, производная в этих четырёх точках отрицательна:
f'(x3)<0, f'(x4)<0, f'(x7)<0, f'(x8)<0.
Ответ: 4.
№3
На рисунке изображен график функции y=f(x), определенной на интервале (−6; 12). Определите количество целых точек, в которых производная функции положительна.
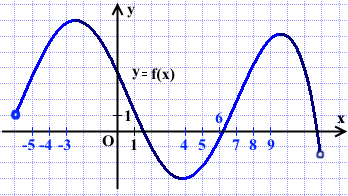
Решение:
Производная функции f'(x) положительна там, где функция y=f(x) возрастает.
Выделяем промежутки возрастания.
Целые точки, входящие в промежутки возрастания: -5; -4; -3; 4; 5; 6; 7; 8; 9.
Всего девять точек.
Ответ: 9.
09
Авг 2013
Категория: 07 Производная, ПО
07. Применение производной к исследованию функции
2013-08-09
2023-04-30
Cледующая таблица будет весьма полезна при работе с данной темой.
Пожалуйста, будьте предельно внимательны в следующем. Смотрите, график ЧЕГО вам дан! Функции 
или ее производной 
Если дан график производной, то интересовать нас будут только знаки функции 
и нули. Никакие «холмики» и «впадины», как в случае не интересуют нас в принципе!
Задача 1. На рисунке изображен график функции 
, определенной на интервале 
. Определите количество целых точек, в которых производная функции отрицательна.
Решение: + показать
Задача 2. На рисунке изображен график функции , определенной на интервале 
. Найдите количество точек, в которых касательная к графику функции параллельна прямой 
или совпадает с ней.
Решение:+ показать
Задача 3. На рисунке изображен график производной функции , определенной на интервале 
. Найдите количество точек, в которых касательная к графику функции параллельна прямой 
или совпадает с ней.
Решение: + показать
Задача 4. На рисунке изображен график функции , определенной на интервале 
. Найдите количество точек, в которых производная функции равна 0.
Решение: + показать
Задача 5. На рисунке изображён график функции и одиннадцать точек на оси абсцисс:
. В скольких из этих точек производная функции отрицательна?
Решение: + показать
Задача 6. На рисунке изображен график функции , определенной на интервале 
. Найдите сумму точек экстремума функции .
Решение: + показать
Задача 7. На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки возрастания функции . В ответе укажите сумму целых точек, входящих в эти промежутки.
Решение: + показать
Задача 8. На рисунке изображен график производной функции , определенной на интервале 
. Найдите промежутки возрастания функции . В ответе укажите длину наибольшего из них.
Решение: + показать
Задача 9. На рисунке изображен график производной функции , определенной на интервале . В какой точке отрезка ![[-5;-1]](https://egemaximum.ru/wp-content/ql-cache/quicklatex.com-6a13fc362ff43608ffd2dbac0045a6c3_l3.svg "Rendered by QuickLaTeX.com")
принимает наибольшее значение.
Решение: + показать
Задача 10. На рисунке изображен график 
— производной функции , определенной на интервале 
. Найдите количество точек максимума функции , принадлежащих отрезку ![[-8;13]](https://egemaximum.ru/wp-content/ql-cache/quicklatex.com-49fdb01b8008c05932c7deeccb657568_l3.svg "Rendered by QuickLaTeX.com")
.
Решение: + показать
Задача 11. На рисунке изображен график функции и отмечены точки -3, 1, 6, 8. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Решение: + показать
Задача 12. Функция определена на промежутке 
На рисунке изображен график её производной. Найдите точку 
в которой функция принимает наименьшее значение, если 
Решение: + показать
Задача 13. Функция определена и непрерывна на полуинтервале 
На рисунке изображен график её производной. Найдите промежутки убывания функции 
В ответе укажите сумму целых точек, входящих в эти промежутки.
Решение: + показать
Вы можете пройти тест «Применение производной к исследованию функции»
Автор: egeMax |
комментариев 29
Печать страницы
Задание
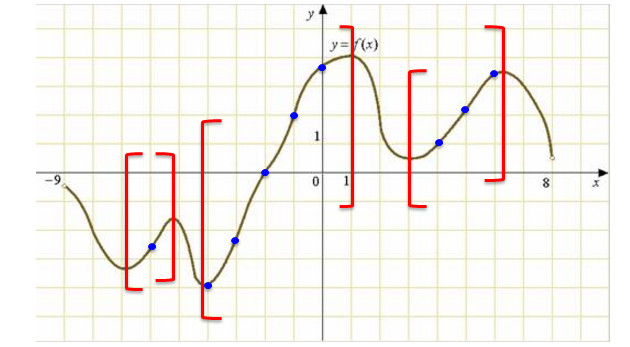
На рисунке изображен график функции y=f(x), определенной на интервале (-9;8). Определите количество целых точек, в которых производная функции f(x) положительна.
Решение
- Для решения данной задачи необходимо знать, что производная функции положительна на отрезках, на которых функция возрастает, и наоборот, производная функции отрицательна на тех отрезках, где функции убывает.
- У нас дан график самой функции, а не её производной, это нужно понимать и не путать.
- Определим участки, на которых функция возрастает, и тем самым определим участки, на которых производная функции положительна. Данные участки выделим красными линиями.
- Получили 3 отрезка. Теперь посчитаем на этих участках количество целых точек (выделяем синим цветом). Целые точки определяются по оси х, а не у.
- Получили 9 точек, в которых производная функции положительна.
Ответ: 9
