Описание задачи
Программа принимает число и выводит количество цифр в нем.
Решение задачи
- Берем значение целого числа и записываем его в переменную.
- Используем цикл
whileи при помощи оператора целочисленного деления «уничтожаем» каждую цифру числа начиная с последней, а при каждой итерации цикла специально созданную переменную (так называемый счетчик цикла) увеличиваем на единицу. После того как введенное в начале число станет равным 0, цикл прекратит свою работу. - Выводим значение этого счетчика на экран.
- Конец.
Исходный код
Ниже дан исходный код для подсчета количества цифр в данном числе. Результаты работы программы также даны ниже.
n = int(input("Введите число:"))
count = 0
while(n > 0):
count = count + 1
n = n // 10
print("Количество цифр равно:", count)
Объяснение работы программы
- Записываем введенное пользователем число в переменную
n. - Задаем переменную
countи инициируем ее значением 0. - Используем цикл
whileи при помощи оператора целочисленного деления «уничтожаем» каждую цифру числа начиная с конца. - При каждой итерации цикла переменная
countувеличивается на 1. - Как только цифры в числе заканчиваются и число
nстановится равным 0, цикл прекращает свою работу. - Выводим переменную
countна экран.
Результаты работы программы
Пример 1: Введите число:123 Количество цифр равно: 3 Пример 2: Введите число:1892 Количество цифр равно: 4
Примечание переводчика
Надо заметить, что опять эту задачу можно решить намного короче, если использовать методы строк.
print("Количество цифр равно:", len(input("Введите число:")))
Здесь введенное число принимается как строка и мы просто выводим ее длину.
Given a number N, the task is to return the count of digits in this number.
Example:
Program to count digits in an integer
Simple Iterative Solution to count digits in an integer
The integer entered by the user is stored in the variable n. Then the while loop is iterated until the test expression n != 0 is evaluated to 0 (false). We will consider 3456 as the input integer.
- After the first iteration, the value of n will be updated to 345 and the count is incremented to 1.
- After the second iteration, the value of n will be updated to 34 and the count is incremented to 2.
- After the third iteration, the value of n will be updated to 3 and the count is incremented to 3.
- In the fourth iteration, the value of n will be updated to zero and the count will be incremented to 4.
- Then the test expression is evaluated ( n!=0 ) as false and the loop terminates with final count as 4.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int countDigit(long long n)
{
if (n == 0)
return 1;
int count = 0;
while (n != 0) {
n = n / 10;
++count;
}
return count;
}
int main(void)
{
long long n = 345289467;
cout << "Number of digits : " << countDigit(n);
return 0;
}
C
#include <stdio.h>
int countDigit(long long n)
{
if (n == 0)
return 1;
int count = 0;
while (n != 0) {
n = n / 10;
++count;
}
return count;
}
int main(void)
{
long long n = 345289467;
printf("Number of digits : %d", countDigit(n));
return 0;
}
Java
import java.io.*;
public class GFG {
static int countDigit(long n)
{
int count = 0;
while (n != 0) {
n = n / 10;
++count;
}
return count;
}
public static void main(String[] args)
{
long n = 345289467;
System.out.print("Number of digits : "
+ countDigit(n));
}
}
Python3
def countDigit(n):
count = 0
while n != 0:
n //= 10
count += 1
return count
n = 345289467
print("Number of digits : % d" % (countDigit(n)))
C#
using System;
class GFG {
static int countDigit(long n)
{
int count = 0;
while (n != 0) {
n = n / 10;
++count;
}
return count;
}
public static void Main()
{
long n = 345289467;
Console.WriteLine("Number of"
+ " digits : " + countDigit(n));
}
}
PHP
<?php
function countDigit($n)
{
$count = 0;
while ($n != 0)
{
$n = round($n / 10);
++$count;
}
return $count;
}
$n = 345289467;
echo "Number of digits : "
. countDigit($n);
?>
Javascript
<script>
function countDigit(n)
{
let count = 0;
while (n != 0)
{
n = Math.floor(n / 10);
++count;
}
return count;
}
n = 345289467;
document.write("Number of digits : "+ countDigit(n));
</script>
Output
Number of digits : 9
Time Complexity : O(log10(n)) or O(num digits)
Auxiliary Space: O(1) or constant
Recursive Solution to count digits in an integer
Keep dividing the number by 10 this reduces the input number size by 1 and keeps track of the number of sizes reduced.
Algorithm:
- The base condition of this recursive approach is when we divide the number by 10 and the number gets reduced to 0, so return 1 for this operation.
- Make a function call by dividing the number by 10, reducing the input size of the given number by 1, and adding 1 for this operation.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int countDigit(long long n)
{
if (n/10 == 0)
return 1;
return 1 + countDigit(n / 10);
}
int main(void)
{
long long n = 345289467;
cout << "Number of digits :" << countDigit(n);
return 0;
}
C
#include <stdio.h>
int countDigit(long long n)
{
if (n/10 == 0)
return 1;
return 1 + countDigit(n / 10);
}
int main(void)
{
long long n = 345289467;
printf("Number of digits : %d", countDigit(n));
return 0;
}
Java
import java.util.*;
class GFG {
static int countDigit(long n)
{
if (n/10 == 0)
return 1;
return 1 + countDigit(n / 10);
}
public static void main(String[] args)
{
long n = 345289467;
System.out.print("Number of digits : "
+ countDigit(n));
}
}
Python3
def countDigit(n):
if n//10 == 0:
return 1
return 1 + countDigit(n // 10)
n = 345289467
print("Number of digits : % d" % (countDigit(n)))
C#
using System;
class GFG {
static int countDigit(long n)
{
if (n/10 == 0)
return 1;
return 1 + countDigit(n / 10);
}
public static void Main()
{
long n = 345289467;
Console.WriteLine("Number of "
+ "digits : "
+ countDigit(n));
}
}
PHP
<?php
function countDigit($n)
{
if ($n/10 == 0)
return 1;
return 1 + countDigit((int)($n / 10));
}
$n = 345289467;
print ("Number of digits : " .
(countDigit($n)));
?>
Javascript
<script>
function countDigit(n)
{
if (n/10 == 0)
return 1;
return 1 + countDigit(parseInt(n / 10));
}
var n = 345289467;
document.write("Number of digits :" + countDigit(n));
</script>
Output
Number of digits :9
Time Complexity : O(log(n))
Auxiliary Space : O(log(n))
Log-based Solution to count digits in an integer
We can use log10(logarithm of base 10) to count the number of digits of positive numbers (logarithm is not defined for negative numbers).
Digit count of N = upper bound of log10(N).
Below is the implementation of the above idea:
C++
#include <bits/stdc++.h>
using namespace std;
int countDigit(long long n) {
return floor(log10(n) + 1);
}
int main(void)
{
long long n = 345289467;
cout << "Number of digits : "
<< countDigit(n);
return 0;
}
C
#include <math.h>
#include <stdio.h>
int countDigit(long long n) {
return floor(log10(n) + 1);
}
int main(void)
{
long long n = 345289467;
printf("Number of digits : %d", countDigit(n));
return 0;
}
Java
import java.util.*;
class GFG {
static int countDigit(long n)
{
return (int)Math.floor(Math.log10(n) + 1);
}
public static void main(String[] args)
{
long n = 345289467;
System.out.print("Number of digits : "
+ countDigit(n));
}
}
Python3
import math
def countDigit(n):
return math.floor(math.log10(n)+1)
n = 345289467
print("Number of digits : % d" % (countDigit(n)))
C#
using System;
class GFG {
static int countDigit(long n)
{
return (int)Math.Floor(Math.Log10(n) + 1);
}
public static void Main()
{
long n = 345289467;
Console.WriteLine("Number of digits : "
+ countDigit(n));
}
}
PHP
<?php
function countDigit($n)
{
return floor(log10($n)+1);
}
$n = 345289467;
echo "Number of digits : ",
countDigit($n);
?>
Javascript
<script>
function countDigit(n)
{
return Math.floor(Math.log10(n) + 1);
}
var n = 345289467;
document.write("Number of digits : " +
countDigit(n));
</script>
Output
Number of digits : 9
Time Complexity: O(1) or constant
Auxiliary Space: O(1) or constant
Converting given number to string solution to count digits in an integer
We can convert the number into a string and then find the length of the string to get the number of digits in the original number.
Note: It gives TLE for numbers other than range of int,example long and long long .
C++
#include <bits/stdc++.h>
using namespace std;
void count_digits(int n)
{
string num = to_string(n);
cout << num.size() << endl;
}
int main()
{
int n = 345;
count_digits(n);
return 0;
}
Java
import java.util.*;
public class GFG {
static void count_digits(int n)
{
String num = Integer.toString(n);
System.out.println(+num.length());
}
public static void main(String args[])
{
int n = 345;
count_digits(n);
}
}
Python3
def count_digits(n):
n = str(n)
return len(n)
n = 456533457776
print(count_digits(n))
C#
using System;
using System.Collections.Generic;
class GFG {
static void count_digits(int n)
{
string num = Convert.ToString(n);
Console.WriteLine(+num.Length);
}
public static void Main(string[] args)
{
int n = 345;
count_digits(n);
}
}
Javascript
<script>
function count_digits(n)
{
let num = n.toString();
document.write(num.length);
}
let n = 345;
count_digits(n);
</script>
Time Complexity: O(1) or constant
Auxiliary Space: O(Number of digits in an integer)
This article is contributed by Suruchi Kumari . If you like GeeksforGeeks and would like to contribute, you can also write an article using contribute.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.
Last Updated :
16 Feb, 2023
Like Article
Save Article
ЗАДАЧА 3.14. Дано натуральное число 


Входные данные: N — целое число.
Выходные данные: сообщение.
Промежуточные данные: i — параметр цикла, возможные делители числа N.
Алгоритм решения этой задачи (рис. 3.33) заключается в том, что необходимо определить, есть ли у числа N делители среди чисел от 2 до N/2. Если делителей нет — число простое. Предположим, что число N является простым (Pr:=true). Организуем цикл, в котором переменная i будет изменяться от 2 до N/2. В цикле будем проверять, делится ли N на i. Если делится, то мы нашли делитель, N не является простым (Pr:=false). Проверка остальных делителей не имеет смысла, аварийно покидаем цикл.
В алгоритме предусмотрено два выхода из цикла. Первый — естественный, при исчерпании всех значений параметра, а второй — досрочный. После выхода из цикла надо проверить значение Pr. Если Pr=true, то число N — простое, иначе N не является простым числом.
При составлении программы на языке Free Pascal досрочный выход из цикла удобно выполнять при помощи оператора break:
var
N, i : integer;
Pr : boolean;
begin
write ( ’N= ’ );
readln (N);
Pr:= true; {Предположим, что число простое.}
for i :=2 to N div 2 do
{Если найдется хотя бы один делитель, то}
if N mod i = 0 then
begin
Pr:= false; {число простым не является и}
break; {досрочный выход из цикла.}
end;
{Проверка значения логического параметра, и}
if Pr then
{вывод на печать соответствующего сообщения.}
writeln ( ’Число ’,N, ’ - простое ’ )
else
writeln ( ’Число ’,N, ’ простым не является ’ );
end.
ЗАДАЧА 3.15. Определить количество простых чисел в интервале от 




Алгоритм решения данной задачи представлен на рис. 3.34.
Обратите внимание, что здесь осуществляется проверка корректности ввода исходных данных. Если границы интервала не положительны, или значение N превышает M, ввод данных повторяется в цикле с постусловием до тех пор, пока не будут введены корректные исходные данные. Далее для каждого числа из указанного интервала (параметр i принимает значения от N до M) происходит проверка. Если число является простым, то переменная k увеличивается на единицу. Подробно определение простого числа описано в задаче 3.14.
Программа на языке Free Pascal, реализующая алгоритм подсчёта количества простых чисел в заданном диапазоне:
var N,M, i, j, k : longint;
Pr : boolean;
begin
repeat
write ( ’N= ’ );
readln (N);
write ( ’M= ’ );
readln (M);
until (N>0) and (M>0) and (N<M);
k : = 0; {Количество простых чисел.}
for i :=N to M do {Параметр i принимает значения от N до M.}
begin
{Определение простого числа.}
Pr:= true;
for j :=2 to i div 2 do
if i mod j = 0 then
begin
Pr:= false;
break;
end;
{Если число простое, увеличиваем количество на 1.}
if Pr then
k:=k+1;
end;
if k=0 then writeln ( ’Простых чисел в диапазоне нет ’ )
else writeln ( ’Простых чисел в диапазоне ’, k );
end.
ЗАДАЧА 3.16. Дано натуральное число 
Входные данные: N — целое число.
Выходные данные: kol — количество цифр в числе.
Промежуточные данные: M — переменная для временного хранения значения N.
Для того чтобы подсчитать количество цифр в числе, необходимо определить, сколько раз заданное число можно разделить на десять нацело. Например, пусть N=12345, тогда количество цифр kol = 5. Результаты вычислений сведены в таблицу 3.8. Алгоритм определения количества цифр в числе представлен на рис. 3.35.
| kol | N |
|---|---|
| 1 | 12345 |
| 2 | 12345 div 10=1234 |
| 3 | 1234 div 10=123 |
| 4 | 123 div 10=12 |
| 5 | 12 div 10=1 |
| 1 div 10=0 |
Текст программы, реализующей данную задачу, можно записать так:
var
M,N: longint;
kol : word;
begin
{Так как речь идёт о натуральных числах,}
{при вводе предусмотрена проверка.}
{Закончить цикл, если введено положительное число,}
{иначе повторить ввод}
repeat
write ( ’N= ’ );
readln (N);
until N>0;
M:=N; {Сохранить значение переменной N. }
kol : = 1; {Пусть число состоит из одной цифры.}
while M div 10 > 0 do
{Выполнять тело цикла, пока число делится нацело на 10.}
begin
kol := kol +1; {Счётчик количества цифр.}
M:=M div 1 0; {Изменение числа.}
end;
writeln ( ’ kol= ’, kol );
end.
ЗАДАЧА 3.17. Дано натуральное число 
Входные данные: N — целое число.
Выходные данные: pos — позиция цифры в числе.
Промежуточные данные: i — параметр цикла, M — переменная для временного хранения значения N.
В связи с тем, что разряды в числе выделяются, начиная с последнего, то для определения номера разряда в числе, необходимо знать количество цифр в
числе1212Алгоритм нахождения количества цифр в числе был рассмотрен в предыдущей задаче.. Таким образом, на первом этапе решения задачи необходимо определить kol — количество цифр в числе. Затем начинаем выделять из числа цифры; если очередная цифра равна нулю, нужно вывести на экран номер разряда, который занимает эта цифра. Процесс определения текущей цифры числа N=120405 представлен в таблице 3.9.
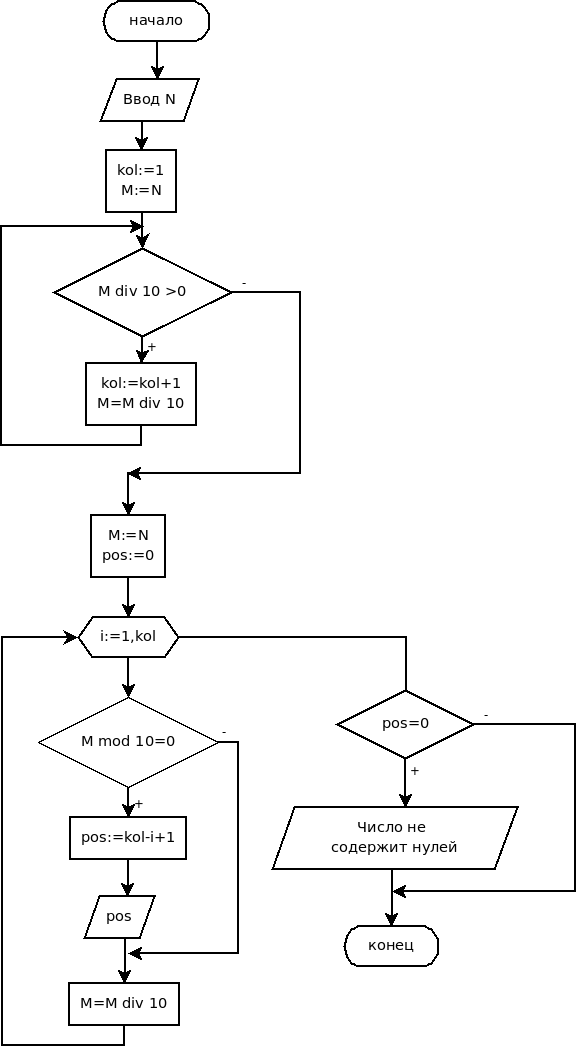
Блок-схема алгоритма решения данной задачи показана на рис. 3.36.
Рис.
3.36.
Алгоритм решения задачи 3.17
| i | Число М | Цифра | Номер позиции |
|---|---|---|---|
| 1 | 120405 div 10=12040 | 120405 mod 10=5 | 6 |
| 2 | 12040 div 10=1204 | 12040 mod 10=0 | 5 |
| 3 | 1204 div 10=120 | 1204 mod 10=4 | 4 |
| 4 | 120 div 10=12 | 120 mod 10=0 | 3 |
| 5 | 12 div 10=1 | 12 mod 10=2 | 2 |
| 6 | 1 div 10=0 | 1 mod 10=1 | 1 |
Текст программы, реализующей данный алгоритм:
var
M,N: longint;
i, pos, kol : word;
begin
{Так как речь идет о натуральных числах,}
{при вводе предусмотрена проверка.}
{Закончить цикл, если введено положительное число,}
{иначе повторить ввод}
repeat
write ( ’N= ’ );
readln (N);
until N>0;
//Определение kol - количества разрядов.
M:=N; {Сохранить значение переменной N.}
kol : = 1; {Пусть число состоит из одной цифры.}
while M div 10 > 0 do
{Выполнять тело цикла, пока число делится нацело на 10.}
begin
kol := kol +1; {Счётчик количества цифр.}
M:=M div 1 0; {Изменение числа.}
end;
writeln ( ’ kol= ’, kol );
M:=N;
pos : = 0; {Пусть в числе нет нулей.}
for i :=1 to kol do
begin
{Выделение цифры из числа и сравнение её с нулем.}
if (M mod 10 = 0) then
begin
pos := kol-i +1; {Позиция нуля в числе.}
writeln ( ’Ноль в ’, pos, ’м- разряде. ’ );
end;
M:=M div 1 0; {Изменение числа.}
end;
if pos=0 then writeln ( ’Число не содержит цифру 0. ’ );
end.
Мой код проходит по всем тестам на 90%, не проходит один тест.
Проблему почему не проходит на все 100 – не нашёл..
Условие: Найти количество цифр заданного целого числа number.
Пример: вводим число 37 должно вывести число 2.
Код:
#include <iostream>
int main() {
long long int number = 0;
int result = 0;
std::cin >> number;
while(number != 0) {
number /= 10;
result++;
}
std::cout << result << "n";
}
insolor
45.7k16 золотых знаков54 серебряных знака95 бронзовых знаков
6
Почти наверняка в том единственном тесте вводится 0.
Делать условие именно на то, что юзер введёт цифру 0, и нужно вывести 1. Както колхозно, как можно реализовать без етого?
Делать отдельно условие нормально, но если есть желание сделать без условия, то можно и без него:
cin >> number;
int result = 1;
while (number /= 10) ++result;
cout << result;
ответ дан 5 мар 2022 в 10:17
Qwertiy♦Qwertiy
121k24 золотых знака121 серебряный знак291 бронзовый знак
3
Если вводите с консоли, то и не нужно рассматривать последовательность цифр как число. Можно просто читать и “выбрасывать” символы_цифры, с увеличением счетчика:
int res{};
while (isdigit(getchar())) ++res;
printf("%d", res);
Вариантов решения много.
Задание должно четко выразить что критично и каким образом задается объект. Потому что “задано число” наталкивает написать функцию с целочисленным аргументом, а пример рождает вопрос “откуда вводится?”…
ответ дан 5 мар 2022 в 10:23
AR HovsepyanAR Hovsepyan
15.8k3 золотых знака13 серебряных знаков30 бронзовых знаков
2
В этой статье мы разберем два способа посчитать, сколько цифр в числе. Первый способ предполагает использование целочисленного деления в цикле while. Второй – применение встроенных функций Python и преобразование числа в строку.
Считаем количество цифр в числе при помощи цикла while
Идея данного подхода состоит в том, чтобы удалять крайнюю правую цифру в числе до тех пор, пока число не станет равно 0.
Вот алгоритм этого метода:
- Получаем от пользователя число и записываем его в переменную
- Создаем переменную-счетчик и инициализируем ее значением 0
- При помощи цикла
whileудаляем крайнюю правую цифру (123 превращается в 12, потом в 1 и потом в 0) - При каждой итерации цикла увеличиваем значение счетчика на 1 и делаем это, пока исходное число не будет равно 0. В конечном итоге в переменной-счетчике будет содержаться значение, соответствующее количеству цифр в числе
- Выводим полученное значение в консоль
count = 0
number = int(input("Enter a number "))
while (number > 0):
number = number // 10
count = count + 1
print("Total number of digits: ", count)
# Результат:
# Enter a number 155
# Total number of digits: 3
Объяснение алгоритма:
- Данный код полностью идентичен алгоритму, который мы привели выше.
count— это переменная-счетчик, используемая для хранения общего количества цифр в числе. Она инициализируется в начале нулем. - Для ввода числа мы используем метод
input(). Данный метод возвращает строку, поэтому мы оборачиваем его в методint(), который преобразует ее в целое число. Оно сохраняется в переменнуюnumber. - Цикл
whileбудет выполняться до тех пор, пока значение переменнойnumberбольше нуля. - В теле цикла мы производим целочисленное деление числа, которое хранится в переменной number, на 10. И далее сохраняем в эту переменную новое число, полученное в результате такого деления. Если значение переменной было равно 123, то после целочисленного деления на 10 оно станет равно 12. Это полностью эквивалентно удалению крайней правой цифры числа.
- После этого мы увеличиваем значение счетчика (переменная
count) на 1. В конце концов исходное число в переменнойnumberстанет равно 0 и цикл прекратит свою работу. - Выводим значение переменной count в консоль.
Считаем, сколько цифр в числе, преобразовав его в строку
Вместо использования цикла while мы можем напрямую преобразовать целое число в строку и получить длину этой строки. В Python получить длину строки легко с помощью встроенного метода len(). Для преобразования числа в строку мы можем использовать метод str().
Встроенная функция abs() используется для получения абсолютного значения числа, то есть наша программа будет обрабатывать и тот случай, когда число будет отрицательным.
Допустим, наше входное значение равно -123. Функция abs() преобразует его в 123, функция str() конвертирует 123 в строку. После этого функция len() возвращает длину строки, то есть значение 3.
Код программы на Python:
count = 0
number = int(input("Enter a number "))
print("Total number of digits: ", len(str(abs(number))))
# Результат:
# Enter a number 123
# Total number of digits: 3
Примечание редакции: возможно, вас также заинтересует статья “Как разбить число на цифры в Python”.
Перевод статьи “Count number of digits in a number in Python”.