Содержание
- II. Молекулярная физика
- Тестирование онлайн
- Тепловой двигатель
- Коэффициент полезного действия
- Цикл Карно
- Цикл теплового двигателя
- Расчет характеристик цикла теплового двигателя.
II. Молекулярная физика
Тестирование онлайн
Тепловой двигатель
Двигатель, в котором происходит превращение внутренней энергии топлива, которое сгорает, в механическую работу.
Любой тепловой двигатель состоит из трех основных частей: нагревателя, рабочего тела (газ, жидкость и др.) и холодильника. В основе работы двигателя лежит циклический процесс (это процесс, в результате которого система возвращается в исходное состояние).
Прямой цикл теплового двигателя
Общее свойство всех циклических (или круговых) процессов состоит в том, что их невозможно провести, приводя рабочее тело в тепловой контакт только с одним тепловым резервуаром. Их нужно, по крайней мере, два. Тепловой резервуар с более высокой температурой называют нагревателем, а с более низкой – холодильником. Совершая круговой процесс, рабочее тело получает от нагревателя некоторое количество теплоты Q1 (происходит расширение) и отдает холодильнику количество теплоты Q2, когда возвращается в исходное состояние и сжимается. Полное количество теплоты Q=Q1-Q2, полученное рабочим телом за цикл, равно работе, которую выполняет рабочее тело за один цикл.
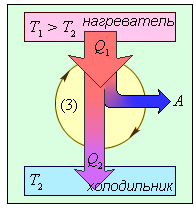
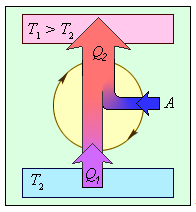
Обратный цикл холодильной машины
При обратном цикле расширение происходит при меньшем давлении, а сжатие — при большем. Поэтому работа сжатия больше, чем работа расширения, работу выполняет не рабочее тело, а внешние силы. Эта работа превращается в теплоту. Таким образом, в холодильной машине рабочее тело забирает от холодильника некоторое количество теплоты Q1 и передает нагревателю большее количество теплоты Q2.
Коэффициент полезного действия


Показатель эффективности холодильной машины:


Цикл Карно
В тепловых двигателях стремятся достигнуть наиболее полного превращения тепловой энергии в механическую. Максимальное КПД.
На рисунке изображены циклы, используемые в бензиновом карбюраторном двигателе и в дизельном двигателе. В обоих случаях рабочим телом является смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного двигателя внутреннего сгорания состоит из двух изохор (1–2, 3–4) и двух адиабат (2–3, 4–1). Дизельный двигатель внутреннего сгорания работает по циклу, состоящему из двух адиабат (1–2, 3–4), одной изобары (2–3) и одной изохоры (4–1). Реальный коэффициент полезного действия у карбюраторного двигателя порядка 30%, у дизельного двигателя – порядка 40 %.
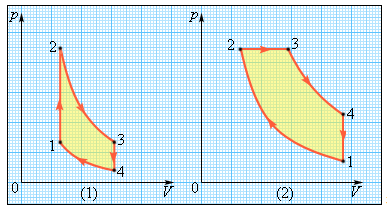
Французский физик С.Карно разработал работу идеального теплового двигателя. Рабочую часть двигателя Карно можно представить себе в виде поршня в заполненном газом цилиндре. Поскольку двигатель Карно — машина чисто теоретическая, то есть идеальная, силы трения между поршнем и цилиндром и тепловые потери считаются равными нулю. Механическая работа максимальна, если рабочее тело выполняет цикл, состоящий из двух изотерм и двух адиабат. Этот цикл называют циклом Карно.

участок 1-2: газ получает от нагревателя количество теплоты Q1 и изотермически расширяется при температуре T1
участок 2-3: газ адиабатически расширяется, температура снижается до температуры холодильника T2
участок 3-4: газ экзотермически сжимается, при этом он отдает холодильнику количество теплоты Q2
участок 4-1: газ сжимается адиабатически до тех пор, пока его температура не повысится до T1.
Работа, которую выполняет рабочее тело — площадь полученной фигуры 1234.
Функционирует такой двигатель следующим образом:
1. Сначала цилиндр вступает в контакт с горячим резервуаром, и идеальный газ расширяется при постоянной температуре. На этой фазе газ получает от горячего резервуара некое количество тепла.
2. Затем цилиндр окружается идеальной теплоизоляцией, за счет чего количество тепла, имеющееся у газа, сохраняется, и газ продолжает расширяться, пока его температура не упадет до температуры холодного теплового резервуара.
3. На третьей фазе теплоизоляция снимается, и газ в цилиндре, будучи в контакте с холодным резервуаром, сжимается, отдавая при этом часть тепла холодному резервуару.
4. Когда сжатие достигает определенной точки, цилиндр снова окружается теплоизоляцией, и газ сжимается за счет поднятия поршня до тех пор, пока его температура не сравняется с температурой горячего резервуара. После этого теплоизоляция удаляется и цикл повторяется вновь с первой фазы.
КПД цикла Карно не зависит от вида рабочего тела
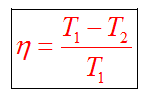

для холодильной машины


В реальных тепловых двигателях нельзя создать условия, при которых их рабочий цикл был бы циклом Карно. Так как процессы в них происходят быстрее, чем это необходимо для изотермического процесса, и в то же время не настолько быстрые, чтоб быть адиабатическими.
Источник
Цикл теплового двигателя
Принцип преобразования тепловой энергии в механическую работу состоит в использовании эффекта значительного объемного расширения газообразных рабочих тел при их нагревании.
Чтобы реализовать этот принцип необходимо иметь машину с рабочей полостью переменного объема, который должен быть заполнен рабочим телом. Один их вариантов такой машины — цилиндр с поршнем, перемещение которого позволяет изменять рабочий объем. При подводе теплоты к газу, последний расширяется и, оказывая силовое воздействие на поршень, перемещает его и производит внешнюю работу:
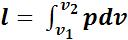 . (1.22)
. (1.22)
Из выражения (1.22) видно, что работа будет производиться только при увеличении объема рабочего тела, и как только возможности его расширения будут исчерпаны, преобразование прекратится. Для возобновления полезного действия машины, рабочее тело надо вернуть в исходное состояние, т. е. переместить поршень, уменьшив объем рабочего тела.
Таким образом, для непрерывного получения механической работы необходимо осуществить круговой процесс, т. е. цикл.
Циклом называется совокупность процессов, происходящих в определенной последовательности, в результате осуществления которых рабочее тело возвращается в первоначальное состояние.
На рис. 12 представлены р— v диаграммы циклов работы тепловых машин.
В реальных тепловых двигателях после осуществления каждого цикла происходит смена рабочего тела. Однако возможны и замкнутые циклы, совершаемые с одним и тем же рабочим телом путем изменения параметров его состояния. С точки зрения термодинамики эти две схемы совершенно эквивалентны.
При уменьшении объема рабочего тела будет происходить его сжатие с изменением параметров состояния. При этом, чем больше повышается давление и температура газа, тем выше поднимается кривая сжатия, и тем больше затраты работы на его осуществление. Возможны случаи, когда линия сжатия располагается выше или ниже линии расширения (см. рис. 12).
Очевидно, что при необходимости получения полезной работы имеют смысл только такие циклы, в которых работа сжатия lсж меньше работы расширения lp. Эти циклы называются прямыми (рис. 12, а). Они лежат в основе работы тепловых двигателей.
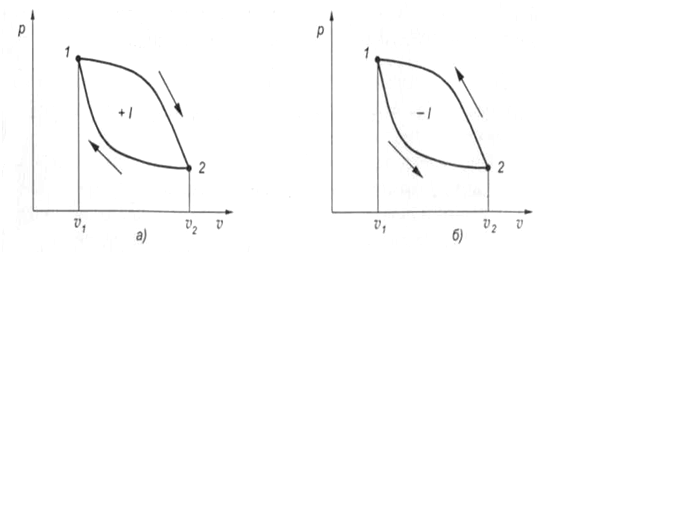
Рис. 12. Прямой (а) и обратный (б) циклы работы тепловых машин
Полезная работа прямого цикла равна разности работ расширения lр и сжатия lсж.
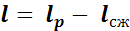 .
.
В обратных циклах
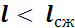 .
.
Работа обратного цикла отрицательна и используется в холодильных машинах.
Таким образом, в непрерывно действующем тепловом двигателе необходимо периодическое повторение прямых циклов, в которых процесс сжатия должен характеризоваться минимальной затратой работы.
Для выполнения последнего условия требуется, чтобы сжатие происходило при наименьшем повышении текущих значений температуры и давления, что может быть достигнуто только в случае отвода теплоты в период возвращения рабочего тела в состояние минимального объема.
Если теплоту не отводить, то работа затраченная на сжатие будет, по крайней мере, равна работе расширения и эффективность такой машины окажется равна нулю.
Таким образом, в любом случае непременным условием преобразования тепловой энергии в механическую, является прямой или косвенный расход теплоты, подведенной в цикле на возвращение рабочего тела в состояние минимального объема. Основным показателем эффективности циклов тепловых двигателей является их термический или термодинамический коэффициент полезного действия (КПД) ηt.
Термодинамический КПД определяет степень преобразования тепловой энергии в механическую в прямом цикле. Он представляет собой отношение величины тепловой энергии, преобразованной в механическую работу Аl, ко всей подведенной теплоте q1:
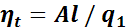 . (1.23)
. (1.23)
В соответствии с законом сохранения энергии [формула (1.4)]
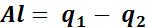 ,
,
где q2 — количество теплоты, отведенной холодильником.
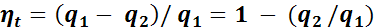 . (1.24)
. (1.24)
Цикл Карно
Одна из формулировок второго закона термодинамики звучит так: непременным условием преобразования теплоты в механическую работу является процесс передачи теплоты холодильнику. Поэтому важным вопросом является определение максимального КПД тепловых двигателей, работающих на идеальных газах.
Изучая эту проблему, французский инженер Карно в 1824 г. предложил цикл, который состоит только из обратимых процессов, совершаемый с идеальным газом. При этом Карно использовал такие процессы, которые наилучшим образом удовлетворяют своему назначению в цикле.
Знание данного цикла важно потому, что ни один из обратимых циклов не может иметь термический КПД выше термического КПД цикла Карно, осуществляемого при тех же перепадах температур.
Подвод и отвод теплоты в цикле Карно осуществляется изотермически, процессы сжатия и расширения протекают адиабатно, т. е. наиболее экономичным способом без тепловых потерь.
Двигатель, работающий по циклу Карно, представляет собой поршневую машину, цилиндр которой заполнен идеальным газом. Газ периодически контактирует с источником тепла, имеющим температуру Т1, или с холодильником, имеющим температуру Т2 (рис. 13).
Пусть газ имеет первоначальную температуру Т1 и давление р1 (точка 1). При нагревании газа от источника тепла происходит медленное изотермическое расширение (кривая 1—2) с подводом теплоты q1. После этого источник тепла удаляется и газ самопроизвольно расширяется без внешнего теплообмена (кривая 2—3) до температуры Т2 (точка 3). В процессе адиабатного расширения работа совершается за счет уменьшения внутренней энергии рабочего тела.
При осуществлении процесса расширения двигатель производит работу.
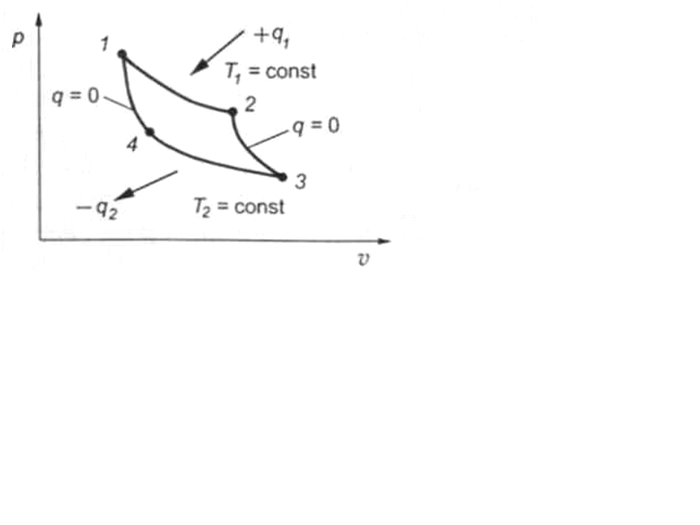
Рис. 13. р—v диаграмма цикла Карно
По окончании расширения цилиндр соприкасается с холодильником и осуществляется отвод тепла q2 в холодильник (кривая 3—4), при этом рабочее тело меняет значения своих параметров, уменьшаясь в объеме, а его давление увеличивается. Затем рабочее тело возвращается в исходное состояние путем адиабатного сжатия (кривая 4—1).
В результате цикла Карно рабочее тело совершает полезную работу, соответствующую площади, заключенной внутри контура 1—2—3—4.
Эта работа эквивалентна разности между подведенной (q1) и отведенной (q2) теплотой, т. е.
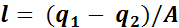 .
.
Тогда термический КПД цикла Карно на основании формул (2) и (3) можно представить как
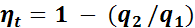 .
.
Для изотермических процессов
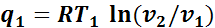 ,
,
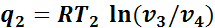 .
.
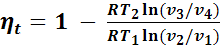 .
.
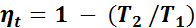 . (1.25)
. (1.25)
Дата добавления: 2017-02-13 ; просмотров: 5292 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
Расчет характеристик цикла теплового двигателя.
1. Цикл отнесен к 1 кг. воздуха;
2. Изобарная теплоемкость СР = 1,005 кДж/кг•К
3. Изохорная теплоемкость СV = 0,71 кДж/кг•К
4. Газовая постоянная R = 287 Дж/кг К
1. Параметры Р, v, T, U, i для узловых точек цикла.
2. Цикл в координатах P –V, в координатах Р – v, используя для этого предыдущее построение. Каждая кривая линия должна быть построена, как минимум по трем точкам.
3. n, C, ΔU, Δi, ΔS, q, l – для каждого процесса.
4. работу цикла lЦ , термический к. п. д. цикла и среднее индикаторное давление Pi .

Рисунок 3. Номер варианта.
Заданные значения:
P1абс= 12 атм = 12•10 5 Па;
P2абс = 14 атм = 14•10 5 Па
 = 0,08 м 3 /кг;
= 0,08 м 3 /кг;
Рассмотрим процессы, происходящие в цикле теплового двигателя:
1-2 – изохорный процесс.
2-3 – изобарный процесс.
3-4 – изохорный процесс.
4-1 – изобарный процесс.
1. Определим параметры p,V,T,U,i для узловых точек цикла:
а) Для точки 1 дано:  = 0,08 м 3 /кг; P1=12•10 5 Па.
= 0,08 м 3 /кг; P1=12•10 5 Па.

 кДж/кг;
кДж/кг;
 кДж/кг;
кДж/кг;
б) Для точки 2 дано: P2абс= 14 атм = 14•10 5 Па, V2=V1=0.08 м 3 /кг.
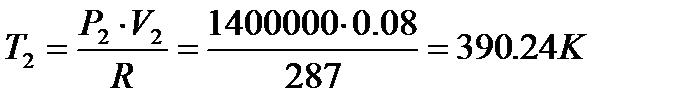
 кДж/кг;
кДж/кг;
 кДж/кг;
кДж/кг;
в) Для точки 3 дано: P2абс =P3абс= 14 атм = 14•10 5 Па, T3=423 К.
 ;
;
 м 3 /кг;
м 3 /кг;
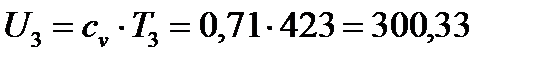 кДж/кг;
кДж/кг;
 кДж/кг;
кДж/кг;
г) Для точки 4 дано: P1абс= P4абс= 12*10 5 Па, V3=V4=0.086 К.

 кДж/кг;
кДж/кг;
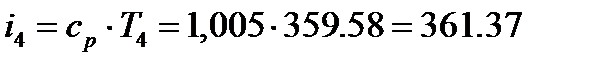 кДж/кг;
кДж/кг;
Результаты представим в виде таблицы 4.
| P, Па | ||||
| V, м 3 /кг | 0,08 | 0,08 | 0,086 | 0,086 |
| T, К | 334,49 | 390,24 | 359,58 | |
| U, кДж/кг | 237,49 | 277,07 | 300,33 | 255,3 |
| i, кДж/кг | 336,16 | 392,19 | 425,11 | 361,37 |
2. Построение цикла.
Данные для построения сведены в таблицу 5
| p, Па | V, м 3 /кг | lg p, Па | lg V*1000, м 3 /кг |
| 0,08 | 6,079 | 1,9 | |
| 0,08 | 6,146 | 1,9 | |
| 0,086 | 6,146 | 1,93 | |
| 0,086 | 6,079 | 1,93 |
Циклы в координатах P-V и LgP-LgV*1000
3. Для каждого процесса находим n, c, ∆U, ∆i, q, ∆S, l, ψ, ε.
n – показатель процесса;
c – теплоемкость процесса;
∆U – удельная внутренняя энергия;
∆i – удельная энтальпия;
q – удельное количество теплоты;
∆S – удельная энтропия;
l – работа изменения объема газа;
а) изохорный процесс 1-2.
 кДж/кг;
кДж/кг;
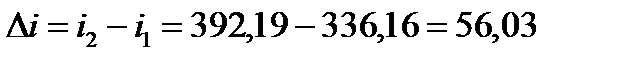 кДж/кг;
кДж/кг;
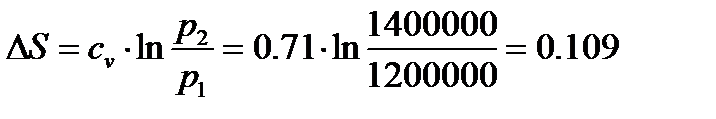 кДж/кг;
кДж/кг;
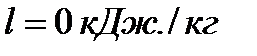
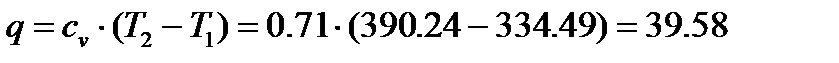 кДж/кг;
кДж/кг;
б) Изобарный процесс 2-3.
 кДж/кг;
кДж/кг;
 кДж/кг;
кДж/кг;
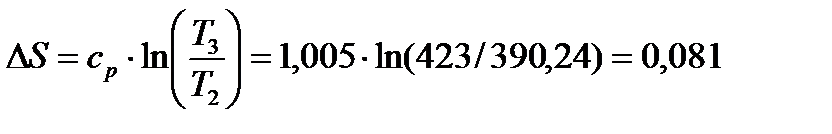 кДж/кг;
кДж/кг;
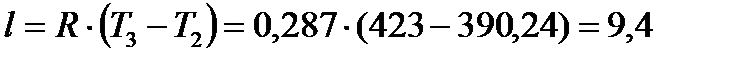 кДж/кг;
кДж/кг;
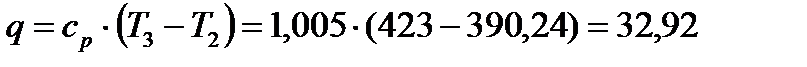 кДж/кг;
кДж/кг;
в) изохорный процесс 3-4.
 кДж/кг;
кДж/кг;
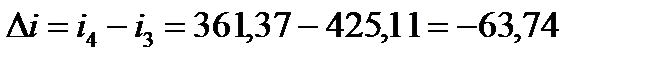 кДж/кг;
кДж/кг;
 кДж/кг;
кДж/кг;
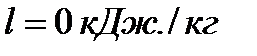
 кДж/кг;
кДж/кг;
г) Изобарный процесс 4-1.
 кДж/кг;
кДж/кг;
 кДж/кг;
кДж/кг;
 кДж/кг;
кДж/кг;
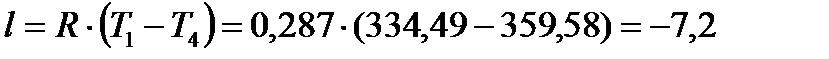 кДж/кг;
кДж/кг;
 кДж/кг;
кДж/кг;
Результаты представим в таблице 6
| 1-2 | 2-3 | 3-4 | 4-1 | |
 , кДж/кг , кДж/кг |
39,58 | 23,26 | -45,03 | -17,81 |
 , кДж/кг , кДж/кг |
56,03 | 32,92 | -63,74 | -25,21 |
 , кДж/кг , кДж/кг |
0,109 | 0,081 | -0,109 | -0,081 |
 , кДж/кг , кДж/кг |
9,4 | -7,2 | ||
 , кДж/кг , кДж/кг |
39,58 | 32,92 | -45,02 | -25,28 |
Проведем проверку:
Сумма изменений внутренних энергий, энтальпий, энтропий, должны быть равными нулю:
 ;
;
 ;
;
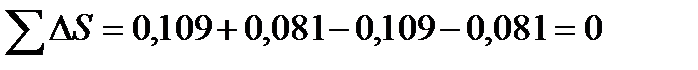 ;
;
Суммы количеств теплоты и работ изменения объема газа должны быть равны:
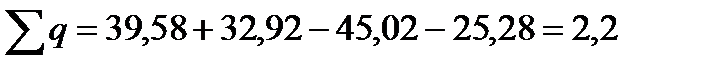 кДж/кг;
кДж/кг;
 кДж/кг;
кДж/кг;
Определим работу цикла lЦ, термический КПД  и среднее индикаторное давление Pi.
и среднее индикаторное давление Pi.
 Дж/кг;
Дж/кг;
 ;
;
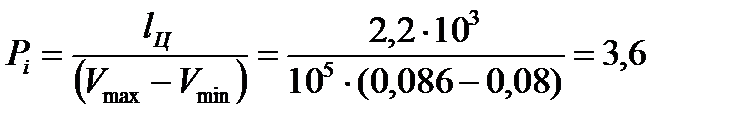 кг/см 2 ;
кг/см 2 ;
Конструктивный тепловой расчет рекуперативного теплообменного аппарата.
Теплообменный аппарат (теплообменник) — это устройство, предназначенное для нагревания, охлаждения или для изменения агрегатного состояния теплоносителя. Чаще всего в теплообменных аппаратах осуществляется передача теплоты от одного теплоносителя к другому, т. е. нагревание одного теплоносителя происходит за счет охлаждения другого.
Теплообменники с двумя теплоносителями в зависимости от способа передачи теплоты от одного теплоносителя к другому можно разделить на несколько типов: смесительные, рекуперативные, регенеративные и с промежуточным теплоносителем.
В рекуперативных теплообменниках теплота от одного теплоносителя к другому передается через разделяющую их стенку. Для уменьшения термического сопротивления стенка выполняется из материала с хорошей теплопроводностью: меди, стали, латуни, сплавов алюминия и т. д.
Провести конструктивный тепловой расчет рекуперативного теплообменника, в котором воздухом при температуре tв =30 0 С охлаждается вода проходящая по трубкам от t I 2 = 91 до t II 2 = 69 . Объемный расход воды V2 = 2,5 л/с .
Материал трубок – латунь (λ = 106 Вт/(м К) диаметром (dвн/ dн = 15/17).
Коэффициент использования поверхности теплообмена ηF – принять равным 0,8. Коэффициент оребрения – К = 10.
Скорость течения воды в трубах теплообменников обычно принимается равной 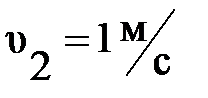 .
.
Определим среднюю температуру воды.
 ;
;
 ;
;
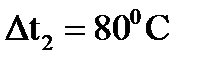 ;
;
Теплофизические свойства воды будем брать из справочника при средней температуре воды  , а воздуха при температуре
, а воздуха при температуре  .
.
Теплофизические свойства воды :
Pr = 2,21; λ = 0, 675 Вт/м∙К; ν= 3,65* 10 -7 ,м 2 /с
Теплофизические свойства воздуха
Pr = 0,701; λ = 0,02675 Вт/м∙К; ν = 16*10 -6 ,м 2 /с
Рассчитаем тепловой поток, который выделится при охлаждении воды:
 ,
,
где  — массовый расход теплоносителя;
— массовый расход теплоносителя;
 — теплоемкость при
— теплоемкость при  ;
;
 — теплоемкость при
— теплоемкость при  ;
;
 — температура воды начальная и конечная соответственно;
— температура воды начальная и конечная соответственно;

 кВт;
кВт;
Рассчитаем средний перепад температур, считается по разности средних температур.
 ;
;
 ;
;
 ;
;
Рассчитаем суммарное сечение труб для прохода воды.
 ;
;
 м 2 ;
м 2 ;
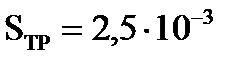 м 2 ;
м 2 ;
Рассчитаем площадь внутреннего сечения одной трубы.
 ;
;
 м 2 ;
м 2 ;
 м 2 ;
м 2 ;
Рассчитаем число параллельно включенных трубок.
 ;
;
 ;
;
 ;
;
Рассчитаем уточнённое значение скорости течения воды в трубках.
 ;
;
 м 2 /с;
м 2 /с;
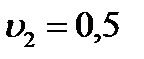 м 2 /с;
м 2 /с;
Для расчёта коэффициентов теплоотдачи, температуру стенки примем равной средней между температурами теплоносителей.
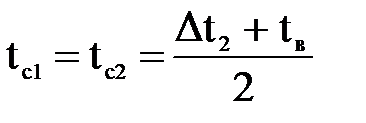 ;
;
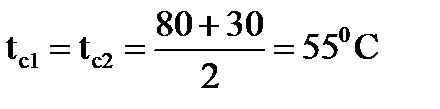 ;
;
 ;
;
Определим число Рейнольдса для воды, движущейся по трубам.
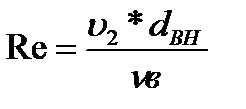 ;
;
 ;
;
 > 10 4 ; Режим движения – турбулентный.
> 10 4 ; Режим движения – турбулентный.
Рассчитаем коэффициент теплоотдачи.
 ;
;


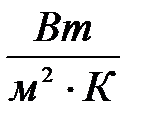 ;
;
Скорость движения воздуха, обтекающего трубы с водой принимаем равной 20 м/с, за определяющий размер принимаем Х = 0,6 м.
Найдём число Рейнольдса для воздуха.
 ;
;
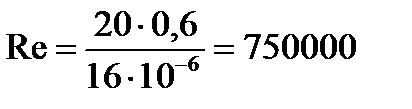 ;
;
 > 10 4 . Режим движения – турбулентный.
> 10 4 . Режим движения – турбулентный.
Так как воздух омывает не одну, а пучок труб, необходимо выбрать тип расположения труб в теплообменнике: шахматный или коридорный. От расположения труб в значительной степени зависят характер движения жидкости, омывание труб каждого ряда и в целом теплообмен в пучке. При коридорном расположении трубы любого ряда затеняются соответственными трубами предыдущего ряда, что ухудшает омывание в лобовой части, и большая часть трубы находится в слабой вихревой зоне. При шахматном расположении труб этого не происходит, поэтому наиболее целесообразно здесь использовать шахматное расположение труб.
Рассчитаем число Нуссельта для шахматного расположения.
 ;
;
 ;
;


Определим коэффициент теплоотдачи.
 ;
;
 ;
;
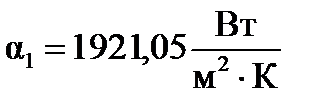 ;
;
Определяем коэффициент теплопередачи теплообменника.
 ;
;

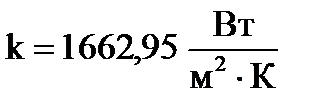 ;
;
Определяем площадь теплообменника.
 ;
;
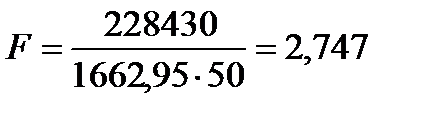 м 2 ;
м 2 ;
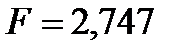 м 2 ;
м 2 ;
Определяем реальную площадь теплообменника по коэффициенту использования поверхности.
 ;
;
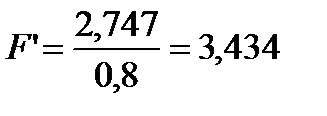 м 2 ;
м 2 ;
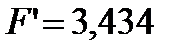 м 2 ;
м 2 ;
Определяем длину трубки.
 ;
;
 м;
м;
 м
м
Компоновка.
Расстояние между трубками в ряду должно находиться в пределах 2 – 4 dн. Расстояние между рядами рекомендуется выдерживать порядка 2 – 3 dн.
Длина и высота теплообменного аппарата не должна превышать 0,6 м.
1. Производим перерасчет площади теплообменного аппарата без учета коэффициента оребрения, с целью определения его реальной площади.
 ;
;
 м 2 ;
м 2 ;
 м 2 ;
м 2 ;
2. Определяем площадь, приходящуюся на оребрение.
 ;
;
 м 2 ;
м 2 ;
 м 2 ;
м 2 ;
3. Согласно компоновке определяем площадь одной пластины. Примем расстояние между трубками в ряду и рядами 3dн.
а = 3dн*6 + 30 = 3*17*6+30 = 336 мм.
b = 3dн*1+30 = 3*17+30= 81 мм.
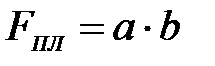 ;
;
 м 2 ;
м 2 ;
 м 2 ;
м 2 ;
4. Находим число пластин.
 ;
;
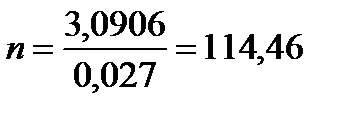 ;
;
 ;
;
Толщина пластины принимается равной 0,5 мм
Список используемой литературы:
1. Баскаков А.П. Теплотехника. – М.: «Энергоатомиздат», 1991. – 224 с.
2. Нащокин В.В. Техническая термодинамика и теплопередача. – М.: «Высшая школа», 1980. – 469 с.
3. Пузанков А.Г. Ремонт автомобиля ГАЗ. – М.: «Транспорт», 1993. – 235 с., ил.
4. Ривкин С.Л. Термодинамические свойства воды и водяного пара. – М.: «Энергия», 1975. – 398 с.
5. Роговцев В.Л. Устройство и эксплуатация автотранспортных средств. – М.: «Транспорт», 1991. – 432 с., ил.
6. Ястрежембский А.С. Техническая термодинамика. – М.: «Высшая школа», 1960. – 413 с.
Источник
Рекомендуемая
литература
-
Нащокин
В.В. Техническая термодинамика и
теплопередача. – М.: Высшая школа, 1980.
– с.230-259. -
Рабинович
О.М. Сборник задач по технической
термодинамике – М.:| Машиностроение,
1969. – с. 137-179. -
Теплотехника/
М.М. Хазен, Г.А. Матвеев, М.Е. Грицевский,
Ф.П.Казакевич/ Под ред. Г.А. Матвеева. –
М.: Высшая школа, 1981. – с. 75-90. -
Юдаев
Б.Н. Техническая термодинамика.
Теплопередача. – М.: Высшая школа, 1988.
– с. 126-142.
КОНТРОЛЬНЫЕ
ВОПРОСЫ И ЗАДАНИЯ
-
Назовите основные
характеристики циклов. -
Что такое степень
сжатия? -
Что такое степень
повышения давления? -
Что такое степень
предварительного расширения? -
Опишите цикл
двигателя с изобарным подводом теплоты. -
Опишите цикл
двигателя с изохорным подводом теплоты. -
Опишите цикл
двигателя со смешанным подводом теплоты. -
Описать цикл ГТУ
с изобарным подводом теплоты. -
В чем отличие
циклов ГТУ от циклов ДВС? -
Изобразить цикл
ГТУ с изобарным подводом теплоты в
 и
и координатах.
координатах. -
Изобразить цикл
ГТУ с изобарным подводом теплоты и
полной регенерацией в
 и
и координатах.
координатах. -
Описать
цикл ГТУ с изобарным подводом теплоты
и полной регенерацией.
Примеры
решения задач
Задача
5.1. Для
идеального цикла двигателя внутреннего
сгорания с изохорным подводом теплоты
определить параметры рабочего тела в
характерных точках цикла, количество
подведенной и отведенной теплоты,
полученную работу и термический КПД,
если начальные параметры рабочего тела
Р1=
0,1
МПа, t1=
17оС,
степень сжатия
=4,0 и степень повышения давления
![]() 3,5
3,5
рабочее тело – воздух. R=287,3 Дж/кг∙К,
ср=1,01Дж/кг∙К,
сv
= 0,72
Дж/кг∙К.
Решение
|
|
Рис.7. К задаче 5.1.
Определим параметры
в характерных точках цикла.
Точка 1. Р1=
0,1 МПа, Т1=
17+273=290 К.
Удельный объем
определим из уравнения состояния:
![]()
![]() м3/кг
м3/кг
Точка 2. Степень
сжатия определяется по формуле:
![]() , (23)
, (23)
тогда
![]()
![]()
м3/кг
Из соотношения
параметров в адиабатном процессе 1-2
определим абсолютное давление:
![]() =
=![]() МПа.
МПа.
Температура из
уравнения состояния:
![]() К. Точка
К. Точка
3. Процесс 2-3 – изохорный, т.е.
![]()
м3/кг.
Из соотношения параметров в изохорном
процессе:
![]()
![]()
![]() ,
,
тогда
![]() К,
К,
![]() МПа
МПа
Точка 4.
![]() =0,83
=0,83
м3/кг.
В адиабатном
процессе 3-4:

![]() МПа.
МПа.
![]()
![]() К.
К.
Подведенная теплота
в процессе 2-3:
![]() ;
;
(24)
отведенная теплота
в процессе 4-1:
![]() ; (25)
; (25)
работа цикла:
![]() ; (26)
; (26)
термический КПД
цикла:
![]() , (27)
, (27)
тогда:
![]() кДж/кг,
кДж/кг,
![]() =
=![]() 540
540
кДж/кг.
![]() 921,6–540=
921,6–540=
381,6 кДж/кг;![]() .
.
Ответ:
Р1=
0,1 МПа, Т1=
17+273=290 К,![]()
![]() м3/кг;
м3/кг;
![]()
![]()
м3/кг,![]() =
=![]() МПа,
МПа,![]() К;
К;![]()
м3/кг,
![]() К,
К,![]() МПа;
МПа;
![]() = 0,83 м3/кг,
= 0,83 м3/кг,
![]()
![]() МПа,
МПа,![]()
![]() К;
К;![]() кДж/кг;
кДж/кг;![]() 540
540
кДж/кг;![]() 381,6
381,6
кДж/кг;
![]() .
.
Задача 5.2. Для
идеального цикла двигателя внутреннего
сгорания с изобарным подводом теплоты
определить параметры рабочего тела в
характерных точках цикла, количество
подведенной и отведенной теплоты,
полученную работу и термический КПД,
если начальные параметры
рабочего тела Р1=
0,16 МПа, t1=
27оС,
степень
сжатия
=13,4 и степень предварительного
расширения
= 1,3,
рабочее тело – воздух. R=287,3
Дж/кг∙К, ср=1,01Дж/кг∙К,
сv
= 0,72
Дж/кг∙К.
Решение
|
|
Рис.8. К задаче 5.2.
Определим параметры
в характерных точках цикла.
Точка 1. Р1=
0,16 МПа, Т1=
27+273=300 К,
![]()
![]() м3/кг
м3/кг
Точка 2.
![]()
![]() м3/кг
м3/кг
![]() =
=![]() МПа;
МПа;![]() К.
К.
Точка 3. Процесс
2-3 – изобарный. Соотношение параметров
в изобарном процессе:
![]() 6,05
6,05
МПа
![]()
![]()
![]() .
.
![]() К,
К,
![]() м3/кг.
м3/кг.
Точка 4.
![]() =0,54
=0,54
м3/кг,

![]() МПа.
МПа.![]()
![]() К.
К.
Подведенная
теплота:
![]() кДж/кг
кДж/кг
Отведенная теплота:
![]() =
=![]() кДж/кг
кДж/кг
Работа цикла:
![]() 255
255
– 93 = 162 кДж/кг
Термический КПД
цикла:
![]() .
.
Ответ:
Р1=
0,16 МПа, Т1=
300 К,
![]()
![]() м3/кг;
м3/кг;![]()
![]() м3/кг,
м3/кг,
![]()
![]() МПа,
МПа,
![]() К;
К;![]() 6,05
6,05
МПа,![]() К,
К,![]() м3/кг;
м3/кг;
![]() =0,54
=0,54
м3/кг,
![]()
![]() МПа,
МПа,![]()
![]() К;
К;![]() кДж/кг;
кДж/кг;![]()
![]() кДж/кг;
кДж/кг;
![]() 162
162
кДж/кг;![]() .
.
Задача 5.3.
Для идеального цикла газотурбинной
установки с изобарным подводом теплоты
определить параметры рабочего тела в
характерных точках, количество подведенной
и отведенной теплоты, полезную работу,
термический КПД, если начальные параметры
рабочего тела р1=
0,1 МПа и t1=
15 оС,
степень повышения давления в компрессоре
= 6,0 и температура рабочего тела в конце
подвода теплоты t3
= 600 оС.
Рабочее тело – воздух. R=287,3 Дж/кг∙К,
ср=1,01Дж/кг∙К
Решение. Точка
1. Р1=
0,1 МПа , Т1=
15+273=288 К,
![]() м3/кг.
м3/кг.
Точка 2.
![]()
МПа.
![]() =
=![]() м3/кг.
м3/кг. ![]()
![]() К.
К.
Точка 3. Т3
= 600+273
= 873
К;
![]() 0,6 МПа;
0,6 МПа;
![]() м3/кг.
м3/кг.
Точка 4.
![]()
= 0,1МПа.
 К;
К;
![]() м3/кг.
м3/кг.
Подведенная
теплота:
![]() =1,01(873-480)
=1,01(873-480)
= 396,93 кДж/кг.
Отведенная теплота:
![]() = кДж/кг.
= кДж/кг.
Работа цикла:
![]() 396,93–237,35=
396,93–237,35=
159,58 кДж/кг.
Термический КПД
цикла:
![]() .
.

Рис. 9. К задачам
5.3. и 5.4.
Ответ:
Р1=
0,1 МПа , Т1=
288 К,
![]() м3/кг;
м3/кг;
![]()
МПа;![]() =
=![]() м3/кг,
м3/кг,
![]() К;Т3
К;Т3
= 873
К;
![]() 0,6 МПа;
0,6 МПа;![]() м3/кг;
м3/кг;
![]()
= 0,1МПа,
![]() К;
К;![]() м3/кг;
м3/кг;
![]()
396,93 кДж/кг;![]() кДж/кг;
кДж/кг;
![]() 159,58
159,58
кДж/кг;
![]() .
.
Задача 5.4.
Решить предыдущую задачу при условии,
что производится полная регенерация.
В цикле с
регенерацией:![]() ;
;![]()
Подведенная
теплота:
![]() =1,01(873-523)
=1,01(873-523)
= 353,5 кДж/кг.
Отведенная теплота:
![]() =
=
1,01(480-288)=193,92
кДж/кг.
Работа цикла:
![]() 353,5
353,5
–193,92= 159,58 кДж/кг.
Термический КПД
цикла:
![]() .
.
Ответ:
![]() =
=
353,5 кДж/кг;
![]() =193,92
=193,92
кДж/кг;![]() =
=
159,58 кДж/кг;
![]() .
.
задачи для
самостоятельного решения
Задача 5.5.
Для идеального
цикла двигателя внутреннего сгорания
с изобарным подводом теплоты определить
параметры рабочего тела в характерных
точках цикла, количество подведенной
и отведенной теплоты, полученную работу
и термический КПД,
если начальные параметры рабочего тела
Р1=
0,15 МПа, t1=
25оС,
степень сжатия
=13,6 и степень предварительного расширения
= 1,4,
рабочее тело – воздух. R=287,3
Дж/кг∙К, ср=1,01Дж/кг∙К,
сv
= 0,72
Дж/кг∙К.
Ответ:
![]() кДж/кг;
кДж/кг;![]() =
=![]() кДж/кг;
кДж/кг;![]() 210,6
210,6
кДж/кг;![]() .
.
Задача
5.6.
Сравнить цикл задачи
4.1
с циклом с изобарным подводом теплоты
при условии, что в сравниваемых циклах
одинаковы отведенная теплота и степень
сжатия.
Ответ:
![]() кДж/кг;
кДж/кг;
![]() .
.
Задача
5.7.
Сравнить цикл задачи
4.2
с циклом с изохорным подводом теплоты
при условии, что в сравниваемых циклах
одинаковы отведенная теплота и
максимальные параметры состояния
рабочего тела.
Ответ:
![]() кДж/кг;
кДж/кг;
![]() .
.
Задача 5.8. Для
идеального цикла газотурбинной установки
с изобарным подводом теплоты и полной
регенерацией определить параметры
рабочего тела в характерных точках,
количество подведенной и отведенной
теплоты, полезную работу, термический
КПД, если начальные параметры рабочего
тела р1=
0,15МПа и t1=
20 оС,
степень повышения давления в компрессоре
= 6,5 и температура рабочего тела в конце
подвода теплоты t3
= 650 оС.
Рабочее тело – воздух. R=287,3
Дж/кг∙К, ср=1,01Дж/кг∙К.
Сравнить данный цикл с циклом ГТУ без
регенерации.
Ответ:![]() =428,24
=428,24
кДж/кг,
![]() кДж/кг,
кДж/кг,![]() 178,77
178,77
кДж/кг,
![]() ;
;![]() =386,83
=386,83
кДж/кг,![]() =208,06
=208,06
кДж/кг,![]() = 178,77
= 178,77
кДж/кг,![]() .
.
Задача 5.9.
Для цикла газотурбинного двигателя с
изобарным процессом подвода теплоты
определить удельное количество подводимой
теплоты, если начальное давление Р1
=0,1 МПа,
начальная температура Т1
=300 К, степень
повышения давления в компрессоре β =
6, максимальная температура цикла Т3
=1500 К. В
качестве рабочего тела принять воздух
R=287,3
![]()
![]() =1,4.
=1,4.
Ответ:
![]() =1009
=1009
кДж/кг.
Задача 5.10. Решить
предыдущую задачу при условии, что
цикл ГТУ
проходит с полной регенерацией.
Ответ:
![]() =607
=607
кДж/кг.
Соседние файлы в папке Термодинамика
- #
- #
- #
- #
- #
- #
- #
- #
Физика, 10 класс
Урок 25. Тепловые двигатели. КПД тепловых двигателей
Перечень вопросов, рассматриваемых на уроке:
1) Понятие теплового двигателя;
2)Устройство и принцип действия теплового двигателя;
3)КПД теплового двигателя;
4) Цикл Карно.
Глоссарий по теме
Тепловой двигатель – устройство, в котором внутренняя энергия топлива превращается в механическую.
КПД (коэффициент полезного действия) – это отношение полезной работы, совершенной данным двигателем, к количеству теплоты, полученному от нагревателя.
Двигатель внутреннего сгорания – двигатель, в котором топливо сгорает непосредственно в рабочей камере (внутри) двигателя.
Реактивный двигатель – двигатель, создающий необходимую для движения силу тяги посредством преобразования внутренней энергии топлива в кинетическую энергию реактивной струи рабочего тела.
Цикл Карно – это идеальный круговой процесс, состоящий из двух адиабатных и двух изотермических процессов.
Нагреватель – устройство, от которого рабочее тело получает энергию, часть которой идет на совершение работы.
Холодильник – тело, поглощающее часть энергии рабочего тела (окружающая среда или специальные устройства для охлаждения и конденсации отработанного пара, т.е. конденсаторы).
Рабочее тело – тело, которое расширяясь, совершает работу (им является газ или пар)
Основная и дополнительная литература по теме урока:
1. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 269 – 273.
2. Рымкевич А.П. Сборник задач по физике. 10-11 класс. -М.: Дрофа,2014. – С. 87 – 88.
Открытые электронные ресурсы по теме урока
http://kvant.mccme.ru/1973/12/teplovye_mashiny.htm
Теоретический материал для самостоятельного изучения
Сказки и мифы разных народов свидетельствуют о том, что люди всегда мечтали быстро перемещаться из одного места в другое или быстро совершать ту или иную работу. Для достижения этой цели нужны были устройства, которые могли бы совершать работу или перемещаться в пространстве. Наблюдая за окружающим миром, изобретатели пришли к выводу, что для облегчения труда и быстрого передвижения нужно использовать энергию других тел, к примеру, воды, ветра и т.д. Можно ли использовать внутреннюю энергию пороха или другого вида топлива для своих целей? Если мы возьмём пробирку, нальём туда воду, закроем её пробкой и будем нагревать. При нагревании вода закипит, и образовавшие пары воды вытолкнут пробку. Пар расширяясь совершает работу. На этом примере мы видим, что внутренняя энергия топлива превратилась в механическую энергию движущейся пробки. При замене пробки поршнем способным перемещаться внутри трубки, а саму трубку цилиндром, то мы получим простейший тепловой двигатель.
Тепловой двигатель – тепловым двигателем называется устройство, в котором внутренняя энергия топлива превращается в механическую.
Вспомним строение простейшего двигателя внутреннего сгорания. Двигатель внутреннего сгорания состоит из цилиндра, внутри которого перемещается поршень. Поршень с помощью шатуна соединяется с коленчатым валом. В верхней части каждого цилиндра имеются два клапана. Один из клапанов называют впускным, а другой – выпускным. Для обеспечения плавности хода поршня на коленчатом вале укреплен тяжелый маховик.

Рабочий цикл ДВС состоит из четырех тактов: впуск, сжатие, рабочий ход, выпуск.
Во время первого такта открывается впускной клапан, а выпускной клапан остается закрытым. Движущийся вниз поршень засасывает в цилиндр горючую смесь.
Во втором такте оба клапана закрыты. Движущийся вверх поршень сжимает горючую смесь, которая при сжатии нагревается.
В третьем такте, когда поршень оказывается в верхнем положении, смесь поджигается электрической искрой свечи. Воспламенившаяся смесь образует раскаленные газы, давление которых составляет 3 -6 МПа, а температура достигает 1600 -2200 градусов. Сила давления толкает поршень вниз, движение которого передается коленчатому валу с маховиком. Получив сильный толчок маховик будет дальше вращаться по инерции, обеспечивая движение поршня и при последующих тактах. Во время этого такта оба клапана остаются закрытыми.
В четвертом такте открывается выпускной клапан и отработанные газы движущимся поршнем выталкиваются через глушитель (на рисунке не показан) в атмосферу.
Любой тепловой двигатель включает в себя три основных элемента: нагреватель, рабочее тело, холодильник.
Для определения эффективности работы теплового двигателя вводят понятие КПД.
Коэффициентом полезного действия называют отношение полезной работы, совершенной данным двигателем, к количеству теплоты, полученному от нагревателя.


Q1 – количество теплоты полученное от нагревания 
Q2 – количество теплоты, отданное холодильнику 
 – работа, совершаемая двигателем за цикл.
– работа, совершаемая двигателем за цикл.
Этот КПД является реальным, т.е. как раз эту формулу и используют для характеристики реальных тепловых двигателей.
Зная мощность N и время работы t двигателя работу, совершаемую за цикл можно найти по формуле

Передача неиспользуемой части энергии холодильнику.
В XIX веке в результате работ по теплотехнике французский инженер Сади Карно предложил другой способ определения КПД (через термодинамическую температуру).
Главное значение этой формулы состоит в том, что любая реальная тепловая машина, работающая с нагревателем, имеющим температуру Т1, и холодильником с температурой Т2, не может иметь КПД, превышающий КПД идеальной тепловой машины. Сади Карно, выясняя при каком замкнутом процессе тепловой двигатель будет иметь максимальный КПД, предложил использовать цикл, состоящий из 2 адиабатных и двух изотермических процессов
Цикл Карно – самый эффективный цикл, имеющий максимальный КПД.
Не существует теплового двигателя, у которого КПД = 100% или 1.
Формула дает теоретический предел для максимального значения КПД тепловых двигателей. Она показывает, что тепловой двигатель тем эффективнее, чем выше температура нагревателя и ниже температура холодильника. Лишь при температуре холодильника, равной абсолютному нулю, η = 1.
Но температура холодильника практически не может быть ниже температуры окружающего воздуха. Повышать температуру нагревателя можно. Однако любой материал (твердое тело) обладает ограниченной теплостойкостью, или жаропрочностью. При нагревании он постепенно утрачивает свои упругие свойства, а при достаточно высокой температуре плавится.
Сейчас основные усилия инженеров направлены на повышение КПД двигателей за счет уменьшения трения их частей, потерь топлива вследствие его неполного сгорания и т. д. Реальные возможности для повышения КПД здесь все еще остаются большими.
Повышение КПД тепловых двигателей и приближение его к максимально возможному — важнейшая техническая задача.
Тепловые двигатели – паровые турбины, устанавливают также на всех АЭС для получения пара высокой температуры. На всех основных видах современного транспорта преимущественно используются тепловые двигатели: на автомобильном – поршневые двигатели внутреннего сгорания; на водном – двигатели внутреннего сгорания и паровые турбины; на железнодорожном – тепловозы с дизельными установками; в авиационном – поршневые, турбореактивные и реактивные двигатели.
Сравним эксплуатационные характеристики тепловых двигателей.
КПД:
Паровой двигатель – 8%.
Паровая турбина – 40%.
Газовая турбина – 25-30%.
Двигатель внутреннего сгорания – 18-24%.
Дизельный двигатель – 40– 44%.
Реактивный двигатель – 25%.
Широкое использование тепловых двигателей не проходит бесследно для окружающей среды: постепенно уменьшается количество кислорода и увеличивается количество углекислого газа в атмосфере, воздух загрязняется вредными для здоровья человека химическими соединениями. Возникает угроза изменения климата. Поэтому нахождение путей уменьшения загрязнения окружающей среды является сегодня одной из наиболее актуальных научно-технических проблем.
Примеры и разбор решения заданий
1. Какую среднюю мощность развивает двигатель автомобиля, если при скорости 180 км/ч расход бензина составляет 15 л на 100 км пути, а КПД двигателя 25%?
Дано: v=180км/ч = 50 м/с, V = 15 л = 0,015 м3, s = 100 км = 105 м, ɳ = 25% = 0,25, ρ = 700 кг/м3, q = 46 × 106 Дж/кг.
Найти: N.
Решение:
Запишем формулу для расчёта КПД теплового двигателя:

Работу двигателя, можно найти, зная время работы и среднюю мощность двигателя:

Количество теплоты, выделяющееся при сгорании бензина, находим по формуле:

Учитывая всё это, мы можем записать:

Время работы двигателя можно найти по формуле:

Из формулы КПД выразим среднюю мощность:
 .
.
Подставим числовые значения величин:

После вычислений получаем, что N=60375 Вт.
Ответ: N=60375 Вт.
2. Тепловая машина имеет КПД 25 %. Средняя мощность передачи теплоты холодильнику составляет 4 кВт. Какое количество теплоты рабочее тело получает от нагревателя за 20 с?
Дано: ɳ = 25%, N = 4000 Вт, t = 20 с.
Найти: Q1.
Решение
 =
= 
 – это количество теплоты, отданное холодильнику
– это количество теплоты, отданное холодильнику


В процессе расширения газ производит работу против сил внешнего давления. Для того чтобы вновь повторить тот же процесс расширения газа и вновь получить работу , нужно возвратить газ в исходное состояние т.е. сжать газ. При этом газ совершит круговой процесс (цикл). На сжатие газа, естественно, должна быть затрачена работа; эта работа подводится к газу от какого-либо внешнего источника.
Понятно, что процесс сжатия газа от давления p2 до давления p1 нужно осуществить по пути, отличному от пути процесса расширения. В противном случае работа, получаемая при расширении газа, будет равна работе, затрачиваемой на сжатие, и суммарная работа, полученная в результате кругового процесса, будет равна нулю. Работа, отдаваемая системой за один цикл (будем называть ее работой цикла), равна разности (алгебраической сумме) работы расширения и работы сжатия. Понятно, что путь процесса сжатия следует выбрать таким образом, чтобы работа сжатия по абсолютной величине была меньше работы расширения, иначе работа цикла будет отрицательной, т.е. в результате цикла работа будет не производиться, а затрачиваться; впрочем, как будет показано в дальнейшем, в определенных случаях (циклы холодильных машин) используется именно такое построение цикла.
Циклические процессы, в результате которых производится работа, осуществляются в различных тепловых двигателях. Тепловым двигателем называют непрерывно действующую систему, осуществляющую круговые процессы (циклы), в которых теплота превращается в работу. Вещество, за счет изменения состояния которого получают работу в цикле, именуется рабочим телом.
Работа цикла находит очень удобную графическую интерпретацию в p, V-диаграмме.
Если 1-а-2 — кривая процесса расширения, а 2-b-1 — кривая процесса сжатия, то площадь под кривой 1-а-2 равна работе расширения, площадь под кривой 2-b-1 — работе сжатия, а площадь, ограниченная замкнутой кривой (кривой цикла) 1-a-2-b-1, представляет собой работу цикла.
Работа цикла Lц равна количеству теплоты, подведенной извне к рабочему телу. В соответствии с первым законом термодинамики: работа, производимая двигателем, строго равна количеству теплоты, отобранной от внешнего источника и подведенной к рабочему телу двигателя. Если бы можно было построить такой тепловой двигатель, в котором количество производимой работы было больше, чем количество теплоты, подведенной к рабочему телу от внешнего источника, то это означало бы, что первый закон термодинамики (закон сохранения и превращения энергии) несправедлив. Из этого следовало бы, что можно построить такой тепловой двигатель, в котором работа производилась бы вообще без подвода теплоты извне, т.е. вечный двигатель.
Что касается теплоты Qц, которая превращается в работу, то следует отметить, что на одних участках цикла теплота к рабочему телу подводится, на других — отводится. Как будет показано далее, отвод определенного количества теплоты от рабочего тела на некоторых участках цикла является неотъемлемым условием осуществимости цикла любого теплового двигателя.
Если обозначить теплоту, подводимую к рабочему телу в цикле, через Q1, а теплоту, отводимую от рабочего тела в цикле, через Q2, то очевидно, что
И тогда в соответствии с первым законом термодинамики:
Введем новое понятие о так называемом термическом коэффициенте полезного действия (КПД) цикла. Термическим КПД цикла называют отношение работы цикла к количеству теплоты, подведенной к рабочему телу в цикле. Обозначая термический КПД цикла ηт, получаем в соответствии с этим определением:
Термический КПД цикла характеризует степень совершенства того или иного цикла: чем больше ηт, тем совершеннее цикл; при подводе к рабочему телу одного и того же количества теплоты Q1 в цикле, у которого ηт больше, производится большая ′ работа Lц.
Введем понятие об источниках теплоты. Систему, от которой отбирается теплота Q1, сообщаемая рабочему телу цикла, принято называть горячим источником теплоты , а систему, которой отдается теплота Q2, отбираемая от рабочего тела, холодным источником теплоты.
Спасибо за прочтение материала. В следующий раз материал про будет про обратимые и необратимые циклы, которые приведут нас к формулировке второго закона термодинамики.
У нас уже была внутренняя энергия и первое начало термодинамики, а сегодня разберемся с задачами на КПД теплового двигателя. Что поделать: праздники праздниками, но сессию ведь никто не отменял.
Присоединяйтесь к нам в телеграме и получайте полезную рассылку каждый день. А приступая к практике, не забывайте держать под рукой памятку по задачам и полезные формулы.
Задачи по физике на КПД теплового двигателя
Задача на вычисление КПД теплового двигателя №1
Условие
Вода массой 175 г подогревается на спиртовке. Пока вода нагрелась от t1=15 до t2=75 градусов Цельсия, масса спиртовки уменьшилась с 163 до 157 г Вычислите КПД установки.
Решение
Коэффициент полезного действия можно вычислить как отношение полезной работы и полного количества теплоты, выделенного спиртовкой:
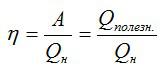
Полезная работа в данном случае – это эквивалент количества теплоты, которое пошло исключительно на нагрев. Его можно вычислить по известной формуле:
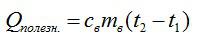
Полное количество теплоты вычисляем, зная массу сгоревшего спирта и его удельную теплоту сгорания.
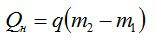
Подставляем значения и вычисляем:
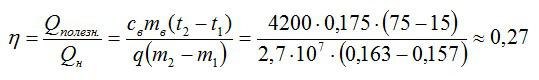
Ответ: 27%
Задача на вычисление КПД теплового двигателя №2
Условие
Старый двигатель совершил работу 220,8 МДж, при этом израсходовав 16 килограмм бензина. Вычислите КПД двигателя.
Решение
Найдем общее количество теплоты, которое произвел двигатель:
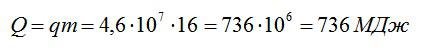
Теперь можно рассчитать КПД:
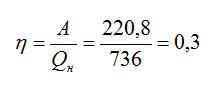
Или, умножая на 100, получаем значение КПД в процентах:
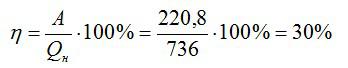
Ответ: 30%.
Задача на вычисление КПД теплового двигателя №3
Условие
Тепловая машина работает по циклу Карно, при этом 80% теплоты, полученной от нагревателя, передается холодильнику. За один цикл рабочее тело получает от нагревателя 6,3 Дж теплоты. Найдите работу и КПД цикла.
Решение
КПД идеальной тепловой машины:
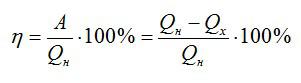
По условию:
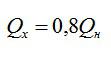
Вычислим сначала работу, а затем КПД:
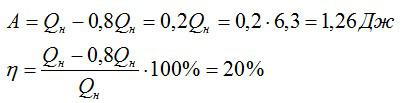
Ответ: 20%; 1,26 Дж.
Задача на вычисление КПД теплового двигателя №4
Условие
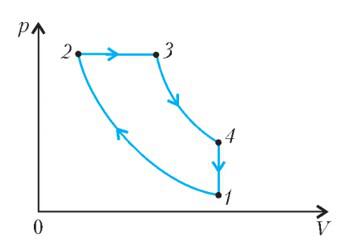
На диаграмме изображен цикл дизельного двигателя, состоящий из адиабат 1–2 и 3–4, изобары 2–3 и изохоры 4–1. Температуры газа в точках 1, 2, 3, 4 равны T1 , T2 , T3 , T4 соответственно. Найдите КПД цикла.
Решение
Проанализируем цикл, а КПД будем вычислять через подведенное и отведенное количество теплоты. На адиабатах тепло не подводится и не отводится. На изобаре 2 – 3 тепло подводится, объем растет и, соответственно, растет температура. На изохоре 4 – 1 тепло отводится, а давление и температура падают.
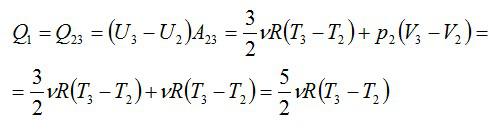
Аналогично:
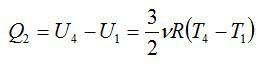
Получим результат:
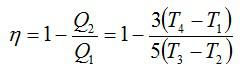
Ответ: См. выше.
Задача на вычисление КПД теплового двигателя №5
Условие
Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 2,94 кДж и отдаёт за один цикл охладителю количество теплоты Q2 = 13,4 кДж. Найдите КПД цикла.
Решение
Запишем формулу для КПД:
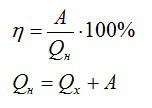
Отсюда:
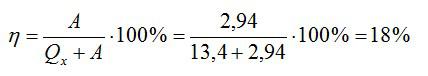
Ответ: 18%
Вопросы на тему тепловые двигатели
Вопрос 1. Что такое тепловой двигатель?
Ответ. Тепловой двигатель – это машина, которая совершает работу за счет энергии, поступающей к ней в процессе теплопередачи. Основные части теплового двигателя: нагреватель, холодильник и рабочее тело.
Вопрос 2. Приведите примеры тепловых двигателей.
Ответ. Первыми тепловыми двигателями, получившими широкое распространение, были паровые машины. Примерами современного теплового двигателя могут служить:
- ракетный двигатель;
- авиационный двигатель;
- газовая турбина.
Вопрос 3. Может ли КПД двигателя быть равен единице?
Ответ. Нет. КПД всегда меньше единицы (или меньше 100%). Существование двигателя с КПД равным единице противоречит первому началу термодинамики.
КПД реальных двигателей редко превышает 30%.
Вопрос 4. Что такое КПД?
Ответ. КПД (коэффициент полезного действия) – отношение работы, которую совершает двигатель, к количеству теплоты, полученному от нагревателя.
Вопрос 5. Что такое удельная теплота сгорания топлива?
Ответ. Удельная теплота сгорания q – физическая величина, которая показывает, какое количество теплоты выделяется при сгорании топлива массой 1 кг. При решении задач КПД можно определять по мощности двигателя N и сжигаемому за единицу времени количеству топлива.
Задачи и вопросы на цикл Карно
Затрагивая тему тепловых двигателей, невозможно оставить в стороне цикл Карно – пожалуй, самый знаменитый цикл работы тепловой машины в физике. Приведем дополнительно несколько задач и вопросов на цикл Карно с решением.
Цикл (или процесс) Карно – это идеальный круговой цикл, состоящий из двух адиабат и двух изотерм. Назван так в честь французского инженера Сади Карно, который описал данный цикл в своем научном труде «О движущей силе огня и о машинах, способных развивать эту силу» (1894).
Задача на цикл Карно №1
Условие
Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 73,5 кДж. Температура нагревателя t1 =100° С, температура холодильника t2 = 0° С. Найти КПД цикла, количество теплоты, получаемое машиной за один цикл от нагревателя, и количество теплоты, отдаваемое за один цикл холодильнику.
Решение
Рассчитаем КПД цикла:
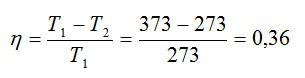
С другой стороны, чтобы найти количество теплоты, получаемое машиной, используем соотношение:
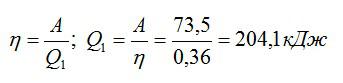
Количество теплоты, отданное холодильнику, будет равно разности общего количества теплоты и полезной работы:
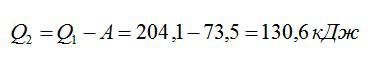
Ответ: 0,36; 204,1 кДж; 130,6 кДж.
Задача на цикл Карно №2
Условие
Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А=2,94 кДж и отдает за один цикл холодильнику количество теплоты Q2=13,4 кДж. Найти КПД цикла.
Решение
Формула для КПД цикла Карно:
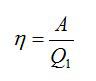
Здесь A – совершенная работа, а Q1 – количество теплоты, которое понадобилось, чтобы ее совершить. Количество теплоты, которое идеальная машина отдает холодильнику, равно разности двух этих величин. Зная это, найдем:
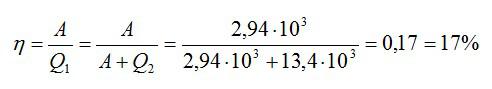
Ответ: 17%.
Задача на цикл Карно №3
Условие
Изобразите цикл Карно на диаграмме и опишите его
Решение
Цикл Карно на диаграмме PV выглядит следующим образом:

- 1-2. Изотермическое расширение, рабочее тело получает от нагревателя количество теплоты q1;
- 2-3. Адиабатическое расширение, тепло не подводится;
- 3-4. Изотермическое сжатие, в ходе которого тепло передается холодильнику;
- 4-1. Адиабатическое сжатие.
Ответ: см. выше.
Вопрос на цикл Карно №1
Сформулируйте первую теорему Карно
Ответ. Первая теорема Карно гласит: КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела.
Вопрос на цикл Карно №2
Может ли коэффициент полезного действия в цикле Карно быть равным 100%?
Ответ. Нет. КПД цикла карно будет равен 100% только в случае, если температура холодильника будет равна абсолютному нулю, а это невозможно.
Если у вас остались вопросы по теме тепловых двигателей и цикла Карно, вы можете смело задавать их в комментариях. А если нужна помощь в решении задач или других примеров и заданий, обращайтесь в профессиональный студенческий сервис.


