Как найти количество диагоналей призмы

Ответы в виде таблицы.
Сколько диагоналей имеют треугольная, четырёхугольная,
шестиугольная и n-угольная
призмы?

Сколько диагональных сечений можно провести через одно
боковое ребро в треугольной, четырёхугольной, шестиугольной и n-угольной призме?

В правильной шестиугольной призме сторона основания равна m, а боковые грани –
квадраты. Найдите диагонали призмы и площади диагоналей сечений.

Формула количества диагоналей у призмы N = n·(n – 3)
где n – количество сторон
треугольная призма- N= 3(3-3)= 0 (диагоналей нет)
четырёхугольная- N=4(4-3)=4
шестиугольная N=6(6-3)=18
n-угольная N=n(n-3)

Сколько диагональных сечений можно провести через одно
боковое ребро в треугольной, четырёхугольной, шестиугольной и n-угольной призме?
в труеуг.-нельзя
четырех.-N=n(n-3)/2=2
шестиуг.-N=6(6-3)/2=9
n-угольной N=n(n-3)/2

Если ответ по предмету Алгебра отсутствует или он оказался неправильным, то попробуй воспользоваться поиском других ответов во всей базе сайта.

Правильная четырехугольная призма

Четырехугольная призма — это многогранник, две грани которого являются равными квадратами, лежащими в параллельных плоскостях, а остальные грани (боковые грани) — параллелограммами, имеющими общие стороны с этими квадратами.

Правильная четырехугольная призма – это четырехугольная призма у которой основания квадраты, а боковые грани прямоугольники.

Данное геометрическое тело по своим свойствам и характеристикам соответствует – параллелепипеду.

Основания призмы являются равными квадратами.

Боковые грани призмы являются прямоугольниками.

Боковые рёбра призмы параллельны и равны.

Размеры призмы можно выразить через длину стороны a и высоту h.

Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.

Формула площади поверхности четырехугольной призмы:

Правильная четырехугольная призма

Элементы правильной четырехугольной призмы

• Основания ABCD и A₁B₁C₁D₁ равны и параллельны друг другу
• Боковые грани AA₁D₁D, AA₁B₁B, BB₁C₁C и CC₁D₁D, каждая из которых является прямоугольником
• Боковая поверхность – сумма площадей всех боковых граней призмы
• Полная поверхность – сумма площадей всех оснований и боковых граней (сумма площади боковой поверхности и оснований)
• Боковые ребра AA₁, BB₁, CC₁ и DD₁.
• Диагональ B₁D
• Диагональ основания BD
• Диагональное сечение BB₁D₁D
• Перпендикулярное сечение A₂B₂C₂D₂ .

Свойства правильной четырехугольной призмы

• Основаниями являются два равных квадрата
• Основания параллельны друг другу
• Боковыми гранями являются прямоугольники
• Боковые грани равны между собой
• Боковые грани перпендикулярны основаниям
• Боковые ребра параллельны между собой и равны
• Перпендикулярное сечение перпендикулярно всем боковым ребрам и параллельно основаниям
• Углы перпендикулярного сечения – прямые
• Диагональное сечение правильной четырехугольной призмы представляет собой прямоугольник
• Перпендикулярное (ортогональное сечение) параллельно основаниям

Формулы для правильной четырехугольной призмы

Указания к решению задач

При решении задач на тему “правильная четырехугольная призма” подразумевается, что:

Правильная призма — призма в основании которой лежит правильный многоугольник, а боковые ребра перпендикулярны плоскостям основания. То есть правильная четырехугольная призма содержит в своем основании квадрат. (см. выше свойства правильной четырехугольной призмы)

Задача.

В правильной четырёхугольной призме площадь основания 144 см 2 , а высота 14 см. Найти диагональ призмы и площадь полной поверхности.

Решение.
Правильный четырехугольник – это квадрат.
Соответственно, сторона основания будет равна √ 144 = 12 см.
Откуда диагональ основания правильной прямоугольной призмы будет равна
√( 12 2 + 12 2 ) = √288 = 12√2

Диагональ правильной призмы образует с диагональю основания и высотой призмы прямоугольный треугольник. Соответственно, по теореме Пифагора диагональ заданной правильной четырехугольной призмы будет равна:
√( ( 12√2 ) 2 + 14 2 ) = 22 см

Задача

Определите полную поверхность правильной четырехугольной призмы, если ее диагональ равна 5 см, а диагональ боковой грани равна 4 см.

Решение.
Поскольку в основании правильной четырехугольной призмы лежит квадрат, то сторону основания (обозначим как a) найдем по теореме Пифагора:

a 2 + a 2 = 5 2
2a 2 = 25
a = √12,5

Высота боковой грани (обозначим как h) тогда будет равна:

h 2 + 12,5 = 4 2
h 2 + 12,5 = 16
h 2 = 3,5
h = √3,5

Площадь полной поверхности будет равна сумме площади боковой поверхности и удвоенной площади основания

S = 2a 2 + 4ah
S = 25 + 4√12,5 * √3,5
S = 25 + 4√43,75
S = 25 + 4√(175/4)
S = 25 + 4√(7*25/4)
S = 25 + 10√7 ≈ 51,46 см 2 .

[spoiler title=”источники:”]

http://mnogogranniki.ru/pravilnaya-chetyrekhugolnaya-prizma.html

http://profmeter.com.ua/communication/learning/course/course7/lesson201/

[/spoiler]

Призма — одна из разновидностей многогранника. Ее определение репетитор по математике вводит на описательном уровне: рассмотрим две параллельные плоскости и и произвольный многоугольник в одной из них. Проведем через все его вершины параллельные прямые до пересечения с другой плоскостью в точках Многогранник называется n-угольной призмой.

Элементы призмы:
Точки  — называются вершинами
Отрезки называются боковыми ребрами
Многоугольники и  — называются основаниями. Также основаниями называют сами плоскости и

Памятка репетитора по математике на призму:

Можно выделить основные понятия, связанные с данным многогранником. К ним относятся:

Высота призмы — любой отрезок , перпендикулярный к плоскостям основания, такой, что ,
Диагональ призмы — это отрезок, соединяющий две любые вершины призмы и не лежащий ни в одной из ее граней.

Площадь полной поверхности — сумма площадей всех граней призмы.

Площадь боковой поверхности — сумма площадей боковых граней.

Поперечные сечение — сечение, проведенное перпендикулярно с боковому ребру призмы.

Диагональная плоскость — это плоскость, проходящая через боковое ребро и диагональ основания. Многоугольник, полученный в ее пересечении с поверхностью призмы называют диагональным сечением.

Заметка репетитора по математике: Можно предложить равносильное определение для диагонального сечения — сечение, содержащее две диагонали: диагональ призмы и диагональ ее основания.

Несложно подсчитать количество диагоналей у n-угольной призмы. Оно вычисляется по формуле

Виды призм:

Прямая призма — такая призма, боковые ребра которой перпендикулярны основаниям
Если этого не происходит, то призма называется наклонной. У прямой призмы длина высоты равна длине бокового ребра.

Правильная призма — такая прямая призма, у которой в основаниях лежат правильные многоугольники. Ее высота равна боковому ребру.

Призма называется параллелепипедом, если в ее основании лежит параллелограмм. Подробнее о параллелепипедах…

Объем призмы:

1) , где  — площадь основания, а  — высота.
2) , где  — площадь поперечного сечения, а  — боковое ребро.

Площадь поверхности:
Площадью поверхности призмы называется сумма площадей всех ее граней.

Площадь боковой поверхности призмы — это сумма площадей всех ее боковых граней. Для прямой призмы боковая поверхность может быть вычислена по формуле: , где P — периметр основания.

При подготовке к ЕГЭ по математике обратите особое внимание на разницу между понятиями правильная и прямая призма. Их часто путают. Если вы решаете задачу при помощи метода координат — вводите систему Oxyz так, как это показано на рисунке справа (кликните для увеличения). На рисунке: начало отсчета является серединой ребра основания, ось абсцисс направлена вдоль стороны основания, ось ординат по высоте основания, а ось аппликат параллельно высоте.

Репетитор по математике в Москве (Строгино). Колпаков А.Н.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Изучением призм занимается пространственная геометрия. Важными их характеристиками являются заключенный в них объем, площадь поверхности и число составляющих элементов. В статье рассмотрим все эти свойства для шестиугольной призмы.

О какой призме пойдет речь?

Призма шестиугольная – это фигура, образованная двумя многоугольниками, имеющими шесть сторон и шесть углов, и шестью параллелограммами, соединяющими отмеченные шестиугольники в единое геометрическое образование.

На рисунке изображен пример этой призмы.

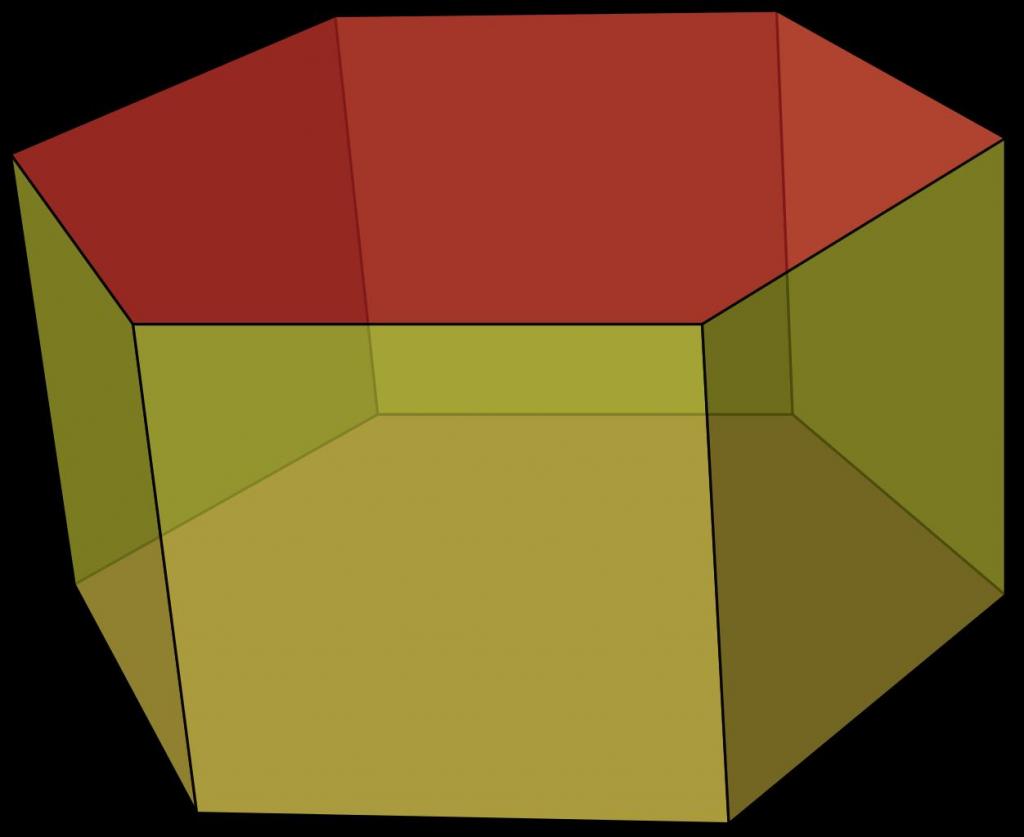
Отмеченный красным цветом шестиугольник называется основанием фигуры. Очевидно, что число ее оснований равно двум, причем оба они идентичны. Желто-зеленоватые грани призмы называются ее боковыми сторонами. На рисунке они представлены квадратами, но в общем случае они являются параллелограммами.

Шестиугольная призма может быть наклонной и прямой. В первом случае углы между основанием и боковыми сторонами не являются прямыми, во втором они равны 90^o. Также эта призма может быть правильной и неправильной. Правильная шестиугольная призма обязательно должна быть прямой и иметь правильный шестиугольник в основании. Приведенная выше призма на рисунке этим требованиям удовлетворяет, поэтому она называется правильной. Далее в статье будем изучать только ее свойства, как общий случай.

Элементы

Для любой призмы главными ее элементами являются ребра, грани и вершины. Шестиугольная призма не является исключением. Приведенный выше рисунок позволяет посчитать количество этих элементов. Так, граней или сторон мы получаем 8 (два основания и шесть боковых параллелограммов), число вершин составляет 12 (по 6 вершин для каждого основания), количество ребер шестиугольной призмы равно 18 (шесть боковых и 12 для оснований).

В 1750-е годы Леонард Эйлер (швейцарский математик) установил для всех полиэдров, к которым относится призма, математическую связь между числами указанных элементов. Эта связь имеет вид:

число ребер = число граней + число вершин – 2.

Указанные выше цифры удовлетворяют этой формуле.

Диагонали призмы

Все диагонали шестиугольной призмы можно разделить на два типа:

• те, которые лежат в плоскостях ее граней;
• те, которые принадлежат всему объему фигуры.

Рисунок ниже показывает все эти диагонали.

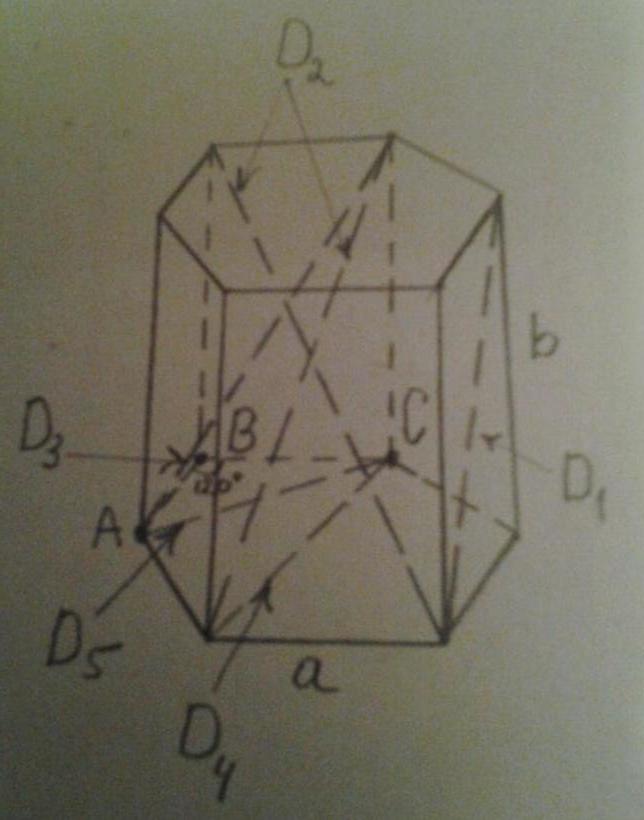
Видно, что D₁ – это диагональ боковой стороны, D₂ и D₃ – диагонали всей призмы, D₄ и D₅ – диагонали основания.

Длины диагоналей боковых сторон между собой равны. Вычислить их легко, используя всем известную теорему Пифагора. Обозначим символом a длину стороны шестиугольника, символом b – длину бокового ребра. Тогда диагональ имеет длину:

D₁ = √(a² + b²).

Диагональ D₄ также легко определяется. Если вспомнить, что правильный шестиугольник вписывается в окружность радиусом a, то D₄ является диаметром этой окружности, то есть получим следующую формулу:

D₄ = 2*a.

Диагональ D₅ основания найти несколько сложнее. Для этого следует рассмотреть равносторонний треугольник ABC (см. рис.). Для него AB = BC = a, угол ABC равен 120^o. Если из этого угла опустить высоту (она же будет биссектрисой и медианой), тогда половина основания AC будет равно:

AC/2 = AB*sin(60^o) = a*√3/2.

Сторона AC является диагональю D₅, поэтому получаем:

D₅ = AC = √3*a.

Теперь остается найти диагонали D₂ и D₃ правильной шестиугольной призмы. Для этого нужно увидеть, что они являются гипотенузами соответствующих прямоугольных треугольников. Воспользовавшись теоремой Пифагора, получаем:

D₂ = √(D₄² + b²) = √(4*a² + b²);

D₃ = √(D₅²+ b²) = √(3*a²+ b²).

Таким образом, самой большой диагональю для любых значений a и b является D₂.

Площадь поверхности

Чтобы понять, о чем идет речь, проще всего рассмотреть развертку этой призмы. Она показана на рисунке.

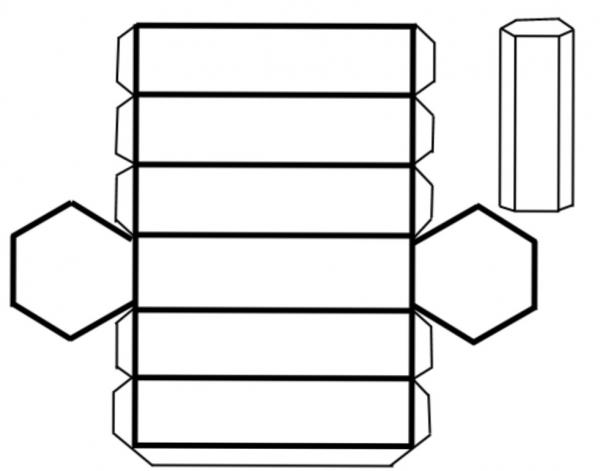
Видно, что для определения площади всех сторон рассматриваемой фигуры необходимо рассчитать отдельно площадь четырехугольника и площадь шестиугольника, затем умножить их на соответствующие целые числа, равные количеству каждого n-угольника в призме, и сложить полученные результаты. Шестиугольников 2, прямоугольников 6.

Для площади прямоугольника получаем:

S₁ = a*b.

Тогда площадь боковой поверхности равна:

S₂ = 6*a*b.

Для определения площади шестиугольника проще всего воспользоваться соответствующей формулой, которая имеет вид:

S_n = n/4*a²*ctg(pi/n).

Подставляя в это выражение число n равное 6, получаем площадь одного шестиугольника:

S₆ = 6/4*a²*ctg(pi/6) = 3*√3/2*a².

Это выражение следует умножить на два, чтобы получить площадь оснований призмы:

S_os = 3*√3*a².

Остается сложить S_os и S₂, чтобы получить полную площадь поверхности фигуры:

S = S_os + S₂ = 3*√3*a² + 6*a*b = 3*a*(√3*a + 2*b).

Объем призмы

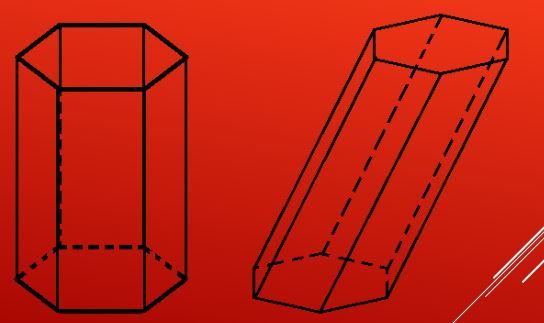
После того как была получена формула для площади шестиугольного основания, вычислить объем, заключенный в рассматриваемую призму, проще простого. Для этого следует лишь умножить площадь одного основания (шестиугольника) на высоту фигуры, длина которой равна длине бокового ребра. Получаем формулу:

V = S₆*b = 3*√3/2*a²*b.

Отметим, что произведение основания на высоту дает значение объема абсолютно любой призмы, включая наклонную. Однако в последнем случае расчет высоты осложняется, поскольку она уже не будет равна длине бокового ребра. Что касается шестиугольной правильной призмы, то значение ее объема является функцией двух переменных: сторон a и b.