Как определить число диагоналей в восьмиугольнике? Есть формула?
Просветленный
(32240),
закрыт
8 лет назад
́§ MEGA VOLT §
Оракул
(93373)
8 лет назад
Есть Катя причём такая простая что ты сама удивишься))))
диагональ в 8 угольнике соединяет 2 противоположные вершины, как и в любом многоугольнике)))
поэтому 8/2
ответ 4 диагонали))))))) улыбнись))
Вячеслав Иванов
Оракул
(70447)
8 лет назад
а я по другому нашел число диагоналей. В треугольнике ноль диагоналей. В четырехугольнике – две диагонали. В пятиугольнике – пять диагоналей. В шестиугольнике – девять. И так далее . В семиугольнике 14 диагоналей а в восьмиугольнике – 20 диагоналей . А в девятиугольнике – 27. А в десятиугольнике – 35. И тд
Загрузить PDF
Загрузить PDF
Нахождение числа диагоналей является важнейшим навыком, который пригодится при решении геометрических задач. Это не так сложно, как кажется – просто нужно запомнить формулу. Диагональ – это отрезок, соединяющий любые две несмежные вершины многоугольника.[1]
Многоугольник – это любая фигура с как минимум тремя сторонами. При помощи несложной формулы можно найти количество диагоналей в любом многоугольнике, например, с 4 сторонами или с 4000 сторон.
-

1
Запомните названия многоугольников. Сначала нужно найти число сторон многоугольника. Это можно сделать по названию любого многоугольника. Вот названия самых распространенных многоугольников:[2]
- Четырехугольник: 4 стороны
- Пятиугольник: 5 сторон
- Шестиугольник: 6 сторон
- Семиугольник: 7 сторон
- Восьмиугольник: 8 сторон
- Девятиугольник: 9 сторон
- Десятиугольник: 10 сторон
- Обратите внимание, что у треугольника диагоналей нет.[3]
-

2
Нарисуйте многоугольник. Чтобы найти число диагоналей в квадрате, нарисуйте его. Самый простой способ найти число диагоналей – это нарисовать правильный многоугольник (в таком многоугольнике все стороны равны) и посчитать количество диагоналей. Запомните: неправильный многоугольник будет иметь такое же количество диагоналей, что и правильный (при одинаковом числе сторон).[4]
- Чтобы нарисовать многоугольник, воспользуйтесь линейкой; нарисуйте замкнутую фигуру со сторонами одинаковой длины.
- Если вы не знаете, как выглядит многоугольник, поищите картинки в интернете. Например, знак «Стоп» – это восьмиугольник.
-

3
Нарисуйте диагонали. Диагональ – это отрезок, соединяющий любые две несмежные вершины многоугольника.[5]
Из одной (любой) вершины многоугольника проведите диагонали к другим (несмежным) вершинам.- В квадрате проведите одну диагональ из нижнего левого угла в правый верхний угол, а вторую – из нижнего правого угла в левый верхний угол.
- Нарисуйте диагонали разных цветов, чтобы быстрее посчитать их.[6]
- Обратите внимание, что применять этот метод к многоугольникам, у которых больше 10 сторон, довольно сложно.
-

4
Посчитайте диагонали. Можно считать диагонали во время того, как вы рисуете их, или после того, как они нарисованы. Отмечайте диагонали, которые уже посчитаны, чтобы не запутаться (особенно когда диагоналей много и они пересекаются).
- У квадрата всего две диагонали – по одной на каждые две вершины.[7]
- У шестиугольника 9 диагоналей: по три диагонали на каждые три вершины.
- У семиугольника 14 диагоналей. Если у многоугольника больше семи сторон, посчитать диагонали довольно сложно, потому что их слишком много.
- У квадрата всего две диагонали – по одной на каждые две вершины.[7]
-

5
Каждую диагональ считайте только один раз. Из каждой вершины выходит несколько диагоналей, но это не значит, что число диагоналей равно произведению числа вершин на число диагоналей, выходящих из каждой вершины. Поэтому аккуратно считайте диагонали.[8]
- Например, у пятиугольника (5 сторон) только 5 диагоналей. Из каждой вершины выходит 2 диагонали; если умножить число вершин на число диагоналей, выходящих из каждой вершины, получите 10. Это неверный ответ, как если бы вы посчитали каждую диагональ дважды.
-

6
Попрактикуйтесь в определении числа диагоналей на некоторых примерах. Нарисуйте разные многоугольники и посчитайте их диагонали. Этот метод применим и к неправильным многоугольникам. В случае вогнутого многоугольника некоторые диагонали лежат вне границ фигуры.[9]
- У шестиугольника 9 диагоналей.
- У семиугольника 14 диагоналей.
Реклама
-

1
Запишите формулу. Формула для вычисления числа диагоналей многоугольника: d = n(n-3)/2, где d – число диагоналей, n – число сторон многоугольника.[10]
Используя распределительное свойство, эту формулу можно записать так: d = (n2 – 3n)/2. Можно пользоваться любой формой представленной формулы.- Эта формула для вычисления числа диагоналей многоугольника.
- Обратите внимание, что эта формула не применима к треугольникам, потому что у треугольников диагоналей нет.[11]
-

2
Определите число сторон многоугольника. Чтобы использовать приведенную формулу, нужно знать число сторон многоугольника. Число сторон можно выяснить по названию многоугольника. Ниже приведены части названий многоугольников.[12]
- Четырех (4), пяти (5), шести (6), семи (7), восьми (8), девяти (9), десяти (10), одиннадцати (11), двенадцати (12), тринадцати (13 ), четырнадцати (14), пятнадцати (15) и так далее.
- Если сторон слишком много, то в название многоугольника включается цифра. Например, если у многоугольника 44 стороны, он называется 44-угольником.
- Если дан рисунок многоугольника, просто посчитайте его стороны.
-

3
Подставьте число сторон в формулу. Сделайте это после того, как найдете число сторон многоугольника. Число сторон подставьте вместо n.[13]
- Например. У двенадцатиугольника 12 сторон.
- Запишите формулу: d = n(n-3)/2
- Подставьте число сторон: d = (12(12 – 3))/2
-

4
Решите уравнение. Для этого не забудьте про определенный порядок выполнения математических операций. Начните с вычитания, затем умножьте, а потом разделите. В итоге вы получите число диагоналей многоугольника.[14]
- Например: (12(12 – 3))/2
- Вычитание: (12*9)/2
- Умножение: (108)/2
- Деление: 54
- У двенадцатиугольника 54 диагонали.
-

5
Попрактикуйтесь на других примерах. Чем больше задач вы решите, тем лучше уясните процесс вычисления. Также вы наверняка запомните формулу для вычисления числа диагоналей, что пригодится на экзамене. Не забывайте, что представленная формула применима к многоугольнику, у которого больше трех сторон.
- Шестиугольник (6 сторон): d = n(n-3)/2 = 6(6-3)/2 = 6*3/2 = 18/2 = 9 диагоналей.
- Десятиугольник (10 сторон): d = n(n-3)/2 = 10(10-3)/2 = 10*7/2 = 70/2 = 35 диагоналей.
- Двадцатиугольник (20 сторон): d = n(n-3)/2 = 20(20-3)/2 = 20*17/2 = 340/2 = 170 диагоналей.
- 96-угольник (96 сторон): 96(96-3)/2 = 96*93/2 = 8928/2 = 4464 диагоналей.
Реклама
Об этой статье
Эту страницу просматривали 175 632 раза.
Была ли эта статья полезной?
|
Сколько диагоналей имеет в частности пентагон и октагон? Так очень же просто вывести формулу. Рассмотрим одну вершину n-угольника. К ней самой, а также к двум ближайшим вершинам диагональ не проведешь. Значит из каждой вершины можно провести (n-3) диагонали. Умножаем на количество вершин, и разделим на 2, так как при таком подсчете каждая диагональ посчитана дважды. Итого получается n*(n-3)/2. Теперь просто подставляем значения n. Остается отметить, что формула пригодна только для полностью выпуклых многоугольников, т.е. не имеющих внутренних углов, превышающих 180 градусов. автор вопроса выбрал этот ответ лучшим
Если брать выпуклые многоугольники, то есть такие у которых только две соседних вершины оказываются лишенными диагоналей – они связаны с третьей боковыми сторонами, то легко подсчитать, что от каждой вершины пятиугольника, в том числе пентагона, можно провести только две диагонали к свободным вершинам. Итого получается десять диагоналей. Но при таком подсчете каждая диагональ оказывается учтена два раза по прямому направлению и обратному. Так что смело делим это количество на 2 и получаем для пятиугольника 5 диагоналей. Для восьмиугольника действуем так же. От каждой вершины проводим пять диагоналей, умножаем на число вершин – 40 диагоналей и делим на 2. Итог – в восьмиугольнике 20 диагоналей. Знаете ответ? |
Восьмиугольник, виды, свойства и формулы.
Восьмиугольник – это многоугольник, общее количество углов (вершин) которого равно восьми.
Восьмиугольник, выпуклый и невыпуклый восьмиугольник
Правильный восьмиугольник (понятие и определение)
Свойства правильного восьмиугольника
Формулы правильного восьмиугольника
Правильный восьмиугольник в природе, технике и культуре
Шестиугольник
Восьмиугольник, выпуклый и невыпуклый восьмиугольник:
Восьмиугольник – это многоугольник с восемью углами.
Восьмиугольник – это многоугольник, общее количество углов (вершин) которого равно восьми.
Восьмиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.
Соответственно выпуклый восьмиугольник – это восьмиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Рис. 1. Выпуклый восьмиугольник
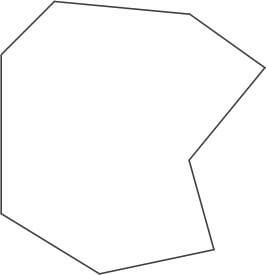
Рис. 2. Невыпуклый восьмиугольник
Сумма внутренних углов любого выпуклого восьмиугольника равна 1080°.

Правильный восьмиугольник (понятие и определение):
Правильный восьмиугольник (октагон) – это правильный многоугольник с восемью сторонами.
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
Правильный восьмиугольник – это восьмиугольник, у которого все стороны равны, а все внутренние углы равны 135°.

Рис. 3. Правильный восьмиугольник
Правильный восьмиугольник имеет 8 сторон, 8 углов и 8 вершин.
Углы правильного восьмиугольника образуют восемь равнобедренных треугольников.
Правильный восьмиугольник можно построить с помощью циркуля и линейки: проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.
Свойства правильного восьмиугольника:
1. Все стороны правильного восьмиугольника равны между собой.
a1 = a2 = a3 = a4= a5 = a6 = a7 = a8.
2. Все углы равны между собой и составляют 135°.
α1 = α2 = α3 = α4 = α5 = α6 = α7 = α8 = 135°.

Рис. 4. Правильный восьмиугольник
3. Сумма внутренних углов любого правильного восьмиугольника равна 1035°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного восьмиугольника O.

Рис. 5. Правильный восьмиугольник
5. Количество диагоналей правильного восьмиугольника равно 20.
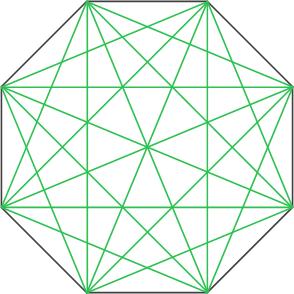
Рис. 6. Правильный восьмиугольник
6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.
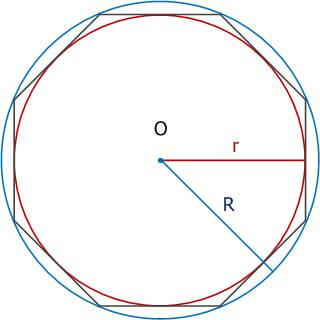
Рис. 7. Правильный восьмиугольник
Формулы правильного восьмиугольника:
Пусть a – сторона восьмиугольника, r – радиус окружности, вписанной в восьмиугольник, R – радиус описанной окружности восьмиугольника, k – константа восьмиугольника, P – периметр восьмиугольника, S – площадь восьмиугольника.
Формула константы правильного восьмиугольника:
![]()
Формула периметра правильного восьмиугольника:
![]()
Формулы площади правильного восьмиугольника:
![]()
Формулы радиуса окружности, вписанной в правильный восьмиугольник:

Формулы радиуса окружности, описанной вокруг правильного восьмиугольника:
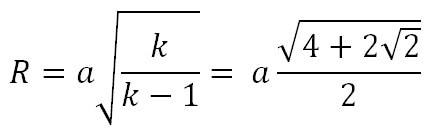
Формулы стороны правильного восьмиугольника:

Правильный восьмиугольник в природе, технике и культуре:
В странах, принявших Венскую конвенцию о дорожных знаках и сигналах (в том числе в России), а также во многих других странах, знак «Движение без остановки запрещено» имеет вид красного правильного восьмиугольника.
Форма правильного восьмиугольника часто используются в изобразительном искусстве, архитектуре. Например, Собор Святого Георгия (Аддис-Абеба, Эфиопия), Купол Скалы (Иерусалим, Израиль), башня Ветров (Афины, Греция), Сан-Витале (в городе Равенна, Италия), Замок Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий (Флоренция, Италия), Ахенский собор (Ахен, Германия), Капелла Карла Великого (Ахен, Германия).
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Шестиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Коэффициент востребованности
7 087
 Популярные ответы
Популярные ответы
- Когда буквы е, ё, ю, я обозначают два звука?
- Каким членом предложения может быть местоимение?
- Как правильно произносятся слова термин, шинель, темп?
- Как найти точки экстремума функции по графику производной?
- Как правильно: по средам (ударение на «а» или на «е»)?
- Какой официальный сайт Московского энергетического института (МЭИ)?
- На какие вопросы отвечает наречие?
- Где найти примеры сравнительных оборотов и других конструкций со словом «как»?
- Как в физике обозначается скорость движения?
- Где скачать задания по английскому языку олимпиады для школьников «Покори Воробьевы горы!»?
Диагональ в многоугольнике (многограннике) — отрезок, соединяющий любые две несмежные вершины, то есть, вершины, не принадлежащие одной стороне многоугольника (одному ребру многогранника).
У многогранников различают диагонали граней (рассматриваемых как плоские многоугольники) и пространственные диагонали, выходящие за пределы граней. У многогранников, имеющих треугольные грани есть только пространственные диагонали.
Подсчет диагоналей
Диагоналей нет у треугольника на плоскости и у тетраэдра в пространстве, поскольку все вершины этих фигур попарно связаны сторонами (ребрами).
Количество диагоналей N у многоугольника легко вычислить по формуле:
N = n·(n – 3)/2,
где n — число вершин многоугольника. По этой формуле нетрудно найти, что
- у треугольника — 0 диагоналей
- у прямоугольника — 2 диагонали
- у пятиугольника — 5 диагоналей
- у шестиугольника — 9 диагоналей
- у восьмиугольника — 20 диагоналей
- у 12-угольника — 54 диагонали
- у 24-угольника — 252 диагонали
Количество диагоналей многогранника с числом вершин n легко подсчитать только для случая, когда в каждой вершине многогранника сходится одинаковое число ребер k. Тогда можно пользоваться формулой:
N = n·(n – k – 1)/2,
которая даем сумманое число пространственных и граневых диагоналей. Отсюда можно найти, что
- у тетраэдра (n=4, k=3) — 0 диагоналей
- у октаэдра (n=6, k=4) — 3 диагонали (все пространственные)
- у куба (n=8, k=3) — 16 диагоналей (12 граневых и 4 пространственных)
- у икосаэдра (n=12, k=5) — 36 диагоналей (все пространственные)
- у додекаэдра (n=20, k=3) — 160 диагоналей (25 граневых и 135 пространственных)
Если в разных вершинах многогранника сходится разное число ребер, подсчет заметно усложняется и должен проводится индивидуально для каждого случая.
Фигуры с равными диагоналями
На плоскости существует два правильных многоугольника, у которых все диагонали равны между собой. Это квадрат и правильный пятиугольник. У квадрата две одинаковых диагонали, пересекающихся в центре под прямым углом. У правильного пятиугольника пять одинаковых диагоналей, которые вместе образуют рисунок пятиконечной звезды (пентаграммы).
Единственный правильный многогранник, у которого все диагонали равны между собой — правильный восьмигранник октаэдр. У него три диагонали, которые попарно перпендикулярно пересекаются в центре. Все диагонали октаэдра — пространственные (диагоналей граней у октаэдра нет, т.к. у него треугольные грани).
Помимо октаэдра есть еще один правильный многогранник, у которого все пространственные диагонали равны между собой. Это куб (гексаэдр). У куба четыре одинаковых пространственных диагонали, которые также пересекаются в центре. Угол между дигоналями куба состаляет либо arccos(1/3) ≈ 70,5° (для пары диагоналей, проведенных к смежным вершинам), либо arccos(–1/3) ≈ 109,5° (для пары диагоналей, проведенных к несмежным вершинам).
Ссылки:
- ru.wikipedia.org — Википедия: Диагональ
- dic.academic.ru — иллюстрация разницы между граневой и пространственной диагоналями многогранника
Дополнительно в базе данных Генона:
- Как найти диагональ прямоугольника?
- Сколько вершин, ребер и граней у тетраэдра?
- Сколько вершин, ребер и граней у куба (гексаэдра)?
