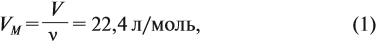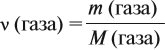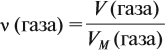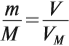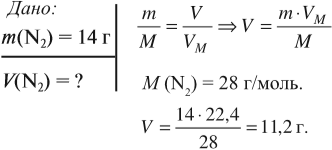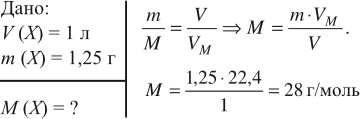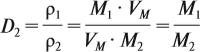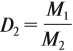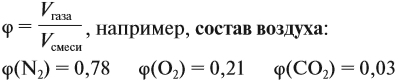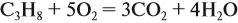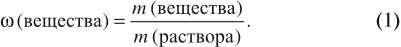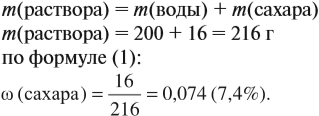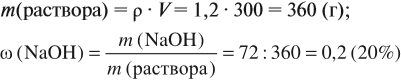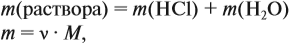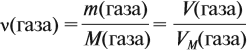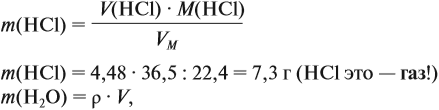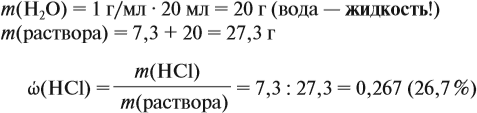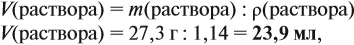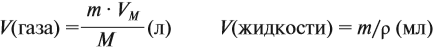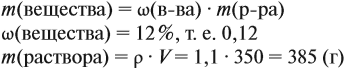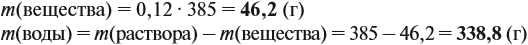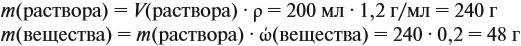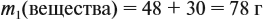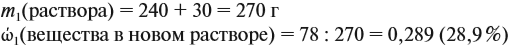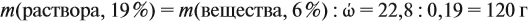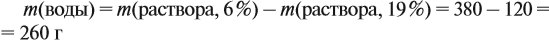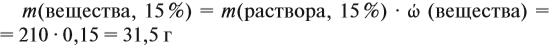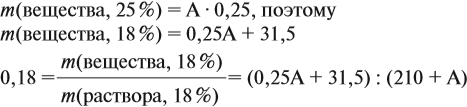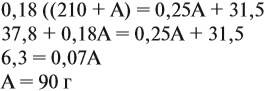Итак, количество вещества в химии обозначается греческой буквой “ню”.
Помню, как в 9-м классе мой учитель физики Игорь Юрьевич учил меня правильно писать букву “ню”. До этого она у меня получалась немного коряво.
Но поскольку на БВ не проходят греческие буквы, я буду обозначать количество вещества латинской буквой v. Латинская v очень похожа на греческую “ню”.
Рассмотрим следующие случаи.
1) Если нам известно количество частиц вещества, то количество вещества можно найти по формуле:
v = n/NA
где
v — количество вещества;
n — количество частиц вещества. Это безразмерная величина, то есть это просто число. Правда, это число бывает очень большим, например, 5*(10^24).
NA — постоянная Авогадро. Постоянная Авогадро представляет собой универсальную константу. NA = 6,022*(10^23) моль^(–1).
2) Если нам известна масса вещества, то количество вещества находится по следующей формуле:
v = m/M
где
v — количество вещества;
m — масса вещества;
M — молярная масса вещества находится по химической формуле вещества, при помощи периодической системы Д. И. Менделеева, путём суммирования атомных масс всех входящих в молекулу атомов с учётом имеющихся индексов.
3) Если нам известен объём газообразного вещества, то мы можем найти количество вещества газа по такой формуле:
v = V/Vm
где
v — количество вещества;
V — объём газа;
Vm — молярный объём газов. Молярный объём газов — это универсальная константа. Vm = 22,414 л/моль = 22414 м3/моль.
Повторюсь, что формула v = V/Vm верна только для газов!
Наконец, рассмотрим Ваш случай.
Вам по условию даны объём и объёмная доля.
Я рискну предположить, что у Вас задача примерно такого рода:
“Объём газовой смеси составляет 240 л. Объёмная доля кислорода в смеси равна 45%. Вычислите количество вещества кислорода в смеси”.
Такая задача решается в два действия.
1) Находим объём кислорода:
V (O2) = V0 * ф / 100 = 240 л * 45 / 100 = 108 л.
(Ф — это объёмная доля, она обозначается греческой буквой “фи”. Вместо неё приходится писать русскую ф).
2) Находим количество вещества кислорода. Кислород — это газ, значит, мы имеем право воспользоваться формулой v = V/Vm.
v (O2) = V/Vm = 108 л : 22,414 л/моль = 4,818 моль. Округление произведено до тысячных.
4.3.3. Расчеты массы вещества или объема газов по известному количеству вещества, массе или объему одного из участвующих в реакции веществ.
На данный момент задачи по этой теме кодификатора идут в КИМе ЕГЭ под номером 29.
Для их решения можно воспользоваться следующим алгоритмом:
1) записать уравнение реакции, о которой идет речь в задаче, и убедиться в правильности расставленных коэффициентов;
2) рассчитать количество молей вещества, масса или объем которого указаны в условии.
Если указана масса некого вещества A, то расчет количества вещества для него следует вести по формуле:
где mA – масса вещества А, а MA – молярная масса вещества А.
Если указан объем газообразного вещества А:
где VA – объем газообразного вещества А, а Vm – молярный объем, одинаковый для всех газов и при н.у. равный 22,4 л/моль.
Иногда вместо массы или объема вещества дается его количество вещества (моль). В таком случае действия по его нахождению не требуются.
3) далее от молей вещества А нужно перейти к молям вещества, массу или объем которого спрашивают в условии.
Допустим спрашивают объем или массу вещества B. Тогда для перехода от количества моль вещества А к количеству моль вещества B следует пользоваться тем правилом, что для любого вещества его количество, деленное на его коэффициент, в уравнении реакции одно и то же. Т.е. количества веществ А и В связаны друг с другом через коэффициенты в уравнении следующим образом:
где n(A) и n(B) – количества вещества А и В соответственно, а k(A) и k(B) – коэффициенты в уравнении перед этими веществами.
Из этого выражения следует, что количество вещества В равно:
4) далее, зная количество вещества B, мы можем найти его массу по формуле:
Если же вещество B является газом и спрашивают его объем, то рассчитать его можно следующим образом:
В общем, последовательность решения таких задач можно изобразить следующей схемой:
1) Зная массу или объем вещества A, рассчитываем его количество вещества.
2) Зная количество вещества A, рассчитываем количество вещества B по формуле:
где n(A) и n(B) – количества веществ А и В соответственно, а k(A) и k(B) – коэффициенты в уравнении перед этими веществами.
3) В зависимости от того, требуется найти массу вещества В или объем газа В, умножаем его количество либо на молярную массу, либо на молярный объем газа:
Пример
Какая масса сульфида алюминия потребуется для того, чтобы в результате его взаимодействия с избытком соляной кислоты образовался газ объемом 33,6 л (н.у.).
Решение:
1) Запишем уравнение реакции:
2) Рассчитываем количество вещества, для которого известна его масса или объем (в случае газа). Нам известен объем сероводорода, рассчитаем его количество вещества:
3) Отношение количества вещества любого фигуранта реакции к его коэффициенту в уравнении этой реакции всегда одно и то же. Т.е. для сульфида алюминия и сероводорода мы можем записать, что:
где k(Al2S3) и k(H2S) – коэффициенты перед Al2S3 и H2S соответственно.
Из этого выражения выразим n(Al2S3):
Подставим известные значения n(H2S) и коэффициентов перед H2S и Al2S3:
Тогда масса сульфида алюминия будет равна:
Задачи с реальных экзаменов ЕГЭ на тему «Расчеты массы вещества или объема газов по известному количеству вещества, массе или объему одного из участвующих в реакции веществ» можно порешать здесь.
Молярный объём
Vm
— это отношение объёма данной порции вещества к его количеству.
Численно молярный объём равен объёму (1) моль вещества.
Обрати внимание!
Молярный объём любого газа при нормальных условиях (давлении (101,3) кПа и температуре (0) °С) равен (22,4) дм³/моль.
Вычисление объёма газа по его количеству
Преобразуем формулу молярного объёма — выразим из неё
V
:
— объём газа равен произведению его количества на молярный объём.
Пример:
вычисли объём (н. у.) метана количеством (1,5) моль.
дм³.
Вычисление количества газа по его объёму
Выразим из формулы молярного объёма
n
:
— количество газа можно вычислить, если его объём разделить на молярный объём.
Пример:
вычисли количество водорода, соответствующее при н. у. его объёму (11,2) дм³.
моль.
В ходе решения таких задач рекомендуется придерживаться алгоритма:
- внимательно прочитать условие задачи и выяснить, что у вас спрашивают;
- написать соответствующую формулу и проанализировать её;
- найти числовые значения требуемых величин, каждый раз записывая вначале формулу, а затем расчёт, учитывая размерность величин.
Содержание
- Задачи по теме «Газы»
- Задачи для самостоятельного решения
- Задачи по теме «Способы выражения концентрации растворов»
- Задачи для самостоятельного решения
Задачи по теме «Газы»
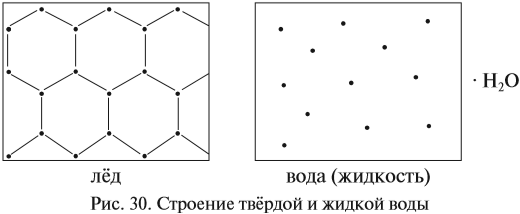
Известно, что вещества при нормальных условиях (н. у.) могут находиться в трёх агрегатных состояниях: твёрдом, жидком, газообразном. В твёрдом и жидком состояниях между молекулами (атомами) вещества имеются довольно сильные взаимодействия, в результате чего частицы находятся на небольших расстояниях друг от друга (рис. 30).
В газах расстояния между частицами очень велики, и силы взаимодействия ничтожны (рис. 31).
Поэтому равные объёмы любых газов содержат одинаковое число молекул. Это формулировка закона АВОГАДРО.
Следствием этого закона является:
1 моль любого газа при нормальных условиях (н. у.) занимает объём 22,4 литра.
Эта величина (22,4 л/моль) является молярным объёмом газа (VМ):
где VM — молярный объём газа, моль/л; V — объём газа, л; ν — количество вещества газа, моль.
Таким образом, зная массу газа, можно определить:
Но для того же газа из формулы (1) имеем:
Отсюда для любого газа выполняется соотношение:
Задача 3. Какую массу имеет кислород объёмом 7 л?
Задача 4. Какой объём занимает азот массой 14 г?
Задача 5. Чему равна молярная масса газа, 1 л которого имеет массу 1,25 г?
Ответ. Молярная масса неизвестного газа 28 г/моль.
Пользуясь этими формулами, можно рассчитать объём, массу, молярную массу газа, например:
Известно, что
где ρ — плотность газа (г/л), поэтому:
ПОМНИТЕ! Эти формулы можно использовать лишь тогда, когда данные задачи (плотность газа, его объём) измерены при н. у.: 273 К, 1 атм.
Из формулы (3) вытекает понятие об относительной плотности газов (Dx). Эта величина, равная отношению плотностей двух газов:
где ρ1 и М1 — плотность и молярная масса одного газа, а ρ2 и М2 — плотность и молярная масса другого газа.
Относительная плотность газа показывает, во сколько раз данный газ тяжелее второго газа. Пользуясь этой формулой, можно легко определить молярную массу данного газа:
Выполняя такие расчёты, следует помнить, что:
- любая смесь газов, например воздух, именуется в задачах словом «газ»;
- средняя молярная масса воздуха, как показывают расчёты, равна 29 г/моль;
- по умолчанию, если не сказано иного, расчёты ведут для н. у.: 273 К, 1 атм.
Задача 6. Определить молярную массу газа, если:
а) плотность его равна 1,25 г/л;
б) плотность его по кислороду равна 0,75.
Решение.
Состав смеси газов, как правило, измеряют в объёмных процентах φ (фи).
Второе следствие, при помощи которого была экспериментально подтверждена гипотеза Авогадро (гипотеза стала законом уже после смерти автора!), заключается в следующем: объемы реагирующих газов относятся как их коэффициенты в соответствующем уравнении реакции.
Это следствие позволяет решать задачи «в уме», если известны объёмы реагирующих газов или количества вещества для них.
Задача 7. Какой объём кислорода потребуется для сжигания 6 л пропана?
Из уравнения реакции:
видно, что молярное соотношение пропана и кислорода составляет 1 : 5. Таким образом, объём кислорода в пять раз больше объёма пропана.
Ответ. Требуется 5 · 6 = 30 л кислорода.
Задачи для самостоятельного решения
3. Определить массы газов:
а) хлороводорода, объёмом 56 л;
б) озона О3, объёмом 14 л.
4. Определить объёмы газов:
а) хлороводорода, массой 72 г;
б) аммиака NH3, массой 3,4 г.
5. Определить молярные массы газов, если:
а) 2 л газа имеет массу 2,86 г;
б) 10 г газа занимает объём 7,47 л.
6. Определить молярную массу газа, если:
а) плотность его равна 1,52 г/л;
б) плотность по кислороду равна 1,81.
7. Какой объем занимает смесь, состоящая из 4 г метана и 22 г пропана?
8. Какой газ имеет большую массу: этан, объёмом 56 л или бутан, объёмом 44,8 л?
9. Существуют ли газообразные соединения серы легче воздуха?
10. Определите, не выполняя расчёт, какой из газов тяжелее воздуха: Не, Ar, CO2, CH4, N2, O2.
Задачи по теме «Способы выражения концентрации растворов»
Для того чтобы определить массовую долю растворенного вещества, нужно воспользоваться формулой:
Ответ может быть дан в долях (единицы): ω = 0,15; или в процентах: ω% = 15 %.
Задача 8. В 200 г воды растворили 16 г сахара. Определить ω(сахара) в полученном растворе.
Решение. В данном случае масса раствора неизвестна. Но:
Задача 9. В 300 мл раствора (ρ = 1,2 г/мл) содержится 72 г NаОН. Определить ω(NаОН) в этом растворе.
Решение. В этом случае масса раствора неизвестна, но известен объём. Найдём массу раствора:
Задача 10. В 20 мл воды растворили 4,48 л хлороводорода. Определить ω(НСl) в соляной кислоте. Плотность раствора равна 1,14 г/мл.
Решение. При растворении хлороводорода в воде получена соляная кислота, её масса равна:
где ν — количество вещества, моль; M — молярная масса вещества, причём для газов
откуда
где ρ — плотность воды (1 г/мл); V — объём воды, мл
Обратите внимание: в 20 мл воды растворили 4,48 л газа, но суммарный объём отнюдь не равен (4,48 + 0,02), т. е. 4,5 литра! Суммарный объём этого раствора равен:
т. е. при растворении более 4 литров газа объём жидкого раствора увеличился менее чем на 4 миллилитра!
Выводы.
- Объёмы жидкостей и объёмы растворяемых газов суммировать нельзя.
- При растворении в жидкости газы сжимаются более чем в 1000 раз.
- Объёмы жидкостей и газов рассчитывают (исходя из значения массы) по-разному:
где m — масса, г; М — молярная масса, г/моль; V — объём (жидкости в мл, газа — в л); ρ — плотность жидкости, г/мл.
Пользуясь формулой (1) нетрудно рассчитать и массу раствора, и массу растворённого вещества. Но при этом следует учитывать, что обычно в задачах говорится (упоминается) о «5 %-ном растворе», «16 %-ном растворе» и т. д., т. е. массовая доля вещества выражена в процентах. В этом случае легко видеть, что:
- в 5 %-ном растворе ω(вещества) = 0,05;
- в 16 %-ном растворе ω(вещества)= 0,16 и т. д.
Зная массовую долю вещества в растворе, можно определить:
Задача 11. Сколько граммов соли и воды нужно взять для приготовления 350 мл (ρ = 1,1 г/мл) 12 %-ного раствора?
Решение. Из формулы (1) получаем формулу (2):
где ρ — плотность раствора (1,1 г/мл); V — объём раствора (350 мл), тогда
Задача 12. Сколько граммов 8 %-ного раствора можно приготовить, имея 64 г NaCl?
Решение. Из формулы (3):
Такие задачи можно решать, составляя пропорции. При этом следует знать, что массовая доля (в %) вещества показывает, сколько граммов вещества содержится (растворено) в 100 граммах раствора: 5 %-ный раствор ⇒ 5 г вещества в 100 граммах раствора.
Задача 13. Сколько мл 15 %-ного раствора (ρ = 1,1 г/мл) можно приготовить из 22,5 г вещества?
Обратите внимание: в пропорции в одном столбце должны совпадать и размерность, и наименование компонента, о котором идёт речь.
Задача 14. К 200 мл 20 %-ного раствора (ρ = 1,2 г/мл) добавили 30 г того же вещества. Определить массовую долю вещества в полученном растворе.
Решение. Определим в начале массу исходного раствора и растворённого вещества:
При добавлении новых порций растворяемого вещества, его масса увеличивается:
На ту же величину увеличивается масса раствора:
Задача 15. Сколько граммов 19 %-ного раствора и воды нужно взять для получения 380 г 6 %-ного раствора?
Решение. При добавлении воды масса растворённого вещества не меняется. Поэтому рассчитаем массу растворённого вещества в 6 %-ном растворе (столько же его будет и в 19 %-ном растворе):
Теперь можно рассчитать массу 19 %-ного раствора:
Теперь задумаемся: почему возросла масса исходного 19 %-ного раствора? Потому, что добавили воду. Значит, масса воды равна:
Ответ. Нужно добавить 260 г воды.
В случаях, когда изменяется и масса раствора, и масса вещества, нужно прибегнуть к приёму, когда неизвестная величина (о ней спрашивается в вопросе задачи), принимается за известную, и обозначается А.
Задача 16. Сколько граммов 25 %-ного раствора нужно добавить к 210 г 15 %-ного раствора, чтобы получить 18 %-ный раствор?
Решение. Пусть нужно добавить А граммов 25 %-ного раствора, тогда масса 18 %-ного раствора составит (210 + А) г. Определим массу вещества в 15 %-ном растворе:
аналогично:
Решим полученное уравнение:
Ответ. Нужно добавить 90 г 25 %-ного раствора.
Задачи для самостоятельного решения
11. В 300 г раствора содержится 45 г поваренной соли. Определить ω (NaСl) в этом растворе.
12. В 300 мл воды растворили 100 г сахара. Определить ω (сахара) в полученном растворе.
13. В 2 л раствора (пл. = 1,05 г/мл) содержится 105 г соли. Определить ω(соли) в этом растворе.
14. В 200 мл воды растворили 56 л аммиака NH3. Определить ω (NH3) в этом растворе.
15. Бромоводород объёмом 5,4 л затрачен на приготовление 8 %-ного раствора (пл. = 1,057 г/мл). Найти объём полученного раствора.
16. Сколько граммов воды и сахара нужно взять для приготовления 3 литров 30 %-ного сиропа? (Пл. = 1,13 г/мл.)
17. Какой объём 25 %-ного раствора можно приготовить из 150 г соли, если плотность раствора равна 1,2 г/мл?
18. К 500 мл 32 %-ной кислоты (ρ = 1,2 г/мл) добавили 1 л воды. Вычислить массовую долю кислоты в полученном растворе.
19. Смешали 25 г 16 %-ного раствора КОН с 30 мл 20 %-ного раствора КОН (плотность 1,2 г/мл). Вычислить массовую долю щёлочи в полученном растворе.
20. К 220 г 20 %-ного раствора поваренной соли добавили 44 мл воды и 36 г этой же соли. Вычислить массовую долю соли в полученном растворе.
21. Определить массу воды, которую нужно выпарить из 1 кг 3 %-ного раствора сульфата меди II для получения 5 %-ного раствора.
22. Сколько граммов воды нужно добавить к 50 г 70 %-ной уксусной кислоты, чтобы получить 5 %-ный уксус?
23. После добавления соды к 200 мл 16 %-ного раствора её (ρ = 1,17 г/мл) массовая доля вещества возросла до 20 %. Определить массу добавленной соды.
24. Какой объём 96 %-ной кислоты (ρ = 1,86 г/мл) необходимо добавить к 5 л 30 %-ной кислоты (ρ = 1,3 г/мл), для того чтобы получить 40 %-ный раствор?
Есть множество формул для нахождения объема. В первую очередь необходимо определить в каком агрегатном состоянии находится вещество, для которого мы ищем объем. Для объема газа подходят одни формулы, а для объема раствора совершенно другие.
Одна из формул объема раствора: V = m/p, где V – объем раствора (мл) , m – масса (г) , p – плотность (г/мл) . Если требуется дополнительно найти массу, то это можно сделать, зная формулу и количество нужного вещества. С помощью формулы вещества мы найдем его молярную массу, сложив атомные массы всех элементов, входящих в его состав. Например, M(AgNO3) = 108+14+16*3 = 170 г/моль. Далее находим массу по формуле: m = n*M, где m – масса (г) , n – количество вещества (моль) , M – молярная масса вещества (г/моль) . Подразумевается, что количество вещества дано в задаче.
2
Следующая формула для нахождения объема раствора выводится из формулы молярной концентрации раствора: с = n/V, где c – молярная концентрация раствора (моль/л) , n – количество вещества (моль) , V – объем раствора (л) . Выводим: V = n/c. Количество вещества можно дополнительно найти по формуле: n = m/M, где m – масса, M – молярная масса.
3
Далее приведены формулы для нахождения объема газа. V = n*Vm, где V – объем газа (л) , n – количество вещества (моль) , Vm – молярный объем газа (л/моль) . При нормальных условиях, т. е. давлении равным 101 325 Па и температуре 273 К молярный объем газа является величиной постоянной и равен 22,4 л/моль.
4
Для газовой системы существует формула: : q(x) = V(x)/V, где q(x)(фи) – объемная доля компонента, V(x) – объем компонента (л) , V – объем системы (л) . Из этой формулы можно вывести 2 другие: V(x) = q*V, а также V = V(x)/q.
5
Если в условии задачи присутствует уравнение реакции, решать задачу следует с помощью него. Из уравнения можно найти количество любого вещества, оно равно коэффициенту. Например, CuO + 2HCl = CuCl2 + H2O. Отсюда видим, что при взаимодействии 1 моля оксида меди и 2 моль соляной кислоты получилось 1 моль хлорида меди и 1 моль воды. Зная по условию задачи количество вещества всего одного компонента реакции, можно без труда найти количества всех веществ. Пусть, количество вещества оксида меди равно 0,3 моль, значит n(HCl) = 0,6 моль, n(CuCl2) = 0,3 моль, n(H2O) = 0,3 моль.