Определение.
Граф называется плоским,
если он представим в пространстве R^2.
Определение.
Гранью в плоском представлении называется
часть пространства R^2, отделенная дугами
этого представления.
Теорема
(формула Эйлера).
Количество граней в плоском представлении
связного графа с n вершинами и m ребрами
равно m − n + 2.
Следствие.
Количество граней в плоском представлении
графа с n вершинами , m ребрами и k
компонентами связности равно m − n + k +
1.
Доказательство
формулы Эйлера для плоских связных
графов
Индукция
по величине t = m − n ≥ −1. База индукции:
если t = m − n = −1, то граф является
деревом
и количество граней равно 1 − 1 + 2 = m −
n + 2.
Индукционное
предположение:
предположим формула Эйлера верна для
всех плоских представлений с m − n = t.
Индукционное
шаг: пусть
дано плоское представление G = (V, E) с n
вершинами и m ребрами, причем
m
− n = t + 1 ≥ 0. Тогда G не является деревом,
и содержит ребро e ∈
E не
являющееся
мостом.
Тогда
граф
U = (V, E {e})
по индукционному предположению имеет
(m − 1) − n + 2 граней.
Но
поскольку e содержалось в некотором
цикле, количество граней в U на единицу
меньше
чем в G. (m − 1) − n + 2 + 1 = m − n + 2 граней.
17
Ориентированные графы. Положительные
и отрицательные степени вершин. Теорема
о суммах положительных и отрицательны
степеней. Изоморфизм ориентированных
графов.
Определение.
Ориентированный
граф состоит
из множества вершин V и множества ребер
E, причем каждому ребру e ∈
E сопоставлена
упорядоченная
пара
вершин
(a, b) ∈
V^2.
В
этом случае говорят, что вершина a ∈
V является
началом,
а b ∈
V —
концом
ребра
e ∈
E.
Определение.
Ребро, сопоставленное паре (a, a) называется
петлей.
Если несколько ребер имеют одинаковое
начало и конец, то такие ребра называют
кратными.
Определение.
Неориентированный граф (V, E) называется
простым,
если среди элементов V нет петель и
кратных ребер. Для случая простых графов
мы будем отождествлять ребра e ∈
E с
соответствующей
парой
вершин
(a, b) ∈
V^2.
Определение.
Путь из A ∈
V в
B ∈
V во
взвешенном
графе
G = (V, E) с
весовой функцией w : E 7→ R+ называется
минимальным,
если его длина не превосходит длины
любого другого пути из A ∈
V в
B ∈
V.
Определение.
Расстоянием d(A, B) из A ∈
V в
B ∈
V во
взвешенном
графе G = (V, E) называется длина
минимального
пути из A в B. Если путей из A в B нет, то
d(A, B) = ∞..
Степень
захода вершины v орграфа D = (V, A) определяется
следующим образом
d+D(v)
= |{u ∈
V | (u, v) ∈
A}|.
Степень
исхода вершины v орграфа D = (V, A) определяется
следующим образом
d−D(v)
= |{u ∈
V | (v, u) ∈
A}|.
Имеет
место следующий аналог леммы о
рукопожатиях.
Лемма
7. Если D = (V,
A) ориентированный граф, то
 d+D(v) = |A| =
d+D(v) = |A| = d−D(v).
d−D(v).
Орграфы
G = (V, E) и G’ = (V’, A’) называются изоморфными,
если существует такая биекция
ϕ
: V → V’, что (u,
v)
∈
A
⇔
(ϕ(u),
ϕ(v))
∈
A’.
Отображение
ϕ называется изоморфизмом.
Таким
образом, как и в случае неориентированных
графов, изоморфизм это биективное
отображение множества вершин при
котором смежным вершинами графа G
соответствуют смежные вершины графа
G’ и наоборот и, кроме того, сохраняются
направления дуг.
18.
Алгоритм Дейкстры нахождения кратчайшего
пути.
Формальное
определение
Дан
взвешенный ориентированный граф G(V,E)
без петель и дуг отрицательного веса.
Найти
кратчайшие пути от некоторой вершины
a графа G до всех остальных вершин этого
графа.
Каждой
вершине из V сопоставим метку —
минимальное известное расстояние от
этой вершины
до
a. Алгоритм работает пошагово — на
каждом шаге он «посещает» одну вершину
и пытается
уменьшать
метки. Работа алгоритма завершается,
когда все вершины посещены.
Инициализация.
Метка
самой вершины a полагается равной 0,
метки остальных вершин — бесконечности.
Это
отражает
то, что расстояния от a до других вершин
пока неизвестны. Все вершины графа
помечаются
как непосещённые.
Шаг
алгоритма.
Если все вершины посещены, алгоритм
завершается. В противном случае, из
ещё
не посещённых вершин выбирается вершина
u, имеющая минимальную метку. Мы
рассматриваем
всевозможные маршруты, в которых u
является предпоследним пунктом.
Вершины,
в которые ведут рёбра из u, назовем
соседями этой вершины. Для каждого
соседа
вершины
u, кроме отмеченных как посещённые,
рассмотрим новую длину пути, равную
сумме
значений
текущей метки u и длины ребра, соединяющего
u с этим соседом. Если полученное
значение
длины меньше значения метки соседа,
заменим значение метки полученным
значением
длины.
Рассмотрев всех соседей, пометим вершину
u как посещенную и повторим шаг алгоритма.
Доказательство
корректности
Пусть
l(v) — длина кратчайшего пути из вершины
a в вершину v. Докажем по индукции,
что
в момент посещения любой вершины z,
d(z)=l(z).
База.
Первой посещается вершина a. В этот
момент d(a)=l(a)=0.
Шаг.
Пускай мы выбрали для посещения вершину
z != a. Докажем, что в этот момент d(z)=l(z).
Для
начала отметим, что для любой вершины
v, всегда выполняется d(v) >= l(v)
(алгоритм
не может найти путь короче, чем кратчайший
из всех существующих).
Пусть
P — кратчайший путь из a в z, y — первая
непосещённая вершина на P, x —
предшествующая
ей (следовательно, посещённая). Поскольку
путь P кратчайший, его часть,
ведущая
из a через x в y, тоже кратчайшая,
следовательно l(y)=l(x)+w(xy). По
предположению
индукции, в момент посещения вершины
x выполнялось d(x)=l(x),
следовательно,
вершина y тогда получила метку не больше
чем d(x)+w(xy)=l(x)+w(xy)=l(y).
Следовательно,
d(y)=l(y). С другой стороны, поскольку сейчас
мы выбрали вершину z, её
метка
минимальна среди непосещённых, то есть
d(z)<=d(y) = l(y)<=l(z). Комбинируя это
с
d(z)>=l(z), имеем d(z)=l(z), что и требовалось
доказать. Поскольку алгоритм
заканчивает
работу, когда все вершины посещены, в
этот момент d=l для всех вершин.
19. Сети
и потоки. Величина потока и его свойства
(сумма потоков из источника = сумме
потоков в сток). Задача о нахождении
максимального потока.
Определение.
Сетью
называется взвешенный граф G
= (E,
V)
с весовой функцией q
: E
→ R+
в котором выделен источник A
∈
V,→deg(A)
= 0, и сток B
∈
V,
←deg(B)
= 0. Значение
q(X,
Y)
называется
пропускной
способностью
ребра (X,
Y)
∈
E.
Если
(X,
Y)
∈/
E
то
считаем,
что
q(X,
Y)
= 0
Определение.
Потоком
называется весовая функция p
: E
→ R+
∪
{0} такая,
что
1.
p(X,
Y)
≤ q(X,
Y)
для всех (X,
Y)
∈
E;
2.
Для всех вершин C
!= A,B
имеет место
 p(C,
p(C,
X)
=
 p(Y,
p(Y,
C).
Если
(X,
Y)
∈/
E
то
считаем,
что
p(X,
Y)
= 0.Теорема. Для потока p
: E
7→ R+
в сети G
= (E,
V,
q,
A,
B)
имеет
место
 p(A,
p(A,
X)
=
 p(Y,
p(Y,
B).
Данная
сумма называется величиной потока.
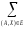 p(A,
p(A,
X) =

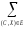 p(C,
p(C,
X) −
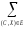 p(C,
p(C,
X) =
 p(Y,
p(Y,
C) −
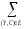 p(Y,
p(Y,
C) =
 p(Y,
p(Y,
B).
Задача
о максимальном потоке.
Дано.
Пусть имеется сеть G
= (E,
V,
q,
A,
B).
Найти
поток p
: E
→ R+
∪
{0} с
наибольшей
величиной
V(p).
Алгоритм
Пусть
к этому шагу в транспортной сети G, c
построен поток f и сток получил пометку
(m+, δ). Тогда увеличиваем поток fms через
дугу (m, s) и полагаем его равным f’ms = fms
+δ. Переходим к рассмотрению вершины
m. Общий шаг: пусть находимся в вершине
j . Возможны две ситуации: вершина имеет
метку вида (i+, γ), либо вершина имеет
метку вида (i−, γ). Тогда в первом
случае,
изменяем поток f’ij = fij + δ, а во втором
случае (здесь дуга идет из j в i) полагаем
поток равным f’ji = fji − δ (необходимо
обратить внимание на то, что поток через
дугу на каждом шаге изменяется на одну
и ту же величину δ). В обоих случаях
переходим к вершине i. Продолжаем
изменение потока, пока не достигнем
источника. Как только источник достигнут,
переходим к этапу расставления пометок.
20.
Разрезы в сетях. Величина потока не
превосходит величины разреза. Величина
разреза.
Определение.
Разрезом в сети G = (E, V, q, A, B) называется
произвольное подмножество U ⊆
V такое,
что
A ∈
U и
B ∈/
U.
Определение.
Величина потока через разрез:
V(p,
U) = V+(p, U) − V−(p, U),
где
V+(p,
U)
=
 p(Y,
p(Y,
X),
V−(p,
U) =
 p(X,
p(X,
Y).
Теорема.
Для потока p : E → R+ ∪
{0} в
сетиG
= (E, V, q, A, B) и произвольного разреза U ⊆
V имеет
место
V(p, U) = V(p).
Доказательство.
Индукция по |U|. Если |U| = 1, то U = {A}, V−(U,
p) = 0и V+(U, p) = V(p).
Предположим,
что теорема верна при |U| = n. Докажем
теорему при |U| = n + 1. Пусть U = W ∪
C},
C
!= A, B и |W| = n. По предположению V(W, p) = V(p).
Тогда
V(U, p) − V(W, p) =(V+(U, p) − V+(W, p)) − (V−(U, p) −
V−(W, p)) =
( p(C,
p(C,
X)
− p(Y,
p(Y,
C))−(
 p(Y,
p(Y,
C)
−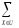 p(C,
p(C,
X))=
 p(C,
p(C,
X)
− p(Y,
p(Y,
C)
= 0.
Значит,
V(U, p) = V(W, p) = V(p).
21.
Алгоритм Форда-Фолкерсона.
Пусть
дана транспортная сеть (G, c). Работа
алгоритма состоит из трех этапов.
1.
Выбор исходного потока.
Строим произвольный поток f в сети (G,
c),
например,
нулевой.
2.
Расставление пометок.
Вершинам будут приписываться метки
состоящие
из
двух элементов. На первом шаге, помечаем
источник меткой (−, ∞). Очеред-
ной
шаг: выбираем одну из уже помеченных,
но еще не обработанных вершин (на-
пример,
с наименьшим номером) и обрабатываем
ее. Пусть требуется обработать
вершину
i с пометкой (x, q), тогда действуем по
следующим правилам:
–
если из вершины i в не помеченную вершину
j идет такая дуга, что fij < cij ,
то
помечаем вершину j парой (i+, min(q, cij −
fij));
–
если в вершину i из не помеченной вершины
j идет такая дуга, что fji > 0,
то
помечаем вершину j парой (i−, min(q, fji)).
После
того как помечены все возможные на
данном шаге вершины, переходим
к
следующему шагу.
Этап
завершается в двух случаях:
–
если помечен сток — в этом случае
алгоритм переходит к этапу изменения
потока;
–
если сток еще не помечен, и нельзя больше
пометить ни одной вершины — в этом
случае алгоритм останавливается.
3.
Изменение потока.
Пусть к этому шагу в транспортной сети
G, c построен
поток
f и сток получил пометку (m+, δ). Тогда
увеличиваем поток fms через дугу
(m,
s) и полагаем его равным f0ms = fms +δ. Переходим
к рассмотрению вершины
m.
Общий шаг: пусть находимся в вершине j
. Возможны две ситуации: вершина
имеет
метку вида (i+, γ), либо вершина имеет
метку вида (i−, γ). Тогда в первом
случае,
изменяем поток f0ij = fij + δ, а во втором
случае (здесь дуга идет из j в i) полагаем
поток равным f0ji = fji − δ (необходимо
обратить внимание на то, что поток через
дугу на каждом шаге изменяется на одну
и ту же величину δ). В обоих случаях
переходим к вершине i. Продолжаем
изменение потока, пока не достигнем
источника. Как только источник достигнут,
переходим к этапу расставления пометок.
22.
Конечные автоматы и регулярные языки.
Примеры регулярных и нерегулярных
языков.
1.
Алфавитом X называется произвольный
набор символов.
2.
Словом над X называется произвольный
набор символов α = x1x2 . . . xl,
где xi ∈
X. Число
l
называется
длиной
слова α.
Пустое слово λ — слово длины 0.
3.
Через X∗
обозначается множество всех слов над
алфавитом X. Если α, β ∈
X∗,
то через αβ ∈
X∗
обозначается
конкатенация слов α и β.
α^n
— конкатенация α с собой n раз.
4.
Языком L над X называется любое подмножество
X∗,
то есть L ⊆
X∗.
Примеры
языков.
1.
X
= {а, б, в, . . . , я};
L
= {α
∈
X∗|
α
— слово русского языка}; мама, папа ∈
L;
ммпа,
аько
∈/
L.
2.
X
= {а, . . . , я} ∪
{,.!?;:-“”}
∪
{А,
. . . , Я};
L
= {α
∈
X∗|
α
— предложение русского языка};
Мама
мыла раму. ∈
L;
Мама
мыло
раме.
∈/
L.
Определение.
Конечный автомат
над — ориентированный граф A
= (Q,
E),
ребра которого помечены функцией f
: E
→ X
таким образом, что для любого символа
x
∈
X
и
любой
вершины q
∈
Q
существует
и
единственно
ребро
e
∈
E
c
началом
q
и
меткой
f(e)
= x.
Вершины
конечного
автомата
называются состояниями. Тогда каждому
состоянию q
∈
Q
и
символу
x
∈
X
однозначно сопоставлено состояние q
0 = δ(q,
x),
являющееся концом ребра с началом q
и меткой x.
Функция
δ
: Q
× X
→ Q
называется функцией перехода.
Определение.
Конечный автомат называется настроенным,
если в нем выделено начальное состояние
q0 ∈
Q и
множество
F ⊆
Q допускающих
состояний.
Определение.
Настроенный автомат A = (Q, X, δ, q0, F)
распознает язык L ⊆
X∗,
если
для любого α ∈
X∗
имеет место α ∈
L ⇐⇒
q0δ(α)
∈
F.
Определение.
Язык L ⊆
X∗
называется регулярным, если он
распознается некоторым (настроенным)
конечным автоматом.
Примеры.
2.

3.
23.
Отношение различимости слов заданным
языком. Ранг языка. Теорема Майхилла-Нероуда.
Бинарное
отношение ∼
на
множестве
M называется
отношением
эквивалентности
если
для всех x, y, z ∈
M выполнены следующие условия:
1.
X ∼
x (рефлексивность);
2.
x ∼
y и
y ∼
z =⇒
x ∼
z (транзитивность);
3.
x ∼
y =⇒
y ∼
x (симметричность).
Фактор-класс
элемента x ∈
M : [x] = {z ∈
M | x ∼
z}. Тогда [x] = [y] ⇐⇒
[x] ∩
[y] 6= ∅
⇐⇒
x ∼
y. Множество
M разбито на непересекающиеся
фактор-классы.
Множество
всех фактор-классов M/ ∼=
{[x] | x ∈
M} называется фактор-множеством
Пусть
задан язык L ⊆
X∗.
Говорим, что слова α, β ∈
X∗
неразличимы
относительно
L(α ∼L
β),
если
αε
∈
L ⇐⇒
βε
∈
L для
любого
ε
∈
X∗.
Примеры.
Для языка L = {a, aab, aba, bb} имеем
1.
a 6∼L
b, так
как
a ∈
L и
b ∈/
L;
2.
a 6∼L
aba, так
как
a ba ∈
L и
aba ba ∈/
L;
3.
aa 6∼L
bb, так
как
aa b ∈
L и
bb b ∈/
L;
4.
aba ∼L
bb, так
как
aba ∈
L, bb ∈
L, abaε
/∈
L, bbε
/∈
L при ε != λ;
5.
aa ∼L
b, так
как
aa ∈/
L, b ∈/
L, , aa b ∈
L, b b ∈
L, aaε /∈
L, bbε
/∈
L при
ε
6= λ,
b;
Бинарное
отношение ∼L
является
отношением
эквивалентности:
1.
α ∼L
α;
2.
α ∼L
β
и
β
∼L
γ
=⇒
α
∼L
γ;
3.
α ∼L
β
=⇒
β
∼L
α.
Кроме
того выполнено условие конгруэнтности:
4.
α ∼L
β
=⇒
αγ
∼L
βγ.
Фактор-класс
строки α ∈
X∗
обозначается через [α]L = {β ∈
X∗|
x ∼
z}.
Количество
элементов в фактор множестве X∗/
∼L=
{[α]L
| α
∈
X∗}
называется
рангом языка L, обозначаемого через rk
L
Теорема
Майхилла-Нероуда
Теорема.
Язык L распознается конечным автоматом
с n состояниями тогда и только тогда,
когда
rk L ≤ n
Пусть
rk L ≤ n. Построим автомат c Q = X∗/
∼L,
q0 = [λ]L,
F = {[α]L | α ∈
L} и [α]Lδx = [αx]L.
Тогда
при α = x1 . . . xk F 3 [λ]Lδ(α) = [λ]Lδ(x1 . . . xk) =
[x1 . . . xk] L = [α]L ⇐⇒
α
∈
L,
то
есть автомат распознает L.
Следствие.
Минимальное количество состояний в
автомате,
распознающим
регулярный язык, равно рангу этого
языка.
?24.
Регулярность объединения и пересечения
языков.
Произведение конечных автоматов

Операции
объединения и пересечения регулярных
языков
Теорема.
Дополнения, объединения и пересечения
регулярных
языков снова являются регулярными
языками

25.
Недетерминированные автоматы и
распознаваемые ими языки.



?24.1
Регулярность конкатенации и L*.
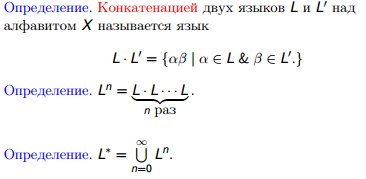


Недетерминированный
автомат для L∗
26.
Регулярные выражения.
Для
обозначения регулярных языков удобно
использовать регулярные выражения.
Каждый регулярный язык можно записать
в виде строки, содержащей символы
алфавита, символ ∅,
круглые
и
фигурные
скобки,
и
символы
∗
и
∪.
На
пример, L
= (({0} ∪
{1})∗)∗
∪({0}{1})
–
регулярный
язык,
принадлежащий
классу
R4 . Регулярным
выражением для заданного регулярного
языка называется строка, полученная
удалением фигурных скобок в записи
этого языка. Так регулярным выражением
для рассмотренного выше языка L будет
строка ((0∪1)∗)∗∪(01).
Для каждого языка существует бесконечно
много регулярных выражений. Например,
строка ∅
∪
((0 ∪
1)∗)∗
∪
(01) является
регулярным
выражением
для
того
же
языка
L. Приведем
более строгое определение регулярных
выражений по индукции.
Определение.
Регулярные выражения в алфавите Σ и
регулярные языки,
для
обозначения которых они служат,
определяются следующим образом:
1.
∅
–
регулярное
выражение,
обозначающее
пустой
язык,
2.
если x ∈
Σ,
то
x –
регулярное
выражение,
обозначающее
язык
{x},
3.
если p и q – регулярные выражения,
обозначающие языки P и Q соответственно,
то
• (pq)
– регулярное выражение, обозначающее
язык P Q,
• (p
∪
q) –
регулярное
выражение,
обозначающее
язык
P ∪
Q,
• (p)∗
– регулярное выражение, обозначающее
язык P∗,
4.
других регулярных выражений в языке Σ
нет.
Подобно
арифметическим выражениям, в регулярных
выражениях можно опускать скобки,
назначив приоритет каждой операции.
Принято считать, что самый высокий
приоритет у звездочки Клини, более
низкий у конкатенации, и самый низкий
у объединения. Так опуская скобки в
регулярном выражении ((0∪1)∗)∗
∪(01),
получим строку (0 ∪
1)∗∗
∪
01.
Теорема
Клини. Язык над алфавитом X является
регулярным тогда и только тогда, когда
он может быть выражен через языки ∅,
{λ},
{a}, где
a ∈
X, и
операции
∪,
·и
∗.
27.
Машины Тьюринга. Вычислимые языки.
Тезис Черча-Тьюринга. Вычислимость
регулярных языков.
Машина
Тьюринга определяется кортежем вида
![]()
где ![]() —
—
конечное множество состояний;![]() —
—
конечный входной алфавит;![]() —
—
символ, называемый маркером начала
ленты;![]() —
—
символ, называемый пустым (или
пробелом);![]() —
—
символы, называемые символами направления
движения головки;![]() —
—
начальное состояние;![]() —
—
заключительное состояние;![]() —
—
функция переходов, являющаяся отображением
вида причем значение![]() ,
,
коль скоро оно определено, есть конечное
(возможно, и пустое) множество упорядоченных
троек из соответствующего декартова
произведения.
Функция
переходов может быть записана в виде
системы команд. Каждая команда есть
слово вида
![]()
где ![]() .
.
Слово ![]() (до
(до
стрелки) называется левой частью
команды, а слово![]() (после
(после
стрелки) — правой частью команды.
Неформально
работу машины Тьюринга можно представить
следующим образом. Машина имеет
устройство управления, которое может
находиться в одном из состояний
множества ![]() ,
,
полубесконечную ленту, разделенную на
ячейки, в каждой из которой может быть
записан символ из алфавита![]() ,
,
причем крайняя левая ячейка хранит
символ![]() ,
,
и головку чтения-записи, которая в
каждый момент дискретного времени
обозревает какую-то одну ячейку ленты.
Символ![]() (пробел)
(пробел)
не следует путать с пустой цепочкой —
это специальный символ, означающий
пустую, т.е. не хранящую символов
алфавита![]() ,
,
ячейку ленты. Команда, записанная выше,
разрешает машине Тьюринга, устройство
управления которой находится в
состоянии![]() ,
,
а головка обозревает ячейку, хранящую
символ![]() ,
,
перевести устройство управления в
состояние![]() ,
,
записав в обозреваемую ячейку
символ![]() (который
(который
может и совпадать с![]() ),
),
и оставить головку на прежнем месте,
если![]() ,
,
сдвинуть ее на одну ячейку влево, если![]() ,
,
или на одну ячейку вправо, если![]() .
.
Будем
говорить, что машина Тьюринга ![]() применима
применима
к слову![]() ,
,
если из конфигурации![]() выводится
выводится
конфигурация![]() для
для
некоторого![]() .
.
Слово ![]() будем
будем
называть в этом случае результатом
применения машины Тьюринга![]() к
к
слову![]() и
и
обозначать его![]() .
.
Факт применимости машины![]() к
к
слову![]() будем
будем
обозначать![]() ;
;
если же![]() не
не
применима к![]() ,
,
то будем записывать![]() .
.
Множество
всех слов ![]() ,
,
таких, что![]() ,
,
называется областью применимости
машины Тьюринга![]() .
.
Словарная
функция ![]() в
в
алфавите![]() называется
называется
вычислимой по Тьюрингу, если существует
такая машина Тьюринга![]() с
с
входным алфавитом![]() ,
,
содержащим![]() ,
,
что
![]()
Тезис
Черча-Тьюринга –
для любой интуитивно вычислимой функции
существует вычисляющая её значения
машина Тьюринга.
28.
Конфигурации и вычисления машин
Тьюринга. Универсальная вычислимая
функция. Теорема Клини о нормальной
форме.
Конфигурация
машины Тьюринга ![]() есть
есть
кортеж
Из
конфигурации ![]() непосредственно
непосредственно
выводится конфигурация![]() ,
,
если![]() .
.
Из
конфигурации ![]() непосредственно
непосредственно
выводится конфигурация![]() ,
,
если![]() .
.
Из
конфигурации ![]() непосредственно
непосредственно
выводится конфигурация![]() ,
,
если![]() .
.
Выводом
на множестве конфигураций машины
Тьюринга называется произвольная
последовательность конфигураций ![]() ,
,
такая, что![]() (
(![]() если
если![]() существует).
существует).
Конфигурация ![]() выводима
выводима
из конфигурации![]() ,
,
если существует вывод![]() .
.
Число![]() называется
называется
при этом длиной вывода. Все обозначения,
касающиеся выводимости на множестве
конфигураций машин Тьюринга, остаются
такими же, как в случае конечных и
магазинных автоматов.
Конфигурация
есть тройка (состояние, часть цепочки
на ленте до головки, часть цепочки на
ленте, первый символ которой обозревается
головкой). При этом, по соглашению, любая
цепочка из множества ![]() (для
(для
фиксированного![]() )
)
отождествляется с цепочкой![]() ,
,
т.е. можно отбрасывать любое число
пробелов в конце слова.
Теорема
Клини.
Любой
граф переходов конечного автомата
всегда можно представить в нормализованной
форме, в которой только одна начальная
вершина только с исходящими ребрами и
только одна заключительная вершина
только с входящими ребрами.
Над
графом переходов, представленным в
нормализованной форме, могут быть
выполнены две операции редукции —
редукция ребра и редукция вершины —
с сохранением допускаемого этим графом
переходов языка. Каждая операция
редукции не меняет языка, распознаваемого
графом переходов, но уменьшает либо
число ребер, либо число вершин.


Следовательно, каждый
автоматный язык является регулярным
множеством.
Для
каждого регулярного выражения R может
быть построен конечный автомат (возможно
недетерминированный), распознающий
язык, задаваемый R. Определение таких
автоматов дадим рекурсивно.

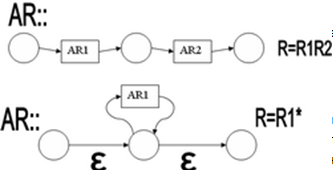
Следовательно, каждое
регулярное множество является автоматным
языком. Теорема
доказана.
Функция
F называется вычислимой,
если существует машина Тьюринга, которая
её вычисляет.
Функция
F называется
универсальной,
если выполняются следующие условия:
для каждой вычислимой функции f одной
переменной x существует постоянная p,
такая что для любого x, F(p,x) = f(x). То есть,
F может быть использована для моделирования
любой вычислимой функции одной
переменной. Нестрого, p представляет
«программу» для вычислимой функции f,
а F представляет эмулятор, которому на
вход поступает программа и он её
выполняет. Следует заметить, что для
любого фиксированного p функция f(x) =
F(p,x) является вычислимой; таким образом,
свойство универсальности утверждает,
что таким путём могут быть получены
все вычислимые функции одной переменной.
?29.
Перечислимые языки. Существование
перечислимых, не вычислимых языков.
Множество ![]() называется
называется
(рекурсивно, или эффективно, или
алгоритмически) перечислимым, если![]() либо
либо
пусто, либо есть область значений
некоторой вычислимой функции или,
другими словами, если существует
алгоритм для последовательного
порождения (перечисления) всех его
элементов.
Другими
словами, ![]() перечислимо,
перечислимо,
если существует такая вычислимая
функция![]() ,
,
что![]() .
.
Функция![]() называется
называется
перечисляющей множество![]() (или
(или
для множества![]() );
);
соответственно алгоритм, вычисляющий![]() ,
,
называется перечисляющим или порождающим
для![]() .
.
Существуют
три основных эквивалентных определения
концепции рекурсивно перечислимого
языка.
-
Рекурсивно
перечислимый формальный язык, это
рекурсивно перечислимое подмножество
множества всевозможных слов над
алфавитом языка. -
Рекурсивно
перечислимый язык — это формальный
язык, для которого существует машина
Тьюринга (или
другая вычислимая
функция),
которая перечисляет все корректные
строки языка. Заметим, что если язык
бесконечен, то можно выбрать алгоритм
перечисления, который избегает
повторений, так как для строки под
номером n можно
проверить, была ли она «уже» выдана
под номером меньшим n.
Если была, то вместо этого использовать
вывод под номером n+1(рекурсивно),
снова проверив, является ли он «новым». -
Рекурсивно
перечислимый язык — это формальный
язык, для которого существует машина
Тьюринга (или
другая вычислимая
функция),
которая остановится и примет любую
входную строку из языка, но остановится
и отвергнет или не остановится вообще
для любой входной строки не из языка.
Рекурсивные языки требуют останова
машины Тьюринга в любом случае.
Все
регулярные, контекстно-свободные,
контекстно-зависимые и рекурсивные
языки являются рекурсивно перечислимыми.
30.
Теорема о рекурсии.
|
Теорема (Клини, |
|
Пусть |
|
Альтернативная |
||||||
|
Доказательство: |
||||||
|
|
||||||
|
Начнём
Теперь Значит, |
$begingroup$
How to count the number of faces or regions of a graph such as the below graph:

The graph has 12 vertices and 17 edges. But I am unable to find the number of faces of the graph. I don’t know how to find the faces. Help me to find the number of faces.
![]()
asked Jun 6, 2017 at 19:21
![]()
$endgroup$
6
$begingroup$
The depicted graph has a $K_{3,3}$ (complete bipartite graph on six vertices) as a minor. By Kuratowski’s theorem such graph is not a planar graph, hence it makes no sense to talk about its faces, unless you embed such graph in a torus or in a surface with genus $geq 1$:

answered Jun 6, 2017 at 21:47
![]()
Jack D’AurizioJack D’Aurizio
348k41 gold badges374 silver badges813 bronze badges
$endgroup$
$begingroup$
Hint:
Use Euler’s formula
$$V-E+F=2$$
Where $V$ is the number of vertices, $E$ is the number of edges, and $F$ is the number of faces.
answered Jun 6, 2017 at 19:22
![]()
$endgroup$
6
$begingroup$
Euler’s theorem $f+n-m=2$.
$n$: number of vertices.
$m$: number of edges.
$f$: number of faces.
answered Jun 6, 2017 at 19:25
$endgroup$
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.
Планарные графы
Геометрический граф
– это плоская фигура, состоящая из вершин –
точек плоскости и ребер – линий, соединяющих некоторые пары вершин.
Всякий граф можно многими способами представить геометрическим графом, и мы уже
не раз пользовались этой возможностью. На рис. 3.6 показаны
два геометрических графа 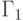 и
и 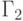 ,
,
представляющих, как нетрудно проверить, один и тот же обыкновенный граф.
Простое устройство этого графа, очевидное на изображении слева, не
так легко обнаружить, рассматривая изображение справа. Главная причина
этого в том, что в  ребра не имеют
ребра не имеют
“лишних” пересечений.

Рис.
3.6.
Геометрический граф, в котором никакие два ребра не имеют общих точек,
кроме инцидентной им обоим вершины, называют плоским графом, а по
отношению к представляемому им обыкновенному графу – его плоской
укладкой. Не каждый граф допускает плоскую укладку. Граф, для
которого
существует плоская укладка, называется планарным графом. Кроме
удобства визуального анализа, есть немало поводов, в том числе и сугубо
практических, для интереса к планарным графам и их плоским укладкам.
Если плоскость разрезать по ребрам плоского графа, она распадется на
связные части, которые называют гранями. Всегда имеется одна неограниченная внешняя грань, все остальные грани называются внутренними. Если в плоском
графе нет циклов, то у него имеется только
одна грань. Если же циклы есть, то граница каждой грани содержит цикл, но
не обязательно является циклом. На рис. 3.7 показан плоский граф с пятью
занумерованными гранями. Граница грани с номером 3 состоит из двух циклов,
а граница грани с номером 2 кроме цикла длины 5 включает еще дерево из
трех ребер.

Рис.
3.7.
Множества ребер, образующие границы граней, могут быть разными для разных
плоских укладок одного и того же графа. На рис. 3.8 показаны две плоские
укладки одного графа. В левой укладке есть две грани, границы которых
являются простыми циклами длины 5. В правой укладке таких граней нет, но
есть грани, ограниченные циклами длины 4 и 6. Однако число граней, как
показывает следующая теорема, не зависит от укладки, т.е. является
инвариантом планарного графа.

Рис.
3.8.
Теорема 6 (формула Эйлера). Количество граней в любой плоской
укладке планарного графа, имеющего  вершин,
вершин,  ребер
ребер
и  компонент связности, равно
компонент связности, равно 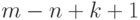 .
.
Доказательство.
Докажем сначала утверждение теоремы при 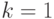 .
.
Рассмотрим связный плоский граф  . Если в нем нет циклов, то
. Если в нем нет циклов, то
имеется единственная грань, а  , и формула верна. Если же есть
, и формула верна. Если же есть
хотя бы один цикл, то возьмем какое-нибудь ребро  , принадлежащее
, принадлежащее
простому циклу  . Это ребро принадлежит границе двух граней, одна
. Это ребро принадлежит границе двух граней, одна
из которых целиком лежит внутри цикла  , другая – снаружи.
, другая – снаружи.
Если
удалить ребро  из графа, эти две грани сольются в одну.
из графа, эти две грани сольются в одну.
Граф  , полученный из графа
, полученный из графа  удалением ребра
удалением ребра  ,
,
очевидно, будет плоским и связным, в нем на одно ребро и на
одну грань меньше, чем в  , а число вершин осталось прежним. Если
, а число вершин осталось прежним. Если
в  еще есть циклы, то, удалив еще одно цикловое ребро,
еще есть циклы, то, удалив еще одно цикловое ребро,
получим
граф 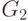 . Будем продолжать удаление цикловых ребер до тех пор,
. Будем продолжать удаление цикловых ребер до тех пор,
пока не получится связный плоский граф 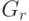 без циклов,
без циклов,
т.е. дерево. У него  ребро и единственная грань. Значит,
ребро и единственная грань. Значит,
всего было
удалено 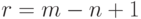 ребер, а так как при удалении каждого ребра число
ребер, а так как при удалении каждого ребра число
граней уменьшалось на единицу, то в исходном графе было 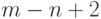
грани.
Таким образом, формула верна для любого связного плоского графа.
Если граф несвязен, то в компоненте связности, имеющей 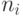
вершин
и  ребер, как доказано выше, будет
ребер, как доказано выше, будет 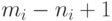
внутренняя грань. Суммируя по всем компонентам и прибавляя 1 для учета
внешней грани, убеждаемся в справедливости формулы в общем случае.
Следствие 1. Если в планарном графе  вершин,
вершин,  , и
, и  ребер, то
ребер, то 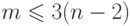 .
.
Доказательство.
Если в графе нет циклов, то 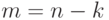
и неравенство выполняется при  . Рассмотрим плоский граф
. Рассмотрим плоский граф  с
с  гранями, в котором имеются циклы. Занумеруем
гранями, в котором имеются циклы. Занумеруем
грани
числами от  до
до  и обозначим
и обозначим
через 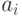 количество ребер,
количество ребер,
принадлежащих грани с номером  . Так как граница каждой грани
. Так как граница каждой грани
содержит цикл, то  для каждого
для каждого  ,
,
следовательно, 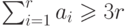 . С другой стороны, каждое ребро
. С другой стороны, каждое ребро
принадлежит границе не более чем двух граней, поэтому  . Из этих двух неравенств следует,
. Из этих двух неравенств следует,
что 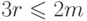 . Применяя формулу Эйлера,
. Применяя формулу Эйлера,
получаем  .
.
Следствие 1 дает необходимое условие планарности, которое в некоторых
случаях позволяет установить, что граф не является планарным. Рассмотрим,
например, полный граф 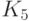 . У него
. У него 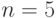 ,
,  , и мы
, и мы
видим, что неравенство из следствия 1 не выполняется. Значит, этот граф
непланарен. В то же время существуют графы, не являющиеся планарными, для
которых неравенство следствия 1 выполняется. Пример – полный двудольный
граф 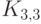 . У него 6 вершин и 9 ребер. Неравенство выполняется,
. У него 6 вершин и 9 ребер. Неравенство выполняется,
но мы сейчас установим, что он непланарен. Заметим, что в этом графе нет
циклов длины 3 (так как он двудольный, в нем вообще нет циклов нечетной
длины). Поэтому граница каждой грани содержит не менее четырех ребер.
Повторяя рассуждения из доказательства следствия 1, но используя
неравенство  вместо
вместо  ,
,
получаем следующий
результат:
Для графа 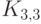 неравенство следствия 2 не выполняется, и
неравенство следствия 2 не выполняется, и
это
доказывает, что он непланарен.
Известно несколько критериев планарности, сформулируем без доказательства
два из них. Два графа называют гомеоморфными,если из них с помощью
подразбиения ребер можно получить изоморфные графы. На рис. 3.9
изображены гомеоморфные графы.

Рис.
3.9.
Сформулируем без доказательства два критерия планарности.
Теорема 7 (критерий Понтрягина-Куратовского). Граф планарен
тогда и только тогда, когда у него нет подграфов,
гомеоморфных 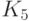 или
или 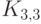 .
.
Граф  называется стягиваемым к графу
называется стягиваемым к графу  , если
, если 
можно получить из  последовательностью операций стягивания
последовательностью операций стягивания
ребер.
Теорема 8 (критерий Вагнера). Граф планарен тогда и только
тогда, когда у него нет подграфов, стягиваемых к 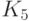
или 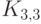 .
.
Отметим, что, несмотря на внешнее сходство двух теорем, фигурирующие в них
понятия гомеоморфизма и стягиваемости существенно различаются.
На рис. 3.10 изображен граф, который называют графом Петерсена. В нем нет подграфа,
гомеоморфного 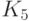 , так как в графе
, так как в графе 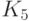 каждая
каждая
вершина имеет
степень  , а в графе Петерсена степень каждой вершины
, а в графе Петерсена степень каждой вершины
равна  .
.
При удалении вершин и ребер и подразбиении ребер степени вершин не
увеличиваются. В то же время легко видеть, что граф Петерсена можно
превратить в 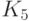 стягиванием пяти ребер.
стягиванием пяти ребер.

Рис.
3.10.
Плана́рный граф — граф, который можно изобразить на плоскости без пересечений рёбер не по вершинам. Какое-либо конкретное изображение планарного графа на плоскости без пересечения рёбер не по вершинам называется плоским графом. Иначе говоря, планарный граф изоморфен некоторому плоскому графу, изображённому на плоскости так, что его вершины — это точки плоскости, а рёбра — кривые на плоскости, которые если и пересекаются между собой, то только по вершинам. Области, на которые граф разбивает плоскость, называются его гранями. Неограниченная часть плоскости — тоже грань, называемая внешней гранью. Любой плоский граф может быть спрямлён, то есть перерисован на плоскости так, что все его рёбра будут отрезками прямых.
Свойства[править | править код]
Формула Эйлера[править | править код]
Для связного плоского графа справедливо следующее соотношение между количеством вершин 


Оно было найдено Эйлером в 1736 г.[1] при изучении свойств выпуклых многогранников. Это соотношение справедливо и для других поверхностей с точностью до коэффициента, называемого эйлеровой характеристикой. Это инвариант поверхности, для плоскости или сферы он равен двум, а, например, для поверхности тора — нулю.
Формула имеет множество полезных следствий. Во-первых, все плоские укладки одного графа имеют одинаковое количество граней. Во-вторых, если каждая грань ограничена не менее чем тремя рёбрами (при условии, что в графе больше двух рёбер), а каждое ребро разделяет две грани, то
следовательно,
то есть при большем числе рёбер такой граф заведомо непланарен. Обратное утверждение неверно: в качестве контрпримера можно взять граф Петерсена. Отсюда следует, что в планарном графе всегда можно найти вершину степени не более 5.
Общая формула также легко обобщается на случай несвязного графа:
где 
Два примера непланарных графов[править | править код]
Полный граф с пятью вершинами[править | править код]

K5, полный граф с 5 вершинами
Лемма. Полный граф с пятью вершинами (К5) нельзя уложить на плоскость.
Доказательство. Для него не выполняется 
«Домики и колодцы»[править | править код]

Граф «домики и колодцы» (K3,3)
Задача о трёх колодцах. Есть три дома и три колодца. Можно ли так проложить дорожки между домами и колодцами, чтобы от каждого дома к каждому колодцу вела дорожка, и никакие две дорожки не пересекались бы. Мосты строить нельзя.
Лемма. Полный двудольный граф с тремя вершинами в каждой из долей (К3,3) нельзя уложить на плоскость.
Доказательство. По формуле Эйлера граф имеет 5 граней.
С другой стороны: любая грань (включая внешнюю) содержит чётное число рёбер — а значит, не менее 4. Поскольку каждое ребро включается в ровно две грани, получается соотношение 
Теорема Понтрягина — Куратовского[править | править код]

В общем случае найти K5 или K3,3 довольно сложно. Граф Петерсена несложно стянуть в K5, но в нём есть и K3,3.
Очевидно утверждение: если граф G содержит подграф, гомеоморфный K5 или K3,3, то его невозможно разложить на плоскости. Оказывается, верно и обратное.
Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных полному графу из пяти вершин (K5) или графу «домики и колодцы» (K3,3).
Теорему также можно сформулировать в следующем варианте (иногда его называют «теорема Вагнера»).
Граф планарен тогда и только тогда, когда не содержит подграфов, стягивающихся в K5 или K3,3.
Компьютерная проверка на планарность[править | править код]
Первый алгоритм, отыскивающий подграф Куратовского за линейное время, разработан в 1974 году Хопкрофтом и Тарьяном[2].
Признаки непланарных графов[править | править код]
- достаточное условие — если граф содержит полный двудольный подграф K3,3 или полный подграф K5, то он является непланарным;
- необходимое условие — если граф непланарный, то он должен содержать больше 4 вершин, степень которых больше 3, или больше 5 вершин степени больше 2.
Планарные графы в задачах[править | править код]
Раскраска карты. Необходимо раскрасить плоскую карту заданным числом красок так, что любые две страны, имеющие общий участок границы, имели различные цвета. Оказывается, что при отсутствии анклавов, всегда достаточно четырёх красок, но это утверждение чрезвычайно сложно доказать, см. Проблема четырёх красок.
Спрямление графа (теорема Фари). Любой плоский граф можно перерисовать так, чтобы он остался плоским, а рёбра стали отрезками прямых.
Обобщения[править | править код]
Граф укладывается на некоторой поверхности, если его можно на ней нарисовать без пересечения рёбер. Уложенный граф называется геометрическим, его вершины — это точки поверхности, а рёбра — линии на ней. Области, на которые граф разбивает поверхность, называются гранями. Плоский граф — граф, уложенный на плоскость.
Число пересечений графа G — наименьшее число пересечений рёбер плоского рисунка графа G. Таким образом, граф является планарным тогда и только тогда, когда его число пересечений равно нулю.
Тороидальный граф — граф, который можно уложить на тор.
См. также[править | править код]
- Словарь терминов теории графов
- Теория графов
- Клетка (теория графов)
- Теорема Фари
- Гамма-алгоритм — алгоритм проверки графа на планарность и его плоской укладки
Примечания[править | править код]
- ↑ Харари Ф. Теория графов УРСС стр. 126
- ↑ Hopcroft, John & Tarjan, Robert E. (1974), Efficient planarity testing, Journal of the Association for Computing Machinery Т. 21 (4): 549–568, DOI 10.1145/321850.321852.
Ссылки[править | править код]
- Видеолекция, посвящённая планарным графам
- А. Ю. Ольшанский. Плоские графы (недоступная ссылка), СОЖ, 1996, No 11, с. 117—122.
- Харари Ф.. Теория графов. М.: «Мир». 1973
- Дискретная математика: Алгоритмы, визуализация графов, апплеты





