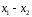-
Определение числа интервалов (классов)
При
отсутствии априорной информации о
необходимом количестве интервалов для
построения гистограммы, число интервалов
вычисляется по формуле:
 n
n
– величина выборки
-
Определение размера интервала (класса)

-
Сортировка
Проводиться
определение (подсчет) числа случайных
величин, попадающих в i-й
интервал (
– абсолютная частота)
Возможны
случаи, когда значение в выборке попадает
точно на границу интервала. Тогда
необходимо относить это значение в
больший или меньший интервал. Принципиально
важно, что бы все подобные пограничные
значения относились либо в следующий
(больший), либо в предыдущий (меньший)
интервал. Обычно пограничные значения
относят к следующему интервалу.
-
Определение
накопленных частот
Подсчитывается
накопленная частота для каждого
интервала, то есть суммируется количество
значений в текущем интервале и всех
предыдущих.

-
Определение
относительной частоты попадания в
каждый интервал

Можно сказать,
что для данной гистограммы эта
относительная частота является и
вероятностью попадания значения в
конкретный интервал.
-
Определение
относительных накопленных частот

-
Определение
высоты прямоугольника гистограммы

-
Табулирование
частотное
|
№ пп |
Границы интервала |
Абсолютная частота |
Относительная частота
|
Относительная накопленная
|
|
|
1 |
|
3 |
0,015 |
0.015 |
h1 |
|
2 |
|
9 |
0,045 |
0.06 |
h2 |
|
|
|
|
|
|
|
|
k |
|
2 |
0,01 |
1 |
hk |
-
Нанесение гистограммы на график
-
На горизонтальной оси выбираем масштаб,
ориентируясь на круглые значения -
Откладываем интервалы на горизонтальной
оси в соответствии с масштабом -
Перед первым интервалом и после
последнего интервала оставляем по 2
интервала свободного места -
Подписываем границы интервалов и
проставляем единицы измерения -
Проводим левую вертикальную ось,
наносим шкалу

подписсываем эту ось. -
Провести две правые вертикальные оси:
-
– на одной нанести
шкалу относительных частот

-
– на другой нанести
шкалу относительных накопленных частот

-
– надписать шкалы
-
Пользуясь интервалом класса как
основанием построить прямоугольник,
высота которого
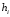
-
Нанести на гистограмме: номинал N;
границы допусков USL
и LSL; среднее
значение, дисперсию -
Построить полигон на гистограмме –
соединить точки середин верхних частей
прямоугольников -
На чистом поле гистограммы показать:
*
время создания гистограммы
*
число данных
*
SR – коэффициент асимметрии
*
ER – коэффициент эксцесса
При
построении кумулятивной гистограммы
на осях откладываются накопленные
частоты, высота прямоугольников
вычисляется на основании накопленных
частот, в остальном последовательность
та же.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
«СЕМЬ ОСНОВНЫХ ИНСТРУМЕНТОВ КОНТРОЛЯ КАЧЕСТВА»
Гистограмма
Гистограмма – это столбиковая диаграмма, предназначенная для графического представления данных, сгруппированных по частоте попадания в определённый интервал.
Интервалы являются основаниями столбиков, на которые разбивается совокупность данных. Высота столбиков пропорциональна частоте попадания результатов наблюдений в соответствующий интервал.
Пример гистограммы представлен на рисунке 1.
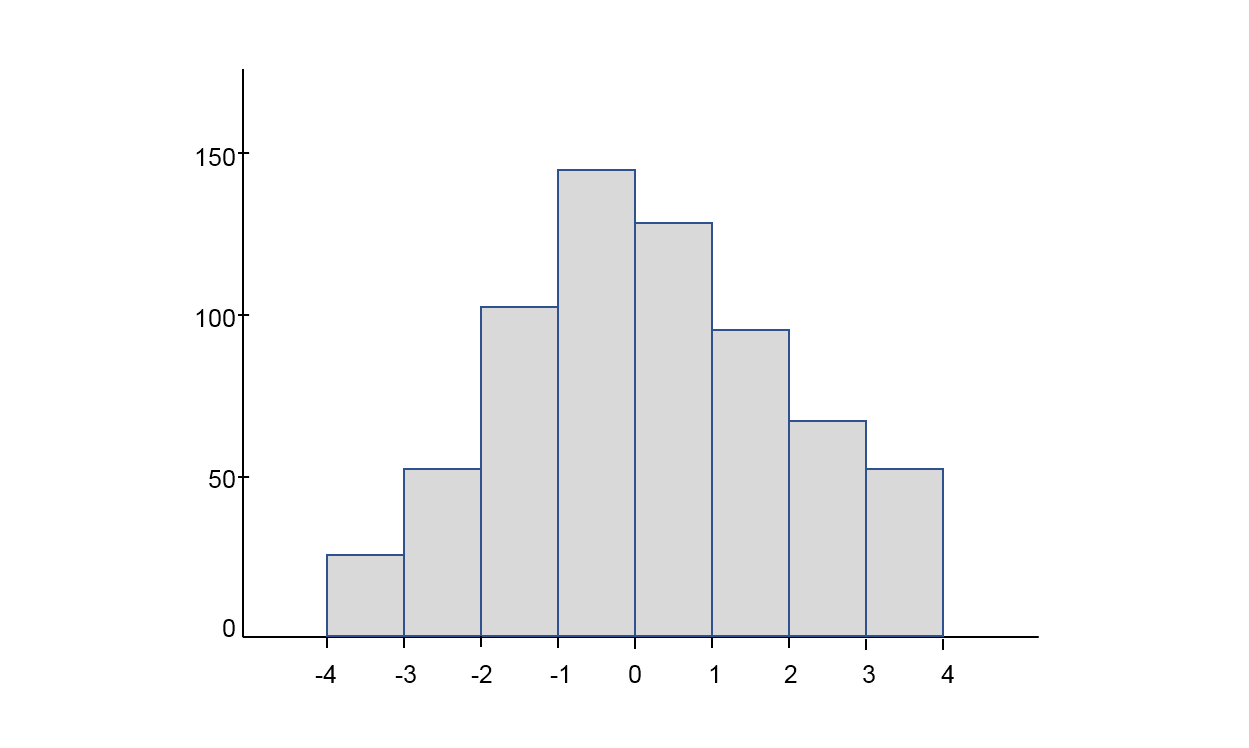
Для ознакомления с сутью, формами и иными особенностями составления, чтения и применения гистограмм предлагаем прочитать приведённый ниже раздел из учебного пособия «Управление качеством продукции» С.В. Пономарева, С.В. Мищенко, B.Я. Белобрагина и др. [1, с. 97–108].
Итак, обратимся к источнику [1]:
“
3.2. Гистограмма
Гистограмма – это инструмент [1, 9–11, 30, 38–45], позволяющий зрительно оценить закон распределения величины разброса данных, а также принять решение о том, на чем следует сфокусировать внимание для целей улучшения процесса.
Гистограмма отображается серией столбиков одинаковой ширины, но разной высоты. Ширина столбика представляет интервал в диапазоне наблюдений, высота – количество наблюдений (измерений), попавших в данный интервал. При нормальном законе распределения данных существует тенденция расположения большинства результатов наблюдений ближе к центру распределения (к центральному значению) с постепенным уменьшением при удалении от центра.
Гистограмма применяется главным образом для анализа значений измеренных параметров, но может использоваться и для оценки показателей возможностей процессов [1, 9–11, 15, 35].
Систематизируя показатели качества и анализируя построенную для них гистограмму, можно легко понять вид распределения, а определив среднее значение показателя и стандартное отклонение, можно провести сравнение показателей качества с контрольными нормативами и таким образом получить информацию высокой точности.
3.2.1. Основные сведения о нормальном законе распределения
В связи с тем что теория управления качеством продукции во многих случаях базируется на использовании так называемого нормального закона распределения, рассмотрим этот закон подробнее.
Плотность р(х) нормального распределения случайной величины х выражается функцией
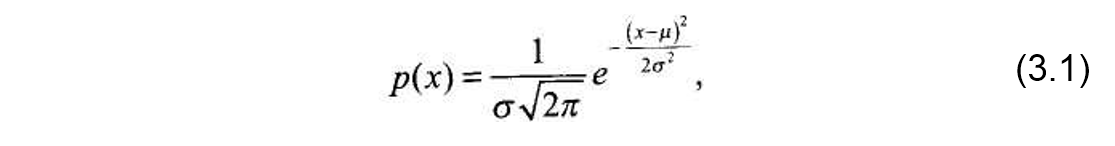
зависящей от двух параметров, а именно: от µ – математического ожидания и σ – среднеквадратичного отклонения нормального распределения.
При статистической обработке экспериментально полученных результатов наблюдений x1, x2, …, хn случайной величины х приблизительные оценки значений µ и σ могут быть вычислены по формулам
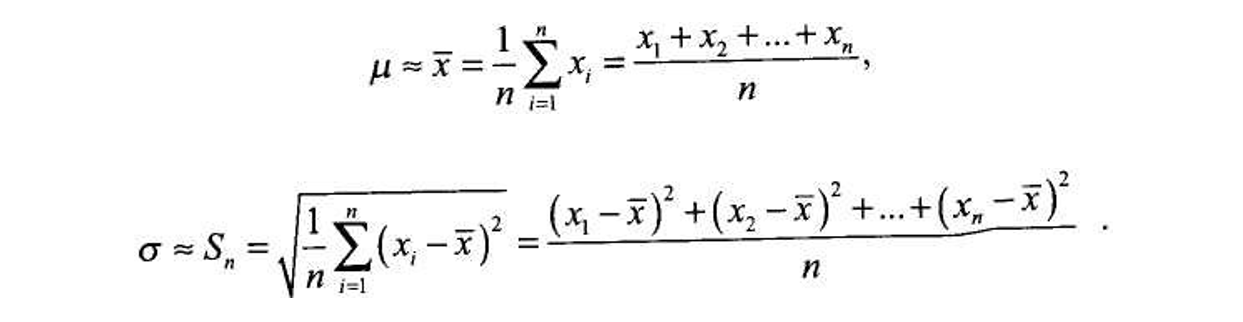
При стремлении n → ∞ оценки x и Sn стремятся к µ и σ, т.е.
lim x = µ, lim Sn = σ.
n → ∞
Графики функции (3.1) приведены на рис. 3.1.
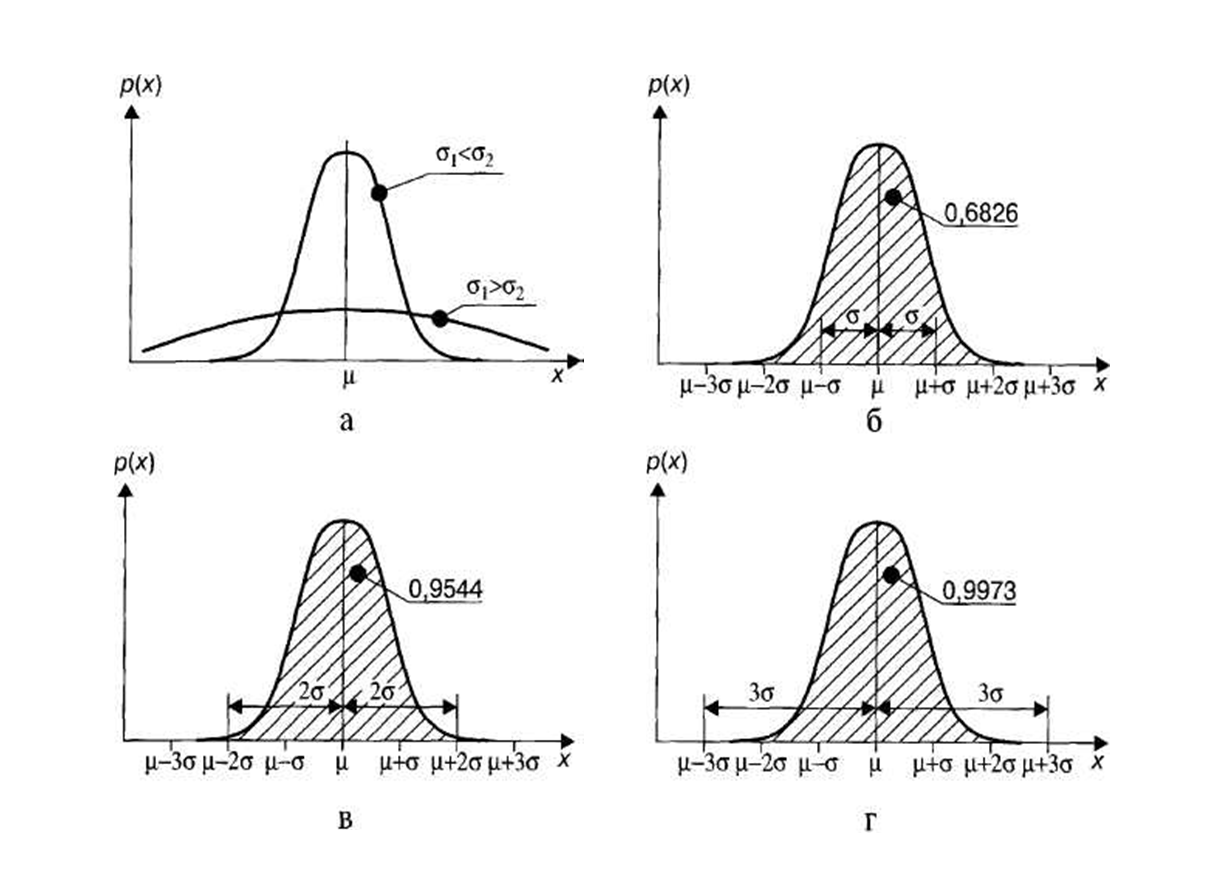
На рис. 3.1а приведены графики функции (3.1) при двух значениях параметра σ. Видно, что при значении σ1 < σ2 колоколообразная кривая падает по обе стороны от вершины более круто, чем при σ2 > σ1. С увеличением параметра σ кривая становится более покатой. Однако независимо от значения параметра σ площадь под кривой, представляющей собой функцию (3.1), равна единице. Колоколообразная кривая имеет две точки перегиба, расстояние от которых до ординаты вершины, т.е. до вертикали, проведенной через математическое ожидание х = µ, равно среднеквадратичному отклонению σ. Заштрихованная на рис. 3.1б площадь криволинейной трапеции, заключенная между ординатами х = µ − σ и х = µ + σ, равна 0,6826.
Это означает, что вероятность того, что случайная величина х, распределенная в соответствии с нормальным законом (3.1), находится в интервале (µ − σ < х < µ + σ), равна 0,6826, т.е. Вер (µ − σ < х < µ + σ) = 0,6826.
Если рассмотреть (см. рис. 3.1в) интервал (µ − 2σ < х < µ + 2σ), то Вер (µ − 2σ < х < µ + 2σ) = 0,9544.
Аналогично (см. рис. 3.1г) получается Вер (µ − 3σ < х < µ + 3σ) = 0,9973.
Приведем дополнительные сведения о вероятности попадания случайной величины х, распределенной по нормальному закону, в часто используемые интервалы:
- Вер (µ − 1,96σ < х < µ + 1,96σ) = 0,95,
- Вер (µ − 2,57σ < х < µ + 2,57σ) = 0,99,
- Вер (µ − 3,291σ < х < µ + 3,291σ) = 0,999.
3.2.2. Этапы построения гистограммы
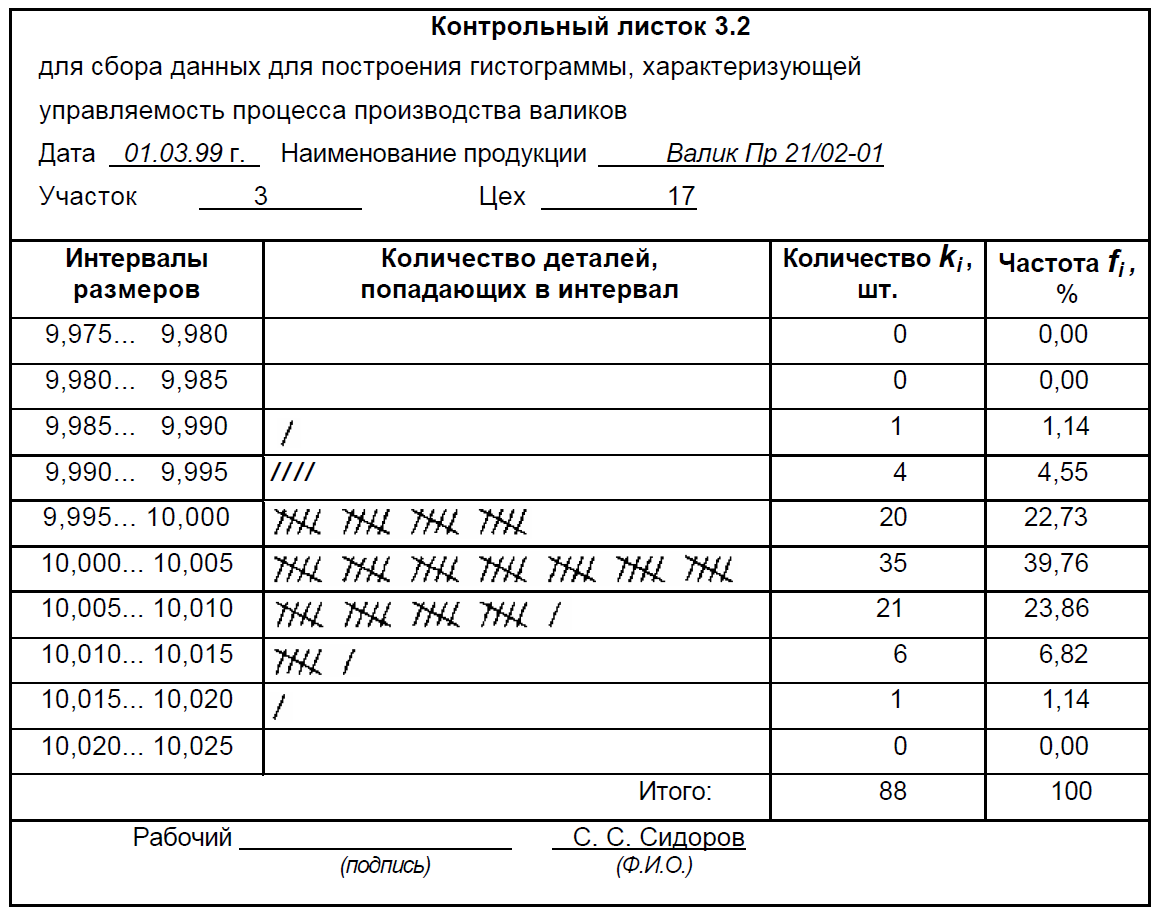
Рассмотрим порядок построения гистограммы, характеризующей управляемость процесса производства валиков, с использованием данных приведенного ниже контрольного листка.
Построение гистограммы, как правило, включает в себя следующие этапы [1, 9–11, 38–42, 45].
- Разработка формы контрольного листка для сбора первичных данных (см. § 3.1). Пример такого контрольного листка для процесса производства валиков приведен ниже.
- Сбор статистических данных xi, i = 1, 2, …, N, характеризующих ход процесса, и заполнение второго столбца контрольного листка. После заполнения контрольного листка приступают собственно к построению гистограммы.
- Вычисление диапазона данных (выборочного размаха):
- Определение количества интервалов n на гистограмме часто осуществляют по формуле Стерджесса [29, 30]
-
Определение размеров интервалов осуществляют так, чтобы размах, включающий максимальное и минимальное значения, делился на интервалы равной ширины. Для получения ширины интервалов h = R/n размах R делят на полученное выше количество интервалов n.
В нашем случае h = 0,035 мм / 7 = 0,005 мм = 5 мкм.
Внимание!
Желательно, чтобы размер интервала был не менее двух делений шкалы измерительного прибора (в рассматриваемом примере данные контрольного листка были получены с использованием микрометрической головки часового типа с ценой деления 1 мкм, т.е. один интервал соответствует пяти делениям шкалы прибора). - Определение границ интервалов.
Сначала определяют нижнюю границу первого интервала и прибавляют к ней ширину этого интервала, чтобы получить границу между первым и вторым интервалами. Далее продолжают прибавлять найденную ширину интервала h к предыдущему значению для получения второй границы, затем третьей и т.д. После завершения такой работы можно удостовериться, что верхняя граница последнего интервала совпадает с максимальным значением xmax. - Вычисление частот.
В третий столбец таблицы контрольного листка вносят количество ki валиков, попавших в каждый интервал. По результатам наблюдений, отмеченных черточками во втором столбце этой таблицы, подсчитывают общее количество наблюдений (в нашем случае N = 88), а затем в четвертый столбец записывают относительные частоты, выраженные в процентах и подсчитанные по формуле - Построение горизонтальной и вертикальной осей графика.
Берется миллиметровая бумага, на ней наносятся горизонтальная и вертикальная оси, а затем на каждой оси выбираются масштабы. - Построение графика гистограммы.
На горизонтальную ось необходимо нанести границы интервалов. На оси абсцисс с обеих сторон (перед первым и после последнего интервалов) следует оставить место, не менее размера одного интервала. Пользуясь шириной интервалов как основанием, строят прямоугольники, высота каждого из которых равна частоте попадания результатов наблюдений в соответствующий интервал. На график (см. рис. 3.2) наносят линию, представляющую среднее арифметическое значение x, а также линии, представляющие границы поля допуска, если они имеются.
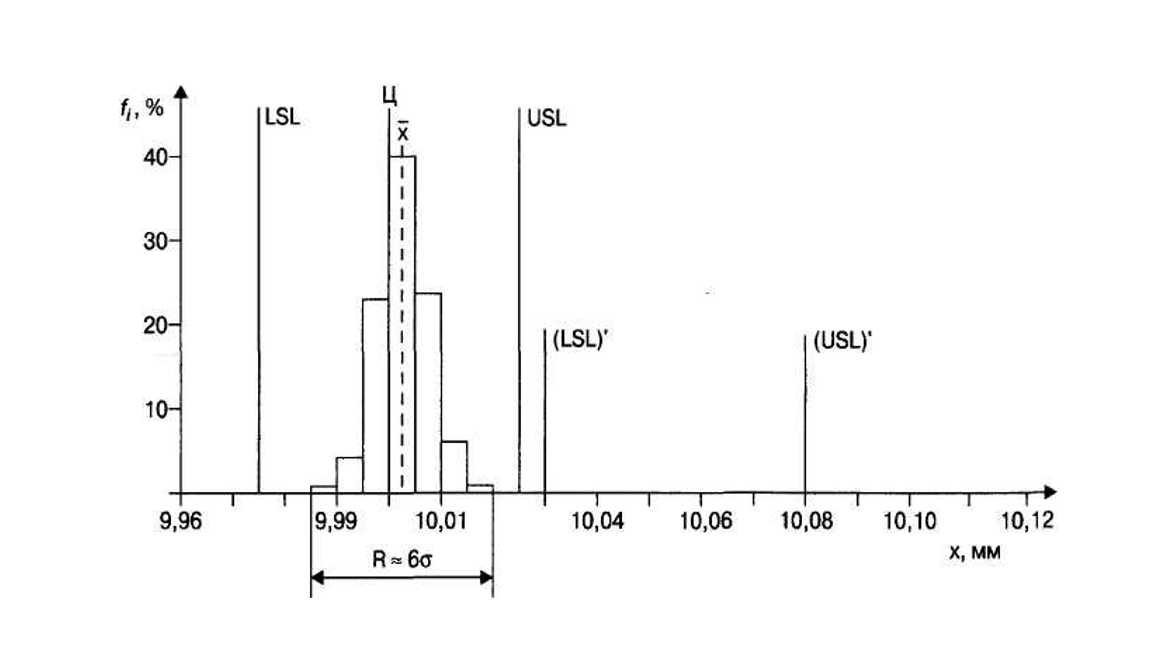
Рис. 3.2. Гистограмма, построенная по данным контрольного листка 3.2
R = xmax − xmin,
где xmax – наибольшее наблюдаемое значение; xmin – наименьшее наблюдаемое значение.
В нашем случае xmax = 10,020 мм, xmin = 9,985 мм, т.е. R = 10,020 − 9,985 = 0,035 мм = 35 мкм.
n ≈ 1 + 3,322 lg N,
где N – общее количество собранных данных в выборке.
Рекомендуемое число интервалов гистограммы, которое получается при использовании формулы Стерджесса, представлено в табл. 3.2.
Таблица 3.2
К выбору рекомендуемого числа интервалов на гистограмме
| Количество данных в выборке | Число интервалов |
|---|---|
| 23 – 45 | 6 |
| 46 – 90 | 7 |
| 91 – 180 | 8 |
| 181 – 361 | 9 |
| 362 – 723 | 10 |
| 724 – 1447 | 11 |
| 1448 – 2885 | 12 |
По данным рассматриваемого нами контрольного листка N = 88, соответственно n = 1 + 3,322 lg 88 = 7,46 – 7.
3.2.3. Вычисление основных характеристик качества процесса по гистограмме
Построение гистограммы на практике производят для того, чтобы оценить качество выпускаемой продукции и качество процесса производства этой продукции. Наиболее часто для оценки качества процесса используют следующие характеристики [9, 10, 34, 39, 41]:
Рр – индекс пригодности процесса удовлетворять технический допуск (без учета положения среднего значения);
k – показатель настроенности процесса на целевое значение;
Ppk = Рр (1 − k) – оценка индекса пригодности процесса удовлетворять технический допуск с учетом положений среднего значения.
Ниже рассмотрены примеры вычисления перечисленных выше индексов (показателей) по параметрам построенной гистограммы.
В нашем случае на рис. 3.2 обозначены:
- среднее арифметическое значение x результатов наблюдений xi
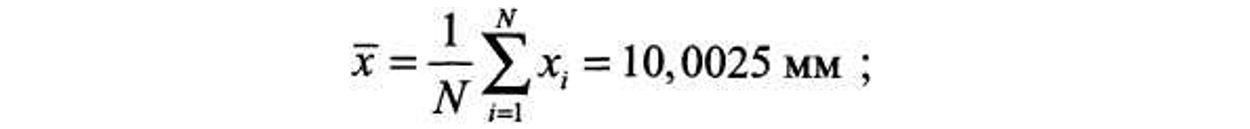
- размах результатов наблюдений R ≈ 6σ = 0,035 мм, равный ширине основания гистограммы и в большинстве случаев близкий к шести значениям стандартных отклонений σ;
Примечание. В качестве приближенного значения стандартного отклонения σ часто используют среднеквадратичное отклонение
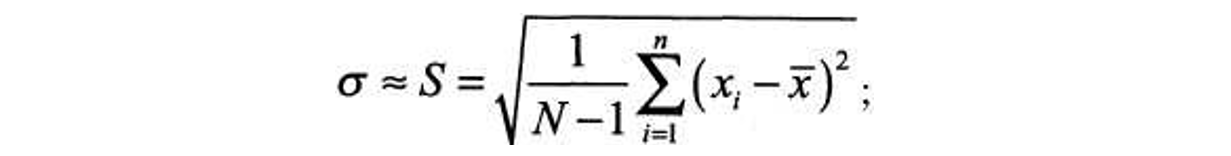
- нижняя граница поля допуска LSL = 9,975 мм;
- верхняя граница поля допуска USL = 10,025 мм;
- середина поля допуска (целевое значение)
Ц = (LSL + USL) / 2 = (10,025 + 9,975) / 2 = 10,000 мм;
- дополнительные (гипотетические) значения нижней (LSL)’ и верхней (USL)’ границ поля допуска, которые нам потребуются далее.
По имеющимся на рис. 3.2 данным могут быть вычислены следующие величины, характеризующие качество процесса производства валиков:
- оценка индекса пригодности процесса удовлетворять технический допуск (без учета положения среднего значения x) [34]
Pp = USL − LSL ≈ USL − LSL = 10,025 − 9,975 ≈ 1,43; 6σ R 0,035 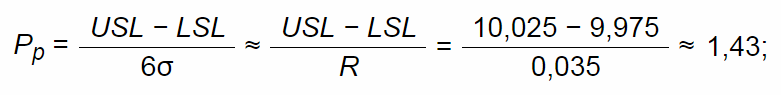
Примечания:
- Если Рр ≥ 1, то ширина гистограммы укладывается в пределах ширины поля допуска, т.е. процесс является управляемым; точнее говоря, имеется возможность осуществить процесс так, что 99,73% изделий будут попадать в пределы поля допуска; если Рр < 1, то процесс является неуправляемым, так как размеры части изделий неизбежно будут выходить за пределы поля допуска; большинство российских заводов работают при значениях Рр ~ 0,95…1,3, а японским специалистам по управлению качеством продукции во многих случаях удается поддерживать на своих предприятиях значения индекса пригодности процессов Рр « 1,5…4,0, что позволяет ограничить дефектность продукции единицами бракованных изделий на миллион выпускаемых изделий.
- Для того чтобы проиллюстрировать, почему Рр называется индексом пригодности процесса, рассмотрим гипотетическую ситуацию, когда нижняя и верхняя границы допуска (LSL)’ = 10,03 мм, (USL)’ = 10,08 мм; тогда получим значение индекса пригодности процесса
Pp = USL − LSL ≈ (USL)’ − (LSL)’ = 10,08 − 10,03 ≈ 1,43; 6σ R 0,035 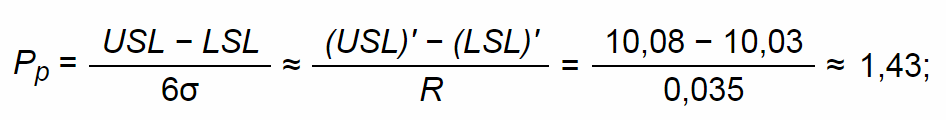
Видно, что при (LSL)’ = 10,03 мм, (USL)’ = 10,08 мм, когда (при представленной на рис. 3.2 гистограмме) ни одно изделие не попадает в пределы границ поля допуска, все равно Рр ≈ 1,43; именно поэтому индекс Рр называется индексом пригодности процесса (он совершенно не учитывает смещение центра x случайного распределения размеров деталей относительно середины поля допуска Ц);
- смещение гистограммы относительно середины поля допуска может быть охарактеризовано показателем настроенности процесса на целевое значение
k = |x − Ц| , (USL − LSL)/2 который в нашем примере равен
k = |10,0025 − 10,0000| = 0,1. (10,025 − 9,975)/2
Примечание. Если среднее значение x случайного распределения результатов наблюдений сместится относительно середины Ц поля допуска на величину половины поля допуска (USL − LSL)/2, то показатель настроенности процесса станет равен k = 1; если же x = Ц, то показатель k = 0;
- наиболее полно качество протекания процесса может быть охарактеризовано [19] величиной индекса пригодности процесса удовлетворять технический допуск с учетом положения среднего значения x
Ppk = Pp · (1 − k),
который в рассматриваемом нами примере равен
Ppk = 1,43 (1 − 0,1) ≈ 1,29.
Таким образом, для повышения качества процесса (уменьшения уровня дефектности) необходимо обеспечить высокое значение индекса Рр и низкое значение показателя k.
Примечания:
- Для лучшего понимания смысла индексов Рр, Ррk рекомендуем внимательно изучить ГОСТ Р 50779.44-2001 [34].
- Согласно [34], индексы Рр, Ррk могут быть использованы в качестве индексов пригодности процессов, стабильность которых по настройке подтверждена, а по разбросу – не подтверждена.
- В случае, когда подтверждена стабильность процесса по разбросу, вместо индексов пригодности Рр, Ррk используются [34]:
– индекс воспроизводимости процесса, оценивающий возможность удовлетворять технический допуск без учета положения среднего значения x и применяемый для стабильных по разбросу процессов;
Срk = Ср (1 − k)
– индекс воспроизводимости процесса, оценивающий возможность удовлетворять технический допуск с учетом фактического положения среднего значения x и применяемый для стабильных и по разбросу, и по настройке процессов.
3.2.4. Типовые формы гистограмм
На рис. 3.3 приведены наиболее часто встречающиеся на практике формы (типы) гистограмм [1, 9–11, 30, 38–42].
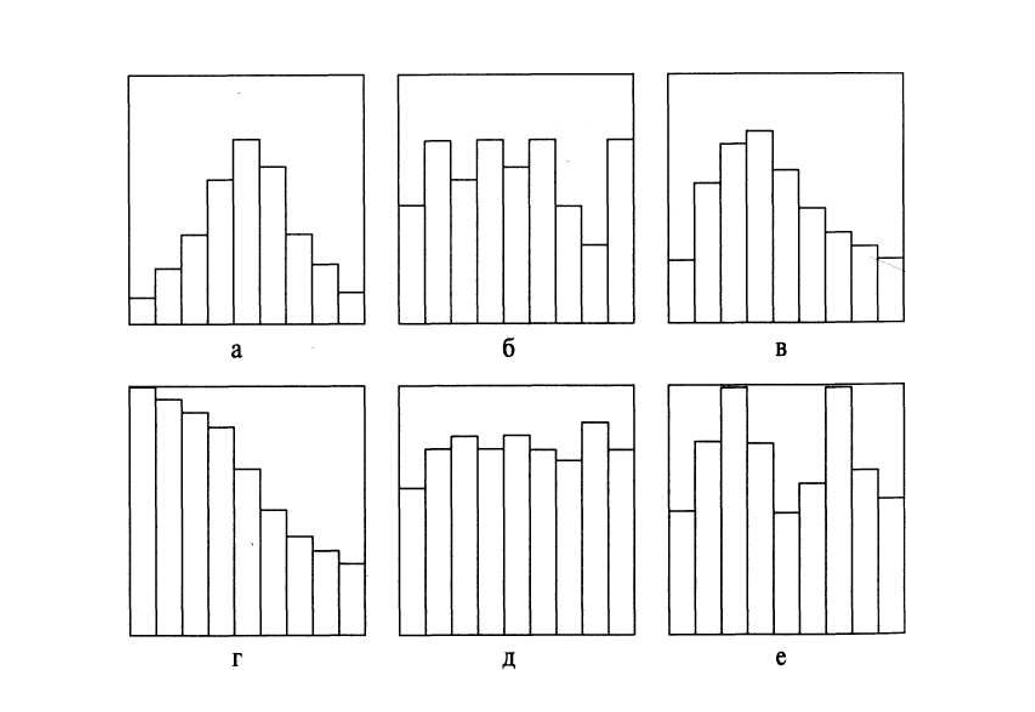
Полезную информацию о характере распределения случайной величины можно получить, взглянув на форму гистограммы. Формы, представленные на рис. 3.3, типичны, и вы можете воспользоваться ими как образцами при анализе процессов.
Обычная форма (симметричная, или колоколообразная). Среднее значение гистограммы приходится на середину размаха данных. Наивысшая частота оказывается в середине и постепенно снижается к обоим концам. Форма симметрична.
Примечание. Это именно та форма, которая встречается чаще всего.
Гребенка. Интервалы через один имеют более низкие (высокие) частоты.
Примечание. Такая форма встречается, когда число единичных наблюдений, попадающих в интервал, колеблется от интервала к интервалу или когда действует определенное правило округления данных.
Положительно скошенное распределение (отрицательно скошенное распределение). Среднее значение гистограммы локализуется слева (справа) от центра размаха. Частоты довольно резко спадают при движении влево (вправо) и, наоборот, медленно – при движении вправо (влево). Форма асимметрична.
Примечание. Такая форма встречается, когда левое (правое) значение поля допуска недостижимо.
Распределение с обрывом справа (распределение с обрывом слева). Среднее арифметическое гистограммы локализуется далеко слева (справа) от центра размаха. Частоты резко спадают при движении влево (вправо) и, наоборот, медленно вправо (влево). Форма асимметрична.
Примечание. Это одна из тех форм, которые часто встречаются при 100%-ной разбраковке изделий из-за плохой управляемости процесса, а также когда проявляется резко выраженная положительная (отрицательная) асимметрия.
Равномерное или прямоугольное распределение (плато). Частоты в разных интервалах образуют плато, поскольку все интервалы имеют более или менее одинаковые ожидаемые частоты.
Примечание. Такая форма встречается в смеси нескольких распределений, имеющих различные средние значения.
Двухпиковая (бимодальная) форма. В окрестностях центра диапазона данных частота низкая, т.е. по пику с каждой стороны.
Примечание. Такая форма встречается, когда смешиваются два распределения с далеко отстоящими средними значениями.
3.2.5. Использование гистограмм при оценке и анализе качества процессов
Анализ формы гистограммы и ее расположения по отношению к технологическому допуску позволяет делать заключения о состоянии изучаемого процесса и вырабатывать надлежащие меры. На рис. 3.4 показаны возможные варианты расположения гистограммы по отношению к допуску [38].
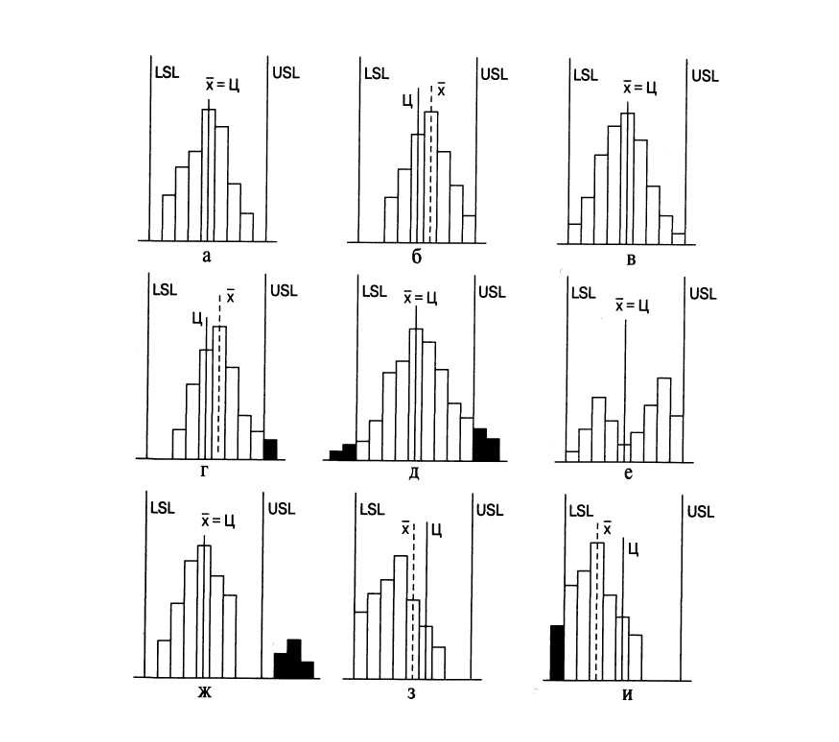
На рис. 3.4а левая и правая стороны гистограммы симметричны, следовательно, форма гистограммы удовлетворительна. Если сравнить ширину гистограммы с шириной поля допуска, то она составляет приблизительно 3/4 (что соответствует Рр ≈ 1,33), т.е. в поле допуска имеется достаточный запас. Поскольку центр x распределения и центр Ц поля допуска совпадают (что соответствует k ≈ 0 и Ррk ≈ 1,33), то качество партии деталей находится в удовлетворительном состоянии. Таким образом, в данной ситуации технологическая операция не нуждается в корректировке [38].
На рис. 3.4б гистограмма сдвинута вправо. В связи с этим имеется опасение, что среди деталей могут находиться некондиционные единицы (выходящие за пределы допуска). В этом случае необходимо проверить, не вносят ли систематическую ошибку используемые средства измерения. Если средство измерения находится в удовлетворительном состоянии, следует продолжить изготовление деталей, отрегулировав технологическую операцию так, чтобы центр x гистограммы совпадал с центром Ц поля допуска [38].
На рис. 3.4в центр гистограммы расположен правильно, т.е. совпадает с центром поля допуска. Однако поскольку ширина гистограммы, характеризующая реальный разброс значений контролируемого показателя, совпадает с шириной поля допуска, то имеется опасение, что со стороны верхнего и нижнего допуска могут появиться некондиционные детали. Следовательно, чтобы сузить ширину гистограммы, необходимо принять меры для обследования технологической операции с точки зрения точности оборудования, условий обработки, технологической оснастки и т. д. В случае невозможности найти техническое решение по данному вопросу рекомендуется (если есть такая возможность) расширить допуск, так как требования к качеству деталей в данном случае трудновыполнимы [38].
На рис. 3.4г центр гистограммы смещен, причем выход одного интервала гистограммы за верхнюю границу допуска USL свидетельствует о наличии дефектных деталей. Кроме того, поскольку ширина гистограммы и ширина поля допуска почти одинаковы, необходимо срочно отрегулировать технологическую операцию, переместив центр гистограммы x в центр поля допуска Ц, либо уменьшить ширину гистограммы, либо изменить допуск [38].
На рис. 3.4д центр гистограммы совпадает с центром поля допуска, но так как ширина гистограммы превышает ширину поля допуска, то обнаруживаются детали несоответствующего качества, о чем свидетельствует выход гистограммы за обе стороны поля допуска. В этом случае целесообразно реализовать рассмотренные выше меры [38].
На рис. 3.4е в гистограмме имеются два пика, хотя образцы деталей взяты из одной партии. Это явление объясняется либо тем, что исходный материал для деталей был двух разных сортов, либо в процессе изготовления деталей была изменена настройка оборудования, либо тем, что в одну партию включили детали, обработанные на двух разных станках. Очевидно, следует провести (см. подробнее § 3.3) расслоение (стратификацию) гистограммы, т.е. разбить ее на две [38].
На рис. 3.4ж главные характеристики гистограммы (ширина и центр) в норме, однако значительная часть деталей выходит за верхний предел допуска и, отделяясь, образует обособленный «островок». Детали в этом «островке», возможно, представляют часть тех деталей несоответствующего качества, которые вследствие небрежности были перемешаны с доброкачественными в общем потоке. В данной ситуации необходимо принять меры для выяснения самых различных и внезапно возникающих обстоятельств, должным образом объясняющих причину этого явления [38].
На рис. 3.4з центр распределения смещен к нижнему пределу допуска. Так как левая сторона гистограммы на границе нижнего предела допуска имеет вид «отвесного берега», можно сделать заключение, что фактически это была партия, которую предварительно рассортировали из-за наличия в ней деталей несоответствующего качества в левой стороне гистограммы (т.е. выходящих за нижний предел допуска) или же детали несоответствующего качества левой стороны при выборочном контроле умышленно распределили как годные для включения в пределы допуска. Следовательно, необходимо выявить причину, которая могла повлечь за собой данное явление [38].
На рис. 3.4и показан случай, аналогичный варианту «з». Возможно, что используемое измерительное средство было неисправно. В связи с этим необходимо обратить внимание на калибровку (поверку) измерительного средства, равно как и на повторное обучение правилам выполнения измерений [38].
”
Источники:
- Пономарев С.В., Мищенко С.В., Белобрагин B.Я. и др. Управление качеством продукции. Инструменты и методы менеджмента качества: учебное пособие / С.В. Пономарев, С.В. Мищенко, B.Я. Белобрагин, В.А. Самородов, Б.И. Герасимов, А.В. Трофимов, C.А. Пахомова, О.С. Пономарева. – М.: РИА «Стандарты и качество». – 2005.
Если вы считаете, что при публикации настоящего материала нарушены ваши авторские права, напишите нам.
If you believe that the publication of this material infringes your copyright, please let us know.
Что такое правило Стерджеса? (Определение и пример)
17 авг. 2022 г.
читать 2 мин
Гистограмма — это диаграмма, которая помогает нам визуализировать распределение значений в наборе данных.
Оказывается, количество бинов, используемых в гистограмме, может иметь огромное влияние на то, как мы интерпретируем данные.
Если мы используем слишком мало бинов, истинный базовый шаблон в данных может быть скрыт:
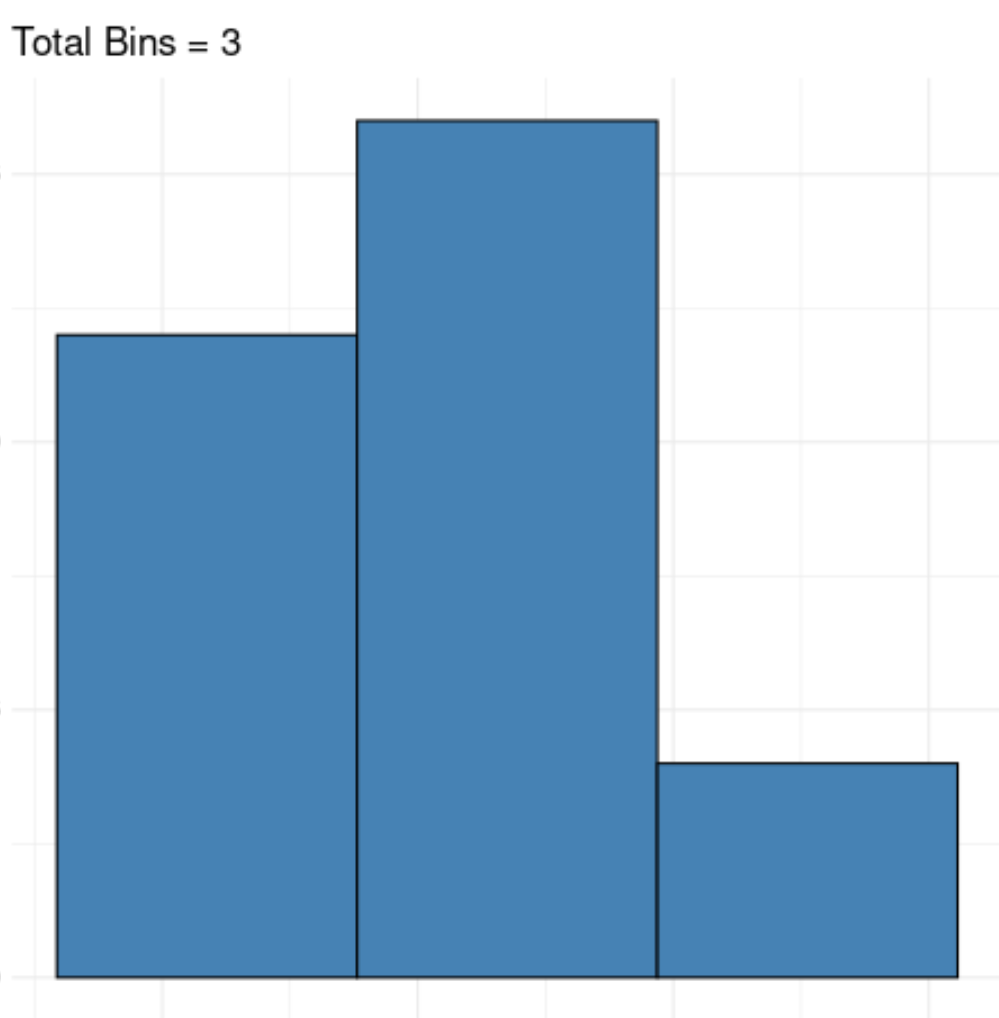
И если мы используем слишком много бинов, мы можем просто визуализировать шум в наборе данных:
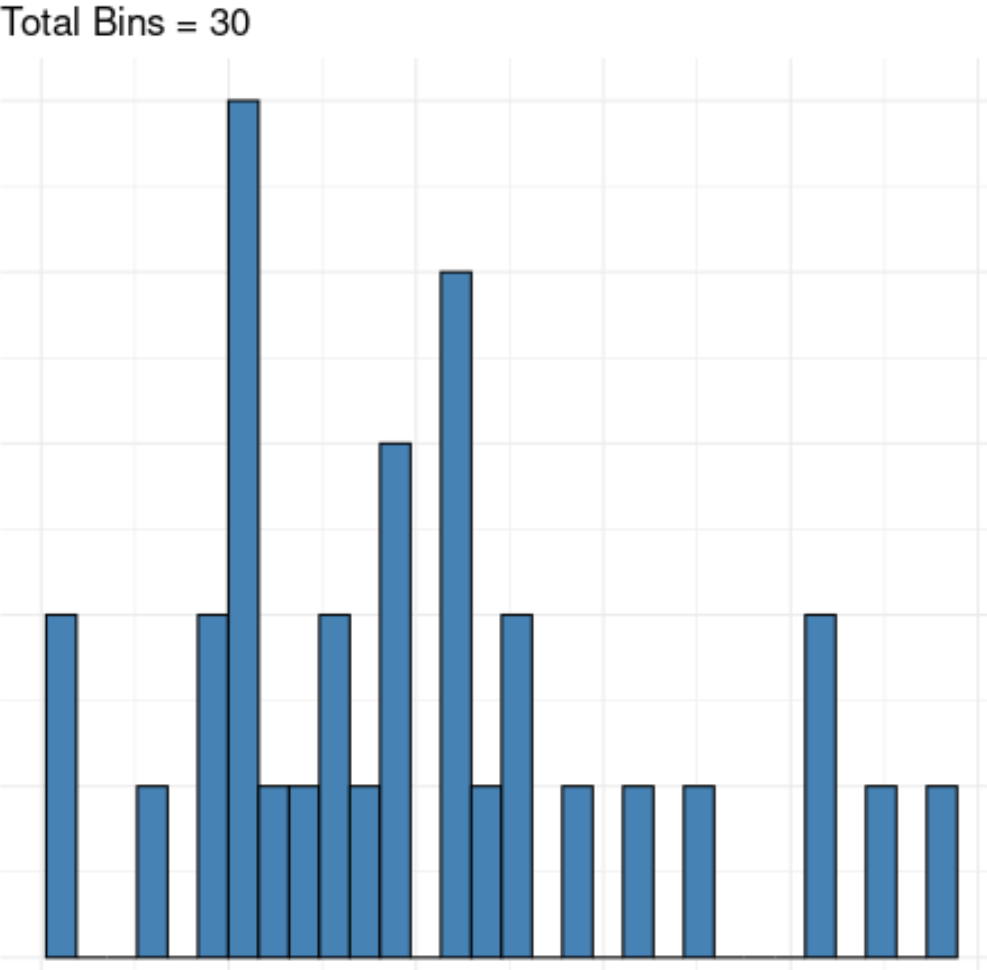
К счастью, мы можем использовать метод, известный как правило Стерджеса, чтобы определить оптимальное количество бинов для использования в гистограмме.
Правило Стерджеса использует следующую формулу для определения оптимального количества интервалов для использования в гистограмме:
Оптимальные интервалы = ⌈log 2 n + 1⌉
куда:
- n: общее количество наблюдений в наборе данных.
- ⌈ ⌉: Символы, означающие «потолок» — т. е. округлить ответ до ближайшего целого числа.
Пример: правило Стерджеса
Предположим, у нас есть следующий набор данных с общим количеством наблюдений n = 31:

Мы можем использовать правило Стерджеса, чтобы определить оптимальное количество бинов для визуализации этих значений на гистограмме:
Оптимальные интервалы = ⌈log 2 (31) + 1⌉ = ⌈4,954 + 1⌉ = ⌈5,954⌉ = 6 .
Согласно правилу Стерджеса, мы должны использовать 6 бинов в гистограмме, которую мы используем для визуализации этого распределения значений.
Вот как будет выглядеть гистограмма с 6 интервалами для этого набора данных:
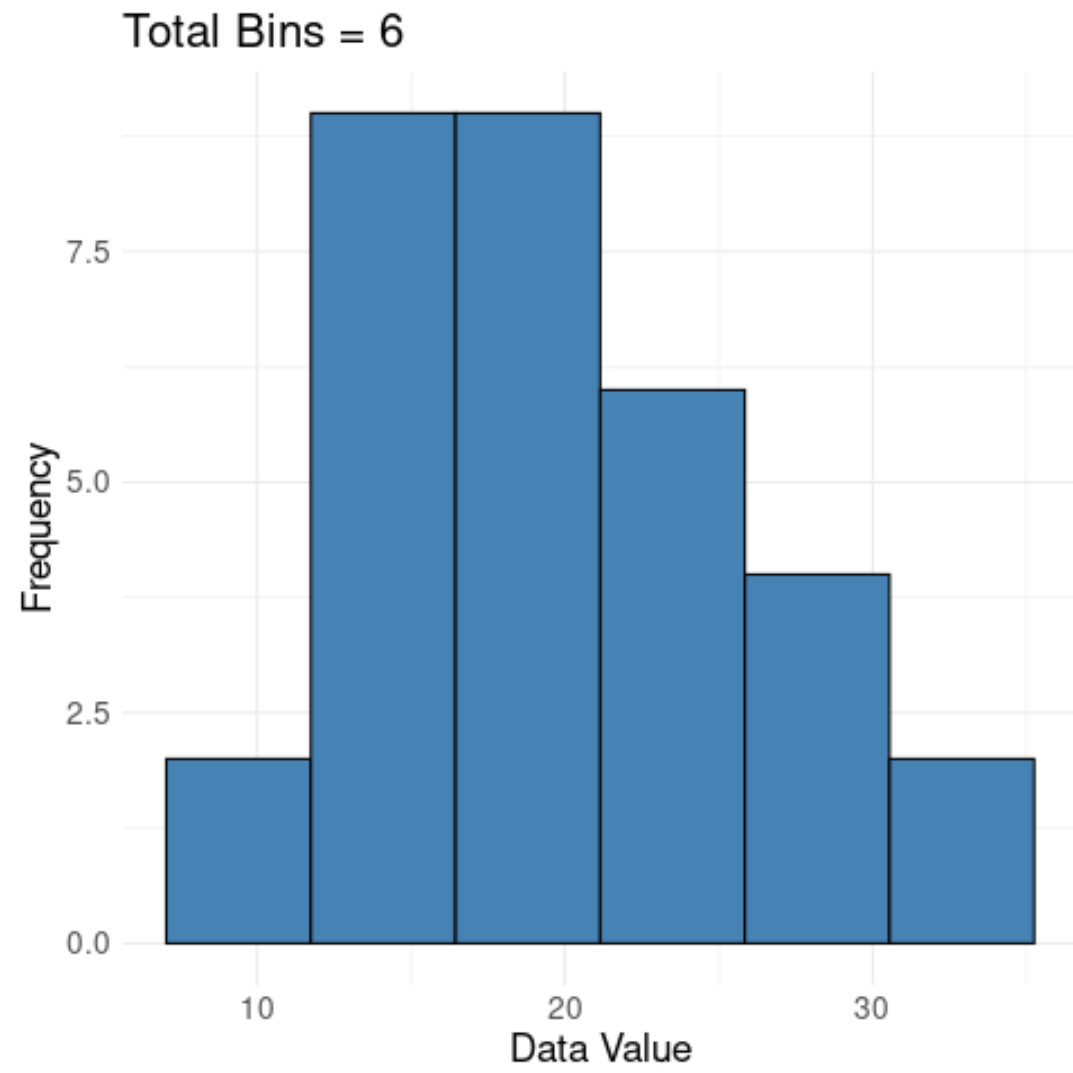
Обратите внимание, что бинов кажется достаточно, чтобы получить хорошее представление о лежащем в основе распределении значений, но их не слишком много, чтобы мы просто визуализировали шум в данных.
Общие значения правила Стерджеса
В следующей таблице показано оптимальное количество бинов для использования в гистограмме на основе общего количества наблюдений в наборе данных в соответствии с правилом Стерджеса:
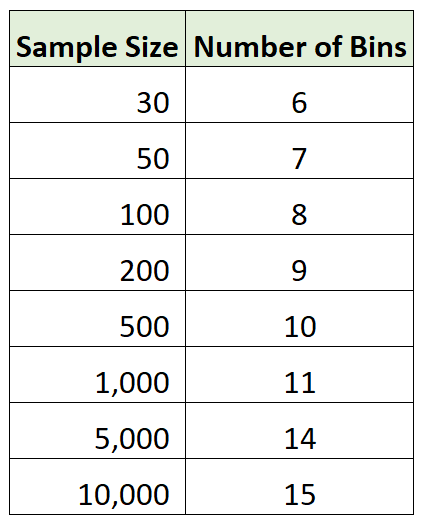
Альтернативы правилу Стерджеса
Правило Стерджеса является наиболее распространенным методом определения оптимального количества бинов для использования в гистограмме, но есть несколько альтернативных методов, в том числе:
Правило квадратного корня : количество ячеек = ⌈√ n ⌉
Правило Райса: количество контейнеров = ⌈2 * 3 √ n ⌉
Правило Фридмана-Диакониса: количество интервалов = (2*IQR) / 3 √ n , где IQR — межквартильный размах.
Бонус: Калькулятор правила Стерджеса
Используйте этот бесплатный онлайн-калькулятор , чтобы автоматически применять правило Стерджеса для определения оптимального количества бинов для гистограммы в зависимости от размера набора данных.
Правило Стёрджеса — эмпирическое правило определения оптимального количества интервалов, на которые разбивается наблюдаемый диапазон изменения случайной величины при построении гистограммы плотности её распределения. Названо по имени американского статистика Герберта Стёрджеса (Herbert Arthur Sturges, 1882—1958).
Количество интервалов 
,
где 



Часто встречается записанным через десятичный логарифм:
,
Основанием для него служит оценка количества событий с разными вероятностями в схеме испытаний Бернулли длительностью в 






Если аппроксимировать значения наблюдаемой случайной величины результатами сложения случайно выпадающих в серии испытаний значений двух чисел 















Распределение получившихся величин (распределение Бернулли) аппроксимируется при больших 
Литература[править | править код]
- Sturges H. (1926). The choice of a class-interval. J. Amer. Statist. Assoc., 21, 65-66.
Ссылки[править | править код]
- Sturges’ rule Архивная копия от 26 января 2013 на Wayback Machine
Гистограмма распределения – это инструмент, позволяющий визуально оценить величину и характер разброса данных. Создадим гистограмму для непрерывной случайной величины с помощью встроенных средств MS EXCEL из надстройки Пакет анализа и в ручную с помощью функции
ЧАСТОТА()
и диаграммы.
Гистограмма (frequency histogram) – это
столбиковая диаграмма MS EXCEL
, в каждый столбик представляет собой интервал значений (корзину, карман, class interval, bin, cell), а его высота пропорциональна количеству значений в ней (частоте наблюдений).
Гистограмма поможет визуально оценить распределение набора данных, если:
- в наборе данных как минимум 50 значений;
- ширина интервалов одинакова.
Построим гистограмму для набора данных, в котором содержатся значения
непрерывной случайной величины
. Набор данных (50 значений), а также рассмотренные примеры, можно взять на листе
Гистограмма AT
в
файле примера.
Данные содержатся в диапазоне
А8:А57
.
Примечание
: Для удобства написания формул для диапазона
А8:А57
создан
Именованный диапазон
Исходные_данные.
Построение гистограммы с помощью надстройки
Пакет анализа
Вызвав диалоговое окно
надстройки Пакет анализа
, выберите пункт
Гистограмма
и нажмите ОК.
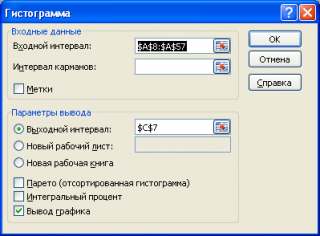
В появившемся окне необходимо как минимум указать:
входной интервал
и левую верхнюю ячейку
выходного интервала
. После нажатия кнопки
ОК
будут:
- автоматически рассчитаны интервалы значений (карманы);
- подсчитано количество значений из указанного массива данных, попадающих в каждый интервал (построена таблица частот);
-
если поставлена галочка напротив пункта
Вывод графика
, то вместе с таблицей частот будет выведена гистограмма.
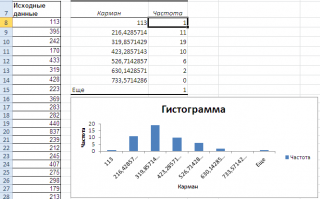
Перед тем как анализировать полученный результат –
отсортируйте исходный массив данных
.
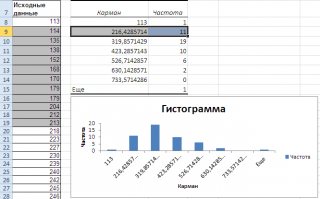
Как видно из рисунка, первый интервал включает только одно минимальное значение 113 (точнее, включены все значения меньшие или равные минимальному). Если бы в массиве было 2 или более значения 113, то в первый интервал попало бы соответствующее количество чисел (2 или более).
Второй интервал (отмечен на картинке серым) включает значения больше 113 и меньше или равные 216,428571428571. Можно проверить, что таких значений 11. Предпоследний интервал, от 630,142857142857 (не включая) до 733,571428571429 (включая) содержит 0 значений, т.к. в этом диапазоне значений нет. Последний интервал (со странным названием
Еще
) содержит значения больше 733,571428571429 (не включая). Таких значений всего одно – максимальное значение в массиве (837).
Размеры карманов одинаковы и равны 103,428571428571. Это значение можно получить так:
=(МАКС(
Исходные_данные
)-МИН(
Исходные_данные
))/7
где
Исходные_данные –
именованный диапазон
, содержащий наши данные.
Почему 7? Дело в том, что количество интервалов гистограммы (карманов) зависит от количества данных и для его определения часто используется формула √n, где n – это количество данных в выборке. В нашем случае √n=√50=7,07 (всего 7 полноценных карманов, т.к. первый карман включает только значения равные минимальному).
Примечание
:
Похоже, что инструмент
Гистограмма
для подсчета общего количества интервалов (с учетом первого) использует формулу
=ЦЕЛОЕ(КОРЕНЬ(СЧЕТ(
Исходные_данные
)))+1
Попробуйте, например, сравнить количество интервалов для диапазонов длиной 35 и 36 значений – оно будет отличаться на 1, а у 36 и 48 – будет одинаковым, т.к. функция
ЦЕЛОЕ()
округляет до ближайшего меньшего целого
(ЦЕЛОЕ(КОРЕНЬ(35))=5
, а
ЦЕЛОЕ(КОРЕНЬ(36))=6)
.
Если установить галочку напротив поля
Парето (отсортированная гистограмма)
, то к таблице с частотами будет добавлена таблица с отсортированными по убыванию частотами.
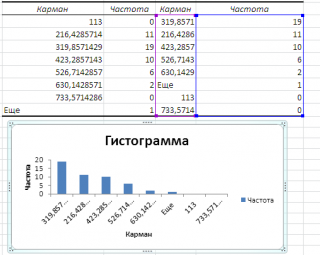
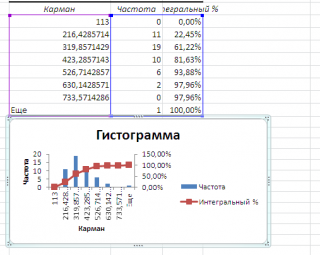
Если установить галочку напротив поля
Интегральный процент
, то к таблице с частотами будет добавлен столбец с
нарастающим итогом
в % от общего количества значений в массиве.
Если выбор количества интервалов или их диапазонов не устраивает, то можно в диалоговом окне указать нужный массив интервалов (если интервал карманов включает текстовый заголовок, то нужно установить галочку напротив поля
Метка
).
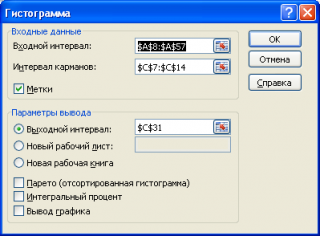
Для нашего набора данных установим размер кармана равным 100 и первый карман возьмем равным 150.
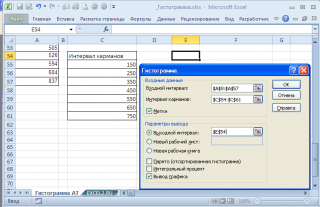
В результате получим практически такую же по форме
гистограмму
, что и раньше, но с более красивыми границами интервалов.
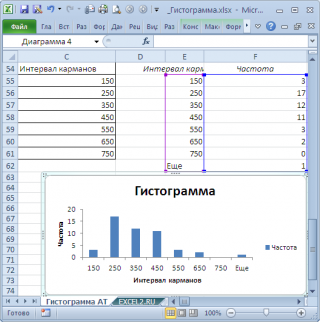
Как видно из рисунков выше, надстройка
Пакет анализа
не осуществляет никакого
дополнительного форматирования диаграммы
. Соответственно, вид такой гистограммы оставляет желать лучшего (столбцы диаграммы обычно располагают вплотную для непрерывных величин, кроме того подписи интервалов не информативны). О том, как придать диаграмме более презентабельный вид, покажем в следующем разделе при построении
гистограммы
с помощью функции
ЧАСТОТА()
без использовании надстройки
Пакет анализа
.
Построение гистограммы распределения без использования надстройки Пакет анализа
Порядок действий при построении гистограммы в этом случае следующий:
- определить количество интервалов у гистограммы;
- определить ширину интервала (с учетом округления);
- определить границу первого интервала;
- сформировать таблицу интервалов и рассчитать количество значений, попадающих в каждый интервал (частоту);
- построить гистограмму.
СОВЕТ
: Часто рекомендуют, чтобы границы интервала были на один порядок точнее самих данных и оканчивались на 5. Например, если данные в массиве определены с точностью до десятых: 1,2; 2,3; 5,0; 6,1; 2,1, …, то границы интервалов должны быть округлены до сотых: 1,25-1,35; 1,35-1,45; … Для небольших наборов данных вид гистограммы сильно зависит количества интервалов и их ширины. Это приводит к тому, что сам метод гистограмм, как инструмент
описательной статистики
, может быть применен только для наборов данных состоящих, как минимум, из 50, а лучше из 100 значений.
В наших расчетах для определения количества интервалов мы будем пользоваться формулой
=ЦЕЛОЕ(КОРЕНЬ(n))+1
.
Примечание
: Кроме использованного выше правила (число карманов = √n), используется ряд других эмпирических правил, например, правило Стёрджеса (Sturges): число карманов =1+log2(n). Это обусловлено тем, что например, для n=5000, количество интервалов по формуле √n будет равно 70, а правило Стёрджеса рекомендует более приемлемое количество – 13.
Расчет ширины интервала и таблица интервалов приведены в
файле примера на листе Гистограмма
. Для вычисления количества значений, попадающих в каждый интервал, использована
формула массива
на основе функции
ЧАСТОТА()
. О вводе этой функции см. статью
Функция ЧАСТОТА() – Подсчет ЧИСЛОвых значений в MS EXCEL
.
В MS EXCEL имеется диаграмма типа
Гистограмма с группировкой
, которая обычно используется для построения
Гистограмм распределения
.
В итоге можно добиться вот такого результата.
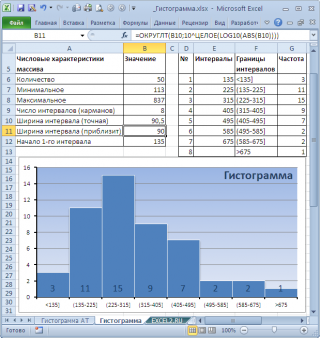
Примечание
: О построении и настройке макета диаграмм см. статью
Основы построения диаграмм в MS EXCEL
.
Одной из разновидностей гистограмм является
график накопленной частоты
(cumulative frequency plot).
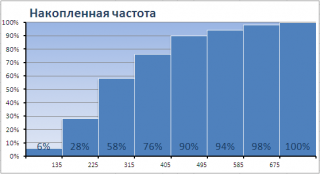
На этом графике каждый столбец представляет собой число значений исходного массива, меньших или равных правой границе соответствующего интервала. Это очень удобно, т.к., например, из графика сразу видно, что 90% значений (45 из 50) меньше чем 495.
СОВЕТ
: О построении
двумерной гистограммы
см. статью
Двумерная гистограмма в MS EXCEL
.
Примечание
: Альтернативой
графику накопленной частоты
может служить
Кривая процентилей
, которая рассмотрена в
статье про Процентили
.
Примечание
: Когда количество значений в выборке недостаточно для построения полноценной
гистограммы
может быть полезна
Блочная диаграмма
(иногда она называется
Диаграмма размаха
или
Ящик с усами
).