Вместе с выбором
группировочного
признака
возникает задача определения количества
групп, на
которые следует подразделить изучаемое
явление.
Число групп зависит
от:
-
задач исследования
-
вида признака,
положенного в основу группировки -
численности
совокупности -
степени вариации
признака
Единицы анализируемой
совокупности могут быть разбиты по
одному и тому же признаку на разное
число групп. Например, при группировке
населения по возрасту с целью определения
трудовых ресурсов страны все население
делится на три группы: население моложе
трудоспособного возраста, трудоспособное
население и население старше трудоспособного
возраста. Если же анализируется
продолжительность жизни, то строится
более детальная группировка и выделяются
группы по 5 лет.
При группировке
по атрибутивному (описательному) признаку
вопрос о количестве групп решается
сравнительно просто – по количеству
градаций, видов состояния этого признака.
Например, группировка
населения по полу образует две группы,
организаций связи по федеральным округам
– 7 групп, по формам собственности – на
пять групп: государственная, муниципальная,
частная, смешанная, собственность
иностранных юридических лиц.
Если атрибутивный
(описательный) признак имеет множество
наименований (например, профессия – в
отрасли связи насчитывается несколько
десятков их наименований), то для
статистической характеристики состава
работников образуют укрупненные
группы (руководители,
специалисты, рабочие, прочие).
Такое объединение основано на изучении
сущности производственных процессов.
Характеристика
типов предприятий по их величине часто
ограничивается тремя группами: мелкие,
средние и крупные, а при изучении
рентабельности – группы нерентабельных,
рентабельных и высокорентабельных.
Группировки по
количественному признаку
очень разнообразны. При выборе числа
групп в совокупности с количественным
признаком необходимо, чтобы в каждую
группу попало достаточное количество
единиц совокупности. Только в этом
случае обобщающие характеристики каждой
группы (средние, относительные показатели)
будут устойчивыми, неслучайными,
характерными.
Сравнительно просто
образуются группы по количественным
признакам, имеющим дискретную (прерывную)
вариацию и принимающим целые значения.
Если количественный
признак изменяется в широких пределах
и имеет множество различных значений,
то каждая группа образуется в виде
интервалов.
Группировка может
быть выполнена с равными
и неравными
интервалами.
Равные
интервалы
употребляются
в тех случаях, когда признак изменяется
более или менее равномерно в ограниченных
пределах, например масса письма, посылки,
заработная плата определенной категории
работников.
Величина интервала
зависит от размаха варьирования признака
и численности изучаемой совокупности
и в случае равных интервалов может
определятся по формуле
Стерджесса.
Формула
Стерджесса
служит для
определения величины интервала:
где
i
– интервал, т.е. разница между максимальным
xmax
и минимальным xmin
значениями признака в каждой группе; N
– численность единиц совокупности; k
– число групп, которое оптимально при
величине 1+3,322 lg
N.
Недостаток формулы
Стерджесса состоит в том, что её применение
дает хорошие результаты для большой
совокупности единиц и когда распределение
единиц по признаку, положенному в
основание группировки, близко к
нормальному.
Число групп можно
определить также по следующей номограмме:
|
Численность |
15..24 |
25..44 |
45..89 |
90..179 |
180..359 |
360..719 |
720..1439 |
|
Число |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
Другим способом
выполнения группировки является
использование среднего
квадратического отклонения
.
Если величина интервала равна 0,5,
то совокупность разбивается на 12 групп,
если 2/3
или,
то совокупность делится на 9 или 6 групп.
При

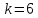
образом:
от
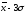
от
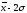
от

от
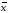
от
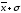
от
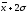
Однако при определении
групп данными методами возможно получение
пустых или малочисленных групп. Если
размах вариации признака совокупности
велик и его значения варьируют
неравномерно, то используют группировку
с неравными интервалами.
Неравные
интервалы
употребляются в тех случаях, когда
признак изменяется неравномерно. Из
неравных интервалов чаще всего
употребляются прогрессивно возрастающие
или убывающие интервалы.
Величина интервалов,
изменяющихся в арифметической прогрессии,
определяется по формуле:
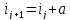
в геометрической
прогрессии:
где a
– постоянная величина (положительная
для прогрессивно-возрастающих интервалов,
отрицательная – для прогрессивно-убывающих);
q
– константа – положительное число (для
прогрессивно-возрастающих интервалов
q
> 1, для прогрессивно-убывающих – q
< 1).
Например, необходимо
построить группировку предприятий
отрасли по показателю выручки от
реализации продукции, который варьирует
от 500 млн. руб. до 4000 млн. руб. в год, то
строить группировку с равными интервалами
нецелесообразно, т.к. как правило,
совокупность предприятий любой отрасли
промышленности и торговли включает
большое число малых предприятий, имеющих
небольшую выручку. С ростом выручки от
реализации продукции значительно
снижается число предприятий. Т.о.
распределение числа предприятий по
величине выручки является неравномерным.
Поэтому следует построить группировку
с неравными интервалами.
Таблица
Группировка
предприятий с неравными интервалами
|
№ группы |
Интервал |
|
I II III IV V |
500-800 800-1300 1300-2000 2000-2900 2900-4000 |
Величина каждого
последующего интервала у этой группировки
больше предыдущего на 200 млн. руб., т.е.
увеличивается в арифметической
прогрессии.
При образовании
интервалов важное значение имеет точное
обозначение границ.
Например, группы
предприятий по численности работников:
200 – 600, 600 – 1000. Такая запись предполагает,
что единица, у которой значение признака
совпадает с верхней границей интервала,
относится к следующей группе.
Обычно границы
интервалов обозначаются указанием
значений признака «от» и «до» (в нашем
примере – 200 – 599, 600 -999). Характер такого
обозначения говорит, что в группу
включаются все значения признака в
указанных границах.
После определения
группировочного признака и границ групп
строится ряд распределения.
Статистический
ряд распределения
– это упорядоченное распределение
единиц совокупности на группы по
определенному варьирующему признаку.
В зависимости от признака, положенного
в основу образования ряда распределения,
различают атрибутивные и вариационные
ряды распределения.
Атрибутивными
называют ряды распределения, построенные
по описательным (качественным) признакам.
Вариационными
называют ряды распределения, построенные
по количественному признаку.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Дана выборка значений признака Х. Требуется:
построить статическую совокупность;
построить гистограмму частот;
найти точечные оценки генеральной средней, генеральной
дисперсии и генерального среднего квадратического отклонения;
найти доверительный интервал для неизвестного математического
ожидания;
проверить нулевую гипотезу о нормальном законе распределения
количественного признака Х генеральной совокупности.
38, 51, 57, 64, 76, 92, 89, 19, 35, 60, 22, 41, 44, 48, 60, 44, 67, 80, 86,
57, 25, 83, 73, 70, 70, 70, 64, 60, 60, 64, 57, 54, 57, 54, 32, 86, 86, 80,
76, 60, 76, 70, 70, 67, 67, 64, 64, 60, 28, 67, 41, 41, 51, 48, 44, 80, 80,
76, 73, 51, 67, 60, 32, 41, 41, 54, 57, 60, 67, 73, 73, 76, 57, 67, 73, 73,
64, 60, 54, 57.
Объем выборки n=80
Наименьшее значение признака Х
MIN:
19
Наибольшее значение
MAX:
92
Определим оптимальное число интервалов разбиения по формуле
Число интервалов:
7,00 – ПОЧЕМУ ???
Шаг интервала h=(92-19)/7=
10,43
Правило Стёрджеса — эмпирическое правило определения оптимального количества интервалов, на которые разбивается наблюдаемый диапазон изменения случайной величины при построении гистограммы плотности её распределения. Названо по имени американского статистика Герберта Стёрджеса (Herbert Arthur Sturges, 1882—1958).
Количество интервалов 
,
где 



Часто встречается записанным через десятичный логарифм:
,
Основанием для него служит оценка количества событий с разными вероятностями в схеме испытаний Бернулли длительностью в 






Если аппроксимировать значения наблюдаемой случайной величины результатами сложения случайно выпадающих в серии испытаний значений двух чисел 















Распределение получившихся величин (распределение Бернулли) аппроксимируется при больших 
Литература[править | править код]
- Sturges H. (1926). The choice of a class-interval. J. Amer. Statist. Assoc., 21, 65-66.
Ссылки[править | править код]
- Sturges’ rule Архивная копия от 26 января 2013 на Wayback Machine
- Авторы
- Файлы
- Литература
Дацковская М.А.
1
Колеснёв А.С.
1
Агишева Д.К.
1
Зотова С.А.
1
1 Волжский политехнический институт (филиал) Волгоградского государственного технического университета
1. Агишева Д.К., Зотова С.А., Матвеева Т.А., Светличная В.Б. Математическая статистика: учебное пособие // Успехи современного естествознания. – 2010. – № 2. – С. 122-123.
2. Булашкова М.Г., Ломакина А.Н., Чаузова Е.А., Зотова С.А. Роль математики в современном мире // Успехи современного естествознания. – 2012. – № 4. – С. 45-45.
Если признак является непрерывным или число различных значений в выборке велико, вычислять частоту каждого из них не имеет большого смысла. В этом случае составляют интервальный вариационный ряд. Весь промежуток измерения значений выборки, от минимального до максимального, разбивают на частичные интервалы (чаще одинаковой длины), т. е. производится группировка.
Число интервалов следует брать не очень большим, чтобы после группировки ряд не был громоздким, и не очень малым, чтобы не потерять особенности распределения признака.
Число интервалов может быть определено по формуле Стерджеса
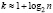
где 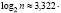
Длина интервала находится по формуле
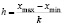
За начало первого частичного интервала, как правило (но не обязательно), выбирается точка
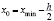
В первую строку таблицы интервального ряда вписывают частичные промежутки 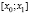
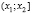
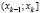
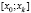
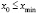
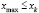
Во второй строке вписывают количество наблюдений 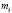
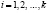
Рассмотрим пример составления интервального вариационного ряда.
В таблице 1 приведена выборка результатов измерения роста 105 студентов (юношей). Измерения проводились с точностью до 1 см.
Требуется составить интервальный вариационный ряд.
Очевидно, что рост юношей есть случайная непрерывная величина. Найдём количество интервалов при
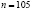
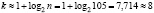
Т. к. 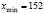
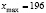
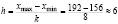
Примем 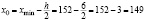
Исходные данные разбиваем на 8 интервалов: 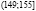
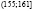
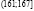
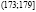
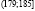
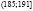
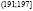
Подсчитав число студентов 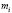
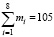
Таблица 1
|
155 |
170 |
185 |
180 |
188 |
152 |
173 |
178 |
178 |
168 |
185 |
172 |
170 |
183 |
175 |
|
173 |
170 |
183 |
175 |
180 |
175 |
193 |
178 |
183 |
180 |
197 |
178 |
181 |
187 |
168 |
|
174 |
179 |
184 |
183 |
178 |
180 |
178 |
163 |
166 |
178 |
175 |
182 |
190 |
167 |
170 |
|
178 |
183 |
170 |
178 |
181 |
173 |
168 |
185 |
175 |
170 |
155 |
169 |
186 |
179 |
189 |
|
156 |
174 |
179 |
179 |
169 |
186 |
174 |
171 |
184 |
175 |
193 |
178 |
184 |
180 |
196 |
|
175 |
181 |
188 |
168 |
179 |
178 |
183 |
184 |
178 |
181 |
177 |
163 |
166 |
178 |
175 |
|
183 |
190 |
167 |
170 |
178 |
183 |
170 |
178 |
182 |
173 |
168 |
186 |
176 |
171 |
188 |
Таблица 2
|
Рост, |
149-155 |
155-161 |
161-167 |
167-173 |
173-179 |
179-185 |
185-191 |
191-197 |
|
Частота, |
3 |
1 |
6 |
22 |
33 |
26 |
10 |
4 |
Библиографическая ссылка
Дацковская М.А., Колеснёв А.С., Агишева Д.К., Зотова С.А. ИНТЕРВАЛЬНЫЙ ВАРИАЦИОННЫЙ РЯД // Международный студенческий научный вестник. – 2015. – № 3-4.
;
URL: https://eduherald.ru/ru/article/view?id=14154 (дата обращения: 21.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Варианты для выполнения работы
I. Установление закономерностей, которым подчинены массовые случайные явления, основано на изучении методами теории вероятностей статистических данных — результатов наблюдений.
Почти все встречающиеся в жизни величины (урожайность сельскохозяйственных растений, продуктивности скота, производительность труда и заработная плата рабочих, объем производства продукции и т.д.) принимают неодинаковые значения у различных членов совокупности. Поэтому возникает необходимость в изучении их изменяемости. Это изучение начинается с проведения соответствующих наблюдений, обследований.
В результате наблюдений получают сведения о численной величине изучаемого признака у каждого члена данной совокупности.
Пример. Имеются данные о размере прибыли 100 коммерческих банков. Прибыль, млн. рублей.
| 30,2 | 51,9 | 43,1 | 58,9 | 34,1 | 55,2 | 47,9 | 43,7 | 53,2 | 34,9 |
| 47,8 | 65,7 | 37,8 | 68,6 | 48,4 | 67,5 | 27,3 | 66,1 | 52,0 | 55,6 |
| 54,1 | 26,9 | 53,6 | 42,5 | 59,3 | 44,8 | 52,8 | 42,3 | 55,9 | 48,1 |
| 44,5 | 69,8 | 47,3 | 35,6 | 70,1 | 39,5 | 70,3 | 33,7 | 51,8 | 56,1 |
| 28,4 | 48,7 | 41,9 | 58,1 | 20,4 | 56,3 | 46,5 | 41,8 | 59,5 | 38,1 |
| 41,4 | 70,4 | 31,4 | 52,5 | 45,2 | 52,3 | 40,2 | 60,4 | 27,6 | 57,4 |
| 29,3 | 53,8 | 46,3 | 40,1 | 50,3 | 48,9 | 35,8 | 61,7 | 49,2 | 45,8 |
| 45,3 | 71,5 | 35,1 | 57,8 | 28,1 | 57,6 | 49,6 | 45,5 | 36,2 | 63,2 |
| 61,9 | 25,1 | 65,1 | 49,7 | 62,1 | 46,1 | 39,9 | 62,4 | 50,1 | 33,1 |
| 33,3 | 49,8 | 39,8 | 45,9 | 37,3 | 78,0 | 64,9 | 28,8 | 62,5 | 58,7 |
Из данной таблицы видно, что интересующий нас признак (прибыль банков) меняется от одного члена совокупности к другому, варьирует. Варьирование есть изменяемость признака у отдельных членов совокупности.
Вариационным рядом называется последовательность вариант, записанных в возрастающем порядке и соответствующих им частот.
Число, показывающее, сколько раз повторяется в данной совокупности каждое значение признака, называется частотой.
Составим ранжированный вариационный ряд (выпишем варианты в порядке возрастания):
| 20,4 | 25,1 | 26,9 | 27,3 | 27,6 | 28,1 | 28,4 | 28,8 | 29,3 | 30,2 |
| 31,4 | 33,1 | 33,3 | 33,7 | 34,1 | 34,9 | 35,1 | 35,6 | 35,8 | 36,2 |
| 37,3 | 37,8 | 38,1 | 39,5 | 39,8 | 39,9 | 40,1 | 40,2 | 41,4 | 41,8 |
| 41,9 | 42,3 | 42,5 | 43,1 | 43,7 | 44,5 | 44,8 | 45,2 | 45,3 | 45,5 |
| 45,8 | 45,9 | 46,1 | 46,3 | 46,5 | 47,3 | 47,8 | 47,9 | 48,1 | 48,4 |
| 48,7 | 48,9 | 49,2 | 49,6 | 49,7 | 49,8 | 50,1 | 50,3 | 51,8 | 51,9 |
| 52,0 | 52,3 | 52,5 | 52,8 | 53,2 | 53,6 | 53,8 | 54,1 | 55,2 | 55,6 |
| 55,9 | 56,1 | 56,3 | 57,4 | 57,6 | 57,8 | 58,1 | 58,7 | 58,9 | 59,3 |
| 59,5 | 60,4 | 61,7 | 61,9 | 62,1 | 62,4 | 62,5 | 63,2 | 64,9 | 65,1 |
| 65,7 | 66,1 | 67,5 | 68,6 | 69,8 | 70,1 | 70,3 | 70,4 | 71,5 | 78,0 |
В нашем случае каждое значение признака (варианта вариационного ряда) повторилось только один раз, т.е. значение частоты для всех вариант равно единице. Перейдем к интервальному вариационному ряду, так как интересующий нас признак принимает дробные, практически не повторяющиеся значения.
Для этого необходимо определить число интервалов (классов) и длину интервала (классного промежутка), после чего произвести разноску, т.е. подсчитать для каждого интервала число вариант, попавших в него.
Количество классов устанавливают в зависимости от степени точности, с которой ведется обработка, и количества объектов в выборке. Считается удобным при объеме выборки (n) в пределах от 30 до 60 вариант распределять их на 6-7 классов, при n от 60 до 100 вариант — на 7-8 классов, при n от 100 и более вариант — на 9-17 классов.
Нужное количество групп также может быть ориентировочно вычислено по формуле Стерджесса:
где — число групп (классов, интервалов) ряда распределения; n — объем выборки.
Можно также использовать выражение:
При они дают примерно одинаковые результаты.
В рассматриваемом примере о размере прибыли коммерческих банков, n=100. Применяя формулу Стерджесса, получим:
Однако Таким образом, число интервалов может быть равно 8, 9, 10 и т.д.
Нахождение нужного количества групп и их размеров часто бывает взаимообусловлено. Для того, чтобы как-то определиться с числом интервалов, найдем размах вариации — разность между наибольшей и наименьшей вариантой:
где — размах вариации,
— наибольшее значение варьирующего признака,
— наименьшее значение варьирующего признака.
Найдем размах вариации для рассматриваемой задачи:
Для того, чтобы найти длину интервала (величину классового промежутка) необходимо разделить размах вариации на число классов и полученную величину округлить таким образом, чтобы было удобно производить сначала разноску, а затем и различные вычисления. Рекомендую округлять до единиц, до которых округлены варианты в исходной таблице, в нашем случае до десятых.
Согласно формуле получаем
Теперь необходимо определиться с началом первого интервала. Для этого можно использовать формулу:
Замечание. За начало первого интервала можно принять некоторое значение, несколько меньшее или само значение
. Далее в табличном виде я покажу оба варианта.
Прибавив к началу первого интервала (нижней границе) шаг, получим верхнюю границу первого интервала и одновременно нижнюю границу второго интервала. Выполняя последовательно указанные действия, будем находить границы последующих интервалов до тех пор, пока не будет получено или перекрыто .
Таким образом, верхняя граница одного интервала одновременно является нижней границей другого интервала. Чтобы не возникало сомнений, в какой интервал отнести варианту, попавшую на границу, условимся относить ее к верхнему интервалу.
Составим теперь рабочую таблицу для построения интервального вариационного ряда и произведем подсчет частот вариант, попавших в тот или иной интервал.
Как и обещал покажу две таблицы построения ряда:
1. Отсчет ведем от , т.е. нижняя граница первого интервала совпадает с
.
|
Группы банков по размеру прибыли (границы интервалов) |
Количество банков, принадлежащих данной группе (частоты, |
Накопленные частоты, |
| 20,4 — 27,6 | 4 | 4 |
| 27,6 — 34,8 | 11 | 15 |
| 34,8 — 42 | 16 | 31 |
| 42 — 49,2 | 21 | 52 |
| 49,2 — 56,4 | 21 | 73 |
| 56,4 — 63,6 | 15 | 88 |
| 63,6 — 70,8 | 10 | 98 |
| 70,8 — 78 | 2 | 100 |
2. Начало первого интервала определяем с помощью формулы: .
|
Группы банков по размеру прибыли (границы интервалов) |
Количество банков, принадлежащих данной группе (частоты, |
Накопленные частоты, |
| 16,8 — 24 | 1 | 1 |
| 24 — 31,2 | 9 | 10 |
| 31,2 — 38,4 | 13 | 23 |
| 38,4 — 45,6 | 17 | 40 |
| 45,6 — 52,8 | 23 | 63 |
| 52,8 — 60 | 18 | 81 |
| 60 — 67,2 | 11 | 92 |
| 67,2 — 74,4 | 7 | 99 |
| 74,4 — 81,6 | 1 | 100 |
Как мы видим в 1-м случае у нас получилось восемь интервалов, что полностью совпадает с результатом, который нам дала формула Стерджесса. Во втором случае у нас получилось девять интервалов, так как при поиске начала первого интервала пользовались специальной формулой.
Для дальнейшего исследования я буду пользоваться результатами второй таблицы, так как там ярко выражен модальный интервал (одна мода) и медиана практически точно попадает на середину вариационного ряда.
Мы получили интервальный вариационный ряд — упорядоченную совокупность интервалов варьирования значений случайной величины с соответствующими частотами попаданий в каждый из них значений величины.
II. Графическая интерпретация вариационных рядов.
| № п/п |
Границы интервалов, |
Середины интервалов, |
Частоты интервалов, |
Относительные частоты |
Плотность относит. частоты |
Плотность частоты |
| 1 | 16,8 — 24 | 20,4 | 1 | 0,01 | 0,001 | 0,139 |
| 2 | 24 — 31,2 | 27,6 | 9 | 0,09 | 0,013 | 1,250 |
| 3 | 31,2 — 38,4 | 34,8 | 13 | 0,13 | 0,018 | 1,806 |
| 4 | 38,4 — 45,6 | 42 | 17 | 0,17 | 0,024 | 2,361 |
| 5 | 45,6 — 52,8 | 49,2 | 23 | 0,23 | 0,032 | 3,194 |
| 6 | 52,8 — 60 | 56,4 | 18 | 0,18 | 0,025 | 2,500 |
| 7 | 60 — 67,2 | 63,6 | 11 | 0,11 | 0,015 | 1,528 |
| 8 | 67,2 — 74,4 | 70,8 | 7 | 0,07 | 0,010 | 0,972 |
| 9 | 74,4 — 81,6 | 78 | 1 | 0,01 | 0,001 | 0,139 |
Строим графики:
Далее найдем моду вариационного ряда:
где
— начало модального интервала;
— длина частичного интервала (шаг);


— частота послемодального интервала.
Определим модальный интервал — интервал, имеющий наибольшую частоту. Из таблицы видно, что модальным является интервал (45,6 — 52,8).
Медиана
Для интервального ряда медиана находится по формуле:
где
— начало медианного интервала;
— длина частичного интервала (шаг);
— объем совокупности;
— накопленная частота интервала, предшествующая медианному;
— частота медианного интервала.
Определим медианный интервал — интервал, в котором впервые накопленная частота превышает половину объема выборки.Так как объем выборки n=100, то n/2=50. По таблице найдем интервал, где впервые накопленные частоты превысят это значение. Таким является интервал (45,6 — 52,8).
Получаем,
III. Расчет сводных характеристик выборки.
Для определения составим расчетную таблицу. Для начала определимся с ложным нулем С. В качестве ложного нуля можно принять любую варианту. Максимальная простота вычислений достигается, если выбрать в качестве ложного нуля варианту, которая расположена примерно в середине вариационного ряда (часто такая варианта имеет наибольшую частоту).
Варианте, которая принята в качестве ложного нуля, соответствует условная варианта, равная нулю. В нашем случае С=49,2.
Равноотстоящими называют варианты, которые образуют арифметическую прогрессию с разностью h.
Условными называют варианты, определяемые равенством:
Произведем расчет условных вариант согласно формуле:
| N п/п |
Середины интервалов, |
Частоты интервалов, |
Условные варианты, |
Произведения частот и условных вариант, |
Произведения частот и условных вариант, |
Произведения частот и условных вариант, |
Произведения частот и условных вариант, |
Произведения частот и условных вариант, |
Произведения частот и условных вариант, |
| 1 | 20,4 | 1 | -4 | -4 | 16 | -64 | 256 | 9 | 81 |
| 2 | 27,6 | 9 | -3 | -27 | 81 | -243 | 729 | 36 | 144 |
| 3 | 34,8 | 13 | -2 | -26 | 52 | -104 | 208 | 13 | 13 |
| 4 | 42 | 17 | -1 | -17 | 17 | -17 | 17 | 0 | 0 |
| 5 | 49,2 | 23 | 0 | 0 | 0 | 0 | 0 | 23 | 23 |
| 6 | 56,4 | 18 | 1 | 18 | 18 | 18 | 18 | 72 | 288 |
| 7 | 63,6 | 11 | 2 | 22 | 44 | 88 | 176 | 99 | 891 |
| 8 | 70,8 | 7 | 3 | 21 | 63 | 189 | 567 | 112 | 1792 |
| 9 | 78 | 1 | 4 | 4 | 16 | 64 | 256 | 25 | 625 |
Контроль:
Контроль:
Равенство выполнено, следовательно вычисления произведены верно.
Вычислим условные моменты 1-го, 2-го, 3-го и 4-го порядков:
Найдем выборочные среднюю, дисперсию и среднее квадратическое отклонение :
Также для оценки отклонения эмпирического распределения от нормального используют такие характеристики, как асимметрия и эксцесс.
Асимметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:
Асимметрия положительна, если «длинная часть» кривой распределения расположена справа от математического ожидания; асимметрия отрицательна, если «длинная часть» кривой расположена слева от математического ожидания. Практически определяют знак асимметрии по расположению кривой распределения относительно моды (точки максимума дифференциальной функции): если «длинная часть» кривой расположена правее моды, то асимметрия положительна, если слева — отрицательна.
Эксцесс эмпирического распределения определяется равенством:
где — центральный эмпирический момент четвертого порядка.
Для нормального распределения эксцесс равен нулю. Поэтому если эксцесс некоторого распределения отличен от нуля, то кривая этого распределения отличается от нормальной кривой: если эксцесс положительный, то кривая имеет более высокую и «острую» вершину, чем нормальная кривая; если эксцесс отрицательный, то сравниваемая кривая имеет более низкую и «плоскую» вершину, чем нормальная кривая. При этом предполагается, что нормальное и теоретическое распределения имеют одинаковые математические ожидания и дисперсии.
Вычисляем центральные эмпирические моменты третьего и четвертого порядков:
Найдем асимметрию и эксцесс:
IV. Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона.
Проверим генеральную совокупность значений размера прибыли банков по критерию Пирсона
Правило. Для того, чтобы при заданном уровне значимости проверить нулевую гипотезу : генеральная совокупность распределена нормально, надо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия:
и по таблице критических точек распределения , по заданному уровню значимости
и числу степеней свободы
найти критическую точку
, где s — количество интервалов.
Если — нет оснований отвергнуть нулевую гипотезу.
Если — нулевую гипотезу отвергают.
Найдем теоретические частоты , для этого составим следующую таблицу.
|
Середины интервалов, |
Частоты интервалов, |
Произведем расчет, |
Произведем расчет, |
Значения функции Гаусса, |
Произведем расчет, |
Теоретические частоты, |
| 20,4 | 1 | -28,152 | -2,23 | 0,0332 | 57 | 2 |
| 27,6 | 9 | -20,952 | -1,66 | 0,1006 | 57 | 6 |
| 34,8 | 13 | -13,752 | -1,09 | 0,2203 | 57 | 13 |
| 42 | 17 | -6,552 | -0,52 | 0,3485 | 57 | 20 |
| 49,2 | 23 | 0,648 | 0,05 | 0,3984 | 57 | 23 |
| 56,4 | 18 | 7,848 | 0,62 | 0,3292 | 57 | 19 |
| 63,6 | 11 | 15,048 | 1,19 | 0,1965 | 57 | 11 |
| 70,8 | 7 | 22,248 | 1,77 | 0,0833 | 57 | 5 |
| 78 | 1 | 29,448 | 2,34 | 0,0258 | 57 | 1 |
Вычислим , для чего составим расчетную таблицу.
| 1 | 1 | 2 | -1 | 1 | 0,5 | 1 | 0,5 |
| 2 | 9 | 6 | 3 | 9 | 1,5 | 81 | 13,5 |
| 3 | 13 | 13 | 0 | 0 | 0 | 169 | 13 |
| 4 | 17 | 20 | -3 | 9 | 0,45 | 289 | 14,45 |
| 5 | 23 | 23 | 0 | 0 | 0 | 529 | 23 |
| 6 | 18 | 19 | -1 | 1 | 0,05 | 324 | 17,05 |
| 7 | 11 | 11 | 0 | 0 | 0 | 121 | 11 |
| 8 | 7 | 5 | 2 | 4 | 0,8 | 49 | 9,8 |
| 9 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| 100 | 100 |
Наблюдаемое значение критерия, |
103,30 |
Контроль:
Вычисления произведены правильно.
Найдем число степеней свободы, учитывая, что число групп выборки (число различных вариант) s=9;
По таблице критических точек распределения по уровню значимости
и числу степеней свободы k=6 находим
Так как — нет оснований отвергнуть нулевую гипотезу. Другими словами, расхождение эмпирических и теоретических частот незначительное. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.
На рисунке построены нормальная (теоретическая) кривая по теоретическим частотам (зеленый график) и полигон наблюдаемых частот (коричневый график). Сравнение графиков наглядно показывает, что построенная теоретическая кривая удовлетворительно отражает данные наблюдений.
V. Интервальные оценки.
Интервальной называют оценку, которая определяется двумя числами — концами интервала, покрывающего оцениваемый параметр.
Доверительным называют интервал, который с заданной надежностью покрывает заданный параметр.
Интервальной оценкой (с надежностью ) математического ожидания (а) нормально распределенного количественного признака Х по выборочной средней
при известном среднем квадратическом отклонении

где — точность оценки, n — объем выборки, t — значение аргумента функции Лапласа
(см. приложение 2), при котором
;
при неизвестном среднем квадратическом отклонении 
где S — исправленное выборочное среднее квадратическое отклонение, находят по таблице приложения по заданным n и
.
В нашем примере среднее квадратическое отклонение известно, . А также
,
,
. Поэтому для поиска доверительного интервала используем первую формулу:
Все величины, кроме t, известны. Найдем t из соотношения По таблице приложения находим t=1,96. Подставив t=1,96,
,
,
в формулу, окончательно получим искомый доверительный интервал:
Интервальной оценкой (с надежностью ) среднего квадратического отклонения

(при q<1), (*)
(при q>1),
где q — находят по таблице приложения по заданным n и .
По данным и n=100 по таблице приложения 4 найдем q=0,143. Так как q<1, то, подставив
в соотношение (*), получим доверительный интервал:
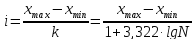
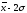
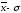
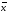
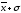
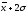
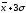
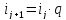

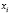
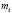





![Rendered by QuickLaTeX.com [chi^2_{nabl}=sum frac{ {(n_i-n_i^{'})}^2}{n_i^{'}}]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-43685ed67e69272b6c950828a97acd89_l3.png)
![Rendered by QuickLaTeX.com [sumfrac{n_i^2}{n_i^{'}}-n=sum frac{{(n_i-n_i^{'})}^2}{n_i^'}]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-6c32fcc2a5c6b3b4b603ae3d99533b4a_l3.png)

