Довольно точно можно вычислить площадь прямоугольной фигуры, но для фигуры неправильной формы можно найти её приближённую площадь. Для этого удобно использовать палетку.
Палетка — это прозрачная плёнка (или калька), расчерченная на равные квадраты со стороной (1) см.
Самостоятельно сделай палетку.
С её помощью ты сможешь быстро находить приближённую площадь разных фигур.
Для нахождения приближённой площади фигуры нужно:
1) наложить палетку на фигуру;
2) посчитать число (a) целых клеток внутри фигуры;
3) посчитать количество (b) клеток, частично входящих в фигуру;
4) вычислить приближённую площадь
S≈a+b:2
.
Поясним также, зачем нужно делить (b) на два.
(b) — число клеток, частично входящих в фигуру. У одних большая часть входит в фигуру, у других — меньшая. Из них можно составить приближённо (b:2) полных клеток (если (b) нечётно, то можно сначала увеличить (b) на (1), а потом уже разделить на (2)).
Обрати внимание!
Для записи приближённого равенства используется знак
≈
.
Найдём с помощью палетки приближённую площадь фигуры (B) неправильной формы.
1. Наложим палетку на фигуру (B).
2. Посчитаем количество (a) клеток, целиком находящихся внутри фигуры (закрашены зелёным цветом):
3. Посчитаем количество (b) клеток, частично входящих в фигуру (B) (закрашены синим). Таких клеток (17) — это нечётное число, поэтому увеличим это число на (1) и поделим на (2):
17+1=18,18:2≈9.
4. Сложим числа, полученные в пунктах (2) и (3), и запишем приближённую площадь фигуры (B):
S≈16+9=25см2.
Обрати внимание!
Нужно понимать разницу между оценкой площади и нахождением её приближённого значения!
Оценка площади записывается неравенством
a<S<b
.
Приближённое значение площади — это число, которое можно найти по формуле
S≈a+b:2
.
Источники:
Изображение: палетка. © ЯКласс.
Изображения: фигура. © ЯКласс.
- Учебники
- 2 класс
- Математика 👍
- Петерсон
- №4
авторы: Петерсон.
издательство: Ювента
Раздел:
- ЧАСТЬ 2
- Урок 16. Площадь фигур
ГДЗ учебник по математике 2 класс Петерсон. Урок 16. Площадь фигур. Номер №4
- Предыдущее
- Следующее
Сколько клеточек в фигуре? Сколько полосок? Какая это величина?
reshalka.com
ГДЗ учебник по математике 2 класс Петерсон. Урок 16. Площадь фигур. Номер №4
Решение
1) m = 6a − площадь фигуры в клеточках a;
2) m = 3b − площадь прямоугольника в полосках b;
3) m = 2c − площадь прямоугольника в полосках c.
- Предыдущее
- Следующее
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
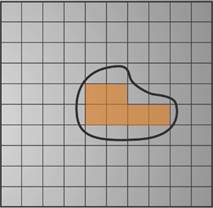
Как найти количество клеток на клеточном листке. На нём обведена подошва ботинка.
Жанна Булычева
Ученик
(151),
на голосовании
5 лет назад
Как быстро посчитать количество полных и не полных клеток.
Голосование за лучший ответ
николай мордовин
Профи
(620)
5 лет назад
самый простой способ посчитать отдельно клетки, находящиеся внутри фигуры, не разрезанные линией а потом прибавить к ним разделенное пополам кол-во разрезанных клеток. Однако этот способ не самый точный но удобный
|
Площадь фигуры (треугольник, четырёхугольник, трапеция и др.) по клеточкам (клеткам). Какие есть формулы? Есть способ, при котором надо воспользоваться формулой, основой которой будет понятие узла, узла внутреннего и узла внешнего. Узел это пересечение линий, образующих эти самые клеточки. Внешние узлы, это узлы, находящиеся на сторонах и вершинах геометрических фигур, площади которых нам надо найти. А внутренние узлы, это узлы внутри этих фигур. Клеточки у нас со сторонами равными одному сантиметру (1 см). Формула, о которой идет речь, называется формула Пика. Выглядит она вот так: И по ней очень просто посчитать площадь фигуры S. В этой формуле M это количество внешних узлов, N – количество внутренних узлов. Приведем пример, возьмем геометрическую фигуру параллелограмм: Внутренние узлы – синие – N – их у нас 20. Внешние узлы – красные – М – их у нас 18 и их количество нам надо поделить на два, получится 18/2 = 9 узлов. Складываем 9 + 20 и вычитаем единицу: 20 + 9 – 1 = 28 см². Еще один пример: S = 14/2 + 43 – 1 = 49 см². система выбрала этот ответ лучшим Ксарфакс 6 лет назад Допустим, у нас есть произвольная фигура, построенная на листе в клетку. Необходимо вычислить её площадь. Площадь фигуры по клеточкам Для того, чтобы найти площадь любой фигуры по клеточкам, можно использовать формулу Пика. Данная формула основана на подсчёте количества узлов, лежащих внутри фигуры и на её границе. Узел – это точка, которая лежит на пересечении 2 линий данной сетки: вертикальных и горизонтальных. Площадь фигуры по клеточкам находится по формуле: N – количество узлов, которые находятся внутри фигуры. M – количество узлов, которые находятся на границах (на вершинах и сторонах). Примеры нахождения площади по клеточкам 1) Найдём площадь треугольника. Будем считать, что одна клетка – это 1 см. Отметим внутренние узлы и узлы, которые находятся на границах. N = 7 (внутренние). M = 8 (узлы на границах). Площадь треугольника S = 7 + 8/2 – 1 = 10 см². 2) Найдём площадь трапеции по клеточкам, одна клетка – это 1 см. Отметим все узлы и подсчитаем их количество. N = 11 (внутренние). M = 12 (узлы на границах). Площадь трапеции S = 11 + 12/2 – 1 = 16 см². 3) Найдём площадь произвольного многоугольника. Одна клетка – это 1 см. Отметим внутренние узлы и узлы, расположенные на границах фигуры. Подсчитаем их количество. N = 6 (внутренние узлы). M = 8 (узлы на границах). Площадь многоугольника S = 6 + 10/2 – 1 = 10 см². Марина Вологда 3 года назад Такие задачи очень часто встречаются, когда известен размер клеточки и дана фигура. Вот пример таких задач: Решение зависит от того, какая фигура дана и как именно она размещена относительно клеточек. Возьмем простой пример, необходимо вычислить площадь вот такого треугольника: Вспоминаем правило: Теперь считаем, сколько клеточек треугольник в длину и сколько в высоту. У нас получается 2 в высоту и 6 в длину. Подставляем к формуле: S = 1/2 х 2 х 6 = 6 см2. Считаем по клеточкам, подставляя формулу Пика: Целых клеточек у нас 3. Теперь считаем, сколько не целых: 6. Делим их на 2. S = 3 + 6:2 = 6 см2. А теперь высчитываем по формуле Пика: количество узлов сетки внутри – 2, количество узлов сетки, лежащих на границах – 10. Подставляем к формуле и получаем – 2 + 10:2 – 1 = 6 см2. Теперь давайте рассмотрим вот такой треугольник: Чтобы найти площадь, вспоминаем правило: Считаем клеточки и подставляем в формулу: S = 1/2 х 2 х 6 = 6 см2. А теперь находим по клеточкам: целых клеточек 2, не целых клеточек 8. Подставляем в формулу: 2 + 8:2 = 6 см2. Пробуем сделать по формуле Пика: количество узлов сетки внутри – 3, количество узлов сетки, лежащих на границах – 8. Подставляем к формуле и получаем – 3 + 8:2 – 1 = 6 см2. Enot-Nina 3 года назад Найти площадь геометрической фигуры можно самыми разными способами: Самый простой вариант – это вручную посчитать клеточки – целые и половинки также поскладывать. Простой, хотя и не самый быстрый и может не самый точный способ, но он работает. Чтобы легче было считать, достаточно расчертить фигуру на более простые. Есть еще один способ – это использовать давно разработанную формулу. Это так называемая формула Пика. Для нее нужно посчитать количество узлов – точек пересечения клеточек, что окружены фигурой (находятся внутри нее), а также подсчитать количество пограничных узлов – по контуру фигуры. Вот на картинке наглядно показано, как ее можно применять, чтоб посчитать площадь любой фигуры по клеточкам: Бархатные лапки 3 года назад Площадь любого многоугольника можно посчитать по клеточкам. Для этого применяем формулу Пика. На нашем рисунке В – количество узловых клеточек внутри фигуры, Г – количество узлов на границе . Узлы – пересечение двух линий. многоугольника. Площадь равна S = В + Г/2 – 1 Считаем точки на рисунке и подставляем в формулу. – 10 + 7/2 -1 = 12,5. Таким образом можно посчитать площадь, если вершины фигуры лежат в узлах. Ann Luka 6 лет назад Чтобы найти площадь фигуры по клеточкам, нужно посчитать сколько в фигуре целых клеточек. Потом нужно посчитать сколько не целых и поделить их количество на 2. Добавить к получившемуся числу количество целых клеточек – это и будет правильный ответ. Например. В треугольнике 3 целых клетки и 4 не целых. 3+4/2=5 пощадь треугольника 5 клеток. Outline 3 года назад Для того, чтобы определить площадь фигуры на бумаге в клеточку есть универсальная формула Пика, позволяющая вычислить площадь изображения, но в только в том случае, если вершины искомой фигуры имеют целые (натуральные числа) координаты. Называется эта формула, в честь Георга Пика: S=В + Г / 2 − 1 В этой формуле буквенные обозначения означают следующее: В — количество целочисленных точек внутри многоугольника; Г — количество целочисленных точек на границе (вершинах и сторонах) многоугольника; S – площадь фигуры. Здесь используется понятие “целочисленные” – это те, точки, которые расположены на пересечениях сетки (в ее узлах). Для примера, найдем площадь треугольника: Обозначим внутренние точки нашей фигуры красными кружками, а те, что на границах – синим цветом. Считаем красные и синие точки: В=12, Г=4. Исходя из подсчетов определяем площадь треугольника по формуле: S=В+Г/2-1=12+2-1=13. Можно убедиться в правильность проведенных выше расчетах. Рассчитываем площадь квадрата, обведенного красным, и вычитаем площади зеленого, синего и фиолетового треугольников: S квадрата равна 36, площади треугольников: синего – 6, зеленого – 2, фиолетового – 15. Исходя из полученных данных, S белого треугольника равна 13: S=36-6-15-2=13. KritikSPb 3 года назад Подсчет клеточек – дело полезное. С их помощью можно найти площадь геометрической фигуры. Достаточно воспользоваться формулой, доказанной Георгом Пиком в 1899 году. Подходит для расчета площади фигур с прямыми сторонами и целым количеством углов, чаще всего применяют для нахождения площади разносторонних треугольников и многоугольников с числом углов больше 4-х. На теорему Пика есть задания в ЕГЭ. 127771 3 года назад Сначала я подумал, что нужно будет фигуру, которая указана на рисунке в клеточку разбить по фигурам так, чтобы можно посчитать площадь каждой фигуры по-отдельности, но оказалось все намного проще. Существует для данной задачи специальная формула Пика, которая выглядит следующим образом: Площадь = В + Г/2 – 1, где:
Теперь разберемся на примере, у нас есть такой пример: Перед нами трапеция. Допустим площадь одной клетки 1 кв.см. Теперь можно воспользоваться формулой: 11+12/2-1=16 кв.см. Бекки Шарп 3 года назад Найти площадь фигуры можно если вершины фигуры находятся в уголках клеточек, так называемые Целочисленные вершины или узловые точки. Решать задачу будем по формуле Пика, где
Вот такая фигура у нас – Считаем точки и подставляем в формулу: S = 17 + 14/2 – 1 = 23 Ответ мы получаем в квадратных единицах, то есть клеточках. Знаете ответ? |
Содержание:
- § 1 Оценка площади
- § 2 Приближенное вычисление площадей
- § 3 Краткие итоги урока
§ 1 Оценка площади
В этом уроке ответим на вопрос: как произвести оценку площади? А также научимся выполнять приближённое вычисление площади.
Давайте представим ситуацию.
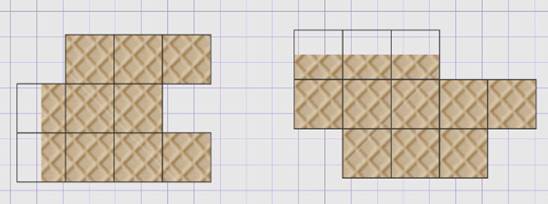
Однажды ученики 4 класса побывали на кондитерской фабрике. Им показывали, как делают вафли. В конце экскурсии кондитер отломил каждому ученику от большой пластины по маленькому кусочку хрустящей вафли. Кусочки были неодинаковые. Петя и Вася стали спорить, чей кусок оказался больше.
Как же им помочь решить их спор? Можно конечно сравнить, наложив один кусок на другой. Но сравнение точным не получится, так как одну из фигур разместить внутри другой нельзя.
Какой же метод сравнения используют в случае, когда наложением сравнить нельзя? Конечно, нужно сделать измерения. Чтобы измерить площадь фигуры, нужно выбрать единицу измерения и определить, сколько раз она содержится в фигуре.
Единицы измерения площади – это квадратный миллиметр, квадратный сантиметр, квадратный метр, квадратный километр.
На рисунке мы видим, что вафли разделены на квадраты. Возьмём их за единицу измерения площади вафель. На рисунке также видно, что площадь вафель состоит из целых и нецелых квадратов.
Определим, между какими числами заключена площадь каждой вафли, т.е. сделаем оценку площади, найдём «нижнюю и верхнюю границы».
«Нижняя граница» – это меньшее число квадратов, значит, мы будем считать только целые квадраты внутри фигуры. Чтобы найти «верхнюю границу», нужно найти большее число квадратов. Значит, нужно найти количество всех целых и всех нецелых квадратов вместе.
Итак, давайте сделаем оценку площади Петиной вафли.
Сосчитаем целые квадраты, их получилось 8. Это «нижняя граница» площади.
Сосчитаем все нецелые квадраты фигуры, их – 2, прибавим к целым, получилось 10. Это «верхняя граница» площади.
Значит, площадь Петиной вафли находится в границах от 8 до 10 квадратов. Это можно записать в виде двойного неравенства.
8 < S < 10
Теперь сделаем оценку площади Васиной вафли. Считаем все целые квадраты внутри фигуры, «нижняя граница» – 8. Считаем все нецелые квадраты фигуры и добавляем к целым, «верхняя граница» – 11. В результате мы получаем следующее неравенство, которое обозначает «нижнюю и верхнюю границы» площади Васиной вафли.
8 < S < 11
Таким образом, у нас получилось, что у мальчиков почти одинаковые по площади вафли.
Давайте обобщим, чтобы произвести оценку площади надо:
1. сосчитать число целых квадратов, расположенных внутри фигуры, то есть определить «нижнюю границу» площади.
2. сосчитать число нецелых квадратов фигуры и прибавить к ним количество всех целых квадратов, расположенных внутри фигуры, то есть определить «верхнюю границу» площади.
3. записать двойное неравенство, указав «верхнюю» и «нижнюю» границы площади.
§ 2 Приближенное вычисление площадей
А теперь вычислим площадь этих вафель.
Внутри вафель мы можем насчитать 8 целых квадратов. Остальные квадраты входят частично, поэтому число нецелых квадратов делим пополам. Итак, в Петиной вафле содержится 8 целых и 2 нецелых квадрата.
Значит, примерно 8 + 2 : 2 = 8 + 1 = 9 квадратов. (8 < 9 < 10).
В Васиной вафле содержится 8 целых и 3 нецелых квадрата.
Значит, 8 + 3 : 2. Так как число 3 нечётное и на 2 не разделится, его нужно увеличить на 1. Давайте 3 увеличим на 1, получим 8 + 4 : 2 = 8 + 2 = 10 квадратов. (8 < 10 < 11).
Так как мы можем посчитать количество квадратов только приблизительно. Мы не имеем право ставить знак «=» между найденным количеством квадратов и площадью. Поэтому для обозначения примерного результата используем знак приближенного равенства «≈».
S ≈ 9 ед2
S ≈ 10 ед2.
Читать следует так:
«Площадь приближенно равна 9 квадратным единицам».
«Площадь приближенно равна 10 квадратным единицам».
Таким образом, мы выполнили приближенное вычисление площади вафель Пети и Васи.
Вычислить приблизительную площадь вафель мы смогли благодаря тому, что фигуры были разделены на квадраты.
Что делать, если таких квадратов нет? Самим расчерчивать фигуры очень долго, поэтому люди придумали особое приспособление – палетку.
Палетка – прозрачная плёнка, разделённая на одинаковые квадраты.
Вычислим площадь фигуры при помощи палетки,
площадь каждой клетки которой равна 1 см2.
1. Наложим палетку на фигуру.
2. Сосчитаем число целых клеток внутри фигуры (а = 6).
3. Сосчитаем число клеток входящих в фигуру частично (b = 14).
4. Вычислим приближенное значение площади 6 + 14 : 2 = 6 + 7 = 13, S ≈13 см2.
Для вычисления приближенного значения площади используют формулу S ≈ а+b:2, где a – это число целых клеток, b – число нецелых клеток.
§ 3 Краткие итоги урока
Для того чтобы произвести оценку площади, необходимо:
1. Сосчитать число целых квадратов, расположенных внутри фигуры, то есть определить «нижнюю границу» площади.
2. Сосчитать число нецелых квадратов фигуры и прибавить к ним количество всех целых квадратов, расположенных внутри фигуры, то есть определить «верхнюю границу» площади.
3. Записать двойное неравенство, указав «верхнюю» и «нижнюю» границы площади.
Для того чтобы вычислить площадь фигуры при помощи палетки, необходимо:
1. Наложить палетку на фигуру.
2. Сосчитать число а целых клеток внутри фигуры.
3. Сосчитать число b клеток, входящих в фигуру частично.
4. Вычислить приближенное значение площади: S ≈ а + b : 2 (если число b нечётно, то увеличить его на 1).
Список использованной литературы:
- Автор конспекта – Курманаева Светлана Валентиновна
- Петерсон Л.Г. Математика. 4 класс. Часть 1./Л.Г. Петерсон. – М.: Ювента, 2014.
- Математика. 4 класс. Методические рекомендации к учебнику математики «Учусь учиться» для 4 класса. / Л.Г. Петерсон. – М.: Ювента, 2014. – 280 с.: ил.
- Зак С.М. Все задания к учебнику математики для 4 класса Л.Г. Петерсон и комплекту самостоятельных и контрольных работ. ФГОС. – М.: Юнвес, 2014.
Использованные изображения: