Как найти количество колебаний в импульсе

дано:   τ = 2,0 мкс,     λ = 15 см    c = 3,0 ⋅ 10⁸ м/с    ν=4000Гц

решение

n=τ/T,     Число колебаний в импульсе

где T — период электромагнитных колебаний;

τ — длительность импульса

Период электромагнитных колебаний найдем из формулы для длины электромагнитной волны (λ = cT):

T=λ/c,   где λ — длина электромагнитной волны,

c — скорость электромагнитной волны в вакууме, .

Подставим выражение для периода электромагнитных колебаний в формулу для числа колебаний в импульсе:

n=τλ/c

Вычислим:

n=2,0⋅10⁻⁶⋅3⋅10⁸/15⋅10⁻²=4000  – Количество колебаний в импульсе

импульс локатора должен успеть достичь объекта и вернуться обратно до того, как послан следующий импульс (для того чтобы не было наложения сигналов); поэтому существует ограничение на число импульсов в единицу времени:

N/t₀ ≤ 1/t,   где N/t ₀ — число импульсов, испущенных локатором за t₀=1c,    t — время распространения импульса до цели и обратно.

по условию

N/t₀  = 4000 с⁻¹

Предельная глубина разведки при заданном количестве импульсов, посланных локатором в секунду, определяется формулой

R=ct/2=c/2(N/t₀).

Рассчитаем ее значение:

R=3⋅10⁸/2⋅4000=3,75⋅10⁵ м=375 км.

Сегодня мы будем рассматривать импульсы и их применение в измерениях. Но что такое импульс? И тут нас поджидает первое затруднение, правда небольшое. Термин импульс оказывается совсем неоднозначным, как и почти все в нашем реальном мире. Давайте попробуем разобраться. Даже не смотря на то, что в предыдущей статье уже давалось одно из определений импульса.

Статья ни в коей мере не является даже малой частью “Теории цепей и сигналов”! Мы рассматриваем импульсы с точки зрения информации и их применения в измерительных приборах.

Пожалуй, первый раз с термином импульс встречаются еще на уроках школьной физики при изучении раздела “Механика”. Произведение массы тела на его скорость и называется импульсом, точнее, импульсом механического движения. Или импульсом тела. Немного позже, когда школьники узнают, что такое вектор, они узнают что скорость, а значит и импульс механического движения являются векторами.

Значительно позже школьники (или сегодня это уже студенты?) узнают про импульс силы. Это произведение силы на время ее действия. То есть, ограниченное во времени. Это тоже векторная величина, так как сила является вектором. Более того, импульс силы является интегральной величиной. Импульс тела и импульс силы связаны между собой. Изменение импульса тела равно импульсу действовавшей на него силы.

Кроме механических импульсов существуют световые, которые на бытовом уровне чаще называют вспышками света. Хотя световым импульсом будет любое изменения яркости (светимости, освещенности) ограниченное во времени. В физике микромира можно встретить импульс Ферми. Существуют волновой импульс, импульс электромагнитного поля, электромагнитный импульс, радиоимпульс, нервный импульс… И конечно, электрический импульс, который мы и будем рассматривать. А еще импульсы не имеющие отношения ни к физике, ни к технике. Душевный импульс мы называем душевным порывом. Есть импульсивный характер. И так далее.

Так что же такое импульс? Импульс это кратковременное, ограниченное во времени, изменение чего либо. Причем не обязательно некой физической величины (а в метрологии мы чаще всего говорим об измерении именно физических величин), но и, например, настроения. Изменение яркости это световой импульс. Изменение напряжения – электрический. Изменение настроения, частые кратковременные перепады настроения, это тот самый импульсивный характер.

Значение физической величины и ее изменение являются информацией, которую мы передаем (и обрабатываем) с помощью сигналов. С этим мы разбирались в предыдущей статье. Поэтому в ней и приводилось определение импульса как “Ограниченный во времени аналоговый сигнал называется импульсным аналоговым сигналом“. Однако, теперь мы уточним это определение.

Что такое импульс?

Прежде всего, давайте уточним, что значит “ограниченное во времени“? Понятно, что бесконечность является лишь теоретической абстракцией, в реальном мире все, так или иначе, имеет свое начало и свой конец. Для примера рассмотрим физическую величину соответствующую высоте дерева, которое живет несколько сотен лет.

Момент прорастания дерева, когда из земли показывается росток, является начальным моментом. Момент падения дерева, век которого закончился, является конечным. Мы можем представить изменение высоты дерева как функцию времени. Аналитическая запись такой функции будет слишком сложной, но мы можем изобразить ее графически. До момента прорастания высота равна 0, причем “от начала времен”. После падения высота тоже будет равна 0, но уже “до конца времен”. Краткий, с точки зрения времени существования Вселенной (или даже просто нашей планеты) миг жизни дерева будет выглядеть небольшим всплеском над нулевым уровнем.

То есть, высота дерева, в виде сигнала ей соответствующего, будет импульсом. Но, обратите внимание, что кроме времени жизни дерева, длительности импульса, здесь присутствует время наблюдения. И это очень важный момент! Если мы будем отображать в виде графика высоту дерева не за время существования планеты, а за время жизни одного человека, мы можем никогда не увидеть высоту равную 0. Более того, высота дерева может оказаться практически неизменной. А значит, мы уже не можем считать изменение высоты дерева импульсом.

Поэтому понятие “ограниченное во времени” следует понимать как “небольшой промежуток времени, значительно меньший времени наблюдения“. И теперь нам понятно, что с точки зрения одного наблюдателя сигнал может являться импульсом, а с точки зрения другого нет.

Но это еще не все. Пример с высотой дерева важен и еще одним нюансом. За пределами “импульса” высота дерева равна 0. От нулевого уровня все начинается, нулевым уровнем все и заканчивается. Начальный уровень не обязательно равен 0. Например, мы можем оценивать высоту дерева от уровня моря, а не от уровня грунта, в котором оно растет. Важно лишь то, что сигнал начинается на некотором уровне и на этом же уровне заканчивается. Вне времени импульса сигнал находится на начальном уровне, которое будем считать нулевым уровнем.

Вот теперь мы можем дать более точное определение импульса:

• Сигнал, который кратковременно, на небольшом интервале времени, значительно меньшем времени наблюдения, отклоняется от начального уровня, называется импульсным.

Это определение учитывает все наши уточнения

А мы можем рассмотреть несколько примеров, когда сигнал нельзя считать импульсом

В данном случае, сигнал не возвращается к начальному уровню за время наблюдения. Конкретные значения начального и конечного уровней, как и их соотношение, не важны. Важен лишь сам факт, что нет возврата к начальному уровню.

В данном случае, сигнал не является импульсным с точки зрения наблюдателя, для которого время наблюдения меньше длительности импульса. Однако, если внимательно присмотреться, оба примера, по своей сути, являются идентичными. Просто в первом примере мы видим начало импульса, но его окончание осталось за пределами времени наблюдения.

А теперь пример посложнее

Это один импульс? Или три следующих друг за другом импульса? Если исходить из того, что за пределами “длительности импульса” уровень должен быть начальным и до начала импульса, и после его окончания, до возможно следующего далее импульса, мы должны считать изображенное на иллюстрации единым импульсом. Однако, исходя из удобства анализа и расчетов, мы можем рассматривать этот случай как комбинацию трех отдельных импульсов. При этом импульс все таки один. Просто мы будем анализировать его по частям.

Какую информацию несет импульс?

Импульс это сигнал, а значит он является носителем информации. Мы не можем знать, чему именно соответствует эта информация. Но мы может получить информацию о собственно импульсе. А с исходной информацией она будет соотноситься с помощью функции преобразования. Мы это рассматривали с предыдущей статье.

Качественная информация, событие

Простейшей информацией, которую несет в себе импульс, является сам факт наличия импульса или его отсутствия. Можно считать эту информацию качественной, так никакие иные параметры импульсы в этом случае не важны. Нас просто интересует есть импульс, или его нет.

Наличие импульса будет соответствовать произошедшему событию. Не важно, что это за событие, например, прошедший через дверной проем человек, загоревшаяся/погасшая лампочка, деталь на ленте конвейера, и т.д.

Количественная информация, количество импульсов и частота

Мы можем подсчитать количество импульсов. При этом сам, отдельно взятый, импульс нас не интересует. Да, каждый импульс по прежнему соответствует некоему событию, но важно именно количество импульсов, количество событий. Например, в одну коробку входит 10 банок консервов. Проходя по ленте конвейера банка замыкает контакт, который и формирует электрический импульс. Когда прошло 10 банок, 10 импульсов, конвейер остановится дав время упаковать коробку.

И именно с количественной информацией связано понятие “частота импульсов“. Термин “частота” применительно к гармоническим колебаниям встречается еще в курсе школьной физики, в том самом разделе “Механика”, когда школьники изучают маятники. Именно тогда и узнают связь между периодом гармонических колебаний и частотой. Гармонические сигналы являются периодическими. Условие периодичности выглядит так

То есть, функция повторяется через определенные, и постоянные, интервалы времени. Интервал времени, через который значения функции повторяются, называется периодом. Из условия периодичности следует, что периодическая функция совершенно не обязана быть гармонической.

Функция описывающая импульсный сигнал может являться периодической. То есть, через интервалы времени равные периоду значения функции, форма импульса, в точности повторяются. Но мы можем немного смягчить условия, ведь нам пока важен лишь сам факт наличия импульса, которые мы подсчитываем. Форма импульса нам пока не важна.

Значит, нам достаточно, что импульсы поступают через равные интервалы времени, без учета формы и прочих параметров импульсов. Такой сигнал нельзя считать периодическим. Это квазипериодический импульсный сигнал.

Можно представить и еще один случай, когда импульсы идентичны, но интервал времени между ними может быть разным. Такой сигнал будет импульсным непериодическим, или апериодическим, сигналом.

Мы можем подсчитывать количество импульсов для любого характера импульсного сигнала. Но понятие “частота импульсов” применимо только к периодическому или квазипериодическому сигналу. При этом частота будет равна не количеству колебаний, как для гармонического сигнала, в единицу времени, а количеству поступивших в единицу времени импульсов.

Мы можем еще больше смягчить условие периодичности допустив изменение времени между импульсами по некоторому закону. Такой импульсный сигнал будет непериодическим, но будет детерминированным. Например, именно таким станет периодический сигнал при плавном изменении частоты. Таким будет и гармонический сигнал при частотной модуляции. Если основой детерминированного сигнала является периодический, то мы не можем говорить просто о частоте сигнала. Но мы можем говорить о мгновенном значении частоты и о средней (интегральной) частоте. Более того, в случае частотной модуляции мы можем выделить несущую частоту и частоту модуляции.

Если интервалы времени между импульсами непериодического импульсного сигнала являются случайными, то и сигнал будет называться импульсным случайным, или стохастическим. Примером такого сигнала может являться сигнал с датчика счетчика Гейгера. Или сигнал шумовой помехи.

Нужно сделать еще одно уточнение. При подсчете количества импульсов мы говорим не об отдельных импульсах, а о последовательности импульсов. Или импульсной последовательности. Импульсная последовательность состоит из бесконечного количества импульсов. Если количество импульсов в последовательности конечно, то это серия импульсов. Как и при определении понятия импульс, здесь мы должны учитывать время наблюдения. Для одного наблюдателя последовательность импульсов может быть импульсной последовательностью, так как его время наблюдения меньше длительности серии импульсов. А для другого наблюдателя, время наблюдения которого позволяет увидеть все импульсы, это будет лишь серия.

Можете считать это своеобразным “эффектом наблюдателя”, только не для элементарных частиц, а для мира импульсов.

Кстати, последовательность импульсов в случайном, стохастическом, непериодическом сигнале называется еще хаотической импульсной последовательностью.

Количественная информация, параметры времени

Давайте обратим более пристальное внимание на собственно отдельный импульс. Но будем пока игнорировать форму импульса. Что у нас остается? Остаются длительность импульса и интервал времени между импульсами, длительность паузы. Оба этих параметра являются параметрами времени. Причем аналоговыми, в отличии от количества импульсов и факта наличия импульса.

Частота импульсов, о которой мы говорили ранее, тоже является параметром времени. Но, в отличии от длительности импульса и длительности паузы, она применима только к периодическим и квазипериодическим сигналам. А значит, это лишь частный случай. Более того, для квазипериодических сигналов длительность импульсов может изменяться при неизменной их частоте.

Количественная информация, параметры формы импульса

Наконец, мы обратив внимание на форму сигнала. Это самый информативный параметр, ведь уровень сигнала, в пределах времени импульса, сам по себе несет множество информации в каждый момент времени. В общем случае, параметр формы сигнала является аналоговой функцией от времени. Причем форма импульса действительно может нести огромный объем информации. Для примера приведу сигнал одной строки черно-белого телевизионного изображения

Обратите внимание, “активная часть строки”, которую я выделил красным цветом, действительно является импульсом сложной формы. Начальным уровнем для этого импульса является “уровень гашения”. Содержащаяся в форме импульса информация соответствует изменению яркости в пределах одной строки телевизионного изображения. То есть, этот импульс и формирует само изображение на экране.

При этом, если мы в качестве времени наблюдения примем длительность импульса, мы можем рассматривать его как просто аналоговый сигнал, но ограниченный во времени. Безусловно, здесь мы не можем уйти от фактора времени, ведь и длительность импульса, и его форма, являются функциями времени. Но все таки нам важна именно форма.

Поскольку мы большей частью будем рассматривать электрические импульсы, мы можем сказать, что совокупность мгновенных значений напряжения в каждой точке импульса является аналоговым сигналом, который и несет информацию. В том случае, если мы рассматриваем именно форму импульса.

Однако, в статьях цикла мы будем рассматривать импульсы куда более простой формы.

“Типовая форма” импульсов

Во многих случаях точная форма импульсов, в импульсных устройствах, не является не столь важной. Достаточно часто важными являются длительность импульсов и длительность паузы, а форма импульсов достаточно “стандартна”. При этом даже амплитуда импульсов не всегда является значимым параметром.

Наиболее распространенной формой импульсов является прямоугольная. Думаю, нет смысла приводить рисунок такого сигнала, все его видели во множестве книг и учебников. Однако, картинки в книгах могут разительно отличаться от того, что вы увидите на экранах осциллографов

Да, это именно импульсы прямоугольной формы снятые с экрана реального осциллографа подключенного к реальному электронному устройству. В данном случае это обмен по последовательной асинхронной шине. Красиво и идеально все выглядит только на страницах учебников. В реальности же прямоугольные импульсы являются трапецеидальными.

Другой распространенной формой импульсов является пилообразная. Пила может быть как нарастающей, так и спадающей. Частным случаем пилообразных импульсов являются импульсы треугольной формы. У треугольных импульсов длительность нарастания равна длительности спада. Опять таки, в реальном мире линейные участки пилообразных импульсов имеют экспоненциальную или логарифмическую форму, хоть это и не всегда видно на глаз.

Импульсы колоколообразной формы могут формироваться как ограниченной гармонической функцией (например, синусом), так и другими функциями. Например, это может быть парабола или перевернутая парабола.

Мы будем в статьях сталкиваться с прямоугольными, причем учет реальной формы импульса будет требоваться не всегда, и пилообразными, включая треугольные, импульсами.

Заключение

Мир импульсных сигналов не менее обширен, чем мир сигналов аналоговых. При этом многие параметры импульсов являются аналоговыми величинами. Да и сами импульсы иногда можно рассматривать как аналоговые сигналы. При этом, в общем случае, импульсный сигнал нельзя считать аналоговым.

Импульсные сигналы являются основой большинства логических схем, не говоря уже о цифровых, например ЭВМ. При этом импульсные сигналы, в общем случае, нельзя считать цифровыми.

Мир импульсных сигналов это отдельная вселенная, со своими правилами. Но эта вселенная пересекается, иногда почти до неразличимости, с мирами аналоговых и цифровых сигналов. И в следующей статье мы будем рассматривать эти пересечения более внимательно. Но не столь абстрактно, а с вполне практической точки зрения. Насколько все это применимо в измерительных приборах. Ведь цикл статей посвящен метрологии и средствам измерения.

Будет интересно!

До новых встреч!

1. Электрические импульсы и их параметры

Под
электрическим
импульсом
понимают отклонение напряжения или
тока от некоторого постоянного уровня
(в частности, от нулевого), наблюдаемое
в течение времени, меньшего или сравнимого
с длительностью переходных процессов
в схеме.

Как
уже было сказано, под переходным процессом
понимается всякое резкое изменение
установившегося режима в электрической
цепи за счёт действия внешних сигналов
или переключений внутри самой цепи.
Таким образом, переходный процесс –
это процесс перехода электрической
цепи из одного стационарного состояния
в другое. Как бы ни был короток этот
переходный процесс, – он всегда конечен
во времени. Для цепей, в которых время
существования переходного процесса
несравненно меньше времени действия
внешнего сигнала (напряжения или тока),
режим работы считается установившимся,
а сам внешний сигнал для такой цепи не
является импульсным. Примером этого
может служить срабатывание электромагнитного
реле.

Когда
же длительность действующих в электрической
цепи сигналов напряжения или тока
становится соизмеримой с длительностью
процессов установления, переходный
процесс оказывает настолько сильное
влияние на форму и параметры этих
сигналов, что их нельзя не учитывать. В
этом случае бóльшая часть времени
воздействия сигнала на электрическую
цепь совпадает со временем существования
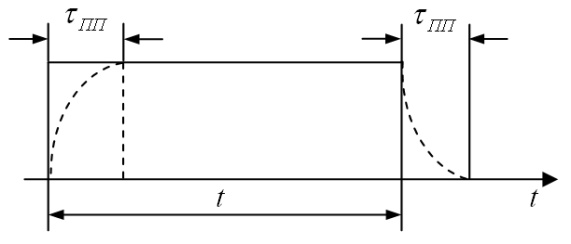
переходного процесса (рис.1.4). Режим
работы цепи во время действия такого
сигнала будет нестационарным, а
воздействие его на электрическую цепь
– импульсным.

а)
б)

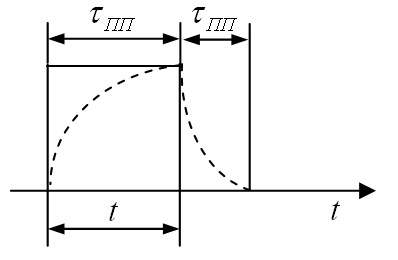
Рис.1.4.
Соотношение между длительностью сигнала
и длительностью

переходного
процесса:

а)
длительность
переходного процесса значительно меньше
длительности

сигнала
(τ_пп
<<
t);

б)
длительность переходного процесса
соизмерима с длительностью

сигнала
(τ_пп
≈
t).

Отсюда
следует, что понятие импульса связывается
с параметрами конкретной цепи и что не
для всякой цепи сигнал можно считать
импульсным.

Таким
образом, электрическим
импульсом для данной цепи называется
напряжение или ток, действующие в течение
промежутка времени, соизмеримого с
длительностью переходного процесса в
этой цепи.
При этом
предполагается, что между двумя
последовательно действующими в цепи
импульсами должен быть достаточный
промежуток времени, превышающий
длительность процесса установления. В
противном случае вместо импульсов будут
возникать сигналы сложной формы
(рис.1.5).

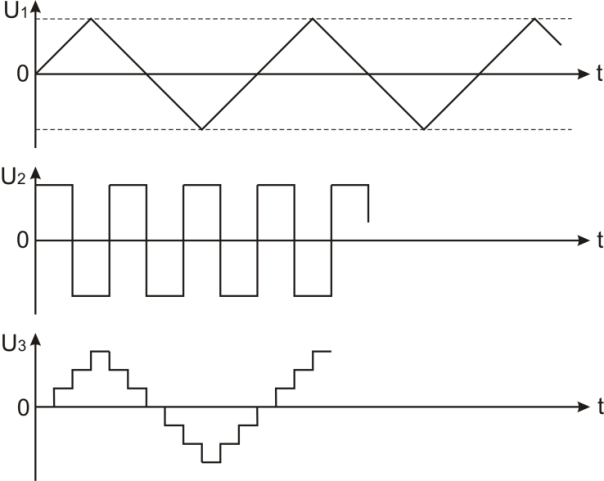
Рис.1.5. Электрические
сигналы сложной формы

Наличие
промежутков времени сообщает импульсному
сигналу характерную прерывистую
структуру. Некоторая условность таких
определений заключается в том, что
процесс установления теоретически
длится бесконечно.

Могут
быть такие промежуточные случаи, когда
переходные процессы в цепях не успевают
практически заканчиваться от импульса
к импульсу, хотя действующие сигналы
продолжают называть импульсными. В
таких случаях возникают дополнительные
искажения формы импульсов, вызванные
наложением переходного процесса на
начало последующего импульса.

Различают
два вида импульсов: видеоимпульсы
и радиоимпульсы.
Видеоимпульсы получают при коммутации
(переключении) цепи постоянного тока.
Такие импульсы не содержат высокочастотных
колебаний и имеют постоянную составляющую
(среднее значение), отличную от нуля.

Видеоимпульсы
принято различать по их форме. На рис.
1.6. показаны наиболее часто встречающиеся
видеоимпульсы.

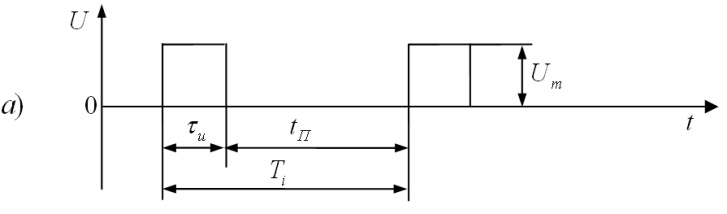
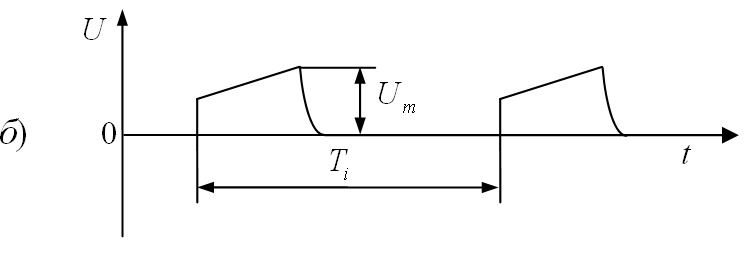
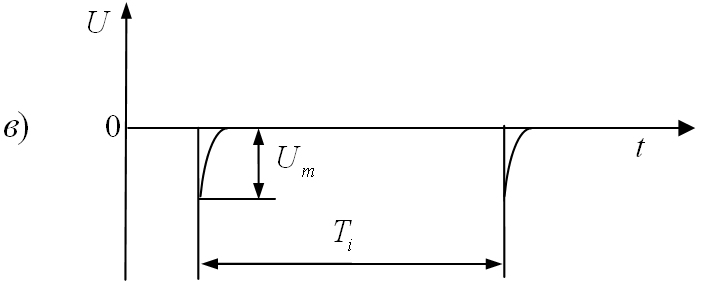
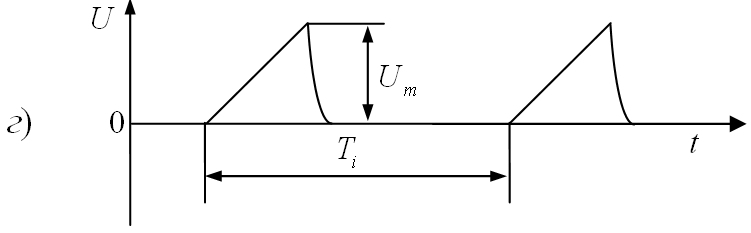
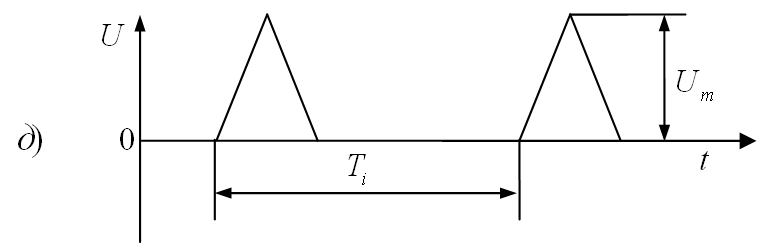
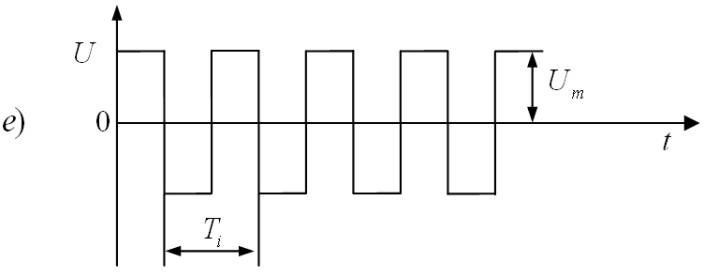
Рис.
1.6. Формы видеоимпульсов:

а)
прямоугольные; б)
трапецеидальные; в)
остроконечные;

г)
пилообразные; д)
треугольные; е)
разнополярные.

Рассмотрим
основные параметры одиночного импульса
(рис.1.7).

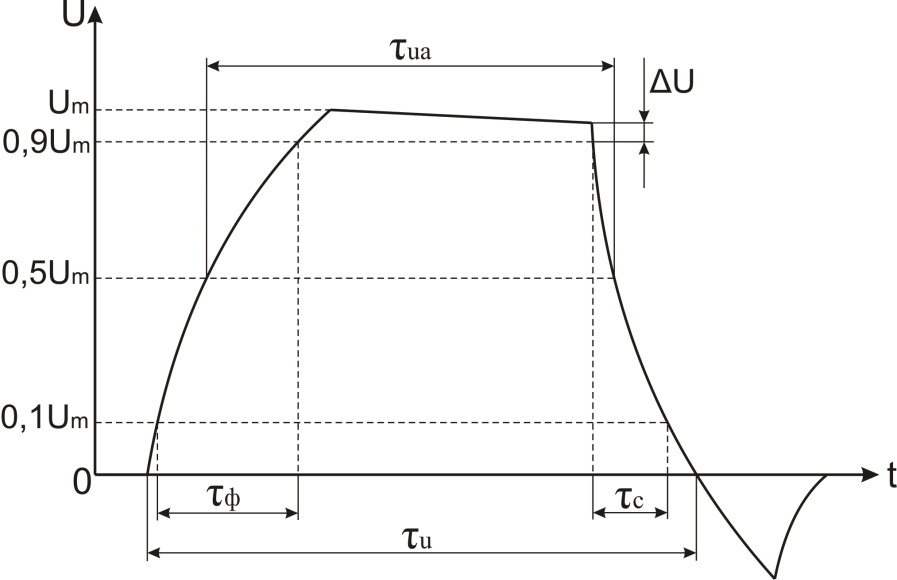
Рис. 1.7. Параметры
одиночного импульса

Форму
импульсов и свойства отдельных его
участков с количественной стороны
оценивают следующими параметрами:

• U_m
  – амплитуда (наибольшее значение)
  импульса. Амплитуда импульса U_m
  (I_m)
  выражается в
  вольтах (амперах).

• τ
  _и –
  длительность импульса. Обычно измерения
  длительности импульсов или отдельных
  участков производят на определённом
  уровне от их основания. Если это не
  оговаривается, то длительность импульса
  определяется на нулевом уровне. Однако
  чаще всего длительность импульса
  определяется на уровне 0,1U_m
  или 0,5U_m,
  считая от основания. В последнем случае
  длительность импульса называется
  активной
  длительностью и обозначается τ
  _иа.
  При необходимости и в зависимости от
  формы импульсов принятые значения
  уровней для измерения специально
  оговариваются.

• τ_ф
  – длительность фронта, определяемая
  временем нарастания импульса от уровня
  0,1U_m
  до уровня 0,9U_m
  .

• τ_с
  – длительность среза (заднего фронта),
  определяемая временем спада импульса
  от уровня 0,9U_m
  до уровня 0,1U_m.
  Когда длительность фронта или среза
  измеряется на уровне 0,5U_m
  , она называется
  активной длительностью и обозначается
  добавлением индекса «а»
  аналогично активной длительности
  импульса. Обычно τ_ф
  и τ_с
  
  составляет единицы процентов от
  длительности импульса. Чем меньше τ_ф
  и τ_с
  по
  сравнению с τ
  _и
  , тем
  больше форма импульса приближается к
  прямоугольной. Иногда вместо τ_ф
  и τ_с
  фронты
  импульса характеризуют скоростью
  нарастания (спада). Эту величину называют
  крутизной
  (S)
  фронта (среза)
  и выражают в вольтах в секунду (В/с)
  или киловольтах в секунду (кВ/с).
  Для прямоугольного импульса
  

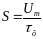
………………………………(1.14).

• Участок
  импульса между фронтами называют
  плоской вершиной. На рис.1.7 показан спад
  плоской вершины (ΔU).

• Мощность в импульсе.
  Энергия W
  импульса,
  отнесённая к его длительности, определяет
  мощность в импульсе:

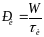
………………………………(1.15).

Она выражается
в ваттах (Вт),
киловаттах (кВт)
или дольных едини-

цах ватта.

В
импульсных устройствах используются
импульсы, имеющие длительности от долей
секунды до наносекунд (10
^{– 9}
с).

Характерными
участками импульса (рис.1.8), определяющими
его форму,

являются:

• фронт
  (1 – 2);

• вершина
  (2 – 3);

• срез
  (3 – 4), иногда называемый задним фронтом;

• хвост
  (4 – 5).

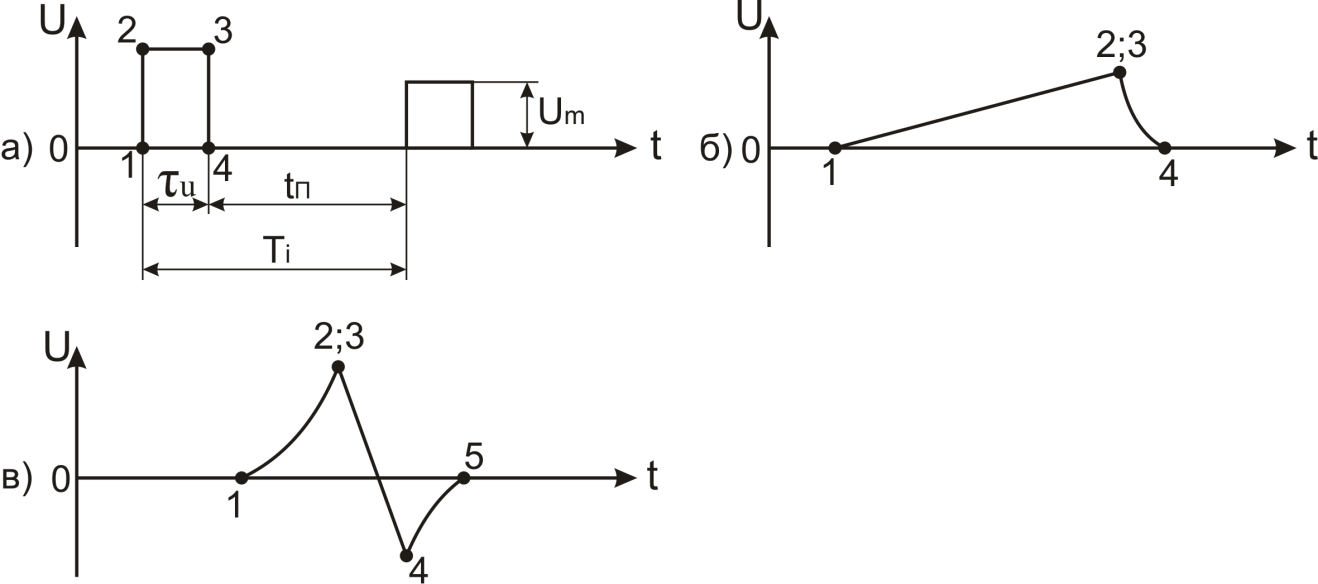
Рис.1.8.
Характерные участки импульса

Отдельные
участки у импульсов различной формы
могут отсутствовать. Следует иметь в
виду, что реальные импульсы не имеют
формы, строго соответствующей названию.
Различают импульсы положительной и
отрицательной полярности, а также
двусторонние (разнополярные) импульсы

(рис.
1.6,е).

Радиоимпульсами
называются импульсы высокочастотных
колебаний напряжения или тока обычно
синусоидальной формы. Радиоимпульсы
не имеют постоянной составляющей.
Радиоимпульсы получают модулированием
высокочастотных синусоидальных колебаний
по амплитуде. При этом амплитудная
модуляция производится по закону
управляющего видеоимпульса. Формы
соответствующих радиоимпульсов,
полученных с помощью амплитудной
модуляции, показаны на рис. 1.9:

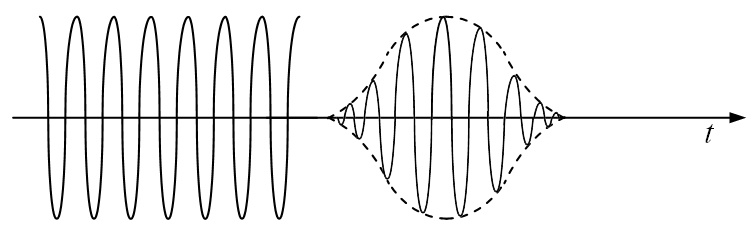
Рис.1.9.
Формы радиоимпульсов

Электрические
импульсы, следующие друг за другом через
равные промежутки времени, называются
периодической
последовательностью
(рис.1.10).

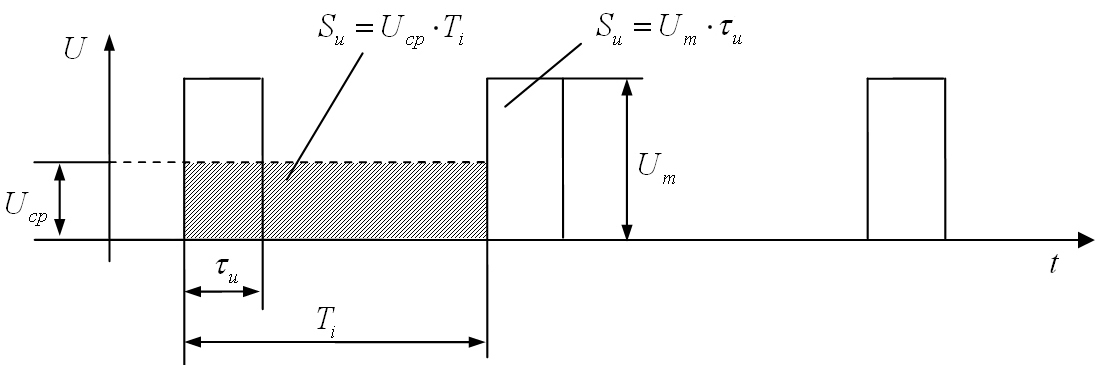
Рис.1.10. Периодическая
последовательность импульсов

Периодическая
последовательность импульсов
характеризуется следующими параметрами:

• Период
  повторения Т_i
  –
  промежуток времени между началом двух
  соседних однополярных импульсов. Он
  выражается в секундах (с)
  или дольных единицах секунды (мс;
  мкс; нс).
  Величина,
  обратная периоду повторения, называется
  частотой повторения (следования)
  импульсов. Она определяет количество
  импульсов, в течение одной секунды и
  выражается в герцах (Гц),
  килогерцах
  (кГц)
  и т.д.

………………………………..
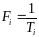
(1.16)

• Скважность
  последовательности импульсов – это
  отношение периода повторения к
  длительности импульса. Обозначается
  буквой q:

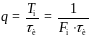
………………… (1.17)

Скважность
– безразмерная величина, которая может
изменяться в очень широких пределах,
так как длительность импульсов может
быть в сотни и даже тысячи раз меньше
периода импульсов или, наоборот, занимать
большую часть периода.

Величина,
обратная скважности, называется
коэффициентом заполнения. Эта величина
безразмерная, меньшая единицы. Она
обозначается буквой γ:

…………………………(1.18)

Последовательность
импульсов с q
= 2 называется
«меандром».
У такой

последовательности

(рис.1.6,е).
Если Т_i
>>
τ_и,
то такая последовательность называется
радиолокационной.

• Среднее
  значение (постоянная составляющая)
  импульсного колебания. При определении
  среднего за период значения импульсного
  колебания U_ср
  (или І_ср)
  импульс напряжения или тока распределяют
  равномерно на весь период так, чтобы
  площадь U_ср
  ·Т_i
  была
  равна площади импульса S_и
  = U_m
  ·
  τ_и
  (рис.
  1.10).

Для
импульсов любой формы среднее значение
определяется из выражения

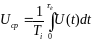
……………………(1.19),

где
U(t)
– аналитическое выражение формы
импульса.

Для
периодической последовательности
импульсов прямоугольной формы, у которой
U(t)
= U_m
, период
повторения Т_i
и
длительность импульса
τ_и,
это выражение
после подстановки и преобразования
принимает вид:

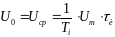
…………………….(1.20).

Из
рис. 1.10 видно, что S_и
= U_m
·
τ_и
= U_ср·Т_i
, откуда
следует:

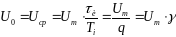
……………(1.21),

где
U₀
– называется
постоянной составляющей.

Таким
образом, среднее значение (постоянная
составляющая) напряжения (тока)
последовательности прямоугольных
импульсов в q
раз меньше
амплитуды импульса.

• Средняя
  мощность последовательности импульсов.
  Энергия импульса W,
  отнесённая к периоду Т_i
  , определяет
  среднюю мощность импульса

……………………………..
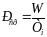
(1.22).

Сравнивая
выражения
Р_и
и
Р_ср,
получим

Р_и·
τ_и
= Р_ср·
Т_i
,

откуда следует

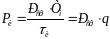
…………………(1.23)

и

……………………. (1.24),

т.е.
средняя мощность и мощность в импульсе
отличаются в q
раз.

Отсюда
следует, что мощность в импульсе, которую
обеспечивает генератор, может в q
раз превосходить
среднюю мощность генератора.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

дано:   τ = 2,0 мкс,     λ = 15 см    c = 3,0 ⋅ 10⁸ м/с    ν=4000Гц

решение

n=τ/T,     Число колебаний в импульсе

где T — период электромагнитных колебаний;

τ — длительность импульса

Период электромагнитных колебаний найдем из формулы для длины электромагнитной волны (λ = cT):

T=λ/c,   где λ — длина электромагнитной волны,

c — скорость электромагнитной волны в вакууме, .

Подставим выражение для периода электромагнитных колебаний в формулу для числа колебаний в импульсе:

n=τλ/c

Вычислим:

n=2,0⋅10⁻⁶⋅3⋅10⁸/15⋅10⁻²=4000  – Количество колебаний в импульсе

импульс локатора должен успеть достичь объекта и вернуться обратно до того, как послан следующий импульс (для того чтобы не было наложения сигналов); поэтому существует ограничение на число импульсов в единицу времени:

N/t₀ ≤ 1/t,   где N/t ₀ — число импульсов, испущенных локатором за t₀=1c,    t — время распространения импульса до цели и обратно.

по условию

N/t₀  = 4000 с⁻¹

Предельная глубина разведки при заданном количестве импульсов, посланных локатором в секунду, определяется формулой

R=ct/2=c/2(N/t₀).

Рассчитаем ее значение:

R=3⋅10⁸/2⋅4000=3,75⋅10⁵ м=375 км.