Как найти количество колебаний зная время - Сайт, где вы сможете решить свои вопросы

Как найти число колебаний математического маятника, еслиизвестны длинв нити и время?

Наталия Дмитриева

Ученик

(98),
закрыт

9 лет назад

g = 10 метров на секунду в квадрате
длина = 2,5 метра
время = 60 секунд

Главное формулу. и как обозначается эта величина

Блондинка=*

Знаток

(445)

10 лет назад

Смотрите, есть такая формула: Т (период) = 2*Pi * на корень из l(длина) / g (ускорение свободного падения)

Если найти период, можно найти и N (число колебаний)

Вот формула, из которой надо выразить N: T(период) = t (время) / N (число колебаний) . Если выразить, получится: N = t / T

Источник: Pi = 3,14

Источник

Период и частота колебаний, теория и онлайн калькуляторы

Период и частота колебаний

Период колебаний

Определение

Период – это отрезок времени, которое необходимо для совершения одного цикла периодического процесса.

Периодом ($T$) колебаний называют время, за которое совершается одно полное колебание.

За время равное периоду колебаний фаза изменяется на величину равную $2pi $, поэтому:

[T=frac{2pi }{{omega }_0}left(1right).]

Разные периодические процессы, (процессы, повторяющиеся через равные промежутки времени) можно представить в виде совокупности наложенных гармонических колебаний.

Гармонические колебания некоторого параметра $xi $ описываются уравнением:

[xi =A{cos ({omega }_0t+varphi ) } left(2right),]

где $A={xi }_{max}$ – амплитуда колебаний; ${omega }_0$ – циклическая (круговая) частота колебаний; $varphi $ – начальная фаза колебаний (фаза при $t=0$); $({omega }_0t+varphi )$ –
фаза колебаний. Величина $xi $ лежит в пределах $-Ale sle $+A.

Формулы для вычисления периода простейших колебательных систем

Период колебаний пружинного маятника определим как:

[T=2pi sqrt{frac{m}{k}} left(3right),]

на упругой пружине, жесткость которой равна $k,$ подвешен груз массой $m$.

Период колебаний математического маятника зависит от ускорения свободного падения ($g$) и длины подвеса ($l$)

[T=2pi sqrt{frac{l}{g}}left(4right).]

Формула для вычисления периода колебаний физического маятника представляет собой выражение:

[T=2pi sqrt{frac{J}{mga}left(5right),}]

где $J$ – момент инерции маятника относительно оси вращения; $a$ – расстояние от центра масс тела до оси вращения.

Единицами измерения периода служат единицы времени, например секунды.

[left[Tright]=c.]

Частота колебаний

Определение

Физическая величина обратная периоду колебаний называется частотой колебаний ($nu $).

Частота – это количество полных колебаний, которые колебательная система совершает за единицу времени.

[nu =frac{1}{T}left(6right).]

Частота колебаний связана с циклической частотой как:

[{omega }_0=2pi nu left(7right).]

Единицей измерения частоты в Международной системе единиц (СИ) является герц или обратная секунда:

[left[nu right]=с^{-1}=Гц.]

Примеры задач с решением

Пример 1

Задание. Каковы период ($T$) и частота ($nu $) колебаний, которые происходят в соответствии с уравнением: $x=A{sin ({omega }_0(t+tau )) }$, где ${omega }_0=2,5 pi (frac{рад}{с})$; $tau =0,4 $с?

Решение. Из уравнения колебаний:

[x=A{sin left({omega }_0left(t+tau right)right)left(1.1right), }]

заключаем, что это гармонические колебания, так как они происходят по закону синуса следовательно, они являются периодическими. Период найдем, зная циклическую частоту колебаний:

[T=frac{2pi }{{omega }_0}left(1.1right).]

Подставляя имеющиеся данные, вычислим период колебаний:

[T=frac{2pi }{2,5pi }=0,8 left(сright).]

Частоту колебаний найдем как величину, обратную периоду:

[nu =frac{1}{T}left(1.2right).]

Вычислим частоту:

[nu =frac{1}{0,8}=1,25 left(Гцright).]

Ответ. $T=0,8$ с; $nu =1,25 Гц$

Пример 2

Задание. Какими будут период и частота малых колебаний тонкого обруча, который висит на гвозде (точка А), вбитом горизонтально в стену (рис.1)? Колебания совершаются в плоскости параллельной стене. Радиус обруча R.

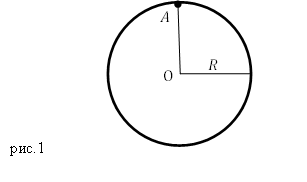
Решение. В этой задаче мы имеем дело с физическим маятником период которого, найдем, используя формулу:

[T=2pi sqrt{frac{J}{mga}left(2.1right).}]

Осью вращения обруча является гвоздь, находящийся в точке А. Цент масс обруча находится в его геометрическом центре, точке О, следовательно, расстояние от центра масс до оси вращения обруча (рис.1) равно:

[a=R left(2.2right).]

Найдем момент инерции обруча относительно оси, перпендикулярной плоскости обруча, проходящей через точку $A$. Для этого воспользуемся теоремой Штейнера:

[J=J_0+mR^2 left(2.3right),]

где $J_0=mR^2$ – момент инерции обруча, относительно оси, проходящей через его центр (т.О), перпендикулярно плоскости обруча; расстояние между осями равно радиусу обруча. Получаем, момент инерции обруча относительно гвоздя равен:

[J=mR^2+mR^2=2mR^2left(2.4right).]

Используя формулы (2.1) (2.2) и (2.4), имеем:

[T=2pi sqrt{frac{2mR^2}{mgR}}=2pi sqrt{frac{2R}{g}}.]

Отталкиваясь от полученного результата, найдем частоту колебаний как:

[nu =frac{1}{T}=frac{1}{2pi }sqrt{frac{g}{2R}}.]

Ответ. $T=2pi sqrt{frac{2R}{g}},$ $nu =frac{1}{2pi }sqrt{frac{g}{2R}}$

Читать дальше: полная энергия колебаний.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

План урока:

Колебательное движение

Период и частота колебаний

Свободные колебания

Амплитуда колебаний

Колебательные системы

Гармонические колебания

Величины, характеризующие колебательное движение

Затухающие колебания

Вынужденные колебания

Колебательное движение

В самом широком смысле, колебательное движение – это любое движение, повторяющееся с течением времени. Например, птица, машущая крыльями вверх-вниз, совершает ими колебательные движения. Ребенок, качающийся на качелях, тоже совершает колебательные движения. Игла швейной машины при шитье – тоже.

Но как же так, ведь в названных примерах тела движутся абсолютно по-разному? Крылья птицы и игла швейной машины движутся вертикально вверх-вниз (прямолинейно), ребенок на качелях движется горизонтально и по дуге (криволинейно). Это все неважно. Главный признак колебательного движения – его повторяемость через определенный промежуток времени, то есть через период колебаний.

Период и частота колебаний

Период колебаний (T) – это время, за которое тело совершает полный цикл движения, т.е. совершает одно колебание.

В случае с движением крыльев птицы, если считать, что один взмах начинается с верхней точки, полным колебанием будет считаться, когда крылья пройдут от верхней точки через середину до нижней и вернутся от нижней точки через середину до верхней (рисунок 1).

Рисунок 1 – Взмах крыльев птицы как пример полного колебания

Период колебаний обозначается латинской буквой T. По определению период – это время, значит, единица измерения периода будет такой же, как и единица измерения времени. В СИ это секунда.

[T] = 1 с

Как же можно вычислить период колебаний?

Самый простой способ – это посчитать количество колебаний и секундомером измерить время, за которое эти колебания были совершены. Например, ребенок на качелях совершает N = 10 колебаний за t = 30 секунд. Нетрудно подсчитать, что время совершения одного полного колебания будет 30/10 = 3 с. Если обобщить, получится формула для нахождения периода колебаний:

где t – время, за которое совершено N колебаний.

Рассмотрим еще одну важную характеристику.

Частота колебаний (ν) – это количество колебаний, совершаемое телом за единицу времени.

Частота колебаний обозначается греческой буквой (читается как «ню»).

Если сравнить определение частоты колебаний с определением периода, можно заметить, что это обратные величины. То есть:

Гц – единица измерения, которую назвали в честь немецкого физика Генриха Герца. При решении задач одинаково часто употребляется и герц, и с^-1. Можно употреблять и то, и другое – в зависимости от того, что удобнее при решении конкретной задачи.

Следует так же отметить, что иногда физики пользуются циклической частотой колебаний:

Свободные колебания

Положение равновесия при колебательном движении

Сравним две ситуации:

1. Родитель толкает качели, на которых сидит ребенок, а потом просто наблюдает, как качели качаются сами по себе.

2. Родитель толкает качели с ребенком, а потом при каждом цикле движения подталкивает качели, поддерживая качания.

Физики говорят, что в первом случае система (качели и ребенок) совершает свободные колебания, то есть колебания под действием только внутренних сил. После выведения системы из равновесия (то есть толчка родителя) к ней больше не прикладывают внешних сил. Во втором случае говорят, что система совершает вынужденные колебания – то есть колебания, под действием периодического внешнего воздействия.

Поговорим о свободных колебаниях. Для простоты рассмотрим систему, состоящую из маленького тяжелого шарика на длинной крепкой нити. Такая система называется нитяным маятником (рисунок 2).

Рис.2 – Нитяной маятник

Без воздействия внешних сил шарик будет находиться в положении 1. Такое состояние называется положением равновесия. Далее к шарику прикладывают силу, направленную влево и он начинает совершать колебания. Траектория шарика будет: 1-2-1-3-1 (см. рисунок 1).

Как при этом будет меняться скорость тела? Для того, чтобы рассмотреть подробно, нужно помнить определения потенциальной и кинетической энергии*, а также в чем заключается закон сохранения энергии (систему считаем замкнутой – потерь энергии не происходит, а, значит, закон сохранения энергии выполняется – энергия колебательной системы остается постоянной):

при движении из точки 1 в 2 шарик постепенно замедляется (уменьшается его кинетическая энергия, а потенциальная увеличивается);
в точке 2 он на мгновенье останавливается (кинетическая энергия равна нулю, потенциальная максимальна);
далее он начинает движение с ускорением, но уже в обратном направлении (кинетическая энергия увеличивается, потенциальная уменьшается) – при движении из 2 в 1 тело будет ускоряться;
когда шарик дойдет до точки 1 его кинетическая энергия будет максимальна, а потенциальная минимальна.

При движении от точки 1 в 3 будет происходить то же самое, что и при движении из 1 в 2 – предлагаем описать процесс изменения величин (скорости и энергии) самостоятельно.

Если обобщить все сказанное, можно сделать вывод: при колебаниях в положении равновесия кинетическая энергия тела максимальна, а потенциальная минимальна (или равна нулю, в зависимости от выбранной точки отсчета). В крайних положениях потенциальная энергия максимальна, а кинетическая равна нулю. То есть положение равновесия маятника – это такое положение, в котором его потенциальная энергия минимальна (или равна нулю, в зависимости от точки отсчета). При удалении маятника от положения равновесия кинетическая энергия будет уменьшаться, а потенциальная увеличиваться.

*Потенциальная энергия тела зависит от его положения в пространстве; кроме того, это относительная величина – она зависит от того, какая точка отсчета выбрана.

Кинетическая энергия зависит от модуля скорости тела.

Амплитуда колебаний

Помимо частоты и периода важной характеристикой колебаний является амплитуда.

Амплитуда колебаний – это модуль максимального смещения тела от положения равновесия. Другими словами, это расстояние между положением равновесия и крайней точкой траектории маятника. Рассмотрим рисунок 3. На нем изображен уже знакомый вам нитяной маятник. В идеальном случае амплитуду колебаний маятника нужно считать как длину дуги от положения равновесия до крайней точки. Но если мы считаем, что колебания малые – то есть длина нити маятника (l) гораздо больше смещения (S), можно считать, что длина дуги совпадает с длиной отрезка между проекциями положения равновесия и крайней точки на ось ОХ.

Рис.3 – Амплитуда колебаний нитяного маятника

Обычно амплитуда обозначается большой латинской буквой A.

Колебательные системы

Для того, чтобы рассмотреть колебательные движения подробнее, рассмотрим несколько колебательных систем, на примере которых будет рассматривать все закономерности.

1. Маятник

В общем случае маятник – это система, способная совершать колебания под действием каких-либо сил, например, сил трения, упругости, тяжести.

2. Пружинный маятник

Пружинный маятник – это система, состоящая из упругой пружины, один конец которой закреплен, а на другой прикреплен груз.

Такой маятник может быть вертикальным (рисунок 4а), тогда колебания будут совершаться под действием сил тяжести и упругости; и горизонтальным (рисунок 4б), тогда на груз будут действовать сил упругости и трения.

Рис.4 – Пружинный маятник

Для пружинного маятника справедливы формулы:

где T –период колебаний пружинного маятника; π ~ 3.14; m–масса груза;k–коэффициент жесткости пружины; – частота колебаний пружинного маятника.

*Ранее говорилось, что существует такая характеристика, как циклическая частота. Формула для ее нахождения будет выглядеть так:

3. Нитяной маятник

Этот вид маятника уже рассматривался ранее (см. рисунок 3), он состоит из длинной нити и тяжелого грузика, подвешенного на ней.

Для нитяного маятника справедливы формулы:

где T – период колебаний нитяного маятника; π ~ 3.14; l –длина нити; g – ускорение свободного падения (~9,8 м/с²), v – частота колебаний.

Интересно отметить, что период нитяного маятника и, следовательно, его частота не зависят от массы грузика, прикрепленного к нити.

*Следует отметить, что все приведенные формулы справедливы только для малых колебаний.

** Циклическая частота нитяного маятника:

Гармонические колебания

При решении задач часто используется не нитяной маятник, а его упрощенная модель – математический маятник. Это идеальная колебательная система, в которой нить считается очень длинной по сравнению с амплитудой колебаний и размерами грузика; сам груз достаточно тяжелым, чтобы пренебречь массой нити. Кроме того, считается, что не происходит потерь энергии.

Рассмотрим подробно, какие силы действуют на такую систему. В первую очередь, на грузик действует сила тяжести mg, направленная вниз (см. рисунок 5). Так же на него действует сила натяжения со стороны нити F, она направлена вдоль нити. Обозначим угол, на который смещается тело от положения равновесия.

Рис.5 – Силы, действующие на математический маятник

Запишем 2-й закон Ньютона:

Рисунок 6 – Силы, действующие на математический маятник при смещении на угол φ

В случае малых углов sinφ можно считать равным φ. Из геометрического определения синуса:

Тогда в крайней точке 2-й закон Ньютона в проекции на ось OX перепишется следующим образом:

То есть ускорение, с которым движется маятник прямо пропорционально его смещению от положения равновесия. Минус в данном выражении означает, что ускорении направлено в противоположную сторону от смещения.

Интересно заметить, что ускорение грузика, подвешенного к ниточке (а значит и самого маятника), не зависит от его массы. Период колебаний математического маятника тоже не зависит от массы грузика:

В случаях, когда колебания происходят под действием силы, пропорциональной смещению тела от положения равновесия, говорят, что тело совершает гармонические колебания.*

График зависимости смещения от времени при гармоническом колебательном движении представляет собой синусоиду или косинусоиду (см. рисунок 7).

Для лучшего понимания, почему график выглядит именно так, можно посмотреть урок в курсе алгебры «Тригонометрические функции»:

Рис. 7 – График зависимости смещения (x) от времени (t) при гармонических колебаниях

На графическом представлении колебаний (рисунок 7) удобно находить период и амплитуду гармонических колебаний.

*Могло сложиться впечатление, что гармонические колебания может совершать только математический маятник. Это не так. Любое тело может совершать колебания, близкие к гармоническим (нужно учитывать не идеальность систем). Например, можно говорить о гармонических колебаниях пружины, если она достаточно жесткая, чтобы она деформировалась упруго, а колебания совершаются с небольшой амплитудой.

Величины, характеризующие колебательное движение

Ранее рассматривались такие характеристики колебаний, как период, частота и амплитуда. Помимо этих величин, колебания характеризуются фазой колебаний.

Фаза колебаний

На рисунке 7 изображен график зависимости смещения от времени при гармонических колебаниях. Такой график называется синусоидой (косинусоидой). В общем случае уравнение зависимости координаты Х от времени t будет выглядеть так:

Разность фаз

Понятие «разность фаз» применяется, когда мы хотим сравнить движение двух маятников. Пусть маятник 1 и маятник 2 двигаются по законам соответственно:

Найдем разность фаз колебаний этих двух маятников.

Если взять конкретный момент времени , фаза гармонических колебаний каждого из маятников в этот момент времени будет:

– это начальные фазы колебания первого и второго маятников соответственно. Эти величины являются начальными условиями, и они не изменяются во время движения, следовательно, при одинаковой частоте колебаний маятников разность фаз остается постоянной.

Затухающие колебания

Во всех рассмотренных ранее случаях считалось, что на колеблющуюся систему не действуют силы извне. На самом деле, идеальных систем не существует, поэтому любой маятник во время движения будет преодолевать внешние силы сопротивления и терять энергию. Например, пружинный маятник (рисунок 8) будет преодолевать силу трению о поверхность.

Рисунок 8 – Пружинный маятник на шероховатой поверхности

Колебания, энергия которых уменьшается с течением времени, называются затухающими.

Амплитуда затухающих колебаний уменьшается со временем. График таких колебаний изображен на рисунке 9.

Рисунок 9 – График зависимости координаты от времени при затухающих колебаниях

Вынужденные колебания

Собственная частота колебаний. Частота вынуждающей силы. Установившиеся вынужденные колебания

В реальных (неидеальных) системах колебания всегда нужно поддерживать внешним воздействием.

Под действием периодической внешней изменяющейся силы возникают вынужденные колебания.

Почему же обязательно сила должны быть периодически изменяющейся? Ответ на этот вопрос легко найти, представив себе качели. Если на них действовать с постоянной по модулю и направлению силой, они никогда не начнут качаться. А толчками (то есть периодической изменяющейся силой) раскачать их не составит труда.

Внешняя сила, заставляющая систему совершать колебания, называется вынуждающей силой.

Так как эта сила периодическая, необходимо ввести частоту вынуждающей силы. А чтобы не запутаться, частоту свободных колебаний называют собственной частотой системы. Как показывают эксперименты, даже если изначально собственная частота системы и частота вынуждающей силы отличались, через некоторое время система начинает колебаться с частотой вынуждающей силы. В таких случаях говорят об установившихся вынужденных колебаниях.

Если частота вынуждающей силы равна собственной частоте системы, возникает резонанс – резкое увеличение амплитуды колебаний.

Источник

Кто не видел белого медведя? В зоопарках он – обычный гость. Нет нужды описывать, каков он на вид. Напомним лишь, что у него только нос черный, сам медведь белый и зимой, и летом (а не как, скажем, песец или заяц-беляк – те лишь зимой белые). Подошвы лап у белого медведя густой шерстью поросли, а пальцы примерно на половину своей длины соединены плавательными перепонками.

Плавают и ныряют белые медведи отлично. Две минуты могут пробыть под водой, но погружаются в нее редко глубже двух метров. Далеко в открытом море не раз видели белых медведей, даже медведиц с медвежатами. Плывут со скоростью 5 километров в час, не беспокоясь, что ни земли, ни льдов нигде вблизи не видно.

Белый медведь и тюленей ловит не только на льду, украдкой к ним подползая. Обычный его прием, так сказать, атаки с моря такой: поблизости от лежбищ тюленей медведь осторожно, без плеска и шума, сползает в воду, плывет туда, где заметил тюленей. Затем он бесшумно ныряет и выныривает уже у самого лежбища, быстро карабкается на лед, отрезая тем самым тюленям путь к спасительной воде. По отвесным ледяным стенам медведь может прямо из воды выпрыгнуть на льдину, даже если высота ее над водой два метра.

Тюлени – главная охотничья добыча белого медведя весной. За год ловит и съедает он примерно 50 тюленей. Летом меню его более разнообразно. Ловит он рыбу на мелкой воде, на берегу – леммингов, песцов, лакомится яйцами птиц. Когда голоден, ест ягоды, водоросли, мхи, лишайник, грибы.

Белый медведь – самый могучий из сухопутных хищных зверей. Лев и тигр в сравнении с ним легковесы: средний вес медведиц 310 килограммов, медведей-самцов – 420 килограммов. Если медведь матерый и хорошо упитанный, то он может весить целую тонну!

Акимушкин И.И. Мир животных: Млекопитающие, или звери. – М., 1988 г

IV. Тест по русскому языку

1. В тексте про белых медведей больше всего предложений:

а) повествовательных; б) вопросительных

2. Восклицательное предложение находится:

а) в начале текста; б) в конце текста

3. Вопросительное предложение находится

а) в начале текста; б) в конце текста

4. Выпиши из второй части текста (из второго абзаца) первое предложение. Разбери его по членам предложения. Что ты можешь сказать о сказуемых? Они являются

а) родственными словами; б) однородными членами предложения

5. Что можно сказать о глаголах, которыми выражены сказуемые? Эти глаголы:

а) I спряжения; б) II спряжения

6. Эти глаголы стоят в форме:

а) настоящего времени; б) будущего времени; в) прошедшего времени

7. Эти глаголы стоят в форме:

а) единственного числа; б) множественного числа

8. Эти глаголы стоят в форме:

а) 1-го лица; б) 2-го лица; в) 3-го лица; г)нельзя определить лицо

9. Эти глаголы стоят в форме:

а) ж.р.; б) м.р.; в) ср.р.; г) нельзя определить род

10. Найди во второй части текста (во втором абзаце) все слова, которые являются родственными существительному, являющемуся подлежащим в первом предложении. Запиши их столбиком, поставив в начальную форму. У тебя получилось:

а) два слова; б) три слова

11. Найди во второй части текста (во втором абзаце) другую форму слова, которое является подлежащим в первом предложении. Выпиши такое словосочетание с формой этого слова, из которого можно определить его падеж. Этот падеж:

а) Р.п.; б) В.п.

Источник

A=v-v0/t
18 км/ч=18*1000/3600=5м/с
а=2,5-5/1,25=-2(м/с^2)
Ответ. Тело тормозит с ускорением равном -2

p = frac{F}{S}

F – сила ( 5000 кН = 5000000 Н )

S – площадь опоры ( 450 м² )

p = frac{5000000}{450} = 11111,1 Па = 11,1111 кПа

В общем так.
Дано
p₁ =768 мм рт ст – атмосферное давление в 1-м случае.
p₁₀ =748 мм рт ст – показание барометра в 1-м случае. соотв. h₁.
L₁=80 мм – высота воздушного пузыря.
p₂₀ – 734 мм рт ст показание барометра во 2м случае соотв. h₂.
p₂₀ – ? атмосферное давление во 2-м случае требуется найти.
Обозначим так же
p₁₁ – Давление воздуха в трубке в 1-м случае.
p₂₁ – Давление воздуха в трубке в 2-м случае.
L₂ – Высота пузыря во 2-м случае
При атмосферном давлении 768 мм рт. ст.
$p_{1}=p_{10}+p_{11}$ (1)
(1) следует из таких соображений. Система в равновесии (ртуть наход. на одном уровне). Рассмотрим давление в трубке на уровне ртути в чашке. С “одной стороны” давит атмосфера 768 мм рт ст, с другой столб ртути 748 мм и воздух над ртутью p₁₁.
Из (1) следует:
$p_{11}=p_1-p_{10}=768-748=20$ мм рт ст (2)

Аналогично во втором случае
$p_{2}=p_{20}+p_{21}$ (3)
Вот в (3) нам p₂₀ известно а вот p₂₁ будем искать.
Объем, занимаемый пузырьком, изменится, значит изменится его давление. Считая процесс изотермическим, (ну со временем температуры воздуха в трубке и атмосферного все равно выравняются), можем записать.
$frac{p_{11}}{p_{21}}= frac{V_2}{V_1}$
$p_{21}= p_{11}cdot frac{V_1}{V_2}$ (4)
V₁, V₂ соответственно объем пузыря в 1-м и 2-м случаях.
Оцениваем изменение объема
V₁=L₁S
V₂=L₂S
S- площадь сечения трубки.
$frac{V_1}{V_2}= frac{L_1 cdot S}{L_2 cdot S} = frac{L_1 }{L_2}$ (5)
L₁ известен, L₂ = L₁+(h₁-h₂)=L₁+(748-734)=80+14=94 мм
Тогда из (5) ⇒ $frac{L_1}{L_2} = frac{80}{94}=0,851$ (6).
А из (4), (2) ⇒
$p_{21}= p_{11}cdot frac{L_1}{L_2}=20 cdot frac{80}{94} =17,02$ мм рт ст
Ну из (3)
$p_{2}=p_{20}+p_{21}=734+17,02=751,02$ мм рт ст
Ответ: p₂≈751,02 мм рт ст≈100127,66 Па.