Молекулярная физика Основные формулы
1. Основы молекулярно-кинетической теории. Газовые законы
1.1 Количество вещества

m — масса;
μ — молярная масса вещества;
N — число молекул;
NA = 6,02·1023 моль-1 — число Авогадро
1.2 Основное уравнение молекулярно-кинетической теории идеального газа

p — давление идеального газа;
m — масса одной молекулы;
n = N/V — концентрация молекул;
V — объем газа;
N — число молекул;
 — среднее значение квадрата скорости молекул.
— среднее значение квадрата скорости молекул.
1.3 Средняя квадратичная скорость молекул идеального газа

k = 1,38·10-23 Дж/К — постоянная Больцмана;
R = kNA = 8,31 Дж/(моль·К) — универсальная газовая постоянная;
T = t+273 — абсолютная температура;
t — температура по шкале Цельсия.
1.4 Средняя кинетическая энергия молекулы одноатомного газа

1.5 Давление идеального газа

n — концентрация молекул;
k — постоянная Больцмана;
T — абсолютная температура.
1.6 Закон Бойля-Мариотта

p — давление;
V — объем газа.
1.7 Закон Шарля
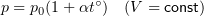
p0 — давление газа при 0 °С;
α = 1/273 °C-1 — температурный коэффициент давления.
1.8 Закон Гей-Люссака

V0 — объем газа при 0 °С.
1.9 Уравнение Менделеева-Клапейрона

1.10 Объединенный закон газового состояния (уравнение Клапейрона)

1.11 Закон Дальтона

pi — парциальное давление i-й компоненты смеси газов.
2. Основы термодинамики
2.1 Внутренняя энергия идеального одноатомного газа

ν — количество вещества;
R = 8,31 Дж/(моль·К) — универсальная газовая постоянная;
T — абсолютная температура.
2.2 Элементарная работа, совершаемая газом,
при изменении объема на бесконечно малую величину dV

p — давление газа.
При изменении объема от V1 до V2

2.3 Первый закон термодинамики

ΔQ — количество подведенной теплоты;
ΔA — работа, совершаемая веществом;
ΔU — изменение внутренней энергии вещества.
2.4 Теплоемкость идеального газа

ΔQ — количество переданной системе теплоты на участке процесса;
ΔT — изменение температуры на этом участке процесса.
Формулы молекулярной физики
Формула концентрации молекул
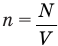
Здесь n — концентрация  , N — количество молекул (безразмерное), V — объем
, N — количество молекул (безразмерное), V — объем  .
.
Формула плотности
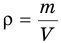
Здесь  — плотность вещества
— плотность вещества  , m — масса вещества (кг), V — объем
, m — масса вещества (кг), V — объем  .
.
Формула относительной молекулярной массы
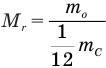
Здесь 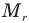 — относительная молекулярная масса (безразмерная),
— относительная молекулярная масса (безразмерная),  — масса одной молекулы (кг),
— масса одной молекулы (кг), 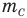 — масса атома углерода (кг).
— масса атома углерода (кг).
Формула количества вещества (количества молей)
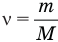
Здесь v — количество вещества (количество молей) (моль), m — масса вещества (кг), М — молярная масса (кг/моль).
Формулы массы одной молекулы
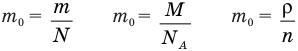
Здесь 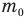 — масса одной молекулы (кг), т — масса вещества (кг), N — количество молекул (безразмерное), М — молярная масса (кг/моль),
— масса одной молекулы (кг), т — масса вещества (кг), N — количество молекул (безразмерное), М — молярная масса (кг/моль), 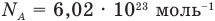 — число Авогадро,
— число Авогадро,  — плотность вещества
— плотность вещества  , n — концентрация молекул
, n — концентрация молекул  .
.
Формулы количества молекул
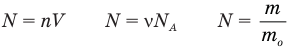
Здесь A — количество молекул (безразмерное), п — концентрация молекул  , V— объем
, V— объем  , v — количество вещества (количество молей) (моль),
, v — количество вещества (количество молей) (моль), 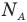 — число Авогадро
— число Авогадро 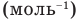 , m — масса вещества (кг),
, m — масса вещества (кг),  — масса одной молекулы.
— масса одной молекулы.
Формулы средней квадратичной скорости молекул
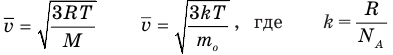
Здесь 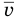 — средняя квадратичная скорость молекул (м/с), R = 8,31 Дж/(моль • К) — молярная газовая постоянная, Т — абсолютная температура (К), М — молярная масса (кг/моль),
— средняя квадратичная скорость молекул (м/с), R = 8,31 Дж/(моль • К) — молярная газовая постоянная, Т — абсолютная температура (К), М — молярная масса (кг/моль), 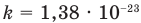 Дж/К — постоянная Больцмана,
Дж/К — постоянная Больцмана,  — масса одной молекулы (кг).
— масса одной молекулы (кг).
Основное уравнение кинетической теории идеального газа

Здесь р — давление газа (Па),  — масса одной молекулы (кг), n — концентрация молекул
— масса одной молекулы (кг), n — концентрация молекул  ,
, 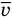 — средняя квадратичная скорость молекул (м/с),
— средняя квадратичная скорость молекул (м/с),  — средняя кинетическая энергия молекул (Дж).
— средняя кинетическая энергия молекул (Дж).
Формула средней кинетической энергии молекул
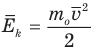
Здесь 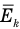 — средняя кинетическая энергия молекул (Дж),
— средняя кинетическая энергия молекул (Дж), 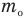 — масса одной молекулы (кг),
— масса одной молекулы (кг), 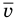 — средняя квадратичная скорость молекул (м/с).
— средняя квадратичная скорость молекул (м/с).
Связь шкал Цельсия и Кельвина
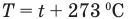
Здесь Т — абсолютная температура (К), t — температура по шкале Цельсия.
Связь средней кинетической энергии молекул идеального газа с абсолютной температурой
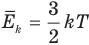
Здесь  — средняя кинетическая энергия молекул (Дж), k — постоянная Больцмана (Дж/К), Т — абсолютная температура (К).
— средняя кинетическая энергия молекул (Дж), k — постоянная Больцмана (Дж/К), Т — абсолютная температура (К).
У равнение состояния идеального газа — уравнение Клапейрона — Менделеева
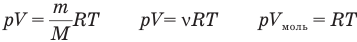
Здесь р — давление газа (Па), V — объем  , т — масса газа (кг), М — молярная масса (кг/моль), R — молярная газовая постоянная (ДжДмоль • К), Т — абсолютная температура (К), v — количество вещества (количество молей) (моль),
, т — масса газа (кг), М — молярная масса (кг/моль), R — молярная газовая постоянная (ДжДмоль • К), Т — абсолютная температура (К), v — количество вещества (количество молей) (моль), 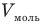 — объем моля
— объем моля 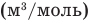 .
.
Объединенный газовый закон — уравнение Клапейрона
при 
Здесь 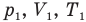 — давление (Па), объем
— давление (Па), объем  и абсолютная температура (К) газа в первом состоянии,
и абсолютная температура (К) газа в первом состоянии, 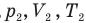 — давление (Па), объем
— давление (Па), объем  и абсолютная температура (К) газа во втором состоянии.
и абсолютная температура (К) газа во втором состоянии.
Закон Бойля — Мариотта (изотермический процесс)
при 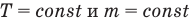
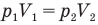
Здесь Т — абсолютная температура газа (К), m — масса газа (кг), 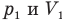 — давление (Па) и объем газа
— давление (Па) и объем газа  в первом состоянии,
в первом состоянии, 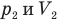 — давление (Па) и объем
— давление (Па) и объем  газа во втором состоянии.
газа во втором состоянии.
Закон Гей-Люссака (изобарный процесс)
при 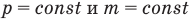
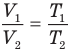
Здесь р — давление газа (Па), m — масса газа (кг), 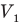 и
и 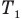 — объем
— объем  и абсолютная температура (К) газа в первом состоянии,
и абсолютная температура (К) газа в первом состоянии, 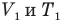 — объем
— объем  и абсолютная температура (К) газа во втором состоянии.
и абсолютная температура (К) газа во втором состоянии.
Закон Шарля
при 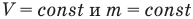
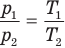
Здесь V — объем газа  , m — масса газа (кг),
, m — масса газа (кг), 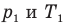 — давление (Па) и абсолютная температура (К) газа в первом состоянии,
— давление (Па) и абсолютная температура (К) газа в первом состоянии, 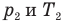 — давление (Па) и абсолютная температура (К) газа во втором состоянии.
— давление (Па) и абсолютная температура (К) газа во втором состоянии.
Связь давления идеального газа с концентрацией его молекул и температурой
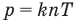
Здесь р — давление газа (Па), к — постоянная Больцмана (Дж/К), п — концентрация молекул газа  , абсолютная температура Т (К).
, абсолютная температура Т (К).
Формулы относительной влажности
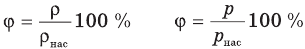
Здесь 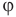 — относительная влажность (безразмерная или в %), р — плотность водяного пара в воздухе при данной температуре
— относительная влажность (безразмерная или в %), р — плотность водяного пара в воздухе при данной температуре 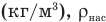 — плотность насыщенного водяного пара при той же температуре
— плотность насыщенного водяного пара при той же температуре 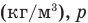 — давление водяного пара в воздухе при данной температуре (Па),
— давление водяного пара в воздухе при данной температуре (Па), 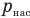 — давление насыщенного водяного пара в воздухе при той же температуре (Па).
— давление насыщенного водяного пара в воздухе при той же температуре (Па).
Работа при изобарном изменении объема газа
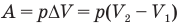
Здесь А — работа (Дж), р — давление газа (Па), 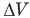 — изменение объема газа
— изменение объема газа 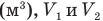 — соответственно начальный и конечный объемы газа
— соответственно начальный и конечный объемы газа  .
.
Внутренняя энергия идеального одноатомного газа
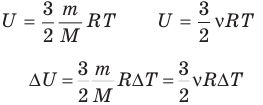
Здесь U — внутренняя энергия газа (Дж), m — масса газа (кг), М — молярная масса газа (кг/моль), R — молярная газовая постоянная (Дж/(моль • К), Т — абсолютная температура (К), v — количество вещества или число молей (моль), 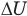 — изменение внутренней энергии (Дж),
— изменение внутренней энергии (Дж), 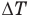 — изменение температуры (К).
— изменение температуры (К).
Первый закон термодинамики
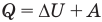
Здесь Q — количество теплоты, переданное термодинамической системе (Дж),  — изменение внутренней энергии системы (Дж), А — работа против внешних сил (Дж)
— изменение внутренней энергии системы (Дж), А — работа против внешних сил (Дж)
Применение первого закона термодинамики к термодинамическим процессам
к изотермическому: при 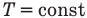
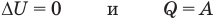
к изохорному: при V = const
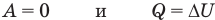
к изобарному: при р = const
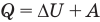
к адиабатному: при Q = 0

Здесь Т — абсолютная температура (К),  — изменение внутренней энергии (Дж), Q — количество теплоты (Дж), А — работа (Дж), V — объем
— изменение внутренней энергии (Дж), Q — количество теплоты (Дж), А — работа (Дж), V — объем 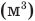 , р — давление (Па).
, р — давление (Па).
Формулы количества теплоты при нагревании или охлаждении тел
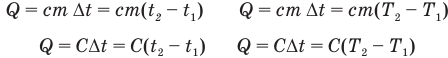
Здесь Q — количество теплоты, переданное телу при нагревании или отданное им при охлаждении (Дж), с — удельная теплоемкость вещества (Дж/(кг • К), т — масса тела (кг), 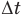 — изменение температуры тела по шкале Цельсия,
— изменение температуры тела по шкале Цельсия, 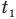 и
и 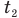 — температуры тела в начале и в конце процесса передачи теплоты по шкале Цельсия,
— температуры тела в начале и в конце процесса передачи теплоты по шкале Цельсия, 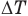 — изменение абсолютной температуры тела (К),
— изменение абсолютной температуры тела (К), 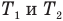 — абсолютные температуры тела в начале и в конце процесса передачи теплоты (К),
— абсолютные температуры тела в начале и в конце процесса передачи теплоты (К), 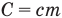 — теплоемкость тела (Дж/К).
— теплоемкость тела (Дж/К).
Формула количества теплоты при плавлении или кристаллизации
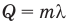
Здесь Q — количество теплоты (Дж), т — масса тела (кг), 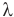 — удельная теплота плавления вещества (Дж/кг).
— удельная теплота плавления вещества (Дж/кг).
Формула количества теплоты при парообразовании или конденсации
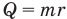
Здесь Q — количество теплоты (Дж), m — масса тела (кг), r — удельная теплота парообразования (Дж/кг).
Формула количества теплоты при сгорании топлива
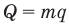
Здесь Q — количество выделившейся теплоты, m — масса топлива (кг), q — удельная теплота сгорания (Дж/кг).
Коэффициент полезного действия теплового двигателя
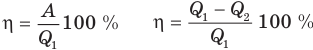
Здесь  — коэффициент полезного действия (безразмерный или в %),
— коэффициент полезного действия (безразмерный или в %), 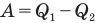 — работа, совершенная двигателем (Дж),
— работа, совершенная двигателем (Дж), 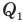 — количество теплоты, полученное рабочим веществом от нагревателя (Дж),
— количество теплоты, полученное рабочим веществом от нагревателя (Дж), 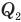 — количество теплоты, отданное рабочим веществом холодильнику (Дж).
— количество теплоты, отданное рабочим веществом холодильнику (Дж).
Коэффициент полезного действия идеального теплового двигателя
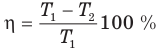
Здесь  — коэффициент полезного действия идеального теплового двигателя (безразмерный или в %),
— коэффициент полезного действия идеального теплового двигателя (безразмерный или в %), 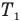 — абсолютная температура нагревателя (К),
— абсолютная температура нагревателя (К), 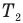 — абсолютная температура холодильника(К).
— абсолютная температура холодильника(К).
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Задачи по физике с решением
Возможно вам будут полезны эти страницы:

Masuma Melimurodova
22 января 2021 · 3,5 K
Помощь c решением задач по химии онлайн от выпускника химфака МГУ с красным дипломом… · 15 февр 2021 · chemhelp.ru
- 0,01 м^3 = 10 литров
Вычислим количество моль газа:
- n = V/Vm = 10/22.4 = 0.446 моль
Найдём количество молекул газа:
- N = n*Na = 0.446*6.02*10^23 = 2.6875*10^23 молекул
1,7 K
Комментировать ответ…Комментировать…
В 22,4 л любого газа при нормальных условиях находится одинаковое число молекул – 6,02*10^23.
В 0,01 м3 таких объемов будет 10^-2/22,4*10^-3 =0, 4464 моль.
Молекул там будет N= v*N0; N= 0, 4464*6,02*10^23 = 2,69*10^23 молекул.
Ответ: 2,69*10^23 молекул
334
Комментировать ответ…Комментировать…
Как найти число молекул в газе
Молекула – это электрически нейтральная частица, обладающая всеми химическими свойствами, присущими данному конкретному веществу. В том числе и газам: кислороду, азоту, хлору и т.д. Как можно определить количество молекул газа?

Инструкция
Если вам необходимо подсчитать, сколько молекул кислорода содержится в 320 граммах этого газа при нормальных условиях, прежде всего, определите, какое количество молей кислорода заключено в этом количестве. По таблице Менделеева, можно увидеть, что округленная атомная масса кислорода – 16 атомных единиц. Поскольку молекула кислорода – двухатомная, масса молекулы составит 32 атомные единицы. Следовательно, количество молей 320/32 = 10.
Дальше вам поможет универсальное число Авогадро, названное в честь ученого, предположившего, что равные объемы идеальных газов при постоянных условиях содержат одинаковые количества молекул. Оно обозначается символом N(A) и очень велико – приблизительно составляет 6,022*10(23). Умножьте это число на вычисленное количество молей кислорода и вы узнаете, что искомое количество молекул в 320 граммах кислорода – 6,022*10(24).
А если вам известно давление кислорода, а также объем, занимаемый им, и температура? Как вычислить количество его молекул при таких данных? И тут нет ничего сложного. Надо лишь записать универсальное уравнение Менделеева-Клапейрона для идеальных газов:
PV = RTM/m
Где P – давление газа в паскалях, V – его объем в кубических метрах, R – универсальная газовая постоянная, M – масса газа, а m – его молярная масса.
Cлегка преобразуя это уравнение, вы получите:
M = PVm/RT
Поскольку у вас есть все необходимые данные (давление, объем, температура заданы изначально, R = 8,31, а молярная масса кислорода = 32 грамма/моль), вы элементарно найдете массу газа при данном объеме, давлении и температуре. А дальше задача решается точно так же, как и в вышеописанном примере: N(A)M/m. Произведя вычисления, вы узнаете, сколько молекул кислорода содержится при заданных условиях.
Можно еще более упростить решение, поскольку в полученной дроби N(A)PVm/RTm молярные массы сокращаются, и остается: N(A)PV/RT. Подставив в формулу известные вам величины, вы получите ответ.
Видео по теме
Полезный совет
Ни один реальный газ (включая кислород), конечно же, не является идеальным, поэтому уравнение Менделеева-Клапейрона можно использовать для расчетов лишь при условиях, не очень сильно отличающихся от нормальных.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
2.1. Основные формулы и законы Молекулярная физика
Количество вещества
(молей) однородного газа находится так:
![]()
,
или
![]() ,
,
где
N
– число молекул газа; NA
– постоянная
Авогадро; m
– масса газа; М – молярная масса газа.
Если система
представляет собой смесь нескольких
газов, то количество вещества системы
равно
![]() ,
,
или
![]() ,
,
где
n,
Nn,
mn,
Mn
– соответственно количество вещества,
число молекул, масса, молярная масса
n-го
компонента смеси.
Уравнение
состояния идеального газа (уравнение
Менделеева-Клапейрона):
![]()
![]() ,
,
где
m
– масса газа; М – молярная масса газа;
R
– молярная газовая постоянная;
– количество вещества; Т – термодинамическая
температура.
Законы,
описывающие состояние газов на основании
опытов и являющиеся частными случаями
уравнения Менделеева-Клапейрона, для
изопроцессов таковы:
а)
закон Бойля-Мариотта (изотермический
процесс: Т=const,
m=const):
рV=const,
или для двух состояний газа p1V1=p2V2;
б)
закон Гей-Люссака (изобарный процесс:
p=const,
m=const):
![]() ,
,
или для двух состояний
![]() ;
;
в)
закон Шарля (изохорный процесс: V=const,
m=const):
![]() ,
,
или для двух состояний
![]() ;
;
г)
объединенный газовый закон (m=const):
![]() ,
,
или
![]() ,
,
где р1,
V1,
Т1
– соответственно давление, объем и
температура газа в начальном состоянии;
р2,
V2,
Т2
– те же величины в конечном состоянии.
Закон
Дальтона определяет давление смеси
газов: р=р1+р2+…+рn,
где рn
– парциальные давления компонентов
смеси; n
– число компонентов смеси.
Парциальным
давлением называется давление газа,
которое производил бы этот газ, если бы
только он находился в сосуде, занятом
смесью.
Молярная масса
смеси газов:
 ,
,
где
mn
– масса n-го
компонента смеси;
![]()
– количество вещества n-го
компонента смеси; n
– число компонентов смеси.
Массовая
доля n
n-го
компонента смеси газа в долях единицы
или процентах находится так:
![]() ,
,
где
m
– масса смеси.
Концентрация
молекул:
![]() ,
,
где
N
– число молекул, содержащихся в данной
системе;
– плотность вещества; V
– объем системы. Формула справедлива
не только для газов, но и для любого
агрегатного состояния вещества.
Основное уравнение
кинетической теории газов:
![]() ,
,
где
![]()
– средняя кинетическая энергия
поступательного движения молекулы.
Средняя кинетическая
энергия поступательного движения
молекулы:
![]() ,
,
где
k
– постоянная Больцмана.
Средняя полная
кинетическая энергия молекулы:
![]() ,
,
где
i
– число степеней свободы молекулы.
Зависимость
давления газа от концентрации молекул
и температуры такова:
p=nkT.
Скорость молекул:
среднеквадратичная
![]() ;
;
среднеарифметическая
![]() ;
;
наиболее
вероятная
![]() ,
,
где
m1
– масса одной молекулы.
Относительная
скорость молекулы:
![]() ,
,
где
![]()
– скорость данной молекулы.
Среднее число
соударений, испытываемых одной молекулой
газа в единицу времени, –
![]() ,
,
где
d
– эффективный диаметр молекулы; n
– концентрация молекул;
![]()
– среднеарифметическая скорость
молекул.
Средняя длина
свободного пробега молекул газа –
![]() .
.
Удельные
теплоемкости газа при постоянном объеме
(сv)
и постоянном давлении (ср):
![]() .
.
Связь между
значениями удельной с и молярной С
теплоемкости:
![]() .
.
Уравнение Майера:
СрСv=R.
Внутренняя энергия
идеального газа:
![]() .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
