Как найти количество отведенной теплоты

Основными процессами в термодинамике являются:

• изохорный, протекающий при постоянном объеме;
• изобарный, протекающий при постоянном давлении;
• изотермический, происходящий при постоянной температуре;
• адиабатный, при котором теплообмен с окружающей средой отсутствует;
• политропный, удовлетворяющий уравнению pvⁿ= const.

Изохорный, изобарный, изотермический и адиабатный процессы являются частными случаями политропного процесса.

При исследовании термодинамических процессов определяют:

• уравнение процесса в p—v иT—s координатах;
• связь между параметрами состояния газа;
• изменение внутренней энергии;
• величину внешней работы;
• количество подведенной теплоты на осуществление процесса или количество отведенной теплоты.

Изохорный процесс

 

Изохорный процесс в p, v— , T, s— и i, s-координатах (диаграммах)

При изохорном процессе выполняется условие v = const.

Из уравнения состояния идеального газа (pv = RT) следует:

 p/T = R/v = const,

т. е. давление газа прямо пропорционально его абсолютной температуре:

 p₂/p₁ = T₂/T₁.

Работа расширения в изохорном процессе равна нулю (l = 0), так как объем рабочего тела не меняется (Δv = const).

Количество теплоты, подведенной к рабочему телу в процессе 1-2 при c_v = const определяется по формуле:

q= c_v(T₂ —  T₁). 

Т. к.l = 0, то на основании первого закона термодинамики Δu = q, а значит изменение внутренней энергии можно определить по формуле:

Δu = c_v(T₂ — T₁).

Изменение энтропии в изохорном процессе определяется по формуле:

s₂ – s₁= Δs = c_vln(p₂/p₁) = c_vln(T₂/T₁).

Изобарный процесс

Изобарный процесс в p, v— , T, s— и i, s-координатах (диаграммах)

Изобарным называется процесс, протекающий при постоянном давлении p = const. Из уравнения состояния идеального газа слуедует:

v/T = R/p = const

или

 v₂/v₁ = T₂/T₁,

т. е. в изобарном процессе объем газа пропорционален его абсолютной температуре.

Работа будет равна:

l = p(v₂ – v₁). 

Т. к. pv₁ = RT₁ и pv₂ = RT₂, то

l = R(T₂ – T₁).

Количество теплоты при c_p = const определяется по формуле:

q = c_p(T₂ – T₁).

Изменение энтропии будет равно: 

s₂ – s₁= Δs = c_pln(T₂/T₁).

Изотермический процесс

Изотермический процесс в p, v— , T, s— и i, s-координатах (диаграммах)

При изотермическом процессе температура рабочего тела остается постоянной T = const, следовательно:

pv = RT = const

или

p₂/p₁ = v₁/v₂,

т. е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении – снижается.

Работа процесса будет равна:

l  = RTln (v₂ – v₁) = RTln (p₁ – p₂).

Так как температура остается неизменной, то и внутренняя энергия идеального газа в изотермическом процессе остается постоянной (Δu = 0) и вся подводимая к рабочему телу теплота полностью превращается в работу расширения:

q = l.

При изотермическом сжатии от рабочего тела отводится теплота в количестве, равном затраченной на сжатие работе.

Изменение энтропии равно:

s₂ – s₁= Δs = Rln(p₁/p₂) = Rln(v₂/v₁).

Адиабатный процесс

Адиабатный процесс в p, v— , T, s— и i, s-координатах (диаграммах)

Адиабатным называется процесс изменения состояния газа, который происзодит без теплообмена с окружающей средой. Так как dq = 0, то уравнение первого закона термодинамики для адиабатного процесса будет иметь вид:

du + pdv = 0

или

Δu+ l = 0,

следовательно

Δu= —l. 

В адиабатном процессе работа расширения совершается только за счет расходования внутренней энергии газа, а при сжатии, происходящем за счет действия внешних сил, вся совершаемая ими работа идет на увеличение внутренней энергии газа.

Обозначим теплоемкость в адиабатном процессе через c_ад, и условие dq = 0 выразим следующим образом:

dq = c_адdT = 0. 

Это условие говорит о том, что теплоемкость в адиабатном процессе равна нулю (c_ад = 0).

Известно, что

с_p/c_v = k

и уравнение кривой адиабатного процесса (адиабаты) в p, v-диаграмме имеет вид:

pv^k = const. 

В этом выражении k носит название показателя адиабаты (так же ее называют коэффициентом Пуассона).

Значения показателя адиабаты k для некоторых газов:

k_{воздуха} = 1,4

k_{перегретого пара} = 1,3

k_{выхлопных газов ДВС} = 1,33

k_{насыщенного влажного пара} = 1,135

Из предыдущих формул следует:

l= — Δu = c_v(T₁ – T₂);

i₁ – i₂= c_p(T₁ – T₂).

Техническая работа адиабатного процесса (l_техн) равна разности энтальпий начала и конца процесса (i₁ – i₂).

Адиабатный процесс, происходящий без внутреннего  трения в рабочем теле, называется изоэнтропийным. В T, s-диаграмме он изображается вертикальной линией.

Обычно реальные адиабатные процессы протекают при наличии внутреннего трения в рабочем теле, в результате чего всегда выделяется теплота, которая сообщается самому рабочему телу. В таком случае ds > 0, и процесс называется реальным адиабатным процессом.

Политропный процесс

Политропным называется процесс, который описывается уравнением:

pvⁿ= const.

Показатель политропы n может принимать любые значения в пределах от -∞ до +∞, но для данного процесса он является постоянной величиной.

Из уравнения политропного процесса и уравнения Клайперона можно получить выражение, устанавливающее связь между p, vи Tв любых двух точках на политропе:

p₂/p₁ = (v₁/v₂)ⁿ; T₂/T₁ = (v₁/v₂)^n-1; T₂/T₁ = (p₂/p₁)^(n-1)/n. 

Работа расширения газа в политропном процессе равна:

В случае идеального газа эту формулу можно преобразовать:

  

Количество подведенной или отведенной в процессе теплоты определяется с помощью первого закона термодинамики:

q = (u₂ – u₁) + l.

Поскольку

представляет собой теплоемкость идеального газа в политропном процессе.

При c_v, k и n = const c_n = const, поэтому политропный процесс иногда определят как процесс с постоянной теплоемкостью.

Политропный процесс имеет обобщающее значение, ибо охватывает всю совокупность основных термодинамических процессов.

Графическое представление политропа в p, v координатах в зависимости от показателя политропа n.

pv⁰ = const (n = 0) – изобара;

pv = const (n = 1) – изотерма;

p⁰v = const, p^1/∞v = const, pv^∞ = const – изохора;

pv^k = const (n = k) – адиабата.

n > 0 – гиперболические кривые,

n < 0 – параболы.

По материалам моего конспекта лекций по термодинамике и учебника «Основы энергетики». Автор Г. Ф. Быстрицкий. 2-е изд., испр. и доп. — М. :КНОРУС, 2011. — 352 с.

2.9.1 Определение количества подведенной теплоты цикла q1

Количество подведенной теплоты графически
определяется площадью под кривой
процесса.

После проведения подсчета количества
клеток под кривой оказалось 285 штук.

Масштаб одной клетки в координатах T-s:

• относительно оси T, K:
  30;

• относительно оси
  
  :
  14.

Следовательно, подведенная теплота
цикла, определенная графическим методом
равна:

2.9.2 Определение количества подведенной теплоты цикла q2

Количество отведенной теплоты графически
определяется площадью под кривой
процесса графика, изображающего весь
цикл. После проведения подсчета количества
клеток по графику оказалось, что всего
их 115 штук.

Масштаб одной клетки в координатах T-s:

• относительно оси T, K:
  30;

• относительно оси

  :
  14.

Следовательно, отведенная теплота
цикла, определенная графическим методом
равна:

Дж/кг

2.9.3 Определение количества теплоты цикла qc

Количество теплоты цикла определяет
площадь полученной в координатах T-s
фигуры. Чтобы определить эту площадь,
необходимо подсчитать количество клеток
внутри фигуры.

Масштаб одной клетки в координатах T-s:

• относительно оси T, K:
  30;

• относительно оси

  :
  14.

После проведения подсчета количества
клеток оказалось, что всего их 170 штук,
следовательно, теплота цикла, определенная
графическим методом равна:

Дж/кг

2.9.4 Определение количества работы цикла lc

Количество работы цикла определяет
площадь полученной в координатах p-v
трапеции. Чтобы определить эту площадь,
необходимо подсчитать количество клеток
внутри трапеции.

Масштаб одной маленькой клеточки в
координатах p-v:

• относительно оси р, Па: 100000;

• относительно оси v, м³/кг:
  0,021.

После проведения подсчета количества
клеток оказалось, что всего их 34 штуки,
следовательно, работа цикла, определенная
графическим методом равна:

Дж/кг

2.10 Сравнение значений
количества подведенной q₁
и отведенной q₂
теплоты, теплоты цикла q_c,
работы цикла l_c
цикла, полученных графическим методом,
с соответствующими величинами, полученными
при выполнении пункта 5

2.10.1 Определение
количества подведенной теплоты цикла
q₁

Графическим методом:

Дж/кг

Расчетным методом:

Дж/кг

Рассчитаем погрешность:

2.10.2 Определение
количества отведенной теплоты цикла
q₂

Графическим методом:

Дж/кг

Расчетным методом:

Дж/кг

Рассчитаем погрешность:

2.10.3 Определение
количества теплоты цикла q_c

Графическим методом:

Дж/кг

Расчетным методом:

Дж/кг

Рассчитаем погрешность:

2.10.4 Определение
количества работы цикла l_c.

Графическим методом:

Дж/кг

Расчетным методом:

Дж/кг

Рассчитаем погрешность:

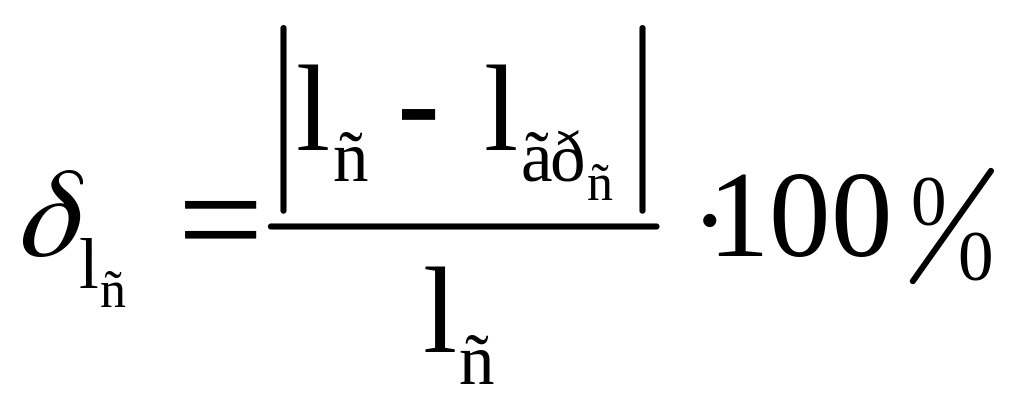
ГЛАВА
III.
РЕЗУЛЬТАТЫ РАСЧЕТОВ.

Таблица 3.1 – Параметры
состояния в характерных точках

Номер точки	p, Па	v, м3/кг	T, К
1	1600000	0,0188	473,15
2	1600000	0,0228	573,15
3	91200	0,4	573,15
4	9694,44	0,4	60,9964

Таблица 3.2 –
Характеристики термодинамических
процессов цикла

Процесс	n	c,	Δu,	Δh,	Δs,	qij,	lij,	si,
1-2	0	158,1961	9472,82	15872,82	30,3317	15819,6	6346,79	-103,9706
2-3	1	∞	0	0	181,8167	104208	104208	-73,6388
3-4	∞	94,7282	-48515,4	-81117,6	-212,2227	-48515	0	108,1779
4-1	1,67	0	39042,57	65244,79	0	0	-39043	-103,9706

Таблица 3.3 –
Характеристики цикла

qс,	q1,	q2,	lс,	ηc
71512,4902	120028	48515,3887	71512,49	0,5958

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Задача 214

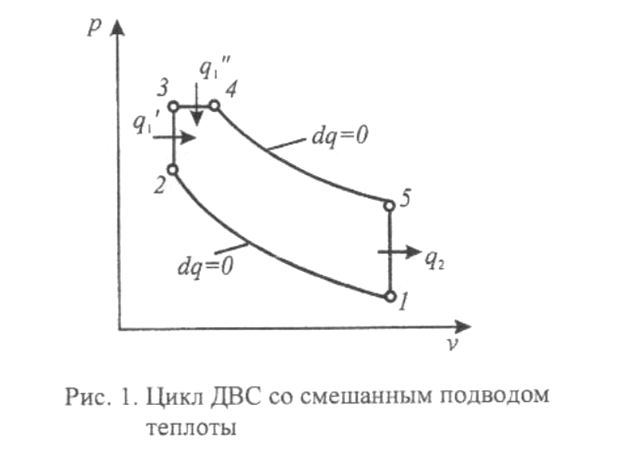
Условие: Для теоретического цикла ДВС со смешанным подводом теплоты, смотри рисунок 1, определить количество подведенной теплоты q1 , количество отведенной теплоты q2, полезную работу цикла lц, и термический КПД цикла ηt,. Определить также, КПД цикла Карно, имеющего одинаковые с заданным циклом минимальную и максимальную температуры. Параметры рабочего тела в начале процесса сжатия: давление – р1=0,1 МПа; начальная температура – t1= -14º С. Заданы безразмерные характеристики цикла: степень сжатия – ε=v1/v2=22; степень повышения давления – λ=р3/р2=1,7; степень предварительного расширения – ρ=v3/v4=1,7. В одном килломоле рабочего тела содержится: 0, 73 кмоль N2; 0, 05 кмоль О2; 0, 04 кмоль CО2; остальное – H2О (т.е. состав смеси задан мольными долями).
Указания (порядок выполнения расчетов):
1. Рассчитать молекулярную массу, газовую постоянную, теплоемкости Cp и Cv газовой смеси, а также показатель адиабаты к. Считать их постоянными для всего цикла. 2. Определить для характерных точек цикла значения давления р, температуры Т, удельного объема v, энтальпии h, и энтропии s. Результаты свести в таблицу.
3. Рассчитать количество подведенной q1 и отведенной q2 теплоты, работу цикла lц, изменение энтальпии, внутренней энергии и энтропии для всех процессов, образующих цикл. Результаты свести в таблицу.
4. Определить термический КПД заданного цикла ηt, а также КПД цикла Карно, имеющего одинаковые с заданным циклом минимальную и максимальную температуры.
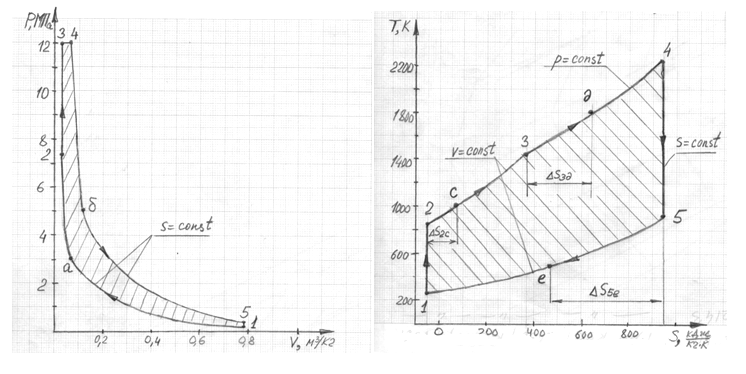
5. По результатам расчетов изобразить цикл ДВС на миллиметровой бумаге в масштабе в координатах р-v и T-s. Величину энтропии определить относительно состояния при нормальных физических условиях (Т0=273 К, р0=0,101 МПа). При изображении процессов кривыми линиями определить параметры, по крайней мере, одной промежуточной точки.

Отведенная теплота

Cтраница 1

Отведенная теплота ft, 3 изображается площадью a. Вся работа I изображается площадью и132Ь, которая на площадь 132 больше, чем / И3) и на площадь 12 3 меньше, чем / ад. Сравнивая рис. 7.12 и 7.13, замечаем, что суммарная работа всасывания и нагнетания при политропном сжатии ( если пК) меньше, чем при адиабатном.
 [1]

Количество отведенной теплоты равно изменению энтальпии, так как процесс протекает в изобарных условиях.
 [2]

Аналогично определяется отведенная теплота 02 в процессе 4 – 1: Q2 г / 4 – щ; м418 мм; Uj2 мм; ц4 – 11 мм.
 [3]

Так как конденсация протекает изохорно, то отведенная теплота равна убыли внутренней энергии.
 [4]

Так как конденсация протекает изохорно, то отведенная теплота будет равна убыли внутренней энергии.
 [5]

Таким образом, в рассматриваемом случае количество выделившейся и отведенной теплоты совпало бы с работой, затрачиваемой в компрессоре.
 [6]

Заметим, что при обратимых процессах подведенная или отведенная теплота в диаграмме s – Т всегда соответствует площади под линией процесса.
 [7]

Заметим, что при обратимых процессах подведенная или отведенная теплота в диаграмме s – Т всегда соответствует площади под линией процесса.
 [8]

Тогда коэффициент сжижения до данного состояния i может быть представлен как отношение отведенной теплоты конденсации к общему количеству тепла, необходимому для полного сжижения хлоргаза.
 [10]

Отсюда следует, что при изобарных процессах изменение энтальпии равно количеству подведенной или отведенной теплоты.
 [11]

Изотермический процесс и в этом случае будет предельным, так как при я1 работа, затраченная на сжатие, эквивалентна отведенной теплоте.
 [12]

Расчет термодинамических процессов паров осуществляется либо аналитическим методом с использованием таблиц и соответствующих формул термодинамики для определения работы, количества подведенной или отведенной теплоты, либо графическим методом с помощью р – v -; Т – s – или / г – s – диаграмм.
 [14]

Как было отмечено ранее, первый закон термодинамики устанавливает эквивалентность различных форм энергии, соотношение между изменением внутренней энергии, количеством подведенной или отведенной теплоты и совершаемой системой ( или над системой) работой, а также постоянство энергии в изолированной системе. Однако первый закон термодинамики не отражает возможность и вероятность возникновения того или иного термодинамического процесса, связанного с превращением энергии или ее перераспределением.
 [15]

Страницы:  

   1

   2

   3