Введите длину в сантиметрах (см):
Количество пикселей равно:
Как перевести сантиметры в пиксели?
Чтобы перевести сантиметры в пиксели, нужно знать плотность пикселей.
Чаще всего плотность пикселей измеряется в количестве пикселей на дюйм.
Для дисплеев (экранов смартфонов, телевизоров, компьютеров и т.д.) используется плотность PPI. PPI — это плотность пикселей на дюйм.
Для печати используется плотность DPI. DPI — это плотность точек на дюйм.
Формула расчета количества пикселей для PPI и DPI одинаковая и имеет следующий вид:
Px = (L ρ) / 2,54, где
Px — количество пикселей;
L — длина в сантиметрах;
ρ — плотность пикселей (точек) на дюйм (PPI или DPI);
2,54 — коэффициент перевода из дюймов в сантиметры.
Например:
Сколько пикселей в 10 сантиметрах при 224 PPI?
Решение: Px = (L ρ) / 2,54 = 10 • 224 / 2,54 = 881,9 px. Ответ: в 10 см при 224 PPI содержится 881,9 пикселей.
Сколько пикселей в 5 сантиметрах при 1200 DPI?
Решение: Px = (L ρ) / 2,54 = 5 • 1200 / 2,54 = 2362 px. Ответ: в 5 см при 1200 DPI содержится 2362 пикселя.
Определение объёма памяти, необходимого для хранения графической информации
Различают три вида компьютерной графики:
- растровая графика;
- векторная графика;
- фрактальная графика.
Они различаются принципами формирования изображения при отображении на экране монитора или при печати на бумаге. Наименьшим элементом растрового изображения является точка (пиксель), векторное изображение строится из геометрических примитивов, фрактальная графика задаётся математическими уравнениями.
Расчёт информационного объёма растрового графического изображения основан на подсчёте количества пикселей в этом изображении и на определении глубины цвета (информационного веса одного пикселя).
Глубина цвета зависит от количества цветов в палитре:
N=2i
.
(N) — это количество цветов в палитре,
(i) — глубина цвета (или информационный вес одной точки, измеряется в битах).
Чтобы найти информационный объём растрового графического изображения (I) (измеряется в битах), воспользуемся формулой
I=i⋅k
.
(k) — количество пикселей (точек) в изображении;
(i) — глубина цвета (бит).
Пример:
Полина увлекается компьютерной графикой. Для конкурса она создала рисунок размером (1024*768) пикселей, на диске он занял (900) Кбайт. Найди максимально возможное количество цветов в палитре изображения.
Дано
(k=1024*768);
(I=900) Кбайт.
Найти: (N).
Решение
Чтобы найти (N), необходимо знать (i):
N=2i
.
Из формулы
I=i⋅k
выразим
i=Ik
, подставим числовые значения. Не забудем перевести (I) в биты.
Получим
i=900∗1024∗81024∗768≈9,3
.
Возьмём (i=9) битам. Обрати внимание, нельзя взять (i=10) битам, так как в этом случае объём файла (I) превысит (900) Кбайт. Тогда
N=29=512.
Ответ: (512) цветов.
На качество изображения влияет также разрешение монитора, сканера или принтера.
Разрешение — величина, определяющая количество точек растрового изображения на единицу длины.
Получается, если увеличить разрешение в (3) раза, то увеличится в (3) раза количество пикселей по горизонтали и увеличится в (3) раза количество пикселей по вертикали, т. е. количество пикселей в изображении увеличится в (9) раз.
Параметры PPI и DPI определяют разрешение или чёткость изображения, но каждый относится к отдельным носителям:
• цифровой (монитор) — PPI;
• печать (бумага) — DPI.
При решении задач величины PPI и DPI имеют одинаковый смысл.
При расчётах используется формула
I=k⋅i⋅ppi2
.
(I) — это информационный объём растрового графического изображения (бит);
(k) — количество пикселей (точек) в изображении;
(i) — глубина цвета (бит),
ppi (или dpi) — разрешение.
Пример:
для обучения нейросети распознаванию изображений фотографии сканируются с разрешением (600) ppi и цветовой системой, содержащей (16 777 216) цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет (18) Мбайт. В целях экономии было решено перейти на разрешение (300) ppi и цветовую систему, содержащую (65 536) цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?
Решение
Заметим, что
16777216=224
, значит,
i1=24
бита.
, значит,
i2=16
бит.
Воспользуемся формулой
I=k⋅i⋅ppi2
.
I1=24⋅k⋅6002;I2=16⋅k⋅3002;I1I2=24⋅k⋅600216⋅k⋅3002=6;18I2=6;I2=186=3.
Ответ: (3) Мбайта.
Определение объёма памяти, необходимого для хранения звуковой информации
Звук — это распространяющиеся в воздухе, воде или другой среде волны с непрерывно меняющейся амплитудой и частотой.
Чтобы компьютер мог обрабатывать звук, непрерывный звуковой сигнал должен быть преобразован в цифровую дискретную форму. Для этого его подвергают временной дискретизации и квантованию: параметры звукового сигнала измеряются не непрерывно, а через определённые промежутки времени (временная дискретизация); результаты измерений записываются в цифровом виде с ограниченной точностью (квантование).
Сущность временной дискретизации заключается в том, что через равные промежутки времени мы измеряем уровень аналогового сигнала. Количество таких измерений за одну секунду называется частотой дискретизации.
Частота дискретизации ((H)) — это количество измерений громкости звука за одну секунду.
Частота дискретизации измеряется в герцах (Гц) и килогерцах (кГц). (1) кГц (=) (1000) Гц. Частота дискретизации, равная (100) Гц, означает, что за одну секунду проводилось (100) измерений громкости звука.
Качество звукозаписи зависит не только от частоты дискретизации, но также и от глубины кодирования звука.
Глубина кодирования звука или разрешение ((i)) — это количество информации, которое необходимо для кодирования дискретных уровней громкости цифрового звука.
В результате измерений звукового сигнала будет получено некоторое значение громкости, при этом все результаты измерений будут лежать в некотором диапазоне — количество уровней дискретизации.
Обозначим за (N) количество уровней дискретизации, тогда глубину кодирования можно найти по формуле:
N=2i
.
Для решения задач на нахождение объёма памяти, необходимого для хранения звуковой информации, воспользуемся формулой:
I=H⋅i⋅t⋅k
, где
(I) — информационный объём звукового файла (бит);
(H) — частота дискретизации (Гц);
(i) — глубина кодирования информации (бит);
(k) — количество каналов (моно — (1) канал, стерео — (2) канала, квадро — (4) канала).
Пример:
для распределения птиц по категориям обучают нейросеть. Для этого загружают звуки, издаваемые птицами. Каждый файл записан в формате монозвукозаписи с частотой дискретизации (128) Гц. При записи используется (64) уровня дискретизации. Запись длится (6) минут (24) секунды. Определи размер загружаемого файла в килобайтах.
Дано
(k=1);
(H=128) Гц;
(N=64);
(t=384) секунды.
Найти: (I) (Кбайт).
Решение
Воспользуемся формулой
N=2i
, (i=6) бит.
Подставим числовые значения в формулу
I=H⋅i⋅t⋅k
и переведём биты в килобайты:
Ответ: (36) килобайт.
Любой файл может быть передан по каналу связи, тогда объём переданной информации вычисляется по формуле:
I=V⋅t
, где
(I) — объём информации (бит);
(V) — пропускная способность канала связи (бит/секунду);
(t) — время передачи (секунды).
Пример:
в дельте Волги орнитологи оцифровывают звуки птиц и записывают их в виде файлов без использования сжатия данных. Получившийся файл передают в Астраханский биосферный заповедник по каналу связи за (56) секунд. Затем тот же файл оцифровывают повторно с разрешением в (8) раз ниже и частотой дискретизации в (3) раза выше, чем в первый раз. Сжатие данных не производится. Полученный файл передают в Кавказский природный заповедник; пропускная способность канала связи с Кавказским заповедником в (2) раза ниже, чем канала связи с Астраханским заповедником. Сколько секунд длилась передача файла в Кавказский заповедник?
Решение
Воспользуемся формулой
I=H⋅i⋅t⋅k
.
I1=k⋅i⋅t⋅H;I2=k⋅i8⋅t⋅3⋅H;I2I1=38.По условиюV2=V12.
Выразим (V) из формулы
I=V⋅t
, получим
V=It
, учтём, что
t1=56 секунд.Тогда I2t2=I156⋅2;t2=56⋅2⋅I2I1=56⋅2⋅38=42.
Ответ: (42) секунды.
Обрати внимание!
1 Мбайт=220 байт=223 бит.1 Кбайт=210 байт=213 бит.
Задание №7
Для хранения произвольного растрового изображения размером 128х320 пикселей отведено 20 Кбайт памяти без учета размера заголовка файла. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении?
Для начала разберемся какие данные у нас уже есть:
- Нам дан размер изображения – 128х320
- Объем в Кбайтах этого изображения равен 20.
Напоминаю вам формулу, которая включает в себя объем памяти, размер изображения и глубину цвета.
Из этой формулы мы можем найти глубину цвета, т.е. объем одного пикселя в битах. Для этого мы общий объем изображения должны поделить на количество пикселей. 128х320 – это и есть количество пикселей.
Обратите внимание, что объем изображения нам дан в Кбайтах. Мы Кбайты умножаем на 1024 – получаем байты. А чтобы получить биты, нужно умножить еще на 8.
По условию задачи нам нужно найти максимальное количество цветов. Для нахождения количества цветов у нас тоже есть формула.
Так как глубину цвета мы уже знаем, нам остается ее только подставить в формулу.
Ответ: 16
Если хотите узнать больше теории про кодирование информации то вам стоит ознакомится со статьей – Информатика. Кодирование информации.
А еще жмите палец вверх и подписывайтесь на мой канал, чтобы не пропустить следующие разборы задач по информатике.
Как много пикселей содержится в одном сантиметре — казалось бы, вопрос очевидный, подвохов тут быть не должно. Но все не так просто, как кажется на первый взгляд. Дело в том, что пиксель не является какой-то фиксированной величиной — это наименьший логический элемент двумерного растрового изображения, имеющий свой размер, прозрачность, координаты, цвет. Потому, рассмотрим подробнее данные свойства пикселей и для решения проблемы познакомимся с такими понятиями, как разрешение печатающего устройства (DPI) и разрешение экрана монитора (PPI).

Содержание
- Что значит понятие «Разрешения»?
- Определение количества пикселей в 1 сантиметре
- Формула № 2 для вычисления PPI
- Как определить размер фото при печати
- 3 на 4 см сколько в пикселях?
- Заключение
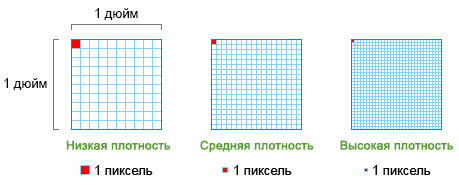
Что значит понятие «Разрешения»?
Количество пикселей, наряду с разрядностью палитры, являются одной из важнейших характеристик, влияющих на качество изображения. Всё это нужно знать, чтобы определить количество пикселей в 1 сантиметре. Чем меньше пиксель, тем более детализированным выйдет конечное изображение. Это происходит вследствие того, что при меньшем размере пикселей увеличивается их количество на единицу площади. Давайте введем величину, характеризующую число пикселей на единицу площади и назовем ее Разрешением. Данная характеристика имеет четыре разновидности, в зависимости вида преобразования изображения — DPI, PPI, LTI и SPI. Основными тут являются величины DPI и PPI, рассмотрим их подробнее.
- DPI — количество точек на дюйм, тип разрешения, применяемый к принтерам при печати изображений. Чем больше данный параметр, тем более детализированным выйдет изображение при печати.
- PPI — количество пикселей на дюйм, применяется для указания разрешающей способности монитора. Данная величина, чаще всего, подсчитывает количество пикселей, которые поместятся на экране вашего монитора.
Таким образом, если говорить об изображениях напрямую, то следует отметить, что оно не имеет собственной разрешающей способности. Данный параметр формируется устройством, на котором изображение было создано. К примеру, если фото A сделано на 3-мегапиксельную камеру, то разрешающая способность его будет равна 2048 пикселей по ширине на 1536 по высоте. Если для снимка B использовалась 4-мегапиксельная камера, то, соответственно, разрешение такого изображения будет составлять 2464 пикселя по ширине и 1632 по высоте.
Логично далее подчеркнуть взаимосвязь разрешения экрана с размером изображения. Возьмем описанные выше примеры. Если вывести изображение A на печать с разрешением 300 DPI, то на выходе мы получим фотографию с размерами 17×13 сантиметров. Если же напечатать фото B, то оно будет иметь размеры 19×14 сантиметров. Та же тенденция будет наблюдаться и при выводе данных изображений на экран монитора. Фото B займет на дисплее большие размеры, чем фото A.

Отсюда следует любопытный вывод — разрешение в чистом виде не является мерой точности и качества изображения, оно лишь формирует конечные размеры, при которых картинка будет иметь наивысшую детализацию. Но, учитывая тот факт, что людям удобней разглядывать более крупные изображения, условно мы можем отнести значение данной характеристики к основному при описании степени детализации.

Настала пора познакомиться с принципом определения размера пикселя в 1 см.
Определение количества пикселей в 1 сантиметре
Перед тем, как познакомиться с вышеописанными терминами и закономерностями, вы, наверняка, были озабочены лишь одним вопросом — количества пикселей в 1 см. Теперь же вы понимаете, что количество пикселей на единицу площади, то есть разрешение — это не фиксированная величина. А зависит она от размеров самого пикселя, более того, она является переменной, если говорить о выводе картинки на плоский носитель.
Ну а как определить размеры пикселя? На самом деле, данный вопрос является очень каверзным. Ведь такого понятия как «размер пикселя» не существует. Пиксель не является какой-то независимой величиной — это часть связи между разрешением экрана, физическим и пиксельным размером данного дисплея. Любые свойства пикселя задаются устройством, в котором происходит обработка изображения. Но, именно отсюда, из данного определения вытекает формула, которая позволяет определить количество пикселей на единицу площади, то есть разрешение PPI:
P/U=R, где P — пиксельный размер экрана, U — физический размер экрана и R — количество пикселей, приходящихся на один дюйм.
К примеру, один из экранов Mac Cinema Display 27 от компании Apple обладает физической шириной в 23.5 дюйма, пиксельная ширина его равна 2560. Исходя из этих данных мы можем вычислить плотность пикселей на дюйм:
2560/23.5=109 пикселей приходится на один дюйм данного дисплея. Давайте попробуем перевести эту величину в сантиметры:
1 дюйм = 2.54 см, следовательно, 109/2.54 = 42 пикселя на сантиметр, так мы рассчитали, сколько пикселей в одном сантиметре данного экрана.
Формула № 2 для вычисления PPI
Существует альтернативная формула, позволяющая также определить PPI. Для этого нам нужно знать диагональ экрана:
[√W^2+H^2]/D=R, где W — ширина экрана в пикселях, H — высота, а D — диагональ, выраженная в дюймах. Предлагаю применить эту формулу к рассмотренному выше примеру:
- Так как соотношение сторон Mac Cinema Display — 16 : 9, а пиксельная ширина 2560, то можем вычислить отсюда высоту дисплея:
(2560/16)*9=1440;
- Диагональ рассматриваемого нами экрана равна 27 дюймов;
- Подставим данные значения в формулу и найдем плотность пикселей на дюйм:
[√2560^2+1440^2]/27=109 PPI, то есть те же 42 пикселя на сантиметр.
Используя эти формулы, можно рассчитать, сколько пикселей в одном сантиметре при условии, что фото сделано с помощью цифрового устройства, например, камеры. При печати используется совершенно другое разрешение, которое называется DPI. Используя его, можно рассчитать конечный размер изображения при выводе его на плоский носитель, что может пригодится на практике, к примеру, если вы увлекаетесь фотографией.
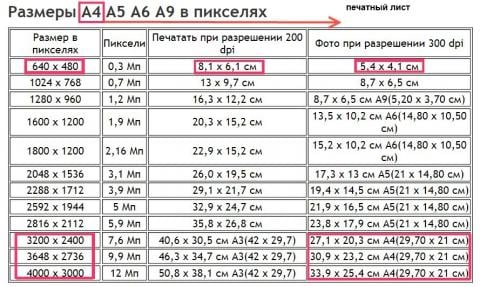
Как определить размер фото при печати
Итак, для начала предлагаю рассчитать, сколько пикселей приходится на один сантиметр при выводе изображения на плоский носитель. Как правило, печатающие устройства имеют разрешение 300 DPI. Это означает, что на один дюйм изображения придется 300 точек. Точки и пиксели — это не всегда одно и тоже, потому как некоторые принтеры печатают точки без смешения красок, что требует большего числа точек для того, чтобы отобразить пиксель. Тем не менее знание этого параметра помогает определить размер изображения, выводимого на печать. Для того, чтобы узнать это, используется следующая формула:
X=(2.54*p)/dpi, где x — длина стороны фото, 2.54 — количество сантиметров в одном дюйме, p — пиксельный размер стороны.
К примеру, нам требуется распечатать фотографию с разрешением 2560 x 1440. Разрешение печатающего устройства — 300 dpi. Воспользуемся формулой, чтобы определить размеры плоского носителя, на который будет распечатано данное изображение.
- X = (2.54*2560)/300=21 сантиметр в ширину;
- X = (2.54*1440)/300=12 сантиметров в длину.
Таким образом, размер фотобумаги, требующейся для распечатки данного изображения, должен иметь размеры 21 x 12 см.

3 на 4 см сколько в пикселях?
При распечатке фото используются разные размеры, 3 x 4 см — один из них. Давайте попробуем определить разрешение такого фото в пикселях при его распечатке (разрешение принтера — 300 dpi). Для этого воспользуемся приведенной выше формулой:
x=(2.54*p)/300, отсюда
p1 = (300*2.3)/2.54 = 271 — пиксельная ширина фото;
p2 = (300*4)/2.54 = 472 — пиксельная длина;
Таким образом, в данной фотографии будет содержаться 271*472=127912 пикселей.
Заключение
С появлением разновидности разрешений, точек, капель и так далее стала возникать путаница в определении плотности пикселей, размере фото и др. Но, приведенные в статье формулы являются актуальными, теперь вы можете определить число пикселей в одном сантиметре.
Если вы хотите узнать больше информации о DPI и PPI, предлагаю взглянуть вам на видеоролики, раскрывающие содержание данных понятий:
