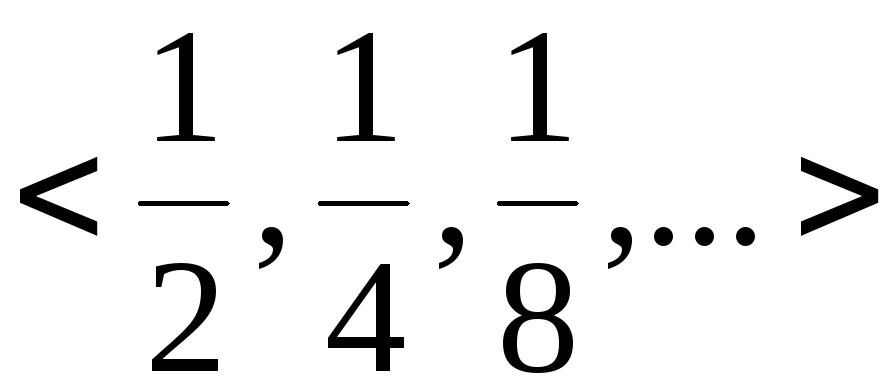Я буду везде говорить о прямых произведениях циклических групп, считая, что операцией является умножение.
Группа из условия имеет примарное разложение (Z8xZ4)x(Z25xZ25). Подгруппа порядка 20 является прямым произведением подгрупп порядка 4 и 5, которые в ней единственны, и она является их произведением. Поэтому надо найти число подгрупп порядка 4 и порядка 5, и эти числа перемножить.
Вспоминаем стандартный факт: в циклической группе Z(n) уравнение X^m=1 имеет d=НОД(m,n) решений. Если m делит n, то получится просто m.
Уравнение X^5=1 достаточно решать в Z25xZ25. Оно имеет по 5 решений в сомножителях, итого 25. Из этих решений одна единица, и остальные 24 имеют порядок 5. В группе Z5 имеется 4 элемента порядка 5. Поэтому подгрупп порядка 5 будет 24/4=6.
Подгруппы порядка 4 изоморфны Z4 или Z2xZ2. Найдём число тех и других в Z8xZ4. Уравнение X^2=1 имеет 4 решения в прямом произведении. Итого 3 элемента порядка 2. С учётом того, что решения уравнения X^2=1 образуют подгруппу, она здесь имеет порядок 4, и такая подгруппа изоморфна Z2xZ2. Она единственна, так как на неё приходятся все три элемента порядка 2.
Уравнение X^4=1 имеет 16 решений в прямом произведении. Чтобы элемент имел порядок 4, нужно, чтобы X^2 было не равно 1, и остаётся 16-6=12 элементов порядка 4. В каждой группе Z4 есть ровно 2 элемента порядка 4. Итого 12/2=6 подгрупп Z4. Вместе с одной Z2xZ2 получается 7 подгрупп порядка 4.
Умножая на 6, имеем 42 подгруппы порядка 20. Это не слишком сложно, если знать стандартные вещи, но всё-таки не “устно”.
Чтобы найти число гомоморфизмов из AxB в CxD, действительно достаточно перемножить 4 числа — количество гомоморфизмов из A,B соответственно в C,D соответственно. Получается произведение четырёх НОДов, то есть 100 * 100 * 100 * 200 = 200000000.
Число биективных гомоморфизмов — это число автоморфизмов. При автоморфизме каждая из примарных компонент отображается на себя. Поэтому надо найти порядки групп Aut(Z8xZ4) и Aut(Z25xZ25), а потом перемножить. Обе эти задачи также являются достаточно “хлопотными”. Замечу, что их лучше давать отдельно, а не “походя”. Создаётся впечатление, что задачи даются не для того, чтобы научить, а для того, чтобы загрузить работой 🙂 Я здесь писать решение не буду — обе задачи заслуживают отдельного вопроса. Его так и надо сформулировать: найти порядки групп Aut(Z8xZ4) и Aut(Z25xZ25).
$begingroup$
Is there a way to calculate the total number of subgroups of a group?
I can imagine that for example if $G=D_n$ is the dihedral group or $G=S_n$ the symmetric group then there exists a formula to calculate the total number of subgroups.
The reason why I started to think about this question is because I was trying to find all subgroups of $D_4$ (the square).
And I found some but I want to prove that I found all of them.
So if the answer is no to the question above then I’d be equally happy
with a way of being sure that given a collection of subgroups to
determine that there cannot be more.
asked Feb 28, 2016 at 3:36
$endgroup$
$begingroup$
You might be interested in this MO thread, which basically says the answer is no. However, it also contains the nice fact that any subgroup is generated by at most $log_2(|G|)$ elements, which does limit the search space somewhat.
For dihedral groups, you can use a much more elementary counting argument: either the group is cyclic (and these are easily counted) or it contains a reflection. If we call one such reflection $r$… can you finish from here?
answered Feb 28, 2016 at 3:55
Eric StuckyEric Stucky
12.6k3 gold badges34 silver badges67 bronze badges
$endgroup$
$begingroup$
The total number of subroups $D_{n}$ are
$$tau(n)+sigma(n)$$
Where $tau(n)$ is the number of divisors of n and $sigma(n)$ is the sum of divisors of $n$
answered Feb 28, 2016 at 5:11
UpstartUpstart
2,62113 silver badges25 bronze badges
$endgroup$
1
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе “Помогите решить/разобраться (М)”.
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
spyphy |
Количество подгрупп в S3
|
|
11/04/08 |
Задачка вроде элементарная, но у меня почему-то не сходится с ответом… Надо найти количество подгрупп в группе Итак, симметрическая группа
|
|
|
|
|
spyphy |
Re: Количество подгрупп в S3
|
|
11/04/08 |
странно, что в задачнике (Белоногов) в ответах написано 5 подгрупп (хотя и вся группа тоже по идее там учитывается в роли подгруппы).
|
|
|
|
|
VAL |
Re: Количество подгрупп в S3
|
||
27/06/08 |
странно, что в задачнике (Белоногов) в ответах написано 5 подгрупп (хотя и вся группа тоже по идее там учитывается в роли подгруппы). У Вас все правильно перечислено.
|
||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы
ЛЕКЦИЯ
4
Собственные
подгруппы
группы
В
любой группе
можно выделить по крайней мере две
подгруппы:
-
– подгруппу,
содержащую только один единичный
элемент.
-
– подгруппу,
совпадающую с самой группой.
В
общем случае количество выделяемых
подгрупп в группе
зависит от мощности группы
.
Если
и множество
– конечно, то конечно и количество
выделяемых подгрупп.
Если
– бесконечно, то количество выделяемых
подгрупп может быть как конечно, так и
бесконечно.
Определение. Подгруппа
называется собственной
подгруппой,
если:
и
.
В
противном случае подгруппа
называется несобственной
или
тривиальной.
Итак,
и
– несобственные
или тривиальные
подгруппы группы
.
Минимальная подгруппа.
Пусть
произвольное подмножество множества
группы
,
попробуем выбрать подгруппу
группы
,
содержащую множество
и такую, что для всякой подгруппы
из того, что
будет вытекать включение
,
т.е.
– минимальная подгруппа, содержащая
множество
.
Лемма. Двух
минимальных подгрупп
и,
содержащих множество
,
не существует.
Доказательство. Действительно,
если
и
,
где
,
– две минимальные подгруппы, то из того,
что
,
а из того, что
,
откуда следует, что
.
Системы образующих.
Пусть
– некоторая группа, и существует
семейство подгрупп
{,
}
группы
G, т.е.
.
Теорема. Пересечение
любого семейства подгрупп
группы G является подгруппой.
Доказательство. Пусть
e – единичный элемент группы
,
тогда свойства:
1. ,
2. Если
,
3.
Если ,
характеризующие
всякую подгруппу, выполнены в
,
т.к. они выполнены в каждой из подгрупп
в отдельности.
Это
свойство групп позволяет находить в
любой группе “наименьшую” или
“минимальную” подгруппу, содержащую
заданное множество
элементов группы G.
Рассмотрим
множество
элементов группы G.
Наименьшая
подгруппа, которой принадлежат эти
элементы, содержится во всякой другой
подгруппе, включающей в себя помимо
элементов множества S, еще какие-то
другие элементы группы
.
Выберем
теперь в качестве семейства
все те подгруппы, которые содержат
данное множество S, тогда их пересечение
(10)
и
будет минимальной “наименьшей”
подгруппой, содержащей множество S.
Определение. Подгруппа
,
определяемая в виде (10),
называется минимальной
подгруппой,
содержащей множество S.
Замечание. На
первый взгляд минимальная подгруппа
задается неконструктивно, поскольку
необходимо перебирать все подгруппы
,
содержащие заданное множество S, а затем
найти их пересечение. Необходимости в
этом, однако, нет.
Покажем
это.
Пусть
.
Поскольку
подгруппа
содержит элементы a, b, c, то три элемента
этой подгруппы уже известны.
Кроме
того, мы знаем, что подгруппе
принадлежит единичный элемент e.
Из
обобщенной ассоциативности следует,
что вместе с каждым из элементов a, b, c
подгруппе
принадлежат и все (целые) степени ее
элементов, а так же все произведения
степеней.
Следовательно,
подгруппа
состоит из элементов вида:
, (11)
где
– целые числа.
Замечание. 1. Некоторые
из произведений вида (11)
могут не содержать какого либо из
элементов {a, b, c}, но их также можно
представить в виде (11),
положив соответствующие показатели
степени равными нулю.
2. Единичный
элемент e также можно представить в виде
(11),
положив все показатели степени равными
нулю.
Вывод. Подгруппа
,
порожденная элементами множества
,
состоит из произведений степеней
образующих элементов вида (11).
Сформулируем
этот вывод в виде следующей
теоремы.
Теорема
о представлении
элементов минимальной подгруппы.
Минимальная
подгруппа
группы G совпадает с множеством T,
состоящим из единичного элемента
и всевозможных призведений
вида:
,
(12)
где:
либо
,
либо
.
Доказательство.
Если
,
следовательно
и
если
Это
означает,
что множество
T является подгруппой H
в G.
С
другой стороны, каждая подгруппа H,
содержащая все
,
должна содержать все их обратные
и, стало быть, все их произведения вида
.
Поэтому
и T совпадает с пересечением всех этих
подгрупп.
Замечание. Далеко
не все произведения
будут различными элементами подгруппы
,
даже если условиться заменять все
встречающиеся пары
,
взаимно обратных элементов единичным
элементом. В общем случае при
вопрос о равенстве произведений
достаточно сложен.
Определение. Если
подгруппа
,
порожденная элементами множества S,
совпадает со всей группой G, то элементы
множества S называются системой
образующих
элементов
группы
.
Определение. Если
множество S конечно, то группа
,
порожденная множеством S, называется
конечнопорожденной группой.
Утверждение. Каждая
группа G порождается какой-либо
системой образующих S.
Доказательство. Пусть
G – группа, порождённая конечным
множеством S своих элементов.
Удаляя
из S “лишние” элементы, которые
записываются в виде произведения
оставшихся и их обратных, мы придем к
минимальной системе образующих
группы G, где
.
Это
означает, что
,
но
,
если система образующих
получена из
удалением хотя бы одного элемента.
Пример 1. Пусть
G – аддитивная абелева
группа
целых чисел, т.е.
.
Необходимо найти минимальную подгруппу
группы G, порожденную множеством S, если:
1. ,
2. ,
3. ,
4. ,
5. .
Решение.
1. Если S={2}, то
;
2.Если
S={4, 6}, то
.
Ясно,
что все элементы подгруппы
четные т.к.
общий
элементэтой
подгруппы можно представить в виде
четного числа
.
Естественно,
возникает вопрос, все ли четные числа
содержатся в данной подгруппе?
Для
ответа на этот вопрос необходимо
проверить, принадлежит ли число два
этой подгруппе. Если число два
принадлежит подгруппе
,
то и все его степени (т.е. четные числа)
принадлежат этой подгруппе.
.
Пусть
Тогда
имеем
,
следовательно,
и подгруппа
будет содержать все элементы, порожденные
числом два, т.е.
3.Если
S={0}, то
4.Если
S={1}, то
5.Если
S={–1}, то
Вывод.
Образующими элементами аддитивной
абелевой
группы
целых чисел
являются числа 1и -1.
Пример 2. Пусть
G – мультипликативная абелева
группа положительных вещественных
чисел, т.е.
.
Необходимо
найти минимальную подгруппу
группы G, порожденную множеством S, если:
1. ,
2. .
Решение. 1. Если
,
то
;
-
Если S={1}, то
Пример 3. Пусть
– аддитивная абелева
группа рациональных чисел.
Необходимо
найти минимальную подгруппу
группы G, порожденную множеством
.
Решение. В
минимальную подгруппу
должны входить все целые кратные
рационального числа
.
Кроме
того, подгруппе
принадлежит любое целое число четвертых,
восьмых и т.д.
Следовательно,
эта подгруппа содержит все дроби, в
знаменатель которых не входят никакие
простые числа, кроме 2 (т.е. в знаменателе
могут стоять лишь степени числа 2).
Но
такие дроби образуют подгруппу, содержащую
все заданные числа.
Следовательно,
минимальная подгруппа
состоит из дробей, знаменателями которых
служит степень числа 2.
ИНДИВИДУАЛЬНЫЕ
ЗАДАНИЯ
Необходимо
найти минимальную подгруппу
группы G, порожденную множеством S, если:
1.ПМ
,S={5,7}
,
S={5,-7}
2.СА
,
S={5,7}
,S={0.5,-7}
3.ИНФ
,S={5,7}
,S={0.5,-0.7}
Соседние файлы в папке ЛЕКЦИИ АиГ
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Добрый день,
задача со студенческой олимпиады:
Найдите количество подгрупп из 4 элементов в прямом произведении группы перестановок [math]S_2 times S_4[/math]
Я начала с записи всех элементов групп [math]S_2, S_4[/math]:
[math]S_4[/math] содержит [math]4!=24[/math] элемента:
[math]S_4={ (1)(2)(3)(4),\ (1)(2)(34),(1)(3)(24), (12)(34), (13)(24), (1)(4)(23), (14)(23), (12)(3)(4), (13)(2)(4), (14)(2)(3), \ (1)(234), (1)(243), (2)(134), (2)(143), (3)(124), (3)(142), (4)(123), (4)(132),\
(1243), (1234), (1342), (1324), (1423), (1432) }[/math]
Группа [math]S_2[/math] довольно проста: [math]S_2 = { (1)(2), (12) }[/math]
В искомой подгруппе должен содержаться нейтральный элемент [math]{ ( (1)(2), (1)(2)(3)(4) )}[/math]. Но как понять как можно выбрать остальные 3 элемента? Для перестановок достаточно выполнения замкнутости и существование обратного элемента. Можно начать перебором, но получается слишком много вариантов.
Как решить такую задачу?
 .
.